Introduction

Noise mitigation has been the focus of research in recent years as disturbance in auditory system may lead to hearing loss as well as impaired cognitive abilities1,2. Reducing noise transmission and enhancing sound absorption has been explored by using micro-perforated panels (MPPs), developing metamaterial configurations, and exploring applicability of sandwich panels in acoustics. However, attenuating low-mid frequency noise remains an area of concern, as the current solutions are too large for practical application. Low-mid frequency noise can travel over large distances without attenuation3. Human ears are sensitive to low-mid frequency noise in that they have been reported to cause feeling of vibration in body parts, irritation, lack of concentration and pressure on eardrum3,4. Eliminating low frequency noise has been reported to cause a sense of relief among individuals3. The focus of this research will remain on low-mid frequency noise attenuation, however, efforts made to mitigate noise in general are also briefly discussed in the following paragraphs.

Recent investigations have focused on reducing sound emissions by either increasing sound transmission loss (STL) or enhancing sound absorption through a higher sound absorption coefficient (SAC). Both parameters are particularly important in acoustics; however, they have different meanings and require distinct analytical, experimental, and numerical methods for measurement5. STL refers to the ratio of sound energy incident on a material to the sound energy transmitted through it and is measured in decibels (dB). SAC represents the proportion of sound energy absorbed by a material and is denoted by α, ranging from 0 to 1.

Several researchers have mitigated noise by using carefully designed structures incorporating porous materials or MPPs6. Andrzej et al. presented comprehensive work in this area, analyzing gypsum-based MPPs both numerically and experimentally, with and without the addition of a porous absorbing material7. These investigations have established the significance of MPPs, perforation shape, and cavity length in achieving high SAC. While these solutions are promising, they are often heavy or occupy substantial volume. Additionally, even lightweight options typically attenuate sound effectively only within narrow frequency bands, limiting their practicality for everyday noise mitigation.

In recent years, acoustic metamaterials have attracted significant interest. Rather than being a distinct category of materials, metamaterials are specialized design frameworks applicable across various research fields. In acoustics, metamaterials are engineered to target specific frequencies through adaptable designs, often based on micro-lattices or repeating cellular structures, such as honeycomb configurations. Complex metamaterial designs have become realizable with Additive Manufacturing (AM) processes. The layer-by-layer approach in AM enables the creation of intricate internal cavities, which can reduce structural weight and serve as Helmholtz resonators for noise attenuation. Moreover, AM is an essential part of sustainable Industry 4.08, as it allows the production of virtually any shape and size, bypassing the limitations of conventional manufacturing, including cost, time, and environmental impact9. Fotsing et al. designed and manufactured three lattices using thermoset AM, demonstrating effective sound attenuation in the mid-frequency range10. Abueidda et al. numerically investigated frequency band gaps of triply periodic minimal surface (TPMS) units, finding that these lattices effectively attenuate sound in specific high-frequency ranges11. Zhao et al. designed modular cavities that could be overlaid on each other to absorb noise within the 500–1000 Hz frequency range12.

Sandwich panels are of interest due to their lightweight nature and high strength. Literature shows that various lattice designs can achieve high specific energy absorption coefficients with only a fraction of the weight13,14,15,16. In acoustics, the cavities within sandwich panels can be optimized to absorb specific frequencies. This multifunctionality has inspired researchers to incorporate lattices into sandwich panel designs, including specially designed cavities, micro-lattices, and hierarchical structures17,18,19,20. Among all existing cellular designs, the honeycomb core has been the most extensively investigated. Ehsan et al. explored natural fiber-reinforced polylactic acid (PLA) MPPs, demonstrating that these materials are easily manufactured using 3D printing and provide a good sound absorption coefficient in the low-frequency range21. Yinmei et al. recently examined the acoustic properties of honeycomb sandwich panels filled with high-strength glass fibers22finding that MPPs with honeycomb designs achieve superior sound attenuation compared to other solutions. Subramanian et al. investigated honeycomb structures made of PLA with nano-fillers, showing that STL improves with the addition of fillers in the cavities23. Another study examined the effects of varying perforation shapes on the honeycomb panel covering, as well as the impact of cavity depth on acoustic performance24. Pierre et al. designed a novel structure and compared its acoustic and structural properties to a honeycomb configuration, suggesting that this design could potentially replace the honeycomb25. Sandwich panels with 2D re-entrant auxetic core are known to exhibit high in-plane and out-of-plane energy absorption26. Fangyi et al. found that 2D re-entrant design can reduce locomotive noise inside cabin while offering good mechanical properties27. This study focused on STL only for a frequency range of 50–1600 Hz. Importantly, the effect of cavities within 2D re-entrant auxetic was not explored in this investigation. Similarly, Kim et al. presented an in-depth STL analysis of tessellated square lattice for a frequency range of 100–1750 Hz for application in electric vehicles28. SAC was not examined in these investigations.

Despite these advancements, low-frequency noise attenuation remains a challenge. Researchers have observed that attenuating low frequencies requires larger cavity sizes, which limits the practicality of such solutions. Common sources of low frequency noise include traffic, industrial processes, home appliances, locomotives, and aircraft. Recently, efforts have focused on designing Helmholtz resonators specifically for low-frequency noise attenuation29. Slagle et al. attempted to create a heterogeneous metamaterial combining melamine foam and steel spheres to absorb frequencies around 500 Hz30. Hedayti et al. recently designed an active and passive noise control device based on Helmholtz resonators, effective in the 160–434 Hz range31. However, these solutions can typically only attenuate a narrow frequency band, allowing noise at other frequencies to pass through easily. Additionally, the necessary dimensions are quite large (approximately 100 mm), posing a further limitation30,31.

Existing acoustic attenuation solutions typically specialize in either sound absorption or transmission loss. While auxetic materials offer unique mechanical properties and MPPs are known for broadband absorption, the strategic architectural fusion of these distinct mechanisms to achieve a multifunctional acoustic response has not been previously investigated. This manuscript introduces a novel hybrid design comprising a 2D re-entrant auxetic structure strategically integrated with MPPs. This investigation primarily assesses the multifunctionality of auxetic designs by embedding MPPs through a systematic design driven methodology. The novelty stems not from simple layer stacking but from leveraging the synergistic interaction between auxetic geometries and multilayered perforated structures. Drawing inspiration from the cellular nature of auxetic designs and established literature, this approach integrates inhomogeneous perforations an innovation not previously reported in auxetic context. It furthermore facilitates targeting a broader frequency range via multilayered MPPs while enhancing both STL and SAC. Optimizing both STL and SAC within a single structure represents a novel approach as these acoustic properties are typically optimized independently. Unlike prior efforts that addressed these phenomena in isolation, our research provides a comprehensive analysis demonstrating this design overcomes conventional limitations achieving significantly enhanced and concurrently high SAC and STL. This dual focus is critical as it highlights how designs with seemingly insignificant SAC still offer substantial acoustic benefits thereby expanding acoustic material performance understanding. Furthermore, the comprehensive parametric analysis in this study generates design maps that provide clear guidelines on how geometric parameters influence acoustic performance. This approach serves both academic understanding and practical design purposes guiding decisions in specific frequency ranges. The resulting structure is compact lightweight and high strength offering tunable features that enable targeting specific wavelengths while maintaining excellent absorption capabilities. Given its broad range noise absorption within the low to medium frequency range and inherent multifunctionality, this design holds significant promise for diverse applications including aviation, automotive, surgical equipment and the locomotive industry32,33,34,35,36,37. Additionally, HVAC compressor systems represent another potential application area for this design38,39. The subsequent sections of this paper detail the methodology in Section “Methodology” followed by a comprehensive presentation and discussion of numerical and experimental results including a detailed parametric study in Section “Results and discussion”. Finally, Section “Conclusion” provides the conclusions drawn from this investigation.

Methodology

The inherent cavities within the re-entrant auxetic design present a unique opportunity to repurpose these voids for acoustic energy attenuation while simultaneously ensuring the structure maintains its superior mechanical properties. The design was precisely modeled in SolidWorks leveraging this principle. It features a consistent wall thickness of 1 mm and all re-entrant angles set at 60 degrees. Selection of these dimensions was directly influenced by constraints of the chosen additive manufacturing process (FDM) as elaborated in Section “Design for additive manufacturing”. MPPs were strategically incorporated to further augment acoustic performance. Existing literature indicates acoustic energy dissipation through MPPs optimizes when perforations are narrow typically within the millimeter to sub-millimeter scale40,41. Literature also indicates that inhomogeneous perforation dimensions are effective in targeting a broader frequency range42.

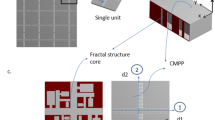
Each re-entrant cell accordingly includes at least one narrow perforation enabling it to function as a compact Helmholtz resonator. The design exhibits a progressive decrease in perforation size along its height ending in a solid base layer. The design also offers flexibility in customizing perforations per cellular cavity. For computational efficiency, however, it was made symmetrical along its width about the sixth perforation and periodic along its length as shown in Table 1; Fig. 1. The top layer exhibits uniform rectangular perforation dimensions. The first and second layer perforation diameter progressively decreased inwards along the MPP until the sixth perforation. The third layer perforations were fabricated at the minimum dimensions constrained by the selected FDM process. This and the selected auxetic dimensions collectively established the maximum and minimum achievable perforation dimensions. Perforations were consistently aligned with the center of each re-entrant auxetic cavity ensuring auxetic cavity walls do not intersect any perforation. The thickness of MPPs remained constant throughout this investigation. Effect of MPP layers, perforation geometry and perforation dimensions are recorded in Section “Parametric study”.

Table 1 provides complete dimensions for one design with additional data available in Table S1 of the Supplementary Information. The complete design demonstrates repeatability as shown in Fig. 1a. Figure 1b depicts the extraction of a 100 mm sample for experimental analysis while Fig. 1c shows the manufactured sample using FDM. The sample diameter is dictated by the internal diameter of the impedance tube used in this investigation. Figure 1d presents dimensional details of the underlying auxetic design. Figure S1 of Supplementary Information provides layer-wise perforation dimensions of one investigated design further expounding on Fig. 1e.

Table 1 Dimensions for auxetic design with MPPs (All dimensions are in mm).
Full size table
Fig. 1
figure 1

Design philosophy for the selected structure: (a) Complete design; (b) 100 mm sample of the design with a 0.6 mm outer wall thickness for additive manufacturing; (c) Manufactured sample using industrial-grade material extrusion additive manufacturing technique; (d) Dimensions of Unit Auxetic (e) Unit lattice of the complete design with each embedded MPP. Designs prepared in SolidWorks 2021 (www.solidworks.com).

Full size image

Numerical model

When evaluating the acoustic performance of series Helmholtz resonator designs, two primary approaches are common in the literature. One method involves developing an analytical model based on the standard Helmholtz resonator equation, then comparing its predictions to a numerical model. However, directly applying the simple Helmholtz resonator equation to complex series designs typically does not yield accurate results. A detailed discussion on this limitation, along with supporting data, is available in Supplementary Information, specifically in Table S2. The alternative, and the approach adopted in this study, involves constructing a numerical model and validating it against established literature. Following this, the numerical results are further corroborated with experimental findings. In this work, numerical models were developed using COMSOL Multiphysics and subsequently validated through comparisons with published literature. Experimental validation has also been performed to confirm these results.

Thermoviscous Acoustics and Pressure Acoustics modules were coupled to simulate the SAC. Thermoviscous Acoustics, Pressure Acoustics, and Solid Mechanics modules were coupled for STL model. As explained in the previous section, STL & SAC denote fundamentally different acoustic measurements. Therefore, experimental & numerical boundary conditions to measure both parameters are different. STL & SAC can be modeled by excluding the Pressure Acoustics module, however, this would increase the computational load. A schematic explaining the boundary conditions and the physics applied to the domains can be seen in Fig. 2 and Figure S2 of the Supplementary Information. Figure 2a shows representative structure with hollow interior while Figs. 2b and c show 3D depiction of numerical model set up in COMSOL Multiphysics. Figure 2b is a numerical model setup of STL and Fig. 2c is the model setup of SAC. For STL, change in sound energy is calculated as it travels through the structure. Therefore, air domain is established on both sides of the structure. SAC is only dependent on cavity design, therefore, computational load can be reduced by considering only the cavity instead of the solid structure as shown in Fig. 2c. Thus, reducing the numerical model to two physics, thermoviscous and pressure acoustics. Normally incident plane wave of 1 Pa pressure was applied using port boundary condition. For all investigated cases, the maximum mesh size was kept at one-sixth of the maximum frequency analyzed. Further, symmetry boundary condition was also used to reduce computation time.

Fig. 2
figure 2

Schematic for numerical model (a) A representative structure with internal cavity (b) Representation of STL model (c) Representation of SAC model. Designs prepared in SolidWorks 2021 (www.solidworks.com).

Full size image

These models were validated using data from published literature. The equations implemented in the software to calculate SAC and STL are shown below43.

$$\alpha = 1 - \left| R \right|^{2}$$
(1)
$$R = \frac{{P_{{ref}} }}{{P_{{in}} }}$$
(2)
$$STL = 10 \times \log _{{10}} \left( {\frac{{\int \left| {p_{i} } \right|^{2} dA}}{{\int \left| {p_{t} } \right|^{2} dA}}} \right)$$
(3)

Here, α denotes SAC and R represents the reflectance coefficient. Pref and Pin denote the power reflected and going in the design, respectively. The incident and transmitted pressures are represented by pi and pt, respectively. The material properties assigned for validation of numerical models and frequency range were kept consistent with the literature. Literature has already provided conclusive evidence for accuracy of equations implemented in FE model provided by COMSOL Multiphysics44. Consequently, an extensive mathematical background is not included.

The frequency range for analysis of the proposed hybrid design was set from 50 to 1800 Hz, with intervals of 25 Hz. The OEM provided material properties of eSUN PLA + were implemented for the design investigated in this work. Table 2 provides the relevant details.

Table 2 Material properties for numerical model.
Full size table

Design for additive manufacturing

The goal was to manufacture the design as a single part to avoid the use of adhesives that could alter the acoustic properties. Internal cavities cannot be created using conventional manufacturing processes in this case. Therefore, FDM was selected due to its availability and ease of operation. FDM uses thermoplastics that are extruded onto a build plate from a heated nozzle, printing the part layer-by-layer. Support structures are automatically generated by the software to ensure structural integrity45,46. It is important to note that any support structure within the designed cavities could affect the acoustic behavior. Hence, geometry was analyzed in 3D printing software to evaluate the need for support in the internal cavities. As shown in Fig. 3a, internal supports were required to print the design using FDM.

A study was conducted to integrate supports within the design that would have minimal impact on the acoustic performance, while also meeting the design requirements for FDM47,48. The designs investigated are shown in Fig. 3b. The selection of these designs was based on the available space, with dimensions kept above minimum datums for FDM. A novel support structure was developed iteratively, featuring the same included angles as the auxetic design, with a thickness of 0.5 mm and a length of 1.5 mm. It was labeled conformal auxetic support. The design was positioned to support the farthest edges of the primary design, while also maintaining adequate cavity volume for improved acoustic properties. A layer-by-layer analysis of the selected support design, conducted in 3D printing simulation software, showed that when the “supports everywhere” option was enabled, excess material was not deposited. This way, the design could be 3D printed as a single part without need of removing support or using other means to assemble the design. The samples were prepared using the INTAMSYS Funmat Pro 410 FDM printer. The print parameters are enlisted in Table S3 of Supplementary information.

Fig. 3
figure 3

Details of the investigation into internal support removal (a) Red circles highlighting the internal support generated by the FDM software. (b) Investigated integral support designs.

Full size image

Experimental setup

Experiments were performed using SW-422 impedance tube (BSWA Technology Co., China), as shown in Fig. 4. The tube requires cylindrical samples with a 100 mm diameter. SAC is measured in accordance with ISO 10534-249 and STL is measured according to transfer function using 4-microphone method. The tube is equipped with four MPA 416 1/4” microphones and MC3242 DAQ. The microphones were calibrated using a calibrator (CA115) provided by OEM. The tests were performed for a frequency range of 50-1800 Hz. As illustrated in Fig. 1b, the 100 mm cylindrical sample was cut from the design, with an outer wall thickness of 0.6 mm to avoid any small features and ensure structural integrity. The goal was to validate the numerical results; therefore, only two selected designs were printed and analyzed. SAC tests were performed with no air gap behind the specimen. Each test was repeated thrice to minimize errors.

Fig. 4
figure 4

SW-422 impedance tube with all parts.

Full size image

Results and discussion

Validation and performance of numerical model

Figure 5 demonstrates the validation of both numerical models using published literature27,41,50. A good agreement was observed between the results of the SAC model and the literature data as shown in Fig. 5a. For STL, experimental as well as numerical data was separately validated. Figures 5b and c represent validation of published experimental data while Fig. 5d represents validation of published numerical data. A good agreement was observed between published data and the numerical model built in COMSOL Multiphysics.

Fig. 5
figure 5

Validation of numerical models (a) SAC numerical model (b) STL numerical model validated from published simulation data (c) STL numerical model validated from published experimental data (d) STL numerical model validated from published theoretical data.

Full size image

Baseline for SAC and STL was established by analyzing auxetic design of 52 mm height without integrating MPPs. It was found that the re-entrant auxetic design does not provide significant sound absorption or sound transmission loss. This can be attributed to the large empty spaces within the design, which allow sound waves to traverse without obstruction.

We modified the design by incorporating MPPs and conducted initial simulations without considering printability, to quickly assess the potential benefits of the proposed design. Once high STL and SAC values were achieved, printability with FDM was then evaluated. The conformal auxetic support had a slight negative impact on the acoustic performance, and Fig. 6 provides a comparison to illustrate this effect. Figure 6a shows comparison of SAC with minimal impact of integrating supports while Fig. 6b shows comparison of STL in same context.

Fig. 6
figure 6

Effect of integrating supports within the design (a) Effect on SAC (b) Effect on STL.

Full size image

Experimental validation

Experimental validation of the numerical findings was performed using the setup shown in Fig. 4. Two designs, D15 and D18, were printed using PLA, with the material properties provided in Table 2. Figure 7 presents a comparison of the numerical and experimental data. Average of experimental data is represented with the grey line while standard deviation is shown with shaded blue region as each test was repeated three times. Figure 7a and c provides a comparison of SAC while Fig. 7b and d shows the comparison of STL. Numerical and experimental results follow the same trend, however, difference in values was observed. A detailed discussion on the reasons behind this deviation has been presented next.

Fig. 7
figure 7

Comparison between experimental & numerical results (a) SAC results for D15 (b) STL results for D15 (c) SAC results for D18 (d) STL results for D18.

Full size image

Stochastic defects: numerical-experimental variance

To investigate the reasons for the differences between the numerical and experimental results, a thorough analysis was conducted by comparing the designed features with those achieved through printing. Figure 8a shows the designed features while Figs. 8b and c show the defects observed. It can be seen in Fig. 8b that designed perforations had polymer stuck in them and Fig. 8c is an image taken from optical microscope showing that the internal supports had material stringing and shape distortion. Table 3 provides a detailed comparison of differences in dimensions using a standard digital vernier caliper. The features were designed based on the limitations of the FDM process, as outlined in the referenced literature47,48and manufacturing was carried out using a high-end printer. However, significant deviations were observed in the printed parts, especially in the D18 design. The 100 mm diameter D18 design, printed with PLA, was expected to have a mass of 230 g. However, after weighing it on a digital scale, the actual mass was found to be 250 g, representing 8.7% increase over the expected mass. This increase in mass can be attributed to manufacturing defects induced by the FDM process.

Table 3 Comparison of designed vs. achieved dimensions for 2nd layer of D18.
Full size table

Literature review indicates that the increase in SAC is attributed to the inherent layer-layer roughness and micro defects generated in designs printed using FDM51,52,53. Consequently, defects of a similar nature were induced in the D18 design, and SAC analysis was conducted. Prior to numerical analysis, the mass difference caused by the induced defects was examined. It was found that mass increased by 7% due to the defects, which is below the 8.7% mass increase observed in the printed sample. Figure 8d compares the SAC of the defective D18 design with the experimental results. The numerical results closely align with the experimental values, suggesting that the defects introduced by the limitations of the FDM process were responsible for the increase in SAC. It should be noted that the computational requirements increased significantly after inducing defects in the design, which led to limiting this analysis to SAC only. The SAC results clearly demonstrate that the deviation observed in the experimental results was due to manufacturing defects.

Fig. 8
figure 8

Investigation of the reasons for the difference between experimental and numerical results: (a) Designed conformal supports and 0.75 mm perforations; (b) Partially closed 0.75 mm perforations; (c) Deformed conformal supports with material stringing observed under optical microscope; (d) Comparison of experimental results with numerical results before and after inducing defects.

Full size image

Parametric study

Consequently, a comprehensive numerical investigation was conducted to examine the effect of geometric and material properties on both STL and SAC.

Effect of geometric parameters

To investigate the effect of different geometric parameters, cavity height, perforation dimensions, base layer thickness, and the number of MPPs were varied, while the underlying re-entrant design and MPP thickness were kept constant. Complete details of the geometric parameters can be found in Table S1 of the Supplementary Information. Dimensions of the perforation were selected in the range that can be easily manufactured by FDM. Figure 9 presents a graphical comparison of the impact of each parametric variation. Designs D1-D5 present the case of auxetic design with a single perforated panel and base layer. Substantial improvement in STL can be seen; however, SAC remains negligible, as seen in Fig. 9a and d. It should be noted that the scale for Fig. 9a has been kept different to clearly indicate curves. Increasing height significantly increases STL in design D1-D5 while, perforation diameter and shape significantly affect SAC as well as the shift of dip in STL. D5 exhibits better SAC than D4, but the dip in STL due to structural resonance is also more pronounced, resulting in minimal transmission loss at 1025 Hz. Designs D6-D9 represent two-layer MPPs where the effect of cavity height has been recorded while keeping perforation dimensions constant. D6 is a combination of D4 and D5, while in D7, the auxetic cavity under the rectangular perforations was modified to create a single large cavity. The cavity interconnection was achieved by removing material from the auxetic design, as shown in Fig. S3 of supplementary information. Interconnection reduced the loss of STL, however, SAC also decreased slightly. Comparison of D7-D9 in Fig. 9b provides conclusive evidence that cavity height has a significant impact on the peak SAC. Peak SAC also shifts to lower frequencies with increase in cavity height. Similarly, STL also improves significantly with the increase in sample height as seen by curves of D7-D9 in Fig. 9e.

Designs D10 & D12-D13 represent three-layer MPP while D11 represents a special case where perforation diameter has been abruptly changed. Comparing SAC of D9-D13 reveals that, as we move down the height, adding MPPs with progressively decreasing perforation diameter has a positive impact on average SAC, peak SAC as well as frequency range for which SAC is above 0.5. Sharp decline in SAC is observed when perforations size is changed abruptly as visible in data of D11. STL curves shown in Fig. 9e for these samples do not show significant deviation as no major change is made to overall height of the sample and structural density. Comparison of D12 & D13 further reveals that progressive decrease in perforation diameter as we move down the height of design has positive impact and vice versa. The results for D13 show the lowest frequency at which 0.5 SAC is achieved, but this design exhibits lower SAC values at higher frequencies, with an average STL of 51 dB.

Designs D14-D18 represent four-layer MPPs where the effects of varying perforation dimensions have been examined. Comparing D13-D15, Fig. 9c shows significant shift of peak SAC to higher frequencies. D16, when compared to D13, has more MPP layers and smaller diameter of perforations which has kept SAC above 0.5 from about 620 Hz to 1800 Hz. Similarly, as evident from Fig. 9f average STL has also improved to 55dB avoiding the sharp dip observed in D13. Top layer perforation has been reduced while increasing perforation dimensions of lower layers in D17 & D18. This has resulted in improved STL while SAC is significantly reduced.

The drop in STL observed in all designs can be attributed to structural resonance at a specific frequency, known as the natural frequency. At this frequency, the entire structure vibrates, allowing sound to propagate more easily through it, thereby significantly lowering STL capabilities. However, by carefully controlling the perforation dimensions, this dip can be kept below 20 dB, ensuring high STL performance across the investigated frequency range. A detailed analysis of this phenomenon can be found in the referenced literature27. As the height of the structure increases, the natural frequency shifts to higher values, as shown in Fig. 9e evident by comparing D7(22 mm) to D11(52 mm).

Fig. 9
figure 9

Results of geometric study for STL & SAC (a) Effect of sample height on SAC with comparison of baseline Auxetic (b) Effect of MPPs on SAC (c) Effect of perforation dimensions on SAC (d) Effect of sample height on STL with comparison of baseline (e) Effect of MPPs on STL (f) Effect of perforation dimensions on STL.

Full size image

It can also be inferred from Fig. 9f that STL is not significantly affected by the perforation design but rather by the overall structural density and height. However, perforations do impact the natural frequency of the design. Therefore, a suitable combination of perforations can be selected to minimize the STL dip at the natural frequency while maximizing SAC. The best SAC and STL results were achieved for the design labeled D16, where SAC above 0.5 was achieved for broad frequency range with an average STL of 55 dB, which is a remarkable achievement. This result is highlighted by the black dotted line in Fig. 9c and f. The improvement is attributed to energy dissipation occurring within the designed perforations, significantly enhancing the absorption capability of the auxetic design.

These findings also align with literature on Helmholtz resonators, where air particles oscillate violently as they approach the resonant frequency. This oscillation leads to increased friction between the internal walls of the structure and the air particles, causing a significant loss of kinetic energy from the incoming pressure wave. This phenomenon can also be visualized in Fig. 10. The design investigated in this research is such that single sectional view for all the auxetic cavities is not possible. Therefore, Fig. 10 gives the view of only three alternate auxetic cavities of unit lattice for D16 design obtained by creating sectional view at the center of unit lattice. Figure 10a proves that viscous losses in the narrow regions dominate overall sound absorption while minimal thermal losses are also observed as shown in Fig. 10b. Figure 10c provides total thermoviscous losses achieved in the cavities shown at 1700 Hz. It is also deduced that neck diameter has significant contribution to the intensity of viscous losses, represented by red color in neck regions of perforation. Also, Maa’s theory of MPPs does not consider thermal effects54. However, since viscous losses serve as the primary source of sound absorption, the theory provides precise sound absorption portrayal. The smaller squares are showing the losses occurring within the interconnected region of the top cavity.

The results are exceptional, as even with a small sample height, the design was able to absorb frequencies with wavelengths as large as approximately 0.5 m, making it a true subwavelength structure. In terms of normalized height (ratio of height to wavelength of 0.5 absorption peak) results varied from 1/6 for D9 (worst) to 1/11 for D13 & D16 (best) when samples with 52 mm height are compared. Similar result were achieved by Tang et al. for corrugated sandwich panel with square lattice hybrid41. The sandwich panel used in that study had been modified to the extent that its mechanical properties would be significantly affected. Also, investigation into STL of the proposed design was not performed. A direct inference drawn from Eq. (1) by researchers is that at a state of high SAC, STL will be high. That might be true for peak SAC, however, the exact quantification of STL deems necessary to authors since it will vary throughout a frequency range. Also, the STL dip at resonance frequency needs to be investigated and reported for a comprehensive acoustic solution. This investigation shows that STL dip can be appropriately managed by optimizing perforation dimension and height of the design. Moreover, results conclusively indicate that at low frequency the proposed design has exceptional STL which might not be true for designs where STL data is not presented.

Fig. 10
figure 10

2D contour for energy dissipation (in W/m3) at central sectional plane of unit lattice of D16 at 1700 Hz (a) Viscous dissipation (b) Thermal dissipation (c) Total thermoviscous energy dissipation.

Full size image

Effect of material properties

The impact of varying material properties was also investigated. Details of the parameters considered are provided in the supplementary information Table S4. Figure 11 illustrates the effect of material properties on the design. To record the effect of material properties, analysis was performed on D1 for STL and D13 for SAC.

To study the impact of material properties on SAC, a third numerical model was developed by coupling thermoviscous acoustics, pressure acoustics, and solid mechanics. The key difference from the STL model was that, for SAC, pressure calculations after the pressure wave passed through the structure were not required. As a result, the air domain after the solid domain was excluded from the model.

It is important to note that varying the material properties had no significant impact on SAC, which further confirms the accuracy of the numerical model used in this study. This supports the approach of excluding the Solid Mechanics module to limit computational load, a technique also employed by Tang et al.41. Additionally, it is well-documented in the literature that structural thickness, density, and porosity significantly affect SAC55,56,57,58,59. However, no change in SAC is observed when only intrinsic material properties are varied. Thus, SAC is primarily dependent on cavity design, rather than the intrinsic material properties.

Regarding STL, increasing the Young’s modulus (E) enhanced STL and shifted the resonance frequency to a higher value. Changes in Poisson’s ratio had no discernable effect, as shown in Fig. 11c and d. Since SAC was unaffected by changes in E, it can be inferred that a stiffer structure reflects more sound energy. Furthermore, by comparing Figs. 9 and 11, it is evident that higher structural density, material stiffness, and height tend to increase STL, while the opposite is true for lower values of these parameters.

The results suggest that appropriate modification to any cellular design might make it capable of high SAC & STL. Sound insulation is essential in surgical devices, locomotive, automotive and aerospace structures. If the target is only high STL (sound insulation), D1 design with a 15 mm height can achieve an average STL of 34 dB. A similar case was investigated by Kim et al. where a square shaped meta panel of 22 mm height was proposed to provide an average STL of 19 dB for application in electric vehicles28. Hence, the application of the proposed hybrid geometry in similar equipment has the potential to suppress noise even with a small height of 15 mm.

Investigation also sheds light on the potential tunability of the proposed design to target specific frequencies. Ensuring high SAC while maintaining high STL over a wide frequency range offers a unique advantage to the proposed design, making it a strong candidate for applications in HVAC systems, jet engine nacelle panels, and other enclosed environments where elevated noise levels are commonly encountered, such as operating theatres with bone saws and jet engine test beds. Furthermore, FDM was employed in this study due to its ease of availability and widespread use in industry & academia. The results show that in acoustics, FDM has limited application as the intricate features required for high STL & SAC are difficult to produce. Future studies will include improving the proposed design by reducing weight and overall height. Also, a detailed comparison between other AM technologies will be made.

Fig. 11
figure 11

Effect of material properties on STL & SAC (a) Effect of material stiffness on SAC of D13 (b) Effect of Poisson ratio on SAC of D13 (c) Effect of material stiffness on STL of D1 (d) Effect of Poisson ratio on STL of D1.

Full size image

Conclusion

Re-entrant auxetic structures are known for their exceptional mechanical properties. In this research, noise mitigation in low-mid frequency range was investigated by exploiting the cellular nature of 2D re-entrant auxetic design. Multi-layer MPPs were integrated, where each cavity has different perforation dimensions and each layer has different cavity height, realizing a truly multifunctional structure. The design was subjected to detailed numerical & experimental analysis. Industrial grade FDM setup was used to manufacture samples, however, numerical results showed slight deviations from experimental data. A thorough investigation revealed that introducing stochastic defects in numerical modelling yield results that are much closer to experimental results. Thus, FDM, while fast and cost-effective, has limitations in producing intricate features. Future studies will explore the impact of different AM techniques on acoustic properties and further optimizations to reduce density, height, and mass while expanding the frequency range. Other key findings of this study are:

  1. 1.

    The study demonstrated that lattice-based designs can achieve effective acoustic attenuation through modifications that are unlikely to affect their mechanical properties.

  2. 2.

    SAC is solely a function of architected design, while STL depends on density of the architected design, stiffness of the material used for manufacturing, and the overall height of the structure.

  3. 3.

    Good STL may be ensured at peak SAC based on the assumptions used in SAC calculations; however, STL was found to remain variable. This variation can be effectively controlled through the careful selection of perforation diameter and overall design height. Therefore, both SAC and STL must be evaluated for each design to ensure a comprehensive acoustic solution.

  4. 4.

    A gradual decrease in perforation diameter across successive MPPs leads to increased SAC, whereas abrupt diameter variations have a detrimental effect.

  5. 5.

    In environments requiring sound emission reduction, a compact design with a height of 15 mm—as demonstrated in Design D1—can be effective, offering an average STL of 34 dB across the 50–1800 Hz frequency range.

  6. 6.

    The proposed design demonstrates substantial improvements in both STL and SAC. An SAC greater than 0.5 was achieved at 620 Hz and sustained beyond 1180 Hz, while Design D16 exhibited a superior average STL of 55 dB across the analyzed frequency range.