Introduction

The problem of accurate prediction of formation pressure has always been one of the focuses in the field of petroleum engineering1,2,3,4,5, especially in areas with abnormally high pressure. According to statistical data, abnormally high-pressure accounts for about 48% of oil and gas fields worldwide6. The parameters of formation pore pressure are the basis for drilling and completion engineering and oil and gas field development. Formation pore pressure is related to safe, fast, effective, and economical drilling and completion7,8,9, and even determines the success or failure of drilling. Risks often occur due to the low prediction accuracy of abnormally high-pressure wells, mainly including blowout, wellbore instability, wellbore scrapping, casing waste, and a surge in drilling economic costs10,11,12,13. Accurate prediction of formation pressure/pore pressure has become crucial to address many oil and gas production related problems14,15,16. When studying the formation pressure of high-temperature and high-pressure wells in the South China Sea, traditional methods have low prediction accuracy and cannot meet the requirements of safe drilling. When exploring solutions, practical research has discovered a simple and significantly improved method for predicting formation pressure, which is the machine learning prediction method based on integrated data.

The study of pore pressure prediction is a complex and challenging task. In recent years, experts and scholars at home and abroad have conducted a large amount of research on pore pressure prediction methods. However, due to the high development of computers, the current prediction methods mainly include two categories.

The first type of prediction is based on empirical or semi-empirical formulas, which are generally fitted and solved based on on-site well logging or mud logging data. The main representatives include the Eaton method, which establishes normal trend lines based on well logging acoustic data17,18,19,20, and the Bowers method, which distinguishes and predicts pressure mechanisms based on well logging acoustic and density data21,22,23,24,25. The Fan method26,27 for calculating the correlation between well logging acoustic waves, porosity, and effective stress, and the Dc index method28,29,30 for calculating formulas based on partial mud logging parameters and data. However, the parameter selection of these empirical or semi-empirical methods is subjective and often leads to significant prediction errors, resulting in poor on-site application results.

The second type is prediction methods mainly based on intelligent algorithms, including neural networks, random forests, deep learning, etc.31,32,33,34,35. Currently, there is relatively little research on these methods, and most of them focus on using logging data for pore pressure prediction, without fully exploring and utilizing favorable on-site data (including well logging and mud logging data). While existing research has investigated the combination of mud logging and well logging data36, the study has limitations such as small sample sizes, shallow formation depth, inadequate predictive evaluation, and the applicability of its conclusions may be restricted by geographical factors. Therefore, there are still many shortcomings in the second type of research, and their methods often have poor results in predicting formation pressure.

Therefore, to improve the accuracy of predicting formation pore pressure and make up for the shortcomings of current research. Well logging and mud logging data are combined in this study to analyze the correlation between various parameters. Based on machine learning algorithms and a large amount of known data, a machine learning formation pressure model with integrated well logging and mud logging data (IWM) was established. The model is predicted and applied to neighboring wells with brand-new data. At the same time, to evaluate the computational accuracy and advantages of the model, conventional machine learning well logging or mud logging models were compared, and the calculation results and accuracy of various data models were obtained. Comprehensively evaluated the integrated data model established in this study. The research method can effectively improve the accuracy of reservoir pressure prediction and provide support for efficient on-site development.

Methods and data handling

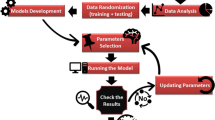
The establishment of IWM datasets and prediction models is the foundation for accurate machine learning prediction of formation pressure. Excellent machine learning model calculation accuracy is often based on accurate and rich datasets. This study established a machine learning prediction model for formation pressure based on well logging and mud logging data using an integrated dataset. The model can then be used for formation pressure prediction and accuracy evaluation and optimization.

Therefore, a prediction dataset and a modeling dataset were established based on well logging and mud logging data. The study conducted data correlation analysis and normalization on the modeling dataset and processed the formatted data. Subsequently, the processed data is randomized and sorted, and training and validation sets are established proportionally. Different machine learning models are selected for training. When the training accuracy cutoff condition is met, the training is completed and the optimal model and random order relationship are obtained. Finally, the model and its relationship are used to perform weighted prediction analysis and inverse normalization on the predicted data. The modeling and processing flow of this study is shown in Fig. 1.

Fig. 1
figure 1

The process of research and analysis.

Full size image

Data source and relationship analysis

It is often considered reasonable to predict unknown adjacent wells by utilizing modeling and fitting information from known drilling data. This approach helps avoid overfitting of data and enhances the reliability or credibility of evaluation studies. All data used in this study originates from the Ledong and Dongfang blocks in the Yingqiong Basin, China. A notable feature of this region is the presence of strata with abnormally high pore pressure. The known well dataset used for modeling in the Ledong block is designated as A1, while the known well dataset used for modeling in the Dongfang block is designated as B1. The adjacent well datasets used for final prediction and evaluation are designated as A2 and B2, respectively.

The IWM dataset and prediction accuracy evaluation validation dataset mainly include well logging and mud logging data. The key parameters of logging data mainly include vertical depth (DEP), rate of penetration (ROP), weight on bit (WOB), weight of hanging (WOH), rotation per minute (RPM), torque (Tor), slurry pump pressure (SPP), mud weight (MW), etc. The key parameters of logging data mainly include acoustic time difference (ADT), density (DEN), and volume of clay (VCL) Wait. The integrated dataset used for model training, validation, and prediction is a data matrix composed of mud logging parameters and well logging parameters. The first eleven columns of the matrix are vertical depth, rate of penetration, weight on bit, weight of hanging, rotation per minute, torque, slurry pump pressure, mud weight, acoustic time difference, density, and volume of clay respectively. The last column of the matrix contains pore pressure data. The input condition of the model is the first eleven columns of the data matrix. The output result is pore pressure (Pp). Therefore, the established data input and output matrix relationship is shown in Eq. (1).

$$Pp = f([DEP \; ROP \; WOB \; WOH \; RPM \; Tor \; SPP \; MW \; ADT \; DEN \; VCL])$$
(1)

At the same time, to select the correlation characteristics of the parameters, correlation analysis was conducted on each parameter in the dataset, and a correlation coefficient matrix was established. The main methods for analyzing parameter correlation include Pearson, Spearman, and Kendall methods. The Pearson method generally requires parameters to satisfy continuity and normal distribution characteristics, and variables are linearly correlated, so the requirements for use are relatively strict; The Spearman method and Kendall method generally do not consider the sample distribution morphology and are general nonparametric methods. In this study, the Spearman method was used for correlation analysis, and the calculation formula is shown in Eq. (2). The correlation coefficient matrix obtained through calculation is shown in Fig. 2.

$$\rho_{j} = \frac{{\sum\nolimits_{i = 1}^{i = n} {\left( {x_{ij} - \overline{x}_{j} } \right)\left( {p_{{i_{j} }} - \overline{p}_{j} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {x_{ij} - \overline{x}_{j} } \right)^{2} \sum\nolimits_{i = 1}^{n} {\left( {p_{ij} - \overline{p}_{j} } \right)^{2} } } } }}$$
(2)

where \(\rho_{j}\) is the combination relationship, \(x_{ij}\) is the variable value of the combination relationship, \(\overline{x}_{j}\) is the mean value of the combination relationship variable, \(p_{ij}\) is the observation value of the combination relationship, and \(\overline{p}_{j}\) is the mean of the combination relationship observation value, j = 1, 2, 3, … 11, 12.

Fig. 2
figure 2

Spearman correlation coefficient matrix.

Full size image

According to the Spearman correlation coefficient matrix, it can be found that pore pressure has different correlation relationships with various parameters. Pore pressure has a strong correlation with DEP, WOH, and MW. While it has a medium to high correlation with ROP, WOB, TOR, SPP, ADT, DEN, and VCL. Pore pressure has a medium to low correlation with RPM.

Data processing and partitioning

The data used for model training in this study consists of 6520 entries, each containing 12 parameters as shown in Eq. (1). The initial dataset for training the model comprises a total of 78,240 data points. The statistical parameters of data can provide a comprehensive overview of the data, which is crucial for the transparency and credibility of research. Therefore, to clearly describe data characteristics and evaluate data quality. This study provides some statistical parameters of the research data, mainly including mean value, standard deviation, median value, and quartiles. The statistical results are shown in Supporting Table 1.

The unified processing of data mainly includes removing outliers, completing missing values, randomizing data, partitioning the dataset, and normalizing the data.

Firstly, to make the training model more reliable, the outliers in the dataset are treated as 3σ37. Abnormal data outside the range of three standard deviations were excluded by using this principle. The data on standard deviation can be found in Supporting Table 1. 39 and 26 abnormal data were removed from the A1 and B1 datasets, respectively. At the same time, for partially missing data, interpolation of neighboring values is used to complete.

Secondly, this study trained and validated the pore pressure prediction model using partitioned data from wells A1 and B1. The accuracy and rationality of model training are crucial. Randomly dividing and selecting the training set has many benefits38. It reduces the bias caused by data order or specific patterns and makes the model more generalizable. It helps to avoid overfitting the model to specific training data patterns. Meanwhile, randomly selecting partitioned datasets is a cross-validation method that can help evaluate the robustness of models on different datasets. Therefore, 85% of the data from datasets A1 and B1 were randomly selected as the model training data to train the machine learning model. The remaining data (15%) from datasets A1 and B1 were selected as the model validation test data to validate the model. Among them, Well A1 has a total of 4046 pieces of data. 3439 pieces of data were randomly selected for model training, and the remaining 607 pieces of data were selected for model validation; B1 well has a total of 2409 data pieces, of which 2047 were randomly selected for model training, and the remaining 362 were selected for model validation. At the same time, establish datasets A2 and B2 as input conditions for evaluating the accuracy of the trained prediction model, to evaluate the reliability or accuracy of the model. Among them, the A2 well has 698 data pieces, and the B2 well has 1918 data pieces.

Finally, to eliminate the influence of parameter magnitude on the model results and obtain reasonable input feature parameter values, all dataset parameters are normalized. After the model is established, reverse normalization can be performed to obtain the parameter results of the original morphological features.

Modeling and prediction with integrated well logging and mud logging data

To evaluate the accuracy and model optimization of the IWM model, this study established commonly used machine learning models based on IWM, including the back propagation (BP) neural network, the support vector machine (SVM), the BP model with genetic algorithm (GABP), the random forest algorithm (RF), the radial basis function (RBF) neural network, and the convolutional neural network (CNN). The IWM model was trained, validated, and used to predict formation pressure through recorded data. The following machine learning models are used to train and verify the existing data to achieve the best and approximate training and verification effect. Based on the approximate training effect, another prediction data set is applied. The accuracy of each model is evaluated by observing the prediction results.

Modeling with integrated well logging and mud logging data

Construction of IWM prediction model based on the BP

The neural network algorithm is one of the algorithms with self-learning ability, high-speed search for optimal solutions, and good practical application effects. The Back Propagation Neural Network was proposed by Rumelhart et al.39, which has excellent function approximation ability through iteration and updating. According to the BP model structure, an integrated data model based on the BP neural network (IWM-BP) was established, as shown in Fig. 3. The main steps involved in the implementation are as follows: random initialization of weights, forward propagation calculation, loss calculation, backpropagation, and weight updates. Both the forward and reverse modules have undergone weight training. The loss function is trained using synthetic data. A crucial aspect of training the weights is the gradient calculated during backpropagation. These gradients are utilized to adjust the weights in each iteration, gradually reducing the loss function. In this study, the integrated data model for measurement and recording has 11 input neurons, hidden layer ranges of 2, 3, and 5 layers, one output neuron, a maximum iteration of 2000, and a learning rate of 0.01.

Fig. 3
figure 3

IWM-BP model structure.

Full size image

Construction of IWM prediction model based on the GABP

The genetic algorithm theory is an algorithm designed based on Darwin’s theory of evolution, which can cause data to evolve in a positive direction to obtain the optimal solution40. This study established an integrated data model based on the GABP neural network (IWM-GABP). The input data was normalized measurement and recording integrated data. Firstly, the BP neural network and genetic algorithm parameters (including genetic algebra, race size, etc.) were initialized, and then fitness and iterative calculations were repeated to determine the initial weights and thresholds of the optimized BP network. Finally, the weights and thresholds were input into the BP model for training and validation, The model established through this process can be used for predicting formation pressure. This model obtains a more adaptive model by changing the population size and genetic algebraic parameters and uses this to predict pore pressure.

Construction of IWM prediction model based on the SVM

The support vector machine is a classic binary model41, which works by identifying decision hyperplanes and completing data planning. A more common model is the linear SVM model. This study uses a nonlinear SVM model to handle input nonlinear problems. The nonlinear problem is transformed into a linear problem in the feature space through a Gaussian kernel function, and a linear SVM model is used in a high-dimensional feature space. Therefore, the decision function of the nonlinear SVM model is obtained as shown in Eq. (3). SVM itself does not have a backpropagation mechanism. This study obtained a more adaptive model by changing the penalty factor and radial basis function parameters and established an integrated data prediction model based on the SVM (IWM-SVM) to predict pore pressure.

$$f(x) = sign\left( {\sum\limits_{i = 1}^{n} {\alpha_{i}^{*} y_{i} \exp \left( { - \left\| {\left. {x - {\varvec{x}}_{i} } \right\|^{2} /2\sigma^{2} } \right.} \right)} + b^{*}} \right)$$
(3)

where \(\alpha_{i}^{*}\) is the optimal solution of the Lagrange multiplier, \(y_{i}\) is the class marker, \(x_{i}\) is the eigenvector, \(\sigma\) is the width parameter of the Gaussian function, and \(b^{*}\) is the optimal intercept.

Construction of IWM prediction model based on the RF

The random forest algorithm is one of the most used and powerful supervised learning algorithms42, which can obtain regression prediction problems through the output of decision trees. This algorithm has obvious advantages, high accuracy, and processing large amounts of data without the need for dimensionality reduction design. The input condition of the model is standardized IWM, and a more adaptive model is obtained by changing the number of decision trees and leaves parameters, which is used for predicting pore pressure. The algorithm does not have a display weight and backpropagation mechanism. The construction of trees is based on random samples and feature selection. This study obtained a more adaptive model by changing the decision tree parameters, and an integrated data prediction model based on the RF (IWM-RF) was established to predict pore pressure.

Construction of IWM prediction model based on the RBF

The radial basis function neural network is a structure activated by radial basis functions, typically consisting of input layer, hidden layer, and output layer43. The input layer of the model in this study is the standardized measurement and recording IWM matrix, the transformation functions of each unit in the hidden layer are radial basis functions, and the activation function in this study is the Gaussian function, as shown in Eq. (4). The function of the hidden layer is to map the data input to a high-dimensional space and then perform fitting. The function of the output layer is to weight the data calculated by the hidden layer. The weights of the output layer are adjusted through the gradient descent method. Finally, the RBF neural network structure was obtained, as shown in Eq. (5). The structure of the integrated data prediction model based on the RBF (IWM-RBF) in this study is shown in Fig. 4.

$$R\left( {x_{j} ,x_{i} } \right) = \exp \left( { - \frac{1}{{2\sigma^{2} }}\left\| x \right._{j} - \left. {x_{i} } \right\|^{2} } \right)$$
(4)
$$F(x) = \sum\limits_{i = 1}^{n} {w_{ij} } \exp \left( { - \frac{1}{{2\sigma^{2} }}\left\| x \right._{j} - \left. {x_{i} } \right\|^{2} } \right)$$
(5)

where xj is the input sample, xi is the center point, \(\left\| x \right._{j} - \left. {x_{i} } \right\|\) is the norm, and wij is the weighted value.

Fig. 4
figure 4

IWM-RBF model structure.

Full size image

Construction of IWM prediction model based on the CNN

The convolutional neural network is a deep learning algorithm that generally includes operations such as convolution, pooling, activation, loss, and output44. This study is based on CNN and integrated measurement and recording data. The data is tiled into 11 × 1 × 1 images and zero-centered, and then subjected to two-dimensional convolution to form 16 feature maps with a convolution kernel size of 5 × 1. Then, an optimized parametric rectified linear unit is used as the activation function to perform nonlinear mapping on the data, which avoids the disadvantage of a gradient of zero in the negative range, as shown in Eq. (6). Then, perform a second convolution to form 32 feature maps and activate them. Form a fully connected layer and a regression layer for model training, set the maximum number of model training times to 800, and reduce the learning rate by half after 400 times, with an initial learning rate of 0.01. The model training utilizes a gradient descent algorithm to update the weights of convolutional kernels and fully connected layers, and an integrated data prediction model based on the CNN (IWM-CNN) was established.

$$f(x) = \max (ax,x)$$
(6)

where a is the backpropagation learning parameter.

Model training and validation

The hyperparameters for training the model are accuracy values, as shown in Fig. 1. Hyperparameters start from 100% during the training process. If the hyperparameter requirements are still not met after reaching the iteration number, the hyperparameter value will be reduced and the next iteration calculation will be carried out. The training will be stopped when the optimal parameter values are obtained. The hyperparameter reduction step size is 0.01%. Therefore, the accuracy value of the training model obtained when the training stops is the hyperparameter value, also known as the training set goodness of fit in the study.

The study established an IWM-BP model through the computer and optimized model training on the A1 and B1 well datasets. Finally, the model training process and results were obtained.

According to the model, after data training for well A1, the goodness of fit of the training set was 0.9956, and the goodness of fit of the validation test set was 0.9941. The best validation performance is 0.0032146, achieved at epoch 17. The regression state and validation performance of the training process data is shown in Fig. 5, and the results of the model training data and validation data are shown in Fig. 6. The results of the B1 well model training and validation data are shown in Fig. 7. The goodness of fit of the training set is 0.9740, and the goodness of fit of the validation test set is 0.9763. According to the observed values of goodness of fit, the model training results are in line with expectations.

Fig. 5
figure 5

Regression state and validation performance.

Full size image
Fig. 6
figure 6

A1 well model training data and validation data results.

Full size image
Fig. 7
figure 7

B1 well model training data and validation data results.

Full size image

Similarly, data based on IWM and other models (GABP, SVM, RF, RBF, CNN) were established separately. The optimal model training was performed on the A1 and B1 well datasets to obtain the model training process and results. The training and validation data of the A1 and B1 well models are shown in Figs. 6 and 7. After calculation, the goodness of fit of the A1 well training set was 0.9958, 0.9988, 0.9991, 0.9911, and 0.9922, respectively. The goodness of fit of the A1 well testing validation set was 0.9952, 0.9986, 0.9987, 0.9908, and 0.9927, respectively. The goodness of fit of the B1 well training set were 0.9909, 0.9672, 0.9943, 0.9496, and 0.9391, respectively. The goodness of fit of the B1 well testing validation set were 0.9093, 0.9768, 0.9908, 0.9357, and 0.9411, respectively. Based on the observed values of goodness of fit for each result, the model training results also meet expectations.

Prediction of formation pore pressure

Based on the established and trained IWM models, pore pressure prediction was performed on adjacent wells A2 and B2. The prediction results are shown in Fig. 8. Based on the calculation results, the prediction accuracy of each model was calculated, as shown in Table 1.

Fig. 8
figure 8

Prediction results of pore pressure.

Full size image
Table 1 Prediction accuracy of each model.
Full size table

According to Fig. 8 of the model prediction results and Table 1 of the prediction accuracy calculation, it can be found that except for IWM-RBF, the prediction accuracy of all models is greater than 90%. The IWM-GABP model has the highest prediction accuracy. The average prediction accuracy is over 96%. When predicting formation pressure, it is advisable to use IWM-BP or IWM-GABP models, and it is not advisable to use IWM-RBF models.

Comparison and evaluation of prediction effects

Simply looking at the prediction results and accuracy of formation pressure made above cannot intuitively demonstrate the advantages of the integrated data model in this study. Therefore, to evaluate the advantages and calculation accuracy of the IWM data model, this study compared conventional machine learning logging and logging models and obtained the calculation results of various data models.

The calculation results and comparison of the data models for wells A2 and B2 are shown in Figs. 9 and 10. Based on the calculation results, the prediction accuracy of each model was calculated, as shown in Fig. 11.

Fig. 9
figure 9

Comparison of prediction results for well A2.

Full size image
Fig. 10
figure 10

Comparison of prediction results for well B2.

Full size image
Fig. 11
figure 11

Comparison bar chart of prediction accuracy.

Full size image

According to the calculation results, for well A2, it can be found that the IWM-GABP model has the highest prediction accuracy, with a formation pressure prediction error of 5.34%, the IWM-SVM model has the lowest calculation accuracy, and the formation pressure prediction error is 16.20%. Compared to traditional logging and logging data models, the calculation errors of the IWM-BP model are reduced by 6.21% and 5.82%, respectively. The calculation errors of the IWM-SVM model are reduced by 41.7% and 11.77%, respectively. The calculation errors of the IWM-GABP model are reduced by 1.96% and 4.52%, respectively. The calculation errors of the IWM-RF model are reduced by 3.50% and 7.48%, respectively. The calculation errors of the IWM-RBF model are reduced by 19.93% and 16.97%, respectively. The calculation errors of the IWM-CNN model are reduced by 3.50% and 1.74%, respectively. Overall, compared to traditional methods, the prediction accuracy of this model has improved by an average of 12.80% and 8.05%.

According to the calculation results, for well B2, it can be found that the IWM-GABP model has the highest prediction accuracy, with a formation pressure prediction error of 2.02%, the IWM-RBF model has the lowest calculation accuracy, and the formation pressure prediction error is 10.47%. Compared to traditional logging and logging data models, the calculation errors of the IWM-BP model are reduced by 11.32% and 9.58%, respectively. The calculation errors of the IWM-SVM model are reduced by 2.81% and 10.28%, respectively. The calculation errors of the IWM-GABP model are reduced by 4.49% and 6.47%, respectively. The calculation errors of the IWM-RF model are reduced by 1.25% and 3.17%, respectively. The calculation errors of the IWM-RBF model are reduced by 3.96% and 12.51%, respectively. The calculation errors of the IWM-CNN model are reduced by 3.64% and 5.01%, respectively. Overall, compared to traditional methods, the prediction accuracy of this model has improved by an average of 4.58% and 7.84%.

Therefore, it can be found that compared to traditional mud logging or well logging data models, the integrated mud logging and well logging data model has higher accuracy in predicting formation pressure, with an average improvement of 8.69% and 7.95% in predicting formation pore pressure.

Conclusions and discussion

The study integrates mud logging and well logging data to analyze relationships among various parameters. Based on commonly used machine learning models for formation pressure, a formation pressure prediction model was established based on integrated combination data. Formation pressure prediction and analysis were conducted, and the accuracy of the integrated data model was evaluated by comparing it with traditional data methods. Research has found that:

  1. 1.

    Analysis using the Spearman correlation coefficient revealed that pore pressure exhibits varying correlation relationships with different parameters. Pore pressure is closely related to factors such as depth, weight of hanging, and mud weight. Pore pressure has a medium to high correlation with the rate of penetration, weight on bit, torque, slurry pump pressure, acoustic time difference, density, and volume of clay. Pore pressure has a medium to low correlation with the rotation per minute.

  2. 2.

    All integrated data models have a prediction accuracy exceeding 90%. The integrated data model utilizing the back propagation neural network method combined with a genetic algorithm achieves the highest prediction accuracy, averaging over 96% accuracy. To predict formation pressure, it is advisable to use an ensemble data model employing the backpropagation neural network method, ideally in combination with a genetic algorithm. Using the integrated data prediction model based on the radial basis function method is not advisable.

  3. 3.

    A comparative evaluation and analysis revealed that the integrated combination data model outperforms traditional mud logging and well logging data models. It not only predicts the formation pressure but also maintains high prediction accuracy. Specifically, there is an average improvement of 8.32% in predicting formation pressure accuracy.

According to the results, this model indeed has high prediction accuracy. However, this model also has certain limitations in field applications. Current machine learning models’ parameters or algorithm layers may not apply to all blocks worldwide, but the methods proposed in current research are universally applicable. Different intelligent models should be trained in different regions. In practical applications, some older wells lack advanced measurement techniques. There may be a situation of insufficient parameters, which require specific analysis based on the situation. In addition, adding new data parameters may also improve prediction accuracy, as long as the parameter is meaningful and economically measurable. However, overall, this method is meaningful for improving the accuracy of reservoir pressure prediction and provides new ideas. Of course, if this method can be improved in the future to establish a real-time prediction model for formation pressure, it may be more suitable for engineering practice.