Introduction

In recent years, significant progress has been observed in research on metal-free organic ferroelectrics. Interest in such materials is stimulated by both fundamental and technological aspects. Compared with their heavy metal counterparts, organic ferroelectrics are promising for future applications because of their low processing cost, light weight, flexibility, and low negative environmental impact1. The high ferroelectric performance of organic materials is expected to be associated with long-term mechanical and chemical stability, as well as resistance to environmental conditions such as UV irradiation, temperature, and moisture. Therefore, the design and search for new organic ferroelectrics is still a challenging task.2,3,4.

Ferroelectrics are multifunctional materials whose practical use is continuously expanding5,6,7. Recently, it has been shown that in addition to areas such as information storage, electronics, sensors, spintronics, or nonlinear optics, ferroelectric functionalities can also be implemented in biotechnological and medical fields8,9,10. For such purposes, organic ferroelectrics, the structures of which are most often stabilised by hydrogen bonds, may be ideal candidates for the engineering of biocompatible devices. Ferroelectric amino acid salts fit very well into this scenario. The history of this family began in 1956 with the discovery of ferroelectricity in triglycine sulfate (TGS)11. Subsequent extensive research has resulted in numerous ferroelectric materials based on glycine and its derivatives.12,13,14,15,16,17,18 Ferroelectricity has also been reported for the γ polymorph of glycine19,20,21,22, which can shed new light on numerous biophysical processes involving the simplest amino acid. Recent studies focused on new salts and adducts of dimethylglycine [(CH3)2NCH2COOH, DMG] with organic and mineral acids have resulted in a wide range of new compounds23,24, including those with polar symmetry, which can be candidates for new ferroelectrics. Indeed, further research revealed ferroelectricity in dimethylglycinium-dimethylglycine chloride, (DMGH···DMG)Cl25, which is built of dimeric H-bonded monocations (DMGH···DMG)+ and Cl− anions. The crystal exhibits ferroelectric properties over a wide temperature range, since its Curie point is situated at 401 K. Continuing research on DMG-based compounds, we synthesized the dimethylglycinium hydrogen maleate-maleic acid salt (CH3)2NHCH2COOH·(COOH)C2H2(COO)·C2H2(COOH)2 (DMG·2MA). Unlike previously reported (DMGH···DMG)Cl, the DMG·2MA crystal was designed as a combination of simple DMGH+ monocations with complex dimeric H-bonded monoanions (2MA)−. A comprehensive study of the structural and physical properties has shown that the crystal undergoes an unusual sequence of two phase transitions. At 295 K, high-temperature centrosymmetric phase I transforms into modulated incommensurately phase II, and next, at around TC = 271 K, the crystal enters low-temperature phase III, which exhibits spontaneous polarization and ferroelectric switching.

Experimental section

Synthesis and crystal growth

High-quality single crystals were grown at a constant temperature of 301 K by slow evaporation of water from an aqueous solution containing dimethylglycine and maleic acid in a 1:2 molar ratio. The unidirectional growth method was used to obtain large single crystals of the desired orientation (Fig. 1). For this purpose, a single crystal seed was mounted at the bottom of a conical glass test tube and heated at 303 K for one day. The test tube was filled with a saturated solution filtered through a 0.45 μm PTFE membrane filter. The tube was loosely closed to reduce the evaporation rate. After one week, the crystal was carefully removed. The apparent opacity visible in Fig. 1c is due to the rough surface formed at the interface with the tube wall. The stoichiometry and purity of the crystals grown were confirmed by powder X-ray diffraction (Fig. S1) and elemental analysis (Supporting Information).

Fig. 1
figure 1

The DMG·2MA single crystal (a) used as a seed in the unidirectional growth method (b) to obtain the crystal in the desired orientation (c).

Full size image

Single-crystal X-ray diffraction

Single-crystal X-ray diffraction experiments were carried out on an Oxford Diffraction Gemini A Ultra diffractometer operating with graphite-monochromated MoKα radiation. The diffraction data were collected as a function of the temperature in the range between 150 and 350 K. The temperature of the crystals was stabilized within ± 0.1 K with a nitrogen stream via a Cryostream Plus attachment (Oxford Cryosystems). For data collection and processing, CrysAlisPro software26 was used. The crystal structures in phases I and III were solved and refined using SHELX27. Details of the refinements and selected structural parameters are presented in Table S1. Crystallographic information files (CIFs) have been deposited with the Cambridge Crystallographic Data Centre as CCDC 2430734‒2430736.

Differential scanning calorimetry and thermogravimetric analyses

The range of thermal stability of the DMG·2MA compound was determined by thermogravimetric analysis (TGA) using a TGA Q50 thermogravimetric analyser (TA Instruments). The polycrystalline sample was heated in a nitrogen atmosphere at a temperature rate of 10 K/min.

Differential scanning calorimetry (DSC) measurements were performed with a Q2000 calorimeter (TA Instruments) calibrated with the indium standard and synthetic sapphire. The powdered sample, which was prepared from a single crystal, was cooled/heated at a rate of 10 K/min.

Spontaneous polarization and electric permittivity measurements

The polarization‒electric field (P − E) hysteresis loops were examined using a Keithley 6517B electrometer. The loops were recorded at a low-frequency electric field sweep ranging from 10 mHz to 1 Hz. An electric field was applied along the polar c direction of the oriented single-crystal plate with painted silver electrodes.

The relative complex electric permittivity ε = ε’ - iε” was measured on the oriented single crystal plates cut perpendicular to the main crystallographic directions. Silver paste was applied to deposit the electrodes on the crystal plates. The real part of the electric permittivity and the tangent of the dielectric loss were measured in the frequency range from 1 kHz to 10 MHz with a Hewlett-Packard 4192 A impedance analyser. The amplitude of the ac measuring electric field varied for different samples between 2.5 and 4 V/cm. The temperature of the samples was changed at rates of 0.2 and 0.5 K/min in the phase transitions region and outside the transitions region, respectively.

Results and discussion

Characterization of thermal properties

The TGA measurements (Fig. S2) revealed that DMG·2MA is stable up to approximately 390 K. The substantial weight loss of the sample above this temperature indicates crystal decay. The salt melts at 392 K, which coincides with the onset of decomposition, and the substance does not crystallize in the subsequent cooling run, as evidenced by the DSC plots in Fig. S1.

The DSC study revealed that DMG·2MA undergoes two phase transitions near room temperature. The character of the thermal anomalies recorded in the cooling and heating runs (Fig. 2a) proves that at 295 K the crystal undergoes a second-order phase transition followed by a first-order transition at around 271 K. Despite the first-order character, the temperature hysteresis of the low-temperature transition is very small. For DSC runs recorded at the rate of temperature changes of 10 K/min, the hysteresis was about 0.5 K, as seen in Fig. 2a, while for much lower temperature rates used in dielectric measurements (0.2 K/min), it was observed to be even lower than 0.2 K. In this respect, the transition resembles the ferroelectric-to-paraelectric transition in KH2PO428. The three phases of DMG·2MA are denoted by Roman numbers I, II, and III, starting from the high-temperature phase.

Fig. 2
figure 2

DSC heating and cooling runs (a) and the temperature dependence of specific heat and the entropy change (b) for DMG·2MA. The dashed line in part (a) marks the transition temperature, which for the second-order phase transition corresponds to the position of the anomaly minimum and the onset, respectively, in the heating and cooling runs; the arrows indicate the transition temperatures of the first-order transition.

Full size image

As shown in Fig. 2, the thermal anomalies accompanying the transitions partially overlap. Therefore, the integration of the anomalous part of Cp(T) was performed across both transitions with the baseline marked in Fig. 2b. The total entropy gain, ΔS = (4.2±0.4) Jmol− 1K− 1, is close to Rln1.7 indicating a possible order-disorder contribution to the transition mechanism.

Crystal structure

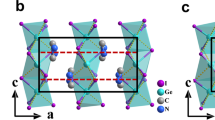
Temperature-dependent structural studies have shown that all DMG·2MA phases exhibit a layered architecture (Fig. 3a). In low-temperature phase III, the crystal symmetry is polar with the space group Pca21 (Table S1) and the polar axis along the longest lattice parameter c. The interaction between the molecular layers, arranged perpendicular to b, is dominated by van der Waals forces. These weak interactions are responsible for the existence of an excellent cleavage plane (010) in the crystal. As shown in Fig. 3b, DMG+ cations and dimeric monovalent [2MA]− anions are linked through the strong O‒H···O and N‒H···O hydrogen bonds (see also Tables S2 and S3), forming wavy ribbons that extend along c. The adjacent ribbons within the sheetsinterplay through weak C‒H···O hydrogen bonds and van der Waals contacts. In phase III at 160 K the molecular ions are well ordered, but the entropy change during the heating of the crystal through the phase transitions region strongly suggests possible disorder in phase I. The determination of the structure in this phase at 300 K revealed two-site disorder of the DMG+ cations (Fig. 4). This disorder causes the lattice parameter c in phase I to be halved compared with the corresponding parameter a in phase III (compare Figs. 3b and 4a), and the crystal adopts the centrosymmetric space group Pnma (Table S1). In intermediate phase II, the diffraction data revealed the presence of satellite reflections, indicating an incommensurate modulation of the structure. The modulation vector is parallel to the lattice translation that becomes doubled in phase III. This doubling is evident from the temperature dependence of the modulation vector shown in Fig. 5a. Thus, the transition between phases II and III is of incommensurate-commensurate type. The average crystal structure of phase II approximates that of phase I. The lattice parameters and molecular volume (V/Z) in all three phases of DMG·2MA are plotted as a function of temperature in Fig. 5b. Small stepwise changes visible at approximately 271 K confirm the first-order character of the transition between phases II and III, whereas continuous changes at approximately 295 K are consistent with the second-order transition between phases II and I.

Fig. 3
figure 3

Layered packing of the unit cell of DMG·2MA in ferroelectric phase III at 260 K viewed along [100] (a) and a single layer of DMG+ cations and dimeric [2MA]− anions tied through OH···O and NH···O hydrogen bonds (b).

Full size image
Fig. 4
figure 4

Crystal structure of DMG·2MA in phase I at 300 K viewed along [001] (a), the hydrogen-bonded molecular ribbons forming a layer perpendicular to [010] (b), and a comparison of DMG+ cations in phases I and III. Owing to the disorder of DMG+, the lattice parameter c is halved in phase I compared with corresponding parameter a in ferroelectric phase III.

Full size image
Fig. 5
figure 5

Temperature dependence of the modulation vector in phases II and III of DMG·2MA (a) and of the lattice parameters and molecular volume across the three phases I, II and III (b).

Full size image

Ferroelectric polarisation

The polar symmetry of phase III suggests possible spontaneous polarisation and ferroelectric properties of DMG·2MA. These suppositions were verified by a series of experiments showing polarisation switching in an external electric field. The most characteristic polarisation-electric field (P-E) hysteresis loops, recorded in the temperature lowering cycle, are shown in Fig. 6a,b. In phase II, at 274 K (TC-T = -2.6 K), the crystal exhibited linear P(E) dependence as expected for normal dielectrics, but closer to the transition temperature, at 271.8 K (TC-T = -0.4 K), a double hysteresis loop was recorded. This behaviour is characteristic of first-orderferroelectric phase transitions29. The double loop indicates an electric field-induced transition from the incommensurately modulated phase to the commensurate phase with non-zero polarisation. Further lowering of the temperature results in a single hysteresis loop in phase III (Fig. 6b) and an increase in the value of spontaneous polarisation, as illustrated by the plot in Fig. 6c. Just below the transition temperature at 271.1 K, the coercive field is relatively low of 422 Vcm− 1, whereas at 226.1 K, it increases to 595 Vcm− 1. The vertical shift of the hysteresis loop indicates an internal bias field that increases from 65 Vcm− 1 at 271.1 K to 362 Vcm− 1 at 226.1 K. The value of spontaneous polarisation of DMG·2MA is approximately two times greater than that of the archetypical ferroelectric Rochelle salt (0.25 µCcm− 2)29, but it is lower than that of TGS (2.2‒2.8 µCcm− 2 at 293 K)11,12 and the recently discovered (DMGH···DMG)Cl (1.9 µCcm− 2)25.

Fig. 6
figure 6

Polarisation-electric field hysteresis loops recorded in the vicinity of the first-order phase transition (a) and in ferroelectric phase III (b), and the temperature dependence of spontaneous polarisation (c).

Full size image

The occurrence of spontaneous polarisation in the ferroelectric phase is undoubtedly related to the ordering of DMGH+ cations. In phase I, the cations occupy split positions and their ordering takes place through phase II, in which their positions are responsible for structural modulation. The complete ordering of DMGH+ cations occurs after the transition to phase III, which is associated with the mutual shift of molecular ions, resulting in the generation of nonzero spontaneous polarisation.

Dielectric properties

The occurrence of switchable spontaneous polarisation in phase III strongly suggests that the temperature of the transition between phases II and III is a Curie point. This was confirmed by the temperature-dependent measurements of the dielectric response of the crystal that are presented in Fig. 7. Along the polar c direction at around TC = 271 K the crystal exhibits a large dielectric anomaly, characteristic of paraelectric‒ferroelectric phase transitions, whereas in the perpendicular directions the values of electric permittivity are approximately two orders of magnitude smaller. As shown in Fig. 7a,b, below the TC in the ferroelectric phase, the dielectric functions are strongly frequency dependent, indicating a substantive contribution of the ferroelectric domains. In the paraelectric phase of ferroelectric materials the low-frequency electric permittivity usually obeys the Curie‒Weiss law, ε = C/(T-T0), but in the case of DMG·2MA, the plots of 1/εc’ as a function of T are clearly nonlinear (see Fig. S3), demonstrating that this law is not fulfilled. The reason for such electric permittivity behaviour is not clear but may be related to the modulation in phase II, whose average structure approximates that of phase I, but can locally show similarities to that of phase III.

As shown in Fig. 7a,b, there is no dielectric anomaly along the polar direction that could be ascribed to the transition between phases I and II. The continuous anomaly in the electric permittivity at around 295 K, which is consistent with the second-order character of this transition, was detected only along b (Fig. 7c).

Fig. 7
figure 7

The real (a) and imaginary (b) parts of the electric permittivity measured for selected frequencies along the polar [001] direction of [DMG]+[2MA]−, and the real part of the electric permittivity along the perpendicular directions [100] (c) and [010] (d), measured on cooling the sample. The crystallographic directions refer to those of ferroelectric phase III.

Full size image

To analyse the dielectric response of DMG·2MA along the polar direction in the ferroelectric phase, the Cole‒Cole formalism was applied. As illustrated in Fig. 8a, the Cole‒Cole plots form semi arcs with centres located below the ε axis, indicating the polydispersive character of dielectric relaxation. Therefore, the complex electric permittivity (ε) was modelled with the Cole‒Cole function30:

$$\:\epsilon\:={\epsilon\:}_{\infty\:}+\frac{{\epsilon\:}_{s}-{\epsilon\:}_{\infty\:}}{{1+\left(i\tau\:\omega\:\right)}^{1-k}},$$
(1)

where εs and ε∞ are the low- and high-frequency limiting values of the real part of the electric permittivity, ω is the angular frequency, τ is the most probable relaxation time, and k is a measure of the relaxation times distribution. To consider the possible contribution of electric conductivity, an appropriate term has been included in the equation modelling of the experimental dielectric data:

$$\:\epsilon\:={\epsilon\:}_{\infty\:}+\frac{{\epsilon\:}_{s}-{\epsilon\:}_{\infty\:}}{{1+\left(i\tau\:\omega\:\right)}^{1-k}}+\frac{i\sigma\:}{\omega\:{\epsilon\:}_{0}},$$
(2)

where σ is the electric conductivity and ε0 is the vacuum permittivity. The fitting of the equation (2) to the experimental data shows that electric conductivity increases from 0.8 nS m− 1 at 192.7 K to 25.9 nS m− 1 at 267 K, but this contribution to the dielectric response of the crystal is not very high. The temperature dependence of the relaxation time (Fig. 8b) does not obey the Arrhenius law31 but can be well described by the Vogel‒Fulcher relation32,33:

$$\:\tau\:={\tau\:}_{0}\text{exp}\left(\frac{{E}_{a}}{T-{T}_{VF}}\right)\:,$$
(3)
Fig. 8
figure 8

Cole‒Cole plots at selected temperatures (a) and ln τ as a function of temperature (b). The solid red line in the chart (b) represents the best fit of Vogel‒Foulcher equation to the experimental points; the inset in (b) shows the temperature dependence of the parameter k [see Eq. (1)].

Full size image

where τ0 is a parameter related to the limiting response frequency of dipolar entities, Ea is the activation energy (in K), and TVF is a characteristic Vogel‒Fulcher temperature, often described as a static freezing temperature. The best fit of Eq. (3) to τ values determined from the experimental data, showed that the dielectric relaxation in the ferroelectric phase of DMG·2MA can be characterized by Ea = 253.7 K (0.22 eV), TVF = 143.2 K, and τ0 = 8.5·10− 8 s. The temperature dependence of the parameter k, plotted in the inset in Fig. 8b, indicates an anomalous alteration of the relaxation times distribution, which narrows between TC and 240 K and then widens at lower temperatures. The turning point at 240 K is clearly visible in the temperature dependences ε(T) and ɛ”(T) in Fig. 7a,b. This anomalous behaviour can be attributed to the temperature evolution of the ferroelectric domains. The initial decrease in k with decreasing temperature may result from the merging of domains and homogenization of their distribution, whereas the reverse tendency at lower temperatures indicates slowing of the dynamics of domains, which ultimately freeze below the TVF.

Conclusions

We synthesized a new ferroelectric organic salt with a layered structure controlled by hydrogen bonds. The layers in DMG·2MA are formed from corrugated supramolecular ribbons of dimethylglycinium monocations and dimeric maleic monoanions linked through N‒H···O and O‒H···O hydrogen bonds. The crystal undergoes an unusual sequence of phase transitions near room temperature. When cooling, the high-temperature disordered phase I of the space group Pnma transforms at 295 K to the incommensurately modulated phase II, and then at around 271 K a lock-in transition leads to commensurate phase III of the polar space group Pca21. The ferroelectric properties of phase III were experimentally verified by polarisation switching in an external electric field and confirmed by comprehensive studies of the crystal dielectric properties. The structural analysis led us to conclude that ferroelectricity in the DMG·2MA phase III results from the ordering process of DMGH+ cations that is realized through the intermediate modulated phase II. Although the driving mechanism is of the order-disorder type, spontaneous polarisation originates from ionic displacement.