Introduction

Cryopreservation is a rapidly developing field with the potential to extend shelf life of biomaterials such as cells1,2,3,4, tissues5,6,7, and organs8,9,10,11,12,13 for biomedical applications such as cell therapy, regenerative medicine, biomedical and clinical research, fertility treatments, and organ transplant. Various ways to cryopreserve a biomaterial exist from storage at “high subzero” temperatures via supercooling and partial freezing (for days to weeks)11,12, and in lower cryogenic temperatures via freezing and vitrification (up to months or years)14,15. In all these cases, one main objective is to control damage from ice formation during cooling, storage and rewarming. A cryoprotective agent (CPA) is often used in all the cryopreservation techniques which prevent ice formation inside biomaterials. After a biomaterial is cooled to these storage temperatures, it requires “optimum” rewarming before its end use. In all cases, rapidity and spatial control of this warming is critical in minimizing damage. For organ cryopreservation, where vitrification is the most promising technique for indefinite shelf life, this heating demands rapid and uniform rewarming in order to achieve a successful cryopreservation outcome.

Electromagnetic (EM) fields for rewarming a cryopreserved biomaterial have been applied in different forms such as dielectric16,17,18,19,20 at 10–100 s of MHz frequencies, microwave dielectric21,22,23 at 1–10 s of GHz frequencies, nanowarming occurring at 100s of kHz frequencies3,6,9,24,25,26,27,28,29). The first attempts at rewarming a frozen organ using electromagnetic (EM) waves occurred in the mid-1960s using a commercial microwave oven and shortwave diathermy machine18,19 to rewarm canine kidneys. However, most of these attempts failed due to shallow penetration depths and thermal runaway induced overheating and non-uniformity. Those studies also highlight that to control thermal runaway, an accurate knowledge of dielectric properties and electrical conductivity as function of temperature and CPA composition is a must. So far, nanowarming (a form of RF rewarming with magnetic nanoparticles as the on target and CPA as the off target heating) has shown great promise for scalability to larger volumes (size of human organs) in terms of achieving uniformity and rapid warming rates that is scalable independent of sample size30,31. Nanowarming was recently demonstrated in the first reproducible protocol for the vitrification, long-term storage, recovery, and transplant of an organ in an animal model8. During nanowarming, heating is generated in the presence of alternating magnetic fields (100s of kHz) via magnetic nanoparticles perfused inside the vasculature of an organ8,9. For dielectric rewarming techniques (10s to 100s of MHz) and microwave dielectric rewarming (1 to 10s of GHz) heat generation occurs directly from cryoprotectants via relaxation of constituent polar molecules in water and CPAs. Dielectric rewarming has also been used to rewarm rabbit kidneys with successful transplant16. Dielectric properties govern the heating (dielectric loss) and electric polarization (dielectric constant) of a material in the presence of an alternating electric field. Knowledge of dielectric properties and electrical conductivity as a function of temperature is crucial in characterizing and manipulating the heating profiles of a cryopreserved sample from subzero or cryogenic temperatures when applying any rewarming technique that includes an electric field. This includes nanowarming because the alternating magnetic field of nanowarming produces an electric field by magnetic induction that has the potential to create eddy currents resulting in inductive heating of the sample.

Fig. 1
figure 1

Dielectric loss as function of temperature plotted at two different frequencies (100 MHz and 98 MHz) for a representative CPA-glycerol using data values from literature8,9,11. Loss peak is shown with black arrows.

Full size image

One proposed concern when scaling nanowarming for human organs is non-uniformity in heating that may arise due to undesired (also known as “off target”) eddy current heating. Nanowarming is intended to predominantly heat through coupling with the uniformly distributed magnetic nanoparticles and minimally through eddy current heating. Thus, knowledge of dielectric properties and electrical conductivity are needed to evaluate the magnitude of eddy current heating in order to effectively design nanowarming protocols.

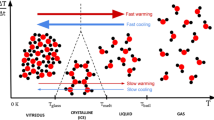
For dielectric rewarming, it is understood that dielectric loss depends upon frequency, temperature and CPA solution composition. It also exhibits a distinct peak with frequency and temperature as shown in Fig. 1. In the presence of an alternating electric field, the polar molecules rotation is resisted by intermolecular viscous forces. Hence, the dielectric relaxation time depends upon the physical state which is governed by temperature and viscosity. At higher temperatures (lower viscosity), relaxation time (tCPA) of CPAs are much shorter than the time period (T = 1/f, f is frequency) of the applied alternating E field. Therefore, the dipoles reorientation can keep up with the changing field and loss values are lower. As the temperature reduces, however, CPA relaxation time (tCPA) of a material increases due to higher viscosity. Thus, when the relaxation time (tCPA) is on the same order as the alternating field time period (tCPA = T), dipoles rotate and align with orientation lagging the field (polarity change at T/2 while relaxation occurs at tCPA) and energy is dissipated as heat. Hence the loss is maximum, and a distinct peak of dielectric loss is observed. At even lower temperatures, the mobility of molecules reduces drastically as the viscosity of CPAs increases exponentially32. Therefore, relaxation time is much longer than the period of the alternating field. Subsequently, no perturbation/energy loss occurs (i.e. dielectric loss decreases to diminishing values) as field is varying too rapidly (polarity changes for dipoles to rotate and align after overcoming intermolecular forces). Also note that this behavior depends on the specific intermolecular interactions within a mixture.

Higher operating frequencies result in shorter periods of an alternating EM field. Hence, the peak value of dielectric loss shifts towards higher temperatures at higher frequencies (i.e., moves from left to right in Fig. 1). As relaxation times of dipolar molecules in CPAs become shorter at higher temperatures due to lower viscosity, it is the same order as the time period of applied alternating field, thereby producing the highest loss peak. Past measurements of CPA dielectric properties and tissues permeated with CPAs are listed in Table 1. These are limited to single component CPAs and in frequency range. To our knowledge, the dielectric properties of contemporary CPA mixtures such as VS55, M22, and DP6 that are showing promise for organ vitrification, are unavailable in literature.

Here we measured dielectric constant (ε’) and dielectric loss factor (ε”) for a range of frequencies (200 MHz − 3 GHz) and temperatures (− 40 to 20 °C). In this paper the dielectric loss factor was also referred to as dielectric loss. We further investigated the effects of individual CPA components, binary mixtures of CPA1 + CPA2, and CPA + water, to try to begin to understand the effective behavior observed in CPA mixtures. Lastly, these measured dielectric properties can be used to evaluate their impact on dielectric heating power (∝ σ = ωεoε” σ: effective electrical conductivity, ω: frequency, εo: permittivity of free space, and ε″: effective dielectric loss) in the MHz - GHz range and on “thermal runaway” where an undesirable positive feedback cycle allows one portion of the system to rewarm faster than others due to increasing dielectric loss as a function of temperature. Furthermore, these dielectric loss values were used to indirectly estimate eddy current heating (∝ σ = ωεoε”) in relevant frequency and temperature ranges to evaluate uniformity of heating during nanowarming. This would allow design and assessment of CPAs for safe rapid and uniform EM rewarming of vitrified large-scale biomaterials, such as organs.

Table 1 Literature summary of prior dielectric property measurement of CPAs and biological tissues in a wide frequency and temperature range relevant for cryopreservation applications (arranged by year).
Full size table

Results

Probe field penetration depth and literature validation

We first calculated penetration depth of RF fields for our open-ended coaxial probe using COMSOL. A depth of ~ 1 mm was found, where the electric field falls to 1/e (~ 37%) of its maximum value as shown in Fig. S2. As expected, the field decays in a radial direction and propagates into the materials under test (MUT) in the z direction. The model used water, which has the smallest dielectric loss of components studied. Therefore, its relative absorption should be the lowest and its penetration depth the largest. Hence, our analysis gives an upper limit (largest) of possible penetration depth as shown in Fig. S2 ~ 0.8 mm at 0.2 GHz. As operating frequency increases, penetration depth will reduce as expected (∝ 1/f). Therefore, the OECP probe was submerged inside the CPA liquid sample at least ~ 5 mm deep (~ 6x penetration depth) to ensure accurate bulk penetration of EM waves into sample. Furthermore, CPA sample depth was chosen as ~ 7x times (~ 37 mm) the submerged depth of probe (~ 5 mm) to ensure an infinite surrounding for EM waves.

The OECP probe measurement values were compared to literature for water and two CPAs: glycerol and DMSO. Good agreement was observed. Measurements of 85% glycerol at room temperature (20°C) produced dielectric constant (ε’) and loss (ε”) values of ~ 20.6 and 16.9, respectively, at 0.98 GHz, and 13.4 and 12.3, respectively, at 2 GHz. These results agree well with ε’ and ε″ literature values of 21 and 17, respectively at 0.98 GHz and of 14 and 12, respectively at 2.02 GHz at 20 °C reported in40. Water dielectric constant (ε’) and loss (ε”) (at room temperature 20 °C) measured were ~ 79 and ~ 0.8 at 0.2 GHz and ~ 78 and ~ 10 at 3 GHz, respectively, which agrees with literature values of ~ 78 and ~ < 1 at 0.2 GHz46,47 and ~ 78 and ~ 13 at 3 GHz46,47,48.

Dielectric behavior for binary CPA water mixtures

First, we measured dielectric constant and loss for binary aqueous CPA mixtures as a function of frequency to understand the effect of components in a CPA mixture. This was performed at room temperature to simplify the comparison. We used 2D heat color maps to visualize the effect of two parameters on dielectric loss: (1) frequency and CPA concentration or (2) frequency and temperature. It was observed that DMSO-water mixtures showed unique non-linear behavior with mixture’s loss values and are higher than the individual component (i.e., 100% DMSO and 100% pure water) as plotted in Fig. 2a. Figure 2b shows the loss response at one representative frequency (2 GHz) versus concentration for DMSO. The red region in heat map plot in Fig. 2a shows the intermediate concentration/mole fraction of DMSO, where the maximum dielectric loss is highest compared to other combinations tested. PG water mixtures also showed a similar non-linear behavior with mixture values higher than individual components as plotted in Fig. 2c. Formamide mixtures, on the other hand, showed simple linear behavior with dielectric loss values within the bounds of pure water and 100% formamide (evident in Fig. 2d).

Fig. 2
figure 2

Heat map plot showing the dielectric loss of binary (a) DMSO + water mixture for the complete frequency range at room temperature (20 °C). (b) Dielectric loss as a function of DMSO mole fraction at a representative frequency of 2 GHz. Heat map plot showing dielectric loss of (c) formamide + water, and (d) PG + water mixtures for the complete frequency range at room temperature (20 °C).

Full size image

Furthermore, binary mixtures of two CPA components such as DMSO + PG and DMSO + Ethanol were studied. It was revealed that a roughly 80:20 (%v/v) mixture of DMSO to PG or ethanol produces the highest dielectric loss (ε”) in the range of 15–17, (the yellow region in Fig. 3a, b). Note that the dielectric constant of all the binary mixtures i.e. CPA + water and CPA + CPA can be found in supplementary Fig. S3 and S4 respectively.

Fig. 3
figure 3

Heat map plot showing the dielectric loss for binary CPA + CPA mixtures (a) DMSO + PG, (b) DMSO + Ethanol for the complete frequency range at room temperature (20 °C). Concentration (%v/v) is listed on bottom and top for each component.

Full size image

Dielectric behavior for CPA cocktail mixtures: VS55, DP6 & M22

Insights from the binary mixture behavior were used to inform our investigation of common organ vitrification CPA cocktail mixtures, namely, M22, VS55 and DP6. Here we aim to understand the contribution of individual components in the effective behavior of the CPA cocktail mixtures. Dielectric properties of individual CPA components were first measured. In general, the dielectric constant (ε’) for all CPAs decreased with an increase in frequency (Fig. 4a) with formamide having the largest drop from ~ 108 to ~ 77. For the most part of frequency range (i.e. 1 to 3 GHz), formamide seemed to have the highest ε” (22 to 46) and PG exhibited the lowest (5–10). In DMSO, loss increased continuously as frequency increases, whereas in PG and EG losses increased to a maximum and then decreased as can be seen in Fig. 4a. Dielectric loss of carrier solutions, such as LM5, decreased from ~ 50 to ~ 10 over the analyzed frequency range of 0.2 to 3 GHz (Fig. 4b). EC loss decreased significantly from 80 to ~ 20 from 0.2 to 1 GHz and then reduced slowly to ~ 14 as frequency increases from 1 to 3 GHz (Fig. 4b). For cocktail mixtures- VS55, DP6 and M22, ε’ decreased with increase in frequency (Fig. 4a) whereas ε” changes only slightly (Fig. 4b).

Fig. 4
figure 4

(a) Dielectric constant, and (b) loss for all the three CPA cocktail mixtures along with individual components at room temperature (20 °C). Note the minimum plotted frequency is 0.2 GHz.

Full size image
Fig. 5
figure 5

Heat map color plots of measured dielectric constant for CPAs: (a) VS55, (b) DP6 and (c) M22 and dielectric loss for CPAs: (d) VS55, (e) DP6 and (f) M22 as function of complete frequency and temperature range measured. Dielectric constant and loss for all the 3 CPA cocktail mixtures M22, VS55, DP6 as function of subzero temperatures at two representative frequencies (g,i) ~ 200 MHz, (h,j) 2 GHz.

Full size image

Figure 5 shows the dielectric behavior of CPA cocktail mixtures (M22, VS55, DP6) in the complete range of frequency and temperature measured. Among all the CPAs, VS55 exhibited the highest dielectric constant (~ 96) followed by M22 (~ 80) and then DP6 (~ 70) in the measured frequency and temperature range (Fig. 5a–c). At the lower end of frequency (~ 0.2 GHz), dielectric constant first increased and then decreased as temperature falls down to subzero range as observed in Fig. 5g. Whereas at the higher end of frequency (~ 2 GHz), dielectric constant decreased continuously for all the CPA cocktails as temperature is lowered from 20 °C to subzero (Fig. 5h). The dielectric loss peak (seen in red in Fig. 5d) moved toward lower temperatures at lower frequencies. Interestingly, all the CPA cocktail mixtures i.e. M22, DP6, VS55 showed a similar dielectric loss trend at room temperature throughout the analyzed frequency range (0.2 to 3 GHz) as seen in Fig. 4. In Fig. 5j, a peak dielectric loss factor occurred at near 0 °C for all CPA cocktail mixtures. This peak shifted to lower temperatures when frequency was reduced though peak was not visible as it was <− 40 °C (Fig. 5i). Hence, at very low frequencies (kHz to few MHz) the dielectric loss peak shifted to even lower/cryogenic temperatures, which has been observed in past studies as well40,43. Note that VS55 showed the highest dielectric loss value (peak ~ 39) when compared to M22 (peak ~ 33) and DP6 (peak ~ 32) in the whole measured frequency and temperature range.

Discussion

Dielectric loss behavior of a CPA mixture tends to be higher than that of its individual components. This has been previously observed for DMSO-water aqueous mixtures49 as well as DMSO-alcohol mixtures50. Interestingly, it was also observed that dielectric rotational relaxation time peaked at an intermediate mole fraction (~ 0.33) of DMSO. Our observations are similar for DMSO water mixtures as seen in Fig. 2b. This increase in relaxation time could be due to hydrogen-bonding between DMSO and water molecules. As the DMSO mole fraction increases, the number of hydrogen (H) bonds among water molecules decrease, whereas the relative number of H-bonds between DMSO and water molecules increase because DMSO-water H-bonds may be potentially stronger and have longer lifetime49,51. It can be conceived that dipole-dipole interactions among these DMSO mixtures would affect the rotational dielectric relaxation in CPA solutions. DMSO molecules seem to reduce the potential barrier for dipole reorientation in a mixture solution due to spatial steric constraints. Another study52 on static dielectric constant and relaxation time for DMSO binary mixtures such as DMSO-ethanol, DMSO-propan-1-ol reported that solute-solvent interactions in a mixture govern the relaxation time behavior. Therefore, CPAs with DMSO rich mixtures may show this increase in dielectric loss at intermediate molar fractions (or concentrations) of DMSO, dominating the mixture dielectric behavior. Our measurements of peak dielectric loss values (~ 30 for M22 & DP6, ~ 40 for VS55- Fig. 5d, e) were higher than that of peak values for glycerol (~ 20)40 or alcohols (~ 5–10)50 in the 1–3 GHz range. These measured peak loss values for VS55, M22 and DP6 were closer to 50%DMSO (30–40) and 55%EG (~ 30)40. Therefore, it showed that these CPA cocktail mixture values should be used for more accurate EM rewarming calculations.

Note that dielectric loss shows a typical peak with temperature (inverted U-curve, Fig. 1, and 5e) because the relaxation heat losses are maximum where the relaxation time τ (governed by physical state and viscosity) is equal to the time of applied alternating electric field (1/fp). As the temperature is lowered to the cryogenic range, the viscosity of CPA solutions increases exponentially. This would imply excessively longer relaxation times (to resist molecular viscous forces) and therefore, negligible dielectric loss values due to lack of mobility of polar molecules in glassy solid-like state. This would be most apparent in the vitrified state, where molecular motion would effectively be arrested. So, while dielectric heating has been shown to provide rapid rewarming at temperatures range between − 100 and 20 °C, rewarming is expected to be negligible at lower temperatures nearing the glass transition16,20,40.

Design of effective dielectric rewarming procedures will also need to be balanced especially at subzero temperatures (above its melt temperature) to control ionic heating and avoid thermal runaway39. Since dielectric loss is a function of temperature, the warming rate will also vary with temperature at a constant electric field amplitude. For a CPA sample with an inverted U-shape for dielectric loss, as the sample is heated from cryogenic temperatures (e.g., from − 100 °C) dielectric loss (and warming rate) will increase until the peak and then falls as the temperature approaches zero degrees (after the peak). This can translate into an inverted U- shape warming rate curve when the electric field is kept constant. However, the most common way to avoid this temperature dependency (or non-uniformity) of the warming rate is by applying constant power which causes electric field amplitude in a resonator to rise (or fall) if the dielectric loss is decreasing (or increasing) in order to obey conservation of energy. If the resonator heating efficiency is high, then the sample warming rate will track the applied power independent of sample temperature or dielectric loss. It is to be noted that for a given applied power going into a sample, and warming rate of the sample, if the dielectric loss decreases to very low values (example in cryogenic temperatures near Tg) then the resulting electric field must become very high to maintain a constant warming rate in which case applied power may not translate proportionally to the heat generation inside the sample. This limits the temperature range over which dielectric warming is practical, especially at a fixed frequency (See supplementary section on dielectric rewarming rate dependence, Eq. S1-S5). Another possible way to eliminate warming rate temperature dependence could be by doing a frequency sweep from lower to higher values (e.g., 27 MHz to 2.5 GHz in case of 50%DMSO43) during warming from ~− 100 °C to ~ 0 °C to maintain constant dielectric loss values. This could provide more uniform (temperature-independent) heating because dielectric loss peak value shifts to larger frequencies at higher temperatures (Fig. 1). On the other hand, spatial non-uniformity in dielectric rewarming would still be a challenge because of shorter penetration depths at higher frequencies and uneven CPA (hence polar molecules) distribution inside tissue, which is itself inhomogeneous. Note that a frequency sweep to achieve constant temperature independent dielectric rewarming can also lead to spatial non-uniformity as frequency is raised to higher values because of shortening penetration/skin depths.

These guidelines will also inform the design of CPAs and their carrier solutions for nanowarming, for which unwanted eddy heating should be minimized (requires lower dielectric loss and electrical conductivity), as well as dielectric rewarming, which requires larger dielectric loss with peak loss at lower subzero temperatures. For nanowarming which operates in 100s of kHz frequencies, a first-order estimate of the eddy heating produced by the induced electric field (see supplementary section on eddy current heating, and Table S2) suggest the impact will be very small (~ 0.9 °C/min) when compared to nanowarming rates (50–100 s of °C/min) at cryogenic temperatures i.e. temperatures well below the melting point of CPAs since the dielectric loss (including dc conductivity) diminishes to negligible values at cryogenic temperatures nearing and below Tg (glass transition) where there is threat of cracking due to non-uniformity.

Lastly, our measurements of CPAs were limited to subzero (~− 40 °C) temperatures and can be directly relevant for evaluating dielectric heating in cryopreservation applications such as supercooling and partial freezing where cryopreserved samples are heated from these subzero temperature ranges ~>− 6 °C and ~>− 15 °C respectively. For example, one can choose the CPA whose loss is highest and frequency at which loss is more or less constant in the temperature ranges such as − 6 to ~ 20 °C for supercooling and − 15 to ~ 4 °C for partial freezing.

Future work should investigate not only the CPA dielectric properties in further lower temperatures (< -40 °C) relevant for EM rewarming from vitrified state but also electrical properties for tissues and organs perfused with CPAs, which can be directly correlated to a cryopreservation protocol.

Conclusion

This study investigated dielectric properties of common organ vitrification CPA solutions (M22, DP6, VS55) and their components. All three CPAs seemed to have similar magnitude of dielectric loss with decreasing loss at subzero temperatures for higher frequencies (~ 2 to 3 GHz) and increasing loss at subzero temperatures for lower frequencies (~ 0.3 to ~ 2 GHz). For CPA mixtures, dielectric loss can be higher than its individual component loss values due to effects such as polar molecules H-bonding arranges. Formamide seemed to be the highest lossy component over other CPAs. It should be included in a CPA design for dielectric rewarming but could be omitted for nanowarming where the intent is minimizing direct EM rewarming. Overall, the temperature heat map plots provide a firsthand guide for choosing the best frequency and CPA for subzero rewarming of cryopreserved biomaterials (such as partial freezing, supercooling). Future work should investigate dielectric properties of CPAs at cryogenic temperatures (<− 40 °C to − 150 °C) for rewarming of vitrified organs.

Materials and methods

Coaxial probe description

An open-ended coaxial probe (OECP) (i.e., Keysight 85070E high temperature probe, Keysight Technologies, CA, USA) was used to determine the dielectric properties of CPAs. The OECP guided-wave method is useful for characterizing a liquid, biological specimen or semi-solids material53,54,55 and is classified as reflectometric method56. It offers high accuracy, a stable platform, and noninvasive measurement of the electrical properties of materials over a wide band of frequencies57,58.

In supplementary Fig. S2, the CPA measurement setup is shown. A calibration method is used to establish a measurement reference plane between the probe aperture plane and CPA using air and DI water. The CPA volume is ~ 10 ml for our study of materials under test (MUT). The dielectric property is represented by relative permittivity εr = εr’-j ε” where εr’ is the relative dielectric constant and εr” is the relative dielectric loss factor. To determine the relative permittivity, the measured reflection coefficient from OECP needs to be transformed. The reflection coefficient loss value \(\:{\Gamma\:}\)is the complex value. The translation of reflection loss to relative permittivity uses the rational function method (RFM), suitable for materials with high loss tangent (> 0.5)59,60,61. RFM offers improved accuracy (εr’ = εr’ + 0.05|εr|, εr” = εr” + 0.05|εr|) and allows the uncertainties in dielectric measurements to be quantified.

The relationship between reflection loss and relative permittivity, as described in62, is

$$\:{\varepsilon\:}_{r}^{{\prime\:}}=\frac{-2\left|{\Gamma\:}\right|\text{s}\text{i}\text{n}{\upphi\:}}{\omega\:{{Z}_{0}C}_{0}(1+2\left[{\Gamma\:}\right]\text{c}\text{o}\text{s}{\upphi\:}+{\left|{\Gamma\:}\right|}^{2})}-\frac{{C}_{f}}{{C}_{0}}$$
(1)
$$\:{\varepsilon\:}_{r}^{{\prime\:}{\prime\:}}=\frac{1-{\left|{\Gamma\:}\right|}^{2}}{\omega\:{{Z}_{0}C}_{0}(1+2\left|{\Gamma\:}\right|\text{c}\text{o}\text{s}{\upphi\:}+{\left|{\Gamma\:}\right|}^{2})}\:$$
(2)

where \(\:{\upphi\:}\) is the phase, \(\:{C}_{0}\) is the capacitance, \(\:{C}_{f}\) is fringing capacitance of the probe, which was determined by the calibration of water and air, and \(\:{\varepsilon\:}_{r}\) is the relative permittivity of MUT.

CPA Preparation

Individual CPA components include dimethyl sulfoxide (DMSO), ethylene glycol (EG), propylene glycol (PG), ethanol and formamide, which were bought from Sigma Aldrich (St. Louis, MO). CPA binary mixtures were prepared using graduated cylinders based on volume ratios (%v/v), later converted to mole fraction. Preparation of CPA cocktail mixtures was performed based on components and composition listed in literature for M2263, DP664 and VS559. Carrier solutions used were Euro-Collins (EC) for VS55, DP6 and LM5 for M22. These carrier solutions were also tested as individual components of CPA cocktail mixtures.

COMSOL modeling

Finite element analysis (FEM) was performed using the RF module in COMSOL Multiphysics Software v5.4. Figure S2 illustrates the modeled geometry. It includes the CPA sample volume and coaxial probe. The wave equation was solved numerically to find spatial distribution of the electric field generated by the OECP in the sample for the 1–3 GHz frequency range. Probe aperture diameter was estimated as 3.5 mm. The boundary conditions and initial conditions are listed in supplementary Table S1. A lumped coaxial port was used as the input to the coaxial probe with 1.78 V (15dB) voltage for 50-ohm impedance and a 90° port phase. Material properties were chosen from COMSOL default options for steel and glass in the probe and water for sample.

Dielectric measurement setup at room temperature and subzero temperatures

The measurement setup included various components such as vector network analyzer (VNA), open-ended coaxial probe (OECP), control rate freezer (CRF), laptop, thermometer and the sample CPA subjected to various temperatures. Figure S1 describes the permittivity measurement sequence steps. The VNA measures signals from one port only to obtain the reflection coefficient of the liquid-MUT in the frequency range from 0.2 to 3 GHz after performing an one-port calibration with deionized water.

Ten ml of CPA was measured in a beaker with the coaxial probe immersed (~ 5 mm) into the sample as shown in Fig. S1. A T-type thermocouple (Omega Engineering, Norwalk, CT) was placed at the interface of the probe and sample to monitor and measure temperature. Both probe and sample setup were placed inside the control rate freezer (CRF) (Planar Kryo 560-II, Middlesex, UK). The chamber was cooled at the fastest rate (40°C/min), and samples were equilibrated for 10 minutes at subzero measurement temperatures (DP6, M22: 20, 10, 0, − 10, − 20, − 30°C; VS55: 25, 10, 0, − 10, − 20, − 30, − 38°C) before measuring the reflection coefficient with the VNA. The reflection coefficient was then transformed to relative dielectric properties εr’ and εr″ as described earlier. Note that our measurement temperature range was limited by the commercial probe (Keysight 85070e) recommended temperature (> − 40 °C). All the plots were created using GraphPad Prism. A total of n = 3 repeats were performed for all the room temperature measurements of CPAs whereas only n = 1 for subzero temperature measurements. The probe was validated with water and air before the start of each experiment.