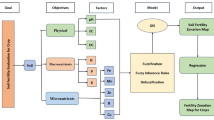
Abstract
Expansive soil spatial variability plays a key role in the over- and under-application of fertilizers, contributing to environmental pollution. Assess soil variability and delineate it into management zones to adopt site-specific nutrient management for balanced fertilization and sustainable agriculture. To assess spatial variability by geostatistical methods and delineate and evaluate nutrient management zones for site-specific nutrient management and variable rate fertilizer application using fuzzy c-means clustering. Overall, 200 soil samples (0–15 cm depth) with geographical coordinates were collected with a grid size of 14.2 m × 14.2 m from a 4-ha maize cultivated 4-ha of Mahagoan village of Bhainsa Mandal, Nirmal district, Telangana, India. The collected samples were tested with different reagents to determine the soil reaction and available nutrient status. Soil spatial variability was assessed by the geostatistical method, and delineation of nutrient management zones was carried out by integrating principal component analysis and fuzzy c-means clustering. Geostatistical analysis revealed spherical (pH, electrical conductivity, organic carbon, available sulfur, and available Zn) and Gaussian (available nitrogen, available P2O5, available K2O, available Fe, available Zn, and available Cu) as the best-fit semivariogram model with strong spatial dependence. Five management zones were delineated by principal component analysis and fuzzy c-means clustering based on fuzzy performance index (FPI) and normalized classification entropy (NCE) indices. Variable rates of fertilizer recommendations in different management zones were calculated using a soil test crop response equation. The results show the highest grain yield and fertilizer saving in MZ−5, followed by MZ−4, MZ−3, MZ−2, and MZ−1, compared to farmer fertilizer practices. The study aims to delineate the management zone to reduce fertilizer application, ensure balanced fertilizer application, minimize environmental pollution, and increase crop grain yield and profitability.
Similar content being viewed by others
Introduction
The hot and dry semi-arid climate poses significant challenges to sustainable crop production due to high variability in physical and chemical properties of soil and even in soil fertility by complex interaction among geology, topography, climate, and land use practices1. Irregular rainfall pattern in terms of intensity and distribution exacerbates negative plant-nutrient balances in many cropping systems and hinders sustainable crop production in semi-arid climatic regions. Persistent land degradation in the semi-arid areas has compromised the sustainability of many existing cropping systems over the long term2. Typically, soil in the semi-arid areas is low in organic matter, highly susceptible to degradation, and subject to mechanical deterioration. Nutrient use efficiency (NUE) in semi-arid areas is generally less than 25%, and the response to the applied fertilizer is poor and inconsistent3. A Precise nutrient management approach is essential and crucial to address this limitation. The targeted fertilizer application based on soil need substantially improves nutrient use efficiency, which increases crop grain production4. Therefore, effective methods should be developed to assess soil spatial variability to delineate uniform fertility zones for efficient nutrient management5. The management zones (MZs) approach emphasizes dividing a field-bounded area into smaller, homogeneous zones. These zones represent portions of land with similar characteristics, such as nutrient levels. However, accurately identifying management zones remains challenging due to the highly complex relationships among the various factors that influence crop productivity. Furthermore, demonstrating the coexistence of multiple influencing variables within a given approach may make subfield-level management assessments particularly difficult6,7,8.
The spatial and temporal variability in soil properties limits crop productivity within agricultural areas. Typically, this heterogeneity is neglected in soil sampling time, laboratory analysis, and agronomic management practices. As a result, soil-specific recommendations within the paradigm of precision agriculture can present a valuable opportunity in soil management9,10. Recently developed advanced technology can measure and map soil properties precisely at a spatial scale. The introduction of novel spatial technology in precision agriculture allows farmers to gather data from different farm regions to facilitate specific differential management11,12. Soil nutrient mapping is adopted to monitor soil fertility status, evaluate fertilizer treatments, and recommend agronomical management practices. Today, site-specific nutrient management (SSNM) approach is needed to recommend fertilizer based on soil demand and need by understanding spatial and temporal variability in soil properties. Geospatial tools and techniques have been adopted to delineate management zones for site-specific nutrient management. Delineation of MZs is possible with geospatial tools, principal component analysis, and fuzzy clustering algorithms. Some conventional methods used to delineate MZs include soil nutrient mapping, slope percent, yield mapping, and nutrient indexing approaches4,13,14.
Over the last two decades, soil scientists have widely used geostatistical analysis to determine spatial variability in soil properties across both small and large geographical scales15,16. Geostatistical analysis is used to model, predict, and interpret the spatial variability of soil properties. The semivariogram is a core concept in geostatistical analysis that measures the degree of spatial dependence between paired observations based on the distance separating them17,18. Some clustering techniques have been widely adopted to classify continuous spatial variability into different clusters for delineation of management zones. Among these, the fuzzy C mean (FCM) clustering algorithm is most widely used for delineation of management zones for better understanding and management of spatial variability in soil properties18,19,20.
In precision agriculture (PA), land areas are classified into different homogeneous management zones using the fuzzy C-means clustering algorithm. This algorithm assigns a fuzzy membership value to each data point based on a membership function, allowing observations to be classified into multiple clusters with varying degrees of association1,21,22.
Distinguishing the individual effect of soil properties on soil quality is often difficult, making it challenging to delineate the boundaries between management zones clearly. To address this complexity, advanced analytical techniques such as principal component analysis (PCA) and fuzzy C-means (FCM) clustering analysis have been widely adopted to delineate management zones. PCA reduces data dimensionality by identifying the principal components (PCs) that account for most variance within the dataset, thereby highlighting the most influential soil variable23,24. These PCs are further used as input for fuzzy cluster analysis, which is the most effective method for spatial autocorrelation and delineation of management zones. This integrated approach improves the accuracy of delineation of management zones (MZs) by condensing most correlated soil variables into fewer components. Consequently, the accuracy of delineation of management zones using PCA and the FCM clustering approach can be assessed by the difference in grain yield across zones. This study underscores the utility of combining PCA and FCM techniques for identifying MZs in precision agriculture based on spatially correlated soil data12,13,25.
Spatial heterogeneity typically influences field management decisions regarding soil properties. The high degree of soil variability in soil characteristics at one location spatially changes over time. Therefore, there is a need for reliable recommendations for management-based zones. In light of the foregoing, this current investigation served to (1) assess the temporal variation in soil properties by geostatistics, (2) delineate MZs by principal component analysis (PCA) & fuzzy C mean (FCM) clustering, & (3) evaluate delineated management zones (MZs) for vil in Telangana’s Northern area.
Materials and methods
Study area
This study was conducted at a farmer’s field located in Mahagoan village, Bhainsa Mandal, Nirmal district, in northern Telangana, India (latitude 19.18424 N to 19.18244 N and Longitude 77.96867 E to 77.96959 E) (Fig. 1). A total area of four hectares under maize cultivation was selected for soil sampling. The site lies within the Deccan Plateau agro-climatic zone and is classified as a hot, moist, semi-arid ecological subregion, characterized by a growing period of 120 to 150 days. The region experiences a predominantly dry climate, with hot summers and cool winters. Average annual rainfall ranges from 867 mm to 1189 mm, of which approximately 86% occurs during the southwest monsoon (June to September), while the remaining is received from the northeast monsoon (December to January)26. Maximum temperatures during the pre-monsoon period (March to early June) range from 31 °C to 39 °C, whereas minimum temperatures during winter (December to February) range from 14 °C to 25 °C. The dominant soil type is deep black soil, which is calcareous, fine-textured, and neutral to strongly alkaline. It has a medium to strong subangular blocky structure with irregular aggregates. According to Soil Taxonomy, these soils are classified as hyperthermic, udic Chromusterts, characterized by very fine montmorillonitic clay27. The prevailing cropping system in the region is cotton–maize. The recommended fertilizer application rates are 150 kg N ha⁻¹, 60 kg P₂O₅ ha⁻¹, and 60 kg K₂O ha⁻¹ for kharif cotton, and 250 kg N ha⁻¹, 40 kg P₂O₅ ha⁻¹, and 40 kg K₂O ha⁻¹ for rabi maize. Groundwater serves as the primary source of irrigation for this cropping system.
Collection and analysis of soil
A total of 200 composite topsoil samples (0–15 cm) were collected in 2020 on a 14.2 m × 14.2 m sampling grid using a handheld GPS unit (Garmin eTrex) (Fig. 2). The samples were air-dried, thoroughly mixed, and gently crushed with a wooden mallet before passing through a 2 mm sieve. The < 2 mm fraction was stored in polyethylene bags for laboratory analysis; a sub-sample was further ground to < 0.2 mm for organic-carbon determinations. Soil pH and electrical conductivity (EC) were measured potentiometrically and conductometrically, respectively28. Soil organic carbon (SOC) was determined by the Walkley–Black wet-digestion method29. Available nitrogen (N) was estimated with the alkaline KMnO₄ method30. Available phosphorus (P₂O₅) was extracted with 0.5 M NaHCO₃ at pH 8.531; available potassium (K₂O) with 1 N NH₄OAc32. Available sulphur (S) was measured turbidimetrically33. Micronutrients (Fe, Mn, Zn, Cu) were extracted with 0.005 M DTPA34.
Statistical analysis
The studied soil properties were subjected to a descriptive statistical analysis, which included minimum, maximum, mean, standard deviation (SD), coefficient of variation (CV), skewness, and kurtosis. Pearson’s correlation coefficient was used to evaluate the relationships among the soil parameters. All statistical analyses were performed using XLSTAT software (version 2020).
Geostatistical analysis
Geostatistical analyses were performed using ArcGIS 10.8 software, developed by Environmental Systems Research Institute (ESRI), to assess soil spatiotemporal variability35. Prior to geostatistical analysis, a normality test was conducted to verify whether the soil data followed a normal distribution. The quantile–quantile (Q-Q) plot technique was employed for this purpose. In geostatistics, the spatial distribution of soil variables is represented by the semivariogram, which measures the degree of similarity between data points separated by distance h (Fig. 3). The semivariogram \(\:\widehat{\gamma\:}\left(h\right)\) for soil properties was calculated using Eq. 317:
where N(h) represents the number of data pairs at a specified distance and direction, \(\:Z\left({\text{x}}_{\left(\text{i}\right)}\right)\) denotes the value of the variable at position \(\:{\text{x}}_{\left(\text{i}\right)}\), \(\:Z{({x}_{\left(i\right)}+h)}^{}\) denotes the value of the variable at a distance of h from a position \(\:{\text{x}}_{\left(\text{i}\right)}\). The above semivariogram equation fits the standard model and calculates the spatial variation parameters: nugget, sill, and range. Semivariogram models, such as spherical, exponential, and Gaussian, were selected based on cross-validation indices like root mean square error (RMSE) to explain the spatial correlation of soil parameters. A preferred model was then applied using an ordinary kriging (OK) technique for interpolation and spatial mapping of predicted soil properties data (Fig. 3).
The root mean square error was used as a comparison criterion to evaluate the predictive accuracy of semivariogram model, as calculated using Eq. 4:
Where, Z(Xi) represents the observed value at position \(\:{x}_{\left(i\right)},\) \(\:\stackrel{-}{Z}\left({x}_{\left(i\right)}\right)\:\)denotes the predicted value at position \(\:{x}_{\left(i\right)}\:\)and N is the total number of data points.
Principal component analysis
PCA is a multidimensional technique that extracts the underlying structure of a dataset by identifying components that explain the most variance (Fig. 4). The data were transformed by rotating the coordinate system along its principal axes to allocate the variance into distinct components. This analytical method emphasizes capturing the highest variation in the first principal component, with decreasing variance in subsequent components. In place of a correlation matrix, a covariance matrix was used for PCA better to reflect the relationships among the selected soil parameters. All soil variables were considered as inputs for PCA. Principal components with eigenvalues greater than or equal to one were retained for further analysis in delineating MZs. The loading values of each soil property on the principal components were analyzed to interpret the contribution and variability of each variable across components.
Fuzzy cluster algorithm analysis
There are many unsupervised machine learning methods used to group similar data points, such as Fuzzy C-Means (FCM), K-Means Clustering, Gaussian Mixture Models (GMM), and DBSCAN (Density-Based Spatial Clustering of Applications with Noise). In this study, the FCM clustering algorithm was selected for delineating management zones due to its ability to handle the inherent uncertainty and gradual transition in soil characteristics, which is a typical feature of agricultural fields. Unlike hard clustering algorithms such as K-means, which assign each data point to a single cluster, FCM allows each data point to belong to multiple clusters with varying degrees of membership. This soft partitioning is particularly suitable for spatial data in soil science, where boundaries between soil zones are rarely distinct. Moreover, FCM is computationally efficient and integrates seamlessly with PCA to reduce dimensionality and multicollinearity, which is essential when dealing with multiple soil attributes. While Gaussian Mixture Models (GMMs) are probabilistic and flexible, they assume normal distribution and are sensitive to initialization, which may lead to convergence issues in heterogeneous soil datasets. Similarly, DBSCAN is effective for detecting clusters of arbitrary shape but struggles with datasets of varying density and is highly sensitive to parameter selection. Therefore, the FCM algorithm was preferred as it balances robustness and interpretability for delineating management zones, especially when combined with PCA to enhance spatial classification accuracy in precision agriculture.
The FCM clustering approach is applied to develop distinct homogeneous management zones. It’s a modified form of cluster analysis. This algorithm assigns a fuzzy membership value to each data point based on a membership function, classifying observations into multiple clusters with varying degrees of association. This approach mitigates the impact of outliers and captures the inherent fuzziness in the dataset. In this study, the number of clusters varied from a minimum of three to a maximum of eight to identify the optimal number of MZs. The algorithm was initialized with randomly assigned cluster centers. Each data point was then assigned a membership grade based on its proximity to the cluster centers. These centers were subsequently updated iteratively using weighted means, recalculated from the membership grades. The Euclidean distance metric assessed the similarity between data points and cluster centers, assuming equal variance and statistical independence across variables. MZA software was used for the task, with the following parameters set: maximum number of iterations = 300, halting criteria = 0.0001, minimum and maximum number of clusters 3 & 8, respectively, and fuzziness component = 1.5. The optimal number of clusters was determined based on the FPI and NCE, calculated using Eqs. 3 and 4, respectively.
.
where c is the number of clusters, n is the number of observations, µik is the fuzzy membership degree of point i in cluster k, and loga is the natural logarithm.
The FPI evaluates the degree of fuzziness a given number of clusters introduces. Its values range from 0 to 1, where values close to 0 indicate well-defined clusters with minimal membership overlap, while values approaching 1 imply indistinct clustering with significant membership sharing among clusters. The NCE quantifies the level of disorder or uncertainty associated with a specific number of clusters. The optimal number of MZs is indicated by the lowest values of both FPI and NCE (Fig. 5). A one-way analysis of variance (ANOVA) was conducted on soil parameters across the different MZs using SPSS software to evaluate statistical differences. Finally, a management zone delineation map was generated using ArcGIS 10.8 software.
Results and discussion
Descriptive statistics of soil parameters
The descriptive statistics of the soil parameters are presented in Table 1. The study site exhibits moderate to strongly alkaline conditions, as indicated by the pH range of 8.26–8.79, and a low coefficient of variation (CV) of 1.57%. Previous studies have also reported minimal variation in soil pH compared to other soil parameters36,37,38,39,40,41,42,43. The alkaline nature of the soil is attributed to its development from basic parent material27,44. The low variability in soil pH can be explained by the logarithmic nature of the pH scale, which reflects hydrogen ion concentration; direct measurement of proton concentration would show greater variability. Moreover, the buffering capacity of soils generally resists abrupt changes in pH, even under diverse agricultural systems and management practices in the region Electrical conductivity (EC) also exhibited low variability, as reflected by a CV of 16.33%, and low skewness (−0.14) and kurtosis (−0.95). This low variation is likely due to using non-saline groundwater for irrigation. Soils with EC values below 2 dS m⁻¹ are classified as non-saline and have been similarly reported in various parts of Telangana45,46,47,48,49.
The average soil organic carbon (SOC) content in the study area was found to be 3.3 g kg⁻¹, which is considered low, with a range from 2.3 to 4.2 g kg⁻¹. These findings are consistent with those reported in various districts of Telangana and other parts of India, where SOC levels have also been found to be low, with average values around 5 g kg⁻¹49.
The soil organic carbon in the area may be attributed to lower organic manure application, and the farmers in that area barely retain crop residues1,50,51. The CV values of SOC, available nitrogen, available P2O5, and available K2O were low (CV of < 25%), anging from 12.90% to17.52%. Tis indicates minimum heterogeneity and uniform distribution of these soil properties across the study area15,52,53,54. Available nitrogen varied from 81 to 161 kg N ha−1 with a mean value of 127 kg N ha−1. The low variability and nitrogen content are accounted for by the leaching of dissolved organic nutrients and inorganic nitrogen43. Similar patterns have been found in different parts of India with low available nitrogen content in soil, particularly in areas with minimal organic matter and poor nutrient management practices41,42,54. The available P2O5 and K2O content were high, varying from 98 to 159 kg ha−1 and 292 kg ha−1– 647 kg ha−1 with a mean of 128 kg ha−1 and 426 kg ha−1, respectively, which was mainly because of the production of recalcitrant Ca–P compounds and fixing of potassium in a soil environment. Similar trends in the increase of phosphorus and potassium content in soil have been found in other studies47,49,55.The prolonged consumption of P fertilizer might cause a high level of phosphorus in the soil without testing the soil56. Another reason for the increase of phosphorus content in the rhizosphere was the fixation of P with Ca57.
Previous studies have reported high levels of available K₂O ranging from 406 to 572 kg ha⁻¹ in various districts of Telangana State58. The elevated potassium levels may be attributed to several factors, including the mineralization of potassium from organic residues, the release of potassium from non-exchangeable sites in 2:1 type clay minerals, the weathering of primary minerals, excessive application of potassic fertilizers, and the upward movement of potassium from deeper soil layers due to capillary rise of groundwater.
The variability of available Sulphur was moderate, with a CV value of 45.20%. Previous studies have reported a moderate coefficient of variability, i.e., between 25 and 75%, which represented moderate heterogeneity in available Sulphur content in the soil59. The available sulfur content was low to high, varying from 4 mg kg−1 − 27 mg kg−1, with a mean value of 14.0 mg kg−1. According to Wilding’s classification, the distribution of micronutrients Fe, Mn, Zn, Cu, and B exhibits moderate variability in the area based on CV > 25–75%. Ths region’s mean values of Fe, Mn, Zn, and Cu were 29.2, 21.0, 7.8, and 7.6 mg kg−1, respectively, indicating high micronutrient status (Fe, Mn, Zn, and Cu) in the Warangal soil of Telangana state58. Soil management activities, such as fertilizer application and other crop management techniques, may be to responsible for the observed differences in soil properties across study regions60. The spatial heterogeneity of crop production may be attributed to the fact that the uniform application of nutrients led to a variable amount of nutrients in terms of quantity at different locations within the studied region.
Geostatistical analysis
Table 2 presents the parameters of the best-fitting semivariogram models for soil characteristics. Three models, i.e., Spherical, Exponential, and Gaussian, were observed as strongly fitted to the analyzed soil parameters based on minimum RMSE value. Other researchers employed similar procedures to identify the best model for interpolation using kriging42,61,62. Figure 6(a-k) illustrate the spatial distribution maps of various soil parameters. The best-fitted model for soil pH, EC, SOC, available sulfur, and Zn was the spherical semivariogram model (Fig. 7. (a, b, c, g and j). In contrast, the Gaussian semivariogram model was the best-fitting model for available nitrogen, P2O5, available K2O, Fe, Mn, and Cu (Figs. 7. (d, e, f, h, I and k)). The best-fit semivariogram models for different soil parameters represent whether human activities and local factors affect the spatiotemporal variation of soil attributes41,63,64. The nugget value denotes the microvariability and variance measurement resulting from sampling errors43. The nugget value denotes micro-variability and potential measurement errors or sampling inaccuracies. In this study, the nugget values for all soil parameters were nearly zero, suggesting minimal measurement error and strong spatial continuity. The sill represents the semivariance level at which the semivariogram flattens, theoretically equating to the total variance of the dataset at large lag distances65,66. The lowest sill value was observed for pH (0.0000732), while the highest was recorded for iron (Fe) (9.4136). Spatial dependence was assessed using the nugget-to-sill ratio, classified into three categories: strong (< 0.25), moderate (0.25–0.75), and weak (> 0.75)35,67. These classifications provide insight into the degree of spatial structure in the observed soil properties.
The observed variability in soil nutrient concentrations may be attributed to farmers’ improper or inconsistent fertilizer application in the study area41. In geostatistical analysis, the range parameter defines the distance the semivariance reaches the sill, indicating the extent of spatial dependence for a particular soil property42. This range reflects the maximum distance over which two samples are spatially correlated. A shorter distance between sampling points generally corresponds to more similar soil characteristics41. In this study, the range of spatial dependence for soil parameters varied between 28 and 61 m. According to Moharana et al.41the range also represents the radius of influence or area of impact for a given soil property, providing insights into the scale at which management practices might be effectively applied. Maps depicting the spatial distribution of all soil parameters are shown in Figs. 6(a-k). Heterogeneous management and fertilizer application mostly led to high levels of all soil nutrients except Zn in the southeast, east, and south, and low levels in the north and northwest direction. The concentration of pH, EC, available nitrogen, available P2O5, available K2O, available sulfur, Fe, Mn, and Cu increased from northeast to southeast, north to south, and west to east. Zn had the opposite distribution pattern. Its contents decrease from northeast to southeast, north to south, and west to east. This was most likely brought by the parent material, irrigation, fertilizer use, and crop planting. The quantitative data derived from such mappings are sometimes utilized to alter site-specific nutrient management (SSNM) and introduce variable rate technology (VRT) for long-term sustainability. The soil fertility location maps could serve as a tool to develop an SSNM plan for maximizing agricultural production while reducing adverse effects on the ecosystem and cost of cultivation.
(a) Spatial distribution map of pH, (b) Spatial distribution map of EC, (c) Spatial distribution map of organic carbon, (d) Spatial distribution map of available N, (e) Spatial distribution map of available P2O5, (f) Spatial distribution map of available K2O, (g) Spatial distribution map of available S, (h) Spatial distribution map of available Fe, (i) Spatial distribution map of available Mn, (j) Spatial distribution map of available Zn, (k) Spatial distribution map of available Cu.
(a) Best fitted semivariogram model of pH, (b) Best fitted semivariogram model of EC, (c) Best fitted semivariogram model of organic carbon, (d) Best fitted semivariogram model of available N, (e) Best fitted semivariogram model of available P2O5, (f) Best fitted semivariogram model of available K2O, (g) Best fitted semivariogram model of available S, (h) Best fitted semivariogram model of available Fe, (i) Spatial distribution ma Best fitted semivariogram model of available Mn, (j) Best fitted semivariogram model of available Zn, (k) Best fitted semivariogram model of available Cu.
Principal components analysis
A correlation analysis of the soil variables revealed significant relationships among the measured parameters, as shown in Table 3. To reduce data complexity and identify the underlying structure of variability, Principal Component Analysis (PCA) was employed. PCA helps in transforming a large set of correlated variables into a smaller number of uncorrelated variables known as Principal Components (PCs). This study generated eleven PCs, corresponding to the number of independent variables analyzed (Table 4). Of these, the first five PCs, each having an eigenvalue greater than 1, were retained for further interpretation based on Kaiser’s criterion, as they collectively accounted for 100% of the total variance in the data set. A principal component with an eigenvalue > 1 explains more variation than any original variable. Tables 4 and 5 illustrate the results of the component. PC1 accounted for 96.9% of total variability, whereas available K2O, N, EC, available P2O5, available S, Mn, OC, Cu, Fe, Zn and pH dominated it. available P2O5, available S and available K2O were the dominant factors for PC2 and accounted 1.8% of the variability. PC3 contributed 0.8% of the variance, whereas it was dominated by pH, available N, and EC. The PC4 accounted for 0.3% of the variance and was mostly influenced by the Fe, cu, and available S. The PC5 accounted for 0.2% of the variance and was dominated by Mn. The PC6 accounted for 0.09% of the variance and was mostly influenced by the available S. PC7 accounted for 0.01% of the variance and was mostly influenced by the available Zn.
Several studies have found three PCs from PCA by aggregating and summarizing the variability of soil properties in different regions of India38,59,64. Other studies have reported the four PCs from PCA by aggregating and summarizing the variability of soil properties in different regions such as Nigeria, north Iran, and east India36,43,68. Additionally some research found 12 PCs, whereas five PCs explained 78.66% of the vaiability that occurred in the study area69.
Clustering analysis for delineating management zones
The seven principal components (PCs) were used to delineate MZs through cluster analysis. To determine the optimal number of MZs, the FCM clustering algorithm was applied to the PC scores using MZA software. This approach facilitates classifying areas with similar soil characteristics and distinct variability. The FPI and NCE were calculated and plotted against varying cluster numbers (Fig. 8). The optimal number of MZs was determined based on the lowest values of both FPI and NCE, indicating the most suitable clustering solution.
As can be seen in Fig. 8, the optimal number of management zones for this study was determined to be six, but six management zones were statistically insignificant. Therefore, five management zones (MZs) were selected for evaluation. Previous studies have reported four management zones, indicating the heterogeneity of soil properties in MZs due to soil types, soil, and nutrient management practices37,38,40,41,64,70. The management zone map (Fig. 9) was developed using ArcGIS 10.3.1 software. Several studies have shown that the analysis of variance is a useful tool for determining the differences between zones. Therefore, a one-way ANOVA was conducted to assess the efficiency of PCA and fuzzy c-means cluster method in defining MZs and their spatial variability.
The variability in soil parameters between management zones was clarified via findings (Table 6). Means of pH, EC, organic carbon, and available nutrients between MZs exist statistically distinct at P < 0.01 (Table 6). Management zone 4 occupied the largest sampling site region (30%), then MZ−3 (28%). MZ−5 (24%), MZ-2 (12%) and MZ−1 (6%). The highest value of soil variables except Zn was recorded in MZ- 5, and the lowest value except Zn was recorded in Management Zone−1. The maximum value of Zn was in MZ −1, whereas the lowest value was in MZ-5. A significant variation in soil parameters between the five management zones is due to the soil type, soil & nutrient management practices59. The zonation approach may benefit the scientific management of nutrients efficiently and effectively. The geospatial assessment revealed spatial variability in the fertility status of sampling sites. Therefore, farmers and other stakeholders might utilize knowledge about MZs for site-specific nutrient management.
Fertilizer recommendation strategies
The wide spatial variability in soil properties, resulting from diverse production techniques, underscores the importance of SSNM practices. SSNM enables the recommendation of precise fertilizer quantities tailored to the nutrient status of specific land parcels, thereby enhancing nutrient use efficiency. In India, where small and fragmented farm holdings dominate agricultural landscapes, implementing field-specific fertilizer schedules poses significant challenges. One viable solution is to cluster farms with similar soil fertility characteristics into uniform MZs, which can then be treated as single units for nutrient management purposes.
To address this, Professor Jayashankar Telangana State Agricultural University (PJTSAU) has developed targeted yield equations for crop- and soil-specific fertilizer recommendations. For maize cultivation, the required NPK doses to achieve a target yield of 70 quintals per hectare are calculated using the Soil Test Crop Response (STCR) equations, as presented in Eq. 5.:
It is possible to connect these equations with the MZs map by utilizing the soil tests results to determine precise fertilizer doses. The amount of fertilizer saved within each of the five MZs in maize production was quantified (Table 7). Among the five management zones, the highest quantity of fertilizer was saved in MZ −5 (up to 42 kg N ha−1, 85 kg P2O5 ha−1 and 28 kg K2O ha−1) compared to farmer fertilizer practices, followed by MZ −4 (up to 36 kg N ha−1, 79 kg P2O5 ha−1 and 25 kg K2O ha−1), MZ −3 (up to 32 kg N ha−1, 74 kg P2O5 ha−1 and 23 kg K2O ha−1), MZ−2 (up to 28 kg N ha−1, 71 kg P2O5 ha−1 and 21 kg K2O ha−1) and MZ −1 (up to 21 kg N ha−1, 66 kg P2O5 ha−1 and 18 kg K2O ha−1). Previous studies have saved 40–46 kg ha−1 nitrogenous fertilizer, 13–15 kg ha−1 phosphorus fertilizer, and 6–12 kg ha−1 potassic fertilizer in rice crops after adopting management zone approach41. The amounts of fertilizer needed to produce the targeted yield of maize @ 70 q ha−1 in MZ−1, MZ−2, MZ−3, MZ−4, and MZ-5 were 280:34:82, 272:29:79, 268:26:77, 264:21:75, and 258:15:72 NPK kg ha−1, respectively. The variation of fertilizer doses between management zones was based on the relative fertility of each management zone. Owing to soil fertility differences amongst the five management zones, MZ−1 received the largest fertilizer dosage due to its low fertility status, while MZ−5 received the lowest dose due to its high fertility status (Table 7). Table 8 shows the effects of fertilizer application in various management zones on maize grain production, cultivation costs, gross return, net return, and the B: C ratio. Overall, MZ −5 had the highest grain yield and B: C ratio, whereas MZ −1 had the lowest. Since less fertilizer was applied to MZ-5, its grain yield and B: C ratio were higher than those of MZ-2, MZ-1, and farmer fertilization practices (Table 8). Previous studies have reported the highest grain yield in maize with the soil test crop response (STCR) based fertilizer recommendation compared to farmer fertilizer practices due to the proper allocation of fertilizer71,72,73,74,75. Based on the results of this research, it seems that SSNM greatly decreases nutrient quantity in similar environments & production systems. As a result, the MZ approach could decrease the need for fertilizer in agriculture, reduce the damage caused to the environment, and boost farmer earnings. Aggregation of the dataset into a number of clusters, as is done by clustering method, which decreases the level of variability within each cluster and offers certain facts to make location-wise fertilizer application, with the ultimate goal of optimizing grain yield over a whole area41.
Conclusion
This study demonstrates that delineating agricultural land into homogeneous MZs using geostatistical analysis, PCA, and FCM clustering is an effective strategy to address spatial variability in soil properties. The spatial heterogeneity of eleven soil parameters was successfully modeled using spherical, exponential, and Gaussian semivariogram models, indicating strong spatial dependence across the study area. Based on these models, five distinct management zones were identified. Integrating Soil Test Crop Response (STCR) equations with MZ maps enabled more precise fertilizer recommendations. Compared to conventional farmer fertilizer practices, this approach significantly reduced the need for NPK fertilizer requirements, enhanced maize grain yield, and enhanced overall profitability. Implementing site-specific SSNM through management zones also offers environmental advantages by reducing nutrient losses and lowering the risk of pollution.
While this study focused on a single crop (maize), the approach demonstrates a scalable framework that can be adapted to other regions and cropping systems with appropriate calibration. Although temporal variability was not the primary focus, the strong spatial correlations identified provide a solid foundation for future research incorporating seasonal dynamics. Moreover, applying advanced geostatistical and clustering techniques has shown high potential for delineating meaningful management zones. Building on this, future studies can expand the validation through long-term trials to further reinforce the robustness and applicability of the methodology across diverse agro-ecological conditions. In conclusion, this study enhances the utility of precision agriculture tools for sustainable nutrient management. Future work should validate these management zones across different crops, years, and broader agroecological zones to fully harness their agronomic and environmental benefits.
Data availability
Data available upon request to the first author (vaibhavsoil39@gmail.com).
References
Venugopal, A. et al. Nutrient variability mapping and demarcating management zones by employing fuzzy clustering in Southern coastal region of Tamil nadu, India. Sustainability (Switzerland) 16, 1–12 (2024).
Jinger, D. et al. Degraded land rehabilitation through agroforestry in India: Achievements, current understanding, and future prospectives. Frontiers in Ecology and Evolution vol. 11 Preprint at (2023). https://doi.org/10.3389/fevo.2023.1088796
Singh, S. K., Kumar, M., Sharma, B. K. & Tarafdar, J. C. Depletion of organic carbon, phosphorus, and potassium stock under a Pearl millet based cropping system in the arid region of India. Arid Land. Res. Manage. 21, 119–131 (2007).
Chatterjee, S. et al. Characterization of field-scale soil variation using a Stepwise multi-sensor fusion approach and a cost-benefit analysis. Catena (Amst) 201, 1–18 (2021).
Peralta, N. R. & Costa, J. L. Delineation of management zones with soil apparent electrical conductivity to improve nutrient management. Comput. Electron. Agric. 99, 218–226 (2013).
Ramzan, S. et al. Management zone delineation and Spatial distribution of micronutrients in cold-arid region of India. Environ Monit. Assess 193, 1–16 (2021).
Wang, N. et al. Delineation and optimization of cotton farmland management zone based on time series of soil-crop properties at landscape scale in South xinjiang, China. Soil Tillage Res 231, 1–17 (2023).
Zeraatpisheh, M. et al. Spatial variability of soil quality within management zones: homogeneity and purity of delineated zones. Catena (Amst) 209, 1–14 (2022).
Futa, B., Gmitrowicz-Iwan, J., Skersienė, A., Šlepetienė, A. & Parašotas, I. Innovative Soil Management Strategies for Sustainable Agriculture. Sustainability (Switzerland) vol. 16 Preprint at (2024). https://doi.org/10.3390/su16219481
Sharma, M., Goel, S. & Elias, A. A. Predictive modeling of soil profiles for precision agriculture: a case study in safflower cultivation environments. Sci Rep 15, 1–15 (2025).
Bullock, D. S., Kitchen, N. & Bullock, D. G. Multidisciplinary teams: A necessity for research in precision agriculture systems. Crop Sci. 47, 1765–1769 (2007).
Shukla, A. K. et al. PCA and fuzzy clustering-based delineation of soil nutrient (S, B, zn, mn, fe, and Cu) management zones of sub-tropical Northeastern India for precision nutrient management. J. Environ. Manage. 365, 121511 (2024).
Kumar, P., Sharma, M., Butail, N. P., Shukla, A. K. & Kumar, P. Spatial variability of soil properties and delineation of management zones for Suketi basin, Himachal himalaya, India. Environ. Dev. Sustain. 26, 14113–14138 (2023).
Shashikumar, B. N., Kumar, S., George, K. J. & Singh, A. K. Soil variability mapping and delineation of site-specific management zones using fuzzy clustering analysis in a Mid-Himalayan watershed, India. Environ. Dev. Sustain. 25, 8539–8559 (2023).
Wickramasingha, W. S. B. & Weerasinghe, V. P. A. The Spatial variability of physicochemical parameters of Mangrove soil and Mangrove species in Negombo lagoon, Sri Lanka. Environ. Nanotechnol Monit. Manag. 21, 100944 (2024).
Chatterjee, S. et al. Geostatistical approach for management of soil nutrients with special emphasis on different forms of potassium considering their Spatial variation in intensive cropping system of West bengal, India. Environ. Monit. Assess. 187, 183 (2015).
Goovaerts, P. Geostatistical tools for characterizing the Spatial variability of Microbiological and physico-chemical soil properties. Biol. Fertil. Soils. 27, 315–334 (1998).
Muniammal Vediappan, D., Godi, A. & Golla, B. Geospatial mapping of soil properties of forest types using the k-Means fuzzy clustering approach to delineate Site-Specific nutrient management zones in goa, India. J. Indian Soc. Remote Sens. https://doi.org/10.1007/s12524-024-02082-y (2025).
Guastaferro, F. et al. A comparison of different algorithms for the delineation of management zones. Precis Agric. 11, 600–620 (2010).
Zihad, S. M. R. et al. Fuzzy logic, geostatistics, and multiple linear models to evaluate irrigation metrics and their influencing factors in a drought-prone agricultural region. Environ. Res. 234, 116509 (2023).
Bezdek, J. C. Pattern Recognition with Fuzzy Objective Function Algorithms (Springer US, 1981). https://doi.org/10.1007/978-1-4757-0450-1Boston, MA.
Yuan, Y. et al. Delineating soil nutrient management zones based on optimal sampling interval in medium- and small-scale intensive farming systems. Precis Agric. 23, 538–558 (2022).
Zeraatpisheh, M. et al. Spatial variability of soil quality within management zones: homogeneity and purity of delineated zones. Catena (Amst). 209, 105835 (2022).
Salem, H. M. et al. Evaluating Intra-Field Spatial variability for nutrient management zone delineation through Geospatial techniques and multivariate analysis. Sustainability 16, 645 (2024).
Neupane, J. et al. Spatial and Temporal patterns of cotton profitability in management zones based on soil properties and topography. Precis Agric. 25, 2140–2163 (2024).
Professor Jayashankar Telangana State Agricultural University. PJTSAU - Crop of Telanagna. PJTSAU. (2021).
Kumar, T. V., Suryanarayan Reddy, M. & Gopalakrishna, V. Characteristics and Classification of Soils of Northern Telangana ’Zone of Andhra Pradesh. Agropedology 4, (1994).
Rathje. Jackson, M. L. & Cliffs, E. Soil chemical analysis. Verlag: Prentice Hall, Inc., NJ. 498 S. DM 39.40. Zeitschrift für Pflanzenernährung, Düngung, Bodenkunde 85, 251–252 (1959). (1958).
Walkley, A., Black, I. A. & An examination of the degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil. Sci. 37, 29–38 (1934).
Subbiah, B. V. & Asija, G. L. A rapid procedure for the Estimation of available nitrogen in soils. Curr. Sci. 25, 259–260 (1956).
Olsen, S. R., Cole, C. V. & Watanabe, F. S. Estimation of Available Phosphorus in Soils by Extraction with Sodium Bicarbonate. USDA Circular No. 939, US Government Printing Office, Washington DC.
Hanway, J. J. & Heidal, H. Soil analysis methods as used in Iowa state college soil testing laboratory. Iowa State Coll. Agric. Bull. 57, 1–31 (1952).
Chesnin, L. & Yien, C. H. Turbidimetric determination of available sulfates. Soil Sci. Soc. Am. J. 15, 149–151 (1951).
Lindsay, W. L. & Norvell, W. A. Development of a DTPA soil test for zinc, iron, manganese, and copper. Soil Sci. Soc. Am. J. 42, 421–428 (1978).
Webster, R. & Oliver, M. A. Geostatistics for Environmental Scientists (Wiley, 2007). https://doi.org/10.1002/9780470517277
Aliyu, K. T. et al. Delineation of soil fertility management zones for Site-specific nutrient management in the maize belt region of Nigeria. Sustainability 12, 9010 (2020).
Amer, B. S., Moussa, K. F., Sheha, A. A. & Fattah, M. K. A.-. Delineation of site-specific management zones using multivariate analysis and geographic information system technique. Plant Arch 21, 1–10 (2021).
Davatgar, N., Neishabouri, M. R. & Sepaskhah, A. R. Delineation of site specific nutrient management zones for a paddy cultivated area based on soil fertility using fuzzy clustering. Geoderma 173–174, 111–118 (2012).
Gorai, T. et al. Site specific nutrient management of an intensively cultivated farm using Geostatistical approach. Proc. Natl. Acad. Sci. India Sect. B: Biol. Sci. 87, 477–488 (2017).
Jena, R. K. et al. Geospatial modelling for delineation of crop management zones using local terrain attributes and soil properties. Remote Sens. (Basel). 14, 2101 (2022).
Moharana, P. C. et al. Geostatistical and fuzzy clustering approach for delineation of site-specific management zones and yield-limiting factors in irrigated hot arid environment of India. Precis Agric. 21, 426–448 (2020).
Reza, S. K., Nayak, D. C., Mukhopadhyay, S., Chattopadhyay, T. & Singh, S. K. Characterizing Spatial variability of soil properties in alluvial soils of India using geostatistics and geographical information system. Arch. Agron. Soil. Sci. 63, 1489–1498 (2017).
Verma, R. R., Srivastava, T. K., Singh, P., Manjunath, B. L. & Kumar, A. Spatial mapping of soil properties in Konkan region of India experiencing anthropogenic onslaught. PLoS One. 16, e0247177 (2021).
Alnaimy, M., Elrys, A., Zelenakova, M., Pietrucha-Urbanik, K. & Merwad, A. R. The vital roles of parent material in driving soil substrates and heavy metals availability in arid alkaline regions: A case study from Egypt. Water (Basel). 15, 2481 (2023).
Naik Malavath, R., Gech, V. & Mahesh, C. C. Genesis, classification and evaluation of some sugarcane growing black soils in semi arid tropical region of Telangana. ~ 81 ~ J. Pharmacognosy Phytochemistry 7, 1–10 (2018).
Narsaiah, E., Ramprakash, T., Chandinipatnaik, M., Reddy, D. V. & Raj, G. B. Classification and characterization of soils of Eturunagaram division of Warangal district in Telangana state. Int. J. Curr. Microbiol. Appl. Sci. 7, 582–594 (2018).
Ramulu, C. & Kamalakar, J. Soil fertility status and correlation of available macro and micronutrients in Warangal district of Telangana state. Int. J. Environ. Clim. Change. 119–126. https://doi.org/10.9734/ijecc/2022/v12i121446 (2022).
Shalini, V., Krishna Chaithanya, A., Aruna Kumari, C., Chandrashaker, K. & The Pharma Innovation Journal ; 11(5): 607–612 Depth wise Physico-chemical properties of soils under different cropping systems in Inceptisols and Vertisols of Northern Telangana Zone. The Pharma Innovation Journal 11, 607–612 (2022). (2022).
Vilakar, K. et al. Soil fertility status of Sesame growing soils of Northern Telangana zone. ~ 267 ~ Pharma Innov. J. 10, 267–271 (2021).
Nogiya, M. et al. Spatial variability of soil variables using Geostatistical approaches in the hot arid region of India. Environ. Earth Sci. 83, 432 (2024).
Tripathi, R. et al. Delineation of soil management zones for a rice cultivated area in Eastern India using fuzzy clustering. Catena (Amst). 133, 128–136 (2015).
Belay, A. M., Selassie, Y. G., Tsegaye, E. A., Meshaeshe, D. T. & Addis, H. K. Spatial analysis of some soil chemical properties of the Amhara region in Ethiopia. Arab. J. Geosci. 17, 205 (2024).
Qinghuo, L. et al. Sampling size requirements to delineate Spatial variability of soil properties for Site-Specific nutrient management in rubber tree plantations. J. Resour. Ecol. 10, 441 (2019).
Tagore, G. S., Bairagi, G. D., Sharma, R. & Verma, P. K. Spatial variability of soil nutrients using Geospatial techniques: A case study in soils of Sanwer tehsil of Indore district of Madhya Pradesh. Int. Archives Photogrammetry Remote Sens. Spat. Inform. Sci. XL–8, 1353–1363 (2014).
Himabindu, R., Kumar, S., Anjaiah, T., Naaiik, R. B. & Shashikala, T. Soil fertility status of forage growing soils of Suryapet district, Telangana. ~ 4624 ~ Pharma Innov. J. 11, 4624–4631 (2022).
Sathish, A. et al. Assessment of Spatial variability in fertility status and nutrient recommendation in Alanatha cluster villages, Ramanagara district, Karnataka using GIS. J. Indian Soc. Soil Sci. 66, 149 (2018).
MALAVATH, R. & MANI, S. Nutrients status in the surface and subsurface soils of dryland agricultural research station at chettinad in Sivaganga district of Tamil Nadu. ASIAN J. SOIL. Sci. 9, 169–175 (2014).
Ramulu, C. H., Raghu, P. & Reddy, R. Soil fertility status of regional agricultural research station, Warangal (Telangana). ~ 1852 ~ J. Pharmacognosy Phytochemistry. 7, 1852–1856 (2018).
Behera, S. K., Mathur, R. K., Shukla, A. K., Suresh, K. & Prakash, C. Spatial variability of soil properties and delineation of soil management zones of oil palm plantations grown in a hot and humid tropical region of Southern India. Catena (Amst). 165, 251–259 (2018).
Shukla, A. K. et al. Spatial distribution and management zones for sulphur and micronutrients in Shiwalik Himalayan region of India. Land. Degrad. Dev. 28, 959–969 (2017).
Verma, R. R. et al. Soil mapping and delineation of management zones in the < scp > western ghats of coastal < scp > india. Land. Degrad. Dev. 29, 4313–4322 (2018).
Pal, S., Panwar, P. & Bhatt, V. K. Evaluation of Spatial variability of soil properties based on Geostatistical analysis:acase study in lower shivaliks. Indian J. Soil. Conserv. 38, 178–183 (2010).
BEHERA, S. K. et al. Distribution variability of soil properties of oil palm (Elaeis guineensis) plantations in Southern plateau of India. Indian J. Agricultural Sci. 85, 1170–1174 (2015).
Rahul, T. et al. Assessing soil Spatial variability and delineating site-specific management zones for a coastal saline land in Eastern India. Arch. Agron. Soil. Sci. 65, 1775–1787 (2019).
Benedito, M. et al. Spatial variability of soil physical properties in archeological dark earths under different uses in Southern Amazon. Soil. Tillage Res. 182, 103–111 (2018).
Mulla, D. J. Modeling and Mapping Soil Spatial and Temporal Variability. in Hydropedology 637–664Elsevier, (2012). https://doi.org/10.1016/B978-0-12-386941-8.00020-4
Cambardella, C. A. et al. Field-Scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 58, 1501–1511 (1994).
Khaledian, Y., Kiani, F., Ebrahimi, S., Brevik, E. C. & Aitkenhead-Peterson, J. Assessment and monitoring of soil degradation during land use change using multivariate analysis. Land. Degrad. Dev. 28, 128–141 (2017).
Zeraatpisheh, M., Ayoubi, S., Sulieman, M. & Rodrigo-Comino, J. Determining the Spatial distribution of soil properties using the environmental covariates and multivariate statistical analysis: a case study in semi-arid regions of Iran. J. Arid Land. 11, 551–566 (2019).
Xin-Zhong, W. et al. Determination of management zones for a tobacco field based on soil fertility. Comput. Electron. Agric. 65, 168–175 (2009).
Giri, Y. Y., Reddy, D. R. & Balaguravaiah, D. Soil test based fertilizer nitrogen recommendations for yield targets of Kharif maize under Alfisols. Int. J. Pharm. Chem. Biol. Sci. 2, 270–274 (2015).
Madhavi, A., Srijaya, T., Babu, P. S. & Dey, P. Popularization of STCR targeted yield for optimum fertilizer use and enhanced yields of maize crop through field level demonstrations. Int. J. Curr. Microbiol. Appl. Sci. 9, 2209–2214 (2020).
Rajamani, K., Madhavi, A., Srijaya, T., Babu, P. S. & Dey, P. On-farm fertility management through target yield approach for sustenance of tribal farmers. Curr. J. Appl. Sci. Technol. 58–65. https://doi.org/10.9734/cjast/2020/v39i4331140 (2020).
SHREENIVAS, B. V., RAVI, M. V. & LATHA, H. S. Effect of targeted yield approaches on growth, yield, yield attributes and nutrient uptake in maize (Zea mays L.)-chickpea (Cicer arietinum L.) cropping sequence in UKP command area of Karnataka. ASIAN J. SOIL. Sci. 12, 143–150 (2017).
Suresh, R. & Santhi, R. Validation of soil test and yield target based fertiliser prescription model for hybrid maize on vertisol. Int. J. Curr. Microbiol. Appl. Sci. 7, 2131–2139 (2018).
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number ‘‘NBU-FFR-2025-1850-06.’’.This paper was supported by the RUDN University Strategic Academic Leadership Program.
Author information
Authors and Affiliations
Contributions
PVB: Conceptualization; methodology; software; validation, formal analysis; investigation. TA: Writing, reviewing, editing, and visualization. Chitteti Ravali: Writing, reviewing, editing, and visualization. DSC: writing, reviewing, editing, and visualization. ATZ: Writing, reviewing, editing; visualization, funding, and project management. SU: Writing, reviewing, editing, and visualization. NYR: Writing, reviewing, editing, and visualization. AT: Writing, reviewing, editing, and visualization.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bhagwan, P.V., Anjaiah, T., Ravali, C. et al. Delineation and evaluation of management zones for site-specific nutrient management using a geostatistical and fuzzy C mean cluster approach. Sci Rep 15, 20991 (2025). https://doi.org/10.1038/s41598-025-07283-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-07283-0