Introduction

Coalbed methane (CBM) is a high-quality clean energy resource associated with coal1,2,3, and it is also a major cause of mine gas disasters4,5. In China, CBM development has dual attributes of energy exploitation and gas disaster prevention, achieving the coupling construction of carbon emission reduction targets and mine safety systems. Enhancing coal permeability is the key to efficiently extracting CBM6,7,8,9,10, and common CBM extraction techniques include hydraulic parting, hole perforation, slotting, and deep-hole blasting11,12,13,14,15. However, these measures have certain limitations in improving permeability16. For example, hydraulic parting with vertical advancement is suitable for well-structured coal seams, but its productivity enhancement is poor in loose and low-strength coal seams. This is mainly due to crack development and water leakage during parting, which can lead to cavity collapse and fail to form complete fluid channels17,18,19,20,21. Surface water jet radial well drilling technology uses high-pressure water jets to erode rock for drilling, enabling the creation of multiple radial tree-like horizontal branch holes in one or more vertical wells, ultimately forming a fracture network in the coal seam22– 23 to enhance permeability and achieve CBM extraction. Therefore, the generation of a fracture network is crucial for efficient CBM development.

Over the past few decades, many researchers have been dedicated to revealing the mechanism of water jet rock-breaking using theoretical frameworks, numerical simulations, and experimental results. For rock masses with different mechanical properties, jet parameters (velocity, water pressure, nozzle diameter, and incidence angle, etc.)24 and the stress state of the rock (unstressed state and triaxial stress state)25 will both influence the rock-breaking effect of water jets. In the early stages of water jet rock-breaking research, scholars primarily established theories such as the tensile-water wedge theory, dense core-splitting theory, stress wave theory, and cavitation corrosion theory26– 27. Subsequently, due to the widespread application of water jets in the oil and gas industry, more in-depth research was conducted on water jet rock-breaking technology. Lu et al.28 investigated the differences in rock damage morphology under different jet velocities, finding that rocks undergo three distinct damage modes depending on the jet velocity: circumferential cracks around the damage pit and within the coal body, radial cracks, and conical cracks. Additionally, as jet velocity increases, the macroscopic cracks on the sides transition from transverse cracks to splitting cracks. Xue et al.29 simulated the rock-breaking processes of water jets and abrasive water jets on coal, comparing the evolution rates of impact holes, damage field distributions, and jet flow stress states. They found that the expansion of impact holes induced by both jet types follows a cyclic damage pattern. Li et al.30 and Tripathideng et al.31 studied the rock-breaking performance of self-excited oscillating pulsed water jets, as well as the erosion resistance of rock samples under different jet pressures and confining pressures, comparing them with continuous water jets. Under the same jet conditions, the former outperformed the latter. Crack growth and the formation of the broken zone led to brittle failure and plastic behavior, respectively, with larger pulse amplitudes resulting in more severe rock damage. Huang et al.32 and Ge et al.33 utilized the SPH method and finite element coupling method to establish numerical models for the erosion of coal and rock, finding that gangue impedes the stress transmission and fissure development of water jets within coal and rock. These findings were validated through physical experiments.

Previous studies have predominantly focused on homogeneous coal or coal-rock composites, neglecting the inherent variability within the same coal seam or even the same working face, particularly for composite coal seams where mechanical strength characteristics are more complex. Traditional coalbed methane (CBM) extraction technologies are unable to provide effective hydraulic rock-breaking measures tailored to the characteristics of composite coal seams34. Therefore, to address the inherent complexities in CBM extraction within composite coal seams, it has become imperative to thoroughly investigate the complexity of stress wave propagation and fracture mechanisms during water jet impacts. This study begins by establishing a numerical model describing the effects of water jets on composite coal, followed by laboratory experiments to investigate the coal-breaking process under water jet impacts. Additionally, the influence of soft coal and hard coal interfaces on the impedance of compression waves was analyzed, and the fracture modes of soft and hard coal were compared. Consequently, the crack development patterns within composite coal seams were identified, providing a solid theoretical foundation for CBM extraction engineering in composite coal seams.

Methods

The hydrodynamics of smooth particles theory

To create the numerical model of the water-jet impacting composite coal, coal samples, and water-jet models were created using the smooth particle hydrodynamics (SPH) method. The method for meshless numerical simulation is based on difference theory, which can describe the rock boundary and material fracture comprehensively while overcoming the problem of mesh distortion35,36,37. In the problem area, discrete particles can successfully evade the element distortion-induced termination of non-linear calculations. Its kernel function is38– 39:

$$f(x) = \mathop \smallint \nolimits_{\Omega } f\left( {x^{\prime}} \right)W\left( {x - x^{\prime},h} \right)dx^{\prime}$$
(1)

In the context of this expression, f(x) represents the kernel approximation function, W(x-x’,h) stands for a meticulously crafted smooth kernel function, x-x’ denotes the inter-particle spacing, h signifies the smooth length associated with each particle, and Ω delineates the supportive domain of the smooth kernel function centered at x. The continuous formulation of Smoothed Particle Hydrodynamics (SPH) particles takes on an approximated discrete manifestation through the following integral representation.

$$f\left( {x_{i} } \right) = \mathop \sum \limits_{j}^{N} \frac{{m_{j} }}{{p_{j} }}f\left( {x_{j} } \right) \cdot W_{{ij}}$$
(2)
$${W_{ij}}=W\left( {{x_i} - {x_j},h} \right)$$
(3)

In the given context, f(xi) denotes the approximated value of the function at particle i, where mj stands for the mass of the particle j (j = 1, 2, 3, 4 …, n), and the variable N represents the cumulative count of particles encompassed by the supportive region of particle j. Formula (2) elucidates that the approximation of any function value at particle i can be achieved by averaging the function values associated with all particles within its supportive domain, through smooth kernel function.

Model of a water-jet

The material model designated for the water jet was identified as the NULL model, and the representation of the water jet’s pressure under conditions of high-speed impact was elucidated through the utilization of the Gruneisen equation of state, as given by40– 41:

$$P=\frac{{{\rho _0}{C^2}\mu \left[ {1+\left( {1 - \frac{{{\gamma _0}}}{2}} \right)\mu - \frac{a}{2}{\mu ^2}} \right]}}{{{{\left[ {1 - \left( {{S_1} - 1} \right)\mu - {S_2}\frac{{{\mu ^2}}}{{\mu +1}} - {S_3}\frac{{{\mu ^3}}}{{{{(\mu +1)}^2}}}} \right]}^2}}}+\left( {{\gamma _0}+a\mu } \right)E$$
(4)

In this context, the intercept of the velocity-dependent curve νs(νp) is denoted by C, the Gruneisen coefficient is represented by γ0, the first-order correction factor for γ0 is denoted by ɑ, the initial internal energy per unit volume is represented by Ε, and the slope coefficients of the velocity-dependent curve νs(νp) are indicated by S1, S2, and v. The specific values of the parameters constituting the water constitutive model can be found in Table 142.

Table 1 Parameters of the water constitutive model.
Full size table

Coal composite material model and fracture standard

Subject to the impact of a water jet, rocks with distinct characteristics will experience varying degrees of damage. Analyzing the mechanical properties of coal with diverse strengths under water-jet impact will involve the utilization of the Johnson-Holmquist-Concrete model. This choice is attributed to the model’s exceptional capacity to accurately depict coal stresses resulting from substantial deformation, heightened strain rate, increased hydrostatic pressure, and elevated overall pressure.

Typically, the fracture types of hydraulic impact rock materials are compression-shear or tensile failure. To scrutinize the stress distribution characteristics in regions of fractured and cracked coal under water-jet impact, the failure modes of coal during different temporal phases of water-jet impact were delineated using a dynamic fracture criterion, as given by:

$${\sigma _1} \geqslant \left[ {{\sigma _t}} \right],\quad {\tau _{\hbox{max} }} \geqslant [\tau ]$$
(5)

In this context, σ1 represents the maximum principal stress, τmax signifies the maximum shear strength of coal, [σt] denotes the dynamic tensile strength of the coal body, and [τ] represents its dynamic shear strength. The pertinent parameters associated with the Johnson-Holmquist-Concrete model are detailed in Table 2.

Table 2 Material parameters of coal.
Full size table

Model setting and verification

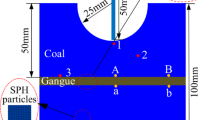
The impact of a water jet on coal is an example of a nonlinear dynamic process that involves a high value of strain rate. The LS-DYNA software for non-linear dynamic analysis has been successfully applied to a variety of non-linear problems, including blasting and impact scenarios. The models involved have not considered the influences of cracks, pores, and jet impact on the coal, and the coal is assumed to be a continuous, uniform, isotropic material. Figure. 1 depicts the impact model of a water jet that strikes soft and hard composite coal. The model’s coal body can be broadly categorized into two sections: the soft coal, which is in direct contact with the jet, and the hard coal, which maintains continuous contact with the soft coal medium at the lower end of the soft coal. Firstly, a composite coal model measuring 50 mm × 50 mm (w × h) was established. Subsequently, a water jet measuring 0.6 mm × 30 mm (w × h) was put in place. Finally, the coal was divided into 65,000 SPH particles, and the water jet into 750 SPH particles according to the different components. Coal of both hard and soft varieties has a consistent particle count and a 25 mm thickness. The water jet was designed to simulate a vertical impact with the coal body at a speed of 400 m/s, with a distance of 1 mm between the two.

Fig. 1
figure 1

Geometric model and boundary of composite coal body.

Full size image

The SPH method is the earliest meshless particle method43. For the SPH method, boundary setting is critical; because the initial setting of the model is a free boundary, to improve its accuracy, virtual particles with the same density, pressure, velocity, and the opposite direction as the internal particles were respectively arranged in the two sides and the lower end of the coal model, to meet the conditions of simulating rock in an infinite domain.

In this experiment, solely coal samples obtained from the No. 2 coal seam in the Jiulong Mine, Hebei Province, China, were utilized. This composite coal was composed of soft coal samples and hard coal samples of the same size (with soft coal at the upper end and hard coal at the lower end). The interface between soft coal and hard coal was bonded with marble glue with high bonding strength. After solidification reached a certain strength, the joints were polished and smoothed. The experimental samples are shown in Figure. 2.

Fig. 2
figure 2

Three kinds of coal rock samples.

Full size image

To validate the formulated model, by the rock sample size stipulated in ASTM D7012-201044, a standard cylindrical specimen of coal was prepared, measuring 50 mm × 50 mm, with upper and lower end faces exhibiting a flatness level not exceeding 0.02 mm. Subsequently, mechanical experiments were conducted to calibrate the chosen soft and hard composite coal samples. Table 3 provides a detailed breakdown of the physico-mechanical parameters for the three samples.

Table 3 Physico-mechanical parameters of coal samples.
Full size table

To substantiate the results of the simulations, experiments involving impact contrast were carried out on three distinct coal sample types(composite coal, hard coal, and soft coal) employing identical parameters. Figure 3 presents a schematic depiction of the experimental setup, consisting primarily of a high-voltage system and a test platform. The high-pressure water pump provides the high-pressure water jet, reaching a maximum pressure of 50 MPa. The 0.6 mm-diameter high-pressure nozzle is fixed to the three-axis moving table, while the 50 mm × 50 mm (width × height) coal specimen is securely held in place on the supporting table using a specialized clamp designed for rock samples. The control panel facilitates the precise modification of the coal sample’s distance from the impact target (nozzle). For the duration of the experiment, a consistent impact target distance of 10 mm was upheld.

Fig. 3
figure 3

Water jet impact experimental equipment.

Full size image

By comparing the three coal samples after the experiment, we were able to ascertain their fracture morphology when subjected to the same initial parameters. The results of the simulation and the tests are displayed in Fig. 4. The propagation of the crack is shown by the red portion of the simulation. At the outset of the water-jet effect on coal samples. At the early stage of water-jet impacting coal samples, the primary objective is to create a crushing pit and induce cracks through the combination of surge and stagnation pressures. For soft coal, when the jet touches the coal surface in the initial stage, the contact surface will be pressed to form a broken area under the action of the instantaneous shock wave. Then it will spread evenly in the internal area of coal due to a stress wave, which causes numerous macroscopic fissures within, and the overall volume of coal will be broken without the action of triaxial stress, in line with findings reported in the literature25. Following the water-jet impact on hard coal samples, a 23 mm wide erosion crater emerges on the impact surface (matching the simulated crater width), and numerous small circumferential cracks and large radial through-cracks appear on the coal’s top and sides. The coal’s mechanical strength and firmness play a significant role in this process, as they generate reflection of stress waves to form a high quasi-static pressure, which in turn causes the sample to crack. For composite coal, the crushing characteristics of water jets are different from those of soft coal and hard coal. Moreover, the composite coal experiences an uneven distribution of stress due to the reflection and attenuation of the stress wave on the contact surface, when the stress wave collides with the soft and hard coal contact surface. Since the majority of high-stress regions are situated in the upper portion of the soft and hard coal contact surface, cracks are present above the contact surface. Thus, only a small amount of stress waves propagates below the contact surface, which generates initial radial cracks and shear cracks in hard coal. In a word, there is concurrence between the experimental and simulated outcomes from the perspective of crack development.

Fig. 4
figure 4

Comparison of different coal samples impacted by water-jet.

Full size image

Results

Water-jet coal-breaking process

Intending to compare the crushing process of hard coal-soft coal-composite coal under water loading impact, Figure. 5 shows the dynamic evolution of the damage degree of coal samples with the impact time. When t = 0.005 ms and t = 0.016 ms, the three coal samples had similar forms of crushing, the initial crushing pit was mainly formed by the action of impact pressure, and then conical, transverse, and radial cracks began to form. However, the conical crack length of hard coal was larger than that of soft coal and composite coal. As the impact time continues, when t = 0.066 ms and t = 0.080 ms, the crack development among the three coal samples is different from one another. In the composite and soft coals, the conical crack opening angle was greater than in the hard coals when subjected to a constant water-jet pressure, and gradually expanded towards the free boundary. However, the cracks of hard coal mostly formed in the sample’s center, following the pattern of radial crack development (Figure. 4b). Besides, the contact surface of composite coal exhibited interface cracks, circumferential cracks, and radial cracks are observed to extend in both radial and circumferential directions from the top to the sides of the contact surface of the composite coal. Conversely, the contact surface exhibits a limited quantity of conical cracks. As the primary crack propagation adheres to the maximum energy criterion, circumferential and radial cracks discharged considerably less energy than contact surface crack propagation33. When t = 0.122 ms, the dimensions of the crater’s depth and width gradually increased due to the high-speed reflective flow formed on both sides of the coal during the water jet’s rapid impact on the coal. Simultaneously, as the stress wave exerted its influence, the fractures in both the soft and hard coals extended persistently toward the lower extremity of the coal sample. In contrast, the cracks in the composite coal ceased their progression in proximity to the contact surface. The interface cracks, however, exhibited ongoing development on either side. This observation implies that, in the context of composite coal seams featuring both soft and hard components, the impact load from the water jet primarily propagated along the interface, undergoing substantial attenuation. Meanwhile, the reflected wave caused by the contact surface led to severe fragmentation of the soft coal at the upper end, which can be confirmed by the test results in Figure.4c.

The crushing mechanism of coal

Different coal bodies have different strength and hardness coefficients, and there is a need to explore the crushing mechanism of different structural coal seams in order to facilitate the extraction of coalbed methane using a water jet. As far as the research object selected by the authors was concerned, the crushing modes of the three coal samples were quite different under the same jet parameters (Figure. 4). Therefore, the crushing modes of coal samples with different structures will be studied separately in the following sections.(Fig 5).

Fig. 5
figure 5

Simulation of soft coal hard coal composite coal water jet impact crushing process.

Full size image

Soft coal crushing mechanism

Integrating the findings from both laboratory experiments and simulations, it is evident that the water hammer pressure from the water jet has a consistent effect on the formation pattern of craters within the liquid-solid contact areas of the three coal samples. As the water hammer effect disappears, the stress wave induces a greater degree of particle damage at the base of the crushing crater, which ultimately results in the formation of initial cracks. In light of the coal samples’ comparatively low hardness coefficient, modulus of elasticity, and shear strength, partial or complete volumetric damage may result when the water jet’s shear strength surpasses the coal samples’ inherent tensile and shear capacities. As illustrated in Fig. 6, the initial cracks dominated by shear waves gradually expanded, and the formidable stress wave generated by the water jet surpassed the inherent strength of the coal enormously. Consequently, amidst the mutual interference of the initial compression wave and the low-energy base reflection wave, the tensile and compressive stresses generated inside the coal sample generated many macroscopic tensile cracks caused by the water-wedge effect in the whole specimen.

Fig. 6
figure 6

Crushing mechanism of soft coal under water-jet impact.

Full size image
Fig. 7
figure 7

Crushing mechanism of hard coal under water-jet impact.

Full size image

Hard coal crushing mechanism

The findings of the experiment indicate that the stress wave damage pattern and propagate pattern of hard coal under water-jet impact is slightly different from that of soft coal. For hard coals, due to their higher strength, lower brittleness, lower Poisson’s ratio (compared with soft coals), and bedding, reflected waves are easily observed on both sides of the coal samples, which leads to intact fractured pieces falling on the samples instead of large broken bodies. This is a characteristic not found in ordinary soft coals, indicating that the number of macroscopic cracks in coal examples is mainly governed by the rock’s mechanical characteristics when subjected to identical impact conditions (Fig. 4a,b). As described in Figure. 745, Following the high-speed impact of the water jet on the coal wall, a crater initially takes shape through the water hammer pressure within the compression concentration area. Subsequently, this pressure transpires into the application of stress in the form of shear waves and wall reflection waves, inducing the development of tensile cracks at the crater’s base. The hydrostatic pressure facilitates the secondary progression of cracks and amplifies the crack opening. Throughout the stage of stagnant pressure, primary cracks with larger openings advance toward the direction of the maximum tensile stress. This behavior is elucidated by the fact that the minimum initial pressure cracks were promoted to undergo fracture when the maximum tensile stress attained the zenith of stress and caused the coal sample to be subject to uniaxial tensile fracture. Consequently, the fracture zone predominantly manifests in the direction of maximum tensile stress within a specified range. Meanwhile, hard coal fracture pits are shallower than soft coal. As the duration of the impact increased, the water flow in the fracture increased, and the water wedge action caused an approximately symmetrical split block in the coal body. These results indicated that under a certain impact pressure, hardness values differ with the degree of crushing and depth of destruction of coal samples.

Compound coal crushing mechanism

The findings of the experiment indicate that the internal stress wave propagation form of composite coal under water-jet impact is completely different from that of soft coal and hard coal. Due to the different material properties, the failure mode is also different. As shown in Fig. 8, the crushing mechanism of coal is as follows: during the first stage of jet impact, the upper soft coal takes the brunt of the impact stress wave, while the compression and shear waves are concentrated at the top of the contact surface. Given that the lower hard coal possesses significantly greater strength and hardness coefficients compared to the soft coal, the reflected wave originating from the bottom free surface ascended towards the coal sample and settled on the contact surface. At this time, the upper soft coal began to crack, while the lower hard coal was less affected by the stress wave. Then, as the jet continued to impact the coal sample, the attenuated stress and reflected waves overlapped each other near the contact surface, as a consequence, preliminary fissures developed at the lower extremity of the interface of contact. As a result, no significant damage was caused to the lower whole hard coal, and only a small number of shorter extending radial and conical cracks were formed. The upper soft coal is crushed most severely, as evidenced by the experimental results presented in Fig. 4c, resulting from the wedging effect of water within the coal body. The author believes that when hydraulic fracturing is used to mine structurally complex coal seams, to enable the hydraulic fracturing of structurally intricate coal seams, the analysis of damage patterns at coal seam interfaces under the influence of water-jet impact and varying mechanical strengths and hardness coefficients is deemed essential. Then effective impact pressure parameters are selected to improve the punching efficiency.

Fig. 8
figure 8

Crushing mechanism of soft-hard composite coal under water-jet impact.

Full size image

Formation of a compound coal crack

Formation of crushing pit

When high-speed jet particles strike the coal surface, water hammer effect is triggered, leading to a rapid elevation of pressure in the compressed-dense area (refer to Figure. 9). Under the surge pressure, the central region of the liquid-solid contact zone primarily experiences heightened compressive stress, exemplified by the distinctive particle P1 in Figure. 5. At t = 0.00116 ms, the maximum principal stress σ1 reaches − 17.6 MPa, surpassing the uniaxial compressive strength of the coal. This stress peaks at t = 0.00156 ms before gradually diminishing, a behavior attributed to the brief duration of surge pressure action, causing unloading as the pressure decreases to stagnation levels. At t = 0.00156 ms, the shear stress of particle P2 (Figure. 5) on the crater boundary is 13.1 MPa, exceeding the dynamic shear strength [τ] of soft coal. Remarkably, the compressive stress variation of this particle aligns with the shear stress, signifying that the crater’s formation is primarily a consequence of pressure-shear mixed stress within a condensed timeframe. The simulation reveals localized regions A and B appear, due to the unsustainable nature of surge pressure, a phenomenon consistent with experimental outcomes, attributed to the straight conFigureuration of the water-jet impact port’s front end46– 47.

Fig. 9
figure 9

Stresses on particles P1 and P2.

Full size image

Formation of conical, transverse, and radial cracks

At t = 0.016 ms, cone cracks, transverse cracks, and radial cracks are formed. Different stress curves for typical particles P3, P4, and P5 (Figure.5 were extracted to explore their internal mechanisms of action (Figure. 10). Region A was the first to form as a result of the compression wave that the water jet had on the coal. After the surge pressure disappears, the instantaneous high pressure of the jet on the coal gradually decreases., and tensile cracks at the bottom of the crater dominated by stagnation flow pressure begin to form, creating region B. There are two phenomena of P3 particles – regions A and B – which are mainly due to the lower downward pressure on the particles piled up on both sides of the crushing pit under the influence of the reflected flow. Except for that, the maximum shear stress τmax of the P3 particles peaks at 6.6 MPa, which is significantly weaker than the dynamic shear force [τ] of soft coal, as a result, coal rupture is prevented. At t = 0.0052, the maximum principal stress σ1 is 2.35 MPa as well as reaches the dynamic tensile failure strength [σ] of bituminous coal. Particle P4 attains peak values for both the maximum principal stress σ1 and maximum shear stress τmax at 2.88 MPa and 11.4 MPa, respectively. These values exceed the dynamic tensile strength [σ] and dynamic shear strength[τ] of soft coal. However, it’s noteworthy that the time for the principal stress to reach the dynamic tensile strength of soft coal (t = 0.00439 ms, σ1 = 1.94 MPa precedes the corresponding time for the shear stress. In the case of particle P5, the maximum principal stress σ1 and maximum shear stress τmax peak at 2.86 MPa and 19 MPa, respectively, occurring at t = 0.00298 ms and t = 0.0153 ms. However, it remains noteworthy that the time for the principal stress to reach the dynamic tensile strength [σ] of soft coal still preceded the time for the shear stress to reach the dynamic shear strength [τ]. These findings indicate that tensile fracture is the causative factor behind the formation of transverse and radial cracks. As the jet continues to strike the coal body, shear fracture also affects the transverse and radial cracks. Since the radial cracks are perpendicular to the jet, a compressive stress field was generated at the lower end of the crushing pit under stagnant flow pressure, resulting in compression of the coal particles. Consequently, the maximum principal stress σ1 on the P5 particles nearly maintained a negative value, as evidenced by the presence of the green dividing line in Figure. 10c.

Fig. 10
figure 10

Stresses on particles P3, P4, and P5.

Full size image

Deterioration of the contact surface near its base

At t = 0.066 ms and t = 0.080 ms, the pressure exerted on the coal by the jet reached the interface between the soft and hard coals, resulting in cracks on both sides and at the lower end of the interface (Figure. 5). Stress-time curves for representative particles, P6 and P7 (Figure. 5), at the lower end of the contact surface are illustrated in Fig. 11. Notably, regions A and B also manifested in the initial stages of the test; however, the principal stress curves from region B to region C exhibited substantial fluctuations. This indicates that particles at both the upper and lower ends of the contact surfaces were subjected to complex compressive and tensile stresses, with a higher prevalence of tensile stress waves.

Fig. 11
figure 11

Stresses on particles P6 and P7.

Full size image

The peaks of the maximum principal stress σ1 were 6.89 MPa and 6.68 MPa (dynamic tensile strength [σ] of 1.7 MPa for soft coal) and 6.68 MPa (dynamic tensile strength [σ] of 3.1 MPa for hard coal), respectively. Nevertheless, the peak of the maximum shear strain τmax within the cracks at the contact surface and the lower end of the contact surface did not attain the dynamic shear strength [τ] of the soft and hard coal. Consequently, cracks could not be initiated under these conditions. Therefore, it was believed that the cracking of coal particles was dominated by tensile fracture. When the compression wave collides with the contact surface, a reflected wave will be formed at the contact surface due to the fact that the hard coal has a higher hardness coefficient than the soft coal. Under the superposition of the compression wave and reflected wave, the coal particles at the contact surface will stretch to both sides. The maximum principal stress σ1 of P6 particles was larger than that of P7 particles. This suggests that the stretching wave originating at the lower end of the contact surface is weakened, and the radial fissures in the upper portion of the contact surface gradually compress the stretching wave (Region D).

Effective stress propagation and attenuation in composite coal

To research the propagation and attenuation characteristics of the effective stress wave in the composite coal, the effective stress curves of four particles P8, P9, P10, and P11 (Figure. 4c) above and below the contact surface at different positions with the duration of the water jet impact were selected respectively (Figure. 12). The effective stress caused by the impact pressure on the coal increased significantly after the water jet hit it. When t = 0.0364 ms, the stress on the P8 particle closest to the bottom of the crushing pit reached 8.8 MPa. At t = 0.0376 ms, the effective stress on the P9 particle dropped to 7.52 MPa, indicating that the stress wave’s propagation in the coal has dissipated. When it reached the P10 and P11 particles, the effective stresses were only 6.26 MPa and 5.86 MPa, respectively, inferring that the propagation of the stress wave in the composite coal experienced a significant reduction in its intensity during the early stage of the injection process. After the surge pressure disappeared, within a brief timeframe, it decreased to the stagnation pressure, leading to an abrupt decline in effective stress (depicted as Area A). At this time, it was in the early stage of crack development, and the four particles were subjected to similar pressures. The water wedge effect led to the formation of more crack networks in the upper part of the soft coal, which lost the ability to block the compression wave, leading to another rise in the effective stress on the four particles, and then a final drop. This showed that the action of the stress wave on the composite coal particles was a loading and unloading process, and the impact of the water jet on the composite coal specimen can also be considered as a loading or unloading process48. This phenomenon lays a theoretical basis for water jet mining of coalbed methane.

Fig. 12
figure 12

Changes in the effective stress on particles in different positions with time.

Full size image

Discussion

This paper takes composite coal seams as examples to investigate the fracture development patterns of soft-hard composite coal under water jet impact. The stress distribution in both soft and hard coals (compressive stress at the bottom and shear stress at the boundaries) is consistent with the results reported by Xue et al.29. Additionally, the observed volume fracturing in soft coal and radial blocky fragmentation in hard coal align with the stress-dependent failure modes reported by Lu et al.28. However, while they linked fracture development to water jet velocity gradients, our findings emphasize the influence of the mechanical strength difference between soft and hard coals on macroscopic fracture development. This differs from studies31 that focus on the effects of jet parameters and confining pressure on fracture development, as our work highlights the role of material heterogeneity in regulating fracture development. Regarding interfacial effects in composite structures, the coexistence of full reflection and transmission domains of stress waves at the coal-rock interface, as described by Ge et al.33, and the spatially heterogeneous fracturing patterns of the coal body are consistent with our observations. Compared to the strong crack-crossing inhibition at the coal-rock interface, the soft-hard coal interface exhibits weaker reflection effects due to material continuity (as seen in Fig. 5, some cracks can cross the soft-hard coal interface and develop on both sides).

Furthermore, variations in coal mechanical properties are widespread and not limited to composite coal seams. Geological structures, mining-induced disturbances, and even differences in samples collected from the same location can all lead to changes in coal mechanical properties. The fracture development patterns of soft-hard composite coal under water jet impact investigated in this study can provide guidance for the application of water jet technology in multi-source heterogeneous coal seams.

Conclusion

A numerical model of water jetting in soft and hard composite coals was devised, and the accuracy of the numerical simulation was verified through laboratory experiments. The inquiry examined the fracture characteristics of hard and soft coals, the composite coal-intrinsic fracture mechanisms, and the dynamics pertaining to the transmission and attenuation of stress waves. The following deductions can be drawn based on the results obtained:

  1. (1)

    Soft and hard coals have different mechanical strength and firmness coefficients so the fracture of soft coals is characterized by large-scale volumetric fracture and that of hard coals by complete radial fracture blocks. This shows that under the same impact parameters, the number of macroscopic cracks in coal samples is largely dictated by the rock’s mechanical characteristics;

  2. (2)

    The fracture patterns within the liquid-solid contact zone exhibit similarities between hard and soft coals. The bottom of the crushing pit is predominantly influenced by compressive stress, whereas the boundary of the crushing pit is predominantly affected by shear stress. Conical cracks are caused by tensile stresses, and the development and expansion of transverse and radial cracks are caused by pressure-shear mixed stress

  3. (3)

    The composite coal structure is special in that when the stress wave collides with the soft and hard coal contact surface, the high-stress area caused by the water-jet impact load is mostly concentrated above the soft and hard coal contact surface, and the stress wave reflects and attenuates on the contact surface, which inhibits crack propagation. At the same time, due to the superposition of the reflection wave and compression wave caused by the contact surface, the cracks at the contact surface and its lower end are primarily induced by tensile stress.

  4. (4)

    During the initial stage of water jet impact on coal, the propagation of effective stress waves in composite coal is hindered due to the hindrance of the contact surface. However, when the upper part of the contact surface composed of soft coal undergoes fragmentation, this hindrance weakens, leading to a subsequent rise and subsequent decline in effective stress. Therefore, the fragmentation of composite coal caused by water jet impact can be conceptualized as a cyclic loading and unloading process.