Decision algorithm with fuzzy framework and evaluation of advanced financial management policy

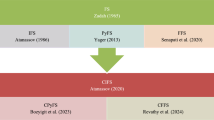
Abstract

In this paper, we introduce a new decision-making algorithm based on the circular picture fuzzy heronian mean (C-PFHM) operator to assess sophisticated financial management policies under uncertainty. The method combines the advantages of picture fuzzy sets and heronian mean aggregation so that more sophisticated management of expert views with hesitation, indeterminacy, and vagueness is possible. Multi-criteria decision-making framework is developed with data collection, normalization, C-PFHM-based aggregation, defuzzification, and ranking. To test the approach, an actual financial case study is provided wherein several policy options are compared against major financial performance measures like return on investment, liquidity, and resistance to market volatility. Quantitative findings indicate that the new approach has a high correlation with reference methods resulting in a weighted Spearman’s rank correlation coefficient of 0.9815 when compared with C-PFHM-TOPSIS. This validates the performance and reliability of the proposed algorithm in high-fidelity decision-making environments.

Introduction

Financial management policies exist as strategic architecture to facilitate organizations and governments in their efforts to obtain the best possible benefit from financial resources, minimize risk, and attain sustainable growth. These policies cover various decisions of investment planning, capital structure, liquidity, and risk assessments. The establishment of a well-structured financial policy would allow an organization to achieve financial stability and foster profitability while maintaining resilience to uncertainties of the economy. Moreover, an effective financial management system balances acute requirements for liquidity with long-term policies for mutual fund investments so that resources can be appropriately assigned toward the achievement of organizational objectives and the minimization of financial risk. Financial risk assessment and mitigation are other key aspects of financial management policies. Financial risks can hamper an organization in areas where market conditions are volatile and fluctuate, interest rates sway up and down, or there remain looming credit risks. Such afflictions, therefore, impose a lot of relevance in the contexts of financial encroachments upon existing chances. MODM has been integrated into the financial decision-making process, so that investment alternatives can be considered, with financial stability and risk management mechanisms being a basis upon which such considerations can be resolved. Because of methods that may incorporate fuzzy logic and uncertainty modeling of such types as picture fuzzy sets (PFSs), decision-makers identify managing the determined connections of financial data and ambiguity in the market more effectively. Consequently, financial policies become improved through the efficient employment of advanced decision algorithms in a manner that enhances economic performance, strengthens support for strategic planning, and improves investment decisions.

In the fast-changing financial landscape of today, organizations are being pushed more and more to make high-stakes decisions in the face of uncertainty, imprecision, and missing information. Conventional decision-making models frequently neglect the intricacies of financial systems, especially when expert opinion is based on doubt or conflicting judgments. Practical situations like corporate investment choices during economic crises or policy assessment in times of crises like the COVID-19 pandemic express the necessity for more stringent models that can deal with ambiguity and interdependence between multiple criteria. Notwithstanding increasing studies on ]MCDM methods, there is still a large gap in approaches that manage effectively the subtleties of uncertainty and expert reluctance in financial policy assessment. To fill this gap, in this research, a new C-PFHM operator is proposed, which captures positive, neutral, and negative expert views in a more mathematically coherent and flexible way. This is intended to enhance the accuracy and reliability of financial policy analysis under complex decision-making situations.

Decision-making is an integral and basic part of our daily life since it allows us to realize the problems from a variety of views and successfully tackle them. DM is a technique of choosing the most apt and best possible alternative out of the various possibilities against the numerous criteria to achieve given goals and objectives. Thus, when we deal with decisions involving many criteria that must be weighted, MCDM helps us methodically examine these alternatives and pick the best alternative since it enables the decision-maker to assign weight to such criteria and order the alternatives on the basis of them. For the MCDM problem, traditionally two methods have been followed, i.e., conventional methods such as TOPSIS¹, VIKOR², ELECTRE³, etc., and the other is AO. The former ones only provide us with the Ranking of alternatives. However, the latter ones are more effective and efficient to process the information pertaining to the alternatives and provide us with full information pertaining to other options and ranking values. In the DM process, these methods cannot handle ambiguity and imprecision in linguistic terms and need numerical values. Therefore, keeping this in mind, Zadeh⁴ proposed the idea of fuzzy set (FS), which only represents the elements by its membership value μ and its complement, i.e., non-membership ν. But the limitation involved in the sets is not our requirement that includes MCDM, Thus, an interval-valued fuzzy set (IVFS)⁵, an extension of FS that gives greater detail of $\mu$ over the interval, has been proposed. Next, to address the hesitancy value, Atanassov⁶ proposed IFS, which, in comparison to classical FS, gives a more sophisticated explanation of ambiguity and uncertainty. In many real-world situations, decision-makers not only had to handle uncertain data but also struggled to make precise decisions. A structure to better represent this vagueness is provided by IFSs, and through them, decision-makers can better specify the degree of membership (DOM) and non-membership (DONM) and refusal associated with each element. We can utilize classical FS to improve AI-based decision-making and for hard transportation problems^7,8. IFS offers a wider view of uncertainty, which allows more accurate modeling of complicated decision-making situations, and it is further extended to an interval-valued intuitionistic fuzzy set (IVIFS)^9,10. Further research on FS and IFSs can be observed from^10,11,12,13. Furthermore, this idea was further extended to Pythagorean FS (PyFS)¹⁴ by Yager, picture fuzzy set (PFS)¹⁵ by Cuong, and q-rung FS (q-RFS)¹⁶ by Yager. picture fuzzy sets (PFSs), introduced as a generalization of Intuitionistic Fuzzy Sets (IFSs), provide a more flexible approach to handling uncertainty and vagueness occurring in decision-making issues. PFSs incorporated another level, referred to as neutrality, for hesitation or indifference to a specific evaluation. A PFS is characterized on the basis of three membership functions: DOM ($\mu$), DONM ($v$), and degree of Abstinence ($\pi$), so that $0\le \mu +\nu +\pi \le 1$. This extra flexibility proves very useful in intricate decision-making issues involving finance, medical usage, and risk analysis, where specialists are likely to disagree partially or hesitate on a certain criterion. The capability to express a broad range of opinions also further increases the usability of PFSs in real-world applications with a view to providing reliable decision results. Later on, a neutrosophic set (NS)¹⁷ was introduced, which addresses vagueness, imprecision, and indeterminacy more thoroughly.

To solve the particular situations where DoM includes circular attributes, Atanassov¹⁸ generalized the IFS and proposed the theory of circular intuitionistic fuzzy sets (C-IFS), which enables a better description of circular phenomena. C-IFS was symbolized by a circle with radius r, whose μ and ν degrees are centered. Similar to IFS, C-IFS is also engaged in MCDM issues throughout the discipline. Cakır¹⁸ established the DM application in C-IFS environment, Irem et al.¹⁹ established the C-IFS by applying AHP and VIKOR methodology for supplier selection problem, Alkan et al.²⁰ established the C-IFS TOPSIS method and its application in pandemic hospital location selection, Otay et al.²¹ established the interval-valued C-IFS and its application in digital transformation, Cakır et al.²² introduced the C-IFS and its application in Covid-19 medical waste landfill site evaluation, Garg et al.²³ extended EDAS Method with C-IFS and its application in MCDM.

Literature review

In the recent past, decision-making in uncertain financial settings has been studied using fuzzy and hybrid models extensively. For example, introduced hybrid risk assessment techniques integrating FS with failure mode analysis have emerged as eminent for risk prioritization in intricate projects. As an example, the work of Karamoozian and Wu^24,25 introduced a hybrid risk prioritization model in construction projects through failure mode and effective analysis that proved more accurate in identifying pivotal risk factors with uncertainty during covid 19. DM methodology was used to choose the best industrial housing building system in Tehran, showing the efficiency of multi-criteria methods for complicated project situations²⁶ and the risk assessment of renewable energy projects and occupational safety in construction project gets using a novel hybrid fuzzy approach^27,28 . Though these models enhance the handling of data in more complicated settings, they cannot always maintain interrelationships between several criteria. In addition, most methods use traditional aggregation operators that do not necessarily capture expert opinion hesitation and neutrality. A new fuzzy decision-making method was utilized for green supplier selection for the construction sector, demonstrating the significance of sustainable factors in the evaluation of suppliers when faced with uncertainty²⁹ by Karamoozian et al. More work on Risk Assesment can be seen here^30,31, The Table 1 below outlines recent contributions and emphasizes limitations overcome in our research.

Table 1 An overview of related works Emphasising the Research Gaps, Limitations, Application Areas, and Methods the Proposed Study Addresses.

Recent research has developed decision-making methods for financial risk and performance assessment based on fuzzy and hybrid models. For example³², proposed a hybrid MEREC-RAFSI model based on spherical fuzzy numbers for the determination of banking financial assistance receivers to demonstrate the ease of evolving fuzzy systems in critical financial decisions. The authors of³³ explored the effect of financial decision-making authority on the risk-taking behavior of individuals, focusing on the behavioral aspects of financial analysis. An extensive risk analysis process for decentralized finance (DeFi) was put forward in³⁴, unifying multi-criteria decision-making in a blockchain environment. In the same way³⁵, offered an upgraded decision support system through the union of fuzzy logic and machine learning, proving to be more robust in risk assessment. Lastly³⁶, conducted a comparative financial performance analysis using different MCDM methods, further showcasing the benefits of incorporating fuzzy-based models into financial environments. These studies confirm the increasing significance of hybrid fuzzy models but identify a gap in methodology that can cope with picture fuzzy data and interdependent criteria exactly the concern of this research.

Motivation and objectives

In modern financial settings, administrations are challenged with greater complexity and uncertainty in evaluating management policies. Conventional decision-making techniques frequently fail to manage imprecise, vague, or conflicting information. This becomes more critical in risk-sensitive fields like investment analysis, liquidity management, and market volatility evaluation. In addition, due to the emergence of more refined fuzzy models as well as complex aggregation methods, it is now increasingly necessary to create decision tools that are more capable of portraying real-world ambiguity. Inspired by these challenges, this research advances a solid decision algorithm founded upon the PFHM operator in an attempt to improve financial policy assessments of uncertainty.

This work presents the hybrid architecture of C-PFHM, which solves DM problems with circular features while considering the viability and effectiveness of AO. Furthermore, it has proven its theorems and properties for the circular Picture fuzzy weighted heronian mean (C-PFWHM), circular Picture fuzzy geometric heronian mean (C-PFGHM), and circular Picture fuzzy weighted geometric heronian mean (C-PFWGHM). Furthermore, as the literature study explains, we need an air purifier to clean the air because of the rise in airborne contaminants in the environment, which significantly affects the air quality index (AQI). A practical situation was then described based on the C-IFHM and how it operates.

The study has the following key objectives:

• 1. To devise a decision-making model based on CPFS for evaluating financial policies under uncertain conditions.

• 2. To examine financial policies against important criteria such as rate of return, liquidity, market volatility, and risk management towards an all-encompassing financial assessment.

• 3. To clearly illustrate the advantages of CPFS over classical fuzzy models, in particular, its superior treatment of neutrality and hesitation.

• 4. To explore the applications of an MCDM approach (e.g., CPFS-TOPSIS, CPFS-WASPAS, or CIFHM) to rank financial policies with comparative analysis for validation.

• 5. To furnish a structured, reliable, and flexible decision support tool for investment planning, policy formulation, and risk assessment for financial institutions and policymakers.

This will act to stimulate developments in financial decision-making models by these objectives, thus assisting strategic planning and risk management amid complex and uncertain financial realms.

Justification of using picture fuzzy sets

PFS further develops IFS by introducing one more dimension-neural (hesitant) membership-along with things normal DoM and DoNM. In any decision-making under real-world situations particularly in environments that are complex like evaluation of air purifiers, financial management, or risk assessment, the decision-makers often face situations in which either neutrality or hesitation, for instance, becomes an important factor. PFS gives a structured approach to represent those uncertain opinions more suitably. Alongside conventional FSs and IFS, which employ the theory of two degrees (memberships and non-memberships), PFS introduces a further “neutral” response, thereby offering greater flexibility in cases where stakeholders or experts may neither fully support nor completely reject an option. This is an exceptionally powerful feature for cases involving environmental assessment, medical diagnosis, or financial policy evaluations, in which experts may have mixed opinions. The key condition in PFS, the sum of the square of the triplets should be between $0$ and $1$, serves to ensure that the total uncertainty of the element does not exceed a logical boundary. This helps to reduce inconsistencies in decision-making and ensures better balancing of aggregation of expert opinions. In many real decision-making problems, there are multiple conflicting criteria. PFS offers a good instrument to handle subjective judgments in methods such as TOPSIS, WASPAS, CoCoSo, and aggregation operators. With such a tool, better rankings and evaluations of alternatives can be made in case studies ranging from air quality management to financial policy assessment, healthcare decisions, and industrial optimization. Thus, the application of PFSs is justified because it can model more effectively the uncertainties, neutrality, and expert hesitation in contrast to traditional fuzzy models, making it a potent tool for decision-making under fuzzy and imprecise conditions.

Key contributions of the study

The key contributions of this paper are outlined as follows:

• 1. Formulation of a new decision-making algorithm under a C-PF setting, which provides for greater representation of uncertainty, hesitancy, and indeterminacy in expert ratings about financial management policies.

• 2. Introduction of a novel aggregation operator, the C-PFHM, which efficiently captures the interdependencies between decision criteria and enhances the credibility of aggregated expert opinions.

• 3. Development of an exhaustive computational framework consisting of expert data gathering, normalization, fuzzy aggregation, defuzzification, and ranking of alternatives for financial policy assessment.

• 4. Implementation of a real-life case study of advanced financial management, proving the practical efficiency and flexibility of the suggested algorithm.

• 5. Validation by comparative assessment, employing the weighted Spearman’s rank correlation coefficient and confusion matrix visualization, proving the reliability and strength of the suggested approach compared to the existing MCDM methods.

Organization of study

The organization of the paper is as follows: Section “Preliminaries” addresses the basic properties of Complex Pythagorean Fuzzy Sets (C-PFS) and their operations, the heronian mean (HM) and its properties, and the generalized heronian mean (GHM) and its related properties. Section “Proposed aggregation operators” introduces a hybrid framework with the C-PFHM, C-PFWHM, C-PFGHM, and C-PFWGHM operators and their properties and supporting theorems. In Section “Methodology”, an approach based on C-PFS is presented to solve MCDM problems. Section “Case study (decision algorithm with fuzzy framework and evaluation of advanced financial management policy)” presents a practical application in the context of a case study on evaluation of a complex financial management policy. Later, in Section “Advantages and disadvantages”, a numerical example is presented to justify the proposed approach, and an analytical comparison between the proposed and current methods is made. Lastly, Section “Conclusion” concludes the research by providing an overview of the major benefits, limitations, and suggesting possible avenues for future research. A detailed list of the symbols, variables, and indices employed throughout the paper and their descriptions is given in Table 2.

Table 2 This Table provides a mathematical symbol, parameters, sets, and indices used throughout the paper.

Preliminaries

This part will cover some fundamental ideas of C-PFS, its geometric representation, operation, HM and GHM AO, and properties.

Circular picture fuzzy set (C-PFS)

The idea of C-PFS was proposed by Kaya³⁷ in 2023, which is the generalization of PFS, where every element is represented by a circle and is defined by a DOM ${\mu }_{\mathfrak{c}}$, DOA ${\mathfrak{y}}_{\mathfrak{c}}$ and DONM ${\nu }_{\mathfrak{c}}$, as follows.

Definition 1

³⁸ Let ${\mathbb{U}}$ be any non-empty set. Then, a C-PFS ${\mathfrak{c}}_{\mathfrak{r}}$ is defined by using Eq. 1.

$${\mathfrak{c}}_{\mathfrak{r}}=\left\{\left(\vartheta ,\left({\mu }_{\mathfrak{c}}\left(\vartheta \right),{\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right),{\nu }_{\mathfrak{c}}\left(\vartheta \right) \right);\mathfrak{r}\left(\vartheta \right)\right);\vartheta \in \mathfrak{c}\right\}$$

(1)

where ${\mu }_{\mathfrak{c}}\left(\vartheta \right):{\mathbb{U}}\to \left[{0,1}\right]; {\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right)\to \left[{0,1}\right]$ and ${\nu }_{\mathfrak{c}}\left(\vartheta \right)\to \left[{0,1}\right]$

And

$$0\le {\mu }_{\mathfrak{c}}\left(\vartheta \right)+{\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right)+{\nu }_{\mathfrak{c}}\left(\vartheta \right)\le 1$$

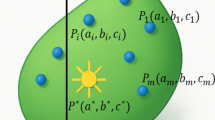
Here, $r\in [{0,1}]$ represents the radius of a circle centered around every element $\vartheta \in \mathfrak{c}$, and ${\mu }_{\mathfrak{c}}\left(\vartheta \right),{\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right)$ and ${\nu }_{\mathfrak{c}}\left(\vartheta \right)\in \left[{0,1}\right]$. Furthermore, the degree of hesitancy denoted by ${\mathbbm{h}}_{\mathfrak{c}}\left(\vartheta \right)=1-{\mu }_{\mathfrak{c}}\left(\vartheta \right)-{\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right)-{\nu }_{\mathfrak{c}}\left(\vartheta \right)$ of $\vartheta$ in $\mathfrak{c}$. Unlike traditional Pythagorean Fuzzy Sets (PFS), in Complex Pythagorean Fuzzy Sets (C-PFS), each element is represented by a circle with its center at the point $\left({\mu }_{\mathfrak{c}}\left(\vartheta \right),{\mathfrak{y}}_{\mathfrak{c}}\left(\vartheta \right),{\nu }_{\mathfrak{c}}\left(\vartheta \right)\right)$ with radius $\mathfrak{r},$ which means that C-PFS cannot be expressed in the framework of standard PFS. This geometric definition indicates that C-PFS cannot be represented by the standard PFS. The geometrical interpretation of this idea is shown in Fig. 1.

Fig. 1

Geometrical representation of C-PFS.

Definition 2

³⁷ Let ${\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}=\left\{\left({\vartheta }_{\mathfrak{T}},\left({\mu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right),{\mathfrak{y}}_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right),{\nu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right)\right);\mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)\right);\vartheta \in \mathfrak{c} \right\}$ be a Circular-Picture Fuzzy Set. Then the score function is expressed by using the following Eq. 2.

$${\mathcal{S}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}=\left({\mu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\mathfrak{y}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\nu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)\right)\times \mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)$$

(2)

Example

Consider a C-PFS element with the following values:

${\mu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)= 0.7$, ${\mathfrak{y}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)=0.1$, ${\nu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)=0.2$ and $\mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)=0.9$

Then the score is calculated as:

$${\mathcal{S}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}=\left({\mu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\mathfrak{y}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\nu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)\right)\times \mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)=$$

$$\left(0.7-0.1-0.2\right)\times 0.9=0.36$$

This score value $(0.36$) is then used in subsequent decision-making steps such as aggregation or ranking using TOPSIS. Ensuring that the final decision considers both expert judgment and fuzzy uncertainty in a mathematically consistent way.

Definition 3

³⁷Let ${\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}=\left\{\left({\vartheta }_{\mathfrak{T}},\left({\mu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right),{\mathfrak{y}}_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right), {\nu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right)\right);\mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)\right);\vartheta \in \mathfrak{c} \right\};\left(\mathfrak{T}={1,2}\right)$ be two Circular-Picture Fuzzy Set. Subsequently, a set of basic operational laws for Complex Pythagorean Fuzzy Sets is defined in Eqs. (3)–(10).

$${\mathfrak{c}}_{{{\mathfrak{r}}_{1} }} \oplus_{{\mathcal{T}}} {\mathfrak{c}}_{{{\mathfrak{r}}_{2} }} = \left\{ {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}l} {\vartheta ,\left( {\mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + \mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - \mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),} \\ {\left( {{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),\left( {\nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right)} \\ \end{array} } \right);} \\ {{\mathfrak{r}}_{{\vartheta_{1} }} + {\mathfrak{r}}_{{\vartheta_{2} }} - {\mathfrak{r}}_{{\vartheta_{1} }} .{\mathfrak{r}}_{{\vartheta_{2} }} } \\ \end{array} } \right\}$$

(3)

$${\mathfrak{c}}_{{{\mathfrak{r}}_{1} }} \oplus_{{{\mathcal{T}\mathfrak{c}}}} {\mathfrak{c}}_{{{\mathfrak{r}}_{2} }} = \left\{ {\left( {\begin{array}{*{20}l} {\vartheta ,\left( {\mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + \mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - \mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),} \\ {\left( {{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right), } \\ {\left( {\nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right)} \\ \end{array} } \right);\left( {{\mathfrak{r}}_{{\vartheta_{1} }} .{\mathfrak{r}}_{{\vartheta_{2} }} } \right)} \right\}$$

(4)

$${\mathfrak{c}}_{{{\mathfrak{r}}_{1} }} \oplus_{\mu } {\mathfrak{c}}_{{{\mathfrak{r}}_{2} }} = \left\{ {\left( {\begin{array}{*{20}l} {\vartheta ,\left( {\mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),\left( {{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + {\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - {\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),} \\ {\left( {\nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + \nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - \nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right)} \\ \end{array} } \right);\left( {{\mathfrak{r}}_{{\vartheta_{1} }} .{\mathfrak{r}}_{{\vartheta_{2} }} } \right)} \right\}$$

(5)

$${\mathfrak{c}}_{{{\mathfrak{r}}_{1} }} \oplus_{{\mu {\mathbbm{c}}}} {\mathfrak{c}}_{{{\mathfrak{r}}_{2} }} = \left\{ {\begin{array}{*{20}l} {\left( {\vartheta ,\left( {\mu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\mu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right),\left( {{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + {\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - {\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).{\mathfrak{y}}_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right)} \right),} \\ {\left( {\nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right) + \nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right) - \nu_{{\mathfrak{c}}} \left( {\vartheta_{1} } \right).\nu_{{\mathfrak{c}}} \left( {\vartheta_{2} } \right)} \right);} \\ {{\mathfrak{r}}_{{\vartheta_{1} }} + {\mathfrak{r}}_{{\vartheta_{2} }} - {\mathfrak{r}}_{{\vartheta_{1} }} .{\mathfrak{r}}_{{\vartheta_{2} }} } \\ \end{array} } \right\}$$

(6)

$${\Bbbk }\vartheta^{\mu }_{1} = \left( {1 - \left( {1 - \mu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,\left( {{\mathfrak{y}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} , \left( {\nu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ; 1 - \left( {1 - {\mathfrak{r}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} } \right)$$

(7)

$${\Bbbk }\vartheta^{{\mu {\mathbbm{c}}}}_{1} = \left( {1 - \left( {1 - \mu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,\left( {{\mathfrak{y}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,\left( {\nu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ; \left( {{\mathfrak{r}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} } \right)$$

(8)

$$\left( {\vartheta^{\mu }_{1} } \right)^{{\Bbbk }} = \left( {\left( {\mu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,1 - \left( {1 - {\mathfrak{y}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,1 - \left( {1 - \nu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ;\left( {{\mathfrak{r}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} } \right)$$

(9)

$$\left( {\vartheta^{{\mu {\mathbbm{c}}}}_{1} } \right)^{{\Bbbk }} = \left( {\left( {\mu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,1 - \left( {1 - {\mathfrak{y}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ,1 - \left( {1 - \nu_{{\vartheta_{1} }} } \right)^{{\Bbbk }} ;1 - \left( {1 - {\mathfrak{r}}_{{\vartheta_{1} }} } \right)^{{\Bbbk }} } \right)$$

(10)

Heronian mean (HM) operator

DM in actual life problems is usually compromise between cost, time, quality, and other conflicting priorities. Thus, the combined consideration of all the concerned parameters is necessary to attain optimal solutions since it allows a better understanding of the issue. In this regard, AOs are critically important by combining heterogeneous numerical inputs into a common output. The HM AO is the topic of this article, which is a mathematically sound and powerful operator that takes into consideration the interdependent nature of the input arguments³⁹. This unique aspect makes it more useful and applicable in decision-making situations⁴⁰. Because it is efficient and adaptable, the HM AO has been highly utilized by scholars and practitioners for data aggregation and best decision-making.

For example, Liu et al.⁴¹ developed a linguistic HM for group decision-making; Zhang et al.⁴² presented the Dombi HM and discussed its applications; Hussain et al.⁴³ constructed the Aczel-Alsina HM for solar panel evaluation; Mishra et al.⁴⁴ developed the Fermatean fuzzy HM for assessing climate change policy; and Peng et al.⁴⁵ developed the Frank HM for coal mine assessment. The HM AO successfully reflects the interconnections among input parameters, providing credible results in MCDM problems, especially in cases dealing with uncertain and complicated information.

Definition 4

⁴⁰ Consider a set of positive numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then,

$${HM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}\sqrt{{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}}\right)$$

(11)

HM AO holds the following properties:

• i. ${{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{0}},{\boldsymbol{0}},\dots ,{\boldsymbol{0}}\right)={\boldsymbol{0}}$; If $\forall {\boldsymbol{\vartheta }}_{\mathfrak{T}}=0, \forall \mathfrak{T}$.

• ii. ${{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)=\boldsymbol{\vartheta }$; If $\forall {\boldsymbol{\vartheta }}_{\mathfrak{T}}=\boldsymbol{\vartheta }, \forall \mathfrak{T}$.

• iii. ${{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)\ge {{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\mathbbm{b}}_{1},{\mathbbm{b}}_{2},\dots ,{\mathbbm{b}}_{\mathfrak{z}}\right)$; If ${\boldsymbol{\vartheta }}_{\mathfrak{T}}\ge {\mathbbm{b}}_{\mathfrak{T}}, \forall \mathfrak{T}$.

• iv. $\bigwedge \left( {\boldsymbol{\vartheta }}_{\mathfrak{T}}\right)\le {{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)\le \bigvee \left( {\boldsymbol{\vartheta }}_{\mathfrak{T}}\right)$.

Definition 5

⁴⁰ Let a set of positive numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then,

$${GHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)={\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}$$

(12)

If $\mathfrak{T}=\mathfrak{J}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, Eq. (12) reduced to Eq. (11). The generalized heronian mean AO satisfies the following properties:

• i. ${{\varvec{G}}{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left(0,0,\dots ,0\right)=0$; If $\forall {\boldsymbol{\vartheta }}_{\mathfrak{T}}=0, \forall \mathfrak{T}$.

• ii. ${{\varvec{G}}{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)=\boldsymbol{\vartheta }$; If $\forall {\boldsymbol{\vartheta }}_{\mathfrak{T}}=\boldsymbol{\vartheta }, \forall \mathfrak{T}$.

• iii. ${{\varvec{G}}{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)\ge {{\varvec{G}}{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\mathbbm{b}}_{1},{\mathbbm{b}}_{2},\dots ,{\mathbbm{b}}_{\mathfrak{z}}\right)$; If ${\boldsymbol{\vartheta }}_{\mathfrak{T}}\ge {\mathbbm{b}}_{\mathfrak{T}}, \forall \mathfrak{T}$.

• iv. $\bigwedge \left( {\boldsymbol{\vartheta }}_{\mathfrak{T}}\right)\le {{\varvec{G}}{\varvec{H}}{\varvec{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)\le \bigvee \left( {\boldsymbol{\vartheta }}_{\mathfrak{T}}\right)$.

Proposed aggregation operators

The PFS extends the classical FS by considering both DoM ($\mu$), DoA (η), and DoNM ($\nu$) simultaneously. This augmentation provides PFS with the ability to deal with uncertainty and vagueness encountered in real-life decision-making problems. Nevertheless, PFS cannot adequately handle situations that involve circular characteristics. The shortcoming introduced C-PFS, meaning Circular Picture Fuzzy Set. AOs are a tool that helps decisions, taking multiple inputs into one collective representative value within an MCDM setting. Circular Picture Fuzzy Hamy Mean (C-PFHM) and its aggregates, such as Generalized Hamy Mean (GHM), Weighted Hamy Mean (WHM), and Weighted Generalized Hamy Mean (WGHM), along with their basic properties, are included in this section.

Circular picture fuzzy heronian mean (C-PFHM) operators

Definition 6

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then, the succeeding operator mathematically defined by using Eqs. (13–14),

$$C{{PFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}\sqrt{{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}}\right)$$

(13)

$$C{{PFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}\sqrt{{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}}\right)$$

(14)

Definition 7

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and the weight vector is defined by ${\mathbbm{w}}_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ s.t $\sum {\mathbbm{w}}_{\mathfrak{T}}=1$ which defined the importance of ${\vartheta }_{\mathfrak{T}}$. Then, the succeeding operator is mathematically defined by using Eqs. (15–16),

$$CPFWHM_{\mu }^{{{\mathfrak{T}},{\mathfrak{J}}}} \left( {\vartheta_{1} ,\vartheta_{2} , \ldots ,\vartheta_{{\mathfrak{z}}} } \right) = \left( {\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {{\mathfrak{z}}^{2} + {\mathfrak{z}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{z}}^{2} + {\mathfrak{z}}}$}}} \right)\mathop \sum \limits_{{{\mathcal{P}} = 1}}^{{\mathfrak{z}}} \mathop \sum \limits_{{{\mathcal{Q}} = 1}}^{{\mathfrak{z}}} \sqrt {\left( {{\mathbbm{w}}_{{\mathcal{P}}} \vartheta_{{\mathcal{P}}} } \right)^{{\mathfrak{T}}} \times \left( {{\mathbbm{w}}_{{\mathcal{Q}}} \vartheta_{{\mathcal{Q}}} } \right)^{{\mathfrak{J}}} } } \right)$$

(15)

$$CPFWHM_{{\mu {\mathbbm{c}}}}^{{{\mathfrak{T}},{\mathfrak{J}}}} \left( {\vartheta_{1} ,\vartheta_{2} , \ldots ,\vartheta_{{\mathfrak{z}}} } \right) = \left( {\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {{\mathfrak{z}}^{2} + {\mathfrak{z}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{z}}^{2} + {\mathfrak{z}}}$}}} \right)\mathop \sum \limits_{{{\mathcal{P}} = 1}}^{{\mathfrak{z}}} \mathop \sum \limits_{{{\mathcal{Q}} = 1}}^{{\mathfrak{z}}} \sqrt {\left( {{\mathbbm{w}}_{{\mathcal{P}}} \vartheta_{{\mathcal{P}}} } \right)^{{\mathfrak{T}}} \times \left( {{\mathbbm{w}}_{{\mathcal{Q}}} \vartheta_{{\mathcal{Q}}} } \right)^{{\mathfrak{J}}} } } \right)$$

(16)

Theorem 1

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then, the succeeding operator mathematically defined by using Eqs. (17–18)

$${{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(17)

And

$${{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({1-\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(18)

Proof

Please See the Appendix A for Proof.

Theorem 2

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and the weight vector is defined by ${\mathbbm{w}}_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ s.t $\sum {\mathbbm{w}}_{\mathfrak{T}}=1$ which defined the importance of ${\vartheta }_{\mathfrak{T}}$. Then, the succeeding operator is mathematically defined by using Eqs. (19–20),

$${{CIFWHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({1-\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(19)

And

$${{CIFWHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({1-\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(20)

Properties of circular-picture fuzzy heronian mean AO

The properties of circular-picture fuzzy heronian mean AO are defined as:

• i. Idempotency:

  Let ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}},{\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs and ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{\vartheta },{\mathfrak{y}}_{\vartheta }, {\nu }_{\vartheta },{\mathfrak{r}}_{\vartheta }\right)=\vartheta ;\forall \mathfrak{T}$ . Then,

  $${{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\vartheta$$
  $${{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\vartheta$$

• ii. Boundedness:

  Consider ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}, {\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs and

  $${\vartheta }^{-}=\left(\underset{\mathfrak{T}}{{\min}}\left({\mu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\nu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right)\right) ; {\vartheta }^{+}=\left(\underset{\mathfrak{T}}{{\max}}\left({\mu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\nu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right)\right);\forall \mathfrak{T}$$

  Then,

  $${\vartheta }^{-}\le {{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {\vartheta }^{+}$$
  $${\vartheta }^{-}\le {{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {\vartheta }^{+}$$

• iii. Monotonicity:

  Consider ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}},{\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and ${{\vartheta }_{\mathfrak{T}}}{\prime}=\left({{\mu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}}{\prime},{{\nu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs, and if ${\vartheta }_{\mathfrak{T}}\le {{\vartheta }_{\mathfrak{T}}}{\prime};\forall \mathfrak{T}$ s.t ${\mu }_{{\vartheta }_{\mathfrak{T}}}<{{\mu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}>{{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}, {\nu }_{{\vartheta }_{\mathfrak{T}}}>{{\nu }_{{\vartheta }_{\mathfrak{T}}}}{\prime}$ and ${\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}<{{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}$. Then,

  $${{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({{\vartheta }_{1}}^{{{\prime}}},{{\vartheta }_{2}}^{{{\prime}}},\dots ,{{\vartheta }_{\mathfrak{z}}}^{{{\prime}}}\right)$$
  $${{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({{\vartheta }_{1}}^{{{\prime}}},{{\vartheta }_{2}}^{{{\prime}}},\dots ,{{\vartheta }_{\mathfrak{z}}}^{{{\prime}}}\right)$$

Circular picture fuzzy generalized heronian mean (C-PFGHM) AO

Definition 8

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then, the succeeding operator mathematically defined by using Eqs. (21–22),

$$CPF{{GHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)={\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}$$

(21)

$$CPF{{GHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)={\left(\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)\sum_{\mathcal{P}=1}^{\mathfrak{z}}\sum_{\mathcal{Q}=1}^{\mathfrak{z}}{\vartheta }_{\mathcal{P}}^{\mathfrak{T}}{\vartheta }_{\mathcal{Q}}^{\mathfrak{J}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}$$

(22)

Definition 9

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and the weight vector is defined by ${\mathbbm{w}}_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ s.t $\sum {\mathbbm{w}}_{\mathfrak{T}}=1$ which defined the importance of ${\vartheta }_{\mathfrak{T}}$. Then, the succeeding operator is mathematically defined by using Eqs. (23–24),

$$CPFWGHM_{\mu }^{{{\mathfrak{T}},{\mathfrak{J}}}} \left( {\vartheta_{1} ,\vartheta_{2} , \ldots ,\vartheta_{{\mathfrak{z}}} } \right) = \left( {\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {{\mathfrak{z}}^{2} + {\mathfrak{z}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{z}}^{2} + {\mathfrak{z}}}$}}} \right)\mathop \sum \limits_{{{\mathcal{P}} = 1}}^{{\mathfrak{z}}} \mathop \sum \limits_{{{\mathcal{Q}} = 1}}^{{\mathfrak{z}}} \left( {{\mathbbm{w}}_{{\mathcal{P}}} \vartheta_{{\mathcal{P}}} } \right)^{{\mathfrak{T}}} \times \left( {{\mathbbm{w}}_{{\mathcal{Q}}} \vartheta_{{\mathcal{Q}}} } \right)^{{\mathfrak{J}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{\mathfrak{T}} + {\mathfrak{J}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{T}} + {\mathfrak{J}}}$}}}}$$

(23)

$$CPFWGHM_{{\mu {\mathbbm{c}}}}^{{{\mathfrak{T}},{\mathfrak{J}}}} \left( {\vartheta_{1} ,\vartheta_{2} , \ldots ,\vartheta_{{\mathfrak{z}}} } \right) = \left( {\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {{\mathfrak{z}}^{2} + {\mathfrak{z}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{z}}^{2} + {\mathfrak{z}}}$}}} \right)\mathop \sum \limits_{{{\mathcal{P}} = 1}}^{{\mathfrak{z}}} \mathop \sum \limits_{{{\mathcal{Q}} = 1}}^{{\mathfrak{z}}} \left( {{\mathbbm{w}}_{{\mathcal{P}}} \vartheta_{{\mathcal{P}}} } \right)^{{\mathfrak{T}}} \times \left( {{\mathbbm{w}}_{{\mathcal{Q}}} \vartheta_{{\mathcal{Q}}} } \right)^{{\mathfrak{J}}} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{\mathfrak{T}} + {\mathfrak{J}}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\mathfrak{T}} + {\mathfrak{J}}}$}}}}$$

(24)

Theorem 3

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ where, $\mathfrak{T},\mathfrak{J}>0$. Then, the succeeding operator mathematically defined by using Eqs. (25–26)

$${CPF{GHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(25)

And

$${CPFG{HM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(26)

Proof

Please See the Appendix B for proof.

Theorem 4

Let a set of circular picture fuzzy numbers ${\vartheta }_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and the weight vector is defined by ${\mathbbm{w}}_{\mathfrak{T}}\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ s.t $\sum {\mathbbm{w}}_{\mathfrak{T}}=1$ which defined the importance of ${\vartheta }_{\mathfrak{T}}$. Then, the succeeding operator is mathematically defined by using Eqs. (27–28),

$${{CPFWGHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({1-\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(27)

and

$${{CPFWGHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({1-\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(28)

Properties of circular-picture fuzzy generalized heronian mean AO

The properties of circular-picture fuzzy generalized heronian mean AO are as follows:

• i. dempotency:

  Consider ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}},{\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs and ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{\vartheta },{\mathfrak{y}}_{\vartheta }, {\nu }_{\vartheta },{\mathfrak{r}}_{\vartheta }\right)=\vartheta ;\forall \mathfrak{T}$. Then,

  $${CPF{GHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\vartheta$$
  $${CPF{GHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\vartheta$$

• ii. Boundedness:

  Consider ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}},{\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs and

  $${\vartheta }^{-}=\left(\underset{\mathfrak{T}}{{\min}}\left({\mu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\nu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right)\right) ; {\vartheta }^{+}=\left(\underset{\mathfrak{T}}{{\max}}\left({\mu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\min}}\left({\nu }_{{\vartheta }_{\mathfrak{T}}}\right),\underset{\mathfrak{T}}{{\max}}\left({\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right)\right);\forall \mathfrak{T}$$

  Then,

  $${\vartheta }^{-}\le {CPFG{HM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {\vartheta }^{+}$$
  $${\vartheta }^{-}\le {CPFG{HM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {\vartheta }^{+}$$

• iii. Monotonicity:

  Consider ${\vartheta }_{\mathfrak{T}}=\left({\mu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}},{\nu }_{{\vartheta }_{\mathfrak{T}}},{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ and ${{\vartheta }_{\mathfrak{T}}}{\prime}=\left({{\mu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{{{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}}{\prime},{\nu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}\right);\left(\mathfrak{T}={1,2},\dots ,\mathfrak{z}\right)$ be a collection of C-PFNs, and if ${\vartheta }_{\mathfrak{T}}\le {{\vartheta }_{\mathfrak{T}}}{\prime};\forall \mathfrak{T}$ s.t ${\mu }_{{\vartheta }_{\mathfrak{T}}}<{{\mu }_{{\vartheta }_{\mathfrak{T}}}}{\prime},{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}>{{\mathfrak{y}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}, {\nu }_{{\vartheta }_{\mathfrak{T}}}>{{\nu }_{{\vartheta }_{\mathfrak{T}}}}{\prime}$ and ${\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}<{{\mathfrak{r}}_{{\vartheta }_{\mathfrak{T}}}}{\prime}$. Then,

  $${CPFG{HM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {CPFG{HM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({{\vartheta }_{1}}^{{{\prime}}},{{\vartheta }_{2}}^{{{\prime}}},\dots ,{{\vartheta }_{\mathfrak{z}}}^{{{\prime}}}\right)$$
  $${CPFG{HM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)\le {CPFG{HM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({{\vartheta }_{1}}^{{{\prime}}},{{\vartheta }_{2}}^{{{\prime}}},\dots ,{{\vartheta }_{\mathfrak{z}}}^{{{\prime}}}\right)$$

Methodology

In this section, we explore the MCDM technique with the C-PFHM operator and show the real-world application of the designed operators. A real-world case study is also provided to show how the proposed approach can be used effectively in real-world decision-making situations.

Comparative analysis of aggregation operators

This sub-section elaborates on the main distinctions among the suggested C-PFHM operator and previous aggregation operators like PFWA and PFHG. It identifies enhancements in model capability, aggregation reasoning, and circular educability with circular picture fuzzy settings.

The main differences are outlined as follows:

Circular Membership Modeling: The new C-PFHM operator applies a circular model of picture fuzzy sets, which provides a more flexible and geometrically uniform methodology for representing indeterminacy and hesitancy than conventional linear approaches.

Heronian Mean-Based Aggregation: As opposed to the PFWA operator which solely takes into consideration weighted averages and the PFHG which takes geometric mean into account, the C-PFHM applies interrelationships between criteria using Heronian mean logic. This makes it a stronger and informative aggregation particularly when there are interdependent criteria.

Enhanced Sensitivity and Precision: The new operator improves the sensitivity of the decision-making function to minute changes in expert inputs and is thus ideal for sophisticated and uncertain environments like financial policy analysis.

Compatibility with C-PF Environment: Although former operators are usually implemented in regular fuzzy or picture fuzzy environments, the C-PFHM is uniquely suited to perform within the circular picture fuzzy framework, providing a more efficient mechanism for managing uncertainty and ambiguity.

Computational steps of the proposed C-PFHM-based MCDM algorithm

Here, we introduce a complete computational process for measuring financial policy options based on the C-PFHM operator within an MCDM environment. Let a set of alternatives $\left\{{\mathcal{P}}_{1},{\mathcal{P}}_{2},{\mathcal{P}}_{3}, {\mathcal{P}}_{4}\right\}$ through several different criteria: return on investment (C₁), risk management (C₂), Liquidity (C₃), and Market volatility resistance (C₄). Assuming that the experts assign some hypothetical weight values for each criterion $w_{t} = \left\{ {0.25, 0.35, 0.10, 0.30} \right\}$ for $T = 1,2,3,4$ such that the sum of the weights of all criteria is equal to $1 \left( {\sum w_{t} = 1} \right)$.

Steps for solving a problem

Step 1: Construct the Circular Picture Fuzzy Decision Matrix.

An MCDM problem consists of ${\mathbbm{m}}$ alternatives ${\mathcal{P}}_{1},{\mathcal{P}}_{2},{\mathcal{P}}_{3},\dots ,{\mathcal{P}}_{\mathbbm{m}}$ and $\mathfrak{z}$ criteria ${\mathcal{C}}_{1},{\mathcal{C}}_{2},{\mathcal{C}}_{3},\dots ,{\mathcal{C}}_{\mathfrak{z}}$, from which the experts ${\mathbb{D}}_{\mathfrak{T}\mathfrak{J}}$ accumulate valuable data according to the demand. The experts assess these alternatives under the C-PF environment s.t the values assigned to each alternative in the form of C-PFN and store these in matrix form, which is given below;

$${\left({\mathbb{D}}_{\mathfrak{T}\mathfrak{J}}\right)}_{{\mathbbm{m}}\times \mathfrak{z}} =\begin{array}{c}{\mathcal{P}}_{1}\\ {\mathcal{P}}_{2}\\ \vdots \\ {\mathcal{P}}_{\mathbbm{m}}\end{array} \left[\begin{array}{cccc}{\mathcal{C}}_{1}& {\mathcal{C}}_{2}& \dots & {\mathcal{C}}_{\mathfrak{z}}\\ {\vartheta }_{11}& {\vartheta }_{12}& \dots & {\vartheta }_{1\mathfrak{z}}\\ {\vartheta }_{21}& {\vartheta }_{22}& \dots & {\vartheta }_{2\mathfrak{z}}\\ \vdots & \vdots & \ddots & \vdots \\ {\vartheta }_{{\mathbbm{m}}1}& {\vartheta }_{{\mathbbm{m}}2}& \dots & {\vartheta }_{{\mathbbm{m}}\mathfrak{z}}\end{array}\right]$$

For the selection of an optimized alternative, the following steps are summarized as follows:

Step 2: Normalize the Decision Matrix (if necessary)

If data are not in C-PF form or need to be normalized (e.g., benefit/cost criteria), normalize to transform the inputs to legitimate C-PFS triplets. Normalize the accumulated data that is stored in matrix form, but if all ${\mathcal{C}}_{\mathfrak{z}}$ are of the same type, then it doesn’t require normalization; otherwise, values must be normalized from $\left({\mathbb{D}}_{\mathfrak{T}\mathfrak{J}}\right)$ to $\left({\mathbb{R}}_{\mathfrak{T}\mathfrak{J}}\right)$ as;

$${\left({\mathbb{R}}_{\mathfrak{T}\mathfrak{J}}\right)}_{{\mathbbm{m}}\times \mathfrak{z}}=\left\{\begin{array}{c}{\left({\mathbb{D}}_{\mathfrak{T}\mathfrak{J}}\right)}^{{{\prime}}};cost\\ \left({\mathbb{D}}_{\mathfrak{T}\mathfrak{J}}\right) ;benefit\end{array}\right.$$

Step 3: Determine Criteria Weights

Employ pre-defined weights $w_{t} = \left\{ {0.25, 0.35, 0.10, 0.30} \right\}$ or compute weights via the entropy method or another weighting.

Step 4: Aggregate the Evaluations Using the C-PFHM Operator.

Employ the picture fuzzy heronian mean operator in aggregating expert opinions by alternative.

To process the data, apply the proposed operators given below in Eqs. 29–36 ;

$${{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(29)

$${{CPFHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({1-\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(30)

$${{CPFWHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({1-\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(31)

$${{CPFWHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right),\\ \left({\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({1-\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

(32)

$${CPF{GHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(33)

$${CPFG{HM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(34)

$${{CPFWGHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({1-\left(1-{\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(35)

$${{CPFWGHM}_{\mu {\mathbbm{c}}}}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right),\\ {\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({1-\left({\mathfrak{r}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{r}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

(36)

Step 5: Calculate Score Values for All Alternatives

Apply the score function to defuzzify the aggregated C-PFS: We assess the scored values corresponding to each operator using Eq. (37).

$${\mathcal{S}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}=\left({\mu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\mathfrak{y}}_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)-{\nu }_{{\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}}\left(\vartheta \right)\right)\times \mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)$$

(37)

This gives a scalar score for every alternative.

Step 6: Rank the Alternatives

Rank the alternatives based on their score value and select the most optimized alternative. The best alternative is the one with the highest score and is thus the most favorable policy.

Computational complexity analysis

The computational complexity of the suggested algorithm is analyzed in terms of the number of alternatives $m$, the number of criteria $n$, and the number of decision-makers or expert opinions

$e$. The key steps and their complexities are as follows:

Step 1: Data gathering and construction of the C-PFS matrix $O(m\cdot n\cdot e)$

Step 2: Aggregation via C-PFHM operator

Each heronian mean computation is $O(n)$, used for each alternative:$O(m\cdot n)$

Step 3: Computation of scores

One operation per alternative:$O(m)$

Step 4: Ranking – Sorting score values:$O(mlogm)$

Therefore, the overall computational complexity is: $O(m\cdot n\cdot e+m\cdot n+m+mlogm)\approx O(m\cdot n\cdot e)$

This shows that the algorithm is efficient and scalable for moderate-to-large MCDM problems and can thus be deployed in practice in financial decision systems.

Decision-making implications

The developed C-PFHM-based decision model provides the following essential managerial advantages:

Management of Uncertainty and Ambiguity: It gives decision-makers a method of capturing uncertainty in terms of CPFSs, thus allowing for more credible policy assessment with imprecise or contradictory expert opinions.

Flexible and Data-Driven: Managers can provide weights or utilize data-driven methods (e.g., entropy method), allowing for adaptability based on inner financial priorities or business conditions.

Risk-Sensitive Ranking: Through the incorporation of positive and negative impressions (through the score function the framework facilitates risk-sensitive choice of financial policies.

Strategic Policy Evaluation: This approach can help in assessing capital structure choices, risk-reduction strategies, and investment strategies consistent with long-term financial goals. Overall, the algorithm suggested in this paper facilitates evidence-based, transparent, and systematic decision-making in intricate financial settings.

Case study (decision algorithm with fuzzy framework and evaluation of advanced financial management policy)

Efficient financial management defines sustainable economic growth and alleviation of financial risk. Nowadays, however, financial systems have become complex, uncertainties pose increasingly uncomfortable situations for economic conditions, and financial markets are subject to extreme volatility. Therefore, decision-making entails more and more challenges in the context of financial management. With the development of fuzzy mathematical approaches, an integrated decision-making environment can therefore be created to handle varying uncertainties and imprecise information. This case study focused on the application of the fuzzy-based decision algorithm for assessing advanced financial management policies.

Assessing financial management policies

Evaluation of financial management policies would involve a few critical questions: What are the critical financial risks in an organization? How could they be mitigated through both quantitative and qualitative models? What are the financial strategies that work best under uncertain economic conditions? Where does advanced data analysis come into play in financial decision-making? The decision-making process should therefore look at these questions in a structured way in which fuzzy logic forms a central role in describing the uncertain financial data so that useful information can be generated. The MCDM approach using fuzzy mathematics provides a systematic way of ranking and evaluating financial management policies as shown in Fig. 2.

Fig. 2

Financial management proccess.

Some major questions related to the evaluation of financial management policies include: What are the major financial risks that exist in an organization? How can they be mitigated through quantitative and qualitative models? Which financial strategies perform best in an uncertain state of the economy? What role is assumed by advanced data analysis in the making of financial decisions?

The fuzzy MCDM methodology gives structure to the ranking and evaluation of financial management policies whereby decision-makers can optimize financial strategies based on uncertain and imprecise information.

The proposed fuzzy framework advances financial decision-making through various components like C-PFS theory, HM aggregation operators, and MCDM methods.

Basic Components:

CPFSs: Represent uncertain and imprecise financial information.

Membership Functions: Riskiness or profitability of different financial policies.

HM Aggregation Operators: A unification of the various financial criteria for objective decision-making.

Defuzzification Techniques: From fuzzy results, derive a crisp ranking that can be put to practical use.

According to the fuzzy decision algorithm, for instance, in the case of an investment decision, the organization would identify three alternative financial management policies under uncertain economic conditions.

Step 1: Definition of Decision Criteria

The decision criteria of the organization are as follows:

Risk Management (${\mathcal{C}}_{1}$)

Risk management is systematically looking at the identification, assessment, and control of some potential risks that can adversely affect the organization, project, or person. This process starts with the identification of risks that may arise from inside (operational risks) or outside (market fluctuations and natural calamities). At this point in risk management, potential risks are assessed against the frequency of occurrence and severity of impact. This prioritizes risks and allows organizations to focus their efforts on those representing the highest threats to the achievement of their objectives. The second step in risk management is to devise strategies for mitigating or managing the identified risks. Strategies may involve risk avoidance (eliminating the risk), risk reduction (taking measures to reduce the frequency or impact), risk transfer (such as through the purchase of insurance), and risk acceptance (acknowledging the risk and making plans to deal with its consequences) as shown in Fig. 3⁴⁶.

Fig. 3

Risk assesment.

As situations are constantly changing, continuous monitoring and review of risks and mitigation measures are very important to ensure risks are effectively managed over some time. Such proactive means will help safeguard their assets, ensure that the stated objectives are achieved, and minimize uncertainties in industries like finance, healthcare, and project management.

Rate of Returns (${\mathcal{C}}_{2}$)

Rate of return (RoR) is a concept that assigns the profits or performances of given investments in a stipulated timeframe. It indicates the percentage gain or loss derived from the investment to the investment’s initial cost or value. Mathematically, RoR can be computed as follows:

$$Rate \,of\, Return=\frac{Final \,Value\, of\, Investment-Initial\, Value\, of\, Investment}{Initial\, Value \,of \,Investment} \times 100$$

The formula results in a percentage value that indicates the appreciation or depreciation of an investment. Here, a positive Rate of Return signifies profit, whereas a negative rate indicates loss. The RoR is oftentimes used to contrast the performance of various investments, thereby allowing the investor to identify the most lucrative investments. RoR can be used in several types of investments such as stock, bond, real estate, or business ventures, and is a key factor in determining whether an investment strategy worked or is financially healthy. Figure 4⁴⁷ shows the graphical representation of the Rate of return.

Fig. 4

Rate of return.

Liquidity (${\mathcal{C}}_{3}$)

The aspect of liquidity is basically how an asset can easily be converted into cash without causing much distortion in prices. In financial terms, an asset can be classified as highly liquid when someone could sell or use it almost as cash without losing significant value. Cash, in the case of other non-cash assets, such as real estate or specialized equipment, would be the asset least liquid since it takes much longer and requires effort. More generally, liquidity would also mean that an organization, a business, or a person can meet short-term obligations using liquid assets. As shown in Fig. 5⁴⁸, A high liquidity status means that there are enough available cash funds to be utilized for covering short-term liabilities, while low liquidity indicates possible difficulties in meeting obligations. Liquidity relates to individuals’ finances and businesses because it gives them financial continuity and flexibility.

Fig. 5

Liquid assests.

Market Volatility Resistance (${\mathcal{C}}_{4}$)

Market volatility resilience is that aspect of some investments, portfolios, or investment strategies that can insulate them from the noise of price movements, particularly during moments when maximum uncertainty dominates the market. A portfolio or asset can shield itself from destruction or sustain value at times of higher volatility like market crashes, economic crises, or events involving geopolitics. These occurrences are typically followed by several different price movements in the market. Investments with long-lasting characteristics in the face of market volatility seem secure but are most resistant to extreme price movements. This may be caused by diversification and hedging tactics, or by outright investment in properties commonly thought to be less correlated with the major markets, such as certain bonds, defensive equities (e.g., utilities or healthcare), or alternative investments like gold. Risk management tools such as stop-loss orders or options may also assist in preventing loss on account of volatility. In the end, this is a strategy whose primary goal would be to preserve value and reduce the effect of sudden market movements, and keep an investment portfolio in tact even in times of turmoil, as represented by Fig. 6.

Fig. 6

US uncertainty percent.

Step 2: Gathering Experts’ Opinions and Converting into C-PFNs

A collection of experts’ opinions is done which are then converted into C-PFNs.

Step 3: Applying the Proposed HM Model

Evaluation of each policy is carried out based on the proposed method through which it has been ranked as close to the ideal solution.

Step 4: Decision Making and Verification

Thus, the best-ranked policy is selected, while the results validate the selection via correlation analysis with those of traditional decision-making models, as illustrated in Fig. 7.

Fig. 7

Decision-making algorithm.

Numerical example

To evaluate an advanced financial management policy, the organization may engage the services of financial analysts who will make assessments of various policy alternatives $\left\{{\mathcal{P}}_{1},{\mathcal{P}}_{2},{\mathcal{P}}_{3}, {\mathcal{P}}_{4}\right\}$ through several different criteria: return on investment (C₁), risk management (C₂), Liquidity (C₃), and Market volatility resistance (C₄). Assuming that the experts assign some hypothetical weight values for each criterion $w_{t} = \left\{ {0.25, 0.35, 0.10, 0.30} \right\}$ for $T = 1,2,3,4$ such that the sum of the weights of all criteria is equal to $1 \left( {\sum w_{t} = 1} \right)$. The weight values can also be determined using the entropy method where the relative importance of each criterion is derived from the data available for them. The evaluation of the policy alternatives under a C-PF environment makes it possible to accommodate the vagueness and uncertainty in decision-making situations, thereby ensuring a more accurate and reliable evaluation of policy effectiveness in complex financial management settings. Data accumulation from the experts’ opinions is given in Table 3. It involves gathering and organizing the visions and evaluations provided by issue matter experts.

Table 3 Data accumulation from the experts’ opinions involves gathering and summarizing their evaluations.

Normalization is not necessary because all ${\mathcal{C}}_{\mathfrak{z}}$ are of the same type. For data assessment, the suggested operators specified in Eqs. 29–36 are used and shown in Table 4.

Table 4 Analyzing and interpreting the information gathered is part of the data evaluation process.

Analyze the score values for each operator shown in Table 5 using Eq. 37.

Table 5 Score values and alternate ranking according to evaluation criteria.

Rank the alternatives based on their score value and select the most optimized alternative display in Fig. 8.

Fig. 8

Ranking of alternatives based on the proposed method, describing an order of preference.

Using the HM, WHM, GHM, and WGHM AO in the C-PFS environment, an MCDM technique chooses the best air purifier. By taking into account the various criteria and giving each criterion a weight value, the expertise accumulated in the data relates to each purifier. The suggested operators were then used to execute the gathered data, and each operator’s score value matched the data. Although we got different results using different operators, the majority of the operators indicate that ${\mathcal{P}}_{2}$ is the best option. But it really depends on their preferred operator and the level of competence they choose.

Result discussion and comparison

Table 6 provides a comparison between the former approaches and the current method, with the most important limitations of former models highlighted. In particular, former approaches fail to express the radius between membership and non-membership degrees or express the interdependent relations between criteria. In order to overcome these problems, the C-PFS structure combined with the heronian mean (HM) has been proposed, providing better uncertainty handling and more effective support for decision-making.

Table 6 Comparison between proposed and former approaches highlighting improved uncertainty handling and decision-making precision.

previous methods including IFS⁶ proposed by Atanassov, PyFS¹⁴ proposed by Yager, and q-RFS¹⁶ proposed by Yager, are capable of handling the μ and ν value Nonetheless, they cannot be flexible to represent interdependencies between criteria and are not structured to deal with circular contexts. Çakır's introduction of CPFS¹⁸ came to alleviate some of these deficiencies by enabling the representation to be circular, though it still didn’t represent interdependencies between interdependent criteria. In an effort to close this gap, a new hybrid model C-PFHM has been proposed. Circular fuzzy logic and an aggregation operator that can portray interdependencies have been merged. This presents a more practical and resilient decision-making solution in intricate and uncertain systems.

If we take $\mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)=0$ from ${\mathfrak{c}}_{{\mathfrak{r}}_{\mathfrak{T}}}=\left(\left({\mu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right),{\mathfrak{y}}_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right),{\nu }_{\mathfrak{c}}\left({\vartheta }_{\mathfrak{T}}\right)\right);\mathfrak{r}\left({\vartheta }_{\mathfrak{T}}\right)\right)$ then it will be reduced into standard PFS, which is defined by Atanassov⁶, and

• i. ${{CPFHM}_{\mu }}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)$ reduced into ${PFHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)$ i.e., Eq. 17 reduced to Eq. 38.

  $${PFHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

  (38)

  Which is defined by Liu et al.⁵¹.

• ii. ${{{{C}}{{P}}{{F}}{{W}}{{H}}{{M}}}_{{{\mu}}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ reduced into ${{{P}}{{F}}{{W}}{{H}}{{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ i.e., Eq. 19 reduced to Eq. 39.

  $${PFWHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\sqrt{\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)}\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right),\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\\ \left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left(\sqrt{{\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)\end{array}\right)$$

  (39)

  Which is defined by Dejian et al.⁴⁰.

• iii. ${{{{C}}{{P}}{{F}}{{G}}{{H}}{{M}}}_{{{\mu}}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ reduced into ${{{P}}{{F}}{{G}}{{H}}{{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ i.e., Eq. 25 reduced to Eq. 40.

  $${PFGHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left({\mu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left({\mu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\mathfrak{y}}_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\mathfrak{y}}_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\nu }_{\mathcal{P}}\right)}^{\mathfrak{T}}{\left(1-{\nu }_{\mathcal{Q}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

  (40)

  Which is defined by Dejian et al.⁴⁰.

• iv. ${{{{C}}{{P}}{{F}}{{W}}{{G}}{{H}}{{M}}}_{{{\mu}}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ reduced into ${{{P}}{{F}}{{W}}{{G}}{{H}}{{M}}}^{\mathfrak{T},\mathfrak{J}}\left({\boldsymbol{\vartheta }}_{1},{\boldsymbol{\vartheta }}_{2},\dots ,{\boldsymbol{\vartheta }}_{\mathfrak{z}}\right)$ i.e., Eq. 27 reduced to Eq. 41.

  $${PFWGHM}^{\mathfrak{T},\mathfrak{J}}\left({\vartheta }_{1},{\vartheta }_{2},\dots ,{\vartheta }_{\mathfrak{z}}\right)=\left(\begin{array}{c}{\left({1-\prod_{\mathcal{Q}=1, \mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left(1-{\mu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left(1-{\mu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.},\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\mathfrak{y}}_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\mathfrak{y}}_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\\ {\left({\prod_{\mathcal{Q}=1,\mathcal{P}=1}^{\mathfrak{z}}\left(1-\left({\left(1-{\left({\nu }_{\mathcal{P}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{T}}{\left(1-{\left({\nu }_{\mathcal{Q}}\right)}^{{\mathbbm{w}}_{\mathfrak{T}}}\right)}^{\mathfrak{J}}\right)\right)}^{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{${\mathfrak{z}}^{2}+\mathfrak{z}$}\right.\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathfrak{T}+\mathfrak{J}$}\right.}\end{array}\right)$$

  (41)

  Which is defined by Dejian et al.⁴⁰.

Statistical comparison of ranking scores

To verify the reliability and consistency of the suggested algorithm, we compared its ranking scores with other existing methods using the weighted Spearman’s rank correlation coefficient (WSRCC). The WSRCC is calculated as:

${\rho }_{w}=1-\frac{6\sum_{i=1}^{m}{w}_{i}{d}_{i}^{2}}{\sum_{i=1}^{m}{w}_{i}\left({m}^{2}-1\right)}$​

where ${w}_{i}$​ is the weight of the $ith$ alternative, $di$ is the rank position difference between the proposed and a comparative approach, $m$ is the number of options.

Correlation analysis and confusion matrix

The performances of the WSRCC are shown in Table 7:

Table 7 Weighted Spearman’s rank correlation coefficient (WSRCC) between the proposed C-PFHM method and other comparative MCDM algorithms.

These values of high correlation $(> 0.94$) validate that the proposed method corresponds with known techniques, and it also showcases its distinguishing ability in ranking (Fig. 9).

Fig. 9

Illustrates the weighted Spearman’s rank correlation coefficient (WSRCC) between the proposed algorithm and other comparative methods.

Advantages and disadvantages

The HM AO in the C-PF framework offers different benefits in MCDM problems. Some of its benefits and possible disadvantages with respect to others are described below and presented in Table 8:

Table 8 Summary of Advantages and limitations of the suggested work.

Overall, the HM provides strength in managing uncertainties and captures interrelatedness, thus being a useful statistical measure. Its sensitivity to outliers, restricted use in dealing with positive values, and computationally intensive nature could, however, be problematic. The applicability of the HM relies on the data’s context as well as the demands of the analysis.

Conclusion

A newly advanced decision-making framework has been developed in this study aimed at evaluating financial management policies through Circular Picture Fuzzy Sets (CPFS). CPFS models capture more realistically and flexibly experts’ judgments with nonmember ship, hesitation degrees, and circular consistency rendering decision-making in finance amidst uncertainties, risks, and fluctuations in the market. The assessment of financial policies using CPFS is successfully shown to the most important criteria such as rate of return, liquidity, market volatility resistance, and risk management. These rankings can be well structured for decision-making and the selection of the best financial strategies using combinations of multiple criterion decision-making (MCDM) methods with CPFS-TOPSIS or CIFHM. Undoubtedly, CPFS enhances the preciseness of the decision, transparency, and adaptability in those findings, making it significantly useful for financial institutions, policymakers, and investors. HM AO is very important in aggregating the various criteria and is very useful in assessing the information. The suggested approach returns a solution in terms of a singleton set, which allows for the DM process. Based on all the provided aspects, the main contributions and analyses of this research are briefly summed up as follows:

• i. The theory of C-PFS with the heronian mean aggregation operator (HM AO) is proposed, providing an efficient method for solving multi-criteria decision-making (MCDM) problems with circular properties—an aspect where the conventional PFS fail. The corresponding fuzzy sets and score function have been established.

• ii. The HM AO, which can grasp the interrelationship between multiple criteria, was implemented in the C-PFS environment to solve MCDM problems.

• iii. Essential properties of the proposed approach idempotency, monotonicity, and boundedness were mathematically analyzed to prove its theoretical correctness.

• iv. An algorithm for solving MCDM problems by using the proposed operators in a circular fuzzy environment was formulated.

• v. In order to show the efficiency and practical applicability of the method, a numerical example was presented and a comparison with other available methods was given.

Future Work:

Future research can investigate the use of sophisticated computational methods like neural network-based models, whose performance has been encouraging across various applications ranging from pantograph differential models⁵², language learning models⁵³, and hepatitis B virus dynamics⁵⁴. Usage of wavelet-based neural computation, especially in the context of Morlet and Meyer wavelets, could also be used to improve the modeling of delay differential systems, transport networks, and ecological dynamics^55,56,57,58. In addition, the application of Meyer wavelets and heuristic methods to nonlinear singular differential equations and medical modeling e.g., smoking trends and COVID-19 dynamics^59,60,61,62 is an important avenue to explore in developing the analytical powers of our technique. Higher-order neuro-swarm hybrid approaches and fractional-order implementations have also successfully tackled LaneEmden and Emden–Fowler type equations^{63,64,65,66,67}, which could yield powerful tools to expand the present framework. Lastly, stochastic mathematical modeling methods⁶⁸ may be used for the inclusion of uncertainty and probabilistic behavior in intricate decision-making situations. We will also explore the Einstein AO^69,70, Aczel-Alsina power AO⁴³, Schweizer-Sklar prioritized AO⁷¹, trigonometric AO⁷², We can use it for the MCDM method using different frameworks^13,73 including SF and TSF^74,75 environments.