Light weight encryption technique: a cellular automaton based approach for securing health records

Abstract

Digitization has led to enormous data generation that needs to be maintained and shared regularly across different platforms. The healthcare industry strives on this enormous data sharing as it forms the backbone of the industry. But such large platforms always face security concerns in terms of privacy preservation and unauthorized access. To overcome this, a robust encryption mechanism is needed to ensure smooth sharing facility but another consideration is the complexity involved in the encryption process. Although many encryption techniques exist, the need of the present situation is to shift to light weight encryption techniques to facilitate quick and efficient data protection schemes. The paper introduces an ultra light weight encryption technique based on the PRESENT algorithm coupled with cellular automaton to provide an added benefit in key generation. The algorithm has been tested on some benchmark tests like the NIST test suite and Diehard test to show its efficacy.

Introduction

In the past few years, the use of Electronic Health Records (EHRs) have gathered great attention and has become profoundly widespread in the healthcare industry. The healthcare industry generates massive records such as prescriptions, lab reports, scan reports, insurance tracker, etc. and there is an urgent need to digitize them creating EHRs. They contribute towards ease of data storage, data management and storing. An EHR essentially contains details of a patient including his personal details, demographic details and mostly medical history details. These EHRs can be thought of to be ever growing as vast amount of data in generated by the healthcare industry. So any system that manages these data must follow an ethical obligation to protect the patients’ confidentiality and hence provide efficient data security technique without compromising the availability of the data. EHRs are prone to exposure and threat from unauthorized access who can modify or steal the data. Hence, the privacy of the data is of utmost importance, and as a mechanism to achieve this, encryption plays an important role. Encryption is used to maintain the secrecy and integrity of the data without compromising its availability and therefore is a right solution to maintain data confidentiality.

In terms of technical study in the security of EHRs, the foremost aim is to provide trust in the document and secondly, to ensure the security of the same by maintaining privacy which can be handled using suitable encryption technique¹. For securing EHRs, various encryption techniques have been proposed in the literature like the Data Encryption Standard (DES)², Advanced Encryption Standard (AES)³ and Rivest-Shamir-Adleman (RSA)⁴ being the traditional ones. However, with a rapid development in the field of computer hardware, DES has already been proved insecure⁵, AES on the other hand struggles with two important factors: the encryption speed and implementation area⁶ and it is difficult to write constant-time high-speed AES software for general purpose computers to prevent timing attack⁷. RSA being asymmetric algorithm solves the inherent problem of key distribution but suffers from a major drawback owing to its greater computational overhead. Hence, leading to the development of hybrid models^8,9,10. Later encryption techniques like optical encryption¹¹, ECC¹², chaos based¹³, parallel¹⁴, etc. and the hybrid models although improved the security concerns but overall were computational expensive and hence are rendered less likely to be used for on the go platforms which are implemented on smart mobile devices. These smart devices generally have constrained resources in terms of low computation power, limited battery life, small size, small memory, and limited power supply. Hence, the conventional cryptographic primitives might not be suited for low-resource smart devices. Since EHRs compromises of heterogeneous files (images, text, numeric, etc.), these hybrid models are difficult to apply in cases of securing EHRs due to data size limitations, and capacity. These techniques are hence, not suitable for light weight devices and thus, there is a need for more portable, secure devices for scanning and maintaining EHRs. Since, low resource devices have very few GEs (gate equivalent) to spare for security implementation, its essential that the encryption is capable of implementing in few GEs. Lightweight cryptography addresses implementation challenges by minimizing gate equivalents (GEs), power consumption, and memory usage while maintaining strong protection for sensitive patient data. In healthcare data management, where real-time transmission of electronic health records (EHRs) is critical, lightweight algorithms enable secure encryption without compromising system performance or battery life. Furthermore, the heterogeneous nature of healthcare data ranging from high-resolution medical images to real-time vital sign telemetry requires adaptable solutions that can function across devices with varying computational capabilities. This ensures that sensitive patient information remains protected across all endpoints, from cloud servers to resource-constrained edge devices, while supporting the seamless interoperability essential for modern healthcare delivery.

Large-scale healthcare data sharing faces critical security challenges that extend beyond encryption, including privacy breaches through data re-identification, integrity threats from unauthorized tampering, and access control vulnerabilities in interoperable systems. Third-party risks in cloud-based platforms and regulatory complexities in cross-border data flows further exacerbate these concerns, while resource-constrained IoT medical devices demand specialized lightweight solutions. The paper presents an enhanced lightweight encryption technique to achieve data privacy and is considerably useful for EHR encryption as it can be implemented on any mobile or lightweight devices. It directly addresses these challenges by proposing an ultra-lightweight cellular automata-based encryption technique that achieves three key objectives: (1) preserving privacy through NIST-validated cryptographic randomness to prevent re-identification attacks, (2) maintaining data integrity via robust key generation that resists tampering, and (3) enabling efficient implementation on low-GE devices (913 GEs) for practical deployment across healthcare IoT ecosystems. This work thus bridges a critical gap between theoretical security and practical implement ability in resource-constrained medical environments.

Randomness plays a fundamental role in cryptographic key generation because the security of cryptographic systems hinges on the unpredictability of the keys. A key that exhibits patterns, repetitions, or low entropy can be more easily guessed, predicted, or reproduced by an attacker using methods such as brute-force search, statistical analysis, or differential cryptanalysis. High-quality randomness ensures that each key is unique and statistically independent from others, making it computationally infeasible for an adversary to reverse-engineer the key or exploit any underlying structure. This is especially important in symmetric encryption systems like block ciphers, where weak or predictable keys can compromise the entire encryption process. Cellular Automata (CA), particularly in their non-uniform form, offer a powerful mechanism for generating pseudo-random sequences suitable for cryptographic key generation. A CA consists of a grid of cells, each of which updates its state based on a set of local rules and the states of its neighboring cells. In uniform CA, all cells follow the same update rule, which can lead to predictable or repeating patterns over time. In contrast, non-uniform CA assigns different rules to different cells, introducing structural irregularity and chaotic behavior in the evolution of the system. This diversity in rule application enhances the entropy of the generated output and helps eliminate periodic or symmetric patterns. When initialized with a simple binary configuration, a non-uniform CA, especially one that uses a carefully selected set of rules with known chaotic or nonlinear behavior, can evolve into highly complex and seemingly unpredictable configurations. This dynamic, coupled with the use of periodic boundary conditions and multiple iterations, creates an environment where a small change in the initial input leads to a drastically different output. Such characteristics are essential for cryptographic randomness. Furthermore, the deterministic linear or non-linear CA makes it suitable for hardware-based implementation of lightweight and efficient random number generators. As a result, non-uniform CA serves as a promising alternative to traditional PRNGs in cryptographic systems, especially in constrained environments like IoT devices, RFID tags, and embedded systems where simplicity, speed, and low resource consumption are crucial.

The remaining part of this article is structured as: Section "Literature review" provides a comprehensive literature survey of lightweight encryption algorithms with a special focus on their usage in securing electronic health records. Section "Proposed methodology" presents the proposed methodology with a detailed description of PRESENT, a lightweight encryption method, and the use of cellular automaton to reduce the gate equivalent required in the key generation stage of PRESENT. Section "Results and discussion" analyzes the result part which mainly focuses on the randomness of the generated key through cellular automaton through NIST and DIE-HARDER statistical randomness tests.

Literature review

Lightweight encryption algorithms have gained momentum recently due to the advent of ultra light weight devices like IoMT devices. Initially variants of the traditional encryption techniques were proposed as lightweight models by altering the structure of the model. DESL (DES Light), for instance used a single S-box as compared to the S-box used in eight repeated rounds, hence bringing down the computational effort drastically¹⁵. Another scheme based on altering the Feistel scheme, key alternating Feistel (AKF), also made implementation changes in the fiestal structure design to make it computationally less expensive¹⁶. Similar lightweight AES variations also exist taking parameters latency and power as their design considerations for applications in low resource devices like sensor nodes and RFID tags¹⁷. Later researches include a compressive sensing and a modified seven-dimensional hyperchaotic map to generate secret keys and further using non sub-sampled contourlet transform (NSCT) for compressing has been used to generate lightweight encryption¹⁸. A lightweight distributed access control system with keyword search (LDAC-KS) model utilizing user’s device for lightweight computation and redirecting the heavy calculations to an auxiliary computation center (ACC) was proposed in¹⁹. A similar approach, LiST was also highlighted in¹⁹ but although the burden on the user’s device is less but a lot of communication overhead related to task distribution between the user device and the ACC is incurred. These lightweight variations still consume around 2200 GEs for encryption²⁰.

Specific lightweight encryption techniques also gained momentum as these algorithms were not variant of the existing ones but were specifically designed for low resource devices with an aim to minimize the GEs. CLEFIA is a compact algorithm that uses two S-boxes and a differential switching mechanism to achieve encryption²¹. Although the reduced number of S-boxes offer some reprise in GEs but it still results in a higher memory requirement. Another lightweight block cipher HIGHT (high security and light weight) has a 64-bit block length and 128-bit key length, which render it suitable for low-cost, low-power, and ultra-light implementation²². The prominent feature of HIGHT is that it consists of simple operations such as XOR, mod addition and bitwise rotation and can be implemented with 3048 GEs. A similar 64-bit block cipher mCrypton with three key size options (64 bits, 96 bits and 128 bits) was also proposed with a claim to use about 2400–3000 gates for encryption only²³. The tiny encryption algorithm (TEA) uses mixed (orthogonal) algebraic group operations for its 64 Feistel rounds utilizing a total of 2,883 gates²⁴. PRESENT is a Substitution Permutation network (SPN) based on 80 bit or 128 bit key size and 64 bit block size and is capable to be implemented in ultra small applications with 1000 GEs²⁵. Owing to the less GEs, it has promising application in ultra lightweight devices which have very limited resources, and is worth exploring for optimized implementation.

Further advancements in lightweight encryption techniques have further expanded the scope of secure and efficient solutions for Electronic Health Records (EHRs). A model combining Elliptic Curve Cryptography (ECC) with chaotic functions, achieving robust security while maintaining low computational overhead was proposed in²⁶. Similarly, a quantum-resistant lightweight encryption framework leveraging a tree structured encryption, addressing future threats posed by quantum computing was discussed in²⁷. Their work demonstrated significant improvements in key generation speed and resistance to brute-force attacks but the complexity needs to be analyzed. Another notable contribution explored the use of bio-inspired algorithms for dynamic cryptosystems showcasing enhanced randomness and reduced gate equivalents (GEs)²⁸. These recent developments highlight the ongoing evolution of lightweight encryption techniques, emphasizing their critical role in securing sensitive healthcare data while adapting to emerging technological challenges. The field continues to see rapid innovation, with particular focus on balancing security requirements with the stringent resource constraints of modern healthcare IoT ecosystems. This forms the basic ideology of the proposed encryption technique which is based on the following consideration and so is the selection of the encryption technique:

• 1. Smaller block size

• 2. Smaller key size

• 3. Less complex round structure

These requirement prompt the authors to explore the possibility of using cellular automaton in encryption technique reprising its lightweight property. Cellular automata (CA) are known to be capable of modeling complex systems, though the basic model of it is a simple grid-like structure²⁹. It has found application in cryptography because of its inherent simplicity in implementation in hardware or sensor devices. It is capable of predicting the next state by looking at the initial state³⁰. This had also popularized the use of CA in different domain of encryption like in generating stream ciphers³¹, block ciphers³², pseudo-random number/pattern generator³³ to name a few. CA are essentially rule based structure and hence it can be made more cache-efficient to reduce the time to fetch rule vectors³⁴. The paper also utilizes these features of CA and proposes an optimal encryption technique in terms of GEs. Pseudo-random number generation is a critical component in cryptographic systems. While CA have been widely explored for this purpose, most existing research has focused on uniform CA, where all cells follow the same rule. In contrast, non-uniform CA, where each cell can evolve based on a different rule, has received relatively limited attention. Despite this, experimental results indicate that the proposed non- uniform CA setup demonstrates strong potential for generating random keys. Although recent studies have continued to incorporate CA in cryptographic designs, they predominantly rely on uniform rule sets, leaving the advantages of non-uniform CA largely under-explored. A recent paper³⁵ explains elliptic curve cryptography (ECC) using 2-dimensional cellular automata. The paper combines Cellular Automata (CA), sponge construction, and Elliptic Curve Cryptography (ECC) to enhance security in image transactions. It aims to provide high diffusion, strong randomness, and resistance to cryptographic attacks, making it suitable for resource-constrained environments such as IoT and secure communications. On the other hand, our method focuses exclusively on key scheduling using a non-uniform, evolving one-dimensional Cellular Automaton (CA), which aligns naturally with the structure and requirements of block ciphers like PRESENT. By avoiding the computational overhead associated with sponge constructions, permutations, and elliptic curve cryptography (ECC) as in³⁵, the proposed approach remains highly efficient and lightweight, ideal for constrained environments. The use of a non-uniform rule vector introduces high entropy and round-to-round diversity in the generated keys, thereby strengthening resistance against key schedule-related cryptanalytic attacks while preserving hardware simplicity. Unlike the CA-based hashing scheme presented in³⁵, which is designed for image hashing and not directly applicable to block cipher operations, our technique is designed to deliver distinct round keys, a critical requirement for secure multi-round encryption. The major contribution of the paper is summarized as:

• Ultralight weight encryption technique ensures faster implementation.

• Cellular Automaton technique for key generation provides a robust implementation in terms of security concerns.

• The proposed method has been applied on securing electronic health records and shows promising application in the domain in terms of efficiency and security.

Proposed methodology

The proposed model is based on light weight cryptography loosely based on the PRESENT 80 technique. The Present 80 algorithm is an ultra-lightweight block cipher designed for applications where low power consumption, small size, and high efficiency are crucial, such as in embedded systems and Internet of Things (IoT) devices²⁵. It essentially works with a block size of 64 bits, a key size of 80 bits (though it can also support 128 bits) and 31 rounds. Some key features of the PRESENT block cipher are:

• Simplicity: PRESENT is designed with simplicity in mind, using a small number of basic operations to keep the hardware and software implementations straightforward.

• Small Code and Memory Footprint: It has a small code size and memory requirements, making it suitable for devices with limited resources.

• Low Power Consumption: The algorithm is optimized for low-power consumption, making it appropriate for battery-powered devices.

• Speed: Despite its simplicity, PRESENT is designed to provide reasonable encryption and decryption speeds for its target devices.

• Security: Being lightweight, PRESENT aims to provide a reasonable level of security against common cryptographic attacks, although its security margin may not be as high as more complex ciphers like AES.

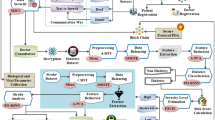
Present 80 follows a Substitution-Permutation Network (SPN) structure, which consists of several rounds of substitutions and permutations. Each round transforms the input data to make it increasingly difficult to deduce the original information or the encryption key without the correct key. The flowchart of the proposed model is depicted in Fig. 1. Ultra-lightweight encryption techniques offer significant advantages over traditional encryption methods, particularly in environments with highly constrained resources such as RFID systems, Internet of Things (IoT) devices, and embedded sensors. These techniques are specifically designed to operate with minimal computational power, memory, and energy consumption. Unlike traditional algorithms such as AES or RSA, which require substantial processing capabilities and storage, ultra-lightweight encryption relies on basic operations like bitwise XOR, rotations, and permutations. This simplicity results in faster execution, lower power consumption, and a reduced code footprint, making it ideal for devices where conserving battery life and minimizing cost are critical. Another key advantage of ultra-lightweight encryption is its suitability for large-scale deployments of low-cost devices. These techniques enable basic yet effective security in systems where implementing full-strength cryptographic algorithms would be impractical or too costly. By balancing security with performance, ultra-lightweight encryption ensures that essential data protection is maintained without overburdening the hardware. While the security provided is generally more limited compared to traditional encryption, it is often sufficient for the low-risk environments these devices operate in. This makes ultra-lightweight encryption a practical and efficient choice for securing communication in modern, resource-constrained applications.

Fig. 1

Workflow of the proposed encryption technique.

Key components

• Substitution Layer (S-Box): The S-box is a non-linear substitution table that takes a fixed number of input bits and transforms them into another fixed number of output bits. Present 80 uses a 4-bit S-box, meaning it operates on 4 bits at a time. This introduces non-linearity into the cipher, which is essential for security.

• Permutation Layer (P-Layer): The P-layer is responsible for the diffusion of bits across the block. It rearranges the bits of the block according to a predefined pattern. This helps to spread the influence of each input bit over the entire block, contributing to the algorithm’s overall security.

• Key Schedule: The key schedule generates round keys from the original key. Each round key is used in a different round of the encryption process. The key schedule of Present 80 involves rotating the key bits and applying an S-box transformation to part of the key.

• S-Box: The S-box is a 4-bit substitution box that introduces non-linearity into the algorithm. It takes a 4-bit input and outputs a 4-bit value according to Table 1:

• P-Layer: The P-layer rearranges the bits of the state to provide diffusion. It maps each bit position to a new position according to Table 2.

• Key Scheduler: The key schedule generates round keys from the original key. Each round key is used in a different round of the encryption process. The key schedule of Present 80 involves rotating the key bits and applying an S-box transformation to part of the key.

Table 1 Substitution (S) Box.

Table 2 Permutation (P) Box.

Encryption process

The encryption process in the existing PRESENT algorithm involves generating round keys which is obtained by performing an XOR operation with the initial round key followed by a series of permutation nad substitution as highlighted in Algorithm 1.

Algorithm 1

Existing PRESENT Algorithm

As discussed in the previous section, the PRESENT block cipher operates on 64-bit blocks of data and supports key lengths of 80 or 128 bits. It uses a combination of substitution-permutation network (SPN) structure and a compact key schedule. The SPN structure involves repeated rounds of substitution and permutation operations. The cipher consists of two main components: a key schedule algorithm and a lightweight substitution-permutation network (SPN) structure. The key schedule algorithm generates round keys from the user-provided key, while the SPN structure performs the encryption and decryption operations.

During encryption, the input plaintext undergoes a series of substitution and permutation operations for a certain number of rounds, determined by the key size. The round keys generated by the key schedule algorithm are XORed with the plaintext at each round to provide confusion and diffusion. This cipher uses a S-Box (Substitution Box) as one of its key components. The S-Box is a fundamental element in symmetric key ciphers and it is responsible for performing substitution operations on the data during the encryption and decryption processes. The specific S-Box used in PRESENT is designed to be compact while providing adequate security for lightweight cryptographic applications. The PRESENT S-Box is defined as a 4 × 4 lookup table, meaning it operates on 4-bit inputs and produces 4-bit outputs.

The key generation process for the 80-bit key variant of the PRESENT cipher involves creating a round key for each round of encryption. Here is a high-level overview of the key generation algorithm:

• Key Expansion: Expand the 80-bit key into 128 bits by appending 48 zero bits to the right. This results in a 128-bit expanded key.

• Round Key Generation: Divide the expanded key into 32-bit words. Then, split these words into two 16-bit halves.

• Key Scheduling: Generate round keys using a round function applied iteratively. Each round key consists of 64 bits (two 32-bit words).

• Round Constants: XOR round constants to the key words at specific positions determined by the round number. This step comprises of the following sub-steps:

  • Initialization: Expand the 80-bit key to 128 bits by appending 48 zero bits.

  • Splitting: Split the 128-bit key into 8 words, each of 16 bits.

  • Round Key Generation:

  • Rotate the key by 61 bits to the left.

  • Apply the S-box (substitution box) to the leftmost 4 bits.

  • XOR the round number (starting from 1) to the rightmost 4 bits.

  • XOR the round number to the leftmost 4 bits.

  • Rotate the key by 61 bits to the left.

• Key Schedule: Repeat step 3 for each round (31 rounds total for 80-bit key).

• Round Constants: XOR round constants to specific key words at each round.

Gate equivalent required for key generation process

PRESENT uses 64-bit XOR operation for key generation for each of the 31 round operations. The 64-bit key for each round is generated from the initial 80-bit key in PRESENT-80. A simple 32-bit XOR operation requires 80 GEs (Gate Equivalents) which for each round of PRESENT-80 is 20 GEs since it performs a 4-bit XOR operation two times in each round. So, a total of 620 GEs is required only in the key generation step of the algorithm. Although, good for lightweight devices but this can cost extra overhead if applied for larger documents such as EHRs. So, in the subsequent section, we present a modified key scheduling algorithm for PRESENT-80. The modified version uses Cellular Automata for round key generation of PRESENT-80 from an initial 64-bit cellular automata.

The key scheduling algorithm for the modified version of PRESENT-80 uses a 64-bit cellular automata. So, we call it PRESENT-64. Cellular automata (CA) are mathematical models used to simulate complex systems, particularly in the fields of physics, biology, and computer science. They consist of a grid of cells, each of which can be in one of a finite number of states. The grid evolves over discrete time steps according to a set of rules based on the states of neighboring cells. Key components of cellular automata include:

• Grid: A regular lattice or grid structure composed of cells, typically arranged in one, two, or three dimensions.

• States: Each cell in the grid can be in one of a finite number of states. Common examples include binary states (0 or 1), colors, or more complex states.

• Neighborhood: The neighborhood of a cell defines which other cells influence its state. Typically, this includes the cell itself and its immediate neighbors, although variations exist such as von Neumann or Moore neighborhoods.

• Transition Rule: A rule determines how the state of each cell evolves over time based on the states of its neighbors. This rule is applied simultaneously to all cells in the grid at each time step.

A vast spectrum of behaviours, from straightforward patterns to extremely complex and unpredictable dynamics, can be seen in cellular automata. Compared to alternative techniques like random number generators (RNG), cellular automata have a variety of benefits, including straightforward hardware implementation and simple algorithms. The low logic required, regularity, modularity, and locality of interconnections are some of the advantageous aspects of CA for VLSI implementation. These characteristics also make them appropriate for on-board applications, such as associative memories, built-in self-test circuits, and specialized massively parallel fine-grained computers. A cellular automaton (CA)³⁶ is a mathematical tool known for producing chaotic patterns. It is a discrete dynamical system composed of a lattice of cells, each of which can be in one of two states, typically represented as 0 or 1. The state of each cell changes based on its neighborhood condition and a local function, often referred to as a ’rule’ as shown in Fig. 3 below. Traditionally, all cells in a CA follow the same rule. However, modern computational techniques introduce non-uniformity, allowing each cell to follow a different local rule. This non-uniform approach can efficiently perform various tasks.

We have employed the use of a linear cellular automata with varying rules to generate 31 round keys from an initial 64-bit key. A more detailed description of PRESENT-64 follows the following steps:

• Key Initialization: A 64-bit initial random key of 0s and 1s is shared between the two parties.

• Round Key Generation: 31 round keys of PRESENT-64 are generated using the cellular automata rule is $\langle 90, 30, 45, 150, 165, 105, 90, 30 \rangle$

The proposed key scheduling algorithm using cellular automata is shown in Algorithm 2 and its corresponding non-uniform CA in Fig. 2 below:

Algorithm 2

Optimized PRESENT with 64-bit Cellular Automata

Fig. 2

Architecture of the key generation module.

The above CA shown in Fig. 2 represent the hardware implementation of the proposed key scheduling algorithm and uses 8 different CA rules viz. 90, 30, 45, 150, 165, 105, 90, 30 to generate 8-bit output from an initial 8-bit input. For generating a 64-bit round key, this CA is repeated 8 times thus giving us the desired 64-bit round key. The input key for each round is the output of the previous round i.e. $K_i = K_{(i-1)}...... 1< i < 31$. This input key in each round goes through 8 CAs as shown in the figure to produce a unique round key for each of the 31 rounds. In this study, we utilize a 3-neighborhood, 2-state non-uniform CA with periodic boundary conditions. Here, a cell’s state may change from 0 to 1 (or vice versa) depending on the states of its left and right neighbors. The periodic boundary condition means that the right neighbor of the rightmost cell is the leftmost cell, and vice versa. We employ a non-uniform CA with the rule vector $\langle 90, 30, 45, 150, 165, 105, 90, 30 \rangle$ evolving over 32 iterations. Given an initial configuration of 8 bits as 0 1 0 1 0 1 0 1, the CA evolves to 0 0 0 0 0 1 1 1 after 32 iterations. Cellular Automaton (CA) rules are typically represented in a tabular format (as shown in Table 3), where each row maps a specific combination of present states (PSs) of a cell and its neighbors to the corresponding next state (NS) of the cell.

Table 3 CA rule table: mapping present states to next states.

In the context of a non-uniform CA consisting of $n$ cells, the behavior of each cell is governed by a distinct rule specified in a rule vector $R = \langle R_0, R_1, \ldots , R_i, \ldots , R_{n-1} \rangle$, where $R_i$ denotes the rule applied to the i-th cell. In contrast, a uniform CA applies the same rule to all cells, meaning $R_0 = R_1 = \cdots = R_{n-1}$. This distinction allows non-uniform CAs to exhibit more complex and less predictable behavior, making them particularly suitable for cryptographic applications such as dynamic key generation.

This type of CA generates unpredictable patterns during evolution with simple rules³⁷. The unpredictable nature can also be seen in the space-time diagram shown in Fig. 3. This unpredictability enhances system security and makes it less vulnerable to attacks.

Fig. 3

State-space Diagram.

PRESENT-80 and PRESENT-64 comparison

As discussed earlier, PRESENT-80 requires 20 GEs in each round for each of the 31 round key generation and thus a total of 640 GEs is required in only the key generation module. The demonstrated PRESENT-64 requires no use of XOR operations for round key generation and employs only different CA rules repeated 8 times in each round. The rules in CA checks for only the neighboring grids/cells and based on each specific rule the output of a grid/cell is selected. Further, since the above demonstrated CA implies the use of 8 different rules so, the generated key stream is random enough to provide efficient security. So, the proposed key generation module efficiently reduces the total GE requirement of PRESENT-80 which is approximately equal to 1533 GEs by 620 GEs giving a total of 913 GEs. This reduced amount of GE makes the modified algorithm much useful for securing larger documents such as EHRs in lightweight devices. Figure 4 below shows the overall architecture of PRESENT 64.

Fig. 4

Architecture of PRESESNT-64.

Results and discussion

PRESENT-80 is specifically optimized for environments with limited computational and memory resources, such as RFID tags and embedded systems. Its compact design allows for efficient execution on small microcontrollers and hardware circuits. In software, the cipher achieves relatively fast encryption speeds for its category, using just over 1000 clock cycles per 64-bit block on 8-bit microcontrollers. In hardware, PRESENT is extremely compact, requiring only around 1570 gate equivalents (GE), and can achieve throughputs of up to 11.7 kbps at a 100 kHz clock rate. Although its speed does not match modern high- throughput ciphers, it is more than adequate for low-bandwidth applications. PRESENT-80 operates on a Substitution-Permutation Network (SPN) structure with 31 rounds, each involving simple operations: XOR with the round key, a 4-bit S-box layer, and a bit permutation layer. These lightweight operations make the cipher computationally efficient, with encryption complexity scaling linearly with the number of rounds. Decryption is similarly efficient, though it requires inverting the key schedule, which introduces a slight overhead. The simplicity of the operations also makes the cipher well-suited for hardware implementations, where area and power consumption are critical metrics. PRESENT-80 has been subject to extensive cryptanalysis and has demonstrated strong resistance to a range of attacks. Differential and linear cryptanalysis are largely ineffective against the full 31-round version, requiring impractically large numbers of plaintexts and computations. Biclique attacks slightly improve over brute force, but still require nearly the full key space (around 2⁷⁹ operations). While algebraic attacks have been explored, they have not broken the full cipher. However, due to its simplicity and regular structure, PRESENT-80 can be vulnerable to side-channel attacks such as power analysis if not properly mitigated in implementation.

NIST random statistical suite

This bar graph in Fig. 5, shows the p-values obtained from multiple randomness tests within the NIST Statistical Test Suite. Each test evaluates a different aspect of randomness for the generated cryptographic keys.

• 1. Frequency (Monobit) Test: The p-value is around 0.8, indicating a good balance of zeros and ones, suggesting no significant bias in the data.

• 2. Frequency Test within a Block: The p-value is very low, close to 0, suggesting some potential non-randomness in specific blocks of the data.

• 3. Runs Test: The p-value is relatively low, indicating possible issues with the number of runs of consecutive bits, which may suggest patterns.

• 4. Test for the Longest Run of Ones in a Block: The p-value is moderately low, pointing to potential deviations from randomness in long sequences of ones.

• 5. Binary Matrix Rank Test: The p-value is moderate, indicating that the matrix rank distribution is reasonably random, showing good independence among bits.

• 6. Discrete Fourier Transform (Spectral) Test: The p-value is around 0.4, suggesting the absence of periodic patterns, which is desirable for randomness.

• 7. Overlapping Template Matching Test: The p-value is low, indicating possible repeated patterns in the data.

• 8. Linear Complexity Test: The p-value is high, suggesting that the generated sequence has a complex structure, indicative of high randomness.

• 9. Serial Test (First and Second): Both p-values are high, indicating that the sequences do not exhibit significant dependencies.

• 10. Approximate Entropy Test: The p-value is very low, suggesting some recurring patterns that affect entropy.

• 11. Cumulative Sums Test (Forward and Backward): Both p-values are moderately high, indicating that the cumulative sums are behaving randomly without significant deviations.

Overall, the graph shows a mixture of high and low p-values, indicating areas where the cryptographic key generation performs well in terms of randomness and areas where improvements could be made.

Fig. 5

P-values of various randomness tests.

Fig. 6

P-values of random excursions test for different states.

In Fig. 6, showcases the p-values for the Random Excursions Test at various levels (from − 4 to + 4). The p-values generally exhibit a wide range, highlighting differences in randomness based on the test criteria. For state − 4, the p-value is around 0.6, indicating good randomness; the p-values for states − 3, − 1, and + 4 are relatively low, suggesting some non-random behavior; and the p-values for states − 2, + 1, + 2, and + 3 are moderate to high, indicating acceptable randomness. The variability in p-values across different states suggests that the generated keys exhibit randomness in some states but show potential areas for improvement in others.

Fig. 7

P-values of random excursions variant test for different states.

As we can see in the Fig. 7, presents the p-values for the Random Excursions Variant Test for different states (ranging from − 9.0 to + 9.0). The bar graph reveals how the p-values fluctuate across these variants, with most values comfortably above common significance thresholds, indicating a random distribution in the tested sequence. The p-values for states − 9, − 5, − 2, + 2, + 3, + 5, + 6, + 7, + 8, and + 9 are high, indicating strong randomness whereas the p-values for states − 8, − 7, − 4, − 3, − 1, + 1, and + 4 are lower, suggesting potential non-random behavior.

Random Excursion and Random Excursion Variant tests are crucial in assessing the randomness of binary sequences generated by our model, which is essential for ensuring the security and robustness of cryptographic keys. In Fig. 6, the Random Excursion Test examines the deviations from an expected random walk within cycle structures, while in Fig. 7, the Random Excursion Variant Test extends this analysis to the total number of visits to each state across the entire sequence. Successfully passing these tests confirms that our model produces sequences with high entropy and without predictable patterns. This level of randomness is crucial for thwarting potential cryptographic attacks, thereby significantly enhancing the security framework of our solution. The results from these tests not only demonstrate the effectiveness of our model in generating cryptographically secure keys but also reinforce the model?s applicability in high-stakes security environments where the integrity and unpredictability of cryptographic keys are paramount.

Diehard test

In another analysis, we meticulously employed the Dieharder statistical test suite, a benchmark for rigor and comprehensiveness in assessing the randomness of numerical sequences, crucial in cryptographic and simulation applications. This advanced suite elevates the standard for randomness testing by integrating a diverse set of robust tests, each tailored to scrutinize various aspects of data. The Dieharder suite?s capacity to identify subtle irregularities and patterns, which might be missed by other methods, is paramount in our analysis. It ensures the data or cryptographic keys under scrutiny are subjected to the highest level of randomness evaluation, thus affirming their strength and reliability in security-critical applications. This rigorous assessment provided by Dieharder is invaluable in our research, offering conclusive insights into the integrity and unpredictability of the data, a cornerstone in maintaining the highest standards of cryptographic security.

Fig. 8

Diehard test suite results.

In Fig. 8, as we can see that the graph visualizes the p-values obtained from various tests in the Diehard Test Suite. Each test is aimed at assessing the randomness of a sequence, with p-values close to 0 or 1 suggesting non-randomness. The graph demonstrates a diverse range of outcomes across different tests, indicating the varying effectiveness and sensitivity of these tests in detecting non-randomness in sequences. The majority of tests have p-values comfortably within typical significance levels, suggesting that the tested sequences generally exhibit good randomness properties.

• Diehard Birthdays Test: p = 0.1843, indicating no unusual clustering, which is a positive sign of randomness.

• Diehard Operm5 Test: p = 0.4608, confirming a random permutation sequence of five consecutive numbers.

• Diehard Rank 32x32 and 6x8 Tests: p = 0.7231 and 0.1020, showing good randomness in the rank distribution of matrices.

• Diehard Bitstream Test: p = 0.4268, suggesting an acceptable level of bit variance.

• Diehard OPSO, OQSO, DNA Tests: p = 0.7609, 0.0182, and 0.1640, showing satisfactory randomness levels, although the OQSO test is close to the critical value.

• Diehard Parking Lot Test: p = 0.5440, indicating a random distribution in the simulated parking lot.

• Diehard 2Dsphere and 3Dsphere Tests: p = 0.7165 and 0.6618, confirming good uniformity and randomness.

• Diehard Squeeze Test: p = 0.3681, showing expected variability in data reduction iterations.

• Diehard Sums Tests (1 and 2): p = 0.3213 and 0.5070, confirming the randomness of sums of random floats.

• Diehard Runs Test: p = 0.7093, indicating a good balance in sequences.

Fig. 9

STS serial test variants.

As we can see in Fig. 9, the STS Serial Test results from the Dieharder suite are promising, demonstrating a strong attribute of randomness across various n-tuples. The p-values range from as low as 0.0131 in the 9-tuple to as high as 0.9832 in the 5-tuple, suggesting a balanced mix in the sequence’s randomness. This diverse spread of p-values indicates that the data is not consistently leaning towards predictability or uniformity. The results, predominantly within the acceptable range, affirm the data suitability for cryptographic and security-related applications where randomness is a critical factor.

Fig. 10

RGB Tests.

From Fig. 10, the results for the RGB tests in the Dieharder suite, covering “rgb_bitdist”, “rgb_minimum_distance”, and “rgb_permutations” display a range of p-values that strongly indicate randomness.

• Rgb_bitdist Tests: p-values range from 0.0889 (for 10-bit) to 0.9007 (for 5-bit), suggesting no bias in bit distribution.

• Rgb_minimum_distance Tests: p-values from 0.2932 to 0.8839, showing good randomness in spatial distribution.

• Rgb_permutations Tests: p-values from 0.3091 to 0.8308, confirming randomness in number permutations.

These findings collectively affirm the data?s randomness across various bit patterns and permutations.

Fig. 11

RGB lagged sum tests.

In Fig. 11, the RGB Lagged Sum tests within the Dieharder suite exhibit a diverse range of p-values, from as low as 0.0295 to as high as 0.9949, as can be seen in Fig. 4, covering a wide spectrum of test scenarios. This range indicates a strong characteristic of randomness in the data, with no consistent pattern of predictability. The variability in these results, especially considering the large number of test cases (0-32), underscores the robustness and reliability of the data?s random nature, vital for cryptographic and security applications.

Fig. 12

Diverse randomness tests.

The results for the RGB KS test, DAB tests, and additional Dieharder suite tests demonstrate commendable randomness attributes, as shown in Fig. 12.

• RGB KS Test: p = 0.6539, aligns well with expectations for random distributions.

• DAB Byte Distribution Test: p = 0.3633, indicating good randomness in byte distribution.

• DAB DCT Test: p = 0.1659, showing some potential non-random behavior in discrete cosine transform.

• DAB Fill Tree Tests: p = 0.5220, 0.7704, 0.4155, and 0.8219, indicating randomness in tree-filling algorithms.

• DAB Monobit 2 Test: p = 0.1950, confirming randomness in bit distribution.

These tests collectively ensure that the cryptographic keys generated by our model are robust and secure. The results indicate that while most tests show good randomness, certain areas (such as the DAB DCT test) highlight the need for further improvement to achieve consistent high randomness across all tests. By passing the Diehard and NIST statistical tests, our model demonstrates its effectiveness in generating high-entropy, cryptographically secure keys, suitable for high-stakes security applications. These results reinforce the model’s capability to produce unpredictable sequences, crucial for maintaining the integrity and security of cryptographic operations.

The proposed cellular automata (CA)-based lightweight encryption technique achieves an optimal security-efficiency balance for real-time healthcare data sharing by combining minimal computational overhead (reducing gate equivalents to just 913 GEs) with provably secure randomness through non-uniform CA rules that pass rigorous NIST and Diehard statistical tests. This approach enables real-time operation on resource-constrained medical devices while maintaining robust protection through multiple security layers: the substitution-permutation network provides AES-grade confidentiality for sensitive EHRs, the dynamic CA-based key scheduler prevents pattern prediction attacks, and the adaptable architecture supports variable security levels based on data sensitivity and device capabilities. By outperforming traditional methods in both speed and resource efficiency, the technique addresses the unique challenges of healthcare ecosystems.

To evaluate the strength and unpredictability of the cryptographic keys generated by our proposed PRESENT-64 algorithm using cellular automata, we conducted rigorous assessments using the NIST Statistical Test Suite and the Dieharder Test Suite. The results from the NIST suite reflect a generally strong level of randomness. For instance, the Frequency (Monobit) Test yielded a p-value of approximately 0.8, indicating a well-balanced distribution of zeros and ones. Similarly, tests such as the Linear Complexity and Serial tests (both first and second order) returned high p-values, signifying the absence of predictable patterns and demonstrating the complexity of the generated sequences. The Discrete Fourier Transform (Spectral) Test also performed well, with a p-value of around 0.4, suggesting no periodicity in the data. However, certain areas indicated scope for refinement. The Frequency Test within a Block returned a very low p-value, implying potential bias within localized regions. Additionally, the Approximate Entropy Test and the Runs Test revealed lower p-values, hinting at minor recurring patterns in the bitstream.

The Random Excursion and Random Excursion Variant tests further explored the behavior of state transitions in the generated sequences. Here, states such as − 4, − 2, +2, + 3, + 5, + 6, and + 9 exhibited high p-values (ranging roughly between 0.6 and 0.9), reinforcing the presence of randomness across most state transitions. Nonetheless, a few states like − 3, − 1, +1, and +4 showed lower p-values, suggesting occasional structural regularities that warrant additional tuning. To complement and deepen the statistical validation, we also utilized the Dieharder suite, known for its robustness in uncovering subtle non-random patterns. The Diehard Birthdays Test produced a p-value of 0.1843, confirming a lack of clustering anomalies, while the Operm5 test (p = 0.4608) and Rank tests (p = 0.7231 for 32 × 32 and 0.1020 for 6 × 8) all indicated healthy randomness. The Bitstream Test and the Parking Lot Test recorded p-values of 0.4268 and 0.5440 respectively, further strengthening confidence in the absence of structural bias. While the OQSO test’s p-value of 0.0182 was close to the critical threshold, the accompanying OPSO (p = 0.7609) and DNA (p = 0.1640) tests balanced out this variance. Spatial randomness was confirmed through the 2Dsphere and 3Dsphere tests (p- values of 0.7165 and 0.6618 respectively), and the STS Serial tests, evaluating n-tuples, produced a diverse but healthy spread of p-values from as low as 0.0131 (for 9-tuples) to as high as 0.9832 (for 5-tuples), indicating neither excessive regularity nor deterministic repetition. Further assurance came from RGB and DAB tests, where bit-level and structural randomness were confirmed. For example, RGB Minimum Distance p-values ranged from 0.2932 to 0.8839, and RGB Permutations ranged between 0.3091 and 0.8308. The RGB Lagged Sum Tests showed a wide spread from 0.0295 to 0.9949, reflecting robust unpredictability across multiple iterations. The DAB Fill Tree tests produced p-values in the range of 0.5220 to 0.8219, while the DAB Byte Distribution and Monobit 2 tests gave results of 0.3633 and 0.1950 respectively. Although the DAB DCT test returned a slightly lower p-value of 0.1659, it remained within acceptable bounds. Collectively, these results affirm that our proposed key generation mechanism based on cellular automata not only reduces computational complexity and hardware requirements but also produces keys with a high degree of statistical randomness and cryptographic robustness. Despite a few isolated areas for potential enhancement, the majority of tests confirmed strong entropy, minimal bias, and effective diffusion, making the technique highly suitable for securing Electronic Health Records on low-resource devices.

Conclusion

Healthcare industry often face the issue of security and privacy preservation in managing the electronic healthcare records of patients. The current study presents an ultralight weight encryption technique that addresses the security concerns and is also computationally less complex owing to its reduced Gate Equivalent (GEs). The concept of linear cellular automata has been leveraged as it provides randomness in the key generation process. Apart from being computationally light, the proposed encryption algorithm was also tested against the benchmarks NIST randomness test and the DieHard test. Both the tests establish the appropriate randomness in the key stream of the proposed algorithm.