Introduction

For several decades now, different studies on fractional derivative have been carried out in relation to various physical potential models within quantum mechanical systems. This interest is traced to the fact that this concept plays a vital role in depicting the inner mechanisms of nature and also explains intricate phenomena relating to various fields including solid state physics, optical fiber, control theory, electric circuit, etc1,2,3,4. This phenomenon which seeks better understanding of the non-integer order differentiation and integration from various definitions have been applied to various concepts in science and engineering studies5,6,7,8,9. By employing the Riemann-Liouville’s definition of fractional derivative, different space-dependent fractional Schrödinger equation with some potential models have been considered numerically10,11,12,13. In another development, The fractional derivative definition proposed by Jumarie was employed by Das and his collaborators in obtaining solutions to relativistic and non-relativistic equations with Mie-type, psudoharmonic and Cornell potentials14,15,16.

A conformable fractional derivative (CFD) technique has been proposed and used to investigate the Schrödinger equation with various potential models17,18,19. Mozaffari et al20 employed the concept of conformable derivative to study the fractional harmonic oscillator, within the quantum mechanical framework. The Heun function has been used to investigate the Schödinger equation for the Killingbeck and hyperbolic potentials, using the conformable derivative21. The CFD has also been used to study the N-dimensional radial Schödinger equation of heavy quarkonia with temperature-dependent potential and Trigonometric Rosen-Morse potential22,23. Jamshir et al24 studied the fractional Schödinger equation for a particle with position-dependent mass in an infinite potential well using the CFD. The solutions of the comformable fractional Bohr Hamiltonian with the Kratzer potential has been developed for triaxial nuclei25. The concept of the CFD has been employed to deduce the mathematical model for the Coronavirus Disease 201926. Okorie et al.27 solved the fractional Schrödinger equation with Morse potential, using the conformable fractional Nikiforov-Uvaraov method. Fractional energies and thermodynamics functional of hydrogen dimer were evaluated in their studies.

Recently, a new fractional derivative has been proposed, also known as the generalized fractional derivative (GFD). The CFD has been seen to be a special case of the GFD28. The GFD has offered a substantial improvement over traditional definitions such as the Caputo and Riemann-Liouville derivatives28. The GFD framework help to preserve essential mathematical properties, including the derivative of the product and quotient of functions, Rolle’s theorem, and the mean value theorem. The generalized fractional parameter in the fractional calculus and its application in quantum mechanics express clearly the space-time’s fractal-like properties and modifies the Schrödinger equation’s solutions. It is physically interpreted as a measure of the underlying anisotropic and fractional dynamics, influencing both the energy and wave functions. While the generalized fractional parameter does not correspond to a directly measurable quantity, its variation provides insight into how quantum systems deviate from classical behaviour under such conditions28. Abu-Shady et al.29 obtained the energy eigenvalues of fractional N-dimensional radial Schrödinger equation with Deng-Fan potential, using the GFD procedures for different diatomic molecules. Their results were reduced to the classical case and compared with existed results in literatures. Also, Abu-Shady and khokha30 employed the GFD to solve the D-dimensional Schrödinger equation with improved Rosen-Morse potential. Their pure vibrational energies for selected diatomic molecules obtained were compared with experimental values in literatures. The CFD has also been seen to produce excellent results consistent with classical results, as proposed before30.

Fractional Schrödinger equation has been studied with different system, in relation to quantum information theory. Solaimani and Dong31 studied the position and momentum information entropies of multiple quantum well systems in fractional Schrödinger equation regime. Their results showed that the position (momentum) probability density tends to be more severely localized (delocalized) in more fractional systems. Also, the Beckner Bialynicki-Birula-Mycieslki (BBM) inequality in the fractional Schrödinger equation was satisfied by adjusting the confining potential amplitude, the fractional the confining potential parameters. In another development, Santana-Carrillo et al.32 investigated the position and momentum entropy for two hyperbolic single-well potentials in the fractional Schrödinger equation. Their findings showed that the wave function moved towards the origin as the fractional derivative number decreased. Also, the position entropy density become heavily localized in more fractional system, while the momentum probability density become heavily delocalized. The Fisher entropy was seen to increase with increase in the depth of the potential wells and decrease in the fractional derivative number.

Many authors have investigated the Schrödinger equation in the presence of various curvature and torsional space-time. The implication of this concept in a curved space-time leads to topological defects33,34,35,36,37,38,39. The topological defects are generally observed in condensed matter physics and gravitation physics. In gravitation physics, the concepts of topological defects were observed in the evolution of the early universe where symmetry breaking phase transition occurs40,41 while topological defects were observed in material synthesis in condensed matter physics42,43.

Relativistic oscillators have been investigated with different topological defects44,45,46,47. Santos and Barros Jr.48 studied the non-inertial effects of Klein-Gordon oscillator in the cosmic string space-time. Ahmed49 also investigated the Klein-Gordon oscillator with linear potential in the background of cosmic string space-time, using the Kaluza-Klein theory. Bouzenada et al.50 investigated the effect of cosmic string and magnetic field on different thermal properties of a 2-dimensional Klein-Gordon oscillator, using the Poisson approximation. The influence of oscillatory frequency in a non-inertial system of Dirac oscillator was studied in the cosmic string space-time background51. The authors obtained Dirac spinors for positive-energies nonrelativistic energies, which were compared with the confinement of a spin-half particle to quantum dot. Bakke and Furtado52 analyzed the influence of Aharonov-Casher effect on the Dirac oscillator in Minkowski, cosmic string and cosmic dislocation space-times. Their study was applied to relativistic quantum dots, especially neutral particles. The influenced of topological defects on the magnetization and persistent current of massless Dirac fermions with quantum dot in a graphene layer were considered53. Here, the Dirac fermions were seen to contribute to the spatial confinement of electrons, and the degeneracy of the Landau levels being broken by the topological defects. Bakke and Mota54 employed the gravity’s rainbow to study the Dirac oscillator within the cosmic string space-time. They deduced that the energy levels of the Dirac oscillator were altered, due to the modification of the cosmic strings line elements by the rainbow functions. Other recent studies on effects of topological defect on thermal, magnetic and optical properties of some potential models can be obtained in Refs.55,56,57,58 and references therein.

It has been established that the superposition of two or more potential model leads to broader range of applications59,60. Therefore, the Hulthén plus Hellmann potential (HHP), which is of interest to us is defined as61

$$\begin{aligned} V_{HHP}(r) = -\frac{H_1e^{-\delta r}}{1-e^{-\delta r}}+\frac{H_2e^{-\delta r}}{r}-\frac{H_3}{r} \end{aligned}$$
(1)

Here, \(H_1, H_2, H_3\) are depths of the combined potential and \(\delta\) the screening parameter, respectively. The HHP model promises to be very relevant in different areas of physics including nuclear and particle physics, atomic and molecular physics, solid state physics and plasma physics. This is because, the Hulthén potential, Coulomb potential and Yukawa potential are special cases of the HHP62.

Our motivation is pivoted on the fact that there is no report on the effect of topological defect on fractional bound state energies of Hulthén-Hellmann potential, to the best of our knowledge. This paper is organized as follows. The framework of the theoretical calculations of the fractional Schrödinger equation of HHP with point-like global monopole can be viewed in Section 2. In section 3, the graphical and numerical results obtained are presented and discussed accordingly. Section 4 gives the concluding remarks.

Theoretical analysis

Quantum energies of fractional Schrödinger equation of HHP in the global monopole space-time

In this section, we introduce the metrics of the line element with a point-like global monopole space-time. Also, the generalized fractional Nikiforov-Uvarov method is used to solve a second-order differential equation with HHP. The line element with a point-like global monopole (PGM) space-time is defined as63

$$\begin{aligned} ds^2=-c^2 dt^2+\frac{dr^2}{\sigma ^2}+r^2 d\theta ^2+r^2\sin ^2\theta d\varphi ^2 \end{aligned}$$
(2)

where \(0<\sigma ^2<1\), \(\sigma ^2=1-8\pi G\eta _0^2\), with \(\sigma\) and \(\eta _0\) being the topological defect parameter of the PGM and the energy scale, respectively and c is the speed of light. The metrics given in Eq. (2) describes a space-time with scalar curvature \(R = \frac{2(1-\sigma ^2)}{r^2}\). The Schrödinger equation (SE) in this context is given as

$$\begin{aligned} -\frac{\hbar ^2}{2\mu }\nabla _{LB}^2\psi \left( \vec {r},t\right) +V(\vec {r},t)\psi \left( \vec {r},t\right) =i\hbar \frac{\partial \psi \left( \vec {r},t\right) }{\partial t} \end{aligned}$$
(3)

where \(\mu\) is the reduced mass of the system and \(\nabla _{LB}^2 = \frac{1}{\sqrt{g}}\partial _i\left( \sqrt{g}g^{ij}\partial _i\right)\) is the Laplace-Beltrami operator, \(g=\det (g_{ij})=\frac{r^2\sin ^2\theta }{\sigma ^2}\) and V(r) is given in Eq. (1). Hence, the SE in the presence of the PGM is given as

$$\begin{aligned} \left. \begin{array}{l} {\frac{-\hbar ^2}{2\mu r^2}\left[ \sigma ^2\frac{\partial }{\partial r}\left( r^2\frac{\partial }{\partial r}\right) +\frac{1}{\sin \theta }\frac{\partial }{\partial r}\left( \sin \theta \frac{\partial }{\partial \theta }\right) +\frac{1}{\sin ^2\theta }\frac{\partial ^2}{\partial \varphi ^2}\right] \psi (r,\theta ,\varphi ,t)} \\ \\ {+ V_{HHP}(r)\psi (r,\theta ,\varphi ,t)= i\hbar \frac{\partial \psi (r,\theta ,\varphi ,t)}{\partial t}} \end{array} \right\} \end{aligned}$$
(4)

By considering a particular solution of Eq. (4) given in terms of eigenvalues of the angular momentum operator \(\hat{L}^2\),

$$\begin{aligned} {\psi (r,\theta ,\varphi ,t) = \exp \left( \frac{-iE_{nl}t}{\hbar }\right) \frac{R_{nl}(r)}{r}Y_{l,m}(\theta ,\varphi )} \end{aligned}$$
(5)

where \(Y_{l,m}(\theta ,\varphi )\) are spherical harmonics and \(R_{nl}(r)\) is the radial wave function. By substituting Eqs. (5) and (1) into Eq. (4), we have the radial SE as

$$\begin{aligned} \begin{aligned}&\frac{d^2 R_{nl}(r)}{d r^2} + \left[ \frac{2ME_{nl}}{\hbar ^2\sigma ^2}+\frac{2\mu H_1e^{-\delta r}}{\hbar ^2\sigma ^2(1-e^{-\delta r}) }-\frac{2\mu H_2\delta e^{-\delta r}}{\hbar ^2\sigma ^2r} +\frac{2\mu H_3\delta }{\hbar ^2\sigma ^2r}-\frac{l(l+1)}{\sigma ^2r^2}\right] R_{nl}(r) = 0 \end{aligned} \end{aligned}$$
(6)

where l represents the angular momentum quantum number.

It has been established in available literatures that Eq. (6) does not have analytical solutions because of the presence of the centrifugal barrier, except for the s-wave where \(l = 0\). Hence, we employ the Greene-Aldrich approximation scheme of the form64,

$$\begin{aligned} \frac{1}{r^2}\approx \frac{\delta ^2}{(1-e^{-\delta r})^2}; \frac{1}{r}\approx \frac{\delta }{(1-e^{-\delta r})} \end{aligned}$$
(7)

It is worthy to note here that the above approximation scheme has been generalized, as mentioned in the following references65,66,67,68,69. By substituting Eq. (7) into Eq. (6) and adopting a coordinate transformation \(y = e^{-\delta r}\), we obtain

$$\begin{aligned} \frac{d^2R_{nl}(y)}{dy^2}+\frac{(1-y)}{y(1-y)}\frac{dR_{nl}(y)}{dy}+\left[ \frac{-\gamma _1y^2+\gamma _2y-\gamma _3}{y^2(1-y)^2}\right] R_{nl}(y)=0 \end{aligned}$$
(8)

Here, the following parameters have been defined:

$$\begin{aligned} \gamma _1&=\epsilon _{nl}+\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}-\frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }; \nonumber \\ \gamma _2&=2\epsilon _{nl}+\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}-\frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta }; \nonumber \\ \gamma _3&=\epsilon _{nl}-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta }+\frac{l(l+1)}{\sigma ^2}; \epsilon _{nl}=\frac{-2\mu E_{nl}}{\hbar ^2\sigma ^2\delta ^2} \end{aligned}$$
(9)

We now adopt the formalism of the generalized fractional derivative, as summarized in the Appendix Section. The generalized fractional form of the Schrödinger equation with point-like global monopole for the HHP can be stated by changing integer orders with fractional orders in Eq. (A.8) as follows:

$$\begin{aligned} D^{\beta }[D^{\beta }R(y)]+\frac{(1-y^{\beta })}{y^{\beta }(1-y^{\beta })}D^{\beta }R(y)+\frac{1}{y^{2\beta }(1-y^{\beta })^2}\left[ -\gamma _1y^{2\beta }+\gamma _2y^{\beta }-\gamma _3\right] R(y)=0. \end{aligned}$$
(10)

By substituting Eqs. (A.7) and (A.8) into Eq. (8), we obtain

$$\begin{aligned}&R^{''}(y)+\frac{\left[ 1+Z(1-\beta )\right] (1-y^{\beta })}{Zy(1-y^{\beta })}R^{'}(y) \nonumber \\&\quad +\frac{1}{Z^2y^2(1-y^{\beta })^2}\left[ -\gamma _1y^{2\beta }+\gamma _2y^{\beta }-\gamma _3\right] R(y)=0. \end{aligned}$$
(11)

By comparing Eq. (11) with Eq. (A.11), we obtain the following functions:

$$\begin{aligned} \tilde{\tau }_{Gf}(y)&=\left( 1+Z(1-\beta )\right) (1-y^{\beta });\nonumber \\ \alpha _{GF}(y)&=Zy(1-y^{\beta }); \nonumber \\ \tilde{\alpha }_{GF}(y)&=-\gamma _1y^{2\beta }+\gamma _2y^{\beta }-\gamma _3 \end{aligned}$$
(12)

By substituting Eq. (12) into Eq. (A.19), the function \(\pi _{GF}(y)\) can be defined as follows:

$$\begin{aligned}&\pi _{GF}(y)=\frac{(Z\beta -1)+(1-2Z\beta )y^{\beta }}{2} \nonumber \\&\quad \pm \sqrt{\left[ \frac{(1-2Z\beta )^2}{4}+\gamma _1-x\right] y^{2\beta } +\left[ \frac{(Z\beta -1)(1-2Z\beta )}{2}-\gamma _2+x\right] y^{\beta } +\left[ \frac{(Z\beta -1)^2}{4}+\gamma _3\right] } \end{aligned}$$
(13)

where

$$\begin{aligned} x=Zky^{1-\beta } \end{aligned}$$
(14)

Equation 13 can be represented in the form:

$$\begin{aligned} \pi _{GF}(y)=\frac{(Z\beta -1)+(1-2Z\beta )y^{\beta }}{2}\pm \sqrt{P_1y^{2\beta }+P_2y^{\beta }+P_3} \end{aligned}$$
(15)

where

$$\begin{aligned} P_1=S_1-x; P_2=S_2+x; P_3=S_3 \end{aligned}$$
(16)

and

$$\begin{aligned} S_1=\frac{(1-2Z\beta )^2}{4}+\gamma _1; S_2=\frac{(Z\beta -1)(1-2Z\beta )}{2}-\gamma _2; S_3=\frac{(Z\beta -1)^2}{4}+\gamma _3. \end{aligned}$$
(17)

To obtain the two possible roots of k, we employ the condition that the discriminant of the expression under the square root of Eq. 15 must be zero. Hence, this gives:

$$\begin{aligned} k_{\pm }&=Q\left[ -(S_2+2S_3)\pm 2\sqrt{S_3(S_1+S_2+S_3)}\right] y^{\beta -1}; \nonumber \\ Q&=\frac{1}{Z} \end{aligned}$$
(18)

By substituting Eq. (18) into Eq. (15), we have

$$\begin{aligned} \pi _{GF}(y)=\frac{(Z\beta -1)+(1-2Z\beta )y^{\beta }}{2}\pm \begin{array}{l} \left( \sqrt{S_3}-\sqrt{S_1+S_2+S_3}\right) y^{\beta }-\sqrt{S_3}, k=k_{+} \\ \left( \sqrt{S_3}+\sqrt{S_1+S_2+S_3}\right) y^{\beta }-\sqrt{S_3}, k=k_{-} \end{array} \end{aligned}$$
(19)

For a physically acceptable solution, the negative sign in Eq. 19 is chosen. Hence, The \(\pi _{GF}(y)\) becomes

$$\begin{aligned} \pi _{GF}(y)^{-}=\frac{(Z\beta -1)+(1-2Z\beta )y^{\beta }}{2}- \left[ \left( \sqrt{S_3}+\sqrt{S_1+S_2+S_3}\right) y^{\beta }-\sqrt{S_3}\right] \end{aligned}$$
(20)

where,

$$\begin{aligned} k_{-}=-Q\left[ S_2+2S_3+2\sqrt{S_3(S_1+S_2+S_3)}\right] y^{\beta -1} \end{aligned}$$
(21)

By employing Eqs. (A.16), (A.20) and (A.21), the expressions for \(\lambda (y)\), \(\tau _{GF}(y)\) and \(\lambda _n(y)\) are obtained respectively as

$$\begin{aligned} \lambda (y)= & \left[ -Q\left( S_2+2S_3\right) +\beta \left( \frac{1}{2}(1-2Z\beta )-\sqrt{S_3}\right) -\sqrt{S_1+S_2+S_3}\left( \beta +2Z\sqrt{S_3}\right) \right] y^{\beta -1} \end{aligned}$$
(22)
$$\begin{aligned} \tau _{GF}(y)= & \left( 2\sqrt{S_3}+Z\right) -\left[ Z(\beta +1)+2\left( \sqrt{S_3}+\sqrt{S_1+S_2+S_3}\right) \right] y^{\beta } \end{aligned}$$
(23)
$$\begin{aligned} \lambda _n(y)= & n\beta \left[ \frac{Z(1+\beta )(n+1)}{2}+2\left( \sqrt{S_3}+\sqrt{S_1+S_2+S_3}\right) \right] y^{\beta -1} \end{aligned}$$
(24)

By equating Eqs. (22) and (24), the energy eigenvalues for HHP in the Global Monopole Space-time is obtained as:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(25)

where,

$$\begin{aligned} A&=\frac{l(l+1)}{\sigma ^2}+\frac{(1-2Z\beta )^2}{4}+\frac{(2\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}; \nonumber \\ B&=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}-\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}+ \frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta }; \nonumber \\ C&=\frac{l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)^2}{4}-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta } \end{aligned}$$
(26)

The corresponding eigenfunction can be determined using Eq. A.15 as follows:

$$\begin{aligned} \phi (y)=y^{Q\left( \frac{(Z\beta -1)}{2}+\sqrt{C-\epsilon _{nl}}\right) }(1-y^{\beta })^{\left( \frac{1}{2}+\frac{Q}{\beta }\sqrt{A+B+C}\right) } \end{aligned}$$
(27)

The weight function m(y) is obtained from Eq. (A.18) as

$$\begin{aligned} m(y)=Qy^{\left( 2Q\sqrt{C-\epsilon _{nl}}\right) }(1-y^{\beta })^{\left( \frac{2Q}{\beta }\sqrt{A+A+C}\right) } \end{aligned}$$
(28)

By employing Eq. (A.17), the function \(W_n(y)\) becomes:

$$\begin{aligned} W_n(y)&=T_ny^{(n+2Q\sqrt{C-\epsilon _{nl}})}(1-y^{\beta })^{(\frac{-2Q}{\beta }\sqrt{A+B+C})} \nonumber \\&\quad \times \frac{d^n}{d\beta ^n}\left[ Z^ny^{\left( n+2Q\sqrt{C-\epsilon _{nl}}\right) }(1-y^{\beta })^{(n+\frac{2Q}{\beta }\sqrt{A+B+C})}\right] \end{aligned}$$
(29)

With the help of Eq. (A.13), we obtain the complete eigensolution of Eq. (8) as

$$\begin{aligned} R(y)&=T_ny^{Q\left( \frac{(Z\beta -1)}{2}+\sqrt{C-\epsilon _{nl}}\right) }(1-y^{\beta })^{\left( \frac{1}{2}+\frac{Q}{\beta }\sqrt{A+B+C}\right) } \nonumber \\&\quad \times \frac{d^n}{d\beta ^n}\left[ Z^ny^{\left( n+2Q\sqrt{C-\epsilon _{nl}}\right) }(1-y^{\beta })^{(n+\frac{2Q}{\beta }\sqrt{A+B+C})}\right] \end{aligned}$$
(30)

It can be noted that when the fractional parameter \(\beta\) and the topological defect parameter \(\sigma\) approach the classical case, Eq. (30) reduces to the radial wavefunction for the Hulthen-Hellmann potential, as obtained in Ref.61.

Fractional energies of related potential models: special cases

In this section, the some parameters of the combined potential are re-adjusted to obtain the fractional energy spectra of other potential models as special cases.

By setting \(H_1 = 0\) in Eq. (25), the fractional energy spectra of Hellmann potential with PGM becomes:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB_1+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(31)

where,

$$\begin{aligned} B_1=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}+ \frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta }; \end{aligned}$$
(32)

By setting \(H_2 = H_3 = 0\) in Eq. (25), the fractional energy spectra of Hulthén potential with PGM becomes:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C_1 \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB_2+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(33)

where,

$$\begin{aligned} B_2&=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}-\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}; \nonumber \\ C_1&=\frac{l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)^2}{4} \end{aligned}$$
(34)

By setting \(H_1 = H_3 = 0\) in Eq. (25), the fractional energy spectra of Yukawa potential with PGM becomes:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C_2 \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB_3+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(35)

where,

$$\begin{aligned} B_3&=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}+ \frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }; \nonumber \\ C_2&=\frac{l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)^2}{4} \end{aligned}$$
(36)

By setting \(H_1 = H_2 = 0\) and as \(\delta \rightarrow 0\) in Eq. 25, the fractional energy spectra of Coulomb potential with PGM becomes:

$$\begin{aligned} E_{nl}=\frac{\mu H_3^2Q^2}{2\hbar ^2\sigma ^2\beta \left( n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta }\right) ^2} \end{aligned}$$
(37)

By setting \(H_2 = 0\) in Eq. (25), the fractional energy spectra of Hulthén-Coulomb potential with PGM becomes:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB_4+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(38)

where,

$$\begin{aligned} B_4=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}-\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}-\frac{2\mu H_3}{\hbar ^2\sigma ^2\delta }. \end{aligned}$$
(39)

By setting \(H_3 = 0\) in Eq. (25), the fractional energy spectra of Hulthén-Yukawa potential with PGM becomes:

$$\begin{aligned} E_{nl}&=\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }C \nonumber \\&\quad -\frac{\hbar ^2\sigma ^2\delta ^2}{2\mu }\left[ \frac{\frac{Z\beta (1+\beta )}{2}(n+\frac{1}{2}+\frac{2\sqrt{A}}{Z(1+\beta )})^2-(\frac{\beta (1-2Z\beta )}{2}-QB_5+\frac{Z\beta (1+\beta )}{8}+\frac{2\beta A}{Z(1+\beta )})}{2\beta (n+\frac{1}{2}+\frac{Q\sqrt{A}}{\beta })}\right] ^2 \end{aligned}$$
(40)

where,

$$\begin{aligned} B_5=\frac{2l(l+1)}{\sigma ^2}+\frac{(Z\beta -1)(1-2Z\beta )}{2}+\frac{(Z\beta -1)^2}{4}-\frac{2\mu H_1}{\hbar ^2\sigma ^2\delta ^2}+\frac{2\mu H_2}{\hbar ^2\sigma ^2\delta }. \end{aligned}$$
(41)

Results and discussion

In this section, the energy spectrum of Hulthén-Hellmann potential obtained in Eq. (25) is analyzed with different potential parameters, under the influence of fractional parameter \(\beta\) and topological defect parameter \(\sigma\). The combined potential parameters employed are as follows: \(H_1=0.025; H_2=-1.00; H_3=1.00\). We have also used the following parameters throughout our analysis: \(\hbar =1, \mu =0.5, \chi =0.5\). The energies of HHP increases with increase in quantum state for any value of topological defect and fractional parameter considered. It can be observed that the there exist a significant increase in the energy eigenvalues from ground state of the exited states of the system. This is illustrated in Table 1. At each quantum state considered, the energy eigenvalues of HHP increases with increase in both topological defect and fractional parameter values. The increase in energy eigenvalues at each quantum state considered is not as significant as that observed between different quantum states. hence, we see that under the dominance of fractional parameter, the energy eigenvalues of HHP are enhanced in the presence of the topological defects. Moreover, the energy eigenvalues of HHP are seen to be more constrained at lower values of topological defect, as compared to their values at classical limit (\(\sigma =1.00\)). Table 2 shows the energy eigenvalues of HHP for Minkowski flat space at different quantum states. These results represent energy eigenvalues in the absence of the topological defect. Our results are seen to be very consistent with the results obtained in Ref.61.

Table 1 Bound state energy eigenvalues (eV) of the HHP at different values of quantum states, topological defect and fractional parameter, with \(\delta = 0.025\).
Full size table
Table 2 Comparison of Bound state energy eigenvalues (eV) of the HHP for Minkowski flat space at different values of quantum states, with \(\delta = 0.025\).
Full size table

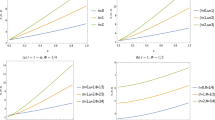
To support our results above, the graphical relationship between the energy eigenvalues of HHP with quantum numbers and screening parameter, for some values of fractional parameter and topological defect. In Fig. 1, the energy eigenvalues are seen to rise monotonously with increase in principal quantum number n, for varying values of fractional parameter \(\beta\) (Fig. 1a) and topological defect \(\sigma\) (Fig. 1b). This indicates that there is a positive shift in energy eigenvalues of HHP as the fractional parameter and topological defect parameter increases.

Fig. 1
figure 1

Variation of energy eigenvalues of HHP with principal quantum number (n) for various values of (a) fractional parameter (\(\beta\)); (b) topological defect (\(\sigma\)), with \(\delta = 0.025\).

Full size image

In Fig. 2, the energy eigenvalues are seen to rise monotonously with increase in angular momentum quantum number l, for varying values of fractional parameter \(\beta\) (Fig. 2a) and topological defect \(\sigma\) (Fig. 2b). For greater values of l, the energy values tend to be constant for each values of \(\beta\) and \(\sigma\) considered.

Fig. 2
figure 2

Variation of energy eigenvalues of HHP with angular momentum quantum number (l) for various values of (a) fractional parameter (\(\beta\)); (b) topological defect (\(\sigma\)), with \(\delta = 0.025\).

Full size image

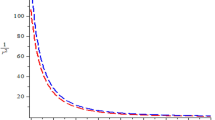
The variation of the energy eigenvalues with screening parameter \(\delta\) is shown in Fig. 3, for varying fractional parameter \(\beta\) and topological defect \(\sigma\). In Fig. 3a, the energies rise together at zero screening parameter for all values of \(\beta\). As \(\delta\) is enhanced, the energy values begin to increase, transiting and shifting with respect to the fractional parameter values considered. At any value of \(\delta\), the energy values increase with decrease in the value of \(\beta\). On the contrary, the energy eigenvalues increase at zero \(\delta\) and later decrease as \(\delta\) increases (Fig. 3b). It can also be observed that the energy eigenvalues shift from negative regime to positive regime, for screening parameters beyond 0.1, at a specific value of topological defect (3a). At a unique value of fractional parameter, the energy eiegenvalues fluctuates between the negative and positive regime, depending on the value of topological defect considered (3b).

Fig. 3
figure 3

Variation of energy eigenvalues of HHP with screening parameter (l) for various values of (a) fractional parameter (\(\beta\)); (b) topological defect (\(\sigma\)), with \(\delta = 0.025\).

Full size image

The variation of the energy eigenvalues with fractional parameter \(\beta\) for varying quantum numbers nandl and topological defect \(\sigma\) are shown in Fig. 4. In Fig. 4a, the energy eigenvalues increase gradually with increase in \(\beta\), for varying \(\sigma\). A fall and rise in energy eigenvalues is observed for \(\sigma\) value in the Minkowski space-time considered, as \(\beta\) value is enhanced. There is a gradual rise in energy, corresponding to increase in \(\beta\) for various values of n and l, as shown in Fig. 4b,c, respectively. In addition, there is a slow drop in energy eigenvalues, as the fractional parameter approaches the classical case (\(\beta =1\)), as shown in Fig. 4c.

Fig. 4
figure 4

Variation of energy eigenvalues of HHP with fractional parameter (\(\beta\)) for various values of (a) topological defect (\(\sigma\)); (b) principal quantum number (n); (c) angular momentum quantum number (l).

Full size image

Figure 5 shows a monotonous increase in the energy eigenvalues of HHP, as they vary with topological defect \(\sigma\). In Fig. 5a, we observe a closer range of energy curves for varying \(\beta\), as compared to Fig. 5b for varying \(\sigma\). Also, the energy eigenvalues increase with an increase in n values, for any value of \(\sigma\) considered. In Fig. 5c, the energy eigenvalues increase with increase in l values, for any value of \(\sigma\) considered. Also, the energy eigenvalues tend to converge at the Minkowski space-time, for various quantum states considered.

The presence of the topological defect parameter changes the quantum dynamic of the HHP. Unlike the Minkowski space-time, which is a flat space, the characteristic properties of the topological effect occur in a curved surface whose values lies between \(0<\sigma ^2<1\) . Within this range, the dynamics of the quantum system will be that of the curved space. As the topological defect parameter approaches unity, the dynamics of the quantum system changes to that of the flat space which is described by the Minkowski space-time. The eigenvalues and the wave function of the particles under the influence of the topological defect changes significantly from the particles moving in the Minkowski space-time. Our discussion clearly points to the fact that the energy eigenvalues of HHP are significantly affected by the global effects of the point-like global monopole, fractional parameter and quantum states of the system.

Fig. 5
figure 5

Variation of energy eigenvalues of HHP with topological defect (\(\sigma\)) for various values of (a) fractional parameter (\(\beta\)); (b) principal quantum number (n); (c) angular momentum quantum number (l).

Full size image

Concluding remarks

Topological defects on the eigensolutions of Hulthén-Hellmann potential have been studied in this work under the framework of generalized fractional Nikiforov-Uvarov method. Greene-Aldrich approximation scheme has been chosen to deal with the centrifugal term. Numerical values of the energy are presented in Table 1 for various quantum states and fractional parameters, in curved space (\(0< \sigma ^2 < 1\)). The corresponding values of the energy in Minkowski flat space (\(\sigma\) = 1) are computed and compared with available results in literature, for some quantum states. This comparison are presented in Table 2. It is observed that these results agree perfectly with each other, for a certain chosen arbitrary values of the potential parameters. It is also observed that the topological defect in the curved space and fractional parameters considered have significant impact in the energy eigenvalues of the system under study.

To authenticate these findings, graphical variations of the energy eigenvalues with quantum numbers and screening parameters, for varying values of topological defect and fractional parameters are presented in Figs. 1, 2, 3, 4 and 5. The significant influence of the topological defect and fractional parameter which results in a shift in the energy eigenvalues of HHP, as demonstrated in the graphs are discussed clearly. We specifically observed consistent influence of the fractional parameter and topological defect parameter on the energy states of the HHP. This phenomena were confirmed to agree with recent studies in literature70,71.

It is our future desire to extend this work to spin-spin interaction, spin-orbit interaction and external fields effects, as they relate to heavy mesons. This is poised out of the fact that the combined potential studied promises to be very efficient in atomic and nuclear physics and their related areas.