Introduction

Pest refers not only to insects that cause damage to crops, gardens or homes, but also to wildlife that cause damage to crops or property, and to any organism that poses a threat to human activities. Agricultural production is inherently susceptible to losses due to pest infestations, which can lead to significant economic and food security implications1. Pest control plays a critical role in sustaining crop yields and ensuring sustainable agricultural practices. The shift towards Integrated Pest Management (IPM) stand for a more comprehensive and sustainable method to pest control2. IPM is an appropriate method, including chemical control, biological control, and artificial control, its aim is to create a potent and detailed system for pest management. Research has shown that biological control, particularly the use of natural enemies, can be an effective component of IPM. The combination of chemical and biological control can yield an optimal control strategy3,4,5. This has sparked interest in pest management strategies.

Several studies have explored different aspects of pest management strategies. For instance, Liu et al.6 studied a Lotka–Volterra predator-prey model with impulsive effect at fixed moment. They analyzed such system from two cases, employing IPM strategy and relying solely on pesticides, finally, they concluded that relying solely on pesticides is less effective than employing an IPM strategy. Shi and Chen7 investigated an SI epidemic model with stage structure. In their model, they considered releasing infected pests to the field at a fixed time periodically, showing that their results could be beneficial for pest management. Literatures8,9,10,11 studied SI models about pest management and considered impulsive releases of infective pests and pesticides sprays, their results provided reliable tactics for the practical pest management. Dai et al.12 proposed and studied a pest control model with impulsive effects that involves periodic spraying of pesticides and the release of natural enemy population, their work showed the significant roles in pest control were played by the sublethal effects of insecticides and the release of natural enemies. Although these studies have contributed to pest management, they did not take into account the effects of hibernation. Hibernation allows animals to achieve a reduction of no less than 90% in their energy requirements and survive for months while slowly breaking down their stored body fat13. Hibernation is regarded as an efficacious strategy for animals to cope with cold environments and scarce food resources14. Jiao et al.15 developed the periodically switching predator-prey model with impulsive harvesting, and prey population with hibernation characteristics in their paper. However, this paper has not been applied to pest management. These literatures16,17,18,19 indicate that many pests exhibit hibernation behavior. Chilo partellus (Swinhoe), known as the spotted stem borer, is a highly destructive pest to sorghum and maize, and undergoes hibernation during harsh winters16. The rice stink bug, Niphe elongata (Dallas) (Hemiptera: pentatomidae), is a serious pest that hibernates during its adult stage17. Psacothea hilaris is a pest that can damage mulberry trees, and it has two hibernation methods, one in the egg stage and the other in the larval stage18. Tarnished plant bugs (TPB), Lygus lineolaris Palisot de Beauvois, are serious pests of cotton and they hibernate during the winter in dead weeds and surface woods trash19. In the literatures mentioned to above, we find that the impulsive release is always a constant. In fact, the limited resources and population density cause pest control strategy has saturation effect or nonlinear characteristics21. Several studies20,21,22,23 have shown the release of natural enemies through impulsive nonlinear methods. However, their studies fail to incorporate the critical factor of pests with hibernation behavior.

Based on the analysis of the mentioned literatures, we find no prior work has integrated both hibernation dynamics and nonlinear impulses within a single switching system. Prior pest management models have largely overlooked the seasonal dynamics of pest hibernation, assuming continuous pest activity throughout the year. This simplification neglects a key biological reality: many pests enter dormancy (overwintering) during unfavorable seasons, drastically reducing their metabolic activity, reproduction, and susceptibility to control measures. Additionally, traditional switching systems often rely on linear or constant-intensity interventions (fixed-rate pesticide application or steady predator release), which fail to account for resource limitation. Based on this, we establish a pest management system with hibernation of pests and nonlinear pulse release of natural enemies, referred to system (1). Our model introduces a switching mechanism that explicitly differentiates between non-hibernation (active pest growth and reproduction) and hibernation (reduced pest activity) periods. Our work introduces a nonlinear impulsive control framework within the switching structure, a feature absent in prior switching models.

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{x}(t)}{dt}=rx(t)(1-\frac{x(t)}{K})-\frac{\beta _1x(t)y(t)}{1+\alpha _1x(t)}, \\&\frac{d{y}(t)}{dt}=\frac{k_1\beta _1x(t)y(t)}{1+\alpha _1x(t)}-d_1y(t), \\ \end{aligned}\right\} ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=-h_1x(t),\\&\bigtriangleup x(t)=-h_2x(t),\\ \end{aligned}\right\} ~~t=(m+\iota )\gamma ,~~m \in Z^{+},\\&\left. \begin{aligned}&\frac{d{x}(t)}{dt}=-cx(t)-\frac{\beta _2x(t)y(t)}{1+\alpha _2x(t)},\\&\frac{d{y}(t)}{dt}=\frac{k_2\beta _2x(t)y(t)}{1+\alpha _2x(t)}-d_2y(t),\\ \end{aligned}\right\} ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=0,\\&\bigtriangleup y(t)=\frac{\mu _{max}}{1+\alpha y(t)},\\ \end{aligned}\right\} ~~t=(m+1)\gamma ,~~m \in Z^{+}.\\ \end{aligned}\right. \end{aligned}$$
(1)

In our research, the pest population has hibernation characteristics is supposed. Pests reproduce logistically in growth phase \((m\gamma , (m+\iota )\gamma ]\). Pesticide spray directly kills pests and indirectly reduces enemies by pesticide at \((m+\iota )\gamma\). Pests enter diapause (as eggs, larvae or adults) with no reproduction in hibernation phase \(((m+\iota )\gamma , (m+1)\gamma ]\), aligning with field observations. Agricultural practices (e.g., straw return, debris removal) expose pests, weakening their defenses. Natural enemies are released to exploit vulnerable pests at \((m+1)\gamma\). Where \(m \in \mathbb {Z}^{+}\) and \(\Delta z(t) = z(t^{+}) - z(t)\) for \(z \in \{x,y\}\).

$$\begin{aligned} f_i(x,y) = \frac{\beta _i x(t) y(t)}{1 + \alpha _i x(t)} \quad (i=1,2), \end{aligned}$$

as \(x \rightarrow \infty\), \(f_i \rightarrow \frac{\beta _i}{\alpha _i}\); as \(x \rightarrow 0\), \(f_i \rightarrow 0\).

$$\begin{aligned} \frac{\mu _{\max }}{1 + \alpha y(t)} {\left\{ \begin{array}{ll} \rightarrow \mu _{\max } & \text {as } y \rightarrow 0, \\ \rightarrow 0 & \text {as } y \rightarrow \infty . \end{array}\right. } \end{aligned}$$

The inverse relationship \(\frac{\mu _{\max }}{1 + \alpha y(t)}\) prevents resource competition among natural enemies, cannibalism at high densities, unnecessary costs when suppression is already effective. Low y triggers aggressive releases (\(\bigtriangleup y(t)\approx \mu _{max}\)) to counter incipient outbreaks, while high y minimizes interventions (Table 1).

Table 1 Model parameters.
Full size table

The framework of this paper is as follows: In Sect. 1, we introduce the background and formulate the model. Section 2 presents a number of significant lemmas along with their proofs. Section 3 provides the sufficient conditions under which the boundary periodic solution of pest eradication is GAS and discusses the sufficient condition under which the model (1) is permanent. Section 4 includes numerical simulations and discussions that validate and explain the main results through diagrams. In Section 5, we give a short summary that concludes this research.

The lemmas

\(Y(t)=(x(t),y(t))^T\) that is the solution of system (1) is a non-smooth function \(Y:R^{+}\rightarrow (R^{+})^2\), Y(t) is continuous on the intervals \((m\gamma ,(m+\iota )\gamma ]\) and \(((m+\iota )\gamma ,(m+1)\gamma ],m\in Z^+\). There are \(Y(m\gamma ^+)=\lim \nolimits _{t\rightarrow m\gamma ^{+}}Y(t)\) and \(Y((m+\iota )\gamma ^+)=\lim \nolimits _{t\rightarrow (m+\iota )\gamma ^{+}}Y(t)\) present. Evidently the smoothness properties of f ensure the global existence and uniqueness of solutions for system (1.3), which shows the mapping is defined on right-side of system (1)24.

Lemma 2.1

(x(t), y(t)) is the solution of system (1), we can be seen a \(R>0\) such that \(x(t)\le R,y(t)\le R\) for t sufficiently big.

Proof

Make \(P(t)=jx(t)+y(t)\), \(j=max\{k_1,k_2\}\), and \(f=min\{d_1,d_2,c\}\). For \(t\in (m\gamma ,(m+\iota )\gamma ]\),

$$\begin{aligned}&D^{+}P(t)+fP(t)<-\frac{jrx^2(t)}{K}+j(r+f)x(t)\\&\quad \le -(x-\frac{K(r+f)}{2r})^2+\frac{Kj(r+f)^2}{4r}\\&\quad \le R_0=\frac{Kj(r+f)^2}{4r}>0. \end{aligned}$$

For \(t\in ((m+\iota )\gamma ,(m+1)\gamma ]\),

$$D^{+}P(t)+fP(t)<j(f-c)x(t)+(f-d_2)y(t)\le R_1<0.$$

For \(t\ne (m+\iota )\gamma\), and \(t\ne m\gamma\),

$$D^{+}P(t)+fP(t)\le R_2=max\{R_0,R_1\}.$$

For \(t=(m+\iota )\gamma\),

$$P((m+\iota )\gamma ^{+})=j(1-h_1)x((m+\iota )\gamma )+(1-h_2)y((m+\iota )\gamma )\le P((m+\iota )\gamma ).$$

For \(t=(m+1)\gamma\),

$$\begin{aligned} P((m+1)\gamma ^{+})&=jx((m+1)\gamma )+y((m+1)\gamma )+\frac{\mu _{max}}{1+\alpha y((m+1)\gamma )}\\&\le jx((m+1)\gamma )+y((m+1)\gamma )+\mu _{max}\\&=P((m+1)\gamma )+\mu _{max}.\end{aligned}$$

For \(t\in (m\gamma ,(m+1)\gamma ]\),

$$P(t)\le P(0^{+})e^{-ft}+e^{-ft}\int _{0}^{t}R_2e^{fs}ds=e^{-ft}P(0^{+})+\frac{R_2}{f}(1-e^{-ft})\rightarrow \frac{R_2}{f},t\rightarrow \infty .$$

According to the definition of ultimate boundedness for the function P(t), there exists a positive constant R such that \(x(t)\le R\) and \(y(t)\le R\) for all t that are sufficiently large.

When \(x(t)=0\), the system (2) is derived

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{y}(t)}{dt}=-d_1y(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y(t)=-h_2y(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{y}(t)}{dt}=-d_2y(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y(t)=\frac{\mu _{max}}{1+\alpha y(t)},\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(2)

By analyzing, the solution to the system (2) is as follows:

$$\begin{aligned} y(t)=\left\{ \begin{aligned}&e^{-d_1(t-m\gamma )}y(m\gamma ^+),t\in (m\gamma ,(m+\iota )\gamma ],\\&e^{-d_2(t-(m+\iota )\gamma )}y((m+\iota )\gamma ^+),t\in ((m+\iota )\gamma , m+1)\gamma ]. \end{aligned}\right. \end{aligned}$$
(3)

Through analysis, the stroboscopic map of system (2) is as follows:

$$\begin{aligned} y((m+1)\gamma ^+)=\frac{\mu _{max}}{1+\alpha (1-h_2)e^{(-d_2(1-\iota )-d_1 \iota )\gamma }y(m\gamma ^+)}+(1-h_2)e^{(-d_2(1-\iota )-d_1 \iota )\gamma }y(m\gamma ^+). \end{aligned}$$
(4)

Letting \(C=(1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }<1\) and setting

$$\begin{aligned} y((m+1)\gamma ^+)=G(y(m\gamma ^+))=\frac{\mu _{max}}{1+\alpha Cy(m\gamma ^+)}+Cy(m\gamma ^+), \end{aligned}$$
(5)

denote \(y(m\gamma ^+)=y_m\), then

$$\begin{aligned} y((m+1)\gamma ^{+})=y_{m+1}=G(y_{m})=\frac{\mu _{max}}{1+\alpha Cy_{m}}+Cy_{m}, \end{aligned}$$
(6)

So we calculate and obtain two fixed points of (5)

$$\begin{aligned} y^*=\frac{-(1-C)+\sqrt{(1- C)^2+4\alpha C\mu _{max}(1-C)}}{2\alpha C(1-C)} \end{aligned}$$
(7)

and

$$\begin{aligned} \widehat{y}=\frac{-(1-C)-\sqrt{(1- C)^2+4\alpha C\mu _{max}(1-C)}}{2\alpha C(1-C)}. \end{aligned}$$
(8)

We can omit \(\widehat{y}\) since \(\widehat{y}<0\).

Lemma 2.2

The fixed point \(y^*\) of (5) is GAS, where \(y^*\) is denoted by (7).

Proof

From (6) we obtain

$$\begin{aligned} \frac{d G(y_{m})}{d y_{m}}=-\frac{\mu _{max} \alpha C}{(1+\alpha C y_{m})^2}+C=\frac{C((1+\alpha y_m)^2-\mu _{max} \alpha )}{(1+\alpha C y_m)^2}. \end{aligned}$$
(9)

\(y^*\) is unique positive fixed point, we derive

$$\begin{aligned} \bigg |\frac{d G(y_{m})}{d y_{m}}\bigg |_{y_{m}=y^*}=\bigg |\frac{C((1+\alpha y^{*})^2-\mu _{max} \alpha )}{(1+\alpha C y^{*})^2}\bigg |<1. \end{aligned}$$
(10)

It implies that the fixed point \(y^*\) is locally asymptotically stable. Let’s continue, when 0<αμmax<1, we have

$$\bigg |y_{m+1}-y^{*}\bigg |= \bigg |(1-\frac{\alpha \mu _{max}}{(1+\alpha C y_{m})(1+\alpha C y^{*})})(y_{m}-y^{*})C\bigg |\le C\bigg |y_{m}-y^{*}\bigg |\rightarrow 0,$$

as \(m\rightarrow \infty\), \(C<1\) implies the fixed point \(y^*\) is globally attractive. When αμmax>1, according to reference23 , it can be similarly proved y* is globally attractive. So \(y^*\) is GAS.

Refer to15, the following Lemma 2.3 can be got.

Lemma 2.3

The periodic solution of (2) \(\widetilde{y(t)}\) is GAS and is given by

$$\begin{aligned} \widetilde{y(t)}=\left\{ \begin{aligned}&e^{-d_1(t-m\gamma )}y^*,t\in (m\gamma ,(m+\iota )\gamma ],\\&(1-h_2)e^{-d_1\iota \gamma }y^*e^{-d_2(t-(m+\iota )\gamma )},t\in ((m+\iota )\gamma , (m+1)\gamma ], \end{aligned}\right. \end{aligned}$$
(11)

where \(y^*\) is denoted by (7).

Lemma 2.4

(i)If \((1-h_1)e^{r \iota \gamma -c(1-\iota )\gamma }>1\), the fixed point \(w^*\) is GAS.

(ii)If \((1-h_1)e^{r \iota \gamma -c(1-\iota )\gamma }<1\), the fixed point \(w_0\) is GAS.

Proof

Seeing as the system is as follow:

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\dot{w}(t)=rw(t)(1-\frac{w(t)}{K}), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup w(t)=-h_1w(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\dot{w}(t)=-cw(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\triangle w(t)=0,\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(12)

By analyzing,

$$\begin{aligned} w(t)=\left\{ \begin{aligned}&\frac{Kw(m\gamma ^+) e^{r(t-m\gamma )}}{K+w(m\gamma ^+)(e^{r(t-m\gamma )}-1)},t\in (m\gamma ,(m+\iota )\gamma ],\\&w((m+\iota )\gamma ^+)e^{-c(t-(m+\iota )\gamma )},t\in ((m+\iota )\gamma , m+1)\gamma ]. \end{aligned}\right. \end{aligned}$$
(13)

By calculating (13), we derive

$$w((m+1)\gamma ^+)=\frac{(1-h_1)Kw(m\gamma ^{+})e^{r \iota \gamma -c(1-\iota )\gamma }}{K+w(m\gamma ^{+})(e^{r \iota \gamma }-1)},$$

let \(A=(1-h_1)e^{(r\iota -c(1-\iota ))\gamma },B=e^{r \iota \gamma }-1\), we analysis show that there are two fixed points:

$$\begin{aligned} w^*=\frac{AK-K}{B} \end{aligned}$$
(14)

and \(w_0=0\).

Let

$$w(m\gamma ^+)=w_{m},$$
$$\begin{aligned} F(w_{m})=\frac{AKw_{m}}{K+Bw_{m}}=w((m+1)\gamma ^+)=w_{m+1}, \end{aligned}$$
(15)

we derive

$$\begin{aligned} \frac{d F(w_{m})}{d w_{m}}=\frac{K^{2}A}{(K+Bw_{m})^2}. \end{aligned}$$
(16)

(i)If \((1-h_1)e^{r \iota \gamma -c(1-\iota )\gamma }>1\), that is \(\frac{1}{A}<1\), then we get

$$\begin{aligned} \bigg |\frac{d F(w_{m})}{d w_{m}}\bigg |_{w_{m}=w^{*}}<\frac{1}{A}<1, \end{aligned}$$
(17)

it implies that the fixed point \(w^*\) is locally asymptotically stable. Next,

$$\bigg |\frac{1}{w_{m+1}}-\frac{1}{w^*}\bigg |= \bigg |\frac{K+B w_{m}}{A K w_{m}}-\frac{K+B w^*}{A K w^*}\bigg |=\frac{1}{A}\bigg |\frac{1}{w_{m}}-\frac{1}{w^*}\bigg |\rightarrow 0,$$

as \(m\rightarrow \infty\). \(\frac{1}{A}<1\) implies the fixed point \(w^*\) is globally attractive. In conclusion \(w^*\) is GAS.

(ii)If \((1-h_1)e^{r \iota \gamma -c(1-\iota )\gamma }<1\), that is \(A<1\), we acquire

$$\begin{aligned} \bigg |\frac{d F(w_{m})}{d w_{m}}\bigg |_{w_{m}=w_0}= A<1, \end{aligned}$$
(18)

it implies that the fixed point \(w_0\) is locally asymptotically stable. Let’s continue,

$$\bigg |w_{m+1}-w_0\bigg |= \bigg |\frac{A K w_{m}}{K+B w_{m}}-\frac{A K w_0}{K+B w_0}\bigg |\le A\bigg |w_{m}-w_0\bigg |\rightarrow 0,$$

as \(m\rightarrow \infty\). \(\frac{1}{A}<1\) implies the fixed point \(w_0\) is globally attractive. So \(w_0\) is GAS.

Refer to15, the following Lemma 2.5 can be got.

Lemma 2.5

If \((1-h_1)e^{r \iota \gamma -c(1-\iota )\gamma }>1\), the periodic solution of (12) \(\widetilde{w(t)}\) is GAS and is denoted by

$$\begin{aligned} \widetilde{w(t)}=\left\{ \begin{aligned}&\frac{Kw^*e^{r(t-m\gamma )}}{K+w^*(e^{r(t-m\gamma )}-1)},t\in (m\gamma ,(m+\iota )\gamma ],\\&\frac{(1-h_1)Kw^*e^{r \iota \gamma }}{K+w^*(e^{r \iota \gamma }-1)}e^{-c(t-(m+\iota )\gamma )},t\in ((m+\iota )\gamma ,(m+1)\gamma ],\end{aligned}\right. \end{aligned}$$
(19)

\(w^*\) is defined as (14).

Extinction and permanence

Assume the following conditions:

  1. (i)

    \(h_1>1-\frac{1}{e^{r \iota \gamma +\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}-c(1-\iota )\gamma +\frac{\beta _2((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)}{d_2}}}\).

  2. (ii)

    \(h_1>1-\frac{1}{e^{r \iota \gamma +\frac{\beta _1y_1^*(e^{-d_1\iota \gamma }-1)}{d_1(1+\alpha _1\varrho )}-\frac{\beta _1\varepsilon \iota \gamma }{1+\alpha _1\varrho } -c(1-\iota )\gamma +\frac{\beta _2((1-h_2)e^{-d_\iota \gamma }y_1^*)(e^{-d_2(1-\iota ) \gamma }-1)}{d_2(1+\alpha _2\varrho )} -\frac{\beta _2\varepsilon (1-\iota )\gamma }{1+\alpha _2\varrho }}}\).

  3. (iii)

    \(h_1<1-\frac{1}{e^{r \iota \gamma +\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}-c(1-\iota )\gamma +\frac{\beta _2((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)}{d_2}}}\).

Stability of pest-eradication periodic solution

Theorem 3.1

If (i) and (ii) hold, the pest-eradication boundary periodic solution of (1) \((0,\widetilde{y(t)})\) is GAS, and \(y^*\) is denoted by (7).

Proof

Let \(u(t)=x(t),v(t)=y(t)-\widetilde{y(t)}\), we obtain

$$\begin{aligned}\left( \begin{array}{c} \frac{du(t)}{dt} \\ \frac{dv(t)}{dt} \end{array}\right) =\left( \begin{array}{cc} r-\beta _1\widetilde{y(t)} & 0 \\ k_1\beta _1\widetilde{y(t)} & -d_1 \end{array}\right) \left( \begin{array}{c} u(t) \\ v(t) \end{array}\right) \end{aligned},t\in (m\gamma ,(m+\iota )\gamma ],$$

and

$$\begin{aligned}\left( \begin{array}{c} \frac{du(t)}{dt} \\ \frac{dv(t)}{dt} \end{array}\right) =\left( \begin{array}{cc} -c-\beta _2\widetilde{y(t)} & 0 \\ k_2\beta _2\widetilde{y(t)} & -d_2 \end{array}\right) \left( \begin{array}{c} u(t) \\ v(t) \end{array}\right) \end{aligned},t\in ((m+\iota )\gamma ,(m+1)\gamma ].$$

Futher, we derive the fundamental solution matrix

$$\begin{aligned}\mathbf {\phi _1(t)}=\left( \begin{array}{cc} e^{\int _{m\gamma }^{t}(r-\beta _1\widetilde{y(t)})ds} & 0 \\ * & e^{-d_1(t-m\gamma )} \end{array}\right) \end{aligned},t\in (m\gamma ,(m+\iota )\gamma ],$$

and

$$\begin{aligned}\mathbf {\phi _2(t)}=\left( \begin{array}{cc} e^{\int _{(m+\iota )\gamma }^{\gamma }(-c-\beta _2\widetilde{y(t)})ds} & 0 \\ \bigstar & e^{-d_2(t-(m+\iota )\gamma )} \end{array}\right) \end{aligned},t\in ((m+\iota )\gamma ,(m+1)\gamma ].$$

We not used \(*\) and \(\bigstar\) in the analysis. Once again, through linearization, we derive

$$\begin{aligned}\left( \begin{array}{c} u((m+\iota )\gamma ^+) \\ v((m+\iota )\gamma ^+) \end{array}\right) =\left( \begin{array}{cc} 1-h_1 & 0 \\ 0 & 1-h_2 \end{array}\right) \left( \begin{array}{c} u((m+\iota )\gamma ) \\ v((m+\iota )\gamma ) \end{array}\right) \end{aligned},t\in (m\gamma ,(m+\iota )\gamma ],$$

and

$$\begin{aligned}\left( \begin{array}{c} u((m+1)\gamma ^+) \\ v((m+1)\gamma ^+) \end{array}\right) =\left( \begin{array}{cc} 1 & 0 \\ 0 & 1-\frac{\alpha \mu _{max}}{(1+\alpha \widetilde{y((m+1)\gamma )})^2} \end{array}\right) \left( \begin{array}{c} u((m+1)\gamma ) \\ v((m+1)\gamma ) \end{array}\right) \end{aligned},t\in ((m+\iota )\gamma ,(m+1)\gamma ].$$

The eigenvalues determine whether the periodic solution is stable.

$$\begin{aligned}\textbf{M}&=\Phi _1(\iota \gamma )\left( \begin{array}{cc} 1-h_1 & 0 \\ 0 & 1-h_2 \end{array}\right) \Phi _2(\gamma )\left( \begin{array}{cc} 1 & 0 \\ 0 & 1-\frac{\alpha \mu _{max}}{(1+\alpha \widetilde{y(\gamma )})^2} \end{array}\right) \\&=\left( \begin{array}{cc} (1-h_1)e^{\int _{0}^{\iota \gamma }(r-\beta _1\widetilde{y(s)})ds+\int _{\iota \gamma }^{\gamma }(-c-\beta _2\widetilde{y(s)})ds} & 0 \\ \sharp & (1-h_2)(1-\frac{\alpha \mu _{max}}{(1+\alpha \widetilde{y(\gamma )})^2})e^{\int _{0}^{\iota \gamma }-d_1ds+\int _{\iota \gamma }^{\gamma }-d_2ds} \end{array}\right) ,\end{aligned}$$

\(\sharp\) is not used in the analysis.

$$\begin{aligned}\lambda _1&=(1-h_1)e^{\int _{0}^{\iota \gamma }(r-\beta _1\widetilde{y(s)})ds+\int _{\iota \gamma }^{\gamma }(-c-\beta _2\widetilde{y(s)})ds}\\&=(1-h_1)e^{r \iota \gamma +\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}-c(1-\iota )\gamma +\frac{\beta _2}{d_2}((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)},\end{aligned}$$

and

$$\begin{aligned}\lambda _2&=(1-h_2)(1-\frac{\alpha \mu _{max}}{(1+\alpha \widetilde{y(\gamma )})^2})e^{\int _{0}^{\iota \gamma }-d_1ds+\int _{\iota \gamma }^{\gamma }-d_2ds}\\&=(1-h_2)(1-\frac{\alpha \mu _{max}}{(1+\alpha \widetilde{y(\gamma )})^2})e^{-d_1\iota \gamma -d_2(1-\iota )\gamma } \le (1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }.\end{aligned}$$

If

$$(1-h_1)e^{r \iota \gamma +\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}-c(1-\iota )\gamma +\frac{\beta _2}{d_2}((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)}<1$$

and

$$(1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }<1,$$

then \(|\lambda _1|<1\),\(|\lambda _2|<1\).i.e.

$$\begin{aligned}h_1>1-\frac{1}{e^{r \iota \gamma +\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}-c(1-\iota )\gamma +\frac{\beta _2((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)}{d_2}}},\end{aligned}$$

and

$$\begin{aligned}(1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }<1\end{aligned}$$

hold, according to Floquet Theorem25, \((0,\widetilde{y(t)})\) is locally stable, and \(y^*\) is denoted by (7). Next, the global attraction will be proven.

Selecting \(\varepsilon >0\) so that

$$\rho =(1-h_1)e^{\int _{0}^{\iota \gamma }(r-\frac{\beta _1(\widetilde{y_1(s)}-\varepsilon )}{1+\alpha _1\varrho })ds -\int _{\iota \gamma }^{\gamma }(c+\frac{\beta _2(\widetilde{y_1(s)}-\varepsilon )}{1+\alpha _2\varrho })ds}<1$$

i.e.

$$r \iota \gamma +\frac{\beta _1y_1^*(e^{-d_1\iota \gamma }-1)}{d_1(1+\alpha _1\varrho )}-\frac{\beta _1\varepsilon \iota \gamma }{1+\alpha _1\varrho } -c(1-\iota )\gamma +\frac{\beta _2((1-h_2)e^{-d_\iota \gamma }y_1^*)(e^{-d_2(1-\iota ) \gamma }-1)}{d_2(1+\alpha _2\varrho )} -\frac{\beta _2\varepsilon (1-\iota )\gamma }{1+\alpha _2\varrho }<\ln \frac{1}{1-h_1}$$

hold. By analyzing the second and sixth equations of system (1),

$$\frac{dy(t)}{dt}\ge -d_1y(t),$$

and

$$\frac{dy(t)}{dt}\ge -d_2y(t)$$

can be obtained. We contemplate the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{y}_1(t)}{dt}=-d_1y_1(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y_1(t)=-h_2y_1(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{y}_1(t)}{dt}=-d_2y_1(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y_1(t)=\frac{\mu _{max}}{1+\alpha y_1(t)},\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(20)

From Lemmas 2.2 and 2.3, by analyzing (20), we obtain

$$\begin{aligned} \widetilde{y_1(t)}=\left\{ \begin{aligned}&e^{-d_1(t-m\gamma )}y_1^*,t\in (m\gamma ,(m+\iota )\gamma ],\\&(1-h_2)e^{-d_1\iota \gamma }e^{d_2(t-(m+\iota )\gamma }y_1^*,t\in ((m+\iota )\gamma ,(m+1)\gamma ].\end{aligned}\right. \end{aligned}$$
(21)

where \(y_1^*\) is defined as

$$\begin{aligned} y_1^*=\frac{-(1-A_1)+\sqrt{(1-A_1)^2+4\alpha \mu _{max} A_1(1-A_1)}}{2\alpha A_1(1-A_1)}, \end{aligned}$$
(22)

and \(A_1=(1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }<1\).

According to the comparison theorem of impulsive differential equations25, \(y(t)\ge y_1(t)\) holds as \(t\rightarrow \infty\) and

$$\begin{aligned} y(t)\ge y_1(t)\ge \widetilde{y_1(t)}-\varepsilon \end{aligned}$$
(23)

for all t large enough. We derive \(x(t)\le w(t)<\widetilde{w(t)}+\varepsilon _1\) for \(t\in (m\gamma ,(m+1)\gamma ]\) by the comparison theorem and Lemma 2.5. We define that \(\max \limits _{0\le t\le \omega }\widetilde{w(t)}=\varrho\) from Lemma 2.5. We posit (23) holds for \(t\ge 0\), from (1) and (23), we derive

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\le (r-\frac{\beta _1(\widetilde{y_1(t)}-\varepsilon )}{1+\alpha _1\varrho })x(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=-h_1x(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\le -(c+\frac{\beta _2(\widetilde{y_1(t)}-\varepsilon )}{1+\alpha _2\varrho })x(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=0,\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(24)

So \(x((m+1)\gamma )\le \rho x(m\gamma )\) for all \(m>M^{'}\), and \(x(m\gamma )\le x(M^{'}\gamma )\rho ^{(m-M^{'})\gamma }\rightarrow 0\) as \(m\rightarrow \infty\). So \(x(t)\rightarrow 0\) as \(t\rightarrow \infty\).

Next, when \(t\rightarrow \infty\), \(y(t)\rightarrow \widetilde{y(t)}\) will be proofed, choose a \(\varepsilon _2\) and satisfies \(0<\varepsilon _2< \min \{\frac{d_1}{k_1\beta _1-d_1\alpha _1},\frac{d_2}{k_2\beta _2-d_2\alpha _2}\}\), there must be \(0<x(t)<\varepsilon _2\) when \(t>t_0>0\), we derive

$$\begin{aligned} -d_1y(t)\le \frac{dy(t)}{dt}\le (\frac{\varepsilon _2 k_1\beta _1}{1+\alpha _1\varepsilon _2}-d_1)y(t), \end{aligned}$$
(25)

and

$$\begin{aligned} -d_2y(t)\le \frac{dy(t)}{dt}\le (\frac{\varepsilon _2 k_2\beta _2}{1+\alpha _2\varepsilon _2}-d_2)y(t). \end{aligned}$$
(26)

So we derive

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{z_1}(t)}{dt}=(\frac{\varepsilon _2 k_1\beta _1}{1+\alpha _1\varepsilon _2}-d_1)z_1(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup z_1(t)=-h_2z_1(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{z_1}(t)}{dt}=(\frac{\varepsilon _2 k_2\beta _2}{1+\alpha _2\varepsilon _2}-d_2)z_1(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup z_1(t)=\frac{\mu _{max}}{1+\alpha z_1(t)},\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(27)

Obviously, \(z_1(t)\rightarrow \widetilde{z_1(t)}\), as \(t\rightarrow \infty\), where \(z_1(t)\) is given by

$$\begin{aligned} \widetilde{z_1(t)}=\left\{ \begin{aligned}&e^{(\frac{\varepsilon _2 k_1\beta _1}{1+\alpha _1\varepsilon _2}-d_1)(t-m\gamma )}z_1^*,t\in (m\gamma ,(m+\iota )\gamma ],\\&(1-h_2)e^{(\frac{\varepsilon _2 k_1\beta _1}{1+\alpha _1\varepsilon _2}-d_1)\iota \gamma }e^{(\frac{\varepsilon _2 k_2\beta _2}{1+\alpha _2\varepsilon _2}-d_2)(t-(m+\iota )\gamma )}z_1^*,t\in ((m+\iota )\gamma ,(m+1)\gamma ],\end{aligned}\right. \end{aligned}$$
(28)

\(z_1^*\) is denoted by

$$\begin{aligned} z_1^*=\frac{-(1-E)+\sqrt{(1-E)^2+4\alpha \mu _{max} E(1-E)}}{2\alpha E(1-E)},\end{aligned}$$
(29)

let \(E=(1-h_2)e^{(\frac{\varepsilon _2 k_1\beta _1}{1+\alpha _1\varepsilon _2}-d_1)\iota \gamma +(\frac{\varepsilon _2 k_2\beta _2}{1+\alpha _2\varepsilon _2}-d_2)(1-\iota )\gamma }<1\). For any positive \(\overline{\varepsilon }\), \(\widetilde{y(t)}-\overline{\varepsilon }<y(t)<\widetilde{z_1(t)}+\overline{\varepsilon }\) holds when \(t>t_0\), making \(\varepsilon _2\rightarrow 0\), we get \(\widetilde{y(t)}-\overline{\varepsilon }<y(t)<\widetilde{y(t)}+\overline{\varepsilon }\) for t sufficiently big, this one shows that \(y(t)\rightarrow \widetilde{y(t)}\) as \(t\rightarrow \infty\).

Permanence of system

Theorem 3.2

If (iii) holds, the system (1) is permanent, \(y^*\)is denoted by (7).

Proof

Assuming that the solution to system (1) is recorded as (x(t), y(t)). From Lemma 2.1, \(x(t)\le R\), and \(y(t)\le R\) hold for \(R>0\), t is sufficiently big. There is \(y(t)>\widetilde{y(t)}-\overline{\varepsilon }\) when t is sufficiently big and \(\overline{\varepsilon }>0\) is sufficiently small. Therefore, \(y(t)\ge (1-h_2)e^{-(d_1\iota +d_2(1-\iota ))\gamma }y^*-\overline{\varepsilon }=\widetilde{R}\) for \(t\ge (m_0+\iota )\gamma\), \(m_0>0\). We simply require to identify a constant \(R^{'}>0\) so that \(x(t)\ge R^{'}\) for t sufficiently big.

First, choosing \(R^{*}\) and \(\varepsilon\), they satisfy \(0<R^{*}<\min \{\frac{d_1}{k_1\beta _1-d_1\alpha _1},\frac{d_2}{k_2\beta _2-d_2\alpha _2}\}\) and \(0<\varepsilon\) so that

$$\sigma =(1-h_1)e^{\int _{0}^{\iota \gamma }[r-\frac{rR^*}{K}-\beta _1(\widetilde{z(s)}+\varepsilon )]ds +\int _{\iota \gamma }^{\gamma }-[c+\beta _2(\widetilde{z(s)}+\varepsilon )]ds}>1.$$

Here \(x(t)<R^{*}\) does not hold as \(t\ge 0\), if not

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{y}(t)}{dt}\le (\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)y(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y(t)=-h_2y(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{y}(t)}{dt}\le (\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2)y(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup y(t)=\frac{\mu _{max}}{1+\alpha y(t)},\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(30)

We contemplate the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{z}(t)}{dt}=(\frac{R^{*}k_1\beta }{1+\alpha _1 R^{*}}-d_1)z(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup z(t)=-h_2z(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{z}(t)}{dt}=(\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2)z(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup z(t)=\frac{\mu _{max}}{1+\alpha z(t)},\\ \end{aligned}\right. ~~t=(m+1)\gamma ,\\ \end{aligned}\right. \end{aligned}$$
(31)

we know \(y(t)\le z(t)\) and \(z(t)\rightarrow \widetilde{z(t)}\) as \(t\rightarrow \infty\) through the comparison theorem. From Lemmas 2.2 and 2.3, we calculate and obtain

$$\begin{aligned} \widetilde{z(t)}=\left\{ \begin{aligned}&e^{(\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)(t-m\gamma )}z^*, ~~t\in (m\gamma , (m+\iota )\gamma ],\\&(1-h_2)e^{(\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)\iota \gamma }e^{(\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2)(t-(m+\iota )\gamma )}z^*,~~t\in ((m+\iota )\gamma , (m+1)\gamma ], \end{aligned}\right. \end{aligned}$$
(32)

\(z^*\) is denoted by

$$\begin{aligned} z^*=\frac{-(1-A)+\sqrt{(1-A)^2+4\alpha \mu _{max} A(1-A)}}{2\alpha A(1-A)},\end{aligned}$$
(33)

where \(A=(1-h_2)e^{(\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)\iota \gamma +(\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2)(1-\iota )\gamma }<1\). So there exists a positive number \(t_1\) that makes \(y(t)\le z(t)\le \widetilde{z(t)}+\varepsilon\) and

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\ge [r-\frac{rR^{*}}{K}-\beta _1(\widetilde{z(t)}+\varepsilon )]x(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=-h_1x(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\ge -[c+\beta _2(\widetilde{z(t)}+\varepsilon )]x(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=0,\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(34)

Further, for \(t>M_1\gamma\), \(M_1\in N\), integrating (34) on \((m\gamma ,(m+1)\gamma ], m\ge M_1\), we derive

\(x((m+1)\gamma )\ge x(m\gamma )\sigma \ge x(M_1\gamma )\sigma ^{m-M_1+1}\rightarrow \infty\) as \(m\rightarrow \infty\) and \(t\rightarrow \infty\), this contradicts the fact that x(t) is bounded. So \(t_1>0\) such that \(x(t)\ge R^{'}\).

Second, the proof is completed when \(x(t)\ge R^{*}\) for \(t\ge t_1\). If not, we will continue to contemplate (I) and (II). Taking \(t^{'}=\inf _{t\ge t_1}\{x(t)<R^{*}\}\). \(x(t)\ge R^{*}\) for \(t\in [t_1,t^{'}]\), where \(t^{'}\in (m_1\gamma ,(m_1+1)\gamma ),m_1\in Z^{+}\).

(I)\(t^{'}=(m+\iota )\gamma\) for all \(m\in Z^+\), \(x(t)\ge R^{*}\) for \(t\in [t_1,t^{'})\) and \(x(t^{'})=R^{*}\), and \(x(t^{'})\le x(t^{'+})\le R^{*}\). Pick \(m_2,m_3\in Z^+\) so that

$$m_2\gamma \ge \frac{1}{\min \{\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1,\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2\}}\ln (\frac{\varepsilon }{(1-h_2)R}),$$
$$(1-h_1)^{m_2}e^{\epsilon m_2\gamma }\sigma ^{m_3}>(1-h_1)^{m_2}e^{\epsilon (m_2+1)\gamma }\sigma ^{m_3}>1,$$

where \(\epsilon =\min \{r-\frac{rR^{*}}{K}-\beta _1R,-(c+\beta _2R)\}<0\). Let \(\overline{T}=m_2\gamma +m_3\gamma\). There exists a \(t_2\in [t^{'},t^{'}+\overline{T}]\) that makes \(x(t_2)>R^{*}\), if not, please contemplate the equation \(z(t^{'+})=y(t^{'+})\) as presented in (31). Similar to the proof of Lemmas 2.2 and 2.3, through calculation, we have

$$z(t)=\left\{ \begin{aligned}&(z(t^{'})-z^*)e^{(\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)(t-m\gamma )}+\widetilde{z(t)}, ~~t\in (m\gamma , (m+\iota )\gamma ],\\&(z(t^{'})-z^*)(1-h_2)e^{(\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1)\iota \gamma }e^{(\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2)(t-(m+\iota )\gamma )}+\widetilde{z(t)},~~t\in ((m+\iota )\gamma , (m+1)\gamma ], \end{aligned}\right.$$

\(m_1+1<m\le m_1+1+m_2+m_3\) (\(m_2\in Z^+\) is large enough), further \(|z(t)-\widetilde{z(t)}|\le (1-h_2)Re^{\min \{\frac{R^{*}k_1\beta _1}{1+\alpha _1 R^{*}}-d_1,\frac{R^{*}k_2\beta _2}{1+\alpha _2 R^{*}}-d_2\}(t-(m_1+1)\gamma )}<\varepsilon\) and \(y(t)\le z(t)\le \widetilde{z(t)}+\varepsilon\), which implies (31) holds for \(t^{'}+m_2\gamma \le t\le t^*+\overline{T}\). So \(x(t^*+\overline{T})\ge x(t^{'}+m_2\gamma )\sigma ^{m_3}\) holds. Then we derive

$$\begin{aligned} \left\{ \begin{aligned}&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\ge (r-\frac{rR^{*}}{K}-\beta _1R)x(t), \\ \end{aligned}\right. ~~t\in (m\gamma ,(m+\iota )\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=-h_1x(t),\\ \end{aligned}\right. ~~t=(m+\iota )\gamma ,\\&\left. \begin{aligned}&\frac{d{x}(t)}{dt}\ge -(c+\beta _2R)x(t),\\ \end{aligned}\right. ~~t\in ((m+\iota )\gamma ,(m+1)\gamma ],\\&\left. \begin{aligned}&\bigtriangleup x(t)=0,\\ \end{aligned}\right. ~~t=(m+1)\gamma .\\ \end{aligned}\right. \end{aligned}$$
(35)

Integrating (35) on \([t^{'},t^{'}+m_2\gamma ]\), we get

$$x(t^{'}+m_2\gamma )\ge (1-h_1)^{m_2}R^{*}e^{\epsilon m_2\gamma },$$

so

$$x(t^{'}+\overline{T})\ge (1-h_1)^{m_2}R^{*}e^{\epsilon m_2\gamma }\sigma ^{m_3}>R^{*},$$

this presents a contradiction. Let \(\overline{t}=\inf _{t\ge t^{'}}\{x(t)\ge R^{*}\}\), thus \(x(\overline{t})\ge R^{*}\) for \(t\in [t^{'},\overline{t}]\), then \(x(t)\ge x(t^{'+})e^{\epsilon (t-t^{'})}\ge (1-h_1)^{m_2+m_3}R^{*}e^{\epsilon (m_2+m_3)\gamma }>(1-h_1)^{m_2+m_3}R^{*}e^{\epsilon (m_2+m_3+1)\gamma }=R^{'}\) holds for \(t\in (t^{'},\overline{t})\). Hence \(x(t)\ge R^{*}\). Given that \(x(\overline{t})\ge R^{*}\), the same perspective can be applied. So \(x(t)\ge R^{'}\) for all \(t\ge t_1\).

(II)\(t\ne (m+\iota )\gamma\), \(m\in Z^+\), then \(x(t)\ge R^{*}\) for \(t\in [t_1,t^*]\), and \(x(t^*)=R^{*}\). Assume \(t^{'}\in ((m_1^{'}+\iota -1)\gamma ,(m_1^{'}+\iota )\gamma )\), so two plausible cases need to be considered:

(i)\(x(t)\le R^{*}\) for all \(t\in (t^*,(m_1^{'}+\iota )\gamma )\), so \(x((m_1^{'}+\iota )\gamma ^+)<R^{*}\) can be derived. Same as (I), there exists a \(t_2^{'}\in [(m_1^{'}+\iota )\gamma ,(m_1^{'}+\iota )\gamma +\overline{T}]\) that makes \(x(t_2^{'})>R^{*}\), omitted. Making \(\underline{t}=\inf _{t>t^{'}}\{x(t)>R^{*}\}\), \(x(t)\le R^{*}\) for \(t\in (t^{'},\underline{t})\) and \(x(\underline{t})=R^{*}\). Choosing a \(t\in (m_1^{'}\gamma +(\iota ^{'}-1)\gamma ,m_1^{'}\gamma +\iota ^{'}\gamma ]\subset (t^{'},\underline{t})\), \(\iota ^{'}\in Z^+\) and \(\iota ^{'}<1+m_2+m_3\), we obtain

$$x(t)\ge x(t^{'})e^{\epsilon (t-t^{'})}\ge (1-h_1)^{m_2+m_3}R^{*}e^{\epsilon (m_2+m_3+1)\gamma }.$$

Let \(R^{'}=(1-h_1)^{m_2+m_3}R^{*}e^{\epsilon (m_2+m_3+1)\gamma }\), we derive \(x(t)\ge R^{'}\) for \(t\in (t^{'},\underline{t})\). For \(t>\underline{t}\), given that \(x(t)\ge R^{'}\), we can continue to discuss.

(ii)There exists a \(t\in (t^{'},(m_1^{'}+\iota )\gamma )\) that makes \(x(t)>R^{*}\). Let \(\widehat{t}=\inf _{m_1^{'}+\iota>t>t^{'}}\{x(t)>R^{*}\}\), then \(x(t)\le R^{*}\) for \(t\in (t^{'},\widehat{t})\). Given that (35) is established, integrating (35) on \((t^{'},\widehat{t})\), then

$$x(t)\ge x(t^{'})e^{\epsilon (t-t^{'})}\ge R^{*}e^{\epsilon \iota \gamma }>R^{'}$$

is obtain. Given that \(x(\widehat{t})\ge R^{*}\) for \(t>\widehat{t}\), we can proceed with the discussion. Therefore \(x(t)\ge R^{'}\) for \(t\ge t_1\). This indicates the system (1) is uniformly permanent.

Numerical simulation and discussion

Because our research is primarily theoretical and has not yet been directly related to actual field data or management practices. But to verify our conditions, we have set the following parameters for the model to conduct numerical simulations: \((x(0), y(0))=(3.3,2.8)\), \((x(0), y(0))=(0.7,0.6)\) and Table 2.

Table 2 Parameter values selection for model (1).
Full size table

We calculate

$$C=(1-h_2)e^{-d_1\iota \gamma -d_2(1-\iota )\gamma }=(1-0.3)e^{(-0.3\times (1-05)-0.38\times 0.5)\times 1}= 0.4413<1,$$
$$\begin{aligned}y^*&=\frac{-(1-C)+\sqrt{(1- C)^2+4\alpha C\mu _{max}(1-C)}}{2\alpha C(1-C)}\\&=\frac{-(1- 0.4413)+\sqrt{(1- 0.4413)^2+4\times 1\times 0.4413\times (1- 0.4413)}}{2\times 1\times 0.4413\times (1- 0.4413)}\\&=2.1246,\end{aligned}$$
$$\frac{\beta _1y^*(e^{-d_1\iota \gamma }-1)}{d_1}=\frac{0.65\times 2.1246\times e^{-0.38\times 0.5\times 1}}{0.38}=-0.6289,$$
$$\begin{aligned}&\frac{\beta _2}{d_2}((1-h_2)e^{-d_1\iota \gamma }y^*)(e^{-d_2(1-\iota )\gamma }-1)\\&=\frac{0.7}{0.3}\times (\Phi 1-0.38\Psi \times e^{-0.38\times 0.5\times 1}\times 2.1246)\times e{-0.3\times (1-0.5)\times 1}\\&=-0.3540,\end{aligned}$$
$$r \iota \gamma -c(1-\iota )\gamma =3.9\times 0.5\times 1-0.4\times (1-0.5)\times 1= 1.7500,$$
$$1-\frac{1}{e^{-0.6289+(-0.3540)+1.7500}}=0.5356<0.6=h_1,$$

so the pest-eradication periodic solution \((0,\widetilde{y(t)})\) of system (1) is GAS (see Figs. 1 and 2). Assuming \(x(0)=0.7, y(0)=0.6\) \(r=3.9, d_1=0.38, c=0.4, \beta _1=0.65, k_1=0.57, \beta _2=0.7, k_2=0.6, d_2=0.3, h_1=0.5, h_2=0.38, \mu _{max}=2.3, \alpha =1,\iota =0.5, \gamma =1\). Based on above calculation \(h_1=0.5<0.5356\), the system (1) is permanent (see Fig. 3). Our result reveal that changes in the population of pests with changes in \(h_1\) during the active period. Consequently we deduce the existence of a critical value \(h^*\approx 0.5356\) for the parameter \(h_1\) in system (1), the pest-eradication periodic solution \((0,\widetilde{y(t)})\) of system (1) is GAS for \(h_1>h^*\). Additionally, the system (1) is permanent when \(h_1<h^*\). So we can choose to spray pesticide appropriately in the active period.

Figure 1
figure 1

The pest-eradication periodic solution of system (1) is GAS for initial values \(x(0)=3.3,y(0)=2.8\) \(r=3.9, d_1=0.38, c=0.4, \beta _1=0.65, k_1=0.57,\), \(\beta _2=0.7,k_2=0.6, d_2=0.3,h_1=0.6,h_2=0.38\), \(\mu _{max}=2.3,\alpha =1,\iota =0.5, \gamma =1\).

Full size image
Figure 2
figure 2

The pest-eradication periodic solution of system (1) is GAS for initial values \(x(0)=0.7,y(0)=0.6\) \(r=3.9, d_1=0.38, c=0.4, \beta _1=0.65\), \(k_1=0.57,\beta _2=0.7,k_2=0.6, d_2=0.3,h_1=0.6,h_2=0.38\), \(\mu _{max}=2.3,\alpha =1,\iota =0.5, \gamma =1\).

Full size image
Figure 3
figure 3

The system (1) is permanent for initial values \(x(0)=0.7,y(0)=0.6\) \(r=3.9, d_1=0.38, c=0.4, \beta _1=0.65\), \(k_1=0.57,\beta _2=0.7, k_2=0.6, d_2=0.3,h_1=0.5,h_2=0.38\), \(\mu _{max}=2.3,\alpha =1,\iota =0.5, \gamma =1.\).

Full size image

Furthermore, our analysis assumes a specific value for the parameter \(\mu _{max}\), where we observe different outcomes for system (1). When we set \(\mu _{max}=1.5\), the system (1) is permanent, see Fig. 4. However, upon increasing \(\mu _{max}\) to 2.3, the system (1) is GAS in Fig. 2. Therefore, we can say that the population of pests changes with variations in the maximum release volume \(\mu _{max}\). So we can flexibly select to release suitable natural enemies.

Figure 4
figure 4

The system (1) is permanent for initial values \(x(0)=0.7, y(0)=0.6\) \(r=3.9, d_1=0.38, c=0.4, \beta _1=0.65, k_1=0.57\), \(\beta _2=0.7, k_2=0.6, d_2=0.3, h_1=0.6, h_2=0.38\), \(\mu _{max}=1.5, \alpha =1, \iota =0.5, \gamma =1\).

Full size image

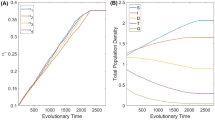
To explore how the nonlinear impulse term affects the system (1), we take \(\mu _{max}\) as a parameter and give the bifurcation diagrams. If we supposed that \(x(0)=2, y(0)=1.8\) \(r=2.5,K=5.5,d_1=0.38,c=0.78,\beta _1=2.52,\alpha _1=1\), \(k_1=0.89,\beta _2=2.06,\alpha _2=0.8,k_2=0.7,d_2=0.82,h_1=0.45\), \(h_2=0.38,\alpha =3.5,\iota =0.63, \gamma =5.5\), we can find that \(\mu _{max}\) increases from 0 to 1.5, the dynamic system (1) behavior has chaos\(\rightarrow\) period-doubling bifurcation\(\rightarrow\) period-halving bifurcation\(\rightarrow\) chaos\(\rightarrow\) period-doubling bifurcation\(\rightarrow\) period-halving bifurcation\(\rightarrow\) chaos, with the increase of \(\mu _{max}\), the stable \(\gamma\)-periodic solution returns eventually, see Fig. 5. We find that the abrupt disappearance of chaos and the sudden emergence of \(\gamma\)-periodic solution, see Fig. 6. The emergence of period-doubling bifurcation leading to the emergence of chaos has been studied in the literature26,27. Therefore a lightly change of the parameters \(\mu _{max}\) can happen dramatic effect, it shows that variation of the parameters \(\mu _{max}\) such that the pest population and natural enemy population appear different periodic oscillation phenomena. We can deduce that the nonlinear impulse term has a significant effect on model (1), and also shows that pest management system with hibernation of pests and impulsive nonlinear release of natural enemies is rich in research value.

Figure 5
figure 5

Bifurcation portrait of system (1) parameterized by the bifurcation parameter \(\mu _{max}\), takes the following parameters: \(x(0)=2, y(0)=1.8\) \(r=2.5, K=5.5, d_1=0.38, c=0.78, \beta _1=2.52, \alpha _1=1\), \(k_1=0.89, \beta _2=2.06, \alpha _2=0.8, k_2=0.7, d_2=0.82\), \(h_1=0.45, h_2=0.38, \alpha =3.5, \iota =0.63, \gamma =5.5\).

Full size image
Figure 6
figure 6

(a,b) Phases portrait of chaos of system (1) for \(\mu _{max}\approx 0.545\). (c,d) Phases portrait of \(\gamma\)-periodic solution for \(\mu _{max}\approx 1.171\).

Full size image

When selecting \(h_1\) as the bifurcation parameter, we define the initial conditions for the system as \(x(0)=1\) and \(y(0)=1.5\). Additionally, we set the model parameters to \(r=1.5, K=8, d_1=0.38, c=0.78, \beta _1=1.52, \alpha _1=1.6\), \(k_1=0.89, \beta _2=1.06, \alpha _2=1.8, k_2=0.7, d_2=0.82\), \(h_2=0.23, \mu _{max}=1, \alpha =2, \iota =0.8, \gamma =4\). By analyzing the results of numerical simulations, the system (1) exhibits a rich and complex dynamical behaviors, the system (1) undergoes chaos when \(0.049<h_1<0.092\), \(0.109<h_1<0.202\), \(0.241<h_1<0.455\) and \(0.469<h_1<0.591\), but as the parameter \(h_1\) increments and \(h_1 >0.591\), the system progressively achieves stability at \(\gamma\)-periodic solution, indicating a convergence towards a stable state within the dynamical framework of the model, see Fig. 7. For example, the Fig. 8 displays the system (1) appear chaos when \(h_1\approx 0.563\) and appear \(\gamma\)-periodic solution when \(h_1\approx 0.654\). Therefore, the parameter \(h_1\) plays a crucial role in pest management strategies, where rational and appropriate pesticide application is beneficial for pest control in our model (1).

Figure 7
figure 7

Bifurcation portrait of system (1) parameterized by the bifurcation parameter \(h_1\), takes the following parameters: \(x(0)=1, y(0)=1.5\) \(r=1.5, K=8, d_1=0.38, c=0.78, \beta _1=1.52, \alpha _1=1.6\), \(k_1=0.89, \beta _2=1.06, \alpha _2=1.8, k_2=0.7, d_2=0.82\), \(h_2=0.23, \mu _{max}=1, \alpha =2, \iota =0.8, \gamma =4.\).

Full size image
Figure 8
figure 8

(a,b) Phases portrait of chaos of system (1) for \(h_1\approx 0.563\). (c,d) Phases portrait of \(\gamma\)-periodic solution for \(h_1\approx 0.654\).

Full size image

Conclusion

The abuse of pesticides and insecticides not only seriously threatens human health but also causes multiple forms of pollution to the ecological environment30. Against this backdrop, the strategy of IPM has emerged, which abandons the traditional model of sole reliance on chemical agents and instead focuses on controlling pest populations within a damage threshold acceptable in terms of economic costs, rather than pursuing their complete eradication31. Natural enemy control is an important pest management tactic within the IPM strategy32,33. Typically, this strategy requires active human intervention-for example, supplementarily releasing natural enemies during critical periods to reduce pest population numbers. However, the implementation of natural enemy release strategies is often constrained by limited agricultural resources, meaning the release quantity of natural enemies should follow a saturation function based on natural enemy population density21. For certain pests (e.g., corn borers), metabolic rates decrease significantly during hibernation, with survival relying on lipid reserves to maintain basic life activities, which provides a time window for precision intervention34.

Our study innovatively constructs a pest management dynamical model that more closely aligns with natural ecosystems-a pest management system with hibernation of pests and impulsive nonlinear release of natural enemies. Unlike previous studies that have overlooked the impact of hibernation of pest, this model precisely incorporates this key biological characteristic-pest hibernation-alongside the nonlinear predator release mechanism, providing a new theoretical perspective for pest control. In this thesis, we apply Floquet theory and the comparison theorem of impulsive differential equations to derive conditions under which the pest-eradication periodic solution is GAS, denoted as \((0,\widetilde{y(t)}\)), which are obtained in Theorem 3.1. These mathematical conditions reveal a critical biological control threshold \(h_1^*\): when the mortality rate of pests killed by pesticide exceeds this value, the pest-eradication periodic solution achieves global asymptotic stability. The biological significance of this threshold \(h_1^*\) lies in its representation of the minimum critical insecticidal efficacy required to successfully suppress pest populations with hibernation habits. Below this critical value, the pest population can permanent, which are obtained in Theorem 3.2. Numerical simulations further show the biological impacts of natural enemy release strategies on pest population dynamics. We observed significant fluctuations in pest population density as it varies with the maximum release quantity of natural enemies (\(\mu _{max}\)). This indicates that \(\mu _{max}\) is a critical operational variable for regulating the survival or extinction of pests, and its setting directly determines whether natural enemies can be effectively utilized to suppress pest populations to low densities or eradication levels. Simulations with \(\mu _{max}\) and \(h_1\) selected as bifurcation parameters revealed that the system exhibits a rich array of dynamical behaviors (e.g., chaos, period-doubling bifurcation, period-halving bifurcation). The biological implications of these complex dynamics are that small changes in control parameters can lead to pest populations abruptly transitioning from predictable periodic fluctuations to unpredictable chaotic states, or result in population outbreaks.

Based on comprehensive theoretical analysis and simulation results, our study clearly identifies the decisive role of two key management factors in controlling hibernating pests: First, the mortality rate of pests killed by pesticide must reach or exceed a critical threshold (\(h_1^*\)), a finding that shows the importance of precise pesticide application and the selection of highly effective insecticides. Second, the maximum release quantity of natural enemies requires scientific optimization-an excessively low release quantity may fail to achieve effective control, while an excessively high release quantity could trigger complex population dynamics or increase management costs. The model established in this study not only provides a mathematical framework for understanding the complex dynamics of hibernating pest-natural enemy systems but also its analytical results offer crucial theoretical foundations and operational decision-making reference points for formulating efficient, stable, and sustainable IPM strategies targeting pests with hibernation behavior. The hibernation integration and nonlinear release strategies emphasized by the model represent a significant biological extension of traditional pest management models.