Introduction

The dense plasma focus (DPF) is a coaxial plasma railgun that concludes its plasma discharge in a Z-pinch configuration1,2,3,4. The discharge between electrodes is initiated during the “breakdown phase” by either a flashover across the primary insulator separating the electrodes, within a working gas, or by plasma injected into the inter-electrode space using fast gas puff valves. During the “axial phase,” the current sheath5,6 formed in the inter-electrode space ionizes and sweeps up the gas along the z-axis, driven by the azimuthal magnetic field generated by the current loop7. When the plasma reaches the end of the inner electrode, it accelerates axis-symmetrically inwards during the “radial phase.” The plasma layer is characterized by a strong shock at the front driven by a magnetic piston at the back. The piston reaches its highest speed just before the shock front coalesces onto the axis, leading to the formation of a reflected shock (RS), which initiates the process of stagnation. The motion of the piston induces a voltage that depends on current, speed, and geometry. For a small focus of 100 kA, this piston induced voltage is typically about 10 kV, whereas for a 1 MA focus, it can exceed 100 kV2,8,9. This high voltage accelerates deuterons, generating an initial pulse of fast deuteron beams with correspondingly high energies. For large PFs it is expected that the dynamics-induced voltages may cause re-strikes just before the start of the stagnation process, resulting in reduced current plasma dynamics2,5,8,9,10.

The RS moves radially outward toward the radially inward-moving piston. When the RS meets the piston, the stagnation process completes, and the stagnated plasma undergoes the pinch phase. Instabilities develop during the pinching process11, disrupting the plasma and interrupting current flow. This leads to significant charge accumulation and the formation of strong, localized electric fields. Ions entering these high-field regions are accelerated into a multitude of micro beams, which collectively form a second pulse of fast ion beam with higher energies than the first, up to MeV, primarily directed away from the anode1,2. Thus, the first dynamics-induced pulse of fast ion beams is produced just before stagnation, while the second pulse is generated toward the end of the pinch phase, merging from a multitude of instability-produced micro ion beams.

In a deuterium or deuterium-–tritium mix, fusion occurs via beam-target fusion6. With deuterium in small PFs, the first neutron pulse is typically insignificant relative to the neutron yield of the second pulse. In a large PF, for example the Poseidon, the first pulse typically contributed one third of the averaged neutron yield and was constant in quantity. The second pulse was more variable, contributing more in good shots, and less in poor shots, averaging twice the neutron production of the first pulse2,12.

In some geometries and conditions, thermonuclear fusion may also significantly contribute to the total neutron yield in DPFs and similar Z-pinch devices8,12,13,14. In any case, the same high voltages that accelerate the ions also accelerate the electrons predominantly toward the anode and generate X-ray pulses through bremsstrahlung emission on impact. Additionally, softer X-rays15 are generated from the plasmas as bremsstrahlung in fully ionized deuterium; but line emissions dominate if operated in or doped with high-Z gases. Both the neutron and X-ray pulses are extremely bright and typically occur within less than 100 nanoseconds. These intense and brief radiation bursts make the DPF an attractive candidate for radiation test facilities.

Such facilities play a critical role in advancing technologies for environments exposed to ionizing radiation, offering invaluable services for radiation hardening and neutron single event effects (nSEE) testing. Radiation hardening ensures the reliability and resilience of electronics and materials under harsh conditions16,17,18. The nSEE testing, which evaluates the susceptibility of components to transient and permanent radiation-induced disruptions due to neutrons, is vital for safeguarding systems against neutron single-event upsets/transients, latch-ups, and burnouts amongst other responses, caused by atmospheric neutrons, particle collisions, or man-made environments. These test capabilities are indispensable for organizations across diverse sectors, including national security, aerospace, medical device manufacturing, nuclear energy, and scientific research. They enable the development of robust technologies, ensuring mission-critical systems operate reliably in high-radiation environments, ultimately supporting innovation, security, and public safety17,18,19.

High voltages at the level of 100 kV are needed for good fusion neutron yields in large deuterium plasma focus devices. Fuse Energy Technologies (Fuse) has designed and built a 100 kV, 125 kJ dense plasma focus device called “FAETON-I” (F-I) to evaluate the radiation effects testing capabilities of the technology. When F-I is directly charged to 100 kV, its discharge generates \(\sim 1\) MA of electrical current with a rise time of \(\sim 3.7\) \(\mu\)s. Extensive experimentation was performed on F-I for over 1100 shots, establishing novel characterization of DPF outputs. The radiation characteristics of F-I and their correlation with the Lee Model Code are presented in this paper.

At such high voltages, three critical questions arise, hitherto unanswered. Do current sheaths form properly with good dynamics? Will re-strikes seriously degrade neutron yields? How does fusion neutron yield correlate with dynamics-induced voltage peak? A major difficulty anticipated for plasma focus operation at high voltage and high current is the likelihood of re-strikes which divert current away from the compressing plasma. The high speeds of the current sheath as the radial shock wave accelerates towards the axis during the radial phase leads to high induced voltages which are known to exceed 100 kV for MA devices20,21. Re-strikes were indeed observed to be commonplace in F-I with dynamics-induced voltages often exceeding 150 kV.

In this study, the Lee code is employed to simulate F-I performance, plasma dynamics, and neutron yield. The Lee code is a computational tool for simulating DPFs. It couples the electrical circuit equations with plasma dynamics, thermodynamics, and radiation to model the entire operation of a DPF machine. The code divides the plasma focus process into five phases (axial acceleration, radial compression, pinch, radiative cooling, and post-pinch expansion), solving normalized equations to maintain energy, charge, and mass consistency while accounting for radiation losses and plasma self-absorption22,23,24.

The Lee Code was modified to accommodate these re-strikes, allowing analysis of the measured current and voltages to be time-correlated to the dynamics. These studies confirm that proper dynamics was achieved and give the first indication that despite these re-strikes, high voltage and high current plasma focus devices can still outperform the universal scaling rule for neutron production of \(Y_\mathrm {D-D}=1.8 \times 10^{10} \times I_{\textrm{peak}}^{3.8}\), \(I_{\textrm{peak}}\) in MA22, compiled from the community of plasma focus devices. The analysis also reveals why the re-strikes are not as detrimental as expected and concludes with the expectation that in D-T operation re-strikes may not matter at all for neutron production. The confirmation that high voltage operation does not preclude good current sheath formation and proper dynamics and that despite restrikes neutron yields outperform the universal scaling law gives confidence for up-scaling to larger devices. Moreover, FAETON-I reveals that the outlook for D-T operation is even better. This is discussed at the conclusion of this paper.

Experimental setup

This section presents a comprehensive overview of the experimental setup, detailing the design and key operational parameters of the F-I device. It also describes the set of diagnostic tools used to analyze plasma dynamics and radiation production. These diagnostics provide essential data for understanding the performance and behavior of F-I under various operating conditions.

FAETON-I design

F-I is a 100 kV, 125 kJ dense plasma focus with two coaxial, concentric electrodes made of oxygen-free copper. The electrodes are isolated at the launching end by a 6.5 cm long, 10 mm thick MACOR insulator, and separated by an A-K (anode-cathode) gap of 5 cm. The anode is 17 cm long with a 5 cm radius and has a taper that starts at 15 cm with a final radius of 1.9 cm. The cathode is made of 24 copper bars, 12 mm in diameter and 25 cm long, that encircle the anode with a radius of 10.6 cm.

Its stainless-steel vacuum chamber is filled with deuterium or a mixture of deuterium and Krypton at a pressure range of 10-40 Torr. The capacitor bank consists of five capacitors, each 5 \(\upmu\)F with rated voltage of 150 kV, and stores 125 kJ when operated at 100 kV. Each capacitor is triggered by a 120 kV, 750 kA self-mounted rail gap switch filled with \(\textrm{SF}_6\) to 1 atm, designed and fabricated in-house. These rail gap switches are individually triggered using a five-channel BFMG19, which delivers -150 kV pulses with a 10-90% rise time of \(\sim 13\) ns to the knife-edge of each switch. The triggering jitter between the rail gap switches is less than 2 ns, ensuring synchronized discharge. The energy from the capacitor bank is transferred to F-I through ten transmission lines made of RG220/U coaxial cables. The static inductance of the system is \(\sim\)220 nH. During a discharge it generates up to \(\sim\)1 MA electrical current with the rise time of \(\sim\)3.7 \(\mu\)s. The main parameters of F-I were simulated using Lee model code22. Table 1 presents the design and operational characteristics of F-I DPF system.

Table 1 Design and operational characteristics of F-I.
Full size table
Fig. 1
figure 1

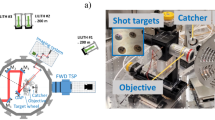
A sectional sketch of F-I with a schematic of the ion beam emitting in a cone and an ion sample being measured by the Faraday Cup. The collector plates are illustrated on the left with several coaxial cables from the capacitor bank. The tapered anode and circle-of-rods cathode are also presented. Positions of two bubble detectors and a photomultiplier-scintillator are shown.

Full size image

Diagnostics

The diagnostic system employed in this study provides a comprehensive evaluation of the DPF, characterizing the current sheath dynamics and dynamics-induced voltage, neutron yield, radiation dose, anisotropy characteristics, and ion energy measurements of F-I. The diagnostics include Pearson current probes, Rogowski coils, voltage probe, bubble detectors, silver activation neutron counters, Lead-shielded PMT scintillators, and a fast Faraday Cup.

Plasma current diagnostics were performed using a Pearson current probe (model 4418) and Rogowski coils made in-house, positioned around individual transmission lines to measure the total current (I) and its time derivative (\(\textrm{d}I/\textrm{d}t\)) in F-I. Additionally, a 100 MHz high-voltage probe was positioned at the back of the anode plate to monitor the dynamics-induced voltage. These measurements, correlated to the Lee code, provide critical insights into the dynamics of plasma discharge. The data acquisition system used for these diagnostics were two Tektronix 4 Series Mixed Signal Oscilloscopes MSO46 with a 350 MHz bandwidth and a 6.25 Gs/s sampling rate.

Neutron dose measurements were performed using bubble detectors BTI models with sensitivities of 43 bubbles/mrem (4 bubbles/\(\upmu\)Sv) and 44 bubbles/mrem (4.1 bubbles/\(\upmu\)Sv). As shown in Fig. 1, these detectors were positioned at two locations: one positioned 5 m axial to the pinch in the z-direction and the other positioned 3 m lateral to the pinch at a \(90^{\circ }\) angle, enabling spatially resolved neutron dose quantification.

In addition, a silver activation neutron counting method was employed in F-I neutron characterization, consisting of a CapeSym \(\textrm{LaBr}_3\)-14x25c-SiPM-T gamma detectors25,26,27 and thin silver foils (2 cm \(\times\) 2 cm \(\times\) 0.3 mm). The gamma detectors were calibrated using known \(^{57}\textrm{Co}\) and \(^{60}\textrm{Co}\) sources. During operation, the foils were placed behind a 7.5 cm thick HDPE moderator to thermalize incident neutrons prior to their interaction with the foils. The corresponding thermalization efficiency was established numerically using the GEANT428,29 and OpenMC30 software. Neutron-induced radioactive isotopes \(^{108\textrm{m}}\textrm{Ag}\) and \(^{110\textrm{m}}\textrm{Ag}\) were analyzed via gamma detectors, providing a quantitative measurement of total neutron counts through the characteristic decay of the activated silver.

Neutron time-of-flight (nToF) measurements were performed using four Lead-Shielded PMT-scintillators31 (Model M540-20x20-6 with EJ-204 scintillator) aligned with lasers and positioned at 5, 10, 20 and 40 m from the pinch. The nToF system measured the temporal delay between prompt X-rays and neutron-induced signals at varying distances, enabling the determination of neutron energies based on their velocities.

A fast Faraday Cup (FC)32 was developed in-house and used to evaluate fast ion beam energies in F-I based on their time-of-flight33,34,35,36. The FC was placed 952.8 mm from the source with a 4 mm aperture hole and used a -136 V bias voltage, as shown in Fig. 1. The response time of this FC is estimated to be about 1 ns.

Together, these diagnostic tools provide precise and complementary data for analyzing the radiation output of F-I, including its current sheath dynamics and dynamics-induced voltage, neutron yields, radiation anisotropy, and fast ion beams.

Simulation

The Lee model code22,23,24 was used to simulate the outputs of F-I. Based on the characteristics of the design, including the inductance, capacitance, operating parameters, and anode geometry of F-I, the Lee code was able to predict the outputs of the device. The Lee code is widely reported to be validated extensively by experimental data especially in dynamics, energetics, yields of fusion neutrons, soft X-rays, fast ion beams, and fast plasma streams. Its physical basis, structure and procedures are widely available in many publications. The “clarion call” of the Lee code over the past four decades is that when the simulated current waveform is identical with the measured current waveform, then all the gross dynamics and energetics of the device are correctly simulated, and the yields, for example, neutrons, and plasma X-rays, are correctly predicted.

For F-I studies, the Lee code had to be modified because of the following. In the radial phase, the current sheath attains the highest speed just before the radial inwards shock front coalesces onto the axis. The induced voltage reaches a peak and typically exceeds the capacitor charge voltage. For large devices with currents of 1 MA or more, the likelihood of secondary breakdowns or re-strikes in the inter-electrode space during this moment, before the start of stagnation, needs to be considered. These re-strikes divert some current from the pinching plasma. The effect is to reduce the parameter \(f_{\textrm{cr}}\) which is the fraction of the circuit current that is flowing into the plasma during the radial phase. This current factor is typically observed to be \(f_{\textrm{cr}} = 0.7\) for the radial phase. When re-strikes occur, \(f_{\textrm{cr}}\) reduces to a value \(f_{\textrm{cr2}}\) less than 0.7; for example, we may have \(f_{\textrm{cr2}} = 0.35\) (half of 0.7), which is the case with half the plasma current diverted away by the re-strikes. The loss of current reduces the severity of the pinch, in particular it reduces the plasma temperature.

It was deduced from the current traces that the higher the operating voltage, the more these re-strikes need to be accounted for. Although the Lee code has been used for simulating plasma focus up to multi-MA and MV, for comparison with real devices it has not been used much for devices operating beyond several tens of kV. Typically, the radial phase is reasonably fitted with one set of radial parameters \(f_{\textrm{mr}}\) and \(f_\textrm{cr}\), fitting the simulated downward slope of the current dip to an averaged slope observed in the measured data of the current dip. When the slope is fitted correctly, it is found that the depth of the dip typically concur. However, for F-I current, such an averaged fitting could not be done satisfactorily, as depicted in Fig. 2a.

Fig. 2
figure 2

(a) Showing the inability of fitting the current dip with one set of radial model parameters. (b) Showing good fitting of the current dip using a second set of radial model parameters at the transition (re-strike) time. Note that the transition time correlates to the time of peak voltage.

Full size image

For this shot, the slope of the dip was fitted with \(f_{\textrm{cr}} = 0.9\), indicating very good plasma current flow when compared with the value of 0.7, typically measured in small to medium size plasma focus devices. However, with this value of \(f_\textrm{cr}\), the simulation showed a current dip, starting at just after 4.0 \(\upmu\)s, with duration 177 ns before the dipping ease off into a very shallow angle (see dashed trace in Fig. 2a). Conversely, the measured current dip was observed to flatten out barely 50 ns after the start of dip, at the point of time when the induced voltage peaked. Despite all attempts to fit, no averaged current dip slope could be found to match the slope of the measured current dip whilst at the same time matching the depth of the dip. Figure 2a represents the best attempt to fit. The discrepancy was far too large to be ignored. The solution was to modify the Lee code to have, in general, several sets of radial mass and current factors. Specifically, for F-I, two sets \(f_{\textrm{mr}}\) and \(f_{\textrm{cr}}\), and \(f_{\textrm{mr2}}\) and \(f_\textrm{cr2}\) were found to be sufficient. For this new version of the Lee code, designated as FF.V5-2, the computation of the radial phase proceeds with the first set \(f_{\textrm{mr}}\) and \(f_{\textrm{cr}}\) until the time \(t=t_{\textrm{transition}}\) when the second set \(f_{\textrm{mr2}}\) and \(f_\textrm{cr2}\) is applied for the rest of the computation. In actual usage, the first set is varied to fit the computed slope to the measured slope for the first part of the dip. The point of time when the measured current slope deviates (by flattening) from the fitted computed slope is noted as the time \(t_\textrm{transition}\). Then the second set \(f_{\textrm{mr2}}\) and \(f_{\textrm{cr2}}\) is introduced and adjusted until the computed slope also flattens sufficiently to match the measured slope, as shown in Fig. 2b.

The re-strikes likely have little primary effect on the mass factor \(f_\textrm{mr}\), the fitting is found to be satisfactorily done with \(f_\textrm{mr2} \le f_{\textrm{mr}}\), varying only \(f_\textrm{cr2}\). The value of \(f_\textrm{cr2}\) that fitted the flattening of the measured current dip was 0.6 for this example. In using the FF.V5-2, we were able to adjust the sets of radial parameters to fit the current waveform with due consideration being given also to the matching of the voltage waveform.

The data acquired from the Pearson probe, Rogowski coils, and voltage probe was used in combination with the Lee code to simulate the experimental outputs of the device. For a given shot, the operating parameters of the device were input into the Lee code control panel. The simulation was run to produce the output current and voltage waveforms. Those waveforms were compared with the waveforms from F-I’s measured data. Then, the mass and current factors (model parameters) from the axial and radial phases were adjusted in the control panel, such that the code’s output waveforms align more with the measured data. This process is repeated, adjusting the model parameters systematically until the computed current and voltage waveforms fit as well as possible with the measured waveforms respectively. Then the Lee model code results of plasma dynamics, energetics and yields are expected to reliably predict the actual experimental values. The computed trajectories of radial inward shock, reflected shock, and piston (current sheath) were superimposed with the computed and measured current and voltage waveforms. These simulation results were compared with the measured results for all diagnostics, including neutron yield, ion energy, and pinch strength to analyze the device. Some results, shown and discussed in the next section reveal important new ideas about high voltage operation of large plasma focus devices with encouraging outlook for eventual operation in deuterium-tritium.

Results and discussion

1100 shots were fired on F-I to condition the device, ensure consistency in outputs, and establish optimal operating parameters. Throughout this conditioning, it was noted that the pressure ranges from 16 Torr to 12 Torr produced good focusing characteristics and good yield. At that stage insufficient systematic data was collected for effective statistical analysis although it was observed that within the above stated range, the diagnostics indicated marginally better performance at the pressures higher than 12 Torr. However, within this good performance pressure range, it was clear that the measured induced voltages were consistently highest at 12 Torr. Hence, for the study of re-strikes 12 Torr was selected as the operational pressure. 100 shots were fired at 12 Torr to achieve a detailed characterization of the technology. Maximum neutrons were observed axially from the pinch in the z-direction with a peak measurement of \(\sim 8 \times 10^{10}\) total neutrons.The peak dynamics-induced voltage measured at 12 Torr D-D was 160.5 kV.

To increase induced voltages, doping with Krypton was attempted. We measured the overall best peak dynamics-induced voltage of 194 kV when the 12 Torr was doped with 0.1 Torr Krypton (Fig. 5c below shows an analysis of that shot for comparison with the pure D-D shots). The mean neutron yields for pure D-D and deuterium-Krypton mixture shots were \(3 \times 10^{10}\) and \(4 \times 10^{10}\), respectively, for shots with pinch voltages above 125 kV. However, due to the very high dynamics-induced voltage, further tests with Krypton doping soon resulted in severe arcing at the back of the device external to the vacuum causing extensive damage to diagnostics. Therefore, we stopped the doping experiments. All results reported in this paper are for pure D-D shots except the shot referred to (Shot 895) in Fig. 5c and Table 3.

A typical example comparing the neutron counts from the silver foil activation, bubble detectors, and Lee code simulations is shown in Table 2. The operating parameters for this shot were 100 kV charging voltage and 12 Torr D-D gas with a peak output voltage of 160.5 kV.

Table 2 Comparison of neutron output between different diagnostic methods and simulation.
Full size table

As shown in Table 2, the neutron yield for each shot was measured by several methods. The maximum neutrons were detected axially from the pinch at the front of the device and measured \(7.92 \times 10^{10}\). Lateral measurements for this shot were acquired using both silver activation foils and bubble detectors, recording \(5.5 \times 10^{10}\) and \(5.44 \times 10^{10}\) neutrons, respectively. The agreement among the various methods of measurement was better than 80%. The agreement with the Lee code was typically within a factor of 2. At 100 kV charging voltage and 12 Torr deuterium, neutron yield data was collected for 85 shots fired over 3 days. For each shot, the yield was recorded by two bubble detectors placed at 3 m and 5 m, respectively, and a silver activation counter. The graph, Fig. 3, was plotted on a logarithmic versus linear scale to show a clearly discernible trend, despite the large scatter of the data points.

Fig. 3
figure 3

Correlation of measured neutron yield versus peak voltage \(V_\textrm{p}\) also designated as \(V_\textrm{max}\) with D-D beam-target fusion cross section \(\sigma (V_\textrm{max})\) versus \(V_\textrm{max}\) and \(\sigma (U)\) vs. \(V_\textrm{max}\), where \(U=3 V_\textrm{max}\) is the effective inductive voltage used in the Lee code.

Full size image

The maximum yield was recorded as \(\sim 8 \times 10^{10}\) in the z-direction, and several shots recorded over \(5 \times 10^{10}\) neutrons. Most of the shots were operated with 5 shots to 1 filling of deuterium. The time interval between each shot was approximately 5 minutes, allowing the electrodes to cool down before performing the next shot. The pressure was observed to rise noticeably after each shot in the 5-shot series, without apparent detriment to the neutron yield. Indeed, the first shot in each of the 5-shot series tended to be the lowest in yield, consistent with our observation, stated earlier, that performance appeared better above 12 Torr. The pressure rise after each shot is primarily caused by electrode sputtering (where high-energy ions eject metal atoms) and thermal evaporation of electrode material, compounded by surface erosion from plasma bombardment. A minor contribution comes from desorption of adsorbed gases from stainless steel walls due to plasma heating and radiation. Figure 3 gave an average of \(2.53 \times 10^{10}\) for 73 shots at 12 Torr. The peak discharge current \(I_\textrm{peak}\) was measured as 870 kA. The universal scaling rule compiled for available plasma focus machines is \(Y_\mathrm {D-D} = 1.8 \times 10^{10} \times I_{\textrm{peak}}^{3.8}\), where \(I_\textrm{peak}\) is in MA22 giving an expected value of \(1.1 \times 10^{10}\). It is noted that F-I outperforms the universal neutron scaling law.

Figure 3 shows that the logarithm of yield increases with measured peak voltage \(V_\textrm{p}\). The highest neutron yield coincides with the highest measured peak voltage of 160.5 kV. A trend line was computed for each of the two sets of results. The trend lines were compared to the D-D beam-target fusion cross section \(\sigma\) versus deuteron energy (\(V_\textrm{max}\) in keV) in the same logarithmic linear scale and presented in Fig. 3. \(V_\textrm{p}\) in kV is the peak voltage and \(V_\textrm{max}\) in keV is the corresponding deuteron energy. They have the same value. The values of the \(\sigma (V_\textrm{max})\) and \(\sigma (U)\) have been relatively scaled so that the trend comparison with the neutron data could be more easily made.

The analysis indicates that for deuteron energies below 45 keV there is a better correlation between the trend of D-D neutron yield vs. \(V_\textrm{max}\) with \(\sigma (U)\) vs. \(V_\textrm{max}\) (unbroken blue line) rather than with \(\sigma (V_\textrm{max})\) vs. \(V_\textrm{max}\). This validates the use in the Lee code of the effective inductive voltage \(U=3V_\textrm{max}\) for general plasma focus devices which generally have induced voltage spikes in the lower tens of kV. However, for deuteron energies in the higher tens of kV, yield vs. \(V_\textrm{max}\) correlates better with \(\sigma (V_\textrm{max})\) vs. \(V_\textrm{max}\). This indicates that the Lee code should be modified accordingly in the case of high voltage, high current focus devices. More importantly, the observation that neutron yield scales with peak measured voltage could illuminate the neutron production mechanism if we could determine in a shot whether the voltage peak occurred before or after the start of stagnation of the inward radial plasma flow. We discuss this with Fig. 4.

Fig. 4
figure 4

The fitting of current traces is shown in the main chart together with the voltage waveforms. The inset shows the correlation of radial phase dynamics with the fitted current dips and voltage spikes. The position of the shock front and piston at the start of the radial phase at 3.64 \(\mu\)s is 19 mm.

Full size image
Fig. 5
figure 5

Comparing current, voltage, and dynamics of 3 shots across the range of yields and voltage spikes. (a) Shot 1062 at 100 kV with D-D mixture at 12 Torr, showing a low yield shot, (b) shot 1036 at 100 kV with D-D mixture at 12 Torr, showing an average yield shot, and (c) shot 895 at 100 kV with D-D mixture doped with 0.1 Torr Kr, showing highest \(f_\textrm{cr}\) and highest \(V_\textrm{p}\).

Full size image

Presently, the current dip is acknowledged to be the indicator of focus strength in terms of neutrons and other radiation. The occurrence of re-strikes in high voltage, high current devices truncates the current dip. Hence, contrary to typical plasma focus devices, for this class of high voltage large plasma focus devices, the current dip is not a good indicator. Likewise, the negative spike of \(\textrm{d}I/\textrm{d}t\) is not a good indicator. The voltage spike becomes the neutron indicator. The higher the voltage spike, the higher the deuteron energy and the higher the beam-target fusion cross section, up to D-D cross section peak of 3 MeV. A proviso is that above 200 keV, the increase in cross section is less than proportional to any further increase in deuteron energy. Thus, it may not be efficient to design for induced voltage above some 200 kV. Further, for D-T, the beam-target fusion cross section peaks at 115 kV and a range of 80–200 kV still gives cross section more than half that at optimum 115 kV. So, for D-T, a good induced peak voltage to aim for may be 80–200 kV. In this context, we note that for high current high voltage devices operating in both D-D and D-T, once the dynamics-induced voltages exceed 200 kV, further increase in neutron yield will have to come from greater number of fast beam ions, greater interaction volume and higher target density. The Lee code is proven to be effective in the optimization of these parameters as a device is scaled up for higher energy and higher voltage. In the upgraded FF.V5-2, the code incorporates the latest features including, importantly, the re-strikes.

An example of a fitting of the current and voltage traces correlated with the computed trajectories of the radial inward shock front, the reflected shock (stagnation phase) and the piston trajectory up to the end of the pinch compression phase is shown in Fig. 4. The radial phase portion is expanded and shown in the inset.

Fig. 6
figure 6

(a) Lead-shielded PM-Scintillator signal at 16 Torr with a time-of-flight of 1794 ns and flight length of 40 m. (b) FC signal at 16 Torr with a time-of-flight of 164.5 ns.

Full size image

For this shot, in order to get a good fit of the simulated current waveform to the measured current waveform, the radial phase current factor \(f_\textrm{cr}\) was adjusted at the transition time, determined from the measured current waveform. The second current factor \(f_\textrm{cr2}\) was reduced in steps, from initial value of \(f_\textrm{cr} = 0.8\) until at \(f_\textrm{cr2} = 0.58\) a good fit of the flattening of the current dip was obtained. Then the trajectories of the incoming radial shock wave, the reflected shock RS and the piston trajectories from the simulation were plotted in the inset. The radial trajectories start at 19 mm, corresponding to the end radius of the tapered anode. It is seen that the transition time is at 3.745 \(\upmu\)s, 105 ns after the start of the radial phase, coinciding with the computed peak of the voltage spike. Before the re-strike, the total discharge current was 830 kA with 665 kA flowing in the collapsing current sheath. The evidence is clear that the spiked voltage of 160 kV is causing re-strikes which divert away some current, leaving only 480 kA in the current sheath. The reduced magnetic drive slows the piston speed from 8.6 cm/\(\mu\)s to 6.1 cm/\(\upmu\)s which correspondingly slows the shock speed from 19.3 cm/\(\mu\)s to 12.2 cm/\(\mu\)s. The slowing of the shock front can be seen in the change in slope of the shock front trace on magnified inspection. At this transition time, the shock front is 0.8 mm and the piston is 8 mm from the axis, the imploding (and elongating) slug of plasma is 14 mm long. The radial shock wave hits the axis 10 ns later, forming the reflected shock RS which starts the stagnation process whereby the plasma motion towards the axis is stopped, the kinetic energy is converted into thermal energy, and the doubly-shocked stagnated plasma is increased in density and temperature. This stagnated region expands as the RS moves outwards towards the incoming piston, hitting the piston 135 ns later, starting the pinch phase, which lasts 86 ns, with the pinch radius slowly compressing from 4.5 mm to 3.9 mm, with a final length of the pinch of 25 mm, extending both sides of the end of the hollow tapered end of the anode. The temperature of the plasma has risen from 513,000 K to 840,000 K during the radial shock acceleration phase, dropped some after the re-strike, increased during the stagnation period reaching 3.1 million K at the start of pinch, with slight decline to 3.04 million K towards the end of the pinch period. Following the 160 kV peak, the measured voltage waveform shows 18 MHz oscillations with reducing amplitude, which appears to be due to ringing of the measurement circuit. There is no sign of any large voltage feature after the 160 kV spike. It would appear that the localized high electric fields of pinch instabilities, well-documented in many publications, are not measured by our probe. This is likely due to the inadequate frequency response of the voltage probe. The neutron yield for this shot was measured as \(5.5 \times 10^{10}\) by silver foil activation and bubble detector, whilst the computed value was \(5.4 \times 10^{10}\). In the above analysis based on simulation merged with real time measurements two key points are noted. First, the 160 kV spike occurs before the start of stagnation, indicating that 160 keV deuteron beams are already produced before the re-strikes. Second, although the re-strikes reduce the severity of the subsequent compressions, the pinch plasma, which forms the target of the deuteron beam for fusion reactions is indeed reduced in temperature, but not sufficiently to change its specific heat ratio or compressibility. Hence, the geometry of the pinch and its areal density exposed to the fast deuteron beam is unchanged. These two points taken together indicate that the re-strikes do not affect the beam-target neutron production much, if at all, for this pre-stagnation (first) neutron pulse. The re-strikes are expected to adversely affect the subsequent instabilities-induced (second) neutron pulse. The total neutron yield which is measured is therefore reduced due to the re-strikes. Thus, the out-performance of F-I compared to the universal rule indicates that this superiority is attributed solely to the superiority of the first neutron pulse, to its higher energy deuterons with the correspondingly higher D-D beam-target fusion cross section.

Furthermore, this study and review has given insight into the effectiveness of the Lee code in the simulation of neutron yield. Like the voltage probe (which is unable to measure the expected sub-nanosecond voltage pulses due to the micro-instabilities), the Lee code also does not account for the instabilities phase. For neutron yield, the code is calibrated against data of compiled machines. One essential feature of the calibration process is to use a factor of 3 for the induced voltage for the beam ion energy. It is well documented that for a small plasma focus, the piston induced voltage spike (in the region of 10 kV) does not produce a neutron pulse (first pulse) so that the neutron yield for the small PF is predominantly from the instability induced deuteron beams (second pulse). Whereas for a large PF, the first voltage pulse of 50 kV to over 100 kV produces deuterons with high fusion cross section so that the first neutron pulse is comparable to the second, instability-produced pulse. For small plasma focus, with induced voltage of about 10 kV, this factor of 3 increases the D-D beam-target fusion cross section by 200 times, thus gives the small PF a reasonable fusion yield from its piston-induced first neutron pulse which apparently on average compensates for the non-inclusion of the instability-produced second pulse in the code calculation. For large plasma focus with piston-induced voltage pulse of say 50-100 kV, increasing the deuteron energy by a factor of 3, increases D-D fusion yield by about 4 times. Reviewing the nature of the variation of fusion cross section and the way the plasma focus produces beam-target neutrons with a first pulse due to piston-induced voltage and a second pulse due to much higher electric fields from micro-instabilities, it appears that the interplay of these circumstances and the various relevant numbers are fortuitous for the Lee code. These combined factors allow a calibration process with a multiplier factor of 3 for the piston-induced voltage, resulting in over-estimation of the first neutron pulse sufficiently to compensate for non-inclusion of the second instabilities-induced neutron pulse; with a remarkable agreement of computed D-D neutron yield to measured yield, to within a factor of 2, for most machines, over the range of machines the code has been applied to.

There is another important point to note from this study. For D-T operation, the optimum fusion cross section is at 115 keV (with factor of 2 from maximum cross section in the optimum fusion range of 80 to 200 keV) contrasting with the way the D-D cross section continues to increase to beyond 1 MeV. For big machines, the first ion pulse from the piston-induced voltage (of about 100-200 kV) is within the optimum D-T fusion cross section range, whereas the second pulse with ions from instability fields at higher energies, say 0.6 MeV, has a fusion cross section reduced by 10 times. This could mean that for big machines operating with D-T, the first neutron pulse is dominant with a negligible second pulse. Hence re-strikes, which does not affect the neutron yield much for D-D (reducing only the second re-strike degraded pulse), will not matter at all for big machines when operating in D-T. Confirmation of this would eliminate the engineering problems involved in re-strike avoidance.

A further note to show the range of the types of shots occurring in F-I. This code has been applied to the analysis of all our shots. Three examples are highlighted in the following Fig. 5, one is a low yield shot, another an average yield shot and the third is a high yield shot. F-I achieved its highest peak dynamics-induced voltage of 194 kV at a total fill pressure of 12 Torr deuterium-Krypton mixture, with 0.1 Torr of Krypton (comprising approximately 0.8% of the gas mixture by mass fraction). Figure 5 shows how well the computed current and voltage waveforms were fitted to the measured waveforms across the whole range of shots, and how these are then correlated in time to the dynamics of the focusing process. The simulated neutron yield in each of the 3 shots shows reasonable agreement to the measured yield.

Shot 895 displays a large radial current factor of 0.9 with a distinctly larger and sharper current drop which is a characteristic of doped (with Kr) shots. Both the two high yield shots (shot 897 and shot 1027) started the radial phase with exceptional current factors significantly larger than the typical 0.7. This seemingly resulted in good neutron yields greater than \(5 \times 10^{10}\). Shot 1062 shows good fit without needing a second current factor (no re-strike), but its current factor starts with such a low value of 0.4, that its dynamics was already degraded, resulting in a poor value of voltage peak of 40 kV. Table 3 shows the current factors \(f_\textrm{cr}\), \(f_\textrm{cr2}\), peak voltage and the measured and simulated neutron yields.

Table 3 Summary of the observed current factors, peak voltage, and neutron yield of a range of shots.
Full size table

This Table indicates that that a good value of \(f_\textrm{cr}\) is the primary factor needed for a large value of \(V_p\) which consistently correlates with a good neutron yield \(Y_\textrm{n}\). An inspection of all the results confirms that a value of \(f_\textrm{cr}\) of 0.7 indicates good current sheath formation leading to proper compression dynamics, an average voltage spike about 100 kV and neutron yield of about \(2.5 \times 10^{10}\). Poor shots have \(f_\textrm{cr}\) substantially lower than 0.7 and shots with exceptional yields have \(f_\textrm{cr}\) of 0.8 or better up to 0.9. The severity of re-strikes (indicated by the fraction \(f_\textrm{cr2}\)/\(f_\textrm{cr}\), the smaller the fraction the more severe is the re-strike) also does not play a role. Re-strikes do not affect the peak voltage. Re-strikes hardly affect the neutron yield. Moreover, it is firmly established that this voltage peak occurs pre-stagnation and is therefore dynamics-induced and not related to the later pinch and instabilities.

These results establish that F-I has good current sheath formation and dynamics, producing a substantial dynamics-induced voltage spike resulting in a good predominantly dynamics-induced neutron yield, that is hardly affected by re-strikes.

The studies on F-I also include other measurements, some of which are reported briefly here. The neutron energy was computed from nTOF using PMT-Scintillator at 40 m distance from the pinch column. The PMT-scintillator, shielded by 30 cm lead blocks, detected gamma photons above 3 MeV at 40 m distance from the pinch column. Looking at the shape and FWHM of these pulses it is necessary to note that the FC is placed about 1 m from the pinch whilst the neutron detector is placed 40 m away. The dispersive effect on the shape of both pulses will increase the FWHM as the distance increases. A set of results are presented in Fig. 6a. The inset of Fig. 6a shows the extraction of neutron energy spectra by an analysis of the neutron pulse shape. The output ion energy of the Faraday Cup was calculated based on the ToF between the X-ray peak and the ion peak as well as the distance between the pinch and the FC and the mass of a deuteron. A set of results are presented in Fig. 6b, showing deuteron energy of \(\sim 350\) keV.

Based on a comparison of the time of occurrence of the hard X-ray pulse and that of the dynamics-induced voltage pulse we identify the neutron pulse and the FC fast ion pulse of 350 keV as the ones corresponding to the dynamics-induced voltage pulse. We have not yet made a systematic study to identify the second pinch-instability ion pulse and related neutron pulse. Due to re-strikes we expect that in F-I these second pulses are very small relative to the corresponding first pulses. Moreover, for the FC at about 1 m away the second hard X-ray pulse would come between the first hard X-ray pulse and the first fast ion pulse, whilst the second fast ion pulse being 2-3 faster than the first ion pulse would reach the FC not differentiated in time from the first fast ion pulse. The expected much reduced amplitude of the second fast ion pulse (compared to the first) combined with the limited time resolution of the FC would make distinguishing the second fast ion pulse very difficult. In any case, a dedicated systematic study would be needed to work out the redesign of the diagnostic components needed to uncover the presently buried second pulse.

Conclusion

FAETON-I, the world’s highest direct-charged voltage plasma focus, i.e. 100 kV, was designed as a testbed for high voltage plasma focus operation. It consistently generates D-D neutron yields of \(2.5 \times 10^{10}\) over five consecutive shots without gas refilling, maintaining pinch voltages above 150 kV. Over 1100 shots were recorded in deuterium, producing exceptional yields up to \(8 \times 10^{10}\) D-D neutrons with an anisotropy factor of 1.6, favoring radiation in the forward on-axis direction. Experimental results, including current sheath dynamics and dynamics-induced voltage data, align with simulations from the Lee model code, confirming the reliability of F-I. A maximum dynamics-induced pinch voltage of 194 kV was achieved with a 99.2% deuterium and 0.8% Krypton mixture at 12 Torr, producing neutron yield of \(6 \times 10^{10}\). Neutron energy peaked at \((2.5 \pm 0.3)\) MeV, verified by PMT-scintillators located at distances of 5 m, 10 m, 20 m, and 40 m. A fast Faraday cup detected fast ion beams with \(\sim 350\) keV energy. PMT-scintillators, shielded by 30 cm lead blocks, detected gamma photons above 3 MeV at 40 m distance from the pinch column.

The measured voltage spikes are observed to occur before the start of stagnation and correspond with the simulated piston-induced voltages. These lead to restrikes which typically reduce the current available to drive the pinch phase. An important observation is that, because of the truncation of the current dip due to restrikes, the severity of the current dip is not a good indicator for high voltage large plasma focus devices. Instead, the peak inductive voltage \(V_{\textrm{max}}\) becomes the preferred indicator. It was observed that the higher this pre-stagnation voltage peaked, the higher the neutron yield was. The data indicated that an underlying cause is the increasing D-D fusion cross section with deuteron energy.

The Lee code was modified for two-step radial fitting to cope with the re-strikes. The code shows, in agreement with measurements, that despite the re-strikes, the neutron yields outperform the universal scaling rule. It is surmised that the re-strikes do not affect substantially the piston-induced neutron pulse (the first pulse) that occurs before the start of stagnation, though are expected to reduce the subsequent pinch-instabilities neutron pulse (the second pulse). Indeed, our code shows a reduction of less than 20% due to the re-strikes. From the results of F-I, it is further surmised that in future operations in D-T in a scaled up FAETON-X, the first pulse could dominate, because the piston-induced voltage is at or near the D-T beam-target fusion cross section peak of 115 kV, whilst the instability-induced voltages are much higher with such degraded cross section that the second pulse becomes insignificant. Such a situation would be good, as the engineering would not have to contend with restrike-avoidance techniques.

It is further noted that F-I is more energy efficient than HAWK in neutron production. Generally, neutron yield is proportional to energy-squared. F-I, with half the operational energy as HAWK, out-performs, delivering same neutron yield as HAWK, which is noted for its record-breaking efficiency in neutron production, based on its current20,21,37.

In summary, FAETON-I has demonstrated that in a high voltage, large plasmas focus, current sheaths are well-formed with good dynamics, and that re-strikes notwithstanding, the D-D neutron yield still outperforms the universal neutron scaling law. Moreover, scaling up to D-T operations the outlook is even better- the re-strikes will not matter at all. Incorporating these new features, a D-T, 14.1 MeV neutron yield of \(2 \times 10^{14}\) is expected for a 65 kV, 1 MJ, 4 MA machine and \(2 \times 10^{15}\) for a 150 kV, 5 MJ, 7 MA plasma focus. These are planned to be developed as dedicated neutron sources for radiation applications.