Anisotropic bounding surface plasticity model for soils

Abstract

This study presents a unified constitutive model capable of simulating monotonic behaviour of clay and sand, incorporating a non-associated flow rule and critical state concept. The bounding surface approach has been used to anticipate a smooth transition from the elastic phase to the plastic phase of the soil. A novel dilatancy relationship is introduced to represent the volumetric behaviour of both sand and clay in a unified way. The model is implemented using the implicit Euler method. To capture anisotropic soil behaviour, the model is extended within a multilaminate framework comprising 13 elastic-plastic planes. The overall response is derived by integrating the behaviour of these individual planes, each governed by unconventional constitutive equations. The model realistically reproduces strain softening and induced anisotropy through a non-classical plasticity approach. Simulations of six soil samples under monotonic drained and undrained loading show good agreement with experimental results, demonstrating the model’s effectiveness.

Introduction

Over recent decades, numerous constitutive models have been developed to simulate the behavior of clay and sand. In this regard, based on the critical state concept, Cam-Clay model was presented by Roscoe¹ and Roscoe et al.². This model has been successful in simulating the behaviour of normally consolidated clay^2,3,4. Subsequently, in the same format, the modified Cam-Clay model was proposed by Roscoe and Burland⁵ for clay with a higher overconsolidation ratio. However, the proposed models have limitations in simulating the behaviour of heavily over-consolidated clay and sand. These limitations include overprediction of yield stress due to the yield surface used in these models for overconsolidated clay^4,6. In fact, the use of the associated flow rule in the above models results in poor prediction of behaviour such as normally consolidated clay under undrained conditions^7,8. In addition, CCM and modified CCM have not been developed for use on sand^8,9,10,11. In this regard, many modifications have been made on these models to achieve a proper and accurate prediction of the behaviour of overconsolidated clay and sand^{3,12,13,14,15,16,17,18,19,20,21}. Nevertheless, the proposed models are only suitable for predicting the behaviour of clay or sand. Yu²² introduced CASM, a unified model for clay and sand that employs a unified yield function, incorporates critical state and state parameter concepts, and utilizes a non-associated flow rule. Yu²² showed that the presented model can be used to predict the behaviour of clay and sand in a unified model. However, the CASM model followed the classical plastic theory, which led to the prediction of sudden behaviour from elastic to plastic state. This model was not able to model the smooth behaviour observed in real soil behaviour. To overcome the limitations of the CASM model, Khong²³ introduced the CASM-b model, incorporating a bounding surface to predict smooth behaviour from elastic to plastic state. Nevertheless, an explicit numerical integration method is used in the presented model. According to the research conducted, it has been shown that the use of the explicit numerical integration method in the implementation of behavioural models converges for small strain increments, but the solutions to the problem do not converge for large strain increments. Research has demonstrated that implicit numerical integration methods provide better convergence, especially under large strain increments^{13,24,25,26,27}. A state-dependent non-associative bounding-surface model within the framework of critical-state soil mechanics is proposed by Sun et al.²⁸. In the research conducted the plastic flow direction is obtained using a state-dependent fractional-order differentiation of the bounding surface. Several articles have been published in the literature relating to the prediction of uniform behaviour of soils^{22,29,30,31,32,33}. Moghadam et al.³³ developed a model for simulating the behaviour of both sand and clay, employing a novel formulation based on bounding surface concepts and an implicit numerical integration scheme. This model can predict the behaviour of overconsolidated smooth clay with proper accuracy and convergence. While the proposed unified models were able to simulate the behaviour of clay and sand, they cannot adequately predict the phase transition behaviour that often occurs in overconsolidated clay and dense sand. This is due to the dilatancy rule considered in these models. According to the research conducted in this field, it has been determined that soil dilatancy depends on the state parameter in addition to the stress ratio^12,34. While the dilatancy rule considered in the CASM model is only a function of the stress ratio. To address this limitation, the proposed model incorporates a generalized dilatancy rule that accounts for both the state parameter and internal soil variables. This paper presents a unified constitutive model for simulating the monotonic, drained, and undrained behaviour of clay and sand. The model is built upon the bounding surface theory using a radial mapping rule, with a non-associated flow rule and isotropic hardening law. Implementation is performed via an implicit return-mapping algorithm to ensure numerical robustness. Additionally, the model is extended to incorporate anisotropic behaviour using a multilaminate framework consisting of 13 elastoplastic planes. Anisotropy, a critical factor in realistic soil modeling, has received growing attention in recent years^{35,36,37,38,39,40,41,42}. In this study, the extended model is validated through comparisons with laboratory data and previous unified model predictions, highlighting the advantages of the multilaminate approach.

Description of the unified model

This section presents a unified constitutive model for simulating the monotonic response of clay and sand under both drained and undrained loading conditions. The model is formulated within a bounding surface framework utilizing a radial mapping rule. Based on critical state soil mechanics and state parameter theory, the model employs a non-associated flow rule to govern the development of plastic strains in both clay and sand. To relate plastic volumetric and deviatoric strain increments, a generalized dilatancy rule is incorporated, capturing the influence of both stress ratio and state parameters. The model is implemented using an implicit numerical integration scheme, specifically a return mapping algorithm, which ensures robust and stable solutions even under large strain conditions. The elastic-plastic formulation used in this implementation is detailed in Section Implementation of the Model by Implicit Method.

General formulation of the model

In the present framework, anisotropic soil behaviour is considered. To describe soil response under triaxial stress conditions, the mean effective stress $\:{p}^{{\prime\:}}$ and deviatoric stress q are employed, defined according to the following relationships²⁹:

$$\:{\text{p}}^{{\prime\:}}=\frac{{{{\upsigma\:}}_{1}+{{\upsigma\:}}_{2}+{\upsigma\:}}_{3}}{3}$$

(1)

$$\:q=\frac{1}{\sqrt{2}}\sqrt{{({{\upsigma\:}}_{1}-{{\upsigma\:}}_{2})}^{2}+{({{\upsigma\:}}_{1}-{{\upsigma\:}}_{3})}^{2}+{({{\upsigma\:}}_{2}-{{\upsigma\:}}_{3})}^{2}}$$

(2)

Similarly, the volumetric strain $\:{\epsilon\:}_{V}\:$and deviatoric strain $\:{\epsilon\:}_{q}$, corresponding to the stress components, are defined by the following expressions:

$$\:{{\upepsilon\:}}_{\text{V}}={{\upepsilon\:}}_{1}+{{\upepsilon\:}}_{2}+{{\upepsilon\:}}_{3}$$

(3)

$$\:{{\upepsilon\:}}_{\text{q}}=\frac{2}{3}({{\upepsilon\:}}_{1}-{{\upepsilon\:}}_{3})$$

(4)

In addition, according to plasticity theory, the total strain increment $\:d\epsilon\:$ is assumed to comprise elastic and plastic components, as expressed in Eq. (5):

$$\:d\varvec{\epsilon\:}={d\varvec{\epsilon\:}}^{e}+{d\varvec{\epsilon\:}}^{p}$$

(5)

Here, $\:{d\varvec{\epsilon\:}}^{e}$ represents the elastic strain increment, which can be determined using the elastic parameters described in the Elastic Behaviour section. The term $\:{d\varvec{\epsilon\:}}^{p}$ denotes the plastic strain increment, calculated based on the non-associated flow rule and the bounding surface concept (refer to the sections Non-Associated Flow Rule and Evolution Rule for the Surface Size Ratio). In this model, compressive deviatoric stresses and strains are considered positive, while tensile components are treated as negative.

Critical state

The critical state represents a condition in which the stress ratio and dilatancy approach zero, while shear deformations continue indefinitely without further changes in stress. In the present model, the critical state is characterized by a line in both the $\:e-ln{p}^{{\prime\:}}$and $\:q-{p}^{{\prime\:}}\:$planes. At this state, the void ratio is dependent on the confining pressure and decreases as the confining pressure increases. The equations defining the Critical State Line (CSL) in the $\:e-ln{p}^{{\prime\:}}\:$and $\:q-{p}^{{\prime\:}}$ planes are given below²⁹.

$$\:{e}_{\text{c}\text{r}}={e}_{{\Gamma\:}}-{\lambda\:}_{\text{c}\text{r}}ln{p}^{{\prime\:}}$$

(6)

$$\:{q=M}_{\text{c}\text{r}}{p}^{{\prime\:}}$$

(7)

Here, $\:{e}_{cr}$ denotes the critical state void ratio. To define the critical state line in the$\:\:e-ln{p}^{{\prime\:}}$ plane, two parameters are used:$\:\:{e}_{{\Gamma\:}}\:$representing the critical state void ratio at a reference pressure of $\:{p}^{{\prime\:}}=1kPa$, and $\:{\lambda\:}_{\text{c}\text{r}}$, indicating the slope of the critical state line in this plane.

As illustrated in Fig. 1, the critical state line in the $\:q-{p}^{{\prime\:}}$ plane is represented by a straight line passing through the origin with a slope of $\:{M}_{\text{c}\text{r}}$. This parameter is derived from the Mohr–Coulomb failure criterion at the yield state and is a function of the internal friction angle $\:\phi\:$, as proposed by Schofield and Wroth⁴³:

$$\:{M}_{\text{c}\text{r}}=\frac{6sin\phi\:}{3\stackrel{\sim}{t}-sin\phi\:}$$

(8)

In this equation, $\:\stackrel{\sim}{t}$ is a scalar parameter that depends on the type of loading. For compressive loading, $\:\stackrel{\sim}{t}=+1$ and $\:{M}_{\text{c}\text{r}}={M}_{cr,c}$; for tensile loading, $\:\stackrel{\sim}{t}=-1$ and $\:{M}_{\text{c}\text{r}}={M}_{cr,e}$ are used.

State parameter

Research has shown that the physical state of a soil sample is influenced by both its void ratio and confining pressure³⁴. Therefore, accurately describing the soil’s state requires a parameter that incorporates both factors. To model the behaviour of both clay and sand using a unified approach, a common and easily determinable parameter is essential.

In the present model, the state parameter is adopted for this purpose. Originally introduced by Been and Jefferies⁸ to characterize sand behaviour, the state parameter is defined as the difference between the current void ratio and the critical state void ratio at the same confining pressure. By combining the effects of void ratio and stress level, the state parameter effectively describes soil behaviour over a wide range of conditions.

Compared to parameters such as the overconsolidation ratio, the state parameter is more versatile and can be directly calculated from the current void ratio and confining pressure for both clay and sand. It provides a robust means of capturing the stress–strain response of soils. In this model, the state parameter is defined as follows⁸:

$$\:\psi\:=\:e-{e}_{\text{c}\text{r}}$$

(9)

Here, $\:e$ is the current void ratio, and $\:{e}_{\text{c}\text{r}}$ is the critical state void ratio (as defined in Eq. 6) corresponding to the same confining pressure. Based on this concept, the model enables simulation of soil behaviour across a wide range of initial states using a consistent set of parameters that depend on the mean effective stress and void ratio.

If the current state of the material is denser than the critical state (i.e., $\:e<{e}_{\text{c}\text{r}}$, such as in overconsolidated clays or dense sands), the state parameter $\:\psi\:$ is negative ($\:\psi\:<0$). Conversely, if the material is looser than the critical state (i.e., $\:e>{e}_{\text{c}\text{r}}$, as in normally consolidated clays or loose sands), the state parameter is positive ($\:\psi\:>0$). On the critical state line, the state parameter equals zero ($\:\psi\:=0$).

Elastic behaviour

The increment in elastic strain is associated with the increment in stress through Eq. 10.

$$\:{d\epsilon\:}^{e}={\left({D}^{e}\right)}^{-1}d{\sigma\:}^{{\prime\:}}$$

(10)

where $\:{\left({D}^{e}\right)}^{-1}$ is the elastic stiffness matrix:

$$\:{D}^{e}=\left[\begin{array}{cc}K&\:0\\\:0&\:3G\end{array}\right]$$

(11)

In the proposed model, the elastic behaviour of soil is described by bulk modulus $\:\text{K}$ and shear modulus $\:\text{G}$³⁰.

$$\:K=\frac{\nu\:{p}^{{\prime\:}}}{\kappa\:}$$

(12)

$$\:G=\frac{3(1-2\mu\:)}{2(1+\mu\:)}K$$

(13)

In these expressions, $\:\nu\:=1+e$ denotes the specific volume, $\:\kappa\:$ is the slope of the loading–unloading line in the $\:e-ln{p}^{{\prime\:}}$ plane, and $\:\mu\:$ represents Poisson’s ratio.

Plastic behaviour

Classical plasticity models typically assume that the material behaviour is entirely elastic within the yield surface^29,44. Under this assumption, the material remains elastic until the stress state reaches the yield surface, at which point the response abruptly transitions to elastic–plastic behaviour. However, laboratory observations have shown that soil exhibits gradual, soft behaviour during loading rather than a sudden transition^29,44.

To better capture this soft transition, non-classical plasticity frameworks have been developed. Notably, the bounding surface theory introduced by Dafalias and Popov⁴⁵and the subloading surface theory proposed by Hashiguchi⁴⁶ and Hashiguchi et al.⁴⁷provide more realistic descriptions of soil response. These frameworks have been successfully applied to model both saturated^25,48,49 and unsaturated soils^50,51.

In the present model, bounding surface theory is adopted to describe plastic behaviour due to its conceptual clarity and relative ease of numerical implementation. According to this theory, plastic strains may develop from the onset of loading, effectively reducing the purely elastic domain to a single point^14,52,53.

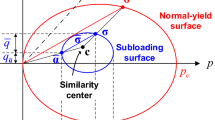
The bounding surface framework defines two surfaces to model elastic–plastic behaviour: an inner surface, referred to as the loading surface, through which the current stress state always passes; and an outer surface, referred to as the bounding surface, on which the image stress state lies^45,52,54. The use of both the loading surface and bounding surface in this framework is illustrated in Fig. 1.

Fig. 1

Loading surface, bounding surface and radial mapping rule according to the bounding surface theory.

To determine the image stress state corresponding to the current stress state, a mapping rule is employed^52,54.

Radial mapping rule

As illustrated in Fig. 1, the current model employs a radial mapping rule to determine the image stress state on the bounding surface. According to this rule, the image stress point on the bounding surface is obtained by extending a straight line from the origin of the stress space through the current stress point located on the loading surface^14,52,54.

Assuming geometric similarity between the loading and bounding surfaces, a proportional relationship can be established between the current stress state and its image, as well as between their corresponding stress components:

$$\:\gamma\:=\frac{\varvec{\sigma\:}}{{\varvec{\sigma\:}}_{j}}=\frac{q}{{q}_{j}}=\frac{{p}^{{\prime\:}}}{{p}_{j}^{{\prime\:}}}=\frac{{p}_{c}^{{\prime\:}}}{{p}_{cj}^{{\prime\:}}}$$

(14)

In this equation, $\:\gamma\:$ represents the ratio of the sizes of the loading and bounding surfaces and indicates the relative distance between them. In the above relationship, $\:\varvec{\sigma\:}$ denotes the current stress state, where $\:{p}^{{\prime\:}}$ is the mean effective stress and q is the corresponding deviatoric stress component. The image stress state on the bounding surface is denoted by$\:\:{\varvec{\sigma\:}}_{j}$, with $\:{p}_{j}^{{\prime\:}}$ and $\:{q}_{j}$ representing the mean effective and deviatoric stress components of the image stress, respectively .

Additionally, $\:{p}_{c}^{{\prime\:}}$ defines the size of the loading surface, while $\:{p}_{cj}^{{\prime\:}}$ is the isotropic hardening parameter that governs the size of the bounding surface.

Loading surface

To describe the unified behaviour of both clay and sand, the yield function proposed by Yu²² is adopted in the present model. The loading surface is defined by the following equation:

$$\:F\left(\varvec{\sigma\:}\right)={\left(\frac{q}{{M}_{cr}{p}^{{\prime\:}}}\right)}^{N}+\text{ln}\left(\frac{{p}^{{\prime\:}}}{{p}_{c}^{{\prime\:}}}\right)/\text{l}\text{n}\left(R\right)$$

(15)

Here, N and R, are material parameters. The parameter N controls the shape of the loading surface, while R represents the ratio between $\:{p}_{c}^{{\prime\:}}$ and $\:{p}^{{\prime\:}}$at the intersection point of the yield surface with the critical state line.

Furthermore, the value of$\:\:{M}_{cr}$, as defined in Eq. (8), depends on the type of loading, where:

$$\:\left\{\begin{array}{c}if\:q>0\:then\:\stackrel{\sim}{t}=+1,\:compressive\:loading\:\\\:if\:q\le\:0\:then\:\stackrel{\sim}{t}=-1,extensive\:loading\end{array}\right.$$

(16)

Bounding surface

In accordance with bounding surface theory, the present model assumes that the bounding surface shares the same shape as the loading surface. The bounding surface is defined by the following equation:

$$\:F\left({\varvec{\sigma\:}}_{j}\right)={\left(\frac{{q}_{j}}{{M}_{cr}{{p}^{{\prime\:}}}_{j}}\right)}^{N}+\text{ln}\left(\frac{{{p}^{{\prime\:}}}_{j}}{{p}_{cj}^{{\prime\:}}}\right)/\text{l}\text{n}\left(R\right)$$

(17)

General dilatancy rule and plastic potential function

A key aspect of modeling the stress–strain behaviour of soils is establishing the relationship between the plastic volumetric strain rate and the plastic deviatoric strain rate—commonly referred to as the general dilatancy rule^34,55. For accurate simulation of plastic deformation in both clay and sand, the dilatancy rule must reliably capture the distinctive behavioural characteristics of each material. Several models describe dilatancy as a function of the stress ratio and internal material properties^56,57. Rowe’s dilatancy rule, incorporated into Cam-Clay models, has proven effective for representing the behaviour of cohesive soils such as clay²⁹. In these models, dilatancy becomes zero when the stress ratio equals the slope of the critical state line, regardless of the soil’s state. This rule is also applied in the CASM unified model. However, when used in CASM, it fails to capture phase transition behaviour—a critical feature in overconsolidated clays and dense sands. Experimental evidence indicates that in granular soils, such as sand and overconsolidated clay, dilatancy depends not only on the stress ratio but also on the degree of compaction^20,58. Therefore, an accurate dilatancy rule must incorporate both stress ratio and the state parameter.

Manzari and Dafalias²⁰ introduced a model that integrates the state parameter into the dilatancy formulation. Similarly, Li et al.⁵⁸ developed a state-dependent dilatancy model for sand, demonstrating its effectiveness across varying confining pressures and void ratios. A more generalized dilatancy relationship was later proposed by Li and Dafalias³⁴which incorporates external variables (e.g., stress ratio) and internal state variables (e.g., void ratio) along with material parameters.

The generalized dilatancy rule adopted in the present model follows the form proposed by Li and Dafalias³⁴and is given by the following equation:

$$\:d=\frac{{d\varvec{\epsilon\:}}_{v}^{p}}{{d\varvec{\epsilon\:}}_{q}^{p}}=\frac{{d}_{0}}{{M}_{\text{c}\text{r}}}({\frac{{M}_{\text{c}\text{r}}}{\stackrel{-}{\eta\:}}\gamma\:}^{\beta\:}\text{e}\text{x}\text{p}(m\psi\:)-1)$$

(18)

In this equation, $\:\text{d}$ denotes the dilatancy; $\:{\text{d}\varvec{\upepsilon\:}}_{\text{v}}^{\text{p}}$ and $\:{d\varvec{\epsilon\:}}_{q}^{p}$ represent the plastic volumetric and deviatoric strain increments, respectively. The terms $\:{\text{d}}_{0}$, $\:m$ and $\:{\upbeta\:}$ are material parameters, and $\:\stackrel{-}{\eta\:}$ is the stress ratio. This formulation effectively captures the behaviour of both clay and sand .

In the proposed model, the direction of the plastic strain increment vector is governed by the gradient of the plastic potential surface, i.e., it is normal to that surface. The plastic potential function is derived by integrating Eq. (18):

$$\:Q\left(\varvec{\sigma\:}\right)=\frac{q}{{p}^{{\prime\:}}}+\frac{{d}_{0}{e}^{\beta\:\psi\:}}{1-\frac{{d}_{0}}{{M}_{\text{c}\text{r}}}}[1-{\left(\frac{{p}_{0}^{{\prime\:}}}{{p}^{{\prime\:}}}\right)}^{1-\frac{{d}_{0}}{{M}_{\text{c}\text{r}}}}]$$

(19)

Here, $\:\:{p}_{0}^{{\prime\:}}$defines the size of the plastic potential surface. However, this parameter does not influence the calculation of plastic strains and is eliminated during the derivation of the plastic potential function. The shapes of the plastic potential surface and the yield surface are shown in Fig. 2.

Fig. 2

Yield surface and plastic potential surface in q- p’ plane.

Non-associated flow rule

To determine the magnitude and direction of plastic strain increments in the present model, a non-associated flow rule is employed. According to this rule, the plastic strain increment vector is directed along the normal to the plastic potential surface, rather than the yield surface. In the proposed model, the flow rule is defined by the following expression²⁹:

$$\:{d\varvec{\epsilon\:}}^{p}=d\lambda\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:=d\lambda\:.\varvec{m}$$

(20)

Here, $\:\varvec{m}=\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:\:$is the unit vector normal to the plastic potential surface, which defines the direction of the plastic strain increment. The scalar$\:\:d\lambda\:$ is the plastic multiplier (or plastic consistency parameter) that determines the magnitude of the plastic strain increment, such that $\:\parallel\:{d\varvec{\epsilon\:}}^{p}\parallel\:=d\lambda\:$.

The volumetric and deviatoric components of the plastic strain increment vector can be computed using the following relationships:

$$\:{d\varvec{\epsilon\:}}_{v}^{p}=d\lambda\:\frac{\partial\:Q}{{\partial\:p}^{{\prime\:}}}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:=d\lambda\:.{m}_{p}$$

(21)

$$\:{d\varvec{\epsilon\:}}_{q}^{p}=d\lambda\:\frac{\partial\:Q}{\partial\:q}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:=d\lambda\:.{m}_{q}$$

(22)

Here, $\:{m}_{p}=\frac{\partial\:Q}{\partial\:{p}^{{\prime\:}}}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:$ and $\:{m}_{q}=\frac{\partial\:Q}{\partial\:q}/\parallel\:\frac{\partial\:Q}{\partial\:\varvec{\sigma\:}}\parallel\:\:$represent the volumetric and deviatoric components, respectively, of the unit vector normal to the plastic potential surface. The application of the non-associated flow rule is illustrated in Fig. 3.

Fig. 3

Non-associated flow rule.

The increment of plastic strain can subsequently be expressed utilizing the dilatancy Eq. 

$$\:{d\epsilon\:}^{p}=d{\Lambda\:}.\varvec{m};\:{\varvec{m}}^{T}=\left[\begin{array}{cc}\frac{d}{\sqrt{1+{d}^{2}}}&\:\frac{\stackrel{\sim}{t}}{\sqrt{1+{d}^{2}}}\end{array}\right]$$

(23)

Isotropic hardening rule

According to the isotropic hardening rule, plastic deformation leads to expansion or contraction of the yield surface in stress space, while its shape and center remain unchanged (Fig. 4). In the present model, the hardening rule assumes that changes in the size of the bounding surface, denoted by$\:\:{dp}_{cj}^{{\prime\:}}$, are linearly related to the plastic volumetric strain increment $\:{d\varvec{\epsilon\:}}_{v}^{p}$³⁰.

$$\:{{dp}^{{\prime\:}}}_{cj}={{p}^{{\prime\:}}}_{cj}\frac{\vartheta\:}{\lambda\:-\kappa\:}{d\varvec{\epsilon\:}}_{v}^{p}$$

(24)

Fig. 4

Isotropic hardening rule.

Evolution rule for the surface size ratio

To allow plastic deformations to develop from the onset of loading, the proposed model assumes that the plastic strain increments are influenced by the ratio of the loading surface size to that of the bounding surface. To account for this, a surface size ratio evolution rule is introduced, defined by the following Eq. ⁴⁴:

$$\:d\gamma\:=U\left(\gamma\:\right)\parallel\:{d\varvec{\epsilon\:}}^{p}\parallel\:,\parallel\:{d\varvec{\epsilon\:}}^{p}\parallel\:=d\lambda\:\:$$

(25)

In this equation, $\:\text{U}\left({\upgamma\:}\right)\:$is a decreasing function of$\:\:{\upgamma\:}$, which must satisfy the following conditions⁴⁴:

$$\:U\left(\gamma\:\right)=+\infty\:\:for\:\gamma\:=0U\left(\gamma\:\right)>0\:for\:0<\gamma\:<1U\left(\gamma\:\right)=0\:for\:\gamma\:=1U\left(\gamma\:\right)<0\:for\:\gamma\:>1$$

(26)

This condition ensures that during the loading process, the loading surface progressively approaches the bounding surface, even in numerically unstable cases where it may extend beyond the bounding surface ($\:\gamma\:>1$). According to the required conditions:

• When the loading surface is very small relative to the bounding surface ($\:\gamma\:=0$), the function $\:U\left(\gamma\:\right)$ must take on a very large value. This results in minimal plastic strain increments, and the material response remains nearly elastic.

• As plastic deformations develop and the loading surface expands (0$\:<\gamma\:<1$), $\:U\left(\gamma\:\right)$ should remain positive, driving the loading surface toward the bounding surface and transitioning the material behaviour into an elastic–plastic state.

• When the loading surface equals the size of the bounding surface ($\:\gamma\:=1$), $\:U\left(\gamma\:\right)$ should approach zero, allowing larger plastic strain increments and representing fully developed elastic–plastic behaviour.

• If the loading surface becomes larger than the bounding surface ($\:\gamma\:>1$), although this condition is physically unrealistic, it may arise due to numerical inaccuracies. In such cases, $\:U\left(\gamma\:\right)$ should be negative to ensure the loading surface is pulled back toward the bounding surface.

To satisfy these criteria, the function proposed by Hashiguchi⁴⁴ is adopted in the present model:

$$\:U\left(\gamma\:\right)=-uln\left(\gamma\:\right)$$

(27)

Equation (27) satisfies the conditions outlined in Eq. (26). In this expression, u is a material parameter.

Implementation of the model by implicit method

In this section, the implementation of the proposed model is described using an implicit approach based on the return mapping algorithm. Unlike conventional return mapping algorithms—which require checking whether the stress state lies inside or outside the yield surface—the present model does not include such a state determination step, as the elastic domain is reduced to a single point.

The implementation algorithm consists of two main steps: (1) elastic trial (prediction of the elastic state) and (2) plastic correction.

Elastic state prediction

In the elastic prediction step, the stress state is computed at each load increment under the assumption that the total strain increment is purely elastic:

$$\:{\varvec{\sigma\:}}^{Trial}={\varvec{\sigma\:}}_{n}+{\varvec{D}}_{n+1}^{e}{d\varvec{\epsilon\:}}_{n+1}$$

(28)

In this equation, $\:{\varvec{\sigma\:}}^{Trial}$ represents the trial stress assuming purely elastic behaviour. The indices $\:n$ and $\:n+1$ denote the previous and current load steps, respectively, and $\:{\varvec{D}}^{e}$ is the elastic stiffness matrix of the material.

Following the trial step, the trial stress and other state variables are updated through the plastic correction phase. Figure 3 illustrates the evolution of the yield surface with plastic deformation, in accordance with the isotropic hardening rule.

It is important to note that the return mapping algorithm used here ensures that, at each loading step, the trial elastic stress state is projected back onto the current loading surface using the elastic–plastic constitutive relations. The full computational procedure based on this algorithm is depicted in Fig. 5.

Fig. 5

Return mapping algorithm.

Plastic correction process

In this step, the trial elastic stress computed during the previous phase is corrected using the flow rule, the isotropic hardening rule, and the surface size ratio evolution rule to ensure that the consistency condition is satisfied. This condition ensures that the updated stress state lies on the loading surface and complies with the plasticity framework.

To enforce this consistency, the following equations are employed during the plastic correction process:

Equilibrium equation

The stress state must always satisfy the equilibrium condition, which ensures internal force balance within the material:

$$\:{d\varvec{\sigma\:}=\varvec{D}}^{e}{d\varvec{\epsilon\:}}^{e}$$

(29)

By applying implicit integration to the above equation over the time interval from step n to n + 1, and substituting Eqs. (5) and (28) into the resulting expression, the equilibrium equation can be reformulated as follows:

$$\:{\varvec{\sigma\:}}_{n+1}={\varvec{\sigma\:}}^{Trial}-{\varvec{D}}_{n+1}^{e}{{d\varvec{\epsilon\:}}_{n+1}}^{p}$$

(30)

Surface size ratio evolution

The initial value of γ is determined based on the over-consolidation ratio. However, to obtain a closed-form system of equations, its evolution must be formulated independently to ensure that the subloading surface remains within the bounding surface. To achieve this, the evolution of γ is derived by integrating Eq. 25.

$$\:{\gamma\:}_{n+1}={\gamma\:}_{n}-uln\left({\gamma\:}_{n+1}\right)d\lambda\:$$

(31)

Isotropic hardening rule

The bounding surface evolves—either expanding or contracting—in response to plastic deformation, in accordance with the isotropic hardening rule. By applying implicit numerical integration to Eq. (24), the following relationship is obtained:

$$\:{{p}^{{\prime\:}}}_{cj,n+1}={{p}^{{\prime\:}}}_{cj,n}\text{e}\text{x}\text{p}\left(\frac{{\vartheta\:}_{n}}{\lambda\:-\kappa\:}{\left({{d\varvec{\epsilon\:}}_{v}}^{p}\right)}_{n+1}\right)$$

(32)

Consistency condition

According to the consistency condition, the stress state must always lie on the loading surface during elastic–plastic loading⁴⁴. Therefore, the current stress state must satisfy the loading surface equation as follows:

$$\:F\left({\varvec{\sigma\:}}_{n+1}\right)={\left(\frac{{q}_{n+1}}{{M}_{cr}{{p}^{{\prime\:}}}_{n+1}}\right)}^{N}+\frac{\text{ln}\left(\frac{{{p}^{{\prime\:}}}_{n+1}}{{{\gamma\:}_{n+1}p}_{cj,n+1}^{{\prime\:}}}\right)}{\text{ln}\left(R\right)}=0$$

(33)

Finally, by simultaneously enforcing Eqs. (30)–(33), a system of nonlinear equations is formed. This system is solved using the Newton–Raphson iterative method.

Calculation of model input parameters

The unified constitutive model requires 17 input parameters, all of which must be determined prior to simulation. These parameters are categorized into five groups: elastic parameters, critical state parameters, bounding surface parameters, dilatancy parameters, and hardening parameters.

Elastic parameters

The elastic response of soil is characterized by two parameters: the shear modulus (G) and the slope of the swelling line (κ).

• The shear modulus, denoted by G, quantifies a soil’s stiffness in response to shear deformation. It is mathematically related to Young’s modulus (E) and Poisson’s ratio (ν). Typical shear modulus values for soils range from approximately 3 MPa for soft clays to around 350 MPa for dense sands and gravels.

• The parameter κ, which represents the slope of the swelling line in the $\:{\vartheta\:-lnp}^{{\prime\:}}$plane, reflects the soil’s compressibility during swelling. Its typical range is 0.001–0.01 for sands and 0.01–0.06 for clays. κ can be determined from isotropic consolidation or unloading tests.

Critical state parameters

The model incorporates three critical state parameters: λ, $\:\:{\vartheta\:}_{{\Gamma\:}}$, and $\:{M}_{cr}$.

• λ represents the slope of the critical state line in the $\:{\vartheta\:-lnp}^{{\prime\:}}$ plane. This slope reflects how compressible the soil is under elastoplastic deformation. Typical values of λ for sands under relatively low pressure conditions (i.e., below 1000 kPa) generally fall within the range of 0.01 to 0.05, although in some soils, higher values may occur at elevated pressures. For clays, λ typically ranges between 0.1 and 0.2.

• $\:{\vartheta\:}_{{\Gamma\:}}$ denotes the reference specific volume on the critical state line at a unit mean effective stress.

• Both λ and $\:{\vartheta\:}_{{\Gamma\:}}\:$can be determined from isotropic or oedometer loading condition using standard laboratory procedures.

• $\:{M}_{cr}$ defines the slope of the critical state line in the q–p′ plane, representing the soil’s shear strength at the critical state. This parameter varies with loading conditions—for example, $\:{M}_{cr,c}$ for compression and$\:\:{M}_{cr,e}\:$for extension. It can be indirectly estimated from the critical state friction angle or directly obtained from drained or undrained triaxial tests. The value of M_cr typically ranges from 0.8 to 1.0 for clays, and from 1.1 to 1.4 for sands.

Bounding surface parameters

The yield surface is characterized by two dimensionless parameters, N and R, as originally introduced in Yu’s unified model:

• N governs the shape of the bounding surface.

• R controls the intersection position of the CSL and the yield surface (i.e. at $\:{p}^{{\prime\:}}$=$\:{p}_{c}^{{\prime\:}}/$R)

For reference, in the original Cam-Clay model, N = 1 and R = 2.718, while in the Modified Cam-Clay model, N ≈ 1.7 and R ≈ 2. N typically ranges between 1 and 5. In natural clays, R typically ranges from 1.5 to 3, with higher values observed in sands. These parameters can be calibrated by analyzing effective stress paths from undrained triaxial tests.

Dilatancy parameters

Assuming elastic strains are negligible compared to plastic strains, the dilatancy parameters d₀, β, and m can be identified by fitting the stress ratio–total dilatancy curve obtained from standard drained triaxial compression tests. Note that β can only take values between 0 and 1.

Hardening parameters

The material constant u, which governs the evolution of the normal-yield ratio ( $\:\gamma\:$), is selected to match the curvature of the stress–strain curve during the transition from elastic to plastic behavior. Lower values of u yield a gradual transition, characteristic of ductile or soft materials, while higher values result in a more abrupt yield, aligning with classical plasticity theory. This parameter is typically identified by fitting the experimental stress–strain data, especially in the region where elastic deformation shifts to plasticity.

Additionally, the initial values of the state variables $\:{p}_{cj}^{{\prime\:}}$ and S need to be established before running simulations. $\:{p}_{cj0}^{{\prime\:}}\:$represents the initial extent of the bounding surface and is equivalent to the over-consolidation pressure. S₀, which denotes the initial location of the similarity center, is currently determined using a trial-and-error approach.

Multilaminate framework

In this theory, the numerical integration of a mathematical function is performed by expanding the function over the surface of a unit-radius sphere. This mathematical function represents variations in physical properties distributed across the sphere’s surface. The surface of the hypothetical unit sphere is approximated using a finite number of flat planes, each tangent to a specific point on the sphere. These tangent planes are referred to as base planes, and their points of contact with the sphere are called base points. The number of base points corresponds to the number of planar facets used to approximate the sphere’s surface.

To evaluate the numerical integral, the function values at each base point are multiplied by corresponding weight factors. The weighted sum of these values provides an approximation of the integral of the function over the sphere. In this way, the integral of a continuous function on the sphere is approximated by the sum of its values at discrete sampling points, each scaled by its weight coefficient. It has been shown that, in one formulation using 26 sampling points, the integration error is of order six. The following equation expresses the relationship between this numerical surface integral and the corresponding three-dimensional integral^{36,37,59,60,61,62}.

$$\:{\int\:}_{\varOmega\:}\int\:f(x,y,z)d\varOmega\:=4\pi\:{\sum\:}_{i=1}^{n}{w}_{i}{f}_{i}({x}_{i},{y}_{i},{z}_{i})$$

(34)

Ω denotes the surface area of the unit sphere, n represents the number of defined base points, and $\:{w}_{i}$ is the weight coefficient associated with the i-th base point. The arrangement of the sphere and the 26 defined base points is illustrated in Fig. 6. For each base point, a tangential plane can be defined on the surface of the sphere such that the direction cosines of the contact point are aligned with the direction cosines of the vector normal to the plane. In this formulation, any change occurring on a plane—such as sliding, opening, or closing—is attributed to the associated base point in a localized manner. By regulating the relative movements (sliding, opening, and closing) of these planes, the internal mechanism of material deformation at a point can be constructed.

Subsequently, by performing a weighted summation (numerical integration), the overall effect of deformation or movement at a material point is obtained. To do this, the function describing deformation on each plane must be properly defined and scaled. The total deformation at a point is thereby related to the stress–strain relationships defined on the base planes. In this framework, nonlinear constitutive equations are applied locally to each plane. When combined through summation, they allow for accurate prediction of the global behaviour of the material.

Fig. 6

The position of the sphere and the 26 mentioned points.

Therefore, it can be stated that the multi-laminate theory is based on a numerical approximation of physical properties—such as strain distribution—around a material point. These properties are considered to be spatially distributed within a representative volume associated with that point. This approximation is achieved by multiplying the value of the physical property at discrete points by their corresponding weight coefficients, and summing the results. This summation provides an estimate of the property (e.g., strain) for the entire domain.

From a geometrical perspective, the base planes are tangent to the surface of a hypothetical unit sphere. When examining pairs of parallel and opposite planes, it is observed that as the radius of the sphere approaches zero, their contact points converge. Consequently, two planes share a single base point. As a result, the original 26 base points are effectively reduced to 13 distinct points, each associated with a single tangential plane. This yields a hemispherical configuration with 13 base planes, which is adopted in the present model.

$$\:{\int\:}_{\varOmega\:}\int\:f(x,y,z)d\varOmega\:=8\pi\:{\sum\:}_{i=1}^{i=13}{w}_{i}{f}_{i}({x}_{i},{y}_{i},{z}_{i})$$

(35)

The direction cosines of the 13 selected planes, along with their corresponding weight coefficients, are presented in Table 1. The spatial arrangement and orientation of these 13 planes, extended from the center of a cube, are illustrated in Fig. 7.

Table 1 Plane numbers, direction cosines and their weighting coefficients⁶¹.

Fig. 7

Extension of the 13 planes in the center of the cube.

In this research, a 13-plane model was employed, with each plane exhibiting elastic–plastic behavior. The overall response of the soil is obtained by summing the contributions from all individual planes. A set of non-classical constitutive equations is applied on each plane, allowing for a more realistic representation of soil softening behavior. This is achieved through the use of a non-classical plasticity framework, which also accounts for the effects of induced anisotropy in the material response. In addition, the explicit Euler method was used to implement the multilaminate model.

Constitutive model for sampling planes

The constitutive equations for the models described within the multilaminate framework are analyzed separately in each plane. Consequently, as shown in Fig. 8, the stress and strain vectors must be transformed on these planes, represented as $\:{\sigma\:}^{T}=\left\{\begin{array}{cc}\tau\:&\:{\sigma\:}_{n}\end{array}\right\}$ and $\:{\epsilon\:}^{T}=\left\{\begin{array}{cc}\gamma\:&\:{\epsilon\:}_{n}\end{array}\right\}$). Additionally, the strain rate for each plane is separated into the elastic and plastic strain rates.

Fig. 8

Transformation of global stress { $\:\sigma\:$} at an integration point into local stresses {$\:{\sigma\:}_{n}$} and { $\:\tau\:$} on a plane.

Assuming the stress components in each element are given by $\:{\sigma\:}^{T}=\left\{{\sigma\:}_{xx}.{\sigma\:}_{yy}.{\sigma\:}_{zz}.{\tau\:}_{xy},{\tau\:}_{yz},{\tau\:}_{zx}\right\}$, the principal stress components on an inclined plane are calculated using the relationships provided in the continuum mechanics.

$$\:\sigma\:=\sqrt{{\sigma\:}_{1}^{2}+{\sigma\:}_{2}^{2}+{\sigma\:}_{3}^{2}}$$

(36)

$$\:\left\{\begin{array}{c}{\sigma\:}_{1}={\sigma\:}_{xx}l+{\tau\:}_{xy}m+{\tau\:}_{xz}n\\\:{\sigma\:}_{2}={\tau\:}_{yx}l+{\sigma\:}_{yy}m+{\tau\:}_{yz}n\\\:{\sigma\:}_{3}={\tau\:}_{zx}l+{\tau\:}_{zy}m+{\sigma\:}_{zz}n\end{array}\right.$$

(37)

The normal stress $\:{\sigma\:}_{n}$ and shear stress $\:{\tau\:}_{n}$ on any plane can be obtained using the following relationships:

$$\:{\sigma\:}_{n}={\sigma\:}_{xx}{l}^{2}+{\sigma\:}_{yy}{m}^{2}+{\sigma\:}_{zz}{n}^{2}+2{\tau\:}_{xy}lm+2{\tau\:}_{yz}mn+2{\tau\:}_{zx}nl$$

(38)

$$\:{\tau\:}_{n}=\sqrt{{\sigma\:}_{1}^{2}+{\sigma\:}_{2}^{2}+{\sigma\:}_{3}^{2}-{\sigma\:}_{n}^{2}}$$

(39)

Modulus matrix for each plane can be calculated as follows:

$$\:{C}^{ep}={C}^{e}+{C}^{p}$$

(40)

The matrix obtained from Eq. (40) is the common modulus matrix, which is used in the finite element method. Following equation facilitates the transformation of this modulus matrix:

$$\:{\left[{C}^{ep}\right]}_{6\times\:6}={\left[T\right]}_{6\times\:2}{\left[{C}^{ep}\right]}_{2\times\:2}{\left[T\right]}_{2\times\:6}^{T}\:$$

(41)

$$\:{T}^{T}=\:\:\left\lfloor\begin{array}{ccc}\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{x}}&\:\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{y}}&\:\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{z}}\\\:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{x}}&\:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{y}}&\:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{z}}\end{array}\:\:\:\:\begin{array}{ccc}\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{yz}}&\:\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{zx}}&\:\frac{\partial\:\tau\:}{{\partial\:\sigma\:}_{xy}}\\ \:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{yz}}&\:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{zx}}&\:\frac{\partial\:{\sigma\:}_{n}}{{\partial\:\sigma\:}_{xy}}\end{array}\right\rfloor$$

(42)

General modulus matrix of a point can then be calculated as follows:

$$\:{\left[{C}^{ep}\right]}_{6\times\:6}=8\pi\:\sum\:_{i=1}^{13}{w}_{i}{\left[{C}_{i}^{ep}\right]}_{6\times\:6}$$

(43)

In the multi-laminate model, the loading surface is related to the shear and normal stresses on each plane as follows:

$$\:F\left(\varvec{\sigma\:}\right)={\left(\frac{\tau\:}{{M}_{cr}{\sigma\:}_{n}}\right)}^{N}+\text{ln}\left(\frac{{\sigma\:}_{n}}{{\sigma\:}_{nc}}\right)/\text{l}\text{n}\left(R\right)$$

(44)

The bounding surface has the same shape as the loading surface, as shown below:

$$\:F\left({\varvec{\sigma\:}}_{j}\right)={\left(\frac{{\tau\:}_{j}}{{M}_{cr}{\sigma\:}_{nj}}\right)}^{N}+\text{ln}\left(\frac{{\sigma\:}_{nj}}{{\sigma\:}_{ncj}}\right)/\text{l}\text{n}\left(R\right)$$

(45)

Modeling triaxial tests

Numerous triaxial test studies have been reported in the literature to investigate soil behaviour under monotonic and cyclic loading in both drained and undrained conditions^{63,64,65,66,67,68,69,70,71}. In the present study, triaxial tests under drained and undrained conditions were numerically modeled for six soil samples using the unified model combined with the multilaminate framework. The results of the simulations were compared against available laboratory data. The input parameters used for the sand and clay samples investigated in this research are summarized in Table 2.

Table 2 The parameters of the studied soils.

A key feature of the proposed model—distinguishing it from previous research—is its ability to simulate induced anisotropy. The model’s performance in capturing anisotropic behaviour is demonstrated in Fig. 9, where shear stress–shear strain responses are shown for Planes 4 and 9 in both weald clay and a kaolinite–silt mixture.

As illustrated, the soil response in plane 4 differs from that in plane 9, confirming direction-dependent behaviour. Specifically, the maximum shear stress in each plane is calculated independently based on the normal stress acting on that plane. This leads to differing peak shear stresses, despite the shear strains corresponding to those peaks being nearly identical. In contrast, classical models typically exhibit significantly different strains corresponding to peak stresses, as they assume uniform behaviour in all directions. This highlights the model’s ability to capture induced anisotropy naturally—without introducing additional assumptions. The essence of induced anisotropic behaviour lies in the directional variation of material response due to accumulated plastic deformation. As loading progresses, the soil experiences different plastic strains in different orientations, leading to non-uniform behaviour across directions.

In conventional continuum mechanics, a single yield surface and plastic potential govern the material behaviour, resulting in uniform plastic variables for the entire volume at each loading step. However, in the multilaminate framework, each of the 13 planes has its own yield and plastic potential surfaces, and the corresponding plastic variables evolve independently based on the local plastic strain in each plane. As a result, the material behaviour becomes direction-dependent, and induced anisotropy is inherently captured by the model.

Fig. 9

Stress–strain curves for weald clay and kaolinit- silt mixtures in plane 4,9.

Drained test on weald clay

The prediction of drained triaxial compressive behaviour under constant lateral pressure for weald clay and a kaolinite–silt mixture using both the unified model and the multilaminate model is presented in Figs. 10 and 11. Overall, the results indicate that the multilaminate model effectively captures the phase transition behaviour from the elastic to plastic state. Furthermore, the model accurately reproduces the concavity and convexity of both the deviatoric stress–axial strain and volumetric strain–axial strain curves. The experimental data for the drained triaxial test on weald clay were originally reported by Skempton and Brown⁶⁶. A comparison between the model predictions and the laboratory results is shown in Fig. 10, demonstrating excellent agreement. The initial mean stress in the test was $\:{{\upsigma\:}}_{0}=-67\text{I}\:\text{k}\text{P}\text{a}.$

Fig. 10

Comparison of modeling results with laboratory data on Weald clay soil for drained triaxial compression test under constant lateral pressure.

Drained test on kaolinite-silt mixtures

A laboratory drained triaxial test on kaolinite–silt mixtures was conducted by Stark et al.⁶⁷. The proposed model demonstrates a good level of agreement with experimental results for both the deviatoric stress–axial strain and volumetric strain–axial strain responses. The predicted trends closely follow those observed in the laboratory data. The initial mean stress in this test was$\:{\:{\upsigma\:}}_{0}=-1275\text{I}\:\text{k}\text{P}\text{a}$.

Additionally, the model accurately captures both contractive and dilative behaviour exhibited by the clay during the drained test, further confirming its capability to simulate complex soil responses under monotonic loading (Fig. 11).

Fig. 11

Comparison of the calculated results from the following models with the test data for the drained triaxial compression test with constant lateral pressure for kaolinite–silt mixtures.

Triaxial undrained test on London clay

The stress paths and stress–strain responses under undrained triaxial loading conditions were simulated using both the unified model and the multilaminate model. The results of the numerical simulations are compared with laboratory test data in Fig. 12. Both models are able to closely replicate the observed laboratory behaviour, demonstrating good agreement with experimental trends. The reference laboratory undrained triaxial test on London clay was conducted by Bishop et al.⁶⁸.

Fig. 12

Comparison of model results with undrained triaxial compression test data under constant lateral pressure for London clay.

Triaxial undrained test on red clay

An undrained triaxial test on red clay was carried out by Wesley⁶⁹ under three different constant lateral pressures: 50, 100, and 250 kPa. As shown in Fig. 13, the multilaminate model provides a significantly better prediction of both the stress–strain response and the stress path compared to the unified model. The multilaminate model closely matches the experimental data across all confining pressure levels, highlighting its enhanced capability in capturing the anisotropic behaviour and complex stress evolution of red clay under undrained loading conditions.

Fig. 13

Comparison of model results with undrained triaxial compression test data for Red Clay.

Triaxial undrained test on Secramanto river sand

This section assesses the performance of the proposed model in simulating the undrained behaviour of Sacramento River sand under monotonic loading at varying confining pressures. Figure 14 presents the numerical results alongside the laboratory data obtained by Seed and Lee⁷¹ for Sacramento River sand. As illustrated in Fig. 14, dense sand initially exhibits dilatant behaviour—expanding before reaching the critical state—after which shear deformation continues along the critical state line. The results clearly demonstrate that the multilaminate model effectively captures this phase transition behaviour, accurately representing the transition from contractive to dilative response. Moreover, the model’s ability to simulate this behaviour confirms the robustness and accuracy of the dilatancy law implemented in the framework.

Fig. 14

Undrained triaxial compression tests on Secramanto river sand subjected to monotonic loading.

Drained triaxial test on hostun sand

In this section, the performance of the proposed model in simulating the behaviour of dense sand under monotonic drained conditions is evaluated using experimental data from tests on Hostun sand, as reported by Gajo and Wood⁷⁰. Monotonic triaxial tests were conducted at initial confining pressures of 200, 300, and 500 kPa, with corresponding initial void ratios of 0.578, 0.574, and 0.588, respectively.

Figure 15 presents a comparison between the simulation results and the experimental observations. The multilaminate model demonstrates superior capability in capturing strain softening behaviour as well as the volumetric response of dense sand. The improved accuracy of the model, particularly in replicating post-peak softening and dilative trends, highlights its effectiveness in representing complex soil behaviour under drained loading conditions.

Fig. 15

Drained triaxial compression tests on Hostun sand subjected to monotonic loading.

Conclusions

In this research, two constitutive models—the unified model and the multilaminate model—were employed to simulate the behaviour of soils under monotonic loading. The unified model is an elastic–plastic constitutive framework designed to capture the behaviour of both clay and sand under drained and undrained conditions. It is formulated based on the bounding surface theory and incorporates key concepts such as the critical state and state parameter to provide a unified description of sand and clay behaviour. To accurately simulate the phase transition behaviour observed in overconsolidated clays and dense sands, a generalized dilatancy rule was implemented. Furthermore, to represent the smooth transition from elastic to plastic response, a new formulation based on the radial mapping rule was adopted. The model was implemented using an implicit Euler integration scheme based on the return mapping algorithm, which ensures stable and accurate results across a wide strain range.

To address anisotropic soil behaviour, the unified model was extended using a multilaminate framework based on the code developed by Moghadam et al.³³. In this extension, a 13-plane model was adopted, with each plane exhibiting elastic–plastic behaviour governed by non-classical constitutive laws. The overall response of the material is obtained by integrating the behaviour across all planes, allowing the model to naturally account for induced anisotropy and directional dependence of plastic deformation.

Six soil samples were modeled under monotonic triaxial loading—both drained and undrained—and the results were compared with experimental data from the literature. The comparison demonstrates that the multilaminate model provides an excellent match with laboratory observations, particularly in capturing key behavioural features such as anisotropy, strain softening, strain hardening, dilatancy, and phase transition behaviour. Additionally, the use of an implicit integration scheme based on the return mapping algorithm proved effective in ensuring numerical stability and convergence for both small and large strain increments. Overall, the multilaminate model offers a robust and accurate tool for simulating the complex behaviour of clay and sand under monotonic loading conditions. The following topics are suggested for future studies:

• Implementation of the proposed model in this paper using the finite element program.

• Incorporating rotational hardening rule into the unified model and comparing the results with those obtained from the multi-laminate method.