Introduction

Among the most common environmental hazards, floods greatly affect human lives and cause major worldwide economic loss1. Depending on the geography and vegetation of the area, too much rainfall—especially in the form of showers—may cause significant runoff. Rapid transformation of this flow into a flood can cause significant damage. Rising damages and casualties have resulted from many areas being prone to recurrent and destructive flooding, which is indicated by recent patterns in flood events. The disturbance of hydrological and ecological equilibrium2, including urbanization (along rivers), climate change3, and deforestation4, explains the regular occurrence of this phenomena.

In recent years, the number of events and financial and human losses is rising globally despite the efforts of decision-makers and professionals to lower the hazards related with floods5. Additionally occurring annually in the Kashkan River basin are devastating floods. Considering the regularity of floods in this area, focus should be on flood susceptibility maps to stop loss of life and financial damage. The Kashkan River suffered sixteen floods with a discharge of more than 1000 cubic meters per second between 1955 and 2011. 2019 had one of the worst floods this basin has experienced6. Thus, it is imperative to arrange to lower, regulate, and forecast high-risk and high-potential dangerous locations during floods7.

First stage in flood management and disaster prevention is to find vulnerable locations and give managerial and executive allocation top priority8. Experiences from many countries imply that identifying and classifying flood-prone locations based on their risk levels is a basic first step in reducing the bad effects of floods. This knowledge can guide choices on land use in the industrial, urban, and agricultural sectors to reduce damage linked to floods9. Actually, one can also get a broad estimate of the flood-prone situation of the area by choosing sites with load potential. This is so because the existence of flood potential in a given location predicts a higher likelihood of flooding in that region. Many mathematical and probabilistic methods have lately been applied for flood susceptibility mapping. Because GIS can analyze vast volumes of spatial data, it has also become a basic analysis tool for spatial data management. Researchers have paid great interest to mathematical and probabilistic models combined with remote sensing and GIS10. Given the importance of identifying flood-prone areas through mathematical models and Geographic Information Systems (GIS)—particularly under financial constraints that hinder the implementation of structural flood control methods—adopting non-structural measures based on such data can serve as an effective strategy for mitigating damages. Non-structural techniques can solve existing flooding problems rather successfully. One such approach is machine learning methods, which have lately been effectively used for flood hazard mapping and the generation of flood sensitivity maps11.

Among the sophisticated machine learning models, the Maximum Entropy (MaxEnt) model stands out for its proven success in many research, owing to its unique benefits and capabilities. Since this offers many difficulties, it is imperative in study to find regions at danger of flooding and guarantee that other sites are not sensitive. Focusing just on places prone to flooding, the MaxEnt model can help to reduce inefficiencies and uncertainty related to non-presence areas12. Furthermore less sensitive to the number of flood episodes13, the MaxEnt model may generate reasonable forecasts even in areas with low frequency of floods. Quantitatively characterizing uncertainty and the information content of random events14 makes benefit from the entropy principle. This approach aids planners in precisely identifying and managing flood-prone areas. Currently, machine learning (ML) methods are widely used for flood modeling. Since ML modeling treats a watershed as an integrated system, it cannot distinguish between sub-watersheds for prioritization purposes. However, beyond flood hazard zonation, the most critical need within a watershed is the prioritization of sub-watersheds and the identification of higher-risk areas. Thus, sub-watershed prioritization requires a distinct approach.

Game theory, as a multi-criteria decision-making method, can determine the contribution of sub-watersheds to flood risk and flood hazard15. Apart from flood risk mapping, it is imperative to give sub-basins top priority and pinpoint the most important sites inside a watershed15. In this regard, game theory offers a consistent instrument for identifying elements influencing flood events and assigning priority watersheds for mitigating measures. A subfield of mathematics, game theory studies strategic decision-making among individuals or groups in situations whereby the decisions of others determine the results. Its ease in addressing multi-objective issues has helped it to move from basic to applied sciences. Furthermore, by providing several modeling approaches, game theory has greatly expanded several spheres of decision-making16.

Research on flood hazard zoning has been carried out extensively all throughout the world.

Using weighting and overlay techniques, Agus and et al. evaluated flood risk and developed a flood risk assessment map in the Sungai Pinang region of Samarinda City. The results showed that 44.21% of the region’s total area was categorized as very vulnerable, 53.57% as vulnerable, 2.19% as slightly vulnerable, and just 0.03% as safe. Furthermore showing a great degree of trust in the outcomes was the kappa value of 90.31%17. Using the Random Forest (RF) algorithm and the Soil Conservation Service (SCS) model, Xie and Shu examined rainstorm and flood hazards in Huangshan City. Examining the primary influencing elements also made use of the Driving forces-Pressure-State-Impact-Response (DPSIR) framework. The findings revealed notable regional variability in rainfall and flood threats; urban outskirts and low-lying areas concentrated the higher risks18. Using Machine Learning Models (MLM) and Geographic Information Systems (GIS) approaches, Adeyemi and Komolafe sought to forecast flood hazard regions in the Niger River basin in Nigeria. These models were designed to predict high-risk flood zones. They were applied to assess flood-prone areas based on 20 contributing factors, classified into topographic, hydrological, environmental/human, and climatic categories. For model training and testing, historical flood event data (1998–2023) from the study area were used, comprising 1164 flood and non-flood point records sourced from diverse databases. They were so included in order to forecast risky locations. With an overall accuracy of 91% compared to 88% and 85% respectively, the results showed XGBoost exceeded SVM and ANN. The flood hazard maps show that areas along the river—especially in the middle and southern portions of the basin—including areas of river confluence—were more vulnerable to flood hazard19.

Using entropy-based analysis, Prince et al. investigated and modeled flash flood hazards in the Himalayan region of Uttarakhand, India, using entropy-based analyses. The researchers employed the Maximum Entropy (MaxEnt) model approach to generate Flash Flood Hazard Susceptibility (FFHS) mapping. For model training, approximately 100 georeferenced field points obtained from the Uttarakhand State Disaster Management Authority were utilized, with an additional 29 points reserved for model validation. Terrain-derived parameters including elevation, slope, aspect, topographic wetness index (TWI), terrain roughness index (TRI), stream power index (SPI), sediment transport index, distance to river, distance to landslide, plan curvature, profile curvature, and land cover were input to the model. Results indicated that approximately five percent of the study area falls within the high to very high potential flash flood hazard classes20.

Using entropy approaches and VIKOR, Derse and Polat evaluated Turkish city urban flooding risk. Their review included several variables, including geographic features, climate, infrastructure, and urban planning. The provinces of Şanlıurfa, Artvin, Zonguldak, and Van were assigned the maximum urban flood risk values, according the results21. Using the MaxEnt model to evaluate and replicate flooding patterns, Li et al. found elements influencing urban flooding and evaluated its hazards in the city center of Tianjin. With population density, impermeable surfaces, and precipitation having the most effect on urban flooding, their results showed that the MaxEnt model is rather good in determining flood risk. The study found that the frequency of impermeable surfaces, building density, and population increase all help to raise the flood risk in the area. Tianjin’s center area, marked by great development and a dense population, concentrated the maximum flood danger in the city22. In a 2024 study, Ullah et al. conducted a sensitivity analysis of a two-dimensional flood inundation model simulating dam breach flooding from Spain’s Taos Dam. Using the SRH-2D model based on shallow water equations, five key parameters (Manning’s coefficient for river and forested areas, time step, turbulence coefficient, and boundary conditions) were analyzed using the Morris method. The results revealed that parameter influence on model output depends on flood stage, with tree resistance (Large_n) being most influential during peak flood conditions, while the time step (DeltaT) showed greater impact during the recession phase. Furthermore, the spatiotemporal analysis emphasized that accurate flood prediction requires consideration of this variability. This study provides strategies for optimizing flood modeling and reducing computational costs23.

Hanif et al. conducted a study examining the impact of land cover classification resolution derived from satellite imagery using machine learning and hydrological simulations. The research focused on the Jhelum River Basin in Kashmir, utilizing Sentinel-2 and Landsat-8 satellite data to classify land cover through two algorithms: Support Vector Machine (SVM) and Random Forest. findings indicated SVM demonstrated superior performance with 82.5% classification accuracy also Land cover changes between 2009 and 2019 (notably forest reduction and urban expansion) resulted in decreased annual runoff from 700 to 600 mm. These results underscore the critical importance of precise land cover classification for effective water resource management24.

Tariq et al. present a novel hydrodynamic-based approach for flood risk management in their study. The authors evaluated Expected Annual Damage (EAD) along Pakistan’s Chenab River both before and after levee installation through probabilistic flood modeling. The results indicate that flood levees reduce overall damages, but they also generate an induced risk (i.e., increased damage in other areas) due to alterations in flow patterns25.

Tariq et al. examine various flood risk management strategies in their research, focusing on alternative approaches for flood damage mitigation. The authors emphasize that while traditional methods rely on fixed return periods (e.g., 100-year flood events), contemporary flood risk management increasingly adopts risk-based approaches. Selecting appropriate mitigation measures requires an understanding of various factors, including flood risk (severity and probability), vulnerability (exposure and sensitivity), and the direct and indirect consequences of flooding. The study comprehensively evaluates diverse risk assessment methodologies and mitigation tools, accounting for varying geographical and socioeconomic contexts26.

Li and Hong investigated employing three deep learning coupling with ensemble learning models by integrating deep learning (DL) with filtered classifier (FC), rotating forest (RF), and random subspace (RSS) in Dingnan County, Jiangxi Province, China. Furthermore under investigation was how the coupling technique affected flood susceptibility modeling. Non-flood points were generated by random sampling; flood data was produced using single flood points. The study of influencing elements revealed that none of the factors show collinearity and that each one of them is efficient in flood occurrence. DL, FC-DL, RF-DL, and RSS-DL were used in preparation of the flood map. At last, the findings revealed that the deep learning couple with ensemble learning models performs more consistently and with more dependability27. Using game theory and machine learning methods, Avand et al. investigated flood likelihood and ranked watershed sub-basins. Thus, the game theory approach made use of the Borda and Condorcet algorithms as well as artificial neural network models and random forest (RF) to accomplish this. Flood occurrence likelihood was modeled using an ANN neural network, and game theory techniques were applied to rank watershed sub-basins in respect to flood occurrence probability. According to the findings, only a very tiny fraction of watershed areas have a high likelihood of flooding based on the forecasts of both models; most of them show rather low probability28.

Oubennaceur et al. introduced a novel sensitivity analysis methodology for two-dimensional flood models in their research, employing Gauss-Quadrature sampling as an alternative to Monte Carlo simulations. This innovative approach modifies the probability distributions of input variables (including flow discharge, Manning’s coefficient, and topography) while calculating relative sensitivity indices, demonstrating superior computational efficiency with fewer hydraulic model runs. The proposed method was tested on a 45-km stretch of the Richelieu River in Canada. The results demonstrated that water depth exhibits the highest sensitivity to topography, whereas its sensitivity to flow discharge and Manning’s coefficient was comparatively lower. These findings hold significant implications for improving hydraulic modeling and reducing uncertainties29.

Using Random Forest, Maximum Entropy, and Enhanced Regression Tree models, Faramarzi et al. zoned floods in Golestan National Park. Their results underlined in this area the important roles of elevation above sea level, distance from streams, precipitation, and road distance in flood occurrence30. Using fuzzy weight of evidence (fuzzy-WofE) and data mining techniques, Hong et al. produced a flood susceptibility map of Poyang County, China. Together with eleven flood-related variables, they employed logistic regression (LR), random forest (RF), and support vector machines (SVM). The fuzzy WofE-SVM model has the best prediction performance (AUC, 0.9865) according to the obtained results31.

Using Borda and Bargaining algorithms from game theory, Arshia et al. concentrated on ranking the sub-basins of the Sezar watershed in order of flood risk. This allowed the most crucial sub-basin and also the most significant parameters in all sub-basins to be found. Running both algorithms revealed that, in terms of flood risk, the two algorithms selected the most effective parameter in very different ways but in rather comparable ways for other effective parameters32.

Developing preventive actions and lessening the effects of flash floods depend on an important work on flood susceptibility, defined as the chance of flood occurrence. Located between the Zagros Mountains, great degree of ruggedness, frequent heavy rainfall due of the penetration of westerly winds, and so on, the Kashkan River basin is regarded as one of the basins that has a high likelihood of flooding. Most of the towns in the area are found in small floodplains next to the basin because of the mountainous character and great degree of roughness. Flooding always affects these places. Several floods have also been recorded in the area recently. For instance, the floods brought quite great damage to infrastructure, natural resource areas, cities and villages in the 2019 downpour events. Identification of the hydrological behavior of the watersheds and creation of management measures depend much on flood susceptibility zonation of the Kashkan River basin and prioritizing of its sub-basins. Consequently, given the significance of the topic, the aim of this research is to flood susceptibility zonation of the Kashkan River basin using machine learning models as well as to identify the most effective factors in flood occurrence and the most critical sub-basins using the game theory model, which in itself can be effective in improving management and decision-making. The innovation of the present research is that it integrates the MaxEnt model with game theory, thereby linking flood risk zoning directly to the decision-making process. The MaxEnt model is capable of predicting maximum probabilities even with incomplete data. Game theory incorporates equilibrium strategies and competitive decision-making, making it effective for addressing complex, multifaceted issues such as land use, environmental management, and resource allocation. In contrast, models like AHP (Analytic Hierarchy Process) or logistic regression may have limitations when dealing with data irregularities or intricate interactions among variables. Therefore, integrating the MaxEnt model with game theory enables a more comprehensive analysis and improved decision-making in scenarios requiring an understanding of interactions and uncertainties.

Materials and methods

Study area

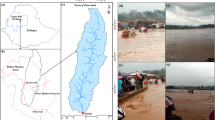
The Kashkan River basin, spanning an area of 917,000 hectare, is situated in the southwestern region of Iran within Lorestan Province. This watershed plays a crucial role in the upper reaches of the Karun River and accounts for approximately one-third of the soil in Lorestan Province. Geographically, it runs between 33° 8′ to 34° 2′ north latitude and 47° 12′ to 48° 59′ east longitude (Fig. 1). Iran is categorized in hydrology as belonging to the Persian Gulf watershed. Before joining the Seimareh River at Gavmishan Bridge, the river runs around 300 km through Pol-Dokhtar, finally becoming the Karun River. The Kashkan River basin is geomorphologically characterized by a variety of features, including low-elevation mountainous units, hills, plateaus, upper terraces, and flat foothill plains. The elevated mountainous areas are marked by rocky formations, steep slopes, and vertical cliffs in the form of erosional escarpments, primarily found in the northern and central regions along the Kashkan River’s course. These features significantly influence the watershed’s hydrological regime, as surface water flows rapidly develop across the slopes during weather events. In terms of land use, over 70% of the watershed consists of high-quality pastures and steppe landscapes interspersed with scattered trees. The soil properties in this area predominantly consist of fine-grained, impermeable soils, composed mainly of clay and silt, which have a high potential for runoff during rainfall events8.

Fig. 1
figure 1

Geographical location of the study area using ArcGIS 10.8 software.

Full size image

Required data

The data used in the present research for the Kashkan River basin was calculated for a 25-year statistical period (1998–2023). The reason for selecting this time series is the occurrence of the 2019 flood within this period. The flood seriously damaged infrastructure, natural resource areas, cities and towns as well as infrastructure during 2019’s annual rainfall. In this study, the single flood event point and random sampling method were used to generate flood and non-flood data, respectively.

In the zoning of flood hazard with the maximum entropy model from rainfall data, flood occurrence points identified by GPS, geological maps, 1:100,000 Lorestan province and other environmental maps such as land use and slope were used.

Table 1 data are applied in the part on game theory. Field research and hydrological studies in the Kashkan basin yielded these results. This data was gathered from topography maps, rainfall statistics, satellite images, and field surveys and covers information about several sub-basins inside this watershed.

Table 1 Parameters used in game theory.
Full size table

Research method

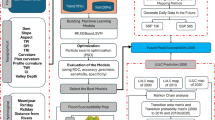
Flood occurrence points were first found by field visits in the Kashkan River basin, then GPS coordinates were recorded in Excel in CSV format. Consequently, the data matrix was constructed after identifying flood occurrence and non-occurrence locations and preparing the environmental variables map. This allowed flood risk zonation to be performed. Then, using the random forest algorithm, among several elements, the most crucial ones influencing the flood sensitivity of the basin were found and their significance was established. The environmental factors were then generated in ASCII form using the SAGA GIS software and the Geographic Information System (GIS) program. The data were loaded using the GeoPandas library in Python. Following binary labeling of flood occurrence and non-occurrence points as 1 and 0 respectively, their correlation was analyzed, and variables exhibiting correlation coefficients above the 0.7 threshold were removed. Subsequently, variable importance was determined using the Random Forest algorithm. The Random Forest algorithm was selected for this purpose due to its robust capabilities in handling noisy data, modeling nonlinear relationships, and addressing multicollinearity among features. At last, the basin’s flood risk zonation map was generated using the Maximum Entropy (MaxEnt) model. In each modeling step, 70% of the data was used for training and 30% for model validation. These training and testing data ratios were chosen depending on past knowledge and studies employing machine learning techniques. Choosing these percentages could help to prevent overfitting among other things. In this study, MaxEnt model outputs—including jackknife tests, receiver operating characteristic (ROC) curves, response curves, and permutation importance values—were utilized not only for statistical model evaluation but also for sensitivity mapping, parameter weighting, and priority analysis. The Borda scoring method incorporated jackknife analysis and variable importance measures for final scoring. Furthermore, the response curves facilitated visual interpretation of variables and were instrumental in identifying high-risk zones and establishing thresholds for regional flood susceptibility classification.

Figure 2 presents the research methodology’s flowchart.

Fig. 2
figure 2

Flowchart of research stages.

Full size image

Maximum entropy model

Recently, the maximum entropy model has attracted major interest as a machine learning technique for evaluating watershed flood susceptibility33. Approved as one of the most often used predictive models in many spheres of natural and environmental sciences, the Maximum Entropy model runs just based on the sites of past floods. By contrast, statistical models and other approaches call for data on both flood events and non-occurrences34.

This model can extract, expressed as raster layers, the probabilistic distribution of data for every environmental variable connected to elements influencing flood occurrence. High forecast accuracy, the abolition of the necessity for absence data, and a free, user-friendly interface are among its benefits33. Environmental variable maps in ASCII form and flood occurrence data with their geographic coordinates in CSV form comprise model inputs. Key outputs of the model include the ROC curve, where the area under the AUC graph indicates the model’s predictive performance; response curves that show the function of environmental factors in the watershed’s flood susceptibility; variable contribution shares, which quantify the significance of each variable in flood susceptibility; and the Jackknife test, which evaluates the impact of each variable on the model by methodically excluding one variable at a time12.

Figure 3 shows steps of the maximum entropy model.

Fig. 3
figure 3

Steps of the maximum entropy model.

Full size image

Evaluation of prediction performance

In this stage, the outcomes of flood risk modeling are validated using the Receiver Operating Characteristic (ROC) curve approach and in line with the occurrence points of the validation group—30% of past flood events. Validation is quantitative measured in the area under this curve (AUC)9. One of the most effective, thorough, and all-around tools for showing the traits of determination, probability identification, and system prediction—that which statistically approximates the model’s accuracy—is the ROC curve. Many times, used to evaluate the susceptibility models of natural hazards is this curve. The model accuracy will be outstanding when the area under the curve exceeds ninety-percent. Actually, the most perfect model boasts the biggest area under the curve35.

In addition to the ROC curve, the F1 Score metric was also employed to evaluate the results.

Factors influencing flood susceptibility in the Kashkan basin

The environmental variables taken into account based on the carried out studies comprise drainage density, slope, slope aspect, topographic moisture, lithology, land use, distance from streams, and soil texture map. The computation and mapping of these variables follow Fig. 4.

Fig. 4
figure 4figure 4

Map of factors affecting flood susceptibility in the Kashkan basin using ArcGIS 10.8 software.

Full size image

Drainage density: This index is the ratio of the total length of rivers in a specific watershed or defined area to the total area of the watershed or region that encompasses those rivers. In watersheds, a high drainage density reduces permeability, hence increasing runoff and raising flood sensitivity. Based on a 30-m resolution DEM, the Line Density tool in GIS software produced a drainage density map.

Slope: The most important factor in determining flow velocity on drainage density, soil moisture, and geomorphological processes; hence, slope and aspect are regarded as effective surface indicators for determining flood-prone areas, the degree of surface runoff, and infiltration possibility. This factor is also significant as the slope map of the watershed was developed using GIS software and categorized into four different classes.

Topographic wetness: This statistic measures the influence of topography on the flood sensitivity of the watershed and reflects its moisture conditions36. SAGA GIS tools helped to produce the topographic wetness map.

$$TWI = \, Ln \, \left( {AS/tan\beta } \right)$$
(1)

where AS is the specific area of the watershed (m2/m) and β (radian) is the slope angle in degrees.

Lithology: The flood sensitivity of watersheds is much influenced by the fine-grained and marly formations as well as alluvial deposits. For Lorestan Province, the lithological map for the watershed was created from geological maps scaled 1:100,000. The studied watershed is covered by various types of geological formations.

Land use: Within the watershed, land use affects permeability and runoff creation. It also plays an important role in the functioning of hydrological and geomorphological processes by controlling surface flows, runoff, and sediment. Developed with data from the Lorestan Province Department of Natural Resources and Watershed Management, the land use map for the Kashkan basin was produced using GIS software.

Distance from streams: The 2019 floods in the Kashkan basin clearly show how important distance from streams is in determining flood danger in a watershed. Euclidean distance function of Geographic Information System (GIS) tools was used to generate a distance map to the streams.

Slope aspect: Slope aspect is an important morphometric component impacting flood risk in watersheds. The slope aspect map for the Kashkan basin was developed using Geographic Information System (GIS) software.

Soil texture map: Evaluating flood risk in watersheds depends on a knowledge of soil texture. Most alluvial soils found in the Kashkan basin are not saline. Geographic Information System (GIS) tools also produced this soil texture map.

Precipitation map: Data from eight rain gauge sites within the watershed over a 25-year period was compiled for the same times for all stations and subsequently, using interpolation in the Geographic Information System, the Precipitation Map of the research area was produced.

Selecting the most important variables using the Random Forest algorithm

The great accuracy, power, and simplicity of use of the Random Forest algorithm for variable selection explain why one should apply it. Originally building training datasets using a variable selection technique, the Random Forest algorithm Decision tree models then are produced and trained by separating the data into training and test sets. The variables with the most significance in dividing the classes then are found by means of the trained data. At last, the very crucial variables are split and their influence shapes the last model33. Data were first loaded in this study using the Geopandas Package in the Jupyter Notebook environment with the Python programming language to ascertain the most significant factors influencing flood susceptibility. The data were split into two sets—training and test—70% for train and 30% for test following normalization. The importance degree of every variable was then computed using feature importances. Scikit-learn and Random Forest algorithms. Figures 5 illustrate the most significant factors chosen by the Random Forest technique.

Fig. 5
figure 5

Feature importance in random forest algorithm.

Full size image

Game theory

Through the design and analysis of scenarios, game theory—a subfield of mathematics—picts the behaviors and results of decision-making entities interacting with one another37. It especially investigates competitive scenarios and emphasizes strategic games over chance ones. Game theory’s main ingredients are players (decision-makers), choices (potential actions), outcomes (payoffs, rewards, etc.), and the choice of the best conclusion. This theory is the study of rational behavior in situations where interdependence exists38. Given that the players’ highest demands are satisfied, its aim is to reach a condition whereby every player’s maximum desires are satisfied39. Game theory stresses the study of strategic conduct among rational agents, in which the choice of strategy by other players influences not just an agent’s utility but also their own strategy37.

Borda algorithm in game theory

Every parameter in the Borda scoring system is handled as a representative and receives linear scores. There will be n rankings for a given n representative. The cumulative score of the influencing variables defines the sub-basin ranking. The representative with lowest priority gets a score of zero; the person ranked first gets n-1. Highest to lowest rank, scores are assigned successively40. Under this scoring system, every representative’s score is computed with the following equation and shown as BS (A):

$$\begin{aligned} & BS\left( A \right) = \left( {1 - n} \right)*\# \left\{ {i| \, i\;ranks\;A\;first} \right\} + \left| {\left( {n - 2} \right)*\# \{ \, i} \right|\;i\;ranks\;A\;second\} \\ & + \cdots + 1*\# \left\{ { \, i|i\;ranks\;A\;second\;to\;last} \right\} + 0*\# \left\{ { \, i|i\;ranks\;A\;last} \right\} \\ \end{aligned}$$
(2)

The representative with the highest score is selected as the primary representative (first priority)41. Steps of the Bodra algorithm for determining flood potential is presented in Fig. 6.

Fig. 6
figure 6

Steps of the Borda algorithm for determining flood potential.

Full size image

The main representative (first priority) is chosen the one with the highest score41. Figure 6 shows the Bodra algorithm’s several steps for determining flood potential.

Results

Flood risk zonation map in the kashkan basin using the MaxEnt model

Figure 7 shows the flood risk zonation map using the Kashkan basin. To prepare the flood susceptibility map, initial reports related to flood-prone areas in the Kashkan basin, pertaining to the 2019 flood, were obtained from the Regional Water Company of Lorestan. Then, through field visits by the authors of the aforementioned article, the location of these points was checked, corrected, and relocated using GPS. Next, using the Random Forest algorithm, 9 factors were selected as the most important, and their significance was determined. The map of each of these variables was prepared using SAGA GIS and Arc GIS 10.8 software, and along with the flood occurrence points, it was entered into MaxEnt software version 3.3.3k. Finally, the output map of the model was drawn in Arc GIS software (Fig. 7) )http://biodiversityinformatics.amnh.org/open_source/maxent/(.

Fig. 7
figure 7

Flood risk zonation map in the Kashkan basin using ArcGIS 10.8 software and MaxEnt3 .3.3k.

Full size image

Five risk classes define the flood risk zonation map for the Kashkan basin: very low (0.0–0.2), low (0.2–0.4), moderate (0.4–0.6), high (0.6–0.8), and very high (0.8–1.0). Five risk categories are chosen in order to evaluate consistency with world standards and accuracy. Figure 7 shows that distance from the streams reduces the sensitivity to flooding. This is so because most of the flow accumulation happens in the channel and so the increase in distance from the streams results in a decrease in flood sensitivity.

Table 2 shows the area and proportion of every flood risk class within the basin. Also shows the area has an inverse relationship with the probability of flood occurrence. The risk of flooding decreases with increasing area of the classes; conversely, the risk of flooding increases with decreasing area of the classes.

Table 2 Area and percentage of every class of flood risk in the Khashkan basin.
Full size table

To evaluate the accuracy of the model, the flood occurrence points are displayed on the flood hazard zonation map in the MaxEnt model (Fig. 8). The high agreement of these points with the simulation output of the MaxEnt model indicates the high accuracy of the model in flood zonation of the Kashkan basin.

Fig. 8
figure 8

Flood occurrence points on the flood risk zonation map using the MaxEnt 3.3.3k and ArcGIS 10.8 software.

Full size image

The alignment of flood occurrence spots in the Kashkan basin in 2019 with the regions and critical sub-basins identified by the Maximum Entropy approach demonstrates that this model efficiently prioritizes the most critical sub-basins in terms of flood risk.

Contribution of factors affecting flood susceptibility in the Kashkan basin

After training the model, the contribution of each factor to flood prediction can be evaluated. By conducting Jackknife test analyses in the Maximum Entropy model, the importance and contribution of input variables in the spatial prediction of flood-prone areas were determined.

The most important variables influencing flood vulnerability in the watershed, according to the results, are distance from the stream contributing 30.9% and slope contributing 32.3% (Table 3). After these, other factors, drainage density, and land use come second in influence. An important issue in this work is the great consistency of the results with this section and the results of variable importance in the Random Forest method.

Table 3 Analysis of variable contributions.
Full size table

The percentage contribution represents the direct share of each variable in reducing the model’s deviation during training. For example, proximity to waterways, with 30.9%, has the greatest impact on improving the model’s fit. On the other hand, permutation importance measures the decline in the model’s performance (AUC) when the values of a variable are randomly shuffled. For instance, in the case of distance from waterways, it shows that disrupting this variable reduces the AUC by 0.32 percent.

The 16.8% contribution of land use indicates its significant role in enhancing model fit, likely due to the influence of land use patterns (e.g., urban areas with low permeability) on flood risk. However, the low permutation importance (6.4%) suggests that random shuffling of land use values results in only marginal reduction in model AUC (Area Under the Curve).

Evaluation of the MaxEnt model

Response curves

Response curves show how factors in the surroundings affect the probability of flooding. While a declining curve indicates a negative relationship, an increasing curve points to a positive one between the action and flooding42.

As shown in Fig. 9, the response curve analysis for soil texture reveals that Brown Step Soils (with a contribution value of 0.55) play the most significant role in watershed flood susceptibility. These clay-textured soils exhibit low permeability and high water retention capacity, promoting water accumulation and increased flood risk. In contrast, sandy soils demonstrate higher permeability, thereby reducing flood potential (A). With values of 0.7, 0.62, and 0.51 respectively, the Aghajari, Kashkan, and Quaternary formations have the most influence in determining flood susceptibility in the basin in the curve related to geology; their fine-grained character and the presence of marl formations in these units explain this. Geological formations such as the Aghajari and Kashkan units exhibit low permeability and high surface runoff due to their characteristic lithology (predominantly marl and clay-rich sediments) (B). In the response plot for land use, areas with irrigated agricultural land use, with a value of 0.73, have the highest influence in the flood vulnerability of the basin (C). As the figure shows in the curve connected to drainage density, the flood susceptibility potential of the basin rises with increasing drainage density. Thus, the flood susceptibility potential is highest, 0.6, at a drainage density of 1.09 (D). The most important element for flood vulnerability in the basin is proximity to a stream, and as the distance from the stream grows, the role of this factor reduces. At the closest distance to the stream, the flood susceptibility potential is 0.7, however as the distance increases, this value rapidly declines and approaches a stable trend. Riparian areas typically exhibit gentler slopes, indicating potential spatial correlation between these two variables. However, prior to modeling, multicollinearity among variables was assessed using Pearson’s correlation coefficient, with variables demonstrating correlation coefficients exceeding the 0.7 threshold being excluded from subsequent analyses (E). Furthermore evident in the slope response curve is the link between slope and flood occurrence. As the figure shows, flood occurrence has an inverse link with slope rise (F).

Fig. 9
figure 9

Response curves indicate the role of environmental parameters using the MaxEnt.

Full size image

Jackknife diagram

Environmental variables significance is assessed using a Jackknife plot. This graph shows how performance varies depending on eliminating every environmental factor. The green hue stands for the whole contribution of all elements save the one under analysis. Stated otherwise, the green shows the model’s performance in cases whereby just one variable is eliminated. The blue hue denotes the performance of the model depending on just one particular variable. Stated differently, a high blue value for a variable indicates the variable by itself can offer rather accurate forecasts. At last, the red color stands for the performance of the model when all the variables are present in the model and acts as a reference benchmark.

Figure 10 shows Jackknife diagram results, stressing the most important influencing factors and their contribution to MaxEnt model prediction. The chart shows that the AUC is around 82% when the model takes just proximity to streams into account. On the other hand, the AUC for slope is rather about 77%. The graph shows that flood sensitivity is least influenced by soil texture.

Fig. 10
figure 10

The results of the Jackknife test to determine the most important parameters.

Full size image

ROC curve

Using the ROC curve and the area under the curve (AUC), the MaxEnt model evaluates its validity. Good accuracy is indicated by an AUC between 0.7 and 0.8; excellent accuracy by an AUC between 0.8 and 0.9; and very great accuracy by an AUC higher than 0.943. While for the test data the AUC is 0.906, for the training data it is 0.945. These principles show that the model has outstanding accuracy. The results of the model evaluation based on the ROC curve are presented in Fig. 11.

Fig. 11
figure 11

The ROC curve for evaluating the MaxEnt model in the Kashkan basin.

Full size image

Given that the MaxEnt model is occurrence-based, both the AUC (Area Under the Curve) and F1 Score metrics were employed to comprehensively evaluate model robustness. For this purpose, the MaxEnt model’s prediction raster file and occurrence point samples were prepared in the Geographic Information System (GIS) and subsequently processed in Python. Using relevant Python libraries, the F1 Score was calculated. The results demonstrated strong model performance with AUC = 0.906 and F1 Score = 0.719.

Game theory

Table 4 lists separately the most crucial factors influencing Flood Susceptibility in the sub-basins of the Kashkan basin. Table 4 presents the ranking of each parameter across sub-watersheds. For instance, Sub-watershed 2221 ranks 3rd for the “Mean Slope” (S) parameter, indicating its relatively steep gradient and consequent erosion potential. This ranking system provides a comparative basis for assessing sub-watershed erosion susceptibility.

Table 4 Influencing factors for flood susceptibility in sub-basins Kashkan basin.
Full size table

The following techniques were applied in order to get the table’s shown results:

  • Data collection: Field surveys and GIS analysis yielded data on area, slope, and drainage density.

  • Hydrological analysis: Hydrological models and rainfall data helped one determine the times of concentration and runoff volume.

  • Land use classification: National Natural Resources Organization produced a land use map.

  • Statistical analysis: Using statistical techniques, rainfall records and other variables were examined.

Additionally acquired from the Country Natural Resources Organization were the eight sub-basins of the Kashkan basin.

Then, all the sub-basins are rated based on the factors under consideration. The score of a parameter for a sub-basin is different from other basins, and each parameter is rated independently (Table 5). Table 5 displays the ranking of each parameter across all sub-watersheds. For example, in the table, the rank of sub-basin 2221 in terms of the average slope parameter (s) is 3, which suggests that the slope parameter has been ranked based on the relationship it has with flood susceptibility production in all sub-basins. The higher the value of this parameter, the larger the sub-basin’s capacity for flood susceptibility production, for which sub-basin 2221 is placed 3rd (Table 5). This ranking system provides a comparative basis for evaluating sub-watershed erosion susceptibility. The rankings presented in Table 4 were derived from raw parameter values, wherein all sub-watersheds were ordered according to each parameter’s actual measurements, with sequential ranks assigned in Table 5. For example, if Sub-watershed 2221 exhibited the second-highest mean slope value among all sub-watersheds, it was assigned a rank of "3" based on the ordinal numbering system (beginning from 2). This process was conducted without classification or normalization, relying solely on the ordering of raw values. To enhance analytical precision and reproducibility, future revisions should consider transforming all numerical raw variables to a common scale prior to ranking, using methods such as linear normalization (Min–Max) or Z-score standardization. This approach would eliminate the influence of parameter scale differences on final rankings and facilitate analysis replication across different regions. Additionally, quantitatively classifying variables (e.g., categorizing slope into 3 or 5 classes) before numerical ranking could establish a more transparent decision-making framework.

Table 5 Ranking of influencing factors for flood susceptibility in sub-basins Kashkan basin.
Full size table

For input into game theory algorithms, the parameters were sorted in ascending order based on their previously assigned rankings, with equally-ranked parameters in each sub-watershed assigned identical colors. This indicates that parameters sharing the same rank within a sub-watershed maintain equivalent ranking status throughout subsequent game theory algorithm processing. Furthermore, uniquely colored cells represent parameters whose scores differ from all other parameters in the target sub-watersheds. In this coding system, the specific color assignment is inconsequential; rather, color uniformity between cells indicates parameter rank equivalence. This approach facilitates rapid identification of equally-ranked parameters for subsequent analytical stages. Within game theory algorithms, parameters sharing the same rank receive identical treatment. This implies that when two parameters demonstrate equivalent ranking within a sub-watershed, they exert identical influence during subsequent analysis and decision-making processes. Parameters assigned unique colors are treated as distinct entities, with their individual impacts evaluated separately in later analytical phases (Table 6).

Table 6 Order of the effect of Influencing factors for flood susceptibility in sub-basins Kashkan basin.
Full size table

Accordingly, Table 6 presents the relative influence of each parameter within every sub-watershed, organized according to the ranking system established in Table 5. This table serves to prioritize parameters by their relative importance within each sub-watershed. For instance, in Sub-watershed 2221, the primary influential parameters include watershed shape (Sh), precipitation (P), and slope (S). The table assigns each parameter a ranked value ranging from 1 (most influential) to 13 (least influential), where a rank of 1 indicates the highest priority and greatest impact on erosion and sediment deposition processes within the respective sub-watershed. For instance, in Sub-watershed 2221, the "Watershed Shape (Sh)" parameter holds rank 1, indicating its predominant role in the sub-watershed’s erosion processes. Conversely, the "Mean Slope (S)" parameter, ranked 10 in this sub-watershed, exerts relatively lesser influence. These rankings serve as inputs for subsequent game theory algorithm implementation.

Notably, parameters sharing identical ranks within a sub-watershed receive equal weighting in subsequent analyses. This equivalence is determined through numerical rankings rather than color-coding. Thus, Table 5 provides both: (1) a tool for assessing each parameter’s relative importance across sub-watersheds, and (2) a foundation for weighting parameters in multi-criteria decision analysis methods such as the Borda Count approach.

In Table 7, following the principles of the Borda method—as explained in the previous section—the sub-basins of Kashkan were scored based on the evaluated parameters and according to Tables 5, 4, and 6. Thus, in Table 7, a numerical rank was assigned to each parameter, and the total score for each parameter in every sub-basin was calculated. According to Table 7, the score for each parameter in each sub-basin was placed in the corresponding column for that parameter, allowing the column-wise summation of each parameter across all sub-basins to be obtained. These scores enable a quantitative comparison of the parameters. Higher values indicate a greater influence of the parameter on erosion. Consequently, parameters that achieve the highest scores across all sub-basins are deemed more critical.

Table 7 Rating of parameters by Borda method in flood susceptibility of sub-basins Kashkan basin.
Full size table

In Table 8, the total score for each parameter across all sub-basins has been calculated, and the parameters are ranked based on their overall significance in the Kashkan Basin. According to Table 8, the most critical—and indeed the most influential—parameter in the Kashkan Basin is the maximum 24-h rainfall with a 25-year return period, followed by the parameters of land use (agriculture) and average slope percentage. In Table 9, the score for each sub-basin was calculated with respect to each parameter, and ultimately, the sub-basin with the highest cumulative row score was identified as the most critical sub-basin. This demonstrates the aggregate impact of all parameters within each sub-basin.

Table 8 Ranking of the most effective parameters by Borda method in flood susceptibility of sub-basins Kashkan basin.
Full size table
Table 9 Ranking of the most critical sub-basins by the Borda method in flood susceptibility of sub-basins Kashkan basin.
Full size table

Table 9 shows the score of every sub-basin computed for every parameter; hence, the most important sub-basin in the row sum would be the one with the highest score. With the greatest total score for the characteristics, Table 9 shows that 2221 was the most important sub-basin in the Kashkan basin. Table 4 lists the primary variables influencing sedimentation and erosion in the sub-basins. Table 5, 6, 7, 8 and 9 present the results of various analysis including ranking of parameters, the effect of every parameter on flood susceptibility and prioritizing of sub-basins and Fig. 12 shows the high-risk map of sub-basins based on the results of analysis. This map demonstrates the link between several characteristics and flood risk as well as graphically points out high-risk sub-basins. Figures 9 and Tables 4, 5, 6, 7, 8 and 9 indicate the link between the investigated parameters and the high-risk sub-basins by means of their merging high-risk sub-basins for example have been found in sub-basins 2221, 2222, and 2223. Agricultural land usage and basin shape in sub-basin 2221 have been noted as high-risk sub-basin given 24-h rainfall with a 25-year return time. With its drainage density, main stream length, time of concentration, and forest land usage, Sub-basin 2223 has been determined as a high-risk sub-basin. Sub-basins 2221, 2222, and 2223 have been found as high-risk sub-basins and demand management and control strategies to lower the danger of flood and sedimentation clearly show when the results of Tables 4, 5, 6, 7, 8 and 9 are integrated with Fig. 12. Based on the Borda technique, Fig. 12 shows the flood prioritizing map of sub-basins Kashkan basins.

Fig. 12
figure 12

Flood susceptibility map of sub-basins Kashkan basin based on Borda algorithm using ArcGIS 10.8 software.

Full size image

Discussion

Using the Maximum Entropy model, flood susceptibility zoning was done in the Kashkan basin producing accurate findings. The MaxEnt model assumes that the spatial distribution of flood risk is primarily influenced by selected environmental variables (such as distance from river and slope). To reduce reliance on this assumption, the Random Forest algorithm was employed to verify variable importance. The study found that, in sequence of importance, the distance from streams at 30.9% and slope at 23.2% define the most important factors affecting flood susceptibility. Less important are other elements like land use, drainage density, lithology, slope orientation, soil texture, and topographic wetness. This underlines how vulnerable places near rivers and with mild slopes (less than 5%) are because of lower soil permeability and higher runoff. This result fits the historical floods of 2019 in the Kashkan basin, where more than eighty percent of the flooded regions fell close to rivers.

In this study, to reduce data bias, a single flood event point and random sampling method were used to generate flood and non-flood data, respectively. Additionally, the MaxEnt model was evaluated using the k-fold cross-validation method, with the data partitioned into 70% for training and 30% for testing. The results demonstrate the model’s stability across all data subsets (AUC = 0.906 ± 0.02). The findings underscore that proximity to streams is the primary factor affecting flood susceptibility in the Kashkan basin. During the floods of 2019, the most flood-prone areas were located near rivers, further validating the predictive capability of the MaxEnt model. To enhance the evaluation of the model’s results, flood occurrence points were compared with the flood susceptibility map, showing a high degree of alignment with the model’s flood hazard points. Additionally, the Jackknife chart for the MaxEnt model indicated that using slope alone in the analysis yields an AUC value of 0.82, highlighting the significant importance of this variable.

Given the intricate interaction of several factors, lowering the dangers of flooding depends on applying good decision-making to give executive operations top priority in watershed management initiatives. If the Maxent model is used independently, since this model only performs prioritization, the lack of integration of quantitative–qualitative analyses leads to incomplete decisions in resource management. Using several techniques—including the two approaches used in this study—game theory and maximum entropy—can be rather successful in prioritizing the elements that affect flooding and spotting important sub-basins at danger of flood occurrence.

According to the results obtained from the game theory method (Table 8), parameters such as 24-h rainfall with a 25-year return period, agricultural land use, and average slope have the most significant impact on erosion and sedimentation. This issue pertains to the physical and ecological characteristics of the region. Intense rainfall increases the kinetic energy of raindrops, which severely displaces the surface soil in areas lacking protective vegetation. The predominant agricultural land use in the Kashkan region employs rain-fed (dryland) farming methods, typically involving slope-parallel tillage practices. This cultivation approach has been shown to exacerbate surface runoff and soil erosion processes. High average slope accelerates overland flow velocity, thereby enhancing sediment transport capacity and soil erosion. Thus, the dominance of these variables is a natural consequence of the region’s physical attributes and land management practices, a conclusion further validated by the quantitative results of the Borda method.

The Borda method is a multi-criteria decision-making approach that offers several advantages, making it particularly suitable for this research:

  1. 1.

    Simplicity and transparency: This method operates based on ranking rather than precise numerical values, making it less susceptible to data uncertainty.

  2. 2.

    Reduced weighting bias: Unlike other methods, the Borda method does not require preliminary weighting of criteria, thereby minimizing analyst subjectivity.

  3. 3.

    Compatibility with ordinal data: Given that the research primarily utilized ordinal data (from Table 5), the Borda method provides a robust framework for integrating these rankings.

Consequently, the selection of the Borda method was scientifically and logically justified, aligning with the nature of the data, the research objectives, and the need for sub-basin prioritization.

Furthermore, Figs. 8 and 12 are complementary to one another. While Fig. 12 illustrates the prioritization of sub-basins based on erosion and sedimentation, Fig. 8 identifies flood-prone areas. The correlation between these two figures clearly demonstrates that the sub-basins at high flood risk in the southwestern region of the basin (shown in Fig. 8) spatially coincide with the sub-basins at high erosion risk (specifically sub-basins 2221, 2223, and 2222 in Fig. 12). Furthermore, the sub-basins located in the northern and northwestern regions of the basin (identified as high flood-risk areas in Fig. 8) exhibit a direct correspondence with sub-basins 2227 and 2226 (classified as high erosion-risk zones in Fig. 12). This spatial consistency underscores the relationship between flood susceptibility and erosion vulnerability across the basin.

Furthermore, Fig. 12 identifies sub-basins 2221 to 2223 as high-risk areas, which aligns with Table 9. The table indicates that sub-basin 2221 has the highest SUM value of 4290.5, derived from the Borda method—a game theory-based multi-criteria decision-making technique. In this method, each sub-basin’s score for each parameter is ranked based on key erosion indicators, and the final score is obtained by summing these rankings. A higher score indicates a greater risk of erosion. The results section includes an analysis of the relationship between each sub-basin’s physical characteristics and its flood/erosion risk levels.

The present work uses the Maximum Entropy model to map flood hazard and the Game Theory model to prioritize flood susceptibility among the sub-basins Kashkan basin. Using Game Theory and Machine Learning algorithms (RF and ANN), flood likelihood and sub-basin prioritizing were also examined in a 2021 Avand et al. paper. The validation findings showed that the machine learning systems attained a suitable degree of accuracy. Analogously, in the present work, the Maximum Entropy model produced respectable findings. The validation data revealed that the machine learning techniques had acceptable accuracy. Furthermore, displaying good results in the present study was the Maximum Entropy model. Consequently, the findings of this study on the applicability of machine learning techniques in flood danger mapping match the present work. Adeyemi and Komolafe also conducted a study on flood-risk zones in the Nigerian basin by integrating machine learning models (MLMs) and geographic information system (GIS) techniques. In their research, they employed three algorithms—XGBoost, SVM, and ANN—and achieved an overall accuracy of 91%, compared to 88% and 85%, respectively. The results indicated that XGBoost outperformed SVM and ANN. However, the present study utilizes the MaxEnt model, which is also a machine learning model. Based on the AUC values—0.945 for training data and 0.906 for validation data—this model demonstrates superior performance19. In contrast to the Kashkan Basin, which has a cold semi-humid climate, the study area in Adeyemi and Komolafe is tropical, with the rainy season typically occurring between April and October. During this period, peak river discharge frequently leads to severe flooding. However, a notable finding is that in both studies, flood hazard maps indicate that riverside areas are consistently more vulnerable to flooding.

Similar to the present study, the research by Ahmad et al. also aimed to improve flood hazard mapping using advanced methodologies44. However, Ahmad et al. proposed an integrated approach for flood susceptibility assessment in the mountainous Hunza-Nagar region. Researchers used hydrodynamic modeling (HEC-RAS) to simulate the 100-year flood, remote sensing to gather regional data, and machine learning algorithms to predict flood-prone areas. he prediction accuracy rates, as measured by AUC values, were 0.912 for Random Forest (RF) and 0.893 for XGBoost. The results demonstrated that these flood hazard maps would serve as valuable tools for disaster management and infrastructure development. In the current study, nine environmental factors were utilized for flood mapping: slope gradient, aspect, precipitation, distance from streams, stream density, lithology, land use, soil texture, and topographic wetness index. The area under the curve (AUC) values from the ROC analysis in the maximum entropy (MaxEnt) method yielded 0.945 for training data and 0.906 for validation data, indicating the model’s high predictive accuracy. Consequently, based on the AUC values, the MaxEnt model demonstrated superior prediction performance compared to both extreme gradient boosting (XGBoost) and random forest (RF) algorithms.

In their investigation on flood zonation, Samanta et al. also applied conventional models including the Frequency Ratio method and the Analytical Hierarchy Process (AHP), but these techniques sometimes lack sufficient accuracy in areas with sparse and non-linear data45. Conversely, the neglect of complicated interactions between natural and human elements and the lack of priority for sub-basins depending on actual risk have made management strategies useless. This is considering in the present work.

Key findings

  • Areas adjacent to waterways and those with gentle slopes (less than 5%)—accounting for 30.9% and 23.2% of the study area, respectively—exhibit the highest vulnerability due to reduced soil permeability and increased surface runoff. These factors were identified as the most critical flood risk determinants in the Kashkan River Basin.

  • Based on the results of the game theory method, parameters such as 24-h rainfall with a 25-year return period, agricultural land use, and average slope were found to have the most significant influence on erosion and sedimentation.

  • The integrated analysis using the MAXENT model and game theory reveals significant spatial correlations between flood-prone and erosion-prone sub-basins:

  • Southwestern sub-basins identified as high flood-risk areas show precise alignment with sub-basins 2221, 2223, and 2222—all classified as high erosion-risk zones.

  • Similarly, northern and northwestern sub-basins with elevated flood risk correspond exactly to sub-basins 2227 and 2226, which are likewise categorized as high erosion-risk areas.

Conclusion

This work aims to map the flood risk and rank the Kashkan basin’s flood-prone sub-basins in order of importance. The proximity to the waterway is the most important determinant of the flood-proneness of the Kashkan basin based on the obtained results; most of the flood-prone areas of this watershed are found close to rivers. The study revealed that proximity to streams was the most significant factor affecting flood vulnerability, accounting for 30.9%, followed by slope at 23.2%. The maximum entropy model demonstrated high accuracy, with an AUC value of 0.945 for training data and 0.906 for validation data, confirming its reliability. Furthermore, noted as high-risk sub-basins based on game theory were sub-basins 2221, 2222, and 2223. Because of agricultural land use, basin shape, and 24-h rainfall with a 25-year return period, Sub-basin 2221 was classified as a high-risk sub-basin.

Particularly in the design and execution of structural and non-structural solutions, knowing flood-prone locations guarantees that resources be used where most needed, therefore ensuring effective and efficient allocation of them. Ultimately, based on the results obtained from the integration of the two methods, managerial strategies can be implemented in the sub-basins 2221, 2222, and 2223—those with the highest flood volumes. Such strategies may include constructing sediment basins, cultivating resistant plants such as Astragalus spp., implementing land use management practices, and preventing land degradation. To manage flooding within sub-basin 2221, non-structural measures such as the implementation of conservation cropping on 30% of the riverbank agricultural lands and the prohibition of construction activities within a 150-m buffer zone from the river are recommended. For sub-basin 2222, the establishment of a flood early warning system in collaboration with Lorestan Regional Water Authority is proposed. Additionally, for sub-basin 2223, it is suggested to cultivate salt-tolerant species (e.g., Atriplex) to stabilize the calcareous soils. These fixes not only lower flood risk but also boost local community resilience against next calamities. Moreover, the findings of this research can help to locate appropriate and secure sites for next local developments.

The framework proposed in this study can be generalized to basins with similar characteristics (semi-arid climate, sedimentary formations, and extensive agricultural activities). However, in basins dominated by groundwater flow or igneous formations, recalibration is necessary. It is recommended that future studies test this framework in basins with different climatic conditions (e.g., humid regions).