Thermal freeze-out and collective signatures in $pp$ collisions with a non-extensive statistical study on energy and pseudorapidity systematics

Abstract

This paper presents a comprehensive analysis of the double-differential $p_T$ distributions of charged particles across twelve pseudorapidity regions ($|\eta | < 2.4$, bin width $\Delta \eta = 0.2$) in $pp$ collisions at $\sqrt{s} = 0.9$, 2.36, and 7 TeV. Using a modified Tsallis function incorporating an effective transverse flow velocity, we achieve excellent agreement between the model and experimental data, with consistent fit quality across all $p_T$ ranges (validated by Data/Fit panels). The extracted parameters including kinetic freeze-out temperature ($T_0$), mean transverse flow velocity ($\langle \beta _T\rangle$), non-extensivity parameter ($q$), and mean transverse momentum ($\langle p_T \rangle$) reveal systematic dependencies on $\eta$ and $\sqrt{s}$. Both $T_0$, $\langle \beta _T\rangle$, and $\langle p_T \rangle$ decrease with $|\eta |$, attributed to reduced energy deposition and weaker thermalization in fragmentation-dominated high-$|\eta |$ regions. These parameters also exhibit marked growth with $\sqrt{s}$, reflecting collision-energy-driven dynamics. In contrast, $q$ increases with $|\eta |$, signaling greater deviation from thermal equilibrium (Boltzmann limit $q \rightarrow 1$) at larger $|\eta |$, while mid-$\eta$ particles ($|\eta | \approx 0$) approach near-equilibrium behavior. Parameter correlations, particularly between $T_0$, $\langle \beta _T\rangle$, $q$, and $\langle p_T \rangle$, highlight interplay between thermal and collective-like dynamics. The results provide critical insights into the interplay of thermalization, effective flow, and non-equilibrium effects in small collision systems, advancing the understanding of bulk hadronic matter in high-energy $pp$ interactions.

Introduction

The study of global properties in proton-proton ($pp$) collisions provides critical insights into non-perturbative Quantum Chromodynamics (QCD) and serves to constrain phenomenological models and event generators^1,2. These collisions are dominated by soft processes or low-momentum-transfer interactions, which remain poorly understood yet essential for understanding the mechanisms governing particle production in high-energy collisions.

A key approach to characterizing $pp$ collisions is the analysis of charged-particle transverse momentum ($p_T$) and pseudorapidity ($\eta$) distributions. These observables reflect the interplay between perturbative (hard) and non-perturbative (soft) QCD processes³. While perturbative methods describe high-$p_T$ particle production, soft processes, such as parton hadronization and low-$p_T$ scattering, require phenomenological modeling. Precise measurements of $p_T$ and $\eta$ distributions at low $p_T$ ($< 5$ GeV/c) are thus vital for refining event generators used in collider and cosmic-ray physics^4,5.

The pseudorapidity $\eta$ discussion is crucial for gaining insights into the jet fragmentation process, energy deposition, and particle flow, which can help distinguish between different types of interactions, such as hard scatterings versus softer processes like collective flow etc. Indeed, $\eta$ represents the direction of the emitted particles produced in the relativistic collision with respect to the beam direction, defined as $\eta = -\ln [\tan (\theta /2)]$ (where $\theta$ is the polar angle relative to the beam axis), serves as a proxy for rapidity in massless approximations. The current study studies different characteristics, parameters, of the produced system at the kinetic freeze-out concerning $\eta$. This directly gives the indication which parameter is prominent in which direction to the beam axis. For instance, in present analysis the kinetic freeze-out temperature is increasing while the non-extensive parameter decreases as one moves towards the mid $\eta$ region, suggesting the formation of a thermalized and equilibrated system along the mid $\eta$ region compared to the beam direction. Similarly, the flow velocity increases towards mid $\eta$, confirming the prominent collectivity of the produced system along the mid $\eta$ region. These results lead us to a tentative conclusion that if the physicists expect the detection of QGP like matter, they need to install detectors in the mid eta region compared to the beam direction. In this work, we analyze the double-differential $p_T$ spectra of primary charged hadrons across twelve pseudorapidity bins ($|\eta | < 2.4$, $\Delta \eta = 0.2$) in $pp$ collisions at $\sqrt{s} = 0.9$, 2.36⁴, and 7 TeV⁵. Primary charged hadrons include particles from strong/electromagnetic decays (lifetime $> 1$ cm), excluding weak-decay products and secondary interactions⁶. These measurements probe the transition between soft and hard QCD regimes, offering a baseline for disentangling nuclear-medium effects in heavy-ion collisions.

Recent advances in statistical modeling have enabled deeper exploration of hadron production dynamics. While Boltzmann-Gibbs (BG) statistics initially described particle spectra^7,8, they fail to capture the non-equilibrium nature of multiparticle production in high-energy collisions³. Tsallis statistics, a nonextensive generalization of BG, address this limitation by introducing a deformation parameter $q$ ($q \rightarrow 1$ recovers BG equilibrium) to quantify deviations from thermal equilibrium^9,10. This framework effectively models systems with long-range correlations, memory effects, or fragmented phase spaces, features inherent to $pp$ collisions¹¹. Modified Tsallis distributions have successfully described $p_T$ spectra at RHIC and LHC energies^12,13,14, particularly when augmented with transverse flow effects.

To account for collective-like dynamics in small systems^15,16, transverse flow velocity ($\langle \beta _T\rangle$) is incorporated into Tsallis-based models such as the Tsallis Blast-Wave (TBW) framework^17,18. While collective flow is well-established in heavy-ion collisions, its interpretation in $pp$ systems remains debated; here, $\langle \beta _T\rangle$ parametrizes effective radial momentum correlations rather than hydrodynamic expansion^19,20. Competing models, including Boltzmann-Gibbs Blast-Wave (BGBW)^21,22 and Hagedorn-inspired functions^23,24, similarly link $p_T$ spectra to freeze-out temperature ($T_0$) and flow velocity.

This paper systematically compares non-extensive Tsallis analyses of charged-hadron spectra as a function of $\eta$ and $\sqrt{s}$. We employ a modified Tsallis distribution with transverse flow¹⁴ to extract $T_0$, $\langle \beta _T\rangle$, $q$, and $\langle p_T \rangle$, elucidating their interdependencies and energy evolution. Section “The data, formalism, and method” details the nonextensive formalism, Section “Results and discussion” presents and discusses results, and Section “Summary and conclusion” summarizes key conclusions.

The data, formalism, and method

This study analyzes $p_T$ distributions of inclusive charged hadrons and $\eta$ in non-single-diffractive (NSD) $pp$ collisions at $\sqrt{s} = 0.9$, 2.36, and 7 TeV, as measured by the CMS experiment^4,5. NSD collisions, comprising non-diffractive and double-diffractive processes, ensure full pseudorapidity coverage ($|\eta | < 2.4$) for charged hadrons. Data are partitioned into twelve $\eta$ bins of width $\Delta \eta = 0.2$. Charged hadron yields are reconstructed using three complementary methods⁴:

• 1. Pixel barrel cluster counting,

• 2. Pixel tracklet reconstruction from correlated clusters,

• 3. Full tracker volume tracking with combined pixel/strip hits.

These methods, as detailed in Refs.^4,5, are used by CMS to obtain combined, high-fidelity $p_T$ spectra. In this analysis, we use the final published spectra that incorporate all three methods and associated systematic uncertainties. We do not select one method over another, as our input data reflects the fully corrected, merged distributions freely available on hepdata.net.

The $p_T$ spectra are modeled using Tsallis statistics, which generalize Boltzmann-Gibbs (BG) thermodynamics to nonequilibrium systems. The simplest Tsallis parametrization is²⁵:

$$\begin{aligned} \frac{1}{N_{ev}} \frac{1}{2\pi p_T} \frac{d^2N}{dydp_T} = C'\left( 1 + (q - 1) \frac{m_T}{T_{\text {eff}}}\right) ^{-q/(q-1)}, \end{aligned}$$

(1)

where $m_T = \sqrt{p_T^2 + m_0^2}$ is the transverse mass ($m_0$: rest mass), $T_{\text {eff}}$ is an effective temperature combining thermal motion ($T_0$) and collective flow ($\beta _T$), $q$ quantifies nonextensivity ($q \rightarrow 1$ recovers BG statistics), and $C'$ normalizes the distribution.

Equation (1) lacks thermodynamic consistency (e.g., violates energy/additivity rules⁹). A modified, consistent form is:

$$\begin{aligned} \frac{1}{N_{ev}} \frac{1}{2\pi p_T} \frac{d^2N}{dydp_T} = C m_T \left( 1 + (q - 1) \frac{m_T}{T_{\text {eff}}}\right) ^{-q/(q-1)}, \end{aligned}$$

(2)

where $C$ is a revised normalization constant.

The thermodynamic consistency of this equation has been shown in Ref.²⁶. It is noteworthy that Eq. (1), does not include the term $m_T$, is the typical Tsallis-like parameterization which has some restrictions in terms of thermodynamic consistency. The quantity $m_T$, which naturally arises from the Lorentz-invariant phase space concerns ($d^3p/E$) that control particle production in relativistic collisions, is included in Eq. (2). There is thermodynamic consistency in this equation. For a meaningful extraction of parameters, the term $m_T$ guarantees that these integrals are executed appropriately over the phase space. Furthermore, the theoretical underpinnings of Tsallis statistics are more closely aligned with Eq. (2). The proper form readily incorporates the $m_T$ dependence when we derive the particle distribution from the maximization of non-extensive entropy. This transforms Eq. (2) into a theoretically sound representation that links to the statistical mechanical foundations of the Tsallis framework, going beyond simply being an empirical fitting function.

To disentangle $T_0$ and $\beta _T$, we adopt a modified Tsallis distribution inspired by Blastwave formalisms²⁶:

$$\begin{aligned} \begin{aligned} \frac{1}{N_{ev}} \frac{1}{2\pi p_T} \frac{d^2N}{dydp_T} =&\; C \langle \gamma _T\rangle \left( m_T - p_T \langle \beta _T\rangle \right) \\& \times \left( 1 + \langle \gamma _T\rangle \frac{(q - 1)(m_T - p_T \langle \beta _T\rangle )}{T_0}\right) ^{-q/(q-1)}, \end{aligned} \end{aligned}$$

(3)

where $\langle \gamma _T\rangle = 1/\sqrt{1 - \langle \beta _T\rangle ^2}$ is the Lorentz factor averaged over the emission profile. Here $T_0$: Kinetic freeze-out temperature at which particles cease interacting. $\langle \beta _T\rangle$: Mean transverse flow velocity, parametrizing radial momentum correlations. $q$: Nonextensivity parameter, capturing deviations from equilibrium ($q > 1$: superstatistics, $q < 1$: subdiffusion).

The detailed models like Tsallis Blastwave or Boltzmann Gibbs Blastwave assume that different parts of the collision zone expand at different speeds, this is called the emission profile. This emission profile is normally used to calculate different properties like temperature and flow rates, etc, at different parts of the produced fireball, normally across different radii. Generally, in the nuclear collision, the fireball produced has a higher thermalization and expansion rate at the center compared to the edges. The current model assumes that the system’s properties are independent of the spatial coordinates and thus assumes the average value of $\beta _T,~ \gamma _T$ and q. Therefore, $\beta _T,~ \gamma _T$ and q show no sensitivity to the emission profile. Thus, the model considers the system as a single big blob with uniform properties and not as a detailed system where properties vary with special coordinates. It is worth noting that in the present analysis, we used $pp$ collisions, where the smaller system size leads to relatively weaker variations in spatial properties. Consequently, employing simplified models, such as the one used here, is unlikely to significantly impact the results.

Equation (3) is fitted to $p_T$ spectra in each $\eta$ bin and $\sqrt{s}$ using $\chi ^2$ minimization. Parameters $T_0$, $\langle \beta _T\rangle$, $q$, and $C$ are extracted, with uncertainties propagated from experimental errors. This approach extends earlier work^14,24,27 by embedding flow effects into a thermodynamically consistent Tsallis framework, validated in $Xe+Xe$ collisions²⁶.

The selected $p_T$ range (0–2 GeV/c) corresponds to the limits of the publicly available CMS data^4,5. Since we are particularly interested in QGP-like matter, whose properties such as flow velocity and collectivity are encoded in the low-$p_T$ region, we focused on this dataset. In contrast, the high-$p_T$ region is dominated by hard processes (e.g., jet production). We used a flow-included Tsallis distribution, because the system formed in relativistic heavy-ion collisions is highly complex and evolves dynamically. As it expands, the mean free path among its constituents increases, reducing the frequency of interactions and causing a deviation from local thermal equilibrium. Applying hydrodynamically inspired models such as the Boltzmann–Gibbs Blast-Wave (BGBW), which assume local equilibrium, may therefore omit critical non-equilibrium information. In contrast, non-extensive Tsallis models with embedded flow, as used here, better describe non-equilibrated systems. The non-extensive parameter q quantifies the deviation from equilibrium, offering a more accurate depiction of the system’s dynamics. Instead of a simple Tsallis distribution which can fit this $p_T$ range, we included flow because the simple Tsallis fit yields an effective temperature that conflates the true kinetic freeze-out temperature and flow effects. By incorporating a transverse flow velocity $\beta _T$ into the Tsallis distribution, we can disentangle these contributions and extract both the real freeze-out temperature and the flow velocity, key to understanding collectivity in high-energy collisions. This approach also facilitates comparison with larger systems (e.g., $Pb-Pb$ or $p-Pb$), where flow is well established. Observing a nonzero $\beta _T$ in $pp$ collisions would suggest collective behavior even in small systems, challenging the conventional view that pp interactions lack hydrodynamic characteristics.

Results and discussion

Figure 1 shows the double-differential $p_T$ spectra of charged particles across twelve pseudorapidity bins ($|\eta | < 2.4$, $\Delta \eta = 0.2$) in $pp$ collisions at $\sqrt{s} = 0.9$, 2.36, and 7 TeV. Experimental data from^4,5 (depicted as geometric symbols) are well-described by the modified Tsallis function (solid lines) over the full $p_T$ range ($0.1< p_T < 5$ GeV/c). The Data/Fit residuals (lower panels) confirm excellent agreement, with deviations $< 10\%$ across most $p_T$ and $\eta$ regimes. Fit quality is quantified by $\chi ^2/\text {ndof} \sim 1.0$–$1.5$ (Table 1), validating the model’s ability to capture both low-$p_T$ exponential and high-$p_T$ power-law regimes^12,13. The newly appeared $N_0$ listed in Table 1, arises during the fitting procedure, where it scales the model to match experimental data. It is the fitting constant that roughly represents the multiplicity parameter, i.e., the number of specific species of hadrons produced in an event.

Fig. 1

The $p_T$ distribution of charged hadrons in various $\eta$ intervals produced in p–p collisions at 0.9, 2.36 and 7 TeV collision energies. The different coloured data points represent the experimental data for different $\eta$ values, while the solid lines are the fit results of Eq. (3). Each plot has a Data/Fit panel at its bottom which measures the fit quality of Eq. (3).

Fig. 2

(a) $T_0$, (b) $\beta _T$, (c) q, (d) fitting constant $N_0$ and (e) $\langle p_T \rangle$ as a function of $\eta$ in $pp$ collision at 0.9, 2.36 and 7 TeV.

Fig. 3

(a) $T_0$ vs $\beta _T$, (b) $T_0$ vs q, (c) $\beta _T$ vs q, (d) $\langle p_T \rangle$ vs $T_0$, (e) $\langle p_T \rangle$ vs q and (f) $\langle p_T \rangle$ vs $\beta _T$ for charged hadrons produced in $pp$ collision at 0.9, 2.36 and 7 TeV.

Table 1 The values of free parameters, the fitting constant, $\chi ^2$ and ndof obtained through the fitting procedure of the experimental data with modified thermodynamically consistent Tsallis distribution function given in Eq. (3).

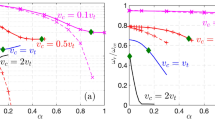
Figure 2a reveals two key trends: (1) $T_0$ decreases with $|\eta |$, reflecting reduced energy deposition in forward/backward $\eta$ regions dominated by beam fragmentation³; (2) $T_0$ grows with $\sqrt{s}$, though the increase diminishes at higher energies ($\Delta T_0(\sqrt{s} = 2.36 \rightarrow 7~\text {TeV}) \approx 5\%$ vs. $\Delta T_0(0.9 \rightarrow 2.36~\text {TeV}) \approx 15\%$).

The $\eta$-dependence of $\beta _T\,($ Fig. 2b) mirrors $T_0$, with mid-$\eta$ values ($\beta _T \sim 0.35$–$0.45c$) exceeding forward $\eta$ values ($\beta _T \sim 0.15$–$0.25c$). This gradient arises from stronger pressure gradients at midrapidity, where energy density peaks¹⁷. $\beta _T$ also rises with $\sqrt{s}$, but the trend flattens above 2.36 TeV, consistent with energy saturation in collective-like momentum transfer¹⁹.

The saturation in $T_0$ and $\beta _T$ can be attributed to the possibility that saturation arises due to non-equilibrium effects and principles of kinetic theory. If the system evolves too rapidly to achieve complete thermalization, non-hydrodynamic modes or viscous damping mechanisms may inhibit further expansion of collective flow. Alternatively, at the highest collision energies, the system may become dominated by instabilities or non-thermal momentum transfer mechanisms, which can suppress additional increases in transverse flow despite the presence of a higher initial energy density.

As shown in Fig. 2c, $q$ increases systematically with $|\eta |$, reaching $q \approx 1.15$ at $|\eta | > 2.0$ compared to $q \approx 1.05$ near mid-$\eta$. This quantifies the departure from thermal equilibrium ($q \rightarrow 1$) in fragmentation regions, where rapid longitudinal expansion suppresses local thermalization^10,11. Notably, mid-$\eta$ values ($|\eta | < 0.5$) approach $q \approx 1.03$–$1.05$, might be suggesting near-Boltzmann behavior in central rapidity⁶. The system produced in the mid $\eta$ region is highly excited because of the greater energy deposition and is highly dense, due to which the system behaves like a hydrodynamic or collective system characterized by the larger $\beta _T$ values. Due to this collectivity, particles of the system have frequent interactions leading to quick thermalization and equilibration, characterized by the smaller values of q. On the other hand, close to the beam direction or along the high $\eta$ region, i.e., along the fragmentation region, the produced system is dilute, more like a hadron gas, having small $\beta _T$, where frequent interactions among the constituents are absent, leading to the suppressed thermalization i.e., larger q values.

Figure 2c also displays the increasing trend of q with collision energy. Although higher-energy collisions do produce systems with greater particle densities that might suggest more efficient thermalization, several competing factors in fact drive the system further away from equilibrium. First, the extremely short lifetimes of the systems formed at high energies lead to rapid expansion and early freeze-out, preventing full thermalization. As a result, non-equilibrium features originating in the early stages of the collision become effectively “frozen in” and persist through to the final state. Secondly, and perhaps more important, the dominant mechanisms of particle production evolve qualitatively with increasing energy. While soft processes, which tend to thermalize quickly, govern particle production at lower energies, hard processes such as mini-jet production, arising from perturbative QCD, play an increasingly significant role at higher energies. These hard scattering events follow inherently non-thermal distributions and are not easily incorporated within a purely thermal framework. Consequently, the presence and growing influence of such processes necessitate larger values of q to adequately describe the observed particle spectra. This reflects a shift away from equilibrium behavior, consistent with the increase in q observed in our analysis.

Figure 2d illustrates the relationship between $N_0$ and $|\eta |$, showing increase in $N_0$ with increasing $|\eta |$. Furthermore, $N_0$ attains higher values at greater center-of-mass energies ($\sqrt{s}$), reflecting the enhanced particle production at higher collision energies and larger pseudorapidities.

The $\eta$-dependence of $\langle p_T \rangle$ (Fig. 2e) parallels $T_0$, declining by $\sim 30\%$ from mid- to forward-$\eta$. This corroborates the link between energy density, radial flow, and transverse momentum²¹. The $\sqrt{s}$-scaling ($\langle p_T \rangle \propto \ln \sqrt{s}$) reflects increased parton multiple scattering at higher energies²⁰. Concerning the observed trend of the mean transverse momentum $\langle p_T \rangle$ as a function of collision energy, the apparent discrepancy can be understood as a transition from equilibrium-dominated dynamics to non-equilibrium-driven behavior. The saturation of the kinetic freeze-out temperature suggests that the system has reached a thermalization limit, beyond which additional energy is diverted into other degrees of freedom rather than contributing to random thermal motion. Similarly, the saturation of the average transverse flow velocity indicates a limit in hydrodynamic expansion, likely caused by viscous damping or reduced system lifetimes that inhibit further buildup of flow. The temporal and spatial scales, along with the finite interaction cross-sections of the hadronic system, impose constraints on both collective flow and thermalization, ultimately giving rise to the observed saturation phenomena. In contrast, the continuous increase of $\langle p_T \rangle$ with collision energy is driven by mechanisms that are not constrained by equilibrium conditions. Chief among these are perturbative QCD (pQCD) processes, whose influence becomes increasingly dominant at higher energies. In the high-$p_T$ tail of the momentum spectrum, hard parton-parton scatterings generate jets and mini-jets, whose production rates grow rapidly with increasing collision energy—from 900 GeV to 7 TeV and beyond. Unlike collective flow, these hard processes are not governed by the system’s thermal or geometric properties. Instead, their momentum scales are determined by fundamental QCD couplings and the available phase space. As a result, pQCD processes can continue to enhance $\langle p_T \rangle$ independently of the saturated collective dynamics, since they do not possess an inherent upper limit on momentum transfer.

Figure 3 displays the correlations among the parameters extracted from the modified Tsallis distribution. Figure 3a shows a direct correlation between $T_0$ and $\beta _T$, where one can see that with increasing the latter the earlier also increases. The values of $T_0$ and $\beta _T$ have a positive correlation. This is in line with the early universe when the system was rapidly expanding and sufficiently heated. It should be noted that different models may produce different results (trends and values of parameters). The Ref.²⁸ has a negative correlation between $T_0$ and $\beta _T$ where they used the Boltzmann Gibbs Blastwave model. Here, in the current study, we used a different model called the modified non-extensive Tsallis model, which brings up the positive correlation between the said parameters. Our results are consistent with the results obtained by K. Olimov et al.^27,29. Furthermore, the current correlation is also consistent with many of our previous publications^{30,31,32,33,34}. Both positive and negative correlations carry physical significance. The negative correlation can be interpreted as indicative of a longer system lifetime (i.e., a lower degree of excitation), associated with a lower $T_0$, alongside a more rapid expansion (stronger radial flow), corresponding to a higher $\beta _T$. Conversely, the positive correlation observed in our study may reflect a scenario with a higher excitation degree, resulting in a higher $T_0$, along with a rapid expansion (strong squeeze), also characterized by a larger $\beta _T$.

Figure 3b shows a negative correlation between $T_0$ and q. This renders that the parameters $T_0$ and q in a system show stronger correlations between its components as it becomes more non-extensive (q increases). The system’s overall dynamics are impacted by the correlations, which lowers the temperature needed for freezeout. Where particles with smaller q correspond to larger $T_0$ confirming that they are closer to equilibration and thermalization. Moreover, Fig. 3c is used to represent the negative correlation among different values of $\beta _T$ and q. The interaction of the QGP’s expansion dynamics with the statistical characteristics of the particle distributions inside of it results in the negative correlation between the $\beta _T$ and the parameter q. Because of the departure from thermal equilibrium, the parameter q rises as the system cools and expands while $\beta _T$ falls. This negative correlation can be explained by the fact that the parameter q is influenced by the expansion dynamics, which also affect the distribution of particles in momentum space. On the other hand, the parameter q may also affect the system’s overall flow patterns. Figure 3d displays the direct correlation between $T_0$ and $\langle p_T \rangle$ which shows that the highly excited system has greater $\langle p_T \rangle$. Although $\langle p_T \rangle$ generally increases with $T_0$, it is not solely determined by it. $\langle p_T \rangle$ is influenced by both the temperature $T_0$ and the radial flow, as well as their interplay. A system with a moderate temperature but strong radial flow can still exhibit a high $\langle p_T \rangle$ due to the enhanced collective motion. Figure 3e represents the inverse correlation between q and $\langle p_T \rangle$, providing evidence that the system closer to thermal equilibrium has larger $\langle p_T \rangle$ i.e., highly excited. Figure 3f shows the direct correlation between $\beta _T$ and $\langle p_T \rangle$, confirming the greater $\langle p_T \rangle$ for the rapidly expanding system, as expected.

We have calculated the Pearson correlation coefficients from the parameter table using the formula:

$$\begin{aligned} r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} \end{aligned}$$

(4)

Values are computed separately for each collision energy ($0.9$, $2.36$, and $7~\text {TeV}$) using all $\eta$ bins.

Figure 3 explores interdependencies between the extracted parameters ($T_0$, $\beta _T$, q, $\langle p_T \rangle$). The Pearson correlation coefficients calculated using Eq. (4) are given in Table 2.

Table 2 Pearson correlation coefficients between model parameters given in Fig. 3 at the three collision energies.

• 1. $T_0$–$\beta _T\,($ Fig. 3a): Strong positive correlations ($r = 0.997$ at $0.9~\text {TeV}$, $r = 0.993$ at $2.36~\text {TeV}$, $r = 0.994$ at $7~\text {TeV}$) confirm that higher freeze-out temperatures correlate with stronger transverse flow. This suggests that, even in small systems like $pp$ collisions, thermal excitation is closely tied to collective expansion dynamics.

• 2. $T_0$–q (Fig. 3b): Strong negative correlations ($r = -0.990$ at $0.9~\text {TeV}$, $r = -0.993$ at $2.36~\text {TeV}$, $r = -0.997$ at $7~\text {TeV}$) indicate that greater deviation from thermal equilibrium (larger q) is consistently associated with lower kinetic freeze-out temperatures. This reflects how increasing non-extensivity corresponds to a more disordered, less equilibrated freeze-out scenario.

• 3. $\beta _T$–q (Fig. 3c): Strong anti-correlations ($r = -0.991$ at $0.9~\text {TeV}$, $r = -0.988$ at $2.36~\text {TeV}$, $r = -0.992$ at $7~\text {TeV}$) suggest that systems with weaker collective flow tend to be more non-extensive. This highlights a strong inverse relationship between flow strength and statistical equilibrium.

• 4. $\langle p_T \rangle$ systematics (Fig. 3d–f): $T_0$–$\langle p_T \rangle$: Strong positive correlations ($r = 0.995$, 0.978, 0.989 at 0.9, 2.36, and $7~\text {TeV}$, respectively) confirm that systems with higher freeze-out temperatures yield harder momentum spectra. q–$\langle p_T \rangle$: Strong inverse trends ($r = -0.992$, $-0.949$, $-0.977$) indicate that as the system approaches equilibrium ($q \rightarrow 1$), the mean transverse momentum rises—consistent with a more thermally equilibrated and collectively expanding system. $\beta _T$–$\langle p_T \rangle$: Very strong correlations ($r = 0.994$, 0.978, 0.990) show that increased transverse flow significantly enhances $\langle p_T \rangle$, reinforcing the role of flow in boosting particle momenta.

These strong and consistent correlations across all energies reveal an interconnected thermal and collective behavior in high-energy $pp$ collisions. The freeze-out temperature, flow velocity, and non-extensivity parameter are not independent but evolve together, shaping the final-state momentum distribution. The $\langle p_T \rangle$ emerges as a natural outcome of this interplay, summarizing the system’s excitation, expansion, and approach to equilibrium. Altogether, the results support the presence of significant, though subdominant, collective dynamics even in small collision systems.

Summary and conclusion

The present study investigates the $\eta$ and energy dependence of $p_T$ spectra in $pp$ collisions at $\sqrt{s} = 0.9$, 2.36, and 7 TeV using a modified Tsallis distribution. The results are summarized as follows:

• The modified Tsallis function provides an excellent fit to the measured $p_T$ spectra across all $\eta$ bins and collision energies, with residuals within 10% and $\chi ^2/\text {ndof} \sim 1.0$–1.5.

• The $T_0$ decreases with $|\eta |$, indicating lower energy densities in fragmentation regions, while increasing moderately with $\sqrt{s}$, with diminishing returns at higher energies.

• The average $\beta _T$ follows a similar $\eta$ and $\sqrt{s}$ dependence as $T_0$, with a plateau suggesting saturation effects in collective dynamics at high energies.

• The parameter $q$ increases with both $|\eta |$ and $\sqrt{s}$, suggesting enhanced non-equilibrium behavior in forward rapidities and at higher collision energies due to limited thermalization and the dominance of hard processes.

• The multiplicity scaling factor ($N_0$) increases with both $|\eta |$ and $\sqrt{s}$, consistent with higher particle production in forward directions and at higher collision energies.

• The $\langle p_T \rangle$ decreases with $|\eta |$ and increases logarithmically with $\sqrt{s}$, showing the combined effects of thermal excitation and high-$p_T$ processes such as mini-jet production.

• Strong parameter correlations are observed:

  • $T_0$ positively correlates with $\beta _T$ and $\langle p_T \rangle$, indicating simultaneous thermal and collective excitation.

  • $q$ shows strong negative correlations with both $T_0$ and $\beta _T$, consistent with reduced equilibrium and collectivity in systems with higher $q$.

  • $\beta _T$ and $\langle p_T \rangle$ exhibit a strong positive correlation, underscoring the role of flow in shaping transverse dynamics.

• The observed saturation of $T_0$ and $\beta _T$, contrasted with the continued growth of $\langle p_T \rangle$, suggests that non-equilibrium processes, including hard QCD scatterings, increasingly dominate particle production at high energies.

This analysis demonstrates that even in small systems like $pp$ collisions, thermal and collective effects play a significant role. The interplay among temperature, flow, and non-extensivity governs the observed momentum distributions, and their inter-correlations point to a unified, though non-equilibrium, picture of particle production dynamics in high-energy collisions.