Introduction

In recent years, due to the fast progress of novel information technology, the requirement for increased integration density in photonic instruments has increased quickly1. Transverse electromagnetic (EM) waves spreading along the metal–insulator junction with declining amplitude are called surface plasmon polaritons (SPPs)2,3,4. Since surface plasmon-based structures have unbelievable features, such as manipulating light at a sub-wavelength scale and overcoming the diffraction limit, they have been widely utilized in different applications5,6,7. In the past few years, researchers have proposed numerous optical devices using SPP structures such as plasmonic filters8,9, demultiplexers10,11,12, splitters13,14, sensors15,16,17, couplers18, absorbers19,20, modulators21,22, logic gates23,24, switches25,26, and so on.

Plasmonic refractive index (RI) sensors have attracted exceptional consideration for detecting RI changes in materials27,28. This is because of their high sensitivity to their surrounding medium and local field increment29. Till now, researchers have designed and investigated numerous surface plasmon-based sensors using various structures and resonator shapes. In30, a plasmonic RI sensor (RIS) using a rectangular resonator incorporating metal nanorods with two baffles and a metal–insulator–metal (MIM) plasmonic waveguide (WG) for biological applications is proposed. In this structure, the sensitivity is 2963.73 nm/RIU, and the figure of merit (FoM) equals 5.1 RIU-1. In another approach31, a nano-plasmonic structure for RI and temperature sensing is designed. The suggested structure comprises a stub cavity, a ring-shaped cavity with a stub, and an MIM plasmonic WG. Its transmission curve has a Fano resonance (FR) mode produced by the interaction between the transmission spectra of the ring-shaped cavity and the stub cavity. The sensitivity and FoM are 1420 nm/RIU, and 76.76 RIU-1, respectively. Also, its temperature sensitivity is 0.8 nm/°C.

Other resonator shapes that have been used to design sensor structures are circular resonators. A plasmonic sensor utilizing two circular resonators and an MIM WG is designed in32. The sensor structure proposed is used for temperature and RI sensing with the temperature and RI sensitivity values of 0.336 nm/°C and 737.71 nm/RIU, respectively. In33, a surface plasmon-based sensor is presented by coupling an MIM plasmonic WG to a U-shaped ring resonator with three stub resonators. This topology generates a band stop spectrum for sensing applications with a sensitivity of 2900 nm/RIU and a FoM of 55.76 RIU-1. It is worth mentioning that there are other various structures for designing plasmonic sensors such as elliptical resonators34, split ring resonators35, triangular resonators36, and so on.

It is worth noting that various structures proposed for optical sensors can generate different transmission spectrum shapes. For example, by coupling two plasmonic WG to a resonator from both sides, a bandpass spectrum is formed37, and a bandstop spectrum is formed by coupling one plasmonic WG to a resonator from one side38. Furthermore, stub-coupled MIM WG systems can produce a Plasmon-induced transparency (PIT) spectrum39. Another transmission spectrum type is the FR spectrum caused by interference between two scattering amplitudes40. The first is because of scattering within a continuum of states (the background process), and the other is caused by an excitation of a discrete state (the resonant process).

To increase the sensitivity of plasmonic sensors with bandpass, bandstop, and PIT resonance modes, the quality factor (Q-factor) of such modes must be increased. To achieve a high Q-factor value, the resonance mode bandwidth should be as narrow as possible34 which has some challenges. The first is that reducing bandwidth is possible to some extent, as it has effects such as increasing losses and reducing resonance transmittance. Also, this issue needs high fabrication accuracy which complicates the fabrication process. Since the transmission spectrum of an FR mode is an asymmetric line and usually has one transient edge, achieving a high-sensitivity sensor with an FR spectrum is easier than sensors with other types of spectra. Therefore, this paper uses a plasmonic structure that can produce an FR spectrum.

Most referenced optical plasmonic sensors have been analyzed using EM simulation software, which is based on time-consuming and repetitive techniques including finite element method (FEM) and finite-difference time-domain (FDTD) method. Using such numerical methods involves extensive trial-and-error searches over structural dimensions. Accordingly, each parameter must be validated and optimized. For this purpose, utilizing machine learning (ML) methods such as regression analysis and neural networks is important41,42,43. ML methods can show the behavior of optical sensors by predicting their transmittance. The relationship between the independent and dependent parameters (wavelength and transmittance) can be observed by regression analysis. Furthermore, to specify patterns over time under various situations, transmittance values or frequency responses, which are data variables, are analyzed with time series analysis. As a result, the ML method is used to analyze the suggested topology.

Here, an optical surface plasmon-based structure is presented and analyzed for RI sensing applications. The presented topology consists of an MIM WG, a U-shaped resonator (USR), and an inverted U-shaped resonator (IUSR). To simulate the structure, the FDTD is utilized. The results show that the designed structure generates two FR modes with sensitivity values of 571.4 and 872.9 nm/RIU for the lower and upper FR modes, respectively. Also, the maximum FoM value is obtained for the lower FR mod that equals 14,987 RIU-1. Furthermore, ML analysis is used to predict transmittance behavior. In other words, utilizing the Extreme Randomized Tree (ERT) regression model (RM) the transmittance values at intermediated wavelengths are forecasted. Using this method reduces the needed resources by 90%.

The next parts are ordered as follows: Part 2 shows the design procedure and FDTD simulation results of the suggested sensor. The ML RM is introduced and used for the presented structure in part 3. Part 4 compares the results with other similar works, and the last part is the conclusion.

Design procedure and simulation results

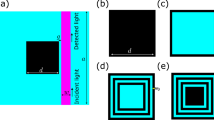
Figure 1 plots the designed surface plasmon-based RIS structure. The suggested structure comprises a USR coupled to an IUSR, both coupled to an MIM WG, and it is symmetrical about the centerline. The values of the defined geometrical dimensions equal l1 = 75, l2 = 40, l3 = 50, l4 = 100, l5 = 240, s = 100, g = 25, and w = 100 (all in nm). The insulator and metal materials utilized for the presented sensor are air and silver, respectively. The air material has the relative permittivity of εd = 1. Furthermore, the Drude model defines the relative permittivity of silver44.

$$\upvarepsilon_{{\text{m}}} \left( \upomega \right) = \upvarepsilon_{\infty } - \frac{{\upomega_{{\text{p}}}^{2} }}{{\upomega \left( {\upomega + {\text{j}}\upgamma } \right)}}$$
(1)
Fig. 1
figure 1

The schematic of the RIS.

Full size image

In Eq. 1, ε∞ = 3.7 denotes the medium dielectric constant for the infinite frequency. Also, \({\omega }_{p}=1.38\times {10}^{16}\) Hz is the bulk plasma frequency, ω shows the angular frequency of incident light, and \(\gamma =2.73\times {10}^{13}\) Hz demonstrates the electron collision frequency.

Figure 2 illustrates the transmission curve of the proposed RIS (Fig. 1), which is obtained using the FDTD method. It is found that two FR modes with sharp edges appear in a wide wavelength range. In Fig. 2, the FR peaks and valleys are labeled with λp1 = 659 nm, λp2 = 871 nm, and λv1 = 598 nm, λv2 = 891 nm, respectively. The transmittance values of λp1 and λp2 are 59.9% and 70.8%, respectively. Furthermore, the transmittance values of λv1 and λv2 are almost near zero.

Fig. 2
figure 2

Transmission spectrum of the RIS58.

Full size image

In the next step, the field profiles of \(|{H}_{z} |\) for the RIS at peaks and valleys of the FR modes are represented in Fig. 3. As observed, two valley wavelengths of 598 and 891 nm do not achieve the right (output) port, while the peak resonance wavelengths of 659 and 871 nm transmit to this port. As observed in Fig. 3b, the energy at λp1 = 659 nm is mainly concentrated within both USR and IUSR. Furthermore, Fig. 3c shows that for λp2 = 871 nm, the most energy is only focused on the USR. It means that both resonators play a key role in the formation of the first peak, while the USR has a more significant influence on the formation of the second peak. In the following, this issue can be seen more clearly by calculating the transmission spectra of each resonator and waveguide separately.

Fig. 3
figure 3

Field profile of \(\left|{H}_{z}\right|\) for the RIS at (a) λv1, (b) λp1, (c) λp2, and (d) λv2. (These figures are obtained by the "Lumerical 2020 R2.4. FDTD solutions" software)58.

Full size image

To more accurately investigate the two generated FR modes, the two building block structures of the MIM WG coupled to IUSR (Structure 1) and USR (Structure 2) are also simulated separately, and their transmission spectra are compared to the transmission curve of the proposed RIS in a single figure. Figure 4a,b show the schematic topologies of Structure 1 and Structure 2, respectively. Also, the transmission curves of the building blocks and the main RIS are presented in Fig. 4c.

Fig. 4
figure 4

The schematic of (a) Structure 1, (b) Structure 2. (c) The transmission spectra of Structure 1, Structure 2, and the RIS58.

Full size image

The transmission curve of Structure 1 (IUSR coupled to the MIM WG) is presented by a green dotted line. It can be observed that Structure 1 creates a wide notch at a wavelength of 620 nm. Also, the transmission curve of Structure 2 (USR coupled to the MIM WG) is displayed by a black dot-dash line. As seen, two narrow notches at wavelengths of 634.2 and 879.4 nm are generated by Structure 2.

The suggested RIS is designed by combining both basic structures (Structure 1 and Structure 2), and its transmission spectrum is illustrated by an orange solid line. By the interaction between the broadband mode of Structure 1 and the narrowband modes of Structure 2, the two FR modes mentioned above are produced.

After designing the sensor structure, its RI sensing performance is examined. The transmission spectra of various filling media with the RI from 1 to 1.05 for Δn = 0.01 is presented in Fig. 5a. It indicates that when the RI of the analyte (insulator media) is increased, the transmittance curve shifts to higher wavelengths, regularly. In order to quantitatively evaluate optical sensors, various parameters have been defined. One of the most important parameters is sensitivity which can be given by45:

$$S = \Delta \lambda /\Delta n\;\left( {\frac{{{\text{nm}}}}{{{\text{RIU}}}}} \right)$$
(2)
Fig. 5
figure 5

(a) The transmission spectra of the RIS for RI changes from 1 to 1.05, (b) Relationship between the wavelengths of λv1 and various values of the RI, (c) Relationship between the wavelengths of λv2 and various values of the RI58.

Full size image

In Eq. 2, Δλ and Δn demonstrate the shift of the resonance wavelength and the variation of the RI, respectively. Also, RIU is the RI unit. To calculate the sensitivity of the RIS, the data points of λv1 and λv2 are fitted by linear functions (Fig. 5b,c). The obtained linear functions for λv1 and λv2 are given in Eqs. 3 and 4, respectively.

$${\lambda }_{v1}=571.4 n+26.22$$
(3)
$${\lambda }_{v2}=872.9 n+18.1$$
(4)

The slops of the linear functions (Δλ⁄Δn) are the RI sensitivity values at valley wavelengths. It can be concluded that the RI sensitivity for λv1 and λv2 are 571.4, and 872.9 nm/RIU, respectively. As observed, sensitivity is a parameter that specifies the value of wavelength shift for a determined RI variation, and it cannot show the resolution of a sensor34. As a result, another more comprehensive parameter to evaluate the sensors’ performance is the FoM parameter. This factor is defined as Eq. 5 for sensors with FR spectra45.

$$FoM = \Delta T/\Delta n.T\;\left( {{\text{RIU}}^{ - 1} } \right)$$
(5)

In Eq. 5, ΔT, Δn, and T are the change of the transmittance, the change of the RI, and the transmittance of the system, respectively. Based on Eq. 5, for the RIS designed in this paper, the FoM distribution of the wavelength is obtained (Fig. 6). Figure 6 shows that the maximum FoM value is obtained for λv1 = 598 nm which equals 14,993 RIU-1. It is worth mentioning that the FoM value obtained for λv2 = 891 nm is 2178 RIU-1. Therefore, the first valley wavelength with the highest FoM is considered for the sensing application of the designed RIS. Considering the remarkable sensitivity and FoM values obtained for the presented topology, it can be a suitable option for RI sensing.

Fig. 6
figure 6

The FoM values of the RIS58.

Full size image

Since the geometrical parameters of the suggested RIS can affect its transmission properties, the transmission performance for numerous values of some parameters (l1, l2, l3, and g) is investigated here. The first column of Fig. 7a,d,g,j displays the transmission curves of the RIS for various values of l1, l2, l3, and g, respectively. Furthermore, the relationship between the FoM and various values of mentioned parameters for λv1 and λv2 are shown in the second column of Fig. 7b,e,h,k and the third column of Fig. 7c,f, i,l, respectively. Figure 7a displays that when the value of l1 is increased, the locations of both FR modes are relatively constant, while Fig. 7b,c demonstrate that increasing l1 increases the FoM of λv1 initially and then decreases, and decreases the FoM of λv2. As discussed, the wavelength of λv1 is chosen for sensing performance, and on the other hand, although the FoM of λv2 also changes, the range of these variations is much smaller than the FoM of λv1. Consequently, the value of 75 nm for l1, which causes the highest FoM for λv1 is chosen.

Fig. 7
figure 7

Transmittances of the RIS for various values of (a) l1, (d) l2 (g) l3, (j) g. Relationship between the FoM and various values of (b) l1, (e) l2 (h) l3, (k) g for λv1. Relationship between the FoM and various values of (c) l1, (f) l2 (i) l3, (l) g for λv258.

Full size image

Figure 7d shows that increasing l2 shifts the first valley wavelength to the lower wavelengths, while the location of the second valley wavelength is constant. Also, by increasing l2, the highest FoM of λv1 is obtained at l2 = 40 nm and the FoM of λv2 increases (Fig. 7e,f). Therefore, for the same reasons as in the previous case (variations of l1), l2 = 40 nm is chosen. Variations of l3 are demonstrated in Fig. 7g–i. Figure 7g demonstrates that changing the l3 value varies the locations of both FR modes. In other words, variations of l3 result in a plasmonic structure with tunable resonance mods. The variations of the FoM of λv1 and λv2 are similar to the previous case (l2). Figure 7h,i show these cases. As a result, l3 = 50 nm is chosen. The gap of g is the last parameter in which its variation is studied (Fig. 7j–l). Figure 7j indicates that increasing the g value shifts the FR modes to the higher wavelengths. Furthermore, the FoM values of both FR modes increase initially and then decrease when the g value is increased (Fig. 7k,l). The highest FoM values for both modes occur at g = 25 nm which is selected.

Machine learning analysis

As known, using FDTD and FEM simulation methods for optical systems is time-consuming and needs extra memory, computational power, and processing time. Therefore, utilizing a method that can reduce the resources and time required to simulate is necessary. ML techniques such as the ERT RM can solve these challenges by predicting essential parameters and specifying missing values. Therefore, this section discusses the RMs briefly and shows how these techniques can reduce the needed resources for the proposed sensor structure by 90%. Regression analysis specifies dependent parameter values (transmittance) according to independent parameter values (wavelength), and uses three steps as follows:

Step 1: Simulating the RIS utilizing a larger wavelength’s step size.

Step 2: Training the RM with the simulation data.

Step 3: Predicting the transmittance of middle wavelengths utilizing the trained model.

Two vital parameters for the regression analysis used in this paper (ERT model) are the minimum needed sample size for node splitting (nmin) and the number of randomly selected properties at each node (K). The parameter of K = 1……p is used to determine the property strength applied to compute the goal. Here p shows the independent variables utilized to anticipate the goal parameter. To have more precision, the K value should be larger46.

In this paper, to forecast the transmittance, six parameters are used. They are l1, l2, l3, g, n, and wavelength (λ). It is worth mentioning that the value of nmin is considered 3. This can be explained below. First, all values between 2 and 10 are considered for nmin, and no significant difference is observed in the outputs. Since different figures for various values of five selected parameters (l1, l2, l3, g, and n) are given in the following, to reduce the number of similar figures and reduce the number of pages, only one case (nmin = 3) is reported. It is worth mentioning that the scope of K is (1 ≤ K ≤ total number of attributes). Since the number of input features of the problem equals one (we only have one input that is wavelength (λ)), k = 1 is considered here. In the ERT RM, a set of "m" unpruned regression trees is produced. They are RT1, RT2, RT3, …, RTm. By calculating the total of each tree’s forecasts and taking the arithmetic mean of the outcomes, the final prediction is attained. Equation 6 demonstrates it47.

$$Predicted \,output=\sum_{j=1}^{m}{RT}_{j}(x)$$
(6)

In Eq. 6, m is the number of trees, and x demonstrates the value of the independent parameter. Some performance indices may be utilized to calculate the accuracy of the trained ERT RM. These indices are R-Square Score (R2S), Adjusted R Square Score (Adj-R2S), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) which are expressed by Eqs. 7–1047

$${R}^{2}s=1-\frac{{\sum }_{i=1}^{N}{({Predicted\, Value}_{i}-{Actual\, Value}_{i})}^{2}}{{\sum }_{i=1}^{N}{({Actual\, Value}_{i}-{Average\, Target\, Value}_{i})}^{2}}$$
(7)
$${Adj-R}^{2}s=1-\frac{(1-{R}^{2}s)(N-1)}{N-p-1}$$
(8)
$$RMSE=\sqrt{\frac{1}{N}{\sum }_{i=1}^{N}{{(Actual\, Value}_{i}-{Predicted\, Value}_{i})}^{2}}$$
(9)
$$MAPE=\frac{1}{N}{\sum }_{i=1}^{N}\left[\frac{{Actual\, Value}_{i}-{Predicted\, Value}_{i}}{{Actual\, Value}_{i}}\right]*100$$
(10)

In these Equations, N illustrates the total number of samples that were used in the validation of the RM. As mentioned, the ERT RM is used to predict the transmission value in this work. This model is applied for the test case of 10% (TC-10). Two distinct subsets of the FDTD-generated data are utilized in TC-10. In the first subset, 10% of the simulation data are selected for training the ERT RM. It is worth mentioning that these data are chosen with equal row spacing. The other 90% of the simulation data are considered for the accuracy of the model’s predictive (the second subset).

Figure 8 displays the heat map of the Adj-R2S of the ERT RM for nmin = 3. It is worth noting that in this figure, all values are rounded to four decimal places, and the exact values ​​are shown in parentheses. Adj-R2S for different values of l1, l2, l3, g, and n are depicted in Fig. 8a–e, respectively. As observed, Adj-R2S values are close to 1. As a result, it can be said that high prediction accuracy is obtained. In other words, a tight link exists between simulated (actual) and predicted values.

Fig. 8
figure 8

Adj-R2S of ERT RM using various values of (a) l1, (b) l2, (c) l3, (d) g, and (e) n for TC-10.

Full size image

Figure 9 illustrates the predicted values by the ERT RM versus the actual values of the transmission curves for various values of l1 (Fig. 9a), l2 (Fig. 9b), l3 (Fig. 9c), g (Fig. 9d), and the RI of n (Fig. 9e). The obtained results for all parameters indicate that predicted and actual values are matched. Therefore, the high accuracy of the prediction is also concluded from this figure.

Fig. 9
figure 9

Predicted vs actual values using various values of (a) l1, (b) l2, (c) l3, (d) g, and (e) n for TC-10.

Full size image

The RMSE generated for various values of all aforementioned parameters (l1, l2, l3, g, and n) using comparative bar charts are demonstrated in Fig. 10. Figure 10a,d,e displays that the RMSE value less than 0.0018 is obtained for all various values of l1, g, and n. Furthermore, for all different values of l2 and l3, the RMSE value less than 0.002 is attained. In fact, these figures show the low error prediction error.

Fig. 10
figure 10

RMSE using various values of (a) l1, (b) l2, (c) l3, (d) g, and (e) n for TC-10.

Full size image

Finally, the predicted versus the simulated transmittances of the suggested RIS are shown in Fig. 11. This figure shows that both curves are in good agreement. Consequently, using the ML-based ERT RM can reduce the simulation time for designing the plasmonic RIS by 90%.

Fig. 11
figure 11

Predicted vs simulated transmission spectra of the RIS58.

Full size image

Comparisons and discussions

To design the RIS presented here, the 2D FDTD simulation technique is used. This means that the thickness of the silver slab is considered to be infinite. As known, 3D simulations are more time-consuming and more complex than 2D simulations. Accordingly, it is more prevalent to use 2D topologies for plasmonic structures48,49,50. It is worth mentioning that most such topologies can be generalized to 3D structures with finite thicknesses. As a result, the suggested surface plasmon-based sensor is also realized based on 2D simulations. Furthermore, air with the dielectric permittivity of 1 and silver are used as insulator and metal materials in the proposed sensor. The dielectric permittivity of silver is characterized by the Drude model. As known, the Drud model is one of the well-known models used to describe the dielectric coefficient of silver in most works, and it can be said that this model can provide an acceptable approximation of the behavior of silver metal in practical situations. The perfectly matched layer (PML) boundary condition is utilized to surround the simulation domain. The thickness of the PML is 200 layers. Furthermore, the mesh size for the total structure equals 2 nm.

It is worth saying that it is currently not possible for us to confirm the obtained results by fabrication data. Since it is not possible to fabricate such devices in our country, the idea of realizing a plasmonic sensor is only proposed in this paper, and it tries to carefully examine the performance of the suggested topology using the well-known FDTD method. Furthermore, ML analysis is utilized to predict transmittance behavior. In other words, using the ERT RM the transmittance values at intermediated wavelengths are forecasted. Applying this method reduces the needed resources by 90%.

In this section, the rest is to compare the proposed design with other similar sensors. For this purpose, Table 1 is suggested to compare the important parameters that include the sensitivity (S) and the maximum value of the FoM (FoMmax). The sensitivity and FoM values of all references in this table are calculated by Eqs. 2 and 5, respectively.

Table 1 Comparisons of the suggested RIS with other papers.
Full size table

As discussed, although sensitivity can be a main parameter for the sensor’s performance, it cannot show the sensor’s resolution, and the FoM parameter is more comprehensive. Therefore, having a high FoM value is more important. For example, Table 1 demonstrates that the sensor proposed in Ref.51 has the highest sensitivity value among the works, while it does not have a high FoM value compared to other works. It is clear that the RIS proposed in this paper simultaneously has optimal features such as high sensitivity and FoM values compared to other similar works. Accordingly, the results indicate that the sensor topology presented here may be applied to numerous RI sensing demands in biomedical, chemical, and environmental fields.

Conclusion

In summary, this article presents a surface plasmon-based RIS composed of a USR, an IUSR, and an MIM WG. According to the FDTD simulations, the design produces two FR modes. The most suitable values of sensitivity and FoM are 571.4 nm/RIU and 14,987 RIU-1 at the wavelength of λv1 = 598 nm. Also, the ML-based ERT RM is applied to learn transmission performance and forecast transmittance values for middle wavelengths. The Adj-R2S nears1, illustrating the prediction efficiency of the ERT RM in calculating the transmittance values in TC-10. Applying this ML-based method reduces needed resources and simulation time by 90%. The proposed RIS designed with the ERT model can be used for RI measurement in biomedical, chemical, and environmental applications.