Introduction

AS the official language of China, Chinese plays a vital role in global economic and cultural exchanges1. Its significance spans various domains, including business, tourism, and employment, leading to a growing number of individuals worldwide embracing Chinese as a second language (L2). Consequently, following English, Chinese has become the second most widely used language globally. China is a multiethnic nation characterized by its diverse ethnic groups. Each group preserves its native language while learning and using Chinese as the official language for everyday communication. For international students and ethnic minorities in China, acquiring Mandarin (the official spoken form of Chinese) is recognized as an essential aspect of L2 learning.

For learners of Mandarin as L2, pronunciation is profoundly influenced by their native language (L1). Mandarin’s phonemes, tones, and prosody pose considerable challenges for these learners. Unlike non-tonal languages such as English, German2, Uyghur, and Kazakh, Mandarin is a tonal language that features four distinct tones: High-Level (Tone1), Low-Rising (Tone2), Falling-Rising (Tone3), and High-Falling (Tone4). These tones are crucial for differentiating word meanings and grammatical structures, making mastery of Mandarin tones a significant hurdle in L2 acquisition2. In light of this, developing tools for detecting and analyzing tone pronunciation errors is of immense academic and practical value. Such tools can empower L2 learners to swiftly and effectively acquire and master the nuances of Mandarin tones.

Currently, the primary methods for facilitating the learning of Mandarin tones include tone pronunciation error detection2,3,4 and analysis5,6. The detection process focuses on identifying tonal inaccuracies through tone recognition. Research in this domain essentially utilizes statistical methods7, deep learning techniques, or neural networks8,9,10 to spot tone pronunciation errors throughout the pronunciation learning journey. Traditional statistical approaches typically employ Hidden Markov Models (HMM)3,11 to construct tone models, with accuracy often improved by refining tone features12,13 or fine-tuning them14,15,16. In contrast, deep learning and neural network techniques can boost performance by adjusting network architectures17 or modifying input data4,17,18. Recently, some studies19 have adopted end-to-end tone pronunciation error detection models, using specific spectrogram data as inputs and integrating contextual features to enhance detection accuracy. On the other hand, tone pronunciation error analysis examines the discrepancies between learners’ tone productions and standard pronunciations, utilizing tone labeling or analysis tools20 such as Praat5. These analyses aim to enhance language learning outcomes for students rather than refine the analysis tools themselves. However, these tools often depend on extensive manual annotation, which can compromise objectivity and lead to subjective results.

Despite the extensive research on tone pronunciation error detection and analysis, several limitations are apparent. First, most studies depend on publicly available corpora, which can vary significantly, and there is currently no dedicated corpus specifically designed for tone research. Second, the tonal features employed for computation and modeling lack standardization. While some studies utilize sophisticated acoustic features, such as Mel Frequency Cepstral Coefficients (MFCC) and Mel spectrograms, others focus primarily on fundamental frequency (F0) features or incorporate additional prosodic elements. This diverse use of features across different models leads to inconsistent results, complicating the comparison of their efficacy. Besides, there is a notable absence of methods or tools for tone pronunciation error analysis that employ automatic annotation. Manual annotation is often costly, inefficient, and prone to subjectivity. Consequently, research in this area remains fragmented. However, Mandarin learners would benefit significantly from integrated tools that simultaneously address detecting and analyzing tone pronunciation errors.

To tackle these issues, namely the lack of a specialized corpus for tone research, the absence of unified tonal features, and the need for a combined approach to tone pronunciation error detection and analysis, we have developed a dedicated Mandarin corpus for tone research and have proposed a method for computing tonal features. Building on this foundation, we integrated large-scale image recognition models to create a tone pronunciation evaluation method based on a Siamese network (SN)21,22,23,24,25,26,27. This method has so far been preliminarily applied in the field of speech, used to predict the discrepancy of speech in different dialects26 or for the discrepancy of speech pronunciation27. We further employed this model to evaluate the tones of each syllable in continuous speech. By determining the accuracy of the tones and providing a discrepancy score, the proposed method enables Mandarin L2 learners to compare their pronunciation with the correct tones. To validate the effectiveness of our proposed method, we employed various subjective and objective experimental analyses and compared the results across different models. The originalities presented in this article are as follows:

  • We introduced an innovative Mandarin tone pronunciation error detection model based on an SN to evaluate whether a pair of tones is identical and quantify the degree of discrepancy between them.

  • We presented two distinct features for tone detection and analysis: the 40D vector (1D feature) and the \(40 \times 50\) binary pixel image (2D feature), enhancing the model’s ability to capture tonal nuances.

  • We developed a comprehensive, large-scale corpus tailored explicitly for tone detection and analysis research, providing a valuable resource for advancing this field.

  • Additionally, we proposed specifically designed subjective and objective evaluation methods for assessing tone differences, enabling a more nuanced and insightful analysis of tone pronunciation.

The article is structured as follows: “Method” section details the proposed method. We present our experimental procedures in “Experiments” section, followed by the results in “Results” section. Subsequently, “Discussion” section analyzes the findings. Finally, we conclude the article in “Conclusion” section and offer suggestions for future research directions.

Method

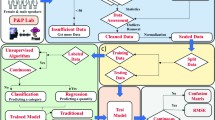
The proposed tone assessment method, which utilizes an SN integrated with two large-scale image recognition models, is illustrated in Fig. 1. The SN is employed in this approach to compute the paired tones’ discrepancies, while ResNet-18 extracts feature information from each tone. To facilitate the experiment, we have developed a dedicated corpus and implemented a method for tone feature extraction. The new tone feature is represented as a 40-dimensional (40D) vector or two-dimensional (2D) matrix, significantly enhancing the performance of the integrated model.

Fig. 1
figure 1

The framework of the proposed ResNet-based SN.

Full size image

Building a corpus for tone assessment in Mandarin

Mandarin can be categorized into standard-accented and non-standard-accented, reflecting the influence of dialects and one’s mother tongue. In everyday situations, most speakers, including most L2 learners, use non-standard-accented Mandarin, while trained broadcasters typically use standard-accented Mandarin. Speakers with non-standard-accented Mandarin exhibit a range of proficiency levels, leading to variations in tone pronunciation and often resulting in subtle tone features that may go unnoticed. While standard-accented Mandarin provides a correct representation of Mandarin tones, it offers limited data and lacks the natural characteristics of authentic reading or conversational contexts. Recognizing that standard-accented Mandarin serves as the benchmark for tone evaluation and understanding that training SN leveraging large-scale image recognition models necessitates extensive corpora, we aimed to integrate the distinguishing features of both types of speech data. Therefore, we constructed a comprehensive corpus comprising standard-accented and non-standard-accented Mandarin. Standard-accented Mandarin served as the baseline sample for tone evaluation in this setup. In contrast, using the twin network architecture, non-standard-accented Mandarin functioned as the test sample for training tone evaluation models. The corpus construction process is depicted in Fig. 2.

Fig. 2
figure 2

Corpus construction process.

Full size image

Initially, we prepared a text corpus for recording standard-accented Mandarin and selecting non-standard-accented Mandarin from the existing speech corpora. Typically, the foundational content for teaching Mandarin pronunciation consists of a systematic tone course tailored for native Mandarin learners aged 5-6 and primary-stage L2 learners. These courses utilize simple and frequently encountered Chinese characters and vocabulary to facilitate tone learning. In designing the text corpus, this study consulted various resources, including textbooks and suggested reading materials for first and second-grade Chinese primary schools, as well as Mandarin proficiency test questions and guidelines from the Chinese language exam outline for primary and secondary education. The text corpus focuses primarily on the combinations and variations of tones rather than the Chinese characters and vocabulary. Consequently, this study created a text corpus encompassing monosyllabic, disyllabic, and polysyllabic vocabulary and sentence structures.

We engaged both male and female professional announcers to record the speech corpus of standard-accented Mandarin based on the carefully curated text corpus. Furthermore, we also sourced speech samples from various open-source Mandarin corpora, including THCHS3028 and AIShell29,30,31, and our self-constructed non-standard-accented Mandarin corpus, ensuring alignment with the designed text corpus. Our self-constructed non-standard-accented Mandarin corpus invited 40 students aged between 10 and 22, whose first language is Tibetan and second language is Mandarin, including 27 females and 13 males. To enhance the diversity and balance of our speech corpus, we deliberately included recordings featuring different speakers and tonal variations for the same content sourced from multiple standard-accented and non-standard-accented Mandarin corpora. Next, the selected Mandarin speech was cleaned to establish an initial corpus. Subsequently, we trained a forced alignment model using all utterances in the initial corpus to generate syllable-level timestamp labels (indicating each syllable’s start and end times). The final corpus was refined through manual cleaning and screening to eliminate unclear boundaries, incomplete data, excessively long silences, or overly brief pronunciations.

Feature extraction and labeling

Unlike images, speech is a time series signal, making it necessary to convert raw signals into sequence features that effectively capture tonal characteristics before they can be used for model training. Commonly utilized features in speech recognition, such as Mel-Frequency Cepstral Coefficients (MFCC), encompass various linguistic dimensions, including initials, finals, tones, rhythm, prosody, stress, and even speaker attributes. However, it is essential to note that the tones, which express relative pitch, remain unchanged despite variations in the initial consonants, final vowels, rhythm, intonation, or the unique characteristics of the speaker. For instance, the tones for “tian1” and “fei1” remain the same even though their initials and finals differ entirely. To address this, and grounded in research on the five-level tone scale, we propose two distinct features for tone representation. These features consist of the 40D vector and the \(50 \times 40\) matrix, which we refer to as 1D and 2D features, respectively. The feature extraction process is illustrated in Fig. 3.

Fig. 3
figure 3

The process of feature extraction.

Full size image

The complexity of continuous speech further exacerbates the challenges associated with tone recognition in Mandarin17, prompting us to adopt syllables as the fundamental unit for tone feature extraction. Each Chinese character’s tone can be effectively represented by its syllable’s pitch contour (F0). To achieve this, we initially utilized the algorithms32 from the WORLD Vocoder33 to extract the F0 for each syllable. Then, zero values are removed from F0 to obtain the non-zero F0 of the syllable, ensuring the continuity of tone variations. Within the non-zero F0, certain outliers still exist, which are eliminated through smoothing processing. So we employ Local Weighted Regression (LWR)34 to achieve F0 smoothing, which significantly preserves the variation trend of F035.

LWR is a robust locally weighted regression smoothing algorithm, which can smooth a scatterplot, (\(x_i\), \(y_i\)), \(i=1\), ..., n, in which the fitted value at \(x_s\) is the value of a polynomial fit to the data using weighted least squares, where the weight for (\(x_i\), \(y_i\)) is large if \(x_i\) is close to \(x_s\) and small if it is not. In implementing the LWR smoothing for non-zero F0, we utilized 25% of the neighborhood data to perform a polynomial fit and estimate the smoothed values \(y_s\).

While the pitch contour is the primary carrier of tone, the perception of tone can vary significantly among individuals. Different speakers, and even the same speaker at other times or under varying conditions, may exhibit pronunciation differences. These variations complicate direct comparisons and analyses of F0, even smoothed non-zero F0. We normalize the F0 using the Five-Degree Tone Model to address this challenge. The Five-Degree Tone Model, proposed by Chao, is a normalization method for marking the pitch counter of tones36,37. This method describes the complex tones of various tonal languages, particularly the tones found in different Chinese dialects. However, he did not provide a specific calculation formula; instead, he referred to the musical scale to categorize pitch variations into five degrees: low, mid-low, mid, mid-high, and high. By doing so, it standardizes the differences, filters out personal characteristics, and allows us to extract consistent parameters with linguistic significance. Consequently, the tones of different speakers or different types can be analyzed and compared against a standard benchmark. Building on this, Shi, F.38,39 introduced the T-value method for calculating the five-degree tone values by Eq. (1). Therefore, we apply Eq. (1) for solving the T-values of the Five-Degree Tone Model to normalize the smoothed non-zero F0 to a scale of 0 to 5, thereby creating a standardized quantitative description of tones that enhances the accuracy of tone comparison.

Typically, Eq. (1) employs 10 annotated points within the spectrogram for computation. 40 values are used for the calculation to characterize tonal variations precisely. Specifically, prior to normalization, the smoothed non-zero F0 is divided into 40 groups, and the mean value is calculated for each group.

$$\begin{aligned} t=5.0 \times {\frac{\log _{10}(F0_{i})-\log _{10}(F0_{min})}{\log _{10}(F0_{max})-\log _{10}(F0_{min})}} \end{aligned}$$
(1)

Here, \(F0_{i}\) refers to the ith mean value of the 40 groups of smoothed non-zero F0, \(F0_{min}\) indicates the lowest F0 produced by the speaker, while \(F0_{max}\) denotes the highest F0 within the same speaker’s range. From the perspective of computational implementation, the calculated five-degree tone values are retained in one decimal place as valid values. Eventually, we get a 40D vector to represent the 1D features.

Additionally, we converted these 1D features to the \(40 \times 50\) 2D features. Since each value of 1D features is normalized to the 0-5 range and the normalized value is retained to one decimal place, multiplying by 10 converts it into an integer value between 0 and 50. We take 50 values from 1 to 50 as the Y-axis, and the index of each F0 as the X-axis, thereby obtaining a \(40 \times 50\) matrix. We regard this matrix as a \(40 \times 50\) binary pixel image representing the 2D feature.

Both types of tone features are designed to train the model to predict tone discrepancies. Therefore, it is crucial to utilize paired tone features and their corresponding labels, indicating whether the two tones are identical or distinct. Specifically, a label of 0 indicates that the paired tones are the same, classifying them as a positive sample. In contrast, a label of 1 signifies that they are different tones, categorizing them as a negative sample.

Tone evaluation model

Our SN-based tone evaluation model is designed to learn and predict the degree of discrepancy between paired tones. The model effectively detects and analyzes tone pronunciation using standard-accented Mandarin tones as a reference. The evaluation framework comprises two essential components: the first utilizes a modified version of large-scale image recognition models, while the second is structured explicitly following the SN architecture.

During the training phase, the model is presented with multiple paired tone features to learn their differences, encompassing various combinations of identical and distinct tones. Labels indicate whether a pair of tones is the same, providing the model with a comprehensive understanding of tone differences. This enriched knowledge enhances the model’s generalization ability, improving its accuracy and realism in predicting discrepancies between target and standard-accented tones. Before input into the branch networks, the labeled paired tone features undergo enhancement via reflection padding. This process allows for more effective training by ensuring the model has a robust dataset. Additionally, the parameters across the two branch networks are shared, promoting efficient learning and reducing computational redundancy. As the neural network processes the paired tone features, it aims to encode similar tones closely together while keeping representations of different tones farther apart. To facilitate this distinction, a contrastive loss function, as detailed in Eq. (2) from40, is employed to train the model effectively for tone discrepancy prediction.

$$\begin{aligned} \mathscr{L}(w) =L\left( w, y, \vec{x}_1, \vec{x}_2\right) = \frac{1}{2}\left\{ (1-y)\left( d_w\right) ^2+Y\left[ \max \left( 0, m-d_w\right) \right] ^2\right\} \end{aligned}$$
(2)

Where y represents the label, \(y=0\) for the same tones, and \(y=1\) for the different tones. \(m>0\) is a margin. The margin defines a radius around \(g_w\). \(g_w\) is the mapping from the model’s input to output with weight (w) sharing across input \(\vec{x}_1\) and \(\vec{x}_2\). Define the parameterized distance function \(d_w\) between \(\vec{x}_1\) and \(\vec{x}_2\) as the Euclidean distance between the outputs of \(g_w\).

The contrastive loss can be calculated using various metrics, including Euclidean distance, cosine similarity, and dot product similarity. Euclidean distance quantifies the spatial discrepancy between features. In contrast, cosine distance considers both the direction and angle of the vectors. Meanwhile, dot product similarity focuses solely on the magnitude of the vectors.

In the testing phase, paired tone features with corresponding labels evaluate the model’s performance (see “Methods for validating model performance” section). The predicted tone discrepancy is normalized on a scale from 0 to 5, with higher scores indicating a more significant discrepancy. The model is supplied with paired tone data, including standard-accented tone and target tone data, to generate the predicted tone pronunciation scores during speech tone assessments.

Methods for validating model performance

Researchers typically conduct subjective analyses of tone pronunciation biases using spectrograms or F0 data, while objective evaluations of tone detection performance are made by calculating error rates. In this article, we introduce both subjective and objective methods for assessing our model’s performance in analyzing discrepancies between paired tones, thereby facilitating a comprehensive evaluation of tone correctness. The specific methods for validating the model’s effectiveness are illustrated in Fig. 4.

Fig. 4
figure 4

Methods for validating model performance.

Full size image

The subjective analysis involves calculating the Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) between the model’s evaluation results and those provided by expert evaluators. This assessment consists of two components: discrepancy scoring and tone pronunciation scoring. Multiple experts evaluate the tone similarity of several paired speech samples, where a higher discrepancy corresponds to a higher score. The subjective evaluation criteria for tone discrepancy are outlined in Table 1. Additionally, the experts evaluate the tone by comparing it to a reference speech with a standard-accented Mandarin tone, using scoring criteria based on the Mean Opinion Scores (MOS), as detailed in Table 2.

Table 1 Tone discrepancy scoring criteria.
Full size table
Table 2 Tone pronunciation scoring criteria.
Full size table

The objective analysis encompasses various metrics, including the MSE and RMSE between the model’s evaluation results and the corresponding labels. It also involves calculating the error rate across different score intervals, the mean tone discrepancy for various tone groups, and the distribution of tone discrepancies within different score intervals. The error rate for different score intervals, as defined in Eq. 3, refers to the observations for n groups of either the same tone (positive data) or different tones (negative data) inputs distributed across specified score intervals. In these results, m groups do not fall within the designated score interval, indicating that \(n - m\) represents the number of samples contained within that interval.

$$\begin{aligned} \text{Error Rate}=\frac{\text{FP}+\text{FN}}{\text{total number of samples}}={\frac{m}{n}}\times {100\%} \end{aligned}$$
(3)

where \(\text{FP}\) is false postive, \(\text{FN}\) is false negative.

The indicator provides some insight into the model’s tone pronunciation error detection capability; however, not all experimental results from the prediction set are equally reliable. To conduct a thorough and credible analysis of the model, we only utilize 97% of the experimental results for our calculations. The top 1.5% of the maximum and the bottom 1.5% of the minimum results are classified as outliers. The data for objective analysis primarily originates from the model’s performance on the prediction set, while the data for subjective analysis is randomly selected from the test set and undergoes additional manual screening.

Experiments

Datasets

The dataset consists of training, validation, and test sets derived from the reconstructed corpus described in “Building a corpus for tone assessment in Mandarin” section. As shown in Fig. 2, the corpus comprises standard-accented and non-standard-accented Mandarin speech recordings. In total, 120,022 speech samples were used to train the Deep Forced Aligner (DFA–DFA is a text-to-speech forced alignment tool that is available at https://github.com/bloodraven66/DeepForcedAligner.git) as a forced alignment tool model, amounting to 145 h of audio. The shortest sample lasts 0.32 s, while the longest spans 16.31 s, with an average duration of 4.35 s. Within this dataset, female speakers contribute 112.81 h, and male speakers account for 32.19 h.

The speech data are aligned with syllables, each consisting of an initial, a final, and a tone. There are 1,801 unique Syllable Tokens (STs), such as “ai1” and “zhou4,” contributing to a total of 1,716,985 syllables. On average, each audio sample includes 14.31 syllables.

We utilized the 80-dimensional Mel spectrograms, extracted from speech and aligned with the corresponding syllable tokens, as the input for the DFA model. The model underwent training for 345,530 steps, equivalent to 737 epochs, as shown by the loss trend in Fig. 5.

Fig. 5
figure 5

DFA convergence.

Full size image

After manual cleaning, the reconstructed corpus was converted into timestamped syllable-level data. This refined corpus, which comprises a total of 79,140 syllables, was subsequently utilized for tone evaluation. We do not specifically distinguish between citation (underlying) forms and sandhi (surface) realizations. For example, both sandhi-modified Tone3 (which acoustically approximates Tone2 while remaining phonemically distinct from Tone2) and canonical Tone3 are systematically categorized under the T3 tonal class. Therefore, there are only four types of tones in the corpus. Detailed tone distribution statistics can be found in Table 3. Additionally, one million pairs of monosyllable speech were randomly generated from this corpus, ensuring an equal distribution of positive and negative samples.

Table 3 Tone distribution statistics of corpus.
Full size table

Positive samples include data from the four kinds of tone categories: “Tone1Tone1(1-1),” “Tone2Tone2(2-2),” “Tone3Tone3(3-3),” and “Tone4Tone4(4-4),” with equal samples allocated to each tone. Negative samples are formed from six combinations of tones: “Tone1Tone2(1-2),” “Tone1Tone3(1-3),” “Tone1Tone4(1-4),” “Tone2Tone3(2-3),” “Tone2Tone4(2-4),” and “Tone3Tone4(3-4).” The order of tones in a pair is non-directional; for instance, “Tone1Tone2” and “Tone2Tone1” are considered the same combination. Each group contains an equal number of samples. The data was shuffled multiple times to ensure randomness and then divided into eight subsets, each containing 125,000 pairs. Finally, the dataset was split into training, validation, and testing sets using a ratio of 6:1:1.

Tone features

The computation of tone features is based on the F0 of the speech signal. Real audio recordings frequently contain noise and other interferences; therefore, for tone analysis, which emphasizes the trend of F0 variation, only non-zero F0 values are utilized for feature extraction. Figure 6 displays the original F0 (Fig. 6a) alongside the processed non-zero F0 (Fig. 6b) for Tone1.

Fig. 6
figure 6

The F0 of Tone1.

Full size image

The smoothed data is grouped and averaged to generate a feature vector of size \(\left( 40,\right)\). The processing steps are illustrated in Fig. 7, where the normalized range is automatically divided into five intervals. The resulting 1D features corresponds to the five-level tone scale values. Figure 8 displays the pixel matrix of size \(\left( 40, 50\right)\), representing the 2D feature, where bright points (F0 value) are assigned a value of 1 and dark points are assigned a value of 0.

Fig. 7
figure 7

The smoothed non-zero F0 of Tone1.

Full size image
Fig. 8
figure 8

The 2D feature of Tone1.

Full size image

Models configuration and training

The model configuration is outlined in Table 4 and described in detail below.

Table 4 Model configuration.
Full size table

  • Baseline The baseline model comprises three convolutional layers, two pooling layers, and one bidirectional LSTM. The first convolutional layer utilizes 64 filters of size \(3 \times 3\), with a stride of 1 and padding of 1. This is followed by a max-pooling layer with a \(3 \times 3\) filter and a stride of 2. The smaller receptive field allows for fine-grained feature extraction, while the max-pooling layer helps retain the most significant features. The second convolutional layer employs 128 filters of size \(5 \times 5\), again with a stride of 1 and padding of 2. The third convolutional layer consolidates features using a single filter of the same size as the first convolutional layer. This is succeeded by an average-pooling layer with a \(3 \times 3\) kernel, a stride of 2, and padding of 1. A bidirectional LSTM layer with 256 neurons is incorporated to preserve temporal sequence characteristics. The final structure includes two FC layers: the first contains 256 neurons, followed by a dropout layer with a rate of 0.25 to mitigate overfitting and enhance regularization during training. The output layer, another FC layer with 32 neurons, encodes the tone features.

  • AlexNet This model41 comprises five convolutional layers, each with more filters than the baseline model. The first convolutional layer utilizes 48 filters of size \(1 \times 1\), with both a stride and padding of 1. The second convolutional layer features 128 filters of size \(5 \times 5\), also with a stride of 1 and padding of 2. The third, fourth, and fifth convolutional layers employ \(3 \times 3\) filters with a stride of 1 and padding of 1; both the third and fourth layers utilize 192 filters, while the fifth layer contains 128 filters. Max-pooling layers, sized \(3 \times 3\) with a stride of 2, follow the first, second, and fifth convolutional layers. Notably, no Local Response Normalization is applied between the convolutional and pooling layers. The final three layers consist of FC layers, with the first two having 2048 neurons each, followed by a dropout layer with a rate of 0.25 to reduce overfitting. Each convolutional and FC layer is activated by a ReLU function, except for the last FC layer, which contains 32 neurons.

  • VGG-16 This model comprises 11 convolutional layers, each utilizing \(3 \times 3\) filters, followed by a ReLU activation function. The convolutional layers are organized into four groups: layers 1-2, 3-5, 6-8, and 9-11. A \(2 \times 2\) max-pooling layer with a stride of 2 is applied after each group of layers. The final section of the model consists of four FC layers, each also followed by a ReLU activation function and a dropout layer with a rate of 0.25, except the last FC layer. The first two FC layers each contain 4096 neurons, while the third FC layer is configured with 1000 neurons to maintain the model’s effectiveness in image classification. The final FC layer consists of 32 neurons.

  • ResNet-18 ResNet-18 architecture comprises 17 convolutional layers, each utilizing a \(3 \times 3\) filter size. Except for the first convolutional layer, every two convolutional layers are organized into groups featuring a residual structure. A ReLU activation function is applied after each convolutional layer. Following the first convolutional layer, a \(3 \times 3\) max-pooling layer with a stride of 2 is incorporated. The model concludes with an average-pooling layer of size \(3 \times 3\) and a stride of 1. The final section includes two FC layers, with the first containing 1000 neurons and the second consisting of 32 neurons.

The model utilizes 1D convolutions and 1D pooling across all convolutional layers for processing 1D features, while 2D features are handled using 2D convolutions and 2D pooling. Before entering the convolutional layers, simple feature enhancement is implemented through padding. The 1D features are expanded from 40 to 100 dimensions, and the 2D features are augmented from a shape of (40, 50) to (100, 100) using padding techniques.

Training is conducted on a setup with 8 NVIDIA 2080Ti GPUs, employing a batch size of 128 and an initial learning rate of 0.005. It can also be conducted on fewer GPUs, even 1 GPU, with appropriate adjustments to the batch size. The dataset is divided into training, validation, and testing sets in a ratio of 6:1:1, resulting in a training process that spans six rounds, with each round utilizing a distinct set of data without repetition. Each round consists of 10 epochs, with one epoch comprising 977 steps. The learning rates for the first and second rounds remain at the initial rate, while the third and fourth rounds are adjusted to 0.001. For the fifth and sixth rounds, the learning rates are halved from the previous rounds, resulting in rates of 0.0005 and 0.00025, respectively. The contrastive loss margin is set to \(m=1\) for both 1D and 2D features. In addition, during the inference phase, the trained models can be deployed on servers or other PC terminals. The models’ size is shown in the Table 5. Inference can be carried out using fewer GPUs or even CPUs.

Table 5 Model size.
Full size table

Results

We used the same test data to conduct experiments across four models—ResNet-18, VGG-16, AlexNet, and baseline model—incorporating both 1D and 2D features. The results were compared to assess the proposed method’s effectiveness through subjective and objective analysis of the outcomes generated from these experiments.

Convergence behavior

Both 1D and 2D features were used to train across different models, each displaying unique convergence behaviors, as depicted in Fig. 9. During the training process, ResNet-18, VGG-16, and AlexNet achieved convergence within a margin of 0.1, irrespective of whether 1D or 2D features were utilized.

Fig. 9
figure 9

Loss variation during model training.

Full size image

Regarding loss value precision, ResNet-18 with the 2D feature (ResNet-2D) converges below 0.02, nearing 0.01, while ResNet-18 with the 1D feature (ResNet-1D) successfully converges below 0.01. Specifically, ResNet-2D reaches convergence around 10,000 steps and stabilizes near 15,000 steps, with a post-convergence oscillation magnitude of approximately 0.01. Meanwhile, ResNet-1D converges around 15,000 steps, stabilizing around 20,000 steps, and exhibits a smaller oscillation magnitude of about 0.005.

VGG-16 similarly demonstrates convergence below 0.02. VGG-16 with the 2D feature (VGG-2D) converges at approximately 13,000 steps and stabilizes near 18,000 steps. Following convergence, it shows oscillation magnitudes ranging from 0.02 to roughly 0.04. VGG-16 with the 1D feature (VGG-1D) also converges around 13,000 steps and stabilizes around 17,000 steps, with oscillations remaining close to 0.01.

For AlexNet with the 2D feature (AlexNet-2D), convergence is achieved below 0.05; however, multiple experiments indicate a tendency to diverge around 7,000 steps, causing loss values to oscillate between 1 and 1.1. In contrast, AlexNet with the 1D feature (AlexNet-1D) effectively converges below 0.02, reaching this point at around 11,000 steps and stabilizing at approximately 15,000 steps. After convergence, AlexNet-2D shows an oscillation magnitude of about 0.03, whereas AlexNet-1D maintains a smaller oscillation magnitude of around 0.01.

Baseline models present a different convergence pattern, losing its downward trend around 1,000 steps and primarily exhibiting oscillations thereafter. The loss value for Baseline with the 2D feature (Baseline-2D) hovers around 1, with an oscillation magnitude of approximately 0.05, while Baseline with the 1D feature (Baseline-1D) stabilizes at a loss value of roughly 0.25, displaying an oscillation magnitude of about 0.01s.

Subjective analysis

Subjective analysis is a comparative evaluation of expert ratings against model predictions using MSE and RMSE. It involves two primary tasks: measuring the paired tone discrepancies between expert assessments and the models’ predictions and assessing the accuracy of the four types of tones as rated by experts and the various models.

We prepared 72 pairs of child speech samples for the first task to evaluate discrepancies. To maintain data balance, these samples included an equal distribution of positive and negative examples. The positive data comprised \(4 tones \times 9 pairs\), while the negative data consisted of \(6 combinations \times 6 pairs\) (refer to “Datasets” section for details on combination types). For the second task, we arranged 24 non-standard-accented Mandarin samples (\(4 tones \times 6 combinations\)) for assessing tone pronunciation, with each tone paired with a standard-accented Mandarin reference sample.

We then invited 19 experts in Mandarin phonetics to complete both tasks, following the scoring criteria outlined in Tables 1 and 2. Concurrently, we employed our models to unify these two tasks by predicting tone discrepancies for the 72 pairs of speech samples and evaluating tone accuracy for the 24 non-standard-accented Mandarin samples based on predefined labels. Additionally, we compiled the experts’ scoring results alongside the model’s predictions, calculating the mean and standard deviation of the scores for each tone.

Comparison of tone discrepancies between model prediction and expert evaluations

This analysis evaluates the consistency and deviation between the model predictions and expert scores, as illustrated in Fig. 10. Lower MSE values indicate greater consistency, while higher RMSE values denote increased deviation. The red line in Fig. 10 highlights the optimal MSE and RMSE, achieved by ResNet-2D, with values of 2.295 and 1.515, respectively. In comparison, ResNet-1D has MSE and RMSE values of 2.442 and 1.563, respectively. ResNet-18 demonstrates superior performance regardless of the feature type used, whether 1D or 2D features. Except for AlexNet, all models show improved performance when utilizing 2D features over 1D features. VGG-2D ranks third overall, achieving an MSE of 2.644 and an RMSE of 1.626. Based on overall performance, the models rank in the following order: ResNet-18 > VGG-16 > AlexNet > Baseline. It’s worth noting that VGG-1D results are slightly lower than those of AlexNet-1D, and AlexNet exhibits the poorest performance when using 2D features.

Fig. 10
figure 10

MSE and RMSE of tone discrepancies between model predicted results and experts’ evaluation.

Full size image

Comparison of tone accuracy between model prediction and expert evaluations

This analysis relies on expert evaluations of 24 individual tone samples, using standard-accented Mandarin samples as references, as illustrated in Fig. 11. Given the limited number of test samples, the expert scores and model predictions’ absolute values are insufficient for drawing comprehensive conclusions. However, by comparing the mean tone pronunciation scores predicted by different models with the mean expert scores, we can assess the models’ ability to distinguish tones and their alignment with expert evaluations.

Figure 11 displays the mean tone pronunciation scores along with their standard deviations, with the red line representing the mean expert scores. The mean scores and standard deviations of expert evaluations for Tone1 to Tone4 are as follows: \(1.25 \pm 0.66\) (Tone1), \(0.75 \pm 0.30\) (Tone2), \(2.90 \pm 2.10\) (Tone3), and \(1.39 \pm 1.23\) (Tone4).

Fig. 11
figure 11

Mean scores ± standard deviations of different tones from models and experts.

Full size image

  • Tone1 The mean predictions of VGG-2D and ResNet-2D are closest to the expert mean scores, recording values of \(1.21 \pm 1.66\) and \(1.05 \pm 1.67\), respectively. Among the models with smaller standard deviations, VGG-1D, AlexNet-1D, and ResNet-1D demonstrate higher reliability, with ResNet-1D achieving a prediction of \(0.38 \pm 0.16\).

  • Tone2 The prediction from ResNet-1D, at \(1.12 \pm 1.85\), is the closest to the experts’ scores, while Baseline-2D achieves the smallest standard deviation with a score of \(1.46 \pm 1.10\).

  • Tone3 ResNet-1D records a prediction of \(2.72 \pm 2.17\), aligning closely with the expert score of \(2.90 \pm 2.10\). Despite its larger standard deviation, ResNet-1D maintains stable performance. Conversely, ResNet-2D and VGG-2D yield lower mean predictions of \(0.93 \pm 1.90\) and \(0.76 \pm 1.61\), respectively, along with standard deviations that are consistent with expert evaluations.

  • Tone4 The predictions from AlexNet-1D, ResNet-1D, and ResNet-2D are closer to the experts’ results, with values of \(1.35 \pm 2.03\), \(1.50 \pm 1.89\), and \(1.18 \pm 1.47\), respectively. Among these, ResNet-2D shows the best consistency.

The comparison indicates that expert evaluations yield the smallest standard deviation for Tone2 (\(\pm 0.30\)) and the largest for Tone3 (\(\pm 2.10\)). Model predictions exhibit varying degrees of consistency and standard deviations compared to expert scores.

Objective analysis

The objective analysis results of this study include the MSE and RMSE between the predicted tone discrepancies and their corresponding labels, as well as the error rates within specific score intervals, the mean tone discrepancy, and the distribution of tone discrepancies. These results are based on predictions derived from two types of tone features across four different models on the same testing dataset.

MSE and RMSE between model predicted tone discrepancies and labels

Figure 12 displays the MSE and RMSE for the predicted tone discrepancies compared to the actual labels across various models. This includes experimental results for different feature types applied to the same model. ResNet-2D achieves the lowest MSE and RMSE, with values of 0.189 and 0.435, respectively. Following closely, VGG-2D ranks second with an MSE of 0.197 and RMSE of 0.444. ResNet-1D secures third place in all eight experiments, recording an MSE of 0.204 and an RMSE of 0.452. Notably, AlexNet consistently outperforms VGG-1D when using both 1D and 2D features. Among the models utilizing 1D features, only the results from ResNet-18 demonstrate MSE and RMSE values below 1, achieving figures comparable to those of VGG-2D. For models employing 2D features, all results fall below 1, except for Baseline models. However, the MSE of AlexNet-2D is more than four times greater than that of ResNet-1D, and its RMSE is over twice as high. Therefore, the performance of ResNet-18 significantly surpasses that of both AlexNet and Baseline models.

Fig. 12
figure 12

MSE and RMSE between tone discrepancies and labels.

Full size image

Error rate within score intervals

Figure 13 presents the error rates for classifying positive and negative data across various score intervals for the four fusion models, with score intervals defined in increments of 0.5 points. Figure 13 specifically highlights results within the intervals [0, 3) (positive data) and (2, 5] (negative data), which account for the lower 60% of the total score range. Additionally, the intervals [0, 1) and (4, 5] represent the lowest 20% of scores. For positive data, the model with the lowest error rate in the [0, 1) interval is AlexNet-1D, achieving an error rate of 0.34%. Other models, including VGG-1D, ResNet-2D, VGG-2D, and ResNet-1D, record error rates of 0.48%, 0.52%, 0.55%, and 0.67%, respectively. In contrast, for negative data, the model exhibiting the lowest error rate in the (4, 5] interval is VGG-2D, obtaining an error rate of 2.42%. ResNet-2D and ResNet-1D follow with error rates of 3.26% and 4.02%, respectively, while the other models perform less favorably. For positive data, AlexNet remains the best-performing model in the [0, 0.5) interval, while for negative data, ResNet-18 shows the strongest performance in the (4.5, 5] interval.

Fig. 13
figure 13

The error rate within score intervals for positive and negative data across different models.

Full size image

Mean score of tone discrepancy

Figure 14 presents the predicted mean tone discrepancy scores and their standard deviations. The data is based on eight experimental groups, where four models utilizing both 1D and 2D features were tested across various tone combinations. The x-axis of Fig. 14 represents the tone combinations in the test dataset, with combinations of identical tones classified as positive and those with differing tones classified as negative. Each combination of identical tones comprises four distinct tones. The tone discrepancy score quantifies the degree of dissimilarity between the sets of tones. To enable a more explicit comparison of the effects of different models, we ranked the results and compiled them in Table 6. For negative data, the highest tone discrepancy is observed in VGG-2D, which records a score of \(4.56 \pm 0.28\), followed closely by ResNet-2D and ResNet-1D, yielding scores of \(4.55 \pm 0.27\) and \(4.53 \pm 0.28\), respectively. In contrast, the lowest tone discrepancy for positive data is reported by the AlexNet-1D, which achieves a score of \(0.02 \pm 0.15\), followed by the AlexNet-2D and VGG-1D.

Fig. 14
figure 14

Predicted tone discrepancy mean ± standard deviation for different models.

Full size image
Table 6 Ranking of predicted tone discrepancy mean ± standard deviation for different models.
Full size table

Distribution of tone discrepancy

Figure 15 illustrates the distribution of tone discrepancy scores across various intervals, based on predictions generated by different models utilizing 2D and 1D features for a range of tone combinations. The numerical values reflect the proportion of samples within each score interval relative to the total dataset. This distribution offers valuable insights into the models’ effectiveness in differentiating between various tone combinations.

Fig. 15
figure 15

Tone discrepancy distribution across different models using various tone features.

Full size image

ResNet-18 exhibits outstanding overall performance in distinguishing tone combinations. For positive samples, predictions utilizing 2D features place over 98.7% of the data within the [0, 1) interval, while predictions for negative samples exceed 95.6% within the [4, 5] interval. When employing 1D features, ResNet-18 predicts scores in the [0, 1) interval for more than 98.2% of positive samples and in the [4, 5] interval for over 93.8% of negative samples.

The prediction result distributions of the other models are generally less effective than those of ResNet-18, with the exception of AlexNet when using 1D features. AlexNet demonstrates a prediction rate exceeding 99.1% for positive samples within the [0, 1) interval. However, for negative samples, a significant portion of predictions occurs within the [3, 4) interval, indicating that it is less effective at differentiating negative samples compared to ResNet-18.

Discussion

This section offers an in-depth discussion of the performance evaluation of different features and models for each tone, drawing insights from both the experimental results and the accompanying subjective and objective analyses.

Features’ performance across different models

1D and 2D features reveal distinct advantages and limitations. Regarding model convergence, those that utilize 2D features generally experience slower rates and encounter greater challenges during training, consistently achieving higher convergence values compared to models that rely on 1D features. Furthermore, models based on 2D features exhibit more significant fluctuations in both amplitude and frequency throughout the training process. This result is consistent with the richer information content of 2D features, which is particularly beneficial for complex and deep architectures. However, in simpler and narrower models like AlexNet, employing 2D features may occasionally result in non-convergence.

An analysis that combines MSE, RMSE, and other objective metrics to assess predicted tone discrepancies indicates that, for the specific model, predictions based on 2D features generally outperform those derived from 1D features. In particular, deeper and more parameter-rich models like VGG-16 show substantial improvements when utilizing 2D features. For instance, in the distribution of tone discrepancy scores across various tone combinations, VGG-2D effectively distinguishes between positive and negative data, clustering predicted scores in the intervals of [0, 1) and [4, 5]. In contrast, both VGG-16 and AlexNet, employing 1D features, categorize a significant amount of negative data within the intervals of [2, 3) and [3, 4). Additionally, an error rate analysis across score intervals reveals that models utilizing 2D features, especially ResNet-18 and VGG-16, consistently achieve lower error rates compared to those using 1D features, with this advantage being especially pronounced in VGG-16.

Based on these observations, several conclusions can be drawn: ResNet-18, notable for its depth and breadth, effectively predicts tone discrepancies using both 1D and 2D features. The model distinguishes between identical and different tones based on the predicted discrepancy scores. In contrast, VGG-16, which prioritizes depth but lacks sufficient breadth, shows limited accuracy when predicting tone discrepancies with a 1D feature. This limitation is especially evident in its ability to differentiate between different-tone combinations as opposed to identical-tone combinations. AlexNet, which lacks both depth and breadth, achieves accurate predictions solely for identical-tone combinations using a 1D feature. Although incorporating 2D features enhances prediction performance, the overall accuracy remains suboptimal. These findings highlight the critical need to align feature types with model architectures to optimize the effectiveness of tone discrepancy predictions.

Models performance

The experimental results confirm the viability of the tone evaluation method proposed in this study. The choice of model significantly influences the effectiveness and accuracy of the method. In terms of convergence, when utilizing the same tone features, ResNet-18 achieves rapid convergence and, once converged, demonstrates minimal fluctuations and improved stability. VGG-16 closely follows, exhibiting similar performance characteristics. Conversely, AlexNet experiences convergence issues with 2D features, occasionally failing to reach convergence. Although Baseline models eventually stabilize their loss, further analysis indicates that this stabilization does not imply true convergence.

An analysis of the MSE and RMSE between predicted and actual tone discrepancies indicates that ResNet-18 outperforms other models when the same tone features are used. The experimental results for VGG-16 do not consistently surpass those of AlexNet, with VGG-16 only fully realizing its potential when utilizing 2D features. When examining the comprehensive analysis of score interval error rates and tone discrepancy distribution, ResNet-18 demonstrates excellent reliability and stability in predicting whether a set of tones is identical. Although ResNet-18’s performance in predicting negative data is slightly lower than that of VGG-16, the difference is negligible. Regarding predicted mean tone discrepancy, ResNet-18 consistently meets expectations, with standard deviations ranging from \(\pm 0.17\) to \(\pm 0.28\) for both 1D and 2D features. Notably, VGG-16 achieves results comparable to ResNet-18 when employing 2D features.

In summary, simpler CNN models, such as Baseline models, are inadequate for identifying and interpreting the tone features developed and computed in this study. VGG-16 is particularly well-suited for processing 2D features, as the complexity of these features leverages the learning capability of deeper architectures. Although AlexNet can extract essential information from tone features, its performance in predicting tone discrepancies, especially for negative data, significantly lags behind ResNet-18 and VGG-16.

ResNet-18 emerges as the top performer, demonstrating a robust ability to understand and differentiate these features, regardless of whether 1D or 2D features are utilized. This may be related to its unique residual blocks. The residual structure can address the issue of vanishing gradients42. At the same time, it can also tackle the problem of learning degradation in deep networks43. The residual blocks endow the model with the capability of identity mapping. With more stable gradient backpropagation, ResNet-18 achieves faster convergence with reduced fluctuations compared to VGG-16, demonstrating more stable loss variations relative to AlexNet.

The deeper ResNet-18 architecture enables shallow-layer features to integrate with deep-layer features during forward propagation when learning complex 2D features. This addresses the potential learning degradation in ResNet-18 (which has greater depth than VGG-16) and allows the 2D data to leverage ResNet-18’s capabilities better. In contrast, AlexNet, with its shallower depth and simpler structure, has a lower learning capacity. Consequently, ResNet-18 performs better in predicting discrepancies between paired tones, especially on negative data.

Performance of different tones during evaluation

When analyzing the performance of different tones across various models, we computed the average tone discrepancy scores and tone discrepancy distributions, focusing on the positive data. We found that different models exhibit varying learning performance for various tones, but ResNet-18 demonstrates a closer alignment with real-world scenarios and shows higher consistency with expert evaluations.

From ResNet-2D, Tone4 has the lowest average discrepancy score, while from ResNet-1D, Tone3 shows the lowest average discrepancy score. The average discrepancy scores for Tone4 in ResNet-2D and Tone3 in ResNet-1D differ from those of other tones by no more than 0.15. By VGG-2D, Tone3 exhibits the lowest average discrepancy score, while Tone1 has the lowest score by VGG-1D. AlexNet yields similar results. These findings suggest that although different models show varying levels of learning for various tones, the differences are not significant.

Regarding the distribution of discrepancy scores, whether using a 1D or 2D feature, Tone3 is best distinguished using ResNet-18, achieving a 100.0% and 99.9% classification rate in [0,1), respectively. For VGG-16 and AlexNet, Tone3 is also distinguished with a 100.0% rate in [0,1). Furthermore, the prediction scores from ResNet-18 show high consistency with expert ratings across all four tones.

In conclusion, while the average discrepancy scores for positive data vary across different models, the score deviations show consistent patterns, with ResNet-18 showing the highest consistency with expert rating deviations. Compared to the other tones, Tone3 is more effectively distinguished and recognized by different models. This suggests that Tone3 is easier for the models to learn and has distinctive recognition features, which remain consistent whether using 1D or 2D features.

Conclusion

This article introduces a tone discrepancy prediction method based on an SN integrated with large-scale image recognition models. The approach extracts specific tone features using a five-level tone scale, facilitating the automatic evaluation of Mandarin tones. Experimental results show the method excels in detecting and analyzing tone pronunciation errors. The extracted tone features, encompassing both 1D and 2D representations, effectively capture the nuances of Mandarin tone information. The proposed method integrates ResNet-18 and is accurate, effective, stable, and reliable for tone pronunciation detection and analysis. It can also achieve tone pronunciation evaluation when incorporated with other models. The method proposed in this study aligns closely with expert evaluation results in tone discrepancy predictions, underscoring its effectiveness in assessing tone pronunciation for Mandarin as an L2 learner. However, the method still relies on the computed tone features, which may oversimplify the complexity of tone characteristics, presenting a limitation of the current approach. Future research will aim to extract raw, deep tone features from speech data using neural networks and effectively integrate these features into the existing framework.