A lightweight certificateless aggregate signature scheme without pairing for VANETs

Abstract

In the secure vehicular ad-hoc networks (VANETs), certificateless aggregate signature schemes(CLAS) have attracted more and more attention because they can efficiently implement message aggregation and authentication without complex certificate management. Recently, Zheng et al. proposed an efficient and privacy-protecting certificateless aggregate signature scheme, which is applicable to VANETs. However, through in-depth analysis, we found that it is vulnerable to temporary rogue key attacks. That is, an adversary can exploit the random numbers in signatures to generate an ephemeral rogue key, enabling him/her to forge an aggregate signature using both this rogue key and his/her private key. Furthermore, the forged signature can pass the verification without being detected. This paper fixes this vulnerability and proposes a security-enhanced CLAS scheme for VANETs. Specifically, our improved solution incorporates an additional aggregator’s signature into the original framework and implements simultaneous verification of both the aggregator’s signature and the aggregate signature to effectively resist rogue key attacks. In terms of security, we conducted a rigorous analysis of the security-enhanced CLAS scheme. In addition, through performance evaluation experiments, we compare the computational complexity and communication overhead of the security-enhanced CLAS scheme and some other schemes. The experimental results show that the security-enhanced CLAS scheme demonstrates significant advantages in both computational efficiency and communication cost while maintaining security. Our method can provide valuable references for the design of security solutions in related fields.

Introduction

Certificateless Aggregate Signature (CLAS) schemes have emerged as a promising approach for securing Vehicular ad-hoc networks (VANETs), enabling efficient and authenticated message aggregation without the burden of certificate management. However, existing pairing-free CLAS schemes remain vulnerable to ephemeral rogue-key attacks, which compromise both security and trustworthiness in vehicular environments^1,2,3,4. VANETs enable several functions that enhance botth the safety and efficiency of transportation systems, such as: Traffic data sharing, vehicle safety, efficient travel, the network integration of VANETs with cellular infrastructures to ensure ubiquitous connectivity^5,6,7. However, the inherent openness of wireless communication in VANETs exposes them to numerous potential threats⁸, such as: data interception and tampering, malicious commands and vehicle control.

A certificateless signature (CLS)^9,10 offers an effective solution to the limitations of traditional Public Key Infrastructure (PKI)^11,12,13 and identity-based cryptography (IBC)^14,15,16,17, avoiding certificate management overhead and eliminating key escrow. To further improve efficiency, certificateless aggregate signature (CLAS) schemes have been proposed, allowing multiple signatures to be compressed into a single, verifiable aggregate. These properties make CLAS particularly well-suited for VANET applications. Several CLAS schemes have been introduced in the literature^{18,19,20,21,22,23}, with pairing-free constructions gaining attention due to their lower computational costs on resource-limited vehicular devices.

Although the research on CLAS has achieved some fruitful results, it still faces many challenges related to safety and efficiency to be further improved. This is directly related to the practical application effect, especially in VANETs. For example, Kamil²⁴ proposed an unpaired CLAS scheme , but it has been found to be susceptible to forgery attacks. Moreover, Liu et al.²⁵ pointed out that there were also loopholes in the CLAS scheme proposed by Gayathri et al.²⁶ and improved the original scheme. However, in their new scheme, there is still a risk point of being attacked by a malicious key generation center (KGC), which may lead to critical information leakage and functional failure of the system. In 2022, Zheng et al.²⁷ also pointed out the vulnerabilities in the CLAS scheme proposed by Han et al.²⁸ and proposed a improvement scheme, which aims to further reduce communication costs while improving security.

Here, it is worth noting that after in-depth research, we found that the above mentioned scheme of Zheng et al.²⁷ was unable to resist transient rogue key attacks²⁹. Specifically, an adversary can exploit the random nonces in signatures to generate an ephemeral rogue key, enabling them to forge an aggregate signature using both this rogue key and their private key. At the same time, We successfully addressed the identified vulnerability and presented a new Lightweight and secure CLAS scheme.Table 1 briefly introduces the comparison and research gaps of recent CLAS schemes. Specific contributions are as follows:

Table 1 Comparative analysis of recent CLAS schemes.

• 1. We analyzed Zheng et al.’s CLAS scheme²⁷ and show that it has a security vulnerability. Malicious node or user can forge AS for arbitrary messages using the ephemeral rogue-key attack method without being detected.Specifically, an adversary can exploit the random nonces in signatures to generate an ephemeral rogue key, enabling them to forge an aggregate signature using both this rogue key and their private key.

• 2. To resist temporary rogue-key attack, we propose an enhanced CLAS scheme, which adds an additional aggregator signature and enhances its security to resist rogue key attacks by simultaneously verifying the aggregator signature and the aggregation signature. This solution provides enhanced protection for the integrity and authenticity of data in VANETs.

• 3. The efficiency, performance and security features of Zheng et al.’s scheme , other existing schemes^{22,30,31,32,33} and the CLAS-VANETs version of $\Gamma$-$\hbox {signature}^*$(we enhance their key generation process by incorporating partial private keys, thereby generating an $\Gamma$-signature$*$that can be applied in VANETs .The $\Gamma$-$\hbox {signature}^*$ scheme incorporates a binding between random challenge hashes and ephemeral elements (e.g., $U_i$), making it computationally infeasible for an attacker to manipulate individual components without knowing the corresponding private key. This design enhances resistance against rogue key forgery.Implementation specifics and cryptographic parameterizations are documented in the appendix.) we slightly modified based on the reference³⁴ are compared with ours. Our experimental results demonstrate that the proposed scheme outperforms existing methods in terms of computational cost, communication overhead, and resistance to forgery, making it highly suitable for VANETs deployment.

The organization of this article is as follows: Section Preliminaries presents the preliminaries, while Section Zheng et al.’s CLAS scheme focuses on the security evaluation of Zheng et al.’s scheme²⁷. In Section Our improved CLAS scheme, we propose our enhanced solution, and Section Correctness and security analysis examines the security and privacy aspects of this approach. Comparative analysis is presented in Section Performance analysis and evaluation, followed by a comprehensive summary of the entire paper. In the appendix, we also introduced the scheme combining $\Gamma$-aggregate³⁴ signature and VANETs.

Preliminaries

To better elaborate the introduced CLAS scheme, this section introduces some preliminary concepts, including the system model and security requirements, etc.

Research methodology

This paper employs an analysis-design-evaluation research framework. First, we identify the efficiency and security challenges confronting existing schemes in VANETs, particularly their susceptibility to temporary rogue key attacks. Guided by this analysis, we proposed improvement methods and validate the scheme’s practicality by comparing its efficiency with state-of-the-art approaches. The detailed workflow is as follows:

• 1. Step 1:Limitation Analysis of Existing Schemes, We first uncover critical weaknesses in current certificateless aggregated signature (CLAS) schemes regarding resistance to transient rogue key attacks. Specifically, we demonstrate how adversaries can exploit their private keys and public parameters to forge valid random numbers, thereby generating verifiable aggregate signatures that evade detection mechanisms. This exposes a fundamental flaw in the security architecture of traditional CLAS schemes.

• 2. Step 2: Design of a Novel CLAS Solution To address the security vulnerabilities and strict real-time demands of VANETs, we proposed a novel CLAS solution. This solution incorporatesa dual-verification mechanism where aggregator-generated signatures and individual signer signaturets collectively ensure resistance against temporary rogue key attacks through cryptographic operations.

• 3. Step 3: Adaptation of $\Gamma$-Signature Framework Concurrently, we investigate the $\Gamma$-signature framework, which inherently resists the identified attacks. Through targeted encryption improvements, we adapt it into an enhanced $\Gamma$-signature scheme suitable for VANETs.

• 4. Step 4: Comparative Evaluation of Schemes We conduct a comprehensive comparative analysis of three schemes: Traditional CLAS scheme (baseline); Enhanced $\Gamma$-signature scheme (adapted framework); Proposed enhanced scheme (our solution). The evaluation focuses on computational costs and communication overhead. Results demonstrate that our proposed scheme achieves a superior balance between security and efficiency, outperforming traditional CLAS in resisting rogue key attacks while maintaining comparable or lower resource consumption compared to the $\Gamma$-signature framework.

VANETs system model

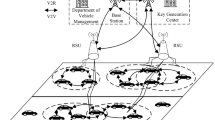
In order to facilitate understanding, based on literature^27,28, we drew a simplified version of the communication system model with a two-layer system, as shown in Fig. 1. It comprises five entities, they are elaborated upon as follows:

• 1. Trust Authority (TA): It provides registration service and never be corrupted. In our scheme, it also can generate pseudonyms for vehicles and trace the vehicle’s identity .

• 2. Key Generation Center (KGC): Its primary role is to generate system parameters and create partial keys for users in VANETs based on their pseudonyms. In generally, it is assumed to be honest.

• 3. Application Server(AS): It has enough computing and storage power to authenticate messages and ASservice requests sent by roadside units or vehicles. It can analyze and process messages and data to complete application service.

• 4. Roadside Unit (RSU): It refers to a base station positioned either alongside the road or at a hotspot location. Within its fixed receiving range. RSU receives and validates traffic information from vehicles. In addition, it can generate AS and transmit them to the application server.

• 5. Vehicles: In VANETs, vehicles have constrained computational resources but can communicate, sign traffic information, and transmit it to RSUs or other vehicles.

Fig. 1

System model of VANETs.

Figure 1 illustrates the architecture of the proposed VANET system model, incorporating three key components: the cloud-based trusted management entities, the roadside infrastructure, and the mobile vehicular nodes. RSU upload the aggregated signature or verification requests to the TA or application server via secure links (red arrows). Each red car represents an On-board Unit (OBU) within a vehicle that participates in VANET communication.Yellow bidirectional arrows indicate V2V (Vehicle-to-Vehicle) communication, enabled by DSRC or 5G.Red arrows show V2I (Vehicle-to-Infrastructure) or RSU-to-cloud communication channels.

To ensure notational consistency throughout this paper, we formalize all cryptographic primitives using standardized symbols with rigorous mathematical definitions, as systematically summarized in Table 2.

Table 2 Notations.

System assumptions

The proposed scheme relies on the following standard assumptions and security model:

• 1. TA: Fully trusted and never compromised. Responsible for identity recovery and pseudonym issuance.

• 2. KGCAssumed to be honest-but-curious. It generates partial private keys but does not collude with malicious users.

• 3. Elliptic Curve Discrete Logarithm Problem (ECDLP): The underlying security of our CLAS scheme is based on the computational hardness of ECDLP over group G.

• 4. Secure Channels: Communication between TA, KGC, and vehicles during initial setup is assumed to be secure. Other channels are insecure and subject to eavesdropping or tampering.

Security requirements for CLAS scheme

Due to the limited computing resources of RSU, vehicle and other devices, weak security protection, and the openness of the network, there are security risks such as eavesdropping, interception, and tampering in the transmission and processing of important data. To safeguard user privacy and ensure security, the CLAS scheme in the VANETs environment needs to meet several basic requirements. They are elaborated upon as follows:

• 1. Message authentication: During the communication process, such as sending a message or signature, it should be ensured that any two entities in the scheme are able to confirm each other’s identity and the legitimacy of the message source.

• 2. Message integrity: The scheme must be capable of ensuring that messages remain free from tampering, replacement, forgery, and similar attacks.

• 3. Conditional anonymity and traceability: To safeguard privacy, the true identity of the vehicle must remain confidential during the communication process in VANETs. However, full anonymity would make all malicious behaviors untraceable. So the best way to balance is to implement conditional anonymity and tracking. That is, vehicle’s real identity is protected anonymously in ordinary times, and traceability ensures that in case of misbehavior, the real identity of a vehicle can be retrieved by the TA using secure mappings.

• 4. Non-Linkability: This property ensures that multiple pseudonyms or messages from the same vehicle cannot be correlated by unauthorized entities.

In addition, CLAS schemes should also be able to resist the common attacks listed below.

• 1. Replay Attack: Replay Attack involves an attacker intercepting and subsequently retransmitting previously legitimate communication data or interactions in an attempt to deceive a system or server into granting unauthorized access or executing illicit operations.

• 2. Impersonation Attack: An attacker impersonates a trusted individual, entity, or system to gain unauthorized access.

• 3. Man-in-the-Middle Attack: Inserting themselves between the communicating parties to monitor, tamper with, or disrupt the communication.

Communication technology

In our proposed VANETs system, different communication technologies are adopted according to the role and network layer of the involved entities:

Vehicle-to-Roadside Unit (V2R) sCommunication: Vehicle communicate with nearby RSUs via Dedicated Short Range Communication (DSRC) or 5G-based Cellular Vehicle-to-Everything (C-V2X), depending on infrastructure support. These links support periodic message signing, certificate querying, and signature aggregation requests.

RSU-to-Trusted Authority Communication: RSUs are assumed to have high-bandwidth, low-latency wired or secure wireless connections to the Trusted Authority (TA), typically via fiber-optic networks or secure IP channels such as TLS-protected APIs.

Vehicle-to-Vehicle (V2V) Communication (Optional): In scenarios requiring local message forwarding or emergency broadcast, V2V communication may utilize ad-hoc DSRC or C-V2X protocols for one-hop or multi-hop message propagation.However, our scheme focuses primarily on V2R communication for aggregation and trust management.

Zheng et al.’s CLAS scheme

Overview of Zheng et al.’s scheme

• 1. System initialization

  • (a) Choose a group G of order q, where P is a generator of the group G.

  • (b) Choose three secure hash functions $H_{1,2,3}$: $\{0, 1\}^*$ $\rightarrow$ $Z_q^*$.

  • (c) KGC, TA ramdomly chooses $a,b \in Z_q^*$ respectively, then computes $K_{pub} = aP$ and $T_{pub} = bP$.

• 2. PID generation

  • (a) Vehicle $V_i$ randomly selects $y_i \in Z_q^*$, then computes $PID_{i,1} = y_iP$, $Y_i = RID_i\oplus y_iT_{pub}$. where $RID_{i}$ is real identity of $V_i$.

  • (b) Once receiving $\{PID_{i,1}, Y_i\}$, TA calculates $RID_i = Y_i \oplus bPID_{i,1}$, $PID_{i,2} = RID_i \oplus H_0(bPID_{i,1} \oplus T_i$). Where $T_i$ means time to live of pseudonym identity.

  • (c) At last, TA generates the $V_i$’s pseudonym $PID_i = \{PID_{i,1}, PID_{i,2}, T_i\}$.

• 3. Partial secret key generation

  • (a) KGC randomly selects $r_i \in Z_q^*$ and computes

    $$\begin{aligned}&R_i = r_iP, \nonumber \\&H_{1i} = H_1(PID_i||R_i||K_{pub}),\nonumber \\&d_i = r_i + aH_{1i}.\nonumber \end{aligned}$$

  • (b) KGC transmits $\{PID_i\}$ and $\{d_i, R_i\}$ over a secure channel to $V_i$ .

• 4. Vehicle key generation

  • (a) $V_i$ randomly selects a number $x_i \in Z_q^*$ and calculates $X_i = x_iP$.

  • (b) Let $SK_i = \{x_i, d_i\}$ be private key and $PK_i = \{X_i, R_i\}$ be public key for $V_i$.

• 5. Signature generation

  • (a) The vehicle $V_i$ selects $u_i \in Z_q^*$ and calculates

    $$\begin{aligned}&U_i= u_iP,\nonumber \\&H_{2i} = H_2(PID_i||X_i||K_{pub}||R_i||t_i),\nonumber \\&H_{3i} = H_3(PID_i||M_i||PK_i||U_i||t_i),\nonumber \\&s_i = u_i + d_iH_{2i} + x_iH_{3i},\nonumber \end{aligned}$$

    where $t_i$ means current timestamp of message.

  • (b) $V_i$ transmits $\{PID_i,PK_i, M_i, t_i, \sigma _i\}$ to receiver, where $\sigma _i = (U_i, s_i)$ is its signature.

• 6. Individual signature Verification

  • (a) About all, verifier checks up the legitimacy of $T_i$.

  • (b) Futhermore, verifier computes $H_{1i}$, $H_{2i}$, $H_{3i}$.

  • (c) At last, verifier examines whether $s_iP = U_i + (R_i + H_{1i}K_{pub})H_{2i} + X_iH_{3i}$ holds.

• 7. Aggregate signature

  • (a) Aggregator firstly examines whether $T_i$ is valid.

  • (b) Aggregator calculates $s = \textstyle \sum _{i=1}^{n}s_i$ for $i =1, \cdots , n$, and generates aggregate signature $\sigma$ = $(U_1, U_2, \cdots , U_n, s)$.

• 8. Aggregate signature Verification

  • (a) At first, aggregate verifier calculates $H_{1i}, H_{2i}, H_{3i}$.

  • (b) Then, aggregate verifier compares whether $\textstyle \sum _{i=1}^{n}U_i + \textstyle \sum _{i=1}^{n}(R_i + H_{1i}K_{pub}) H_{2i} + \textstyle \sum _{i=1}^{n}X_iH_{3i}$ and sp are the same.

Attack of Zheng et al’s scheme

Now, we use a temporary rogue key attack method given by Zhao et al.³⁴ to demonstrate the security vulnerability of the CLAS scheme introduce by Zheng et al.²⁷. We usually assume that there is a attacker whose index is n. The attacker has public keys $\{X_j,R_j\}_{j=1}^n$ and private key $\{x_n,r_n\}$. To forge AS, he may do the following operations:

• 1. The attacker prepares messages $M_1, \cdots , M_n$ and randomly chooses $U_1, \cdots , U_{n-1}$.

• 2. Then, he computes respectively:

  • (a) for $j=1,\cdots ,n$,

    $$\begin{aligned}&\ H_{1j} = H_1(PID_j||R_j||K_{pub}),&\nonumber \\&\ H_{2j} = H_2(PID_j||X_j||K_{pub}||R_j||t_j),&\nonumber \end{aligned}$$

  • (b) for $j=1,\cdots ,n-1$,

    $$\begin{aligned} H_{3j} = H_3(PID_j||M_j||PK_j||U_j||t_j).\nonumber \end{aligned}$$

• 3. the attacker calculates :

  $$\begin{aligned} U_n =-\sum _{j=1}^{n-1}(R_j + H_{1j}K_{pub})H_{2j}-\sum _{j=1}^{n-1}U_j - \sum _{j=1}^{n-1}X_jH_{3j}. \nonumber \end{aligned}$$

• 4. According to $U_n$, he computes :

  $$\begin{aligned}&\ H_{3n} = H_3(PID_n||M_n||PK_n||U_n||t_n)&\nonumber \\&\ s = H_{3n}x_n+H_{2n}d_n&\nonumber \end{aligned}$$

• 5. Finally, the attacker outputs the forged AS $\sigma = (U_1, U_2, \cdots , U_n, s)$ . When the verifier checks the AS, there is

  $$\begin{aligned} \begin{aligned} sP&= H_{3n}x_nP + H_{2n}d_nP \\&= H_{3n}X_n +(R_n + H_{1n}K_{pub})H_{2n}\\&= H_{3n}X_n + (R_n+H_{1n}K_{pub})H_{2n} + U_n+\\&~~~\sum _{j=1}^{n-1}(R_j + H_{1j}K_{pub})H_{2j}+\sum _{j=1}^{n-1}U_j +\sum _{j=1}^{n-1}X_jH_{3j}\\&= \sum _{j=1}^{n}U_j + \sum _{j=1}^{n}(R_j + H_{1j}K_{pub})H_{2j} + \sum _{j=1}^{n}X_jH_{3j} \end{aligned} \end{aligned}$$

Obviously, according to the above formula, forged signatures will pass verification without being detected. There is no doubt that this kind of attack are harmful, especially in the VANETs system, where the attacker can deliberately fake some false information by pretending to be the identity of other users, thus causing a major accident.

In response to these issues, Zhao et al.³⁴ proposed $\Gamma$-signature to address the vulnerability of the Schnorr signature to rogue key attacks. we enhance their key generation process by incorporating partial private keys, thereby generating an $\Gamma$-signature$*$ that can be applied in VANETs. While this approach effectively mitigates tephemeral rogue-key, it introduces a significant decrease in efficiency, which is unacceptable for VANETs. Therefore, an urgent need exists for a solution that can counter temporary rogue key attacks without compromising efficiency.

Our improved CLAS scheme

Fig. 2

Scheme flow chart.

In view of the above security vulnerabilities, we propose an improved CLAS scheme. This scheme can not only block rogue key attacks, but also has high efficiency, which is more suitable for VANET network. The specific explanation of the scheme is as follows (some contents similar to the scheme given by zheng at al.²⁷ will not be repeated here).

To ensure secure communication in VANETs while meeting the requirements for conditional privacy protection of vehicle identities and efficient message signature authentication, we propose a noval privacy protection authentication scheme.

Our scheme addresses the vulnerability to rogue key attacks present in Zheng et al.’s²⁷ scheme. While Zhao et al.’s³⁴ introduction of the $\Gamma$-signature can mitigate this issue, its computational overhead is impractical for VANETs. Therefore, we propose a more efficient solution.

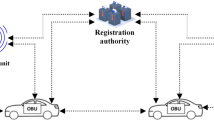
The flow chart is produced according to our proposed scheme in order to make the reader understand our scheme more clearly. As shown in Fig. 2.In our improved CLAS authentication scheme scenario, vehicle Vi joins the VANET using pseudonyms, requests partial private keys from the KGC, and generates its own public-private key pair. During operation, the vehicle broadcasts traffic-related messages with digital signatures. RSUs perform signature verification, forward validated data to the TA, and simultaneously aggregate successfully verified signatures. These aggregated signatures along with message hashes sent to the TA are stored in servers. Validated data is transmitted to the TA, while verification-failed messages are reported with aggregated signatures to enable traceability and penalty enforcement. Vehicles primarily obtain trustworthy messages with verifiable aggregated signatures from RSUs, supplemented by V2V interactions. Furthermore, vehicles join VANETs pseudonymously – if detected as fraudulent entities, they can be reported to the TA, which then traces and identifies malicious message-originating nodes.

The detailed procedure of our proposed solution is outlined below.

System initialization

The content of this step is almost the same as the first one of system initialization in Zheng et al.’s scheme, except that our scheme uses five hash functions $H_0, H_1, H_2, H_3, H_4$.

• 1. Choose a group G of order q, where P is a generator of the group G.

• 2. Selects five collision-resistant hash functions: $H_{0,1,2,3,4}$:{0, 1}$^*$ $\rightarrow$ $Z_q^*$.

• 3. KGC, TA ramdomly chooses $a,b \in Z_q^*$ respectively, then computes $K_{pub} = aP$ and $T_{pub} = bP$, outputs params = $\{P, q, E, G,H_0, H_1, H_2, H_3,H_4 K_{pub}, T_{pub}\}$.

Pseudonym identity generation

In this vehicular pseudonym generation process, the vehicle first selects a secret value x, computes the corresponding parameter X, then encrypts its real identity (RID) using both the secret value and the TA’s public key through a key agreement mechanism. This encrypted RID is transmitted to the TA via public channels, which alleviates the resource constraints associated with dedicated private channels. Only the TA can decrypt the RID using its private key paired with the received X. Subsequently, the TA verifies the legitimacy of the decrypted RID, sets a validity period T for the pseudonym identity, and generates corresponding pseudonymous credentials based on the validated RID.

• 1. Vehicles $V_i$ selects a random $x_i$ from $Z_q^*$.

• 2. Then, $V_i$ computes $X_i = x_iP$, $TID_i = RID_i \oplus H_0(x_iT_{pub})$, and sends $\{X_i, TID_i\}$ to TA.

• 3. TA extracts the value $RID_i = TID_i \oplus H_0( bX_i )$ at first and checks its validity. If $RID_i$ is legal, TA computes pseudonym identity $PID_i = RID_i \oplus H_1( bX_i, T_i, t'_i)$ for $V_i$, where $T_i$ is the validity period of $PID_i$ and $t_i$ is the time when the $PID_i$ was created. Otherwise, TA will discard it and abort the protocol.

• 4. TA transmits $\{PID_i, X_i, T_i,t_i\}$ to KGC.

Partial secret key generation

• 1. After receiving the above message, KGC first checks whether the corresponding time parameter $T_i$ and $t_i$ are valid. If yes, go to the next step. If not, an error is reported to TA and the previous step is returned.

• 2. KGC chooses $r_i \in Z_q^*$ at random and calculates the following equations:

  $$\begin{aligned}&R_i = r_iP,\nonumber \\&H_{2i} = H_2(PID_i||R_i||K_{pub}||X_i||T_i),\nonumber \\&d_i = r_i + aH_{2i},\nonumber \\&D_i = d_i \oplus H_0(aX_i),\nonumber \end{aligned}$$

• 3. KGC sends $\{PID_i, D_i, R_i, T_i,t_i\}$ to $V_i$ over a public channel.

Vehicle key generation

• 1. Above all, $V_i$ computes

  $$\begin{aligned}&d'_i = [D_i \oplus H_0( K_{pub}x_i)],\nonumber \\&H_{2i} = H_2(PID_i||R_i||K_{pub}||X_i||T_i||t_i),\nonumber \end{aligned}$$

• 2. Next, $V_i$ computes $result_{d'_i} =d'_iP - R_i-H_{2i}K_{pub}$ and performs

  • (a) If $result_{d'_i}=0$,this condition confirms that the reconstructed partial private key $d'_i$ correctly corresponds to the received values and the TA/KGC’s master keys. The equation ensures that no tampering has occurred during key generation or transmission, and that Di was computed honestly by the KGC. $V_i$ keeps the private key $SK_i = (x_i, d'_i)$ and publishes the public key $PK_i = (X_i, R_i)$.

  • (b) If $result_{d'_i} \ne 0$, $V_i$ reports an error to KGC and requests to resend the information. Repeat until $result_{d'_i}=0$.

• 3. Key Renewal: When $T_i$ expires, the vehicle:

  • (a) Generates a new pseudonym identity $PID'_i$ with a new validity period $T'_i$.

  • (b) Derives new public/private keys ($x'_i$,$X'_i$) and requests a new partial private key ($d'_i$) from the KGC.

Individual signature generation

• 1. $V_i$ chooses $u_i \in Z_q^*$, and calculates the first part of the signature $U_i = u_iP$.

• 2. $V_i$ computes the remaining signature portion as below:

  $$\begin{aligned}&H_{3i} = H_3(M_i||PID_i||PK_i||K_{pub}||T_i||t_i),\nonumber \\&H_{4i} =H_4(M_i||PID_i||PK_i||U_i||T_i||t_i),\nonumber \\&s_i = u_i + d'_iH_{3i} + x_iH_{4i}.\nonumber \end{aligned}$$

• 3. $V_i$ sets $\sigma _i$ = $(U_i, s_i)$ as the signature of $M_i$ and broadcasts message $\{PID_i,PK_i, M_i, \sigma _i, T_i, t_i\}$.

Individual signature verification

• 1. Verifier (RSU and other vehicle $V_j$) checks if time $t_i$ is valid. If affirmative, proceed to the subsequent step; If negative, “verification failed” is returned and abort the protocol.

• 2. Next, verifier computes :

  $$\begin{aligned}&\ H'_{2i} = H_2(PID_i||R_i||K_{pub}||X_i||T_i),\nonumber \\&\ H'_{3i} = H_3(M_i||PID_i||PK_i||K_{pub}||t_i),\nonumber \\&\ H'_{4i} = H_4(M_i||PID_i||PK_i||U_i||t_i)).\nonumber \end{aligned}$$

• 3. Verifier examines whether $s_iP = U_i + (R_i + H'_{2i}K_{pub})H'_{3i} + X_iH'_{4i}$ is established is or not. If yes, $s_i$ is valid; If not, it is invalid.The corresponding erroneous signature information is then transmitted to the TA, which traces back the real identity of the vehicle disseminating false information using its private key.

Aggregate signature generation

• 1. Aggregator checks if time $t_i$ is valid after receiving $\{PID_i,PK_i, M_i, t_i, \sigma _i\}$ (i = 1, 2,..., n).

• 2. Aggregator collects and collates all individual signatures and related information as follow

  $$\begin{aligned}&\ U_{set} = (U_1, U_2, \cdots , U_n),\nonumber \\&\ PK_{set} = (PK_1, PK_2,\cdots , PK_n),\nonumber \\&\ PID_{set} = (PID_1, PID_2,\cdots , PID_n),\nonumber \\&\ t_{set} = (t_1, t_2,\cdots , t_n),\nonumber \\&M_0 = (U_{set}, PK_{set}, PID_{set}).\nonumber \end{aligned}$$

• 3. According to step (Pseudonym identity generation)-(Vehicle key generation), aggregator generates private key $SK_0 = (x_0, d_0)$, public key $PK_0 = (X_0, R_0)$ and pseudonym identity $PID_0$.

• 4. Aggregator randomly chooses $u_0 \in Z_q^*$ and computes the following equations

  $$\begin{aligned}&U_0 = u_0P,\nonumber \\&H_{30} = H_3(M_0||PID_0||PK_0||K_{pub}||t_{set}),\nonumber \\&H_{40} = H_4(M_0||PID_0||PK_0||U_0||t_{set}),\nonumber \\&s_0 =u_0+d_0H_{30}+ H_{40}x_0,\nonumber \\&\sigma _0 = (U_0,s_0),\nonumber \\&s = \sum _{i=0}^{n}s_i.\nonumber \end{aligned}$$

• 5. Aggregator broadcasts $\{PID_0, PK_0, M_0, t_{set}, \sigma _0\}$ and outputs $\sigma$ = ($U_0, U_1, U_2, \cdots , U_n, s_0, s$) as the AS.

Aggregate signature verification

• 1. Verifier first checks the equation whether $s_0p = U_0 + (R_0+H_{20}K_{pub})H_{30}+ H_{40}X_0$ is true or not. If the equation is correct, proceed to the next step. Otherwise, the signature verification fails and stops. In this process, verifiers can submit reports to the TA to identify the aggregator RSU that distributed incorrect aggregated signatures, and impose penalties accordingly. Simultaneously, by implementing pre-verification checks on aggregator signatures, subsequent massive signature verification computations can be prevented, thereby conserving substantial computational resources.

• 2. Verifier verifies whether $sP = \textstyle \sum _{i=1}^{n}U_i + \textstyle \sum _{i=1}^{n}(R_i + K_{pub}H_{2i})H_{3i} + \textstyle \sum _{i=1}^{n}X_iH_{4i} +s_0p$ is established or not. If yes, the AS is valid. If not, it is invalid.In this process, verifiers can submit reports to the TA to identify the aggregator RSU that distributed incorrect aggregated signatures, and impose penalties accordingly. Simultaneously, by implementing pre-verification checks on aggregator signatures, subsequent massive signature verification computations can be prevented, thereby conserving substantial computational resources.

Correctness and security analysis

Correctness

The correctness proof of the whole scheme is divided into individual signature verification and AS verification two parts.

• 1. Individual signature verification The derivation of the verification equation is as follow:

  $$\begin{aligned} \begin{aligned} s_iP =&(u_i+d'_iH_{3i}+x_iH_{4i}) P\\ =&U_i+d'_iH_{3i}P+x_iH_{4i}P\\ =&U_i+(r_i+aH_{2i})H_{3i}P+X_iH_{4i}\\ =&U_i+(R_i+K_{pub}H_{2i})H_{3i}+X_iH_{4i}. \end{aligned} \end{aligned}$$

• 2. Aggregate signature verification Here, the two-step verification is performed. That is, the individual signature of the aggregator is verified first, and the AS is verified after the first verification is successful.

  • 1. The verification correctness derivation of the aggregator’s personal signature $\sigma _0$ is the same as the derivation above, and will not be repeated here. It is worth noting that when $\sigma _0$ validation fails, the AS will be considered invalid and the validation will not continue. Therefore, this verification step will help to realize the preliminary detection of illegal AS.

  • 2. The correctness of AS verification:

    $$\begin{aligned} \begin{aligned}&sP-s_0P \\ =&\sum _{i=1}^{n}(u_i+d_iH_{3i}+x_iH_{4i}) P\\ =&\sum _{i=1}^{n}u_iP + \sum _{i=1}^{n}d_iH_{3i}P + \sum _{i=1}^{n}x_iH_{4i}P\\ =&\sum _{i=1}^{n}U_i + \sum _{i=1}^{n}(aH_{2i}+r_i)H_{3i}P \sum _{i=1}^{n}X_iH_{4i} \\ =&\sum _{i=1}^{n}U_i + \sum _{i=1}^{n}(K_{pub}H_{2i}+R_i)H_{3i} + \sum _{i=1}^{n}X_iH_{4i}. \end{aligned} \end{aligned}$$

Security analysis

In reference³⁵ defines the security requirements for an AS scheme as follows:

• 1. The underlying CLS scheme should securely withstand two types of attackers: malicious vehicles, capable of substituting vehicle’ public key but unable to acquire information regarding KGC private key. Another type is a malicious KGC, capable of acquiring KGC private key but unable to replace public key of vehicles.

• 2. The employed aggregation algorithm should effectively defend selective key attacks, wherein attacker possesses public and private keys and sets temporary rogue keys, constituting an internal attack.

In our proposed scheme, the underlying CLS scheme is derived from the scheme of Zheng et al.²⁷. Since its security has been officially proven (see zheng at al.²⁷ for more details), we will not go into details here. The difference is that our scheme adopts XOR encryption operation in steps 4.3 and 4.4 to protect the security of intermediate variables. The security of the key $H_0 (aX_i)$ corresponding to the encryption algorithm can be guaranteed by the unidirectional hash algorithm and the confidentiality of the KGC private key, where a is the KGC private key.

In addition, an additional signature is introduced in the aggregation stage when the AS is used in our scheme. The addition of this signature can effectively prevent the attacker from setting temporary illegal keys through authentication. Increase the count of AS from n to n+1.

Our proposed scheme is resistant to temporary rogue key attacks, which Zheng et al.’s scheme fails to achieve. In Section Zheng et al.’s CLAS scheme, we reviewed Zheng et al.’s scheme and provided a detailed explanation of how such a temporary rogue key attack can enable forgery. Below, we will explain how our scheme mitigates temporary rogue key attacks.

In the proposed scheme of this paper, to mount a tephemeral rogue-key attack on AS, assuming the attacker’s index is 1, they first need to set up a tephemeral rogue-key attackas: $U_1$ = - ($\textstyle \sum _{i=1}^{n}R_i$ + $H_{1i}K_{pub})H_{2i}$ - $\textstyle \sum _{i=1}^{n}X_iH_{3i}$ - $\textstyle \sum _{i=1}^{n}U_i$ - $s_0p$).

However, Due to the unidirectionality of the hash function, namely, the irreversible nature of the computation process involved in hashing. Consequently, our scheme can withstand rogue key attacks. It should be noted that in the aggregation process, the signature $s_0$ is computed as $s_0 = u_0 + d_0H_{30} + H_{40}x_0$ (where $H_{30} = H_3(M_0||PID_0||PK_0||U_0||T_0)$,$H_{40} = H_4(M_0||PID_0||PK_0||U_0||t_{0})$, $M_0$ = $\{U_1, U_2, \cdots U_n\}$).

Therefore, the proposed scheme effectively safeguards against tampering attacks.

Our proposed scheme adopts an efficient certificateless aggregate signature mechanism where all individual signatures are of fixed length and can be linearly aggregated without requiring re-randomization or interactive coordination. Given n vehicles in a dynamic VANET cluster, the RSU only needs to perform O(n) signature verification computations, while the final aggregate signature size remains constant.

Furthermore, our aggregation process is non-interactive and stateless, meaning that new vehicles joining or leaving the communication group do not invalidate the aggregate structure. This is particularly suitable for dynamic VANET scenarios where frequent node mobility and topology changes occur.

Compared to schemes that require re-initialization or multiple signature rounds (e.g., in pairing-based systems), our approach minimizes the overhead caused by dynamic behavior.

Privacy requirements analysis

Then, We demonstrate that our improved solution meets the proposed safety objectives.

• 1. Message authentication and integrity: Vehicle $V_i$ signs each message, receiving the message, the RSU determines the legitimacy of the signature using the equation $s_iP = U_i + (R_i + H_{2i}K_{pub})H_{3i} + X_iH_{4i}$. This process serves to ascertain whether the message has been tampered. This implies that attacker are unable to forge legitimate signatures. Consequently, our scheme satisfies the requirements.

• 2. Conditional Anonymity and Traceability: During data transmission and communication, only TA can ascertain vehicle’ real identity. The pseudonymous identity of the vehicle $V_i$ is represented as $\{PID_i, T_i\}$, where $PID_i = RID_i \oplus H_1( bX_i ,T_i)$, and $T_i$ denotes the validity period of the pseudonym. $T_{pub} = bP$, where b is TA’s private key. An attacker would need to derive b from the available $T_{pub} = bP$ and then calculate $bX_i$ to obtain the $V_i$’s real identity. However, due to the computational hardness of the ECDLP, the attacker cannot extract a from $T_{pub}$ within polynomial time. The $RID_i$ of $V_i$ is concealed within the $PID_i$. If vehicle transmits malicious messages, the TA can utilize the private key b to trace back to the $V_i$. The pseudonym $\{PID_i, T_i\}$ is defined as $PID_i = RID_i \oplus H_1(bX_i, T_i)$. The traceability process for $RID_i$ is as follows: $RID_i = PID_i \oplus H_1(bX_i, T_i) = RID_i \oplus H_1(bX_i, T_i) \oplus H_1(bX_i, T_i) = RID_i$. However, since other entities do not possess the master key b, it is not possible to compute $bX_i$.

• 3. Unlinkability: Vehicles have the capability to possess multiple pseudonyms simultaneously, and each pseudonym can be employed with a distinct private key for signing messages. Importantly, there is no inherent linkage between different pseudonyms. Thus, our CLAS scheme adheres to the property of unlinkability.Formally, given multiple pseudonyms $PID_i = RID_i \oplus H_1(bX_i, T_i)$, an adversary without access to TA’s secret key b cannot compute $H_1(bX_i, T_i)$ to recover $RID_i$, nor determine whether two different $PID_i$ values belong to the same vehicle. Since xi is chosen independently per pseudonym, there exists no cryptographic linkage between different $PID_i$ even for the same vehicle.

This scheme is capable of withstanding various types of attacks, detailed as follows:

• 1. Resistance to replay attacks: Receiving the message signature tuple(incorporates two timestamps: the timestamp $t_i$ of message, and the timestamp $T_i$ of the pseudonym $\{PID_i, T_i\}$.), vehicle $V_j$ or RSU can verify the timestamps by examining $\vert t_i' - t_i \vert$ or $\vert T_i'- T_i \vert$. Each aggregated signature includes individual timestamps $t_i$ for all messages. During verification, RSUs or Vehicle check that each timestamp is fresh and within valid time windows, thus preventing replay. Moreover, since the aggregated signature includes a separate signature by the aggregator ($\sigma _0$) that covers the complete set of individual signatures, a dishonest aggregator cannot alter or omit any component without invalidating $\sigma _0$. Consequently, the presented scheme effectively defends against replay attacks.

• 2. Resistance to impersonation attacks: Attacker would need to forge a legitimate traffic-related information tuple {$PID_i$, $M_i$, $PK_i$, $\sigma _i$, $t_i$} that satisfies the verification equation $s_iP$ = $U_i$ + $(R_i + H_{2i}K_{pub})H_{3i}$ + $X_iH_{4i}$ or (sP = $\textstyle \sum _{i=1}^{n}U_i$ + $\textstyle \sum _{i=1}^{n}(R_i + H_{2i}K_{pub})H_{3i}$ + $s_0p$ and $s_0p = U_0 + (R_0+H_{20}K_{pub})H_{30} + H_{40}X_0)$. But the attacker is unable to solve the ECDLP. Thus, our CLAS cheme effectively prevents impersonation attacks.

• 3. Resistance to man-in-the-middle attacks: The attacker’s approach involves forging two private keys to deceive both parties into believing they are engaging in direct communication.. To accomplish this, the attacker must forge signatures using their private keys, and then generate authentic-looking messages to send to them. However, such a scenario is impractical. Consequently, it effectively thwarts attacker.

Furthermore, the scheme adopts a certificateless public key cryptography mechanism, which can effectively defend against eavesdropping attacks and unauthorized data collection by adversaries on sensitive identity or key-related information. Besides, Our scheme ensures data integrity via hash functions to resist modification attacks by adversaries. As the scheme does not require maintaining validation tables or identity-token bindings at verifier side, it is inherently immune to validation table leakage attacks. Furthermore, the scheme also uses ephemeral random values, which can not only prevent replay attacks but also provide forward security.

Performance analysis and evaluation

Computational cost comparison

The execution times of each cryptographic operation in the cited paper is measured using the charm-crypto cryptographic library. We executed each cryptographic operation 100 times using Python code, calculated the average value, and recorded the measured results in Table 3.

For schemes reliant on bilinear pairings, a security level equivalent to that of the 1024-bit RSA algorithm is attained through the bilinear pairing function $e : G_1 \times G_1 \rightarrow G_2$, where $G_1$ denotes a cyclic subgroup of elliptic curves $E$ over a finite field with an embedding degree of 2, defined by $y^2 = x^3 + ax + b$ mod $q$, and $p$ is a 512-bit prime. Conversely, to achieve an analogous security level for schemes built upon elliptic curves, the Koblitz elliptic curves $E : y^2 = x^3 + ax + b$ mod $q$ with a q-order additive cyclic group $G$ is employed, where $p$ and $q$ are 160-bit primes, and $a, b \in {\mathbb {Z}}$. Generally, a 160-bit elliptic curves offers a security level akin to that of the 1024-bit RSA. Furthermore, the computation time for regular multiplications, and additions over $Z{_q}{^*}$ can be neglected compared to the operations listed in Table 3. Therefore, they are excluded from the scheme comparison presented below.

Table 3 Time of each cryptographic operation.

We proceed to offer a comprehensive evaluate of the computational overhead associated with the schemes outlined in references^27,30,31,32, contrasting them with our proposed scheme.Meanwhile, for $\Gamma$-signature resistant to ephemeral rogue key attacks, we enhance their key generation process by incorporating partial private keys, thereby generating an $\Gamma$-$\hbox {signature}^*$ that can be applied in VANETs and compared with our proposed scheme. Table 3 describes the calculated costs for each phase of each scheme.

Table 4 Execution time.

We conducted an evaluation and analysis of the computational overhead across various schemes. We present comprehensive comparison results in Table 4. Based on Table 4.we created a bar chart to illustrate the cost of individual signing and verification, as shown in Fig. 3, and a line chart to represent the cost of aggregate verification, as shown in Fig. 4.

In our proposed scheme, the individual signature entails two hash computations and one point multiplication. In the individual verification, three general hash operations, three point additions, and four point multiplications are required. Furthermore, for the aggregate verification phase, $3(n+1)$ general hash computations to $Z_q^*$ , $4(n+4)$ point additions, $(3n+5)$ point multiplications, and one verification of $s_0'$ are necessary.

Due to the expensive bilinear pairing operations and pairing-based dot product computations proposed in the schemes outlined in references^22,30,31,32, these approaches incur substantial computational overhead at various stages. In contrast, our CLAS scheme, along with the schemes outlined in references²⁷, is designed rooted on Elliptic Curve Cryptography (ECC), thereby reducing overall computational overhead.

Specifically, in the signature generation stage, our CLAS reduces computational overhead by 66.62%, 66.59% , 83.83% and 66.62%,compared to references^22,30,31,32. In individual signature verification , our method reduces computational overhead by 68.62%, 58.17% , 45.85% and 53.26% compared to references^22,30,31,32, while in AS verification (n=100), it reduces computational overhead by 24.89%, 50.91% ,1.62%, 24.06% and 29.35% compared to references^{22,30,31,32,33}. Although our scheme slightly lower than references²⁷, as n increases, it remains comparable to reference²⁷. Since $\Gamma$-$\hbox {signature}^*$ has very good performance, we also try to apply it to VANETs and give the CLAS version of $\Gamma$-signature in Appendix A. In the overall signature verification (n=100), although it meets the security requirements, it is 23.75% less efficient than our proposed scheme. Our solution takes into account both security and computational performance, making it more suitable for VANETs applications.

Moreover, although the computational cost of our proposed method during the validation phase is slightly higher than the solutions presented in references²⁷, the scheme in Zheng at al.²⁷ is susceptible to the ephemeral rogue-key attacks.

Fig. 3

Computation cost.

Fig. 4

Computation cost comparison of aggregate verification.

Communication overhead comparison

Let $\vert G_1 \vert$, $\vert G \vert$, and $\vert Z_q^*\vert$ denote the bilinear pairing, elliptic curve, and the size of the group element in $Z_q$, respectively, where $\vert G_1 \vert$ = 1024bits, $\vert G \vert$ = 320bits, and $\vert Z_q^*\vert$ = 160bits. The timestamp is omitted for brevity.

We conducted an evaluation and analysis of the communication overhead across various schemes. Table 5 evaluates the communication efficiency of our scheme compared to the referenced schemes. We have provided a more intuitive comparison of the communication efficiency by presenting a bar chart in Fig. 5.

Table 5 Communication cost comparison.

Fig. 5

Communication cost comparison bar chart (when $\vert G_1 \vert$ = 1024bits, $\vert G \vert$ = 320bits, and $\vert Z_q^*\vert$ = 160bits).

In reference²⁷ and Aggregate $\Gamma$-signature in VANETS, senders send messages typed {$PID_i$, $PK_i$, $M_i$, $T_i$, $\sigma _i$}, where $PID_i = \{PID_{i,1}, PID_{i,2}, T_i\}, PK_i = \{R_i, X_i\}$ and $\sigma _i = \{s_i, U_i\}$. $\{PID_{i,1}, R_i, X_i, U_i\}\in G, \{PID_{i,2}, M_i, s_i\} \in Z_q^*$, thus communication costs is 4$\vert G \vert + 3\vert Z_q^*\vert$. Similarly, the communication overhead of literature^{22,30,31,32,33} are respectively 4$\vert G_1 \vert + 2 \vert Z_q^*\vert$, 4$\vert G_1 \vert + 2\vert Z_q^*\vert$, 5$\vert G_1 \vert + \vert Z_q^*\vert$,3$\vert G \vert + 2\vert Z_q^*\vert$ and 3$\vert G_1 \vert + 2\vert Z_q^*\vert$.

In references^22,30,31,32, the proposed scheme involves the transmission of group elements based on bilinear pairings, resulting in substantial communication overhead. In comparison, our approach achieves a communication overhead reduction of 67.4%, 66.1% , 72.7% and 62.3% relative to references^22,30,31,32, and a reduction of 18.1% compared to reference²⁷. For AS, assuming n=100, our scheme exhibits communication overhead reductions of 19.1%, compared to²⁷and aggregate $\Gamma$-$\hbox {signature}^*$ in VANETs, and exhibits communication overhead reductions of 63.6%, and 41.4% compared to references^30,31.

Experimental analysis

Fig. 6

Experimental communication cost.

This paper implements our scheme, Zheng et al.’s²⁷ scheme, and the $\Gamma$-$\hbox {signature}^*$ scheme in VANETs using Python, the experiments were conducted on a platform with the Ubuntu 20.04 operating system, an AMD Ryzen 7 7840HS processor, and 16GB of memory, ensuring no network latency during the experimental process, and conducts a practical comparison. Figure 6 below shows the comparison results. From the experimental data, it is evident that when n=20,40,60,80,100, our scheme improves performance by approximately 20% compared to the $\Gamma$-$\hbox {signature}^*$ scheme in VANETs. Additionally, through the improvements made in this scheme, it enhances security compared to Zheng et al.’s scheme while maintaining nearly identical performance. Consequently, our approach achieves an improved trade-off between efficiency and security, making it more suitable for VANETs.

Through the above analysis, it can be observed that by introducing an additional aggregator signature into the aggregate signature process, our improved scheme is capable of resisting ephemeral rogue key attacks. Furthermore, the comparative analysis of computational performance shows that our improved scheme enhances security while still maintaining high efficiency. Specifically, when compared with other CLAS schemes^{22,30,31,32,33}, our approach demonstrates notable performance improvements, especially against schemes^22,30,32 that rely on bilinear pairings. Experimental results further show that the addition of an aggregator signature has a negligible impact on the actual verification process compared to Zheng et al.’s²⁷ scheme.

Conclusion

In this work, we first evaluated the security of the CLAS scheme proposed by Zheng et al.²⁷ for VANETs and identified its vulnerability to temporary rogue-key attacks. We rigorously formalized the attack methodology and proposed an enhanced CLAS scheme to mitigate these security flaws. A key innovation in our improved design is the introduction of an additional aggregator’s signature, which ensures the security of VANETs through dual-layer verification-validating both the aggregator’s signature and the aggregate signatures. This dual-validation mechanism strengthens resistance to collusion attacks and malicious aggregators while preserving the efficiency of the original scheme.

Our scheme is unforgeable against two types of attackers under the ECDLP assumption. Furthermore, the scheme satisfies the requirements of vehicle authentication, anonymity, traceability, non-repudiation, and unlinkability and so on. To validate practicality, we conducted a comprehensive performance analysis comparing our scheme with existing approaches^{22,30,31,32,33}. Experimental results demonstrate that our solution achieves lower computational and communication overhead while maintaining robust security guarantees. This balance positions our scheme as a scalable and efficient choice for resource-constrained VANETs environments.

Combining certificateless aggregated signatures with emerging technologies such as blockchain to promote the implementation of decentralized applications will be a very interesting future direction. Meanwhile, expanding the application to more scenarios (such as healthcare and education, etc.) is also worthy of attention.