Introduction

Cancer remains one of the leading causes of morbidity and mortality worldwide. According to the World Health Organization (WHO), cancer accounted for over 10 million deaths in 2020, representing approximately one in six deaths globally1. In the United States, about 40.5% of men and women are expected to be diagnosed with cancer at some point in their lifetimes2. Early detection significantly improves patient outcomes, as timely intervention and treatment can increase survival rates. For instance, the five-year survival rate for liver cancer detected at a localized stage is about 37%, compared to just 4% when diagnosed at a distant stage3. Similarly, early detection of bladder cancer can increase the five-year survival rate from 8 to 71%4. Despite the clear benefits of early detection, predicting the onset of cancer remains a complex challenge due to the multifactorial nature of the disease and the intricate interplay of genetic, environmental, and lifestyle factors5.

Traditional risk assessment tools are often limited, as they tend to rely on single factors or simplistic models that may not capture the complexity of cancer development6. Machine learning has emerged as a promising solution, offering the ability to model complex biological phenomena and enhance predictive accuracy for cancer diagnosis and prognosis7. Survival analysis techniques, such as the Cox proportional hazards model, are widely used to analyze time-to-event data in medical research, particularly in cases with censored observations8. The semi-parametric nature of the Cox model allows it to handle a variety of covariates without specifying the baseline hazard function, making it versatile for studying the relationship between patient characteristics and cancer development. Incorporating regularization techniques such as elastic net further improves the model by addressing multicollinearity and refining feature selection9. However, despite advancements in predictive modeling, significant challenges remain in translating machine learning tools into clinical practice. While there have been substantial advances in explainable AI10, the technical complexity and specialized expertise required to interpret these methods often render such models inaccessible to most end users11. This challenge is particularly acute in high-stakes settings, where deep learning algorithms—despite their high accuracy—are still widely perceived by clinicians as “black boxes”12. For instance, deep learning models have demonstrated impressive performance in tasks such as cancer detection from imaging data, yet their lack of transparency can undermine clinical trust and impede adoption13. This persistent opacity highlights the need for models that not only achieve strong predictive performance but are also interpretable and aligned with clinical reasoning processes14.

Another critical challenge is the generalizability of many existing machine learning models for cancer prediction. These models are often developed using data from specific populations or regions, which may not account for the demographic and genetic diversity seen across different groups. As a result, their performance may suffer when applied elsewhere15. For instance, a liver cancer risk prediction model developed in Asian populations may perform poorly in Western populations due to differences in hepatitis prevalence and etiological factors16. Moreover, overfitting to specific datasets can limit the model’s real-world utility, potentially exacerbating health disparities and biases inherent in the training data17.

Previous studies have applied machine learning models to predict cancer risk and outcomes, though many have focused on specific types of cancer or endpoints. For example, machine learning approaches have been used to assess lung cancer risk using clinical and imaging features (n = 2537)18 and to predict survival in liver cancer patients based on genomic and clinical data (n = 1136)19. However, these studies often have relatively small sample sizes, limiting the generalizability and robustness of their findings. Additionally, most models have focused on survival post-diagnosis, rather than predicting the time to cancer onset. To date, there has been a lack of well-powered research on predictive models that estimate the time to first cancer diagnosis across diverse populations and multiple cancer types. Our study addresses these gaps by leveraging large cohorts to develop more comprehensive and generalizable models for cancer prediction.

There is a critical need for predictive models that can estimate the time to first cancer diagnosis across various cancer types and populations. These models could help identify high-risk individuals, enabling targeted screening and preventive interventions. Moreover, models that balance high predictive performance with interpretability are essential for their integration into clinical workflows20. In this study, we aim to fill these gaps by developing a traditional Cox model and machine learning models to predict the time to first cancer diagnosis for cancers affecting both sexes. Using the Prostate, Lung, Colorectal, and Ovarian (PLCO) Cancer Screening Trial dataset for training and the UK Biobank (UKBB) cohort for external validation, we focus on cancers with significant incidence and mortality rates, including lung, liver, and bladder cancers. By employing the Cox proportional hazards model with elastic net regularization, we prioritize model interpretability and clinical relevance. We also compare the performance of our models against more complex tree-based methods to assess the trade-offs between model complexity and practical utility. Figure 1 shows the data workflow for model development and evaluation.

Fig. 1
figure 1

Model development and evaluation workflow: This figure outlines the workflow for predicting time-to-first cancer diagnosis using PLCO data. After preprocessing (exclusion criteria, missForest imputation, and feature standardization), three models—Cox proportional hazards, survival decision tree, and random survival forest—were trained on PLCO data and then evaluated on UKBB participants. Key outputs include a coefficient heatmap from the Cox proportional hazards model, a time-dependent AUC curve comparing performance, and a table summarizing C-index values across cancer types, highlighting the Cox model’s superior accuracy.

Full size image

Our objectives are twofold:

  1. 1.

    Develop predictive models of differing interpretability levels to accurately estimate time to first cancer diagnosis over a 10-year period using demographic, clinical, and behavioral variables.

  2. 2.

    Externally validate these models on a different dataset to evaluate their generalizability across different populations.

Through this research, we aim to contribute to the advancement of personalized medicine by providing tools that enhance early detection strategies and support clinical decision-making.

Methods

Datasets

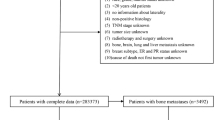
The Prostate, Lung, Colorectal, and Ovarian (PLCO) Cancer Screening Trial, initiated by the National Cancer Institute (NCI), is a large-scale, randomized trial that enrolled 155,000 participants from 1993 to 200121. Originally designed to assess the efficacy of cancer screening on mortality, the PLCO trial has gathered extensive longitudinal data on both cancer incidence and mortality, making it a valuable resource for studying time-to-event outcomes, such as cancer diagnoses21. The PLCO dataset includes detailed demographic, clinical, and behavioral information for each participant, such as age, sex, smoking status, family history of cancer, and comorbid conditions21. Figure 2 represents the major data processing steps for PLCO and UKBB datasets. After applying exclusion criteria, our sample size in PLCO is 141,979. Since our primary objective is to develop models to accurately predict time-to-first cancer diagnosis, we only considered first cancer diagnosis and time to that diagnosis if a patient experienced multiple cancers. For the non-specific cancer model this means the time-to-cancer is based on their first diagnosis. For cancer-specific models patients with multiple cancers were removed if that cancer-type was not their first diagnosis. A full list of the sex-agnostic cancers we modeled can be found in Supplementary Table 1.

Fig. 2
figure 2

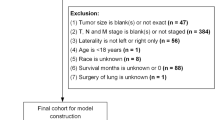
Data processing for PLCO and UKBB datasets: This flowchart summarizes the data exclusion criteria and final cohort sizes for the PLCO (A) and UKBB (B) datasets used in the analysis. For PLCO, patients with a previous history of cancer, diagnosis based solely on death certificates, or zero days to first cancer incidence were excluded, resulting in 141,979 participants, including 25,016 cancer cases and 116,963 non-cancer cases. For UKBB, participants with cancer diagnoses prior to assessment or an assessment date beyond confirmed censoring time were excluded, yielding a cohort of 287,150 participants, with 30,523 cancer cases and 256,627 non-cancer cases.

Full size image

To validate the generalizability of these models in a different population, we evaluated our model on the UK Biobank (UKBB) dataset. The UKBB is a large-scale, prospective cohort study with over 500,000 individuals that provides comprehensive genetic, phenotypic, and lifestyle data linked to national health records, making it an ideal external validation cohort for our U.S.-based PLCO model22. One significant challenge in this study was the absence of precise censoring times in the UKBB dataset. Traditional survival analysis methods rely on exact event and censoring times; however, the UKBB only provides dates for cancer diagnoses and the initial survey22.

To construct time-to-event outcomes, we treated the date of the baseline assessment—defined as the date of the initial clinic visit at one of 22 UKBB assessment centers—as time zero. For individuals with no cancer diagnosis recorded in the linked hospital inpatient data (ICD-10), we treated the most recent non-cancer ICD-10 record as the right-censoring time. This approach assumes that the absence of a cancer diagnosis up to that date implies a cancer-free status, a limitation imposed by the structure of UKBB’s follow-up data. Furthermore, to avoid ambiguity in survival time construction, we excluded individuals whose cancer diagnosis date preceded their baseline assessment, consistent with the framework of left censoring—where the event of interest occurs before the individual enters the study and thus cannot be properly modeled in our setup. We also excluded individuals whose baseline assessment occurred after their most recent non-cancer record, since this implies their time of entry postdates the inferred right-censoring time. The diagnoses prior to baseline assessment are available in UKBB through linkage of participant’s historical ICD-10 medical records. After applying these exclusions, we retained 287,150 participants in the UKBB cohort for model evaluation.

Data mapping and imputation

We utilized 46 sex-agnostic features covering demographics, comorbidities, and family history of cancer. All features used in modeling are shown in Supplementary Table 2. Our input features represent a single baseline snapshot of each participant, consistent with standard survival modeling approaches, which do not require longitudinal measurements. To ensure consistent feature selection across datasets, we mapped each PLCO feature to its corresponding UKBB variable. For example, the PLCO feature “SMKEV” (ever smoked) was matched to UKBB field “20160.” A complete list of feature mappings is provided in Supplementary Table 3. To standardize the baseline assessment, we used the first recorded instance of each UKBB feature. Cancer diagnoses were harmonized by converting ICD-10 codes into the cancer types of interest (Supplementary Table 4).

Although the predictive models are sex-agnostic, imputation was conducted separately for male and female subsets of the PLCO data before recombining them. This approach leveraged sex-specific data distributions, resulting in more accurate imputations given the known differences in health metrics and risk factors by sex. Missing values were imputed using the missForest package in R23, which accommodates both categorical and continuous variables. We optimized the mtry parameter (range: 1–9) and chose mtry = 5 for both sexes, balancing complexity and accuracy (Supplementary Figures 1–4). Iterative imputations continued until convergence, guided by out-of-bag error metrics, thereby maintaining reliable and consistent data relationships within each sex-specific subset. After imputation, the male and female datasets were merged to create a single sex-agnostic dataset for model training. Imputation for UKBB was conducted in the same manner, splitting the male and female data and using missForest with the same hyperparameters.

Before model training and evaluation, we applied standard scaling to all continuous features, normalizing them to a mean of 0 and a standard deviation of 1. This scaling, derived from the PLCO training set, was consistently applied to both PLCO and UKBB datasets. By standardizing feature ranges, we minimized the undue influence of variables with inherently larger numeric values, thus reducing bias and improving model performance, especially for algorithms sensitive to feature magnitude. Additionally, categorical variables were one-hot encoded to avoid ordinal assumptions and allow compatibility with machine learning models.

Evaluation metrics

We assessed predictive performance using three complementary metrics: the concordance index (C-index), the time-dependent area under the receiver operating characteristic curve (AUC), and the Lift metric. Together, these measures provide a comprehensive view of both global and time-specific model discrimination, as well as practical utility in identifying high-risk individuals.

The C-index quantifies how well a model ranks survival times, accounting for censored observations24. It represents the probability that, for a randomly selected pair of individuals, the model correctly identifies which individual experiences the event first. Values range from 0.5 (random guessing) to 1.0 (perfect prediction). The C-index thus offers an overall evaluation of a model’s discriminatory power without focusing on a single time point.

To complement this global perspective, we employed the time-dependent AUC, which extends the conventional AUC metric into the survival setting25. By examining the model’s ability to distinguish between individuals who develop cancer and those who remain cancer-free at various time intervals, the time-dependent AUC captures how discrimination changes over the follow-up period. This temporal view helps identify when a model’s predictive power is strongest and when its performance declines.

To further assess clinical relevance—especially in rare-event settings—we computed the Lift metric, defined as the inverse-probability-of-censoring–weighted positive predictive value (PPV) divided by the baseline event rate at each time point. Lift was evaluated over a grid of our 10-year prediction time interval, using risk thresholds corresponding to the top 1%, 5%, 10%, and 20% of predicted scores. A Lift of 3.0 at a given time, for instance, indicates that individuals in the top-scoring group are three times more likely to develop cancer by that time than the average person. This metric highlights each model’s ability to meaningfully stratify individuals by risk, offering an intuitive and prevalence-normalized view of predictive utility.

By integrating the C-index, time-dependent AUC, and Lift, we capture not only how well a model discriminates overall and across time, but also how effectively it concentrates cancer risk in the highest-scoring individuals—information critical for clinical decision-making and targeted interventions. We constructed 95% confidence intervals for both metrics through 400 bootstrap iterations of training and evaluation.

Statistical and machine learning models

Although over 110 FDA-cleared machine learning algorithms exist in healthcare, clinicians often struggle to trust and understand these tools26,27. To address this, we employed statistical and machine learning approaches that balance predictive accuracy, interpretability, and clinical relevance. For each cancer type, we trained a cancer-specific predictive model using data from PLCO participants diagnosed with that specific cancer and from those who remained cancer-free during the study. We also developed a non-specific “pan-cancer” model that predicted the occurrence of any type of cancer, pooling together all patients who experienced any type of cancer.

We focused on three modeling strategies: a Cox proportional hazards model with elastic net regularization, survival decision trees, and a random survival forest (RSF). The Cox model, known for its interpretability and direct estimation of hazard ratios, was our primary choice8. By incorporating elastic net regularization, which balances L1 (lasso) and L2 (ridge) penalties, we enhanced feature selection and model generalizability, particularly when dealing with correlated variables9,28. We used an L1 ratio of 0.9. This hybrid approach allowed us to retain a parsimonious subset of important features29. Hyperparameters were tuned using 10-fold cross-validation and then fitted on the entire training dataset.

We next explored Survival Decision Trees, which are often viewed as intuitive due to their resemblance to clinical decision-making processes30. These non-parametric models partition the data into regions with similar survival outcomes, capturing complex, non-linear relationships30. However, while decision trees are interpretable in theory, achieving high accuracy often requires deep trees with many splits, which can lead to models that are too large and complex for human comprehension. To mitigate this, we applied randomized hyperparameter tuning with 10-fold cross-validation to balance accuracy with interpretability, optimizing parameters such as tree depth and minimum samples per split. After tuning, we fitted on the entire training set.

Finally, we employed RSF, an ensemble method that builds multiple Survival Decision Trees and averages their predictions31. By aggregating the results from many trees, RSF reduces model variance and enhances stability, particularly when dealing with high-dimensional data31. Though RSF has reduced interpretability compared to Survival Decision Tree, it offers superior predictive performance in scenarios where feature interactions are critical to survival outcomes. We tuned RSF hyperparameters (e.g., the number of trees, the subset of features at each split) through a randomized search of 10-fold cross-validation.

Cox feature coefficient scaling

In the Cox proportional hazards model, coefficients quantify the effect of each feature on survival, making these effect sizes clinically interpretable32,33. Given the importance of understanding these coefficients, we aimed to compare the influence of features across multiple cancer types. In our analysis, we scaled the feature coefficients from the cancer-specific Cox models by the variance of the corresponding features to ensure they were comparable across different cancer types. This standardization was essential because the magnitude of these coefficients, which denote the strength of the association between each feature and the time to cancer diagnosis, can vary significantly across models due to differences in data distributions and feature scaling34. Without such scaling, direct comparisons could lead to misleading conclusions, as discrepancies in feature magnitudes or underlying population characteristics may distort the interpretability of results35.

Results

Our models demonstrated robust predictive performance in estimating time-to-first-cancer diagnosis within the UKBB cohort, particularly excelling in lung, liver, and bladder cancers (Table 1). For most cancer types, our models generalized quite well relative to the averaged C-index from our 10-fold cross-validation on the PLCO dataset (Supplementary Table 5). The Cox proportional hazards model achieved the highest C-index values in all cancers, indicating strong discrimination ability with 0.813 (95% CI: 0.803–0.824) for lung cancer, 0.759 (95% CI: 0.725–0.789) for liver cancer, and 0.747 (95% CI: 0.734–0.759) for bladder cancer. The RSF model also performed well for lung cancer with a C-index of 0.802. Conversely, thyroid cancer had the lowest C-index values for both the Cox (0.584) and RSF (0.544) models, showcasing reduced predictive performance. The Survival Decision Tree displayed consistent results across cancer types, peaking at 0.784 for lung cancer.

Table 1 Performance comparison of predictive models by cancer type (C-Index and 95% confidence intervals) on evaluation set.
Full size table

Enhanced predictive performance of cancer-specific models

Table 1 and Fig. 3 show that cancer-specific models consistently achieve higher time-dependent AUC values compared to the non-specific cancer model predicting any cancer occurrence. For instance, models for lung, bladder, and liver cancers demonstrate significantly better discriminatory ability. The non-specific model performed quite poorly with the second lowest C-index of 0.589 (95% CI: 0.585–0.592), 0.224 points lower than the lung cancer-specific Cox model’s C-index of 0.813. Similarly, the non-specific model’s mean time-dependent AUC was 0.588, 0.222 lower than the lung cancer Cox model.

Fig. 3
figure 3

Time-dependent AUC with 95% Confidence Intervals for (A) Lung, (B) Liver, (C) Bladder, and (D) Any Cancer Models: The figure shows time-dependent AUC curves with 95% confidence intervals for predicting the occurrence of cancer using Cox proportional hazards, Survival Decision Tree, and RSF models. (A)–(C) depict predictions for specific cancer types: lung cancer (A), liver cancer (B), and bladder cancer (C). (D) represents the “any cancer” model, which predicts the occurrence of any type of cancer. The x-axis represents days since baseline assessment, and the y-axis shows the AUC. Mean AUC values for each model are provided within each panel.

Full size image

Cancer-specific models also achieved higher C-index and time-dependent AUC values across multiple cancers and showed more stable predictive performance over time, as evidenced by the time-dependent AUC plots. In contrast, the general model exhibited a flatter AUC curve with less pronounced temporal spikes.

Cox model achieves similar or greater risk concentration in top-ranked groups compared to ML-based models.

To assess how well each model concentrated time-to-first-cancer events into the highest-risk individuals, we computed the IPCW-weighted lift over a 10-year horizon for individuals in the top 1%, 5%, 10%, and 20% of predicted risk (Fig. 4). Across lung, liver, bladder as well as in a pooled non-specific model, the Cox proportional hazards model consistently demonstrated similar or greater enrichment in the highest-risk strata compared to the Survival Decision Tree and RSF models. For instance, in liver cancer models (Fig. 4, Panel B), the Cox model demonstrated markedly higher enrichment than both RSF and the Survival Tree. In the top 1% group, Cox reached up to 30 × lift, substantially exceeding RSF (~ 20 ×) and the tree model (~ 10 ×). This advantage persisted across the top 5% and 10% risk groups, where Cox maintained ~ 2 × higher lift than the nearest model. In lung cancer models (Fig. 4, Panel A), the RSF achieved the highest enrichment in the top 1% risk group, peaking at approximately 18 × within the first two years, while the Cox model followed closely at around 15–17 × . Both models significantly outperformed the Survival Tree, which showed a lift of ~ 10 × in the same stratum. At broader thresholds (top 5–20%), the three models showed similar patterns, with declining enrichment and convergence around a lift of 1 by the top 20%.

Fig. 4
figure 4

Cancer‑specific risk enrichment over time with 95% confidence intervals: Each row shows the inverse‑probability‑of‑censoring‑weighted lift (IPCW‑weighted lift) of the top risk strata, evaluated over ten years since baseline, for three models: Cox proportional hazards (blue), survival decision tree (green), and random survival forest (RSF, orange). Shaded bands denote 95% pointwise confidence intervals; the horizontal dashed line at lift = 1 indicates no enrichment. Within each row, panels correspond to increasing risk‐stratum sizes—Top 1%, Top 5%, Top 10%, and Top 20% for (A) Lung cancer models (B) Liver cancer models (C) Bladder cancer models (D) non‑specific “pan-cancer” models.

Full size image

In contrast, the non-specific models (Fig. 4, Panel D) showed limited stratification ability across all thresholds. Even in the top 1% group, lift values were substantially lower—approximately 2–3 × for RSF and Cox, and below 2 × for the Survival Tree. Across all strata, the non-specific models’ enrichment rapidly declined and plateaued near the baseline.

Cox model coefficients reveal unreported cancer-associated features

The scaled Cox model coefficients (Fig. 5) highlight both well-established risk factors and additional associations across multiple cancer types. Age consistently emerged as a major risk factor for lung (8.6), liver (3.9), and melanoma (3.3) cancers.

Fig. 5
figure 5

Heatmap of scaled coefficients by feature and cancer-specific cox proportional hazards model: This heatmap displays the scaled coefficients of selected features across various cancer types as determined by cancer-specific Cox proportional hazards models. Rows represent features such as age, BMI, cumulative smoking history, family history of cancers (e.g., melanoma, glioblastoma, head and neck cancer), and demographic variables (e.g., race and gender). Columns represent cancer-specific models. Positive coefficients indicate a higher risk, while negative coefficients indicate a protective effect. The color gradient reflects the magnitude and direction of the coefficients, with red indicating higher positive values and blue indicating negative values.

Full size image

Several body composition measures, particularly Body Mass Index (BMI), exhibited distinct patterns across cancer types. Elevated BMI was positively associated with renal (4.4), biliary (1.4), and thyroid (1.4) cancers, while showing negative associations with lung (− 3.3), head and neck (− 1.2), and melanoma (− 1).

Demographic factors also contributed to variation in cancer risk. Female sex was inversely associated with bladder (− 1.1), lung (− 1.1), and head and neck (− 0.94) cancers. White race was associated with increased melanoma risk (2.0), and Pacific Islander ethnicity showed positive associations with biliary (0.97) and renal (0.88) cancers.

Cumulative smoking exposure, measured by pack-years, was associated with lung (3.8), head and neck (3.5), and bladder (2.0) cancers. Family history variables showed notable patterns: a positive family history of upper gastrointestinal (GI) cancer was associated with increased risk of upper GI cancer (0.82) and decreased risk of melanoma (− 2.5). A comprehensive list of scaled feature coefficients is provided in Supplementary Figure 5.

Discussion

Interpretable statistical Cox model outperforms ML-based survival decision tree and random survival forest

Our findings show that cancer-specific Cox proportional hazards models consistently provided more accurate time-to-first cancer predictions than the ML-based Survival Decision Tree and RSF counterparts. This superior performance, combined with the Cox model’s interpretability, underscores the clinical value of well-regularized statistical approaches12. Hazard ratios offer a straightforward means of understanding and communicating risk associated with factors like smoking or genetic variants, thereby aiding clinicians in patient counseling and personalized care6.

In addition to achieving superior discrimination metrics, cancer-specific Cox models demonstrated markedly stronger risk concentration in our IPCW-weighted lift analysis, particularly for liver cancer where the top 1% risk group captured over 30 × the baseline event rate—compared to ~ 20 × for RSF and ~ 10 × for the Survival Tree. While RSF slightly outperformed Cox in the top 1% stratum for lung cancer, the Cox model remained highly competitive, showing comparable enrichment and greater consistency across broader thresholds. Importantly, all cancer-specific models (except for thyroid) outperformed non-specific counterparts, which exhibited substantially attenuated lift across all risk strata. These results highlight the importance of tailoring models to individual cancer types, as aggregating heterogeneous etiologies into pan-cancer models appears to dilute key tumor-specific risk patterns. For example, the lung-specific Cox model achieved a C-index of 0.813—far surpassing the pan-cancer Cox model’s 0.589, reflecting a nearly 38% relative gain. This trend extended even to the rarest cancers we modeled like biliary, where the cancer-specific model outperformed the pooled model in both ranking ability and AUC. These differences likely stem from the ability of cancer-specific models to retain nuanced, site-specific interactions that are lost in broader models. Prior studies echo this pattern: pan-cancer drug response models often achieve inflated accuracy due to between-tissue differences yet perform poorly when evaluated within a single cancer type36,37. Similarly, survival models developed using pooled multi-cancer data often fail to generalize when disaggregated by cancer site, with predictive accuracy retained in only a subset of cancer types38. Together with our findings, this underscores the need for cancer-specific predictive models that reflect the distinct biology and risk factor profiles of each malignancy.

When benchmarked against previous work, the cancer-specific Cox models with elastic net regularization performed competitively, especially given that we only used widely available clinical variables. Although imaging-based analyses such as the study by McWilliams et al. achieved a high AUC of 0.905 for predicting malignancy in pulmonary nodules using a total sample size of 1871 patients18, these methods require specialized imaging data that may not be readily available in routine clinical practice. Our lung cancer model, by contrast, achieved a C-index of 0.813 without specialized biomarkers or imaging, suggesting its utility as a risk stratification tool that can guide clinicians on whether further imaging or more invasive biomarker assessments are warranted. Similarly, our liver cancer model’s time-dependent AUC (0.759) approached the REACH-B model’s static AUC of 0.769 which predicted hepatocellular carcinoma risk16, despite the latter incorporating more specialized factors. Thus, while not replacing advanced diagnostics outright, our models can complement them by identifying patients who would benefit from additional testing.

Moreover, the time-dependent AUC for our cancer-specific models remained stable and comparatively high throughout extended follow-up, contrasting with the declining performance observed in generalized models. This consistency in predictive accuracy was matched by consistent risk stratification over time in our IPCW-weighted lift analysis, where enrichment remained elevated across the top 1% and 5% of predicted risk, particularly for lung and liver cancers. This reliability enhances their suitability for clinical practice, where dependable, long-term risk stratification is crucial. By offering a balance of accuracy, interpretability, and broad applicability, the Cox models can serve as valuable decision-support tools, helping inform interventions, follow-up strategies, and patient communication over the continuum of cancer care.

Interpreting coefficients from the Cox model

The heatmap of scaled coefficients from the Cox models provides valuable insights into the associations between risk factors and cancer types. Age emerged as a significant risk factor across multiple cancers, with substantial effect sizes in lung, liver, and melanoma cancers. This aligns with established knowledge that cancer risk increases with age due to the accumulation of genetic mutations, epigenetic alterations, and decreased immune surveillance5,39,40. For example, telomere shortening and increased oxidative stress in older individuals contribute to genomic instability, facilitating carcinogenesis.

BMI exhibited differential associations across cancer types, reflecting its complex role in cancer etiology. Elevated BMI was positively associated with renal, biliary, and thyroid cancers—consistent with literature linking obesity-related metabolic and inflammatory states to carcinogenesis40. Adipose tissue can secrete adipokines and pro-inflammatory cytokines that promote tumor initiation and progression. In contrast, BMI showed inverse associations with lung, head and neck, and melanoma cancers, highlighting the challenge of interpreting single risk factors in isolation. The negative association between BMI and lung cancer has been reported in prior studies, often attributed to confounding by smoking: individuals who smoke heavily tend to have suppressed appetite and lower body weight, which may artificially inflate the apparent protective effect of higher BMI40. Similarly, the inverse association between BMI and head and neck cancers may reflect this confounding pathway. However, the observed inverse correlation between BMI and melanoma risk is less well understood. It raises important questions about whether this relationship reflects true biological mechanisms, behavioral patterns, or residual confounding—highlighting an area for future investigation.

Smoking remains a critical and well-established risk factor, demonstrated by the strong positive associations between cumulative smoking exposure and increased risk of lung, head and neck, and bladder cancers. These findings reinforce the central role of tobacco-related carcinogens in driving tumorigenesis5,40. Tobacco-specific nitrosamines, for instance, are known to induce DNA damage and mutational signatures in key oncogenes and tumor suppressor genes.

The inverse associations between female sex and bladder, lung, and head and neck cancers align with epidemiological findings indicating that these cancers occur more frequently in males39,40. Possible explanations for this higher incidence in males include greater exposure to known risk factors, such as smoking and occupational hazards, as well as differences in hormonal milieu. Ethnic and racial variations, exemplified by the elevated melanoma risk in White individuals and the positive associations between Pacific Islander ethnicity and biliary and renal cancers, highlight how genetic background, cultural practices, and environmental exposures intersect to shape cancer susceptibility39,40. Such patterns emphasize the importance of targeted interventions and risk stratification strategies that account for demographic and ethnic diversity.

Finally, family history variables showed that risk cannot be fully captured by direct genetic predispositions to the same cancer type. For example, the positive association between a family history of upper GI cancers and upper GI cancer risk is expected, given shared genetic mutations (e.g., in CDH1 and APC)39. Yet the unexpected inverse association between upper GI cancer family history and melanoma risk suggests that certain protective behavioral patterns or environmental exposures might accompany families at risk for GI cancers, inadvertently reducing their melanoma susceptibility. More integrative research that considers cross-cancer family histories—looking beyond straightforward hereditary patterns—is needed to elucidate these complex relationships.

Limitations

While our use of 46 general features—including demographic variables, comorbidities, and family history of cancers—makes our models highly deployable in large-scale, cost-effective clinical settings, this generality may limit predictive performance for certain complex cancer types as shown in Table 1 and Supplementary Figure 6. The advantage of these features lies in their wide availability and ease of collection, facilitating implementation across various healthcare environments without the need for extensive or specialized data gathering.

However, incorporating more detailed clinical variables could enhance the predictive accuracy of our models, particularly for cancers with complex progression patterns. Previous research has demonstrated that including specific clinical variables such as tumor characteristics, treatment information, and pathological findings can improve model performance in predicting cancer outcomes6. For example, Hippisley-Cox and Coupland developed risk prediction algorithms using detailed clinical variables in a prospective cohort study6. Their comprehensive approach allowed for a more nuanced understanding of individual patient risk profiles.

By integrating such detailed clinical variables, future models could better capture the heterogeneity of tumor biology and patient responses, potentially improving predictive performance for complex cancers like glioblastoma and thyroid cancer, where our models showed reduced accuracy. Detailed information on tumor characteristics (e.g., grade, size, lymph node involvement) and treatment modalities could provide deeper insights into disease progression and patient outcomes41. However, the inclusion of these variables also presents challenges. Detailed clinical data may not be readily available in all settings, and collecting this information can be resource-intensive, potentially limiting the scalability and practicality of the models.

Moreover, our study’s observational nature may introduce biases due to unmeasured confounding variables. Important factors such as environmental exposures, occupational hazards, and detailed lifestyle habits were not included but may significantly influence cancer risk17. For instance, exposure to specific carcinogens in the workplace or particular dietary patterns could impact cancer development but were not accounted for in our models.

Differences in population characteristics and data collection methods between the PLCO trial and the UK Biobank may also affect the external validity of our models. The PLCO cohort primarily comprises participants from the United States, while the UK Biobank represents a UK population. Variations in healthcare systems, socioeconomic factors, and genetic backgrounds may limit the generalizability of our findings to other populations15. Additionally, selection bias may be present if the study participants are not representative of the broader population.

Lastly, while the Cox model offers interpretability, it assumes proportional hazards and linear relationships between covariates and the log hazard function, which may not hold true for all variables or cancer types41. Complex interactions and nonlinear relationships might be better captured by more advanced machine learning models, albeit at the expense of interpretability7. Incorporating genetic and molecular biomarkers, as well as detailed clinical variables, could enhance predictive accuracy and provide deeper insights into cancer etiology16. Future research should aim to balance the inclusion of additional clinical variables with the practicality of model deployment, exploring methods to integrate more detailed data without compromising scalability and cost-effectiveness.

Conclusion

In this study, we developed and validated predictive models for estimating time-to-first cancer diagnosis across multiple cancer types, prioritizing both accuracy and interpretability. Our findings demonstrate that tailored Cox proportional hazards models outperformed the more complex ML-based Survival Decision Tree and RSF in predictive accuracy for most cancers, achieving competitive C-index values comparable to existing models for specific cancers like lung and liver. The Cox model’s interpretability enhances its clinical utility, providing actionable insights for clinicians to counsel patients effectively and support personalized care.

Our results also emphasize the limitations of a generalized model across diverse cancers, as cancer-specific models demonstrated superior performance. Tailoring models to individual cancer types allows for better integration of relevant risk factors, underscoring the heterogeneous nature of cancer etiologies. While the use of broadly available clinical and demographic variables improves the scalability of our models, incorporating more specialized clinical and genetic features may further enhance predictive performance, particularly for cancers with complex progression patterns. With these additional features, more complex models may outperform the Cox model.

In conclusion, our research advances the application of interpretable, well-performing cancer prediction models, emphasizing the value of statistical approaches in achieving predictive accuracy while aligning with clinical needs for transparency and usability. Future studies should explore integrating more granular clinical data and biomarker profiles to further refine risk assessment across varied populations and cancer types, enhancing early detection strategies and supporting tailored interventions in clinical practice.