Dynamical description and analytical study of traveling wave solutions for generalized Benjamin-Ono equation

Abstract

The current manuscript deals with the analytical study of the generalized Benjamin-Ono (BO) equation. The underlying model has numerous applications in scientific fields like wave propagation effect and study of the plasma dynamics and complicated modeling of physical systems. The Jacobi elliptic function (JEF) expansion method is employed for employed for the solitary wave and soliton solutions for the underlying model. This technique provides dark, bright and dark periodic solitary wave solutions. Different solutions are chosen to draw their physical behavior. 2D, 3D and their corresponding contours are drawn and their physical behavior is explained in the context of real-life application. The stability analysis, chaotic behavior, sensitivity and bifurcation analysis is derived to analyze its various dynamics and simulations are plotted for various choices of the parameters. These results will create an impact in the existing literature.

Introduction

Nonlinear partial differential equations (NLPDEs) are essential for investigating intricate nonlinear events in various scientific fields, including solid-state physics, plasma physics, and condensed matter physics. Significant improvements have been made in the study of these equations over time. Numerous computational techniques have been developed in the literature to investigate the properties of solutions¹. In a deep ocean, the rotation-modified BO equation is used to study the interaction between a single wave and a long background periodic wave. Grimshaw et al. determined stationary and non-stationary solutions for BO solitons caught in a long sinusoidal wave using a multiple scales approach. However, in a quasi-random wave field, the coherent structure and energy dispersion are eventually destroyed due to the soliton’s feedback on the background wave. The soliton dynamic’s distinctive parameters are estimated for actual oceanic circumstances².

In order to explore certain physical interpretations for the Cahn–Hilliard system solutions, the unified method is introduced. These solutions are of the polynomial type and have various geometrical structures, including conoidal soliton, bright-dark, and M-type solutions³. Tarla et al. investigated the perturbed Chen-Lee-Liu equation with the help of JEF expansion method. Tarla et al. obtained solitary wave solutions such as dark-bright, trigonometric, exponential, hyperbolic, periodic, and singular soliton solutions⁴. Osman et al. worked on the coupled Schrödinger–Boussinesq equation with variable-coefficients to explored the nonautonomous complex wave solutions⁵, also the multiwave solutions of time-fractional (2+ 1)-dimensional Nizhnik–Novikov–Veselov equations⁶. Akbar et al. constructed the solitons for the shallow water waves and superconductivity models⁷, Nisar et al. considered the biological population model to explored the solitary wave solutions⁸. Umar et al. worked on the 2D generalized kadomtsev–petviashvili equation to gained the Hirota D-operator forms, multiple soliton waves, and other nonlinear patterns⁹.

Arafat et al. used the modified Kudryashov technique and the (2 + 1)-dimensional Konopelchenko-Dubrovsky model to derive traveling wave solutions (TWSs), which are represented as several wave profiles such as W-shape, bell shape, anti-bell shape, and kink shape^10,11,12. The Kadomtsev-Petviashvili and Calogero-Degasperis equation models are investigated by Islam and Basak, using the improved F-expansion approach. It reveals visually appealing TWSs in hyperbolic and rational functions as well as kink, dark, periodic, and v-shape¹³. Dey et al. obtained the solitons for the generalized (3+ 1)-dimensional shallow water-like equation using the $(\phi '/\phi , 1/\phi )$-expansion method¹⁴. Khan et al. considered the two distinct equations: the (1+ 1)-dimensional cKdV–mKdV equation and the sinh-Gordon equation to explored the traveling wave solutions¹⁵.

The extended Fan-sub equation technique and the Biswas-Arshed equation are applied by Bilal and Ahmad (2022) to study optical pulses in birefringent fibers. It generates hyperbolic, singular periodic waves and JEF solutions and recovers several shapes of optical pulses, such as bright, dark, singular, bright-dark, and dark-singular solitons¹⁶. Bilal et al. (2021) introduced novel integration norms such as the $(\frac{G'}{G^{2}})$-expansion method and the expansion function technique to achieve solutions such as shock, singular, shock-singular, and singular periodic waves for the Gilson-Pickering equation in plasma physics¹⁷. Khan et al. employed an improved JEF method for the improved modified kortwedge-de vries equation¹⁸.

Benjamin¹⁹ and Ono²⁰ presented the well-known BO equation that models the propagation of long internal waves in stratified fluids. The equation is integrable. Originally developed to simulate waves in shallow water, the BO equation has applications in fluid dynamics, nonlinear optics, and plasma physics. Because the generalized equation has many non-linear components, multiple non-linear phenomena become accessible. Because of its numerous and relevant physical applications, the generalized BO equation has been extensively studied. The BO equation, which was created by Benjamin¹⁹, Ono²⁰, Davis and Acrivos²¹ serves as a model for how waves change in deep sea. It is a dispersive equation that has been researched extensively, and its solutions are well understood^22,23,24. The BO equation was chosen as the first application for a numerical method due to its lower cost of evolution compared to vortex sheets or water waves. It shares features with these types, such as non-locality through the Hilbert transform and Birkhoff-Rott integral. Numerical simulation demonstrates a rich variety of nontrivial time-periodic solutions that connect traveling waves of various wavelengths and speeds like rungs in a ladder. These solutions produce or eliminate oscillatory humps, which gradually increase or decrease in size until they are incorporated into the stationary wave. The dynamics of these solutions are frequently interesting, which resemble low-amplitude traveling waves or interacting solitons passing through or bouncing off each other²⁵. The (2+1)-dimensional generalized BO equation²⁶, which is expressed as follows

$$\begin{aligned} u_{xxxx}+c_{1}u_{tt}+c_{2}u_{xt}+c_{3}u_{xy}+c_{4}(u^{2})_{xx}=0, \end{aligned}$$

(1)

where $c_{1},$ $c_{2},$ $c_{3},$ and $c_{4}$ stand for arbitrary constants. The generalized BO equation serves numerous scientific fields through its ability to model wave propagation analysis in optical fiber communications while advancing communication system designs. Plasma physics depends on the generalized BO equation to study wave behavior in plasma systems because such knowledge finds application in condensed matter physics for describing particular types of material waves that enhance understanding complex physical behaviors. Through the generalized BO equation, the system delivers essential operational functionality as its core instrument to solve various challenges in multiple domains.

The extended direct algebraic method²⁷, $\left( \frac{G'}{G},\frac{1}{G}\right)$-expansion technique²⁸, sub-ordinary differential equations method²⁹, Bilinear method³⁰, generalized Kudryashov method³¹, extended sinh-Gordon equation expansion method³², the unified method³³, Bilinear neural network technique^34,35, the Darboux transformations method³⁶, the new extended hyperbolic function method and the Sine-Gordon equation expansion method³⁷, $\phi ^6$-model expansion method³⁸, new extended direct algebraic method³⁹, the generalized exponential rational function technique^40,41, the generalized Riccati equation mapping approach⁴², and the Weierstrass elliptic function method⁴³ are a few of the well-known techniques. These methods are used to investigate a variety of solutions, like peaks, bright and dark solitons, and more. Nonlinear optics is a place where these solutions are sought, where the unique wave has the same shape as they travel, as a result of a fine balance between nonlinear and dispersion⁴⁴. But in this study we considered the JEF approach. The advantages of this is approach is easy to compute and the results are better then others in the form of both solitary waves and soliton solutions. The JEF method proves itself as an efficient analytical method to discover exact solutions of NLPDEs. The JEF method has successfully obtained solutions to several nonlinear equations, among which are Sine-Gordon, nonlinear Schrodinger, and Korteweg-de Vries (KdV). This approach provides the periodic and solitary wave solutions that improve the comprehension of non-linear wave behavior. But the limitations and the disadvantages of this method is only that, which is not applicable for all types of the NLPDEs. This is only applied to the even order ordinary differential equations. Moreover, the JEF method facilitates the derivation of periodic wave solutions that are of significant interest in physical models exhibiting nonlinear oscillatory behavior. Its algebraic formulation is particularly amenable to symbolic computation, enhancing both the efficiency and tractability of obtaining exact solutions. These attributes make the JEF method an effective and elegant tool for exploring nonlinear wave phenomena in various branches of applied mathematics and physics.

The main novelty of this study is to explore the exact solitary wave solutions for the generalized BO model along with the dynamical analysis and modulation instability analysis. For the analytical results, the JEF expansion method is used to explore various types of solitons and solitary wave solutions like dark, bright, dark-bright, singular, and other mixed solitons with solitary wave solutions. The Galilean transformation is used to convert the system into a planar dynamical system to explore the bifurcation and sensitivity analysis of the model. Lastly, the modulation instability is also derived along with the physical representation as well.

Methodology

The description of the JEF expansion method is described in this section. To pursue these studies, the following procedures will be executed^45,46,47:

Step 1: The mathematical form of the NPDEs is usually as follows

$$\begin{aligned} A(u,u_{t},u_{x},u_{tt},u_{xx},\cdots )=0. \end{aligned}$$

(2)

Step 2: Using the chain rule and converting $eq.(2)$

$$\begin{aligned} u(x,y,t)=\phi (\eta ), \end{aligned}$$

(3)

where $\eta =ax+by-\gamma t$. $eq.(2)$ was transformed into an ordinary differential equation (ODE) by the given following form with modification in $eq.(3)$

$$\begin{aligned} \frac{\partial (.)}{\partial t}=-\gamma k\frac{d(.)}{d\eta },\frac{\partial (.)}{\partial x}=k\frac{d(.)}{d\eta }, \end{aligned}$$

(4)

the general form of ODE is considered as

$$\begin{aligned} A(u',u'',u''',\cdots )=0. \end{aligned}$$

(5)

The principal aim of this approach is to improve the capacity to solve an auxiliary ODE, which is the first kind of three-parameter Jacobian equation,

$$\begin{aligned} (\chi ')^{2}(\eta )=L\chi ^{4}(\eta )+M\chi ^{2}(\eta )+N, \end{aligned}$$

(6)

where $\chi '$ = $\frac{d\chi }{d\eta }$, $\eta$ = $\eta (x, t)$ and L, M, & N are constants. $eq.(6)$’s solution is found in JEF¹⁸. $sn \eta$ = $sn(\eta ,\rho )$, $cn \eta$ = $cn(\eta ,\rho )$ and $dn \eta$ = $dn(\eta ,\rho )$ are the Jacobi elliptic functions (JEFs), and $\rho$(0 < $\rho$ < 1) is the modulus. The following are some characteristics of the double periodic elliptic functions

$$\begin{aligned} & sn^{2}\eta +cn^{2}\eta =1,\\ & dn^{2}\eta +\rho ^{2}sn^{2}\eta =1,\\ & \frac{d}{d\eta }sn\eta =cn\eta *dn\eta ,\\ \end{aligned}$$

$$\begin{aligned} & \frac{d}{d\eta }cn\eta =-sn\eta *dn\eta ,\\ & \frac{d}{d\eta }dn\eta =-\rho ^{2}sn\eta *cn\eta . \end{aligned}$$

Since JEFs, which are presented in JEF¹⁸, were reduced to hyperbolic and trigonometric functions in the restrictive sense for $\rho \rightarrow 0$ and $\rho \rightarrow 1$, we used the JEF expansion technique to find trigonometric function and soliton solutions to the problem, denoting $u(\eta )$ as a finite series of JEFs.

$$\begin{aligned} u(\eta )=\sum _{j=0}^{m} a_{j}\chi ^{j}(\eta ). \end{aligned}$$

(7)

$\chi (\eta )$ is the solution to nonlinear ordinary $eq.(6)$, using the constants m and $a_{j}(j = 0,1,2,...,m)$ that we obtained later. The highest order linear term in $eq.(7)$ can be used to determine the integer m.

$$\begin{aligned} R\left( \frac{d^{a}u}{d\eta ^{a}}\right) =m+a,\; a=0,1,2,3,\cdots , \end{aligned}$$

(8)

Thus, the nonlinear terms of the highest order are

$$\begin{aligned} R\left( u^{b}\frac{d^{a}u}{d\eta ^{a}}\right) =(b+1)m+a,\;a=0,1,2,3,\cdots ,b=1,2,3,\cdots \end{aligned}$$

(9)

Equation 7 is used to solve the nonlinear algebraic equations system for $a_{j}(j = 0, 1, 2,..., m)$, by adjusting all of the coefficients of powers $\chi$ to zero. Wolfram Mathematica 11.1 is used to solve the system and display the values for A, B, and C of $eq.(6)$ in JEF¹⁸, allowing for exact solutions for $eq.(2)$.

Solutions of the generalized Benjamin-Ono equation

Considered the wave transformation as

$u(x,y,t)=\phi (\eta )$, where $\eta =ax+by-\gamma t$.

Taking the derivatives and submit into the $eq.(1)$ and get the ODE as

$$\begin{aligned} a^{4}\phi ^{(4)}+\phi ''\left( \gamma ^{2}c_{1}-c_{2}\gamma a+c_{3}a b\right) +2 a^{2}c_{4}\left( \phi \phi ''+\phi '^{2}\right) . \end{aligned}$$

(10)

By taking integration of eq.(2), we have

$$\begin{aligned} a^{4}\frac{d^{2}\phi }{d\eta ^{2}}+\phi \left( \gamma ^{2}c_{1}-c_{2}\gamma a+c_{3}a b\right) +a^{2}c_{4}\phi ^{2}. \end{aligned}$$

(11)

After resolving the nonlinear term $\phi ''$ and the highest-order derivative term $\phi ^{2}$ in $eq.(10)$, we apply homogeneous balancing principle. By this procedure, we obtain $n = 2$. The solution of $eq.(10)$ is then written of the form:

$$\begin{aligned} \phi (\eta )=\alpha _0+\alpha _{2} \chi (\eta )^2+\alpha _1 \chi (\eta ), \end{aligned}$$

(12)

Taking the derivatives of the $eq.(12)$ along with $eq.(6)$ into $eq.(11)$ and get

$$\begin{aligned} & 6 \alpha _2 a^4 L \chi (\eta )^4+2 \alpha _1 a^4 L \chi (\eta )^3+4 \alpha _2 a^4 M \chi (\eta )^2+\alpha _1 a^4 M \chi (\eta )+2 \alpha _2 a^4N \nonumber \\ & \quad +\alpha _0^2 a^2 c_4+\alpha _2^2 a^2 c_4 \chi (\eta )^4+2 \alpha _1 \alpha _2 a^2 c_4 \chi (\eta )^3+\alpha _1^2 a^2 c_4 \chi (\eta )^2+2 \alpha _0 \alpha _2 a^2 c_4 \chi (\eta )^2 \nonumber \\ & \quad +2 \alpha _0 \alpha _1 a^2 c_4 \chi (\eta )+\alpha _0 a b c_3+\alpha _2 a b c_3 \chi (\eta )^2+\alpha _1 a b c_3 \chi (\eta )-\alpha _0 a \gamma c_2-\alpha _2 a \gamma c_2 \chi (\eta )^2 \nonumber \\ & \quad -\alpha _1 a \gamma c_2 \chi (\eta )+\alpha _0 \gamma ^2 c_1+\alpha _2 \gamma ^2 c_1 \chi (\eta )^2+\alpha _1 \gamma ^2 c_1 \chi (\eta )=0, \end{aligned}$$

(13)

by collecting various powers of $\chi (\eta )$, we obtained:

$$\begin{aligned} \left. \begin{array}{l} 2 \alpha _2 a^4 N+\alpha _0^2 a^2 c_4+\alpha _0 a b c_3-\alpha _0 a \gamma c_2+\alpha _0 \gamma ^2 c_1=0,\\ \alpha _1 a^4 M+2 \alpha _0 \alpha _1 a^2 c_4+\alpha _1 a b c_3-\alpha _1 a \gamma c_2+\alpha _1 \gamma ^2 c_1=0,\\ 4 \alpha _2 a^4 M+\alpha _1^2 a^2 c_4+2 \alpha _0 \alpha _2 a^2 c_4+\alpha _2 a b c_3-\alpha _2 a \gamma c_2+\alpha _2 \gamma ^2 c_1=0,\\ 2 \alpha _1 a^4 L+2 \alpha _1 \alpha _2 a^2 c_4=0,\\ 6 \alpha _2 a^4 L+\alpha _2^2 a^2 c_4=0.\\ \end{array} \right. \end{aligned}$$

(14)

The above mentioned system (14) is solved using Wolfram Mathematica 11.1, now the coefficient values are as follows:

$$\begin{aligned} \alpha _0=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( M^2-3 L N\right) }-a^2 c_4 M\right] , \alpha _1=0, \alpha _2=-\frac{6 a^2 L}{c_4}. \end{aligned}$$

(15)

$$\begin{aligned} \gamma =\frac{\sqrt{a \left( a c_2^2-\frac{4 c_1 \left( 4 a \sqrt{a^4 c_4^2 \left( M^2-3 L N\right) }+b c_3 c_4\right) }{c_4}\right) }+a c_2}{2 c_1}. \end{aligned}$$

(16)

The exact solution of $eq.(1)$ was obtained by applying the previously defined solution approach.

$$\begin{aligned} u(\eta )= \frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( M^2-3 L N\right) }-a^2 c_4 M\right] -\frac{6 a^2 L}{c_4} \chi (\eta )^2. \end{aligned}$$

(17)

Case 1: When we select L= $\rho ^{2}$, M= $-(1+\rho ^{2})$, N= 1, $\chi (\eta )$= $sn(\eta )$ from JEF¹⁸, the solution is:

$$\begin{aligned} u_{1}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( -\rho ^2-1\right) ^2-3 N \rho ^2\right) }-a^2 c_4 \left( -\rho ^2-1\right) \right] -\frac{6 a^2 \rho ^2 }{c_4}\left[ \text {sn}(\eta )^2\right] , \end{aligned}$$

(18)

from JEF¹⁸, suppose $\rho \rightarrow 1$, the solution obtained as:

$$\begin{aligned} u_{2}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2}+2 a^2 c_4\right] -\frac{6 a^2}{c_4}\left[ \tanh ^2(ax+by-\gamma t)\right] . \end{aligned}$$

(19)

Case 2: Setting A= $-\rho ^{2}$, B= $2\rho ^{2}-1$, C= $1-\rho ^{2}$, it conclude from JEF¹⁸, $\chi (\eta )$= $cn(\eta )$, the periodic solution expressed as:

$$\begin{aligned} u_{3}=\frac{6 a^2 \rho ^2}{c_4} \left[ \text {cn}(\eta )^2\right] +\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( 3 N \rho ^2+\left( 2 \rho ^2-1\right) ^2\right) }-a^2 c_4 \left( 2 \rho ^2-1\right) \right] , \end{aligned}$$

(20)

if $\rho \rightarrow 1$, from JEF¹⁸, we get:

$$\begin{aligned} u_{4}=\frac{6 a^2 }{c_4}\left[ \text {sech}^2(ax+by-\gamma t )\right] +\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-a^2 c_4\right] . \end{aligned}$$

(21)

Case 3: Choosing L= −1, M= $2-\rho ^{2}$, N= $\rho ^{2}-1$, from JEF¹⁸, gives $\chi (\eta )$= $dn(\eta )$, we obtained the periodic solution as

$$\begin{aligned} u_{5}=\frac{6 a^2}{c_4} \left[ \text {dn}(\eta )^2\right] +\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( 3 N+\left( 2-\rho ^2\right) ^2\right) }-a^2 c_4 \left( 2-\rho ^2\right) \right] , \end{aligned}$$

(22)

from v, for $\rho \rightarrow 1$, the solution is similar to $eq.(21)$.

Case 4: Supposing L= 1, M= $-(1+\rho ^{2})$, N= $\rho ^{2}$, from JEF¹⁸, gives $\chi (\eta )$= $ns(\eta )$, then obtained the periodic solution as

$$\begin{aligned} u_{6}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( -\rho ^2-1\right) ^2-3 N\right) }-a^2 c_4 \left( -\rho ^2-1\right) \right] -\frac{6 a^2 }{c_4}\left[ \text {ns}(\eta )^2\right] , \end{aligned}$$

(23)

furthermore, from JEF¹⁸, for $\rho \rightarrow 1$, the solution is expressed as:

$$\begin{aligned} u_{7}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }+2 a^2 c_4\right] -\frac{6 a^2 }{c_4}\left[ \coth ^2(ax+by-\gamma t)\right] , \end{aligned}$$

(24)

from JEF¹⁸, if $\rho \rightarrow 0$, $eq.(1)$’s solution is written as:

$$\begin{aligned} u_{8}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }+a^2 c_4\right] -\frac{6 a^2}{c_4}\left[ \csc ^2(ax+by-\gamma t )\right] . \end{aligned}$$

(25)

Case 4(ii): Supposing L= 1, M= $-(1+\rho ^{2})$, M= $\rho ^{2}$, from JEF¹⁸, $\chi (\eta )$= $dc(\eta )$

$$\begin{aligned} u_{9}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( -\rho ^2-1\right) ^2-3 N\right) }-a^2 c_4 \left( -\rho ^2-1\right) \right] -\frac{6 a^2}{c_4} \left[ \text {dc}(\eta )^2\right] , \end{aligned}$$

(26)

for $\rho \rightarrow 0$, by JEF¹⁸, $eq.(1)$’s solution is written as:

$$\begin{aligned} u_{10}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }+a^2 c_4\right] -\frac{6 a^2}{c_4}\left[ \sec ^2(ax+by-\gamma t )\right] . \end{aligned}$$

(27)

Case 5: While L= $1-\rho ^{2}$, M= $2\rho ^{2}-1$, N= $-\rho ^{2}$, from JEF¹⁸, gives $\chi (\eta )$= $nc(\eta )$, then the periodic solution is expressed as

$$\begin{aligned} u_{11}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( 2 \rho ^2-1\right) ^2-3 N \left( 1-\rho ^2\right) \right) }-a^2 c_4 \left( 2 \rho ^2-1\right) \right] -\frac{6 a^2 \left( 1-\rho ^2\right) }{c_4}\left[ \text {nc}(\eta )^2\right] , \end{aligned}$$

(28)

and for $\rho \rightarrow 0$, from JEF¹⁸, solution of $eq.(1)$ is determined as:

$$\begin{aligned} u_{12}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }+a^2 c_4\right] -\frac{6 a^2}{c_4} \left[ \sec ^2(ax+by-\gamma t )\right] . \end{aligned}$$

(29)

Case 6: Supposing L= $\rho ^{2}-1$, M= $2-\rho ^{2}$, N= $-1$, from JEF¹⁸, this relates to $\chi (\eta )$= $nd(\eta )$, so

$$\begin{aligned} u_{13}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( 2-\rho ^2\right) ^2-3 N \left( \rho ^2-1\right) \right) }-a^2 c_4 \left( 2-\rho ^2\right) \right] -\frac{6 a^2 \left( \rho ^2-1\right) }{c_4} \left[ \text {nd}(\eta )^2\right] , \end{aligned}$$

(30)

is found and if $\rho \rightarrow 0$, then from JEF¹⁸, the solution obtained as:

$$\begin{aligned} u_{14}=\frac{6 a^2}{c_4} (ax+by-\gamma t )^2+\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-2 a^2 c_4\right] . \end{aligned}$$

(31)

Case 7: Assuming L= $1-\rho ^{2}$, M= $2-\rho ^{2}$, N= 1, from JEF¹⁸, and $\chi (\eta )$= $sc(\eta )$, we get

$$\begin{aligned} u_{15}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( 2-\rho ^2\right) ^2-3 N \left( 1-\rho ^2\right) \right) }-a^2 c_4 \left( 2-\rho ^2\right) \right] -\frac{6 a^2 \left( 1-\rho ^2\right) }{c_4}\left[ \text {sc}(\eta )^2\right] , \end{aligned}$$

(32)

and if $\rho \rightarrow 0$, then from JEF¹⁸, the solution is given as:

$$\begin{aligned} u_{16}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-2 a^2 c_4\right] -\frac{6 a^2}{c_4}\left[ \tan ^2(ax+by-\gamma t )\right] . \end{aligned}$$

(33)

Case 9: Assigning L= 1, M= $2-\rho ^{2}$, N= $1-\rho ^{2}$, from JEF¹⁸, and $\chi (\eta )$= $cs(\eta )$, the solution determined as

$$\begin{aligned} u_{17}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( 2-\rho ^2\right) ^2-3 N\right) }-a^2 c_4 \left( 2-\rho ^2\right) \right] -\frac{6 a^2}{c_4} \left[ \text {cs}(\eta )^2\right] , \end{aligned}$$

(34)

from JEF¹⁸, if $\rho \rightarrow 1$, then the solution is represented as:

$$\begin{aligned} u_{18}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-a^2 c_4\right] -\frac{6 a^2}{c_4}\left[ \text {csch}^2(ax+by-\gamma t )\right] , \end{aligned}$$

(35)

also for $\rho \rightarrow 0$, from JEF¹⁸, the solution we have:

$$\begin{aligned} u_{19}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-2 a^2 c_4\right] -\frac{6 a^2}{c_4} \left[ \cot ^2(ax+by-\gamma t )\right] . \end{aligned}$$

(36)

Case 10: Assigning L= 1, M= $2\rho ^{2}-1$, N= $\rho ^{2}(1-\rho ^{2})$, from JEF¹⁸, and $\chi (\eta )$= $ds(\eta )$, the solution is determined as

$$\begin{aligned} u_{20}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \left( 2 \rho ^2-1\right) ^2-3 N\right) }-a^2 c_4 \left( 2 \rho ^2-1\right) \right] -\frac{6 a^2}{c_4} \left[ \text {ds}(\eta )^2\right] , \end{aligned}$$

(37)

for $\rho \rightarrow 1$, the solution is same as $eq.(35)$, and if $\rho \rightarrow 0$, from JEF¹⁸, the solution is alike $eq.(25)$.

Case 11: Considering L= $\frac{-1}{4}$, M= $\frac{\rho ^{2}+1}{2}$, N= $\frac{-(1-\rho ^{2})^{2}}{4}$, from JEF¹⁸, and $\chi (\eta )$= $\rho cn\pm dn$, the solution is determined as

$$\begin{aligned} u_{21}=\frac{3 a^2 }{2 c_4}\left[ \text {cn}(\eta ) \rho +\text {dn}(\eta )\right] ^2+\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{3 N}{4}+\frac{1}{4} \left( \rho ^2+1\right) ^2\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2+1\right) \right] , \end{aligned}$$

(38)

additionally for $\rho \rightarrow 1$, the solution is

$$\begin{aligned} u_{22}=\frac{3 a^2}{2 c_4} \left[ (2 \text {Sech})(ax+by-\gamma t )\right] ^2+\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }-a^2 c_4\right] . \end{aligned}$$

(39)

Case 12: When L= $\frac{1}{4}$, M= $\frac{-2\rho ^{2}+1}{2}$, N= $\frac{1}{4}$, from JEF¹⁸, and $\chi (\eta )$= $ns\pm cs$, the solution appeared as

$$\begin{aligned} u_{23}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( 1-2 \rho ^2\right) ^2-\frac{3 N}{4}\right) }-\frac{1}{2} a^2 c_4 \left( 1-2 \rho ^2\right) \right] -\frac{3 a^2}{2 c_4} \left[ \text {cs}(\eta )+\text {ns}(\eta )\right] ^2, \end{aligned}$$

(40)

furthermore,if $\rho \rightarrow 1$, the solution evaluated as

$$\begin{aligned} u_{24}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }+\frac{a^2 c_4}{2}\right] -\frac{3 a^2 }{2 c_4}\left[ \text {Coth}(ax+by-\gamma t )+\text {Csch}(ax+by-\gamma t )\right] ^2, \end{aligned}$$

(41)

also for $\rho \rightarrow 0$, the solution

$$\begin{aligned} u_{25}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }-\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \text {Cot}(ax+by-\gamma t )+\text {Csc}(ax+by-\gamma t )\right] ^2, \end{aligned}$$

(42)

is obtained.

Case 13: Taking L= $\frac{1-\rho ^{2}}{4}$, M= $\frac{\rho ^{2}+1}{2}$, N= $\frac{1-\rho ^{2}}{4}$, from JEF¹⁸, and $\chi (\eta )$= $nc\pm sc$, the solution gets

$$\begin{aligned} u_{26}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2+1\right) ^2-\frac{3}{4} N \left( 1-\rho ^2\right) \right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2+1\right) \right] -\frac{3 a^2 \left( 1-\rho ^2\right) }{2 c_4} \left[ \text {nc}(\eta )+\text {sc}(\eta )\right] ^2, \end{aligned}$$

(43)

if $\rho \rightarrow 0$, acquiring solution as

$$\begin{aligned} u_{27}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }-\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \text {Sec}(ax+by-\gamma t )+\text {Tan}(ax+by-\gamma t )\right] ^2. \end{aligned}$$

(44)

Case 14: Setting L= $\frac{1}{4}$, M= $\frac{\rho ^{2}-2}{2}$, N= $\frac{\rho ^{2}}{4}$, by JEF¹⁸, this $\chi (\eta )$= $ns\pm ds$, results

$$\begin{aligned} u_{28}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2-2\right) ^2-\frac{3 N}{4}\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2-2\right) \right] -\frac{3 a^2}{2 c_4} \left[ \text {ds}(\eta )+\text {ns}(\eta )\right] ^2, \end{aligned}$$

(45)

for $\rho \rightarrow 0$, solution gets

$$\begin{aligned} u_{29}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 }+a^2 c_4\right] -\frac{3 a^2}{2 c_4} \left[ (2 \text {Csc})(ax+by-\gamma t)\right] ^2, \end{aligned}$$

(46)

and for $\rho \rightarrow 1$ the results is similar to $eq.(41)$.

Case 15: If we set L= $\frac{\rho ^{2}}{4}$, M= $\frac{\rho ^{2}-2}{2}$, N= $\frac{\rho ^{2}}{4}$, JEF¹⁸, due to the setting $\chi (\eta )$= $sn\pm icn$, the equation results

$$\begin{aligned} u_{30}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2-2\right) ^2-\frac{3 N \rho ^2}{4}\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2-2\right) \right] -\frac{3 a^2 \rho ^2 }{2 c_4}\left[ \text {sn}(\eta )+i \text {cn}(\eta )\right] ^2, \end{aligned}$$

(47)

so for $\rho \rightarrow 1$, from JEF¹⁸, the solution can

$$\begin{aligned} u_{31}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }+\frac{a^2 c_4}{2}\right] -\frac{3 a^2 }{2 c_4}\left[ \text {Tanh}(ax+by-\gamma t )+i \text {Sech}(ax+by-\gamma t )\right] ^2. \end{aligned}$$

(48)

Case 16: Taking L= $\frac{1}{4}$, M= $\frac{1-2\rho ^{2}}{2}$, N= $\frac{1}{4}$, from JEF¹⁸, $\chi (\eta )$= $\rho cn\pm idn$, the solution can be found as

$$\begin{aligned} u_{32}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( 1-2 \rho ^2\right) ^2-\frac{3 N}{4}\right) }-\frac{1}{2} a^2 c_4 \left( 1-2 \rho ^2\right) \right] -\frac{3 a^2}{2 c_4} \left[ \text {cn}(\eta ) \rho +i \text {dn}(\eta )\right] ^2, \end{aligned}$$

(49)

from JEF¹⁸, for $\rho \rightarrow 1$, the solution is

$$\begin{aligned} u_{33}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }+\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \text {Sech}(ax+by-\gamma t )+i \text {Sech}(ax+by-\gamma t)\right] ^2. \end{aligned}$$

(50)

Case 16(ii): Supposing L= $\frac{1}{4}$, M= $\frac{1-2\rho ^{2}}{2}$, N= $\frac{1}{4}$, from JEF¹⁸, $\chi (\eta )$= $\frac{sn}{1\pm cn}$, the solution can be expressed as

$$\begin{aligned} u_{34}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( 1-2 \rho ^2\right) ^2-\frac{3 N}{4}\right) }-\frac{1}{2} a^2 c_4 \left( 1-2 \rho ^2\right) \right] -\frac{3 a^2}{2 c_4} \left[ \frac{\text {sn}(\eta )}{\text {cn}(\eta )+1}\right] ^2, \end{aligned}$$

(51)

for $\rho \rightarrow 1$, from JEF¹⁸, we have

$$\begin{aligned} u_{35}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }+\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \frac{\text {Tanh}(ax+by-\gamma t )}{\text {Sech}(ax+by-\gamma t )+1} \right] ^2, \end{aligned}$$

(52)

also for $\rho \rightarrow 0$, the periodic solution we have

$$\begin{aligned} u_{36}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }-\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \frac{\text {Sin}(ax+by-\gamma t )}{\text {Cos}(ax+by-\gamma t )+1}\right] ^2. \end{aligned}$$

(53)

Case 17: Considering L= $\frac{\rho ^{2}}{4}$, M= $\frac{\rho ^{2}-2}{2}$, N= $\frac{1}{4}$, from JEF¹⁸, we have $\chi (\eta )$= $\frac{sn}{1\pm dn}$, the solution is written as

$$\begin{aligned} u_{37}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2-2\right) ^2-\frac{3 N \rho ^2}{4}\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2-2\right) \right] -\frac{3 a^2 \rho ^2}{2 c_4} \left[ \frac{\text {sn}(\eta )}{\text {dn}(\eta )+1}\right] ^2, \end{aligned}$$

(54)

for $\rho \rightarrow 1$, the solution is identical to $eq.(52)$.

Case 19: From JEF¹⁸, regarding L= $\frac{1-\rho ^{2}}{4}$, M= $\frac{\rho ^{2}+1}{2}$, N= $\frac{-\rho ^{2}+1}{4}$, $\chi (\eta )$= $\frac{cn}{1\pm sn}$, so the solution is obtained as

$$\begin{aligned} u_{38}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2+1\right) ^2-\frac{3}{4} N \left( 1-\rho ^2\right) \right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2+1\right) \right] -\frac{3 a^2 \left( 1-\rho ^2\right) }{2 c_4} \left[ \frac{\text {cn}(\eta )}{\text {sn}(\eta )+1}\right] ^2, \end{aligned}$$

(55)

if we set $\rho \rightarrow 0$, we have the periodic solution

$$\begin{aligned} u_{39}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }-\frac{a^2 c_4}{2}\right] -\frac{3 a^2}{2 c_4} \left[ \frac{\text {Cos}(ax+by-\gamma t )}{\text {Sin}(ax+by-\gamma t )+1}\right] ^2. \end{aligned}$$

(56)

Case 20: By JEF¹⁸, Taking L= $\frac{(1-\rho ^{2})^{2}}{4}$, M= $\frac{\rho ^{2}+1}{2}$, N= $\frac{1}{4}$, and $\chi (\eta )$= $\frac{sn}{dn\pm cn}$, so the solution is evaluated as

$$\begin{aligned} u_{40}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2+1\right) ^2-\frac{3}{4} N \left( 1-\rho ^2\right) ^2\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2+1\right) \right] -\frac{3 a^2 \left( 1-\rho ^2\right) ^2 }{2 c_4}\left[ \frac{\text {sn}(\eta )}{\text {cn}(\eta )+\text {dn}(\eta )}\right] ^2, \end{aligned}$$

(57)

for $\rho \rightarrow 0$, the solution is obtained as twin of $eq.(53)$.

Case 21: Since L= $\frac{\rho ^{2}}{4}$, M= $\frac{\rho ^{2}-2}{2}$, N= $\frac{1}{4}$, from JEF¹⁸, we have $\chi (\eta )$= $\frac{cn}{\sqrt{1-\rho ^{2}\pm dn}}$, so the solution is

$$\begin{aligned} u_{41}=\frac{2}{c_4^2} \left[ \sqrt{a^4 c_4^2 \left( \frac{1}{4} \left( \rho ^2-2\right) ^2-\frac{3 N \rho ^4}{4}\right) }-\frac{1}{2} a^2 c_4 \left( \rho ^2-2\right) \right] -\frac{3 a^2 \rho ^4 }{2 c_4}\left[ \frac{\text {cn}(\eta )}{\sqrt{\text {dn}(\eta )-\rho ^2+1}}\right] ^2, \end{aligned}$$

(58)

for $\rho \rightarrow 1$, the solution is given as

$$\begin{aligned} u_{42}=\frac{2}{c_4^2} \left[ \frac{1}{4}\sqrt{a^4 c_4^2 }+\frac{a^2 c_4}{2}\right] -\frac{3 a^2 }{2 c_4}\left[ \text {Sech}(ax+by-\gamma t )\right] . \end{aligned}$$

(59)

The exploration of bifurcation analysis, chaotic behavior, and sensitivity analysis

Bifurcation analysis

In this section, $eq.(1)$ will be evaluated using bifurcation theory. Bifurcation happens when slight modifications to the parameters of a dynamic system result in qualitative alterations in the system’s behavior. It frequently results in chaotic behavior, periodic orbits, or novel stable states. Bifurcation theory makes it easier to comprehend these abrupt changes and forecast how the system will behave at various points in time. $eq.(11)$ may be represented as a planar dynamic system through the Galilean transformation^51,52,53,54.

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d u}{d\eta }=z,\\&\frac{d z}{d\eta }=-s_{1} u-s_{2}u^{2}. \end{aligned} \right. \end{aligned}$$

(60)

Where $s_{1}=\frac{\gamma ^{2}c_{1}}{a^{4}}-\frac{c_{2}\gamma }{a^{3}}+\frac{c_{3}b}{a^{3}}$ and $s_{2}=\frac{c_{4}}{a^{2}}$. This system is Hamiltonian and has the following integral.

$$\begin{aligned} H(u,z)=\frac{z^{2}}{2}+s_{1}\frac{u^{2}}{2}+s_{2}\frac{u^{3}}{3}=h. \end{aligned}$$

(61)

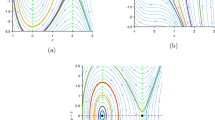
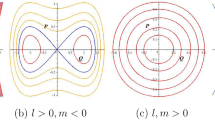
Here, h also known as the energy level or Hamiltonian constant, is an integral constant. It is sometimes referred to as the total energy or energy integral. However, $\frac{z^{2}}{2}$ shows the kinetic energy and $s_{1}\frac{u^{2}}{2}+s_{2}\frac{u^{3}}{3}$ represents the potential energy of the Hamiltonian system. (0, 0) and $(0,-\frac{s_{1}}{s_{2}})$ on the u-axis are two equilibrium points for the given differential equations. The graphical behavior of the bifurcation analysis is represented in Figure (1) and the subfigures (1a,1b,1c,1d) are discuss below.

Case-1: When we choose $s_1>0$ and $s_2<0$ then the center point (Stable) at (0,0) and a saddle exists at $(0,-\frac{s_{1}}{s_{2}})$ which shows in subfigure 1a.

Case-2: When we choose $s_1>0$ and $s_2>0$ then at (0, 0) is center (stable) at origin and $(0,-\frac{s_{1}}{s_{2}})$ shows the saddle point (unstable) shows in subfigure 1b.

Case-3: When we choose $s_1<0$ and $s_2<0$ then at (0, 0) is center (stable) at origin and $(0,-\frac{s_{1}}{s_{2}})$ shows the saddle point (unstable) shows in subfigure 1c.

Case-4: When we choose $s_1<0$ and $s_2>0$ then at (0, 0) is center (stable) at origin and $(0,-\frac{s_{1}}{s_{2}})$ shows the saddle point (unstable) shows in subfigure 1d.

Fig. 1

The figure represents the phase portraits of the systems bifurcation with different parameter values.

Chaotic behavior

We investigate if chaotic behavior⁴⁸ exists in the resultant system eq.(60) by adding a perturbed term. For this system, we examine phase portraits in both 2D and 3D. This dynamical system is taken into consideration:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d u}{d\eta }=z,\\&\frac{d z}{d\eta }=-s_{1} u-s_{2} u^{2}+\omega \cos (\alpha t), \quad \omega \ne 0,\alpha \ne 0. \end{aligned} \right. \end{aligned}$$

(62)

We analyze the impact of the perturbed term $\omega \cos (\alpha t)$ on the dynamical system defined by eq.(62), as shown in the figures (2,3,4,5). The system’s frequency and amplitude are denoted by $\alpha$ and $\omega$, respectively.

Fig. 2

The figure represent chaotic behavior with parameters $s_{1}=1$, $s_{2}=-1$, $\omega =0.01$, and $\alpha =2\pi$.

Fig. 3

The figure represent chaotic behavior with parameters $s_{1}=1$, $s_{2}=-1$, $\omega =1$, and $\alpha =2\pi$.

Fig. 4

The figure represent chaotic behavior with parameters $s_{1}=1$, $s_{2}=-1$, $\omega =2$, and $\alpha =2\pi$.

Fig. 5

The figure represent chaotic behavior with parameters $s_{1}=1$, $s_{2}=-1$, $\omega =2.9$, and $\alpha =2\pi$.

Sensitivity analysis

Here, we investigate the sensitivity of the dynamical system defined by eq.(60)^49,50. In order to do this, we have to solve the following dynamical system^54,55

$$\begin{aligned} \left\{ \begin{aligned}&\frac{d u}{d\eta }=z,\\&\frac{d z}{d\eta }=-s_{1} u-s_{2} u^{2}. \end{aligned} \right. \end{aligned}$$

(63)

The values of parameters are $s_{1}=2$ and $s_{2}=-1$. The initial conditions set as:

$$\begin{aligned} u(0)=x_{1} \quad and \quad u'(0)=y_{1} \end{aligned}$$

This analytical procedure allows us to verify that the stability of the solution was barely impacted by slight modifications to the initial conditions. Figure (6) illustrates the outcomes of this efficient approach. The red ones indicate the dynamics of class u, whereas the blue curves show the dynamics of z. The subfigures (6a,b,c,d,e,f) are shows that how the initial conditions are effects on our model.

Fig. 6

The subfigures represent numerical demonstration of the variables with different parameters.

Graphical representation

In this paper, we emphasize the various soliton behaviors using the JEF expansion technique to demonstrate the obtained solutions in the physical interpretation. These graphs demonstrate various soliton behaviors using Wolfram Mathematica 11.1 to illustrate how we may physically interpret the solutions of the JEF expansion approach. We plotted the following 2D, 3D and contour graphs: Figure (7) is plotted for $u_{2}(x,t)$ which is provided us the dark soliton by selecting various parameter values, Figure (8) for $u_{4}(x,t)$ which shows the bright behavior, Figure (9) is draw for $u_{8}(x,t)$, Figure (10) for $u_{10}(x,t)$ and Figure (11) for $u_{19}(x,t)$ which represents solitary wave solutions, Figure (12) is draw for the solution $u_{27}(x,t)$ and Figure (13) for $u_{36}(x,t)$ shows the complex dark-bright soliton behavior as 2D, 3D, and contour representations. The generalized BO equation describes internal waves in stratified fluids while it enables studies of two-layer fluid solitons which maintain stability as propagating waveforms in oceanographic applications. The solitonic waveforms serve as essential tools for investigating nonlinear deep and intermediate water wave interactions. Geophysical applications use the generalized BO equation for analysis of atmospheric waves together with plasmas under magnetohydrodynamic (MHD) flows. These soliton solutions serve an essential purpose in optical fiber communication systems when used for pulse propagation under weak nonlocal dispersion effects. This equation finds important applications in condensed matter physics through its usage in analyzing the behavior of edge waves in superfluid films and quantum Hall systems.

Fig. 7

The figure represents 3D, 2D & contour of solution $u_2(x,t)$ when $c_2=-0.41, c_3=0.2, c_4=0.6, a=1.4, b=0.1, c_1=0.9, y =1$.

Fig. 8

The figure represents 3D, 2D, and contour for the solution $u_4(x,t)$ when $c_2=0.3, c_3=0.2, c_4=0.4, a=0.3, b=0.1, c_1=0.8, y=1$.

Fig. 9

The figure represents 2D, 3D & contour for solution $u_8(x,t)$ when $c_2=0.4, c_3=0.66, c_4=1.2, a=0.5, b=1.3, c_1=1.9, y=1$.

Fig. 10

The figure represents 3D, 2D, and contour for the solution $u_{10}(x,t)$ when $c_2=0.3, c_3=0.4, c_4=0.3, a=0.3, b=0.3, c_1=0.7, y=1$.

Fig. 11

The figure represents 2D, 3D & contour for solution $u_{19}(x,t)$ when $c_2=0.4, c_3=0.6, c_4=1.3, a=0.5, b=1.2, c_1=1.6, y=1$.

Fig. 12

The figure represents 2D, 3D & contour for solution $u_{27}(x,t)$ when $c_2=0.3, c_3=0.4, c_4=0.5, a=1.3, b=1.2, c_1=0.7, y=1$.

Fig. 13

The figure represents 3D, 2D, and contour for the solution $u_{36}(x,t)$ when $c_2=1.6, c_3=1.2, c_4=1.6, a=0.5, b=1.8, c_1=1.4, y=0.8$.

Modulation instability

Several higher order non-linear PDEs that display instability are examined in relation to the modulation of the steady state caused by an interaction between the non-linear and dispersive effects. Using this method, the perturbed steady-state solution of $eq.(1)$ has the structure shown below⁵⁷

$$\begin{aligned} q(x,y,t) =\left[ f+ \Lambda \psi (x,y,t)\right] , \end{aligned}$$

(64)

where $\psi$ is the perturbation term, $\Lambda$ $\ll$ 1 is the perturbation coefficient parameter, and f is the incident power. We can use $eq.(64)$ to replace $eq.(1)$ after linearizing $\psi$ as, yielding the following result.

$$\begin{aligned} 2 c_4 f \Lambda \psi _{xx} (x,y,t)+c_1 \Lambda \psi _{tt}(x,y,t)+c_2 \Lambda \psi _{xt}(x,y,t)+c_3 \Lambda \psi _{xy}(x,y,t)+\Lambda \psi _{xxxx}(x,y,t). \end{aligned}$$

(65)

In order to investigate instability, we must find the solutions that grow exponentially as

$$\begin{aligned} \psi (x,y,t) =f_1 e^{i (\delta _1 x+\delta _2 y-\rho t)}+f_2 e^{-i (\delta _1 x+\delta _2 y-\rho t)}, \end{aligned}$$

(66)

where $\delta _1$ and $\delta _2$ stand for wave numbers and $\rho$ for frequency, also $f_{1}$ and $f_{2}$ are represented as constants. The following equation is obtained by substituting $f_{1}$ and $f_{2}$ coefficients from $eq.(66)$ into $eq.(65)$.

$$\begin{aligned} & -c_1 f_1 \Lambda \rho ^2 e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }-c_1 f_2 \Lambda \rho ^2 e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }\nonumber \\ & \quad -2 c_4 \delta _1^2 f f_1 \Lambda e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }-2 c_4 \delta _1^2 f f_2 \Lambda e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }\nonumber \\ & \quad +c_2 \delta _1 f_1 \Lambda \rho e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }+c_2 \delta _1 f_2 \Lambda \rho e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }\nonumber \\ & \quad -c_3 \delta _2 \delta _1 f_1 \Lambda e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }-c_3 \delta _2 \delta _1 f_2 \Lambda e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }\nonumber \\ & \quad +\delta _1^4 f_1 \Lambda e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }+\delta _1^4 f_2 \Lambda e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }. \end{aligned}$$

(67)

After collecting the values of $e^{i \left( \delta _1 x+\delta _2 y-\rho t\right) }$ and $e^{-i \left( \delta _1 x+\delta _2 y-\rho t\right) }$, we have set of homogeneous equations that are given below:

$$\begin{aligned} & c_2 \delta _1 f_1 \Lambda \rho -2 c_4 \delta _1^2 f f_1 \Lambda -c_3 \delta _2 \delta _1 f_1 \Lambda -c_1 f_1 \Lambda \rho ^2+\delta _1^4 f_1 \Lambda ,\\ & c_2 \delta _1 f_2 \Lambda \rho -2 c_4 \delta _1^2 f f_2 \Lambda -c_3 \delta _2 \delta _1 f_2 \Lambda -c_1 f_2 \Lambda \rho ^2+\delta _1^4 f_2 \Lambda . \end{aligned}$$

Following the resolution of the above mentioned system, the relevant dispersion relation $\rho$ = $\rho (\delta _1,\delta _2)$ is produced as follows:

$$\begin{aligned} \rho =\frac{c_2 \delta _1 \pm \sqrt{c_2^2 \delta _1^2+4 c_1 \left( -c_3 \delta _2 \delta _1-2 c_4 \delta _1^2 f+\delta _1^4\right) }}{2 c_1}. \end{aligned}$$

(68)

If $\rho$ is real, the steady-state solution is stable, according to the linear stability analysis of the steady-state given by $eq.(68)$.

Conclusions

The current study explored the exact solutions for the generalized BO equation model. It is a nonlinear partial differential equation (NLPDE) and used to explained various physical system such as plasma dynamics and wave propagation phenomena etc.Numerous analytical techniques are used to find exact solutions of NLPDE and one of the them is the JEF expansion method. We explored different soliton solutions such as dark and bright, complex dark-bright, and solitary wave. It demonstrates that the methodologies used are significantly better than conventional approaches in other fields. The generalized BO equation model’s modulation instability dynamics are also covered in this work. Even after fifty years of research, interesting novel problems are continually generated by modulation instability. The most recent findings could contribute to explaining the physical significance of the model as well as other nonlinear models often used in study. Bifurcation is investigated using the theory of planar dynamical systems, then examined the potential existence of chaotic behaviors. A perturbed term was introduced. Comprehensive 2D and 3D phase portraits are presented to further enhance this investigation. The sensitivity analysis is also studied for various initial conditions and it is noted that our model is sensitive.