Introduction

Advancements in quantum computing, particularly in the era of quantum utility1,2 have sparked a growing interest in using intermediate-scale quantum devices across various research fields. Quantum Machine Learning (QML) is a field within quantum computing that aims to leverage quantum principles to enhance machine learning, potentially achieving speed up and performance improvements compared to classical approaches3. In parallel, the field of transfer learning4 has gained much attention since 1995, it enhances the effectiveness of models in new tasks by utilizing information from related source tasks. Transfer learning has shown significant success across various machine learning applications5,6,7,8 and also in computer vision tasks9,10,11. In traditional deep learning, training a neural network from scratch requires vast amounts of data, which is often difficult or expensive to obtain for specific tasks. Transfer learning alleviates this challenge by utilizing pre-trained models, typically trained on large, general datasets like ImageNet, and fine-tuning them for domain-specific tasks. This process allows the model to retain learned features from the general task, such as object edges and textures, which can then be adapted to more specialized tasks with limited data.

Fig. 1
figure 1

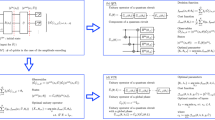
This is a high level end to end flow of the proposed PVCQTL model. The regular parameterized ansatz is replaced by Post Variational Design Strategies: (1) The modified observable construction approach uses a classical combination of predefined trial observables. (2) The hybrid approach uses an ansatz with a single repetition (for reduced depth) and classically combines multiple observables. In this approach, the parameters are not tuned by an optimizer but are predefined by the parameter shift rule. (3) In the variational with post-variational approach, a parameterized ansatz is combined with a modified observable construction. Here, the variational parameters are tuned by an optimizer according to a cost function, and multiple observables are measured, as in the modified observable construction approach.

Full size image

Many QML methods have been proposed to tackle the image classification problem12,13,14,15,16 showcasing the potential accuracy improvement. Hybrid quantum classical transfer learning (CQTL) was introduced by17, wherein a few layers of the classical transfer learning are replaced by quantum circuits. In this method, the quantum circuit learns from the pre-trained classical model to perform a specific task. Their theoretical insights, supported by experiments, affirm that quantum transfer learning is a promising strategy. It is particularly well-suited for near-term quantum devices and is considered a preferred method for quantum image classification, where training on large datasets poses challenges. Classical-quantum transfer learning models (CQTL) combine quantum neural networks (QNN) with classical neural network layers. A QNN uses an ansatz called a parameterized ansatz, which faces significant challenges, particularly when handling large real-world datasets. Some key challenges faced by QNN are as follows: Optimization Difficulties and Slow Convergence: Hybrid quantum-classical algorithms often use hardware-efficient or problem-agnostic ansatz, many of which suffer from the barren plateau problem18, causing gradient vanishing which hinders optimization, requiring exponentially more measurement shots as Qubit increase19. This challenge is especially severe in deep quantum circuits, frequent parameter adjustments in the hybrid classical-quantum feedback loop add to the computational burden making it difficult for classical optimizers to find optimal parameters. Proposed solutions include block identity initialization, layer-wise training, and parameter correlation20,21,22,23. Inefficiency of ansatz: The choice of ansatz significantly impacts optimization, as poor initialization can worsen barren plateaus, necessitating more robust quantum algorithms. Traditional variational methods suffer from optimization inefficiencies, prompting us to explore post-variational strategies that eliminate the need for circuit optimization while maintaining performance.

This paper proposes post variational methods to hybrid classical-quantum transfer learning avoiding the need to optimize quantum circuits. To the best of our knowledge, this is the first attempt to combine both hybrid quantum classical transfer learning and post-variational approaches. Proposing post variational classical quantum transfer learning (PVCQTL) with 3 different post variational strategies are discussed in this work, shown in Fig. 1: (1) modified observable construction, (2) hybrid approach, an ensemble of fixed ansatz with modified observable construction approach, (3) combining parameterized ansatz with modified observable construction approach, where we increase the observability of variational approach. The first two approaches are pure post-variational approaches which sidesteps the Barren Plateaus issue by removing quantum parameter optimization altogether. Instead of optimizing parameters within the quantum circuit, we offload the learning task to a classical model that interprets outputs from fixed quantum measurements. This effectively eliminates the source of vanishing gradients in variational quantum algorithms, as there is no quantum parameter landscape is being navigated, and therefore, no gradients are required from the quantum circuit, removing the core mechanism through which barren plateaus arise. However, this simplification trades off some model expressivity. Third strategy is also the first attempt to combine variational circuit with post variational approach for hybrid quantum classical neural networks. Where Barren Plateaus issue still exists as this approach contains parameterized anstaz which needs fine tuning with quantum back propagation. The variational model had to be dealt as a non-convex optimization problem, wherein the number of local minima is exponential compared to the global minima. The PV model solves a convex quadratic optimization problem of finding the right combination of various fixed quantum circuits, it is therefore guaranteed to find the minima on its landscape.One possibility why this combination might still be interesting or different from one or the other is that the variational part needed to achieve a good fit might be smaller or require less adaptation than a purely variational approach, while still bringing some additional benefit and flexibility over a purely fixed transformation with a pure post variational approach.

As a proof of concept for our proposed methods, we implement PVCQTL on the Deepfake Detection task and three additional binary image classification datasets. The proposed models consistently outperform benchmarked models, as shown in Table 1 for deepfake detection and Table 9 for the other datasets. We conduct an extensive study across various pretrained models including VGG19, ResNet50, ResNet18, and MobileNet for classical feature extraction, along with variations in batch size and number of qubits. A detailed ablation study on model architecture is presented for one representative dataset. And extended the experiments for three more datasets for generalization all of them are doing binary classification. To test the hyperparameters, ablation study on hyperparametrs were also conducted and reported. To analyze the robustness of the proposed model we introduced two types of noise into the input images at different levels, assessing its ability to maintain performance under perturbed conditions. All experiments were implemented using Qiskit24, with the baseline CQTL model also reproduced in Pennylane25.

This paper is organized as follows: Section “Related work” presents an overview of related work. Preliminaries in Section “Preliminaries”, providing the necessary background for understanding our approach. Section “Methods” details the proposed methods, including the post-variational classical quantum transfer learning strategies introduced in this study. Section “Results” describes dataset, experimental setup, benchmark models, evaluation metrics used to assess performance and presents the results comparing PVCQTL with existing hybrid quantum-classical and classical approaches. Section “Extended experiments for generalization” provides a comprehensive analysis of the proposed approach on three additional datasets, including ablation studies on hyperparameter, model architecture, and robustness to noise levels and two different noise induced. Finally, Section “PVCQTL results for deepfake detection binary classification dataset” summarizes the findings and outlines potential future research directions.

Related work

Transfer learning is driven by the idea that humans apply prior knowledge to solve new problems more efficiently. It has become a widely used approach in computer vision, largely due to the extensive collection of pre-trained deep networks that are publicly accessible26. The concept was first highlighted in the NIPS-95 workshop on Learning to Learn5. Since 1995, research on transfer learning has gained attention under various terms, including learning to learn, life-long learning, multitask learning, and meta learning27. Multitask Learning28 improves generalization by sharing knowledge across related tasks. It learns tasks in parallel with a shared representation, boosting performance across domains and algorithms, with strong potential for real-world applications. It is transductive transfer learning7 when labeled data is used to train a classifier, but testing labels are unavailable. The goal is for the classifier to correctly predict the unlabeled testing data. Similarly, there are many different types of transfer learning. In our work, we focus on using transfer learning for image classification8,29,30. Instead of training a neural network from scratch, we leverage the “weights” or learned features of a pre-trained model, applying existing knowledge to the new task.

The selection of VGG19, ResNet50, ResNet18, and MobileNet for quantum transfer learning in image classification is driven by their distinct architectural strengths and empirical performance. VGG19’s deep, uniform structure with stacked 3 × 3 convolutional layers enables robust hierarchical feature extraction, making it suitable for hybrid quantum classical models that require stable input representations31.ResNet50 and ResNet18 leverage residual skip connections to mitigate vanishing gradients, allowing deeper networks without sacrificing accuracy-ResNet50 achieved 95 % accuracy in cervical cancer classification tasks32. MobileNet’s depthwise separable convolutions reduce computational overhead, with training times as low as 52 seconds per epoch, aligning with quantum hardware’s current limitations while maintaining competitive accuracy33. These models also benefit from pre-training on large datasets like ImageNet34, which provides transferable features that reduce data requirements for quantum fine-tuning.

The first classical quantum transfer learning model (CQTL), was introduced by17 for classification between ants and bees, using ResNet18 as a pre-trained model followed by a parameterized ansatz for binary classification. Since then, several works have built on this model with slight modifications. For example,35 tested CQTL with different pre-trained models, comparing the performance of VGG19, DenseNet169, and AlexNet. They found that DenseNet and AlexNet performed best on trash TB, while VGG19 was most effective on crack datasets. In another study,36 applied the same CQTL model from17 to deepfake detection using the Pennylane SDK, without changing the ansatz or data encoding circuit. Additionally,37 applied the CQTL model to X-ray image datasets, comparing the Qiskit and Pennylane SDKs with a common training protocol. In all the CQTL models, there exists an ansatz which needs to be trained which itself poses some challenges as discussed in the introduction section.

Classical shadows38 allows for efficient estimation of quantum observables by replacing the need for repeated single-qubit measurements with multi-observable measurements in a single shot. Applying Classical shadows for quantum observables this work39 shows improved performance of quantum system properties. The Observable Construction Heuristic40, proposed a kernel-based method for quantum states called “projected quantum kernels” applied on the Fashion MNIST dataset. They demonstrated a quantum advantage when such data is present with geometric differences between quantum and classical kernels.41 focused on post variational strategies for Quantum Neural Networks, designing several approaches that showed hybrid quantum classical models could outperform parameterized ansatz-based models in certain cases. None of the approaches mentioned above focus on post-variational strategies for quantum transfer learning.

Preliminaries

A variational quantum circuit (VQC)

A VQC42 employs parameterized ansatz to solve optimization and parametric machine learning problems. An ansatz is a unitary operator \(U(\theta )\), where \(\theta\) represents the set of variational parameters. Let x be a classical input, a feature map encodes the classical input x into quantum state \(\rho (x)\), which is a density matrix representation of the quantum state. The quantum state \(\rho (x)\) is then transformed by this unitary operator \(U(\theta )\) from the initial state \(\rho (x)\) to a final state \(\rho (\theta , x)\) that is given by the quantum state : \(\rho (\theta , x) = U(\theta , x) \rho (x) U^\dagger (\theta , x)\). A VQC operates by optimizing in a manner similar to a neural network, where the goal is to optimize parameters to minimize a cost function and build a learning model to learn an estimator \(E_{\varvec{\theta }}(x)\) via a parameterized ansatzwith parameters \(\varvec{\theta }\). During each iteration a cost function \(C(\theta )\) is employed to approximate its gradient efficiently. The estimator \(E_{\varvec{\theta }}(x)\) is designed to predict the output \(\hat{y}\) based on the input x. Thus, the prediction for each sample i is \(\hat{y} := E_{\varvec{\theta }}(x)\). Where \(E_{\varvec{\theta }}(x) = tr(O \rho (\theta , x))\) is the estimator’s expectation value for the variational form which is calculated through the observable \(O\_j\) in the Pauli Z basis, as below using cost function in Eq. (1). A cost function \(C(\theta )\), can be represented as in Eq. (1). During the optimization process, the gradient of the cost function updates the model parameters in the direction that minimizes the cost, typically using the binary cross-entropy function. This function minimizes the error between the actual and predicted outcomes. The quantum cost function for a machine learning task, such as classification, should include: The expectation of the quantum state with respect to the input data x. The observable values, which will be summed over all the observables \(O_j\). A comparison of the quantum model’s output (after measurement) with the true labels y is done. The cost function could be written as:

$$\begin{aligned} C(\theta ) = \sum _{i} \left[ \sum _j \text {Tr}\left[ O_j U(\theta , x_i) \rho (x_i) U^\dagger (\theta , x_i)\right] - y_i \right] \end{aligned}$$
(1)

Where \(\theta \in \mathbb {R}^k\) represents the set of variational parameters that encodes potential solutions, k indicates that there are k parameters in the model. are the variational parameters of the quantum circuit. \(x_i\) represents the input data, the i-th data point. \(y_i\) is the true label for the i-th data point. \(U(\theta , x_i)\) is the parameterized ansatz that takes as input both the variational parameters \(\theta\) and the data point \(x_i\). \(\rho (x_i)\) is the quantum state or density matrix associated with the data point \(x_i\). \(O_j\) are the observables and j is the index of observables. \(O_j\) is mathematically represented as the tensor product of N Pauli-Z matrices (\(\sigma _z\)) \(O_j = \sigma _z^{\otimes N}\) measurement in Pauli Z basis is the most common method. Tr represents the trace of a matrix that is used to calculate expectation value of the observables. N is the number of qubits and Pauli-Z matrix (\(\sigma _z\)) is a 2 \(\times\) 2 is a Hermitian matrix defined as: \(\sigma _z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\).

Classical quantum transfer learning

In CQTL, the model combines classical neural networks and quantum circuits to represent complex data transformations. For classical layer a fully connected neural network43 is most commonly used in the literature, which are found towards the end of neural network architecture and are responsible for producing final output predictions. The classical component handles data pre-processing, feature extraction, and high-level decision-making, while the quantum component involves a variational algorithm that uses quantum embedding before performing measurements, as described in Section “Modified Observable Construction Approach” to make finer decisions. Figure 2a shows two networks: A, the pre-trained model, and B, the trainable quantum model. Pre-trained model refers to a model that has already been trained on a large dataset before being fine-tuned or adapted for a specific task. Consider a network A pre-trained on dataset \(D_A\) for a task \(T_A\). Upon removing its final layer, we obtain \(A'\), which serves as a pre-processing block, transforming high-resolution input images into abstract features. The final layer is then replaced by network B, a trainable “dressed quantum circuit” \(\tilde{Q}\) defined in Eq. (2) is built with a pre-network, Q layer, and a post-network as shown in the Fig. 2a, forming a classical-quantum loop. Pre-network and post-network are classical layers whereas Q layer is a quantum circuit. The CQTL model, applied to a specific dataset \(D_B\), solves task \(T_B\) by transferring knowledge from the pre-trained model to the quantum model to tackle the specific task. Lets define a dressed quantum circuit \(\tilde{Q}\) with a Q layer which has a parameterized ansatz in the final layer and classical layers for mapping input and output of the pre-trained model.

$$\begin{aligned} \tilde{Q} = L_{n_q \rightarrow n_{out}} \circ Q \circ L_{n_{in} \rightarrow n_q} \end{aligned}$$
(2)

where \(\circ\) indicates a function composition, \(L_{n_{in} \rightarrow n_q}\) is a pre-network and \(L_{n_q \rightarrow n_{out}}\) is a post-network forming a classical layers mapping the input size \(n_{in}\) to \(n_q\) qubits and the quantum output size \(n_q\) to \(n_{out}\), respectively. This hybrid approach is particularly effective for processing high-resolution images, as the quantum computer is applied only to a small set of abstract features, making it far more practical than embedding millions of raw pixels into a quantum system.

Fig. 2
figure 2

Quantum models for image classification.

Full size image

Hybrid quantum classical neural network

In a traditional classical neural network, each artificial neuron is typically built from linearly connected layers, followed by nonlinear activation functions applied at the end. A quantum-classical hybrid neural network integrates a quantum layer with classical layers. It varies in architecture to the classical neural network by the quantum layer placed at the beginning, end, or between classical layers; one such architecture is shown in Fig. 2b. The input is first fed into a classical layer with a classical activation function. Then, its output is encoded into quantum states by a feature map S(x) which maps classical data into quantum states. Next, ansatz \(U(\theta )\) applies transformations on the encoded states. Measurement block corresponds to measurement in Pauli Z basis to collapse the quantum information into classical states by outputting an expectation values for each qubit. During each iteration, a final classical layer in the Fig. 2b has a classical activation function which combines the results of different qubit measurements from previous block, calculates the cost function and updates the gradients based on the cost function to ansatz of the QNN layer. This way, the hybrid classical-quantum loop works on minimizing the cost function in each iteration by updating the QNN layer through classical optimization techniques. The process continues until a stopping criterion is met, such as the cost function reaching a sufficiently low value or the number of iterations exceeding a predefined limit. This approach combines the power of quantum circuits for data encoding and transformation, with classical optimization methods for parameter updating, within a quantum-classical hybrid optimization framework.

Methods

In our proposed Post-Variational Classical-Quantum Transfer Learning (PVCQTL) model Fig. 1, we extend post-variational strategies introduced in41 to modify the quantum Q layer in the dressed quantum circuit of CQTL. While both CQTL and PVCQTL share a similar structure (Section “Classical quantum transfer learning”, Eq. (2)), PVCQTL replaces the trainable variational circuit with alternative post-variational strategies. Each strategy follows the generic form:

$$\begin{aligned} Q = M \circ \mathscr {A} \circ S \end{aligned}$$
(3)

where S is the state preparation (feature map), \(\mathscr {A}\) is the ansatz operator, and M is the measurement. The ansatz \(\mathscr {A}\) takes three forms:

  • \(\mathscr {A} = I\): No ansatz (pure encoding),

  • \(\mathscr {A} = FA\): Fixed, non-trainable ansatz,

  • \(\mathscr {A} = PQC\): Trainable parameterized quantum circuit.

The three strategies are illustrated in Fig. 3:

  1. 1.

    Modified Observable Construction: \(\mathscr {A} = I\), no quantum transformation beyond encoding; measurements are directly applied Fig. 3a, Section “Modified Observable Construction Approach”.

  2. 2.

    Hybrid with Fixed Ansatz: \(\mathscr {A} = FA\), using a non-trainable ansatz circuit with classical parameter tuning Fig. 3b, Section “Hybrid approach: fixed ansatz with modified observable construction”.

  3. 3.

    Variational + Post-Variational: \(\mathscr {A} = PQC\), combining variational training with enhanced post-variational measurements in all three localities (Fig. 3c).

The measurement layer M follows the modified observable construction method (Eq. (5)) with \(n_m\) measurements per locality. In all approaches, the pre-network outputs 2048 features from a ResNet50 model44, mapped to \(n_q\) qubits. These are processed by the Q layer and then transformed by the post-network into \(n_{out}\) output neurons. The first two strategies avoid quantum parameter training, offering efficiency, while the third enriches variational learning through expressive measurements. In our proposed model post variational classical quantum transfer learning (Fig. 1), the post variational strategies are adapted and extended from41 for the quantum part of classical quantum transfer learning settings making the Q layer of the B network to be post variational. In both the original CQTL and our proposed PVCQTL, the B Network is a dressed quantum circuit. Difference with our approach is Q layer of the dressed quantum circuit is implemented with post variational strategies. Where, instead of optimizing the quantum circuit directly, post-variational strategies promotes an alternative approach. We are proposing 2 pure post variational approaches and one variational with post variational strategy :Modified Observable Construction Approach Fig. 3a, Hybrid Approach Fig. 3b and Variational with post variational strategy Fig. 3c. The generic PVCQTL learning scheme follows the same flow as in CQTL described in Section “Hybrid approach: fixed ansatz with modified observable construction” Eq. (2) except for the dressed quantum circuit Q in Eq. (2) which is replaced with post variational strategies.

Fig. 3
figure 3

Three different post variational strategies for CQTL. (a) Modified observable construction approach, which measures a quantum feature map in different Pauli basis, making it post-variational. (b) A hybrid approach where a fixed quantum circuit is parameterized by a classical model. (c) A Variational with Post-Variational measurement approach: a Parameterized Ansatz is measured using all Pauli operators instead of the standard Pauli Z in a regular Parameterized Ansatz, making it a post-variational method.

Full size image
Fig. 4
figure 4

Quantum circuit with feature map S(x) measured in pauli operators \(P \in {I,X,Y,Z}^{\otimes N}\) possible combinations. For N qubits it is \(4^N\) combinations. By applying Pauli truncation and the classical shadows protocol, the number of measurements required is reduced to a logarithmic dependence on the number of qubits.

Full size image

Modified observable construction approach

In quantum neural networks, the quantum state of each neuron (qubit) can be measured using the Pauli observables. These observables capture the effects of quantum operations on qubits at different levels of locality. The measurements corresponding to these observables are critical for determining the state of quantum neurons. In the Observable Construction approach, we directly construct a measurement observable by combining multiple predefined trial observables. A variational observable can be formed using a collection of Pauli operators, which may act as a possible approximation when locality constraints are applied, followed by a classical aggregation of their contributions. It is is achieved through methods such as reduced physical observables or classical shadows38 using classical combination of variational quantum states (CQS)45. CQS-based heuristics enables extraction of classical information from quantum states while retaining essential features. The goal in observable construction method is to solve the equation \(E_\theta (x)\) for post variational forms by combining the ansatz \(U(\theta )\) and observable O into a single parameterized observable \(\hat{O}(\theta )\) and replacing this observable with a collection of predefined trial observables \(O_1\),\(O_2\), \(\cdots\) ,\(O_m\).

Starting from variational observable O which is for a parameterized anstaz, we can combine the parameterized ansatz with observables to obtain parameterized observable. Hence, instead of optimizing over parameterized trial quantum states, we could optimize over a parameterized observable like this: \(\hat{O}(\theta ) = U^\dagger (\theta ) O U(\theta )\) achieving the same result. Expectation values of these observables will be parameterized observables \(\hat{O}(\theta )\) : \(\text {tr}(O \rho (\theta , x)) = \text {tr}(\hat{O}(\theta ) \rho (x))\), where \(\rho (\theta , x)\) is the quantum state associated with input x. By the universal approximation theorem46, we can approximate the function \(\theta\) values classically using a neural network model \(G_\alpha\), parameterized by classical parameters \(\alpha\): \(E_{\theta }(x) \approx G_\alpha \left( \left\{ \text {tr}(\hat{O}_j \rho (x)) \right\} _{j=1}^M\right) = E_\alpha (x)\). Finally, using first approximation and second approximation41 the post-variational algorithm is constructed by ensemble of multiple trial observables. Consider only a subset S of trial observables, where \(|S| = m\). The final target observable can be learned by combining the measurement results based on a learned function: \(E_\theta (x) \approx E_\alpha (x) = G_\alpha \left( \left\{ \text {tr}(\hat{O_j} \rho (x)) \right\} _{j: O_j \in S} \right)\).

Local Observables in Terms of Qubits and Pauli Operators Suppose we are working with N qubits. Without any restrictions, each qubit has four possible choices: I,X,Y,Z. Thus, without locality constraints it would be \(4^N\) if N =8, it will be 65536 possible combinations which is exponential. Applying Pauli truncating and the classical shadows protocol reduces the number of measurements needed for \(\text {tr}(P \rho (x))\) to a logarithmic dependence on the number of qubits. The classical shadows enable the estimation of \({\textbf {tr}}(P \rho (x))\), where \(P \in \{I, X, Y, Z\}^{\otimes N}\) as shown in Figure 4 and \(|P| \le L\).

$$\begin{aligned} \hat{O}_j \rho (x) = \textbf{P} \mid \textbf{P} \in \{I, X, Y, Z\}^{\text {n}} \end{aligned}$$
(4)

Proposition 1

(Required Measurements for observable construction of all Quantum Neurons): We now calculate the number of observables required at different levels of locality according to41. For locality \(L \le 1\) or \(L \le 2\) or \(L \le 3\) , there are 3 possible choices X,Y,Z for the Pauli operators, with the remaining operators being the identity operator I. This results in \(\left( {\begin{array}{c}N\\ L\end{array}}\right)\) distinct local observables. Where P = 3 distinct Paulis from Fig. 4, hence, the number of local observables for N = 8 qubits and locality 1, 2 and 3 are: \(L\le 1\) = \(\left( {\begin{array}{c}8\\ 1\end{array}}\right) \times 3 = 8 \times 3 = 24\). \(L\le 2\) = \(\left( {\begin{array}{c}8\\ 2\end{array}}\right) \times 3 \times 3 = 28 \times 9 = 252\). Additionally, there is 1 extra observable where \(L\le 2\) which makes it 252 + 1 + \(L \le 1\) = 277. \(L\le 3\) = \(\left( {\begin{array}{c}8\\ 3\end{array}}\right) \times 3 \times 3 \times 3 = 56 \times 27 = 1512\) + \(L\le 2\) = 1789

Modified Observables: In the transfer learning setting with dressed quantum circuit the number of observables from the observable construction even when locality constraints are too many as shown in Proposition 1. Although we are freezing parameters for all layers except the final layer, having to measure these many observables from quantum subsystems at each iteration and epoch is time consuming. We need to maintain the computational feasibility of the transfer learning process without losing critical quantum features by reducing the number of observables. We define an additional condition on all combinations of Pauli operators while meeting the locality constraints defined in Proposition 1. The additional condition is to filter observables with Pauli operators acting on qubits in pairs, triplets for \(L\le 2\) and \(L\le 3\) respectively and non-repeated:

$$\begin{aligned} n_m = V_C \left( \left( {\begin{array}{c}N\\ L\end{array}}\right) \times P\right) \end{aligned}$$
(5)

where L is the locality and \(V_C\) represents the valid combinations, which are predefined for different locality values. For \(L\le 2\) = (XY, XZ, YX, YZ, ZX, ZY) and \(L\le 3\) = (XYZ, XZY, YXZ, YZX, ZXY, ZYX). These combinations were chosen based on experimental observations, where these specific sets yielded the best accuracy for the given problem. These Pauli combinations can be changed for different experiments as per the need. With two conditions we emphasized: (1) non-identical Pauli operators and (2) valid combinations pre-defined. We now have a modified observable construction method to ensure that the quantum information retained in the locality-1, locality-2, and locality-3 observables remains meaningful and relevant for the model’s training and testing. This modification is driven by the goal of preserving key quantum features while reducing the potential for redundant or irrelevant information. By preserving meaningful quantum information at each locality, this method enhances the model’s ability to generalize and make accurate predictions in both training and testing scenarios. Modified observable construction method when has fewer observables in locality-2 and locality-3 as described here: \(L\le 1\) , it remains as in Proposition 1, because the 24 observables are non repeated and each single Pauli is acting on one qubit at a time. \(L\le 2\) = Filter observables with Pauli operators acting on pairs of qubits and non repeated. The predefined valid combinations are: (XY, XZ, YX, YZ, ZX, ZY) to choose from Proposition 1 for \(L\le 2\) + \(L \le 1\) = 66 observables. \(L\le 3\) = Filter observables with Pauli operators acting on triplets of qubits and non repeated. The predefined valid combinations are: (XYZ, XZY, YXZ, YZX, ZXY, ZYX) to choose from Proposition 1 + \(L \le 2\) = 102 observables. The algorithm for PVCQTL implementation with modified observable construction is given Algorihtm 1 and pictorially represented in the Figure 1. The featuremap quantum circuits are represented as shown in Fig. 6.

Algorithm 1
figure a

An algorithm for PVCQTL B: dressed quantum circuit

Full size image

Hybrid approach : fixed ansatz with modified observable construction

The goal of post-variational algorithms is to construct the variational algorithm by replacing the parameterized quantum circuit \(U(\theta )\) with an ensemble of p fixed ansatz \(\{ U_a \}_{a=1}^p\), as demonstrated by45. Instead of generating linear combinations of multiple ansatz, this work41 applies derivatives of the ansatz, which is based on variational observable \(O(\theta ) = U^\dagger (\theta ) O U(\theta )\) into a truncated Taylor series. Furthermore, as shown by47, Higher-order gradients of a single parameter can be computed by using finite difference approximations, where the parameter is shifted by \(\{0, \pm \frac{\pi }{2} \}\) from its initial value (typically 0) to calculate the gradient. Specifically, a linear combination of circuits is used to evaluate the derivative with respect to the parameter at these shifted points. By performing a full Taylor expansion of the circuit around \(\theta = 0\), which used for gradient and higher-order derivative calculations. One can express \(U^\dagger (\theta ) O U(\theta )\) for any arbitrary \(\theta \in \mathbb {R}^k\) as a linear combination of \(U^\dagger (\theta ') O U(\theta ')\), where \(\theta ' \in \{0, \pm \frac{\pi }{2} \}^k\). For truncation at derivative order R, the number of circuits grows exponentially with the number of variational parameters, becoming computationally expensive for deep ansatz. Consider the gradient of the variational observable with respect to the u-th parameter \(\theta _u\) using parameter shift rule. We then construct two variational observables: \(O_{\pm }(\theta ) = U^\dagger \left( \theta \pm \frac{\pi }{2} e_u\right) O U\left( \theta \pm \frac{\pi }{2} e_u\right)\) where \(e_u\)is the unit vector in the direction of the u-th parameter. These observables allow us to estimate the gradient of the variational observable with respect to \(\theta\) and the traces will be given by:

$$\begin{aligned} \text {tr} (O_{\pm }(\theta ) = \text {tr} \left( U^\dagger \left( \theta _u \pm \frac{\pi }{2} e_u\right) O U\left( \theta _u \pm \frac{\pi }{2} e_u\right) \right) \end{aligned}$$
(6)

For hybrid strategy: by expanding the ansatz on the shallow layer and replacing deeper layers with modified trial observables for classical combinations, we can combine both fixed ansatz with parameter shift rule as per Eq. (6) and observable construction Eq. (5). Lets say we have p ansatz circuits \(\{U_a\}_{a=1}^{p}\) and q observables \(\{O_b\}_{b=1}^{q}\), such that the output of each circuit for an input state \(\rho\) is given by:

$$\begin{aligned} \text {tr}(O_{a,b} \rho ) = \text {tr}(U_a^\dagger O_b U_a \rho ). \end{aligned}$$
(7)

Since the measurements in a quantum neural network are probabilistic, multiple measurements are required to obtain accurate estimates. We define the matrix \(Q \in \mathbb {R}^{d \times m}\) such that \(Q_{ij}:= \text {tr}(\hat{O_j} \rho (x_i))\), where \(\{\hat{O_j}\}_{j=1}^{m}\) represents the collection of observables produced by this strategy with P ansatz and q observables, and \(m = p \cdot q\). This matrix Q is then used as input to a classical model with a cross-entropy loss function, which minimizes the error between the actual and predicted outcomes: \(\mathscr {L}_{CE}(x_i) = - \left[ y_i \log (P_+) + (1 - y_i) \log (P_-) \right]\). Where, P is the probability derived from the quantum observables, calculated as the traces of the quantum states with \(\theta\) values at random initialization. Given a set of observables \(\hat{O_j}\) for \(j \in [m]\) and data embedding \(\rho (x_i)\), a simple linear Q layer can be constructed by combining the outputs linearly using combination parameters \(\alpha _j\), resulting in the predicted output label \(\hat{y}\).

Variational with post variational approach

In this method we keep a regular parameterized ansatz as shown in Fig. 6c with random initial parameters and update the gradients like a usual parameterized ansatz in each iteration and epochs. In this method, replacing the M block from Pauli Z based measurements with trial observables for classical combinations that is laid out in previous sections. We measure with modified observable construction approach where the parameterized ansatz get updated in each iterations. So this method provides a larger set of observables than typically used for CQTL model. Instead of measuring in Pauli Z basis, we measure the quantum circuit in Paulis X, Y, Z, I basis as shown in Fig. 4, allowing to design a combination of both variational and post variational approach. In the Algorithm 1, instead of fixed anstaz, we put an actual parameterized ansatz \(U(\theta )\) where \(\theta\) is set with some initial weight parameters, hence in the Eq. (2), Q layer will assume any of the forms mentioned in Eq. (3). The weight parameters in the circuit is enabled forming the Q layer for parameter tuning. Training the Q layer involves updating these parameters using a classical-quantum loop, where the quantum circuit’s parameters are updated through gradient-based optimization techniques until convergence (or for a set number of epochs) is reached.

Results

Deepfake detection data set

Assessment of the proposed design approaches for PVCQTL is conducted on the Indian Institute of Technology Patna Indian Fake Face Dataset (IITP-IFFD)48. It Consists of 110,852 labeled images, predominantly featuring female pictures as in Fig. 5. It comprises 57,283 fake pictures and 53,569 real pictures. This dataset presents the first effort to address fake faces in an Indian setting. The dataset consists of a set of facial images as mentioned corresponding binary labels indicating the authenticity of each image. The objective is to learn a function \(f: X \rightarrow y\), where \(f(X_i)\) predicts the label \(\hat{y_i}\) for the image \(X_i\). The labels are provided as a binary classification task where 0 indicates a fake image and 1 indicates a real image.

Fig. 5
figure 5

Real and fake images from the IITP-IFFD datasets that we are using in our experiments.

Full size image

Input: A set of facial images represented by X and their corresponding labels y.Output: A model f(X) that predicts whether a given image is real or fake. \(Let X \in \mathbb {R}^{n \times D}\) be the feature matrix, where n is the number of samples (images) and D is the number of features (dimensions) for each image \(D = 64*64*3\). \(y \in \{0, 1\}^n\) be the label vector, where \(y_i\) is the label corresponding to the i-th image, with: \(y_i = {\left\{ \begin{array}{ll} 0 & \text {if the image is fake} \\ 1 & \text {if the image is real} \end{array}\right. }\)

Data Reduction by Number of Samples We are reducing sample size of the IITP-IFFD dataset which is currently too large for the quantum models available today. For 10 epochs 2000 images, its taking minimum of 58 mins and maximum of 870 minutes depending on configuration and design approaches we simulate Table 4 gives detailed runtime analysis. So considering the results from this work49 that quantum learning models can achieve high-fidelity predictions using a few training data points and proved that generalization error agrees as number of samples varies, we reduce the same size of the dataset. To reduce the number of samples by size we applied random sampling50 from 110,852 images to 2000 images. We selected 6 such random datasets datasets, each containing 2000 images from the larger dataset of 110,852 images for training and testing purposes. We calculate the standard deviation and mean across all test and train accuracy for various methods bench marked and proposed here. The distribution of data points is uniformly represented for fake and real classes of the dataset on both train and valid or test split, \(50\%\) for test and \(50\%\) for train, both has 1000 fake images and 1000 real images. Pre-trained Models : The Pre-trained models that are considered here are VGG1931, ResNet18, ResNet5044, and MobileNet51, which are pretrained on large ImageNet, available through the Pytorch and TensorFlow Keras library. VGG1931 is a deep CNN model that is known for its simplicity and use of multiple layers of convolutions, ResNet18, ResNet5044 is a ResNet architecture with 18 and 50 layers respectively, it is very popular for image recognition tasks due to their residual connections, which help train deeper models. MobileNet51 is a deep CNN architecture with multiple “inception” blocks, where each block has multiple types of convolutions and pooling layers. The selection of VGG19, ResNet50, ResNet18, and MobileNet for quantum transfer learning in image classification is driven by their distinct architectural strengths and empirical performance. VGG19’s deep, uniform structure with stacked 3\(\times\)3 convolutional layers enables robust hierarchical feature extraction, making it suitable for hybrid quantum classical models that require stable input representations. ResNet50 and ResNet18 leverage residual skip connections to mitigate vanishing gradients, allowing deeper networks without sacrificing accuracy-ResNet50 achieved \(95\%\) accuracy in cervical cancer classification tasks. MobileNet’s depthwise separable convolutions reduce computational overhead, with training times as low as 52 seconds per epoch, aligning with quantum hardware’s current limitations while maintaining competitive accuracy. These models also benefit from pre-training on large datasets like ImageNet, which provides transferable features that reduce data requirements for quantum fine-tuning. Table 1 presents the test performance of various pre-trained models benchmarked across six datasets. This benchmarking on pre-trained models, is based of PVCQTL’s modified observable construction approach for 10 epochs with a batch size of 32. ResNet50 with 8 qubits had higher accuracy than ResNet18 and other pre-trained models, hence we keep ResNet50 for future benchmarking experiments on existing models and our proposed PVCQTL approaches.

Quantum circuits

This section gives details on the quantum circuits used for the experiments.

Quantum Data Encoding A quantum embedding \(\psi\) corresponds to the preparation of quantum states based on classical data. Let a quantum circuit \(U_{\psi }\) prepare a quantum state \(\rho _{\psi }(x)\) using a data point x . This procedure is referred to as quantum encoding or quantum embedding, and it can be mathematically represented as a classical-to-quantum feature map that encodes classical data into a quantum state. The formal definition is: \(|\psi \rangle : x \in X \rightarrow \rho _{\psi }(x) \in S(\mathscr {H})\). Where \(\rho _{\psi }(x)\) is the quantum state on a Hilbert space \(\mathscr {H}\), and \(S(\mathscr {H})\) denotes the set of quantum states on that Hilbert space. This quantum embedding can be achieved using various methods such as basis encoding, amplitude encoding, angle encoding, Hamiltonian encoding or other quantum state preparation techniques. We have chosen angle encoding for the feature map quantum circuit.

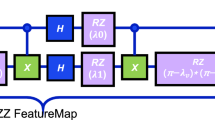
Feature map Ry + Cz is applied for our learning problem, Fig. 6a is a combination of single qubit rotation around Y axis and CZ gate (Controlled-Z gate) is a two-qubit quantum gate that can be used to create entangled states between two qubits by flipping the phase of the target qubit if the control qubit is set to \(|1\rangle\) state. The combined RY + CZ feature map for a 2-qubit system can be represented by the following unitary operation: \(U_{\psi } = \left( R_{Y}(\theta ) \otimes I \right) \cdot \text {CZ}\) where the individual components are: \(RY(\theta ) = \exp {-i(\theta /2)Y}\).

Ansatz After encoding the data, we propose a simple ansatz to be used in the PVCQTL approach that leads to an improved performance. We selected layered circuit ansatz while making it fixed ansatz, each layer consists of Euler rotations applied to each qubit. For each qubit, 4 parameters are associated with the Euler rotation. The first layer consists solely of rotation gates along the X,Y, and Z axis for each qubit \(q_i\), as illustrated in Fig. 6b. The entanglement pattern can either be user-defined or chosen from a predefined set, we have selected linear entanglement for this circuit. Note that there is no parameters (angles) of each gate to be optimized, the angles are already defined with parameter shift rule. This results in 3N single-qubit rotations in each layer, where N is the number of qubits. Figure 6c is an ansatz used for in variational with post variational approach.

Fig. 6
figure 6

Quantum circuits used in this experiment.

Full size image

Quantum circuit characteristics Table 7 presents the quantum circuit depth and gate count for each model. These characteristics are independent of the dataset, as the quantum layer architecture remained unchanged across experiments. All models were executed using a single quantum layer. In contrast, the Pennylane version of CQTL used in prior work17 employed five or more quantum layers, resulting in significantly deeper circuits. Our approach intentionally avoids such depth to reduce circuit complexity, improve efficiency, and enhance transpilation feasibility for execution on actual quantum hardware.

Existing models benchmarked

To evaluate PVCQTL model’s effectiveness, we compare it against both hybrid quantum-classical and fully classical models. CQTL model at Section 1.2.2) is a standard hybrid approach using variational circuits. HQCNN 1.2.3 is a quantum model without transfer learning. MLP (Multilayer Perceptron) a classical baseline for direct comparison. ResNet50 is a powerful pre-trained deep learning model used in image classification. The results of these models are tabulated in Table 2 which serves as a benchmark to assess whether PVCQTL can achieve similar or superior performance while reducing quantum circuit optimization overhead. Experiments were conducted on the 6 sub sampled datasets, which contain random images out of IITP-IFFD dataset. For HQCNN and MLP models, we applied a pre-trained ResNet50 model and trained the model to extract 8 features from 4096 features images on all 6 datasets under test, hence making 8 features dataset. But for ResNet50 model, we trained it as is by only modifying the final fully connected layer for 2-class classification as opposed to 1000 class classification it has been built for. The MLP architecture consists of four fully connected layers, with ReLU activation functions applied after each hidden layer. It takes an input of 8 features, passes through progressively smaller hidden layers (64, 32, 16 units), and outputs a 2-dimensional of fake or real class as shown in the Fig. 7. The HQCNN model is described in Section 1.2.3 which takes 8 features as input from the classical layer. The HQCNN model applies the feature map in Fig. 6a) and ansatz in Fig. 6c, but with parameters and they are randomly initialized. CQTL with Pennylane and Qiskit Software Development Kit: To do a fair study further, we conducted a test to check accuracy score between CQTL model implemented in Pennylane25 vs qiskit for the learning problem with IITP-IFFD dataset. The model uses the feature map and parameterized ansatz as in17 except that the CQTL model implementation in Pennylane includes three repetition layers, whereas in Qiskit, it consists of only one layer. The pre-trained models for both was tested with ResNet50 and ResNet18 and number of qubits 8 qubits instead of 4 qubits as the CQTL17 used ResNet18 and 4 qubits. We observe from Fig. 8 is the historgram plot on accuracy that they both have similar performance in terms of accuracy. Table 1 presents the accuracy of all models discussed in this benchmarking study.

Fig. 7
figure 7

Classical MLP architecture with 8 nodes input layer for 8 features input, 3 hidden layers and one output layer with Relu activation function.

Full size image
Fig. 8
figure 8

Accuracy comparison of CQTL model in qiskit and Pennylane sdk with ResNet50 as the pre-trained model. These are the hyper parameters that was selected for both Pennylane and qiskit performance assessment on CQTL model, batch size: 32, number of qubits: 8, loss function is cross entropy loss function and learning rate: 0.1 with a step size of 10. epochs: 30. CQTL model Implementation in Pennylane was with 3 layers of parameterized ansatz where as in qiskit it was just one layer. Overall time consumed including 3 reps of CQTL in Pennylane is equal to 1 layer of qiskit.

Full size image
Table 1 Test accuracy of the PVCQTL model using VGG19, ResNet18 and ResNet50, MobileNet pre-trained models and for number of qubits: 4 and 8, we tested for modified observable construction approach with pre-trained models in our proposed method from Fig. 1.
Full size table
Table 2 Mean and standard deviation of accuracy for six sub-sampled datasets of size 2000, equally distributed between two classes, with a batch size of 32.
Full size table

PVCQTL results for deepfake detection binary classification dataset

The performance results offer a preliminary understanding of how effective each strategy is. The median accuracy results of all six datasets are tabulated in Table 3 and plotted in Fig. 9 demonstrates that all proposed PVCQTL methods outperforms the variational-CQTL when using the feature map proposed in Fig. 6a and fixed ansatz as in Fig. 6b. The best accuracy of each models are as shown in Table 5 and run time analysis is tabulated at Table 4. The accuracy of all three approaches shows limited variance when averaged over the 6 sub-sampled datasets, indicating the stability of the models. Modified observable construction approach with locality-1, 2 and 3 exhibits a relatively high median accuracy around (0.822–0.827). For hybrid approach, in the preliminary tests when the Fixed ansatz circuit is initialized with random parameters, convergence after 10 epochs was not a satisfactory accuracy. Consequently, we did not proceed with a detailed analysis using random initialization and moved on with parameter shift rules explain in Section “Hybrid approach: fixed ansatz with modified observable construction”. Hybrid approach median accuracy is around (0.818–0.820) enhances accuracy when combined with locality-3 observables and performed the best at Locality-2 as per Table 5. But hybrid approach consumes more time than modified observable construction approach as tabulated in Table 4 to achieve a similar accuracy. However, this outcome suggests that incorporating gradient circuits with parameter shift techniques serves as a more effective heuristic for enhancing the expressivity of observable construction methods. Our third proposal, the variational ansatz with post variational measurement using modified observable construction approach, generally performed similarly to our first proposal and better than our second proposal, with a median accuracy ranging around (0.820–822). However, the time required by the third proposal is significantly higher than that of the hybrid and modified observable construction approaches. For instance, for 10 epochs, the computation time for locality-3 exceeds 800 minutes for 2000 image classification as per Table 4, which creates a bottleneck due to the slow computational speed. For Deepfake dataset, the loss curve Fig. 10 of all approaches show a consistent downward trend in loss, indicating successful convergence. The modified observable construction variant demonstrates slightly faster and more stable convergence, with lower variance and the lowest final loss among the three. The hybrid approach follows closely behind, maintaining low variance as well. The Variational-PV variant exhibits higher variability and a comparatively slower decline in loss, suggesting it may be more sensitive to initialization or training conditions.

Table 3 Mean and standard deviation of accuracy of a PVCQTL model on all proposed approaches for batch size 32 and 8 qubits.
Full size table
Table 4 Time consumed for running the model for three proposed strategies. The recorded time are in minutes and are for batch size 32.
Full size table
Table 5 Deepfake dataset’s best accuracy of each models for batch size of 32 and 8 qubits. We have taken the maximum accuracy from all 9 results pertaining to 6 sub-sampled datasets test for each method and locality.
Full size table
Fig. 9
figure 9

Box plot visualizing the accuracy performance of PVCQTL across all proposed PVCQTL approaches.

Full size image
Fig. 10
figure 10

Loss convergence trends of three PVCQTL approaches on the Deepfake dataset (Section “PVCQTL results for deepfake detection binary classification dataset”), averaged across six sub-sampled datasets to reflect variability and generalization.

Full size image

Statistical significance test

Paired t-tests52 were conducted on Deepfake dataset which was already run on 6 different randomly sampled dataset, to compare three approaches (Modified Observable Construction, Hybrid, and Variational-PV) across three locality settings (L1, L2, L3) and the results are represented in the Table 6. The last column in the table shows whether any paired comparison of approaches were significantly different than the other. It shows that none of the approaches comparisons yielded statistically significant differences at the 0.05 level. The closest to significance was Modified Observable Construction vs Hybrid in Locality 2 resulting a (p = 0.0882) which is still greater than 0.005. Overall, p-values across all comparisons were relatively high, indicating strong evidence of performance similarity in Table 9. These results suggest that no single method consistently outperforms the others across all localities. The conclusion from this test suggests that, we can choose any of the proposed methods to conduct our analysis, but choosing Modified Observable Construction approach consumes lesser time with the same performance.

Table 6 Paired t-test results comparing Mod. Obs. Const., Hybrid, and Variational-PV methods across different locality levels.
Full size table
Table 7 Quantum circuit characteristics for each model implemented on a 4-qubit quantum system.
Full size table

Extended experiments for generalization

We extend our evaluation by considering three additional datasets. Three diverse image classification datasets were selected.. The Ants vs. Bees dataset53 is a binary classification subset commonly used to test fine-grained visual recognition, particularly in natural scenes. The Cats and Dogs dataset is derived from the CIFAR-10 dataset54, which contains low-resolution natural images across ten categories; we extract a binary subset for focused evaluation on animal classes. The Shirts vs. Pullover dataset is selected from Fashion-MNIST55, a modern alternative to MNIST with grayscale clothing images that offer higher complexity and real-world relevance. These datasets were chosen to provide a range of visual features—natural, structured, and fashion-oriented—ensuring robust performance evaluation and generalization across domains. The CQTL model was also implemented using Qiskit, and its results are presented in Table 8. In parallel, we conducted an extensive study of the proposed PVCQTL variants, with the corresponding performance summarized in Table 9. Quantum circuit characteristics for each configuration, evaluated on the statevector simulator, is reported in Table 7. The feature map circuit, common to all three proposed models, has a depth of 5 based on Figure 6(a), comprising only two gate types: ry and cz, one per qubit, unlike CQTL’s feature map, which uses Hadamard gates, our ablation on model architecture Table 10 informs more about the experimental analysis for Hadamard vs no Hadamard in the feature map circuit. The CQTL ansatz circuit is a two-local design with a depth of 5 for a single layer, using gates ry and cx. In contrast, the modified observable construction approach does not use an ansatz, resulting in a depth of 0 and significantly reduced gate count. The hybrid and Variational-PV models use ansatz circuits with a depth of 7, composed of rx, ry, rz, and cz gates, as shown in Figures 6(b) and 6(c). Computational cost of PVCQTL approaches remains comparable to CQTL. Despite introducing more measurements in the PVCQTL framework, the runtime is not significantly increased—this is largely due to the fact that measurements of commuting Pauli operators can be executed simultaneously. Our results show that, for example, the Ants vs. Bees dataset took approximately 15 minutes to train under the CQTL model, and the modified observable construction approach within PVCQTL required a similar runtime. The hybrid variant exhibited a marginal increase of only 2–4 minutes. Although runtime was not the primary focus of this study, we emphasize that our objective is to explore design innovations that improve performance while maintaining efficiency. Additionally, a thorough ablation study analyzing hyperparameter sensitivity was conducted, with detailed results provided in Table 12 is a function of learning rate, whereas Table 13 is a function of batch size.

Table 8 The CQTL model was implemented using Qiskit and evaluated on three datasets.
Full size table
Table 9 PVCQTL performance across three proposed approaches. L1, L2, L3 represents each approach ran at different localities.
Full size table

Ablation study on model architecture

We conduct a detailed ablation study recorded in Table 10 to isolate the contribution of each architectural component within our PVCQTL framework. The ablation results clearly highlight that incorporating Pauli-based measurements (L1, L2, L3) significantly enhances model performance compared to traditional Z-basis readout. Variants with fixed ansatz combined with Pauli measurements (hybrid and post-variational models) often match or exceed the accuracy of fully trainable circuits, showing that expressive measurements can compensate for reduced quantum depth. Additionally, reducing the number of qubits or removing entanglement degrades performance, reaffirming their role in encoding richer representations. Finally, larger classical pretrained models (ResNet50) consistently outperform smaller ResNet18, underscoring the importance of hybrid model capacity in quantum transfer learning. Together, these studies validate our proposed architecture through systematic, component-wise comparisons.

Table 10 Ablation study on architectural elements in quantum transfer learning were conducted varying elements such as qubit count, ansatz trainability, measurement basis, and the presence of Hadamard gates or entanglement, we evaluate their individual impact on model performance.
Full size table

Robustness to noise during inference

In this section we evaluate how well the PVCQTL model handles corrupted inputs at inference time. To assess this, we introduce controlled perturbations into the Ants and Bees dataset using two widely recognized types of noise: Gaussian noise and Salt-and-Pepper noise56. Gaussian Noise models random variations in pixel intensity values, following a normal distribution. Salt-and-Pepper Noise introduces extreme outliers by randomly flipping a subset of pixels to either the minimum (black) or maximum (white) intensity. Experimental results show that all PVCQTL-based models (Modified Observable Construction, Hybrid, and Variational PV) demonstrate strong resilience under noisy inputs. The models perform better under Gaussian noise than Salt-and-Pepper noise as shown Fig. 11 and the results are in the Table 11. This may be due to the less abrupt nature of Gaussian perturbations, which preserve the global structure of the image, whereas Salt-and-Pepper noise disrupts spatial continuity more severely. Despite the difference in performance, the models exhibit overall robustness toward both types of noise, maintaining high classification accuracy and consistent precision/recall levels. These findings highlight the robust generalization capacity of the PVCQTL framework.

Fig. 11
figure 11

Visual comparison of Ants and Bees dataset as input images under different noise conditions used to evaluate the robustness of the PVCQTL model. (a) Clean images with no noise, (b) Images with Gaussian noise at 20% intensity, and (c) Grayscale images corrupted by salt-and-pepper noise at 20%. These augmentations simulate real-world perturbations to assess how well the model generalizes under degraded conditions.

Full size image
Table 11 Performance metrics for the PVCQTL model under two different noise types and varying noise levels, averaged over 5 runs (mean ± std) for Ants and Bees dataset, in each run we selected 100 images for testing.
Full size table

Convergence evaluation

To provide a more comprehensive evaluation of the PVCQTL model’s performance we have analysed the training loss curves with epoch-wise accuracy progression, along with different hyperparameter settings as show in under each datasets at Table 9. The loss curve for Ants and Bees dataset Fig. 12 and Cats and Dogs dataset is at Fig. 13, all models exhibit a steep initial drop in loss, indicating effective learning during early epochs. Notably, modified observable construction and Variational-PV show improved convergence and lower final loss values when configured with higher locality (Locality = 2 or 3), suggesting that increased observable locality contributes to better model performance. In contrast, hybrid approach demonstrates consistent convergence across all locality settings.

Fig. 12
figure 12

Dataset: Ants and Bees, convergence behavior of the three PVCQTL approaches. Hyperparameters in the legend.

Full size image
Fig. 13
figure 13

Dataset: Cats and Dogs, convergence behavior of the three PVCQTL model variants. Hyperparameters in the legend.

Full size image

Ablation study on hyperparameters

An ablation study was performed on the Ants and Bees dataset using the Modified Observable Construction approach to evaluate the model’s sensitivity to key hyperparameters. This analysis explores the impact of varying the learning rate (Lr), batch size (Bs), and number of qubits (Nq) on the model’s accuracy.In the learning rate analysis Table 12, the batch size, number of qubits, and dataset were kept constant while adjusting the learning rate and number of epochs. A higher learning rate tends to accelerate convergence by increasing the step size, potentially reaching a local optimum more quickly but sometimes at the cost of stability. In contrast, a lower learning rate results in more gradual, stable learning, though it may require more training time. This confirms that the learning rate effectively controls the optimization step size. For the batch size evaluation (see Table 13), we fixed the learning rate and number of qubits and varied only the batch size. The results indicate that increasing the batch size from 4 to 8 led to a drop in model accuracy, highlighting the sensitivity of the proposed approach to this parameter.

Table 12 Effect of Learning Rate (Lr), for fixed parameters Nq = 4 and Bs = 4, accuracy decreasing as the learning rate increases taking a bigger jump in the parameter space which is also reflected in the time that it takes lesser time to converge as learning rate increases.
Full size table
Table 13 Effect of Batch Size (Bs), in this case we change batch size and keep same learning rate for each batch and number of qubits is fixed at Nq = 4.
Full size table

Computational settings

The quantum circuits were implemented using the Qiskit Software Development Kit and Pennylane, with integration into neural networks achieved via their respective PyTorch extensions. All implementations were developed in Python. Experiments were executed on a system equipped with an Apple M3 Pro chip, featuring a 12-core CPU (performance cores up to 4.05 GHz, efficiency cores up to 2.06 GHz). No GPU acceleration was used for any experiments. The software environment included Qiskit version 1.3.0, QiskitMachineLearning version 0.8.2, Pennylane version 0.41.1 all in Python programming language version 3.11.4 under a conda virtual environment.

Conclusion

We introduce the Post-Variational Classical-Quantum Transfer Learning (PVCQTL) model as a non-iterative approach to quantum machine learning. Unlike variational CQTL, PVCQTL employs fixed quantum circuits, optimizing only their classical combination instead of variational parameters. With a well-chosen set of fixed ansatz, the optimization reduces to a convex problem, ensuring a global minimum solution in polynomial time. Although the algorithm yields slightly better-performing PVCQTL models compared to CQTL models, we do not claim a proven quantum advantage. The classical hardness of simulating the circuits are preserved, but PVCQTL may require fewer quantum gates and lower circuit depths than previous methods while still outperforming other quantum models such as CQTL and HQCNN. Observable Construction-based approaches exhibit stable accuracy, whereas the hybrid approach introduces more variability. The Variational-based post-variational method demonstrates similar median accuracy compared to modified observable construction approach, but consumes more time per epoch. The statistical significance test results indicate that while all proposed methods perform comparably across localities. The modified observable construction approach offers similar accuracy with lower runtime, making it a more efficient choice for analysis with lesser circuit depth and gate count. The studies reveal that post-variational measurement design, Pauli observables, and hybrid quantum circuits offer clear performance gains. Our model maintains stable performance under varied noise and hyperparameters, with fast and consistent convergence across training scenarios. Additionally, exploring adaptive fixed ansatz selection and hardware-efficient implementations could enhance scalability and robustness to improve generalization. Another promising direction is investigating the expressivity trade-offs between locality-based methods and hybrid approaches, potentially leading to more structured circuit designs for practical quantum advantage. Future work may extend PVCQTL by incorporating experiments under varying noise levels, using both Qiskit-based simulations and real quantum hardware, to investigate whether hardware-induced noise can positively influence model performance. As these experiments were conducted using simulated quantum environments, this work can be easily extended to run on real quantum devices with a heavy hexagonal lattice structure. To achieve this, the full circuit length should be optimized, and gates such as CZ or CNOT to be replaced with swap gates, depending on the native gates supported by the specific quantum device.