Introduction

High-resolution multispectral images are crucial in the field of remote sensing, significantly contributing to areas such as national defense security1target detection2environmental protection3and disaster prevention4. However, the simultaneous achievement of high spatial resolution and high spectral resolution images remains a significant challenge due to the limitations of multispectral imaging devices and sensor technologies. Pan-sharpening provides an effective solution to this issue by fusing multispectral (MS) images with panchromatic (PAN) images from the same region, thereby generating high-resolution multispectral images5. While numerous spectral fusion algorithms are currently available, all pan-sharpening algorithms can be classified into four primary categories6: Component Substitution (CS), Multiresolution Analysis (MRA), Variational Optimization-based (VO), and Deep Learning (DL).

The Component Substitution (CS) method, also referred to as the spectral method, leverages the high spatial resolution of the panchromatic (PAN) image to replace the low spatial resolution components of the multispectral (MS) image, resulting in a fused MS image with enhanced spatial resolution7. Owing to its straightforward implementation, many pioneering pan-sharpening algorithms belong to the CS category8. Notable examples include those utilizing Intensity-Hue-Saturation (IHS)9Principal Component Analysis (PCA)10and Gram-Schmidt (GS)11. Recent contributions in the literature have focused on refining the injection rules, leading to the development of Adaptive GS (GSA)12 and GSA with Clustering (C-GSA)13 methods. The Multiresolution Analysis (MRA) approach extracts spatial details from the panchromatic (PAN) image through multiscale transformations and injects these details into the resampled MS image, yielding a fused multispectral image with high spatial resolution14. These methods can be traced back to fusion techniques based on generalized decomposition, which can be executed using simple low-pass filtering or more complex iterative methods, such as Laplacian pyramids, wavelets15and Smoothing Filter-based Intensity Modulation (SFIM)16.

Variational Optimization-based (VO) techniques are recognized as sharpening methods that depend on the resolution of optimization problems. All techniques within this family are based on a model that defines an objective function, which is typically addressed through variational optimization methods to identify appropriate solutions17. A pioneering VO pan-sharpening approach introduced a regularization model based on Total Variation (TV)18. It is undeniable that the rise of Deep Learning (DL) has significantly impacted the field of panchromatic sharpening19,20. Masi et al. designed and trained the first fully convolutional network specifically developed for panchromatic sharpening, referred to as the Panchromatic Sharpening Neural Network (PNN)21which achieved promising results. An enhanced version of the PNN, known as the Adaptive PNN (APNN)22has also been proposed. Deng et al.23 developed the FusionNet architecture by integrating convolutional neural networks (CNNs) with traditional techniques, achieving commendable performance at both downscale and full scale. Jian et al.24 constructed a multi-scale multi-flow fusion network (MMFN) by extracting diverse features from multispectral (MS) and panchromatic (PAN) images using a multi-scale strategy and multi-flow fusion blocks, enabling the preservation of both spatial and spectral features. Fang et al.25 introduced a lightweight CNN architecture with a single branch and scaling, termed SDRCNN, which incorporates convolutional blocks and dense residual connections to retain spatial and spectral information within the images. Lu et al.26 proposed a self-guided spatial channel adaptive convolution method (SSCAConv) that combines spatial and channel attention, taking into account both spatial and channel differences in features while enhancing sharpening outcomes. Que et al.27 integrated spectral and spatial networks in a bilateral pyramid structure, employing collaborative attention to amplify the correlation between spectral and spatial features, thereby improving the sharpening results. Although deep learning methods can enhance the quality of fused images from various perspectives, they often involve high computational complexity and necessitate a substantial amount of training data, which somewhat limits the advancement of these approaches28,29.

To effectively address the spatial and spectral distortions caused by the previously mentioned methods, a pan-sharpening (PS) approach based on a Component Substitution (CS) model and Side Window Filtering (SWF) has been proposed. This approach, referred to as the Improved Adaptive GS Method Based on SWF (SWGSA), significantly enhances the quality of full-resolution fused images while reducing errors. In the process of generating intensity components, SWF is applied to filter the PAN image, achieving both denoising and improved edge preservation. Furthermore, the gain function has been modified to incorporate references from the PAN image, thereby enhancing detail. The latest parameter metric, RQNR, has been utilized for performance evaluation. Experimental results indicate that the algorithm effectively enhances both spatial and spectral information.

Related works

Component substitution methods are based on projecting the multispectral (MS) image into a new space where spatial structures and spectral information are effectively separated. In this new space, the component containing spatial structures is replaced with the panchromatic (PAN) image, and the transformed MS image is subsequently sharpened. Finally, the sharpening process is completed by applying an inverse transformation to restore the MS image to its original space. This process can generally be described by the following equation:

$$\widehat{{{\bf{MS}}}}_{k} = \widetilde{{{\bf{MS}}}}_{k} + {\bf{G}}_{k} \cdot \left( {{\bf{P}} - {\bf{I}}_{L} } \right)$$
(1)

In Eq. (1), the subscript k indicates the spectral image of the k-th channel; \(\widehat{{{\bf{MS}}}}_{k}\) denotes the fused multispectral image; \(\widetilde{{{\bf{MS}}}}_{k}\) represents the multispectral image interpolated to the resolution of the PAN image; Gk refers to the injected gain matrix; P is the panchromatic image; and IL is the intensity component, which is defined as follows:

$${\bf{I}}_{L} = \sum\limits_{i = 1}^{K} {w_{i} \widetilde{{{\bf{MS}}}}_{i} }$$
(2)

In Eq. (2), K denotes the number of spectral channels, and wi represents the weight coefficient for the i-th channel. In the traditional Gram-Schmidt (GS) method, the intensity component is calculated using a direct averaging approach, specifically wi = 1/K. The calculation of the injected gain matrix in the traditional Gram-Schmidt (GS) method is presented as follows:

$${\bf{G}}_{k} = \frac{{\sigma ({\bf{I}}_{L} )}}{{\sigma ({\bf{P}})}}{\bf{1}}$$
(3)

In Eq. (3), \(\sigma\) represents the standard deviation and 1 indicates a matrix of ones. It is evident that the traditional GS method solely considers the relationship between the intensity component and the panchromatic (PAN) image.

Multiple improved versions have been developed by modifying the methods for generating intensity components and calculating the injected gain matrix. The Gram-Schmidt Adaptive (GSA) method calculates the weight coefficients for each channel by minimizing the mean squared error (MSE) relative to the low-pass filtered version of the Panchromatic (PAN) image through a weighted average of the multispectral (MS) bands. Furthermore, the new injected gain matrix considers the relationship between the MS image and the intensity component, as represented in the following equation:

$${\bf{G}}_{k} = g_{k} {\bf{1}} = \frac{{{\text{cov}} \left( {\widetilde{{{\bf{MS}}}}_{k} ,{\bf{I}}_{L} } \right)}}{{{\text{var}} \left( {{\bf{I}}_{L} } \right)}}{\bf{1}}$$
(4)

In Eq. (4), Cov(X, Y) denotes the covariance between two images X and Y; var(X) represents the variance of image X. The formulas for covariance and variance are provided below:

$${\text{cov}} (X,Y) = \frac{1}{MN}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {(X(i,j) - \overline{X})(Y(i,j) - \overline{Y})} }$$
(5)
$${\text{var}} (X) = \frac{1}{MN}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {(X(i,j) - \overline{X})^{2} } }$$
(6)

In Eq. (5), M and N indicate the resolution dimensions of the image, while \(\overline{X}\) and \(\overline{Y}\) represent the average grayscale values of all pixels in the entire image.

The GSA with Clustering (C-GSA) method employs an injected gain matrix that is consistent with the GSA method, but the generation of intensity components differs. C-GSA segments the MS image using a binary tree segmentation algorithm, and k-means clustering is applied to estimate the weight coefficients for each channel from the segmented images, thereby optimizing the algorithm.

The mathematical foundation of the Gram-Schmidt Adaptive (GSA) method and its improved version, the C-GSA method, which is based on the classical Gram-Schmidt orthogonalization process, is clearly established. The calculations involved are relatively straightforward and easy to implement. Both GSA and its improved methods exhibit high computational efficiency and speed, particularly when handling large-scale image data. Due to their lower algorithmic complexity, these methods can complete panchromatic sharpening tasks within a shorter time frame. Furthermore, they effectively mitigate the impact of noise interference on sharpening results and demonstrate a degree of robustness to variations in input data, allowing for adaptability to different types of multispectral images and providing high-quality outputs.

In contrast, Multiresolution Analysis (MRA) methods typically involve complex wavelet transforms and multiscale analyses. In comparison, GSA and its improved methods are simpler to implement, requiring less frequent scale transformations, which reduces the overall complexity of implementation. These methods directly address the features of the input images, thereby avoiding information loss at various resolution levels and preserving both image detail and contrast.

Variational Optimization (VO) methods generally necessitate iterative calculations to resolve complex optimization problems. In contrast, GSA and its improved methods can produce results in a shorter time, making them suitable for applications requiring rapid responses. While variational optimization methods require an in-depth mathematical background and advanced optimization techniques, the implementation of GSA and its improved methods is relatively intuitive, promoting their widespread adoption and application.

Deep Learning (DL) methods typically demand a substantial amount of training data for model training. Conversely, GSA and its improved methods have relatively lower data requirements and can achieve good performance even on smaller datasets. The training process for deep learning models may consume significant time and computational resources, whereas GSA and its improved methods can rapidly yield results, making them ideal for quick deployment and application.

Proposed method

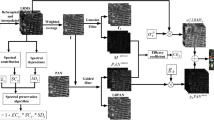
Figure 1 illustrates the flowchart of the algorithm proposed in this paper, with each component to be discussed in detail in the subsequent sections.

Fig. 1
figure 1

Flowchart of the proposed approach.

Full size image

SWGSA fusion model

The Gram-Schmidt (GS) method applies low-pass filtering to the Panchromatic (PAN) image; however, low-pass filtering often diminishes the edge details of the image. Reference30 introduces a Spatial Weighted Filtering (SWF) model that significantly enhances the ability to preserve image edges. Inspired by this model, applying it in the Panchromatic Sharpening (PS) process allows for better extraction of effective and relevant detail features from the image, thereby establishing a foundation for improving the spatial resolution of the Multispectral (MS) fused image while maintaining spectral information after information injection. The introduction of the SWF filtering method aims to better preserve meaningful detail information in the image. By integrating the SWF-filtered image into the weight function, the detail features of the intensity component can be more thoroughly enhanced. Furthermore, since the fused image should consider both the MS and PAN images, the relationship with the PAN image is crucial. The new injection gain strategy modifies the injection gain to utilize the covariance relationship between the PAN image and the MS image, which further elevates the image’s detail level. The implementation of these two strategies will positively influence the detail level of image fusion. The subsequent sections will provide a detailed description of the specific operational steps for the new intensity component and injection gain strategy.

Side window filtering

The original weight coefficients were established through linear regression between the low-pass filtered PAN image and the MS bands, with the goal of minimizing the mean squared error (MSE) between the low-pass filtered PAN image and the intensity component. The new intensity component strategy primarily involves replacing the original low-pass filtered PAN image with the new Spatial Weighted Filtering (SWF) method, which is capable of preserving more details from the MS image. In this study, the weight function is defined by applying weighted averages to the MS bands, aiming to minimize the mean squared error (MSE) between the upsampled MS image and the PAN image processed with SWF filtering. SWF not only retains detail information but also incurs a lower computational cost. This approach is expected to effectively mitigate the detail loss issues that may arise from low-pass filtering.

Compared to traditional filters, Side Window Filtering not only effectively removes image noise but also preserves image edges and details more effectively. The parameters of the side window filter, including window size and the number of iterations, can be flexibly adjusted to meet specific requirements for processing images with varying noise levels. Specifically, the choice of filter window size and iteration count must balance the level of image noise with the retention of detail and edge information. Smaller filter windows are more effective at preserving details and edges; however, they may prove inadequate for effective noise reduction at higher noise levels. In contrast, larger filter windows can smooth the image more effectively and remove noise, but they may also blur details and edges, negatively impacting image clarity. Regarding the number of iterations, fewer iterations typically facilitate rapid noise removal but may not sufficiently smooth the image, resulting in residual noise. Conversely, increasing the number of iterations can enhance the denoising effect to some extent; however, excessive iterations may lead to the loss of image details and cause over-smoothing effects, such as the “block effect.”

Given that remote sensing image data contains rich details and edge information, caution must be exercised during filtering to avoid detail loss due to over-smoothing. Additionally, considering the response modulation transfer function of optical sensors, the collected image data may contain some high-frequency noise. To retain as much detail and edge information as possible while denoising, a window size of 3 × 3 was selected for the side window filter in this study. Taking into account the processing efficiency of the filter and the denoising effect, the number of iterations was set to 1 to achieve an optimal balance between denoising effectiveness and detail retention.

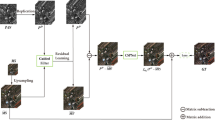
The SWF method effectively captures the edges of the target. We employed data from the Gaofen satellite31 to illustrate the comparison of filtering effects, as depicted in Fig. 2. Figure 2(a) presents the original PAN image, Fig. 2(b) shows the low-pass (LP) filtered version of Fig. 2(a), and Fig. 2(c) displays the SWF filtered version of Fig. 2(a).

Fig. 2
figure 2

Comparison of filtering results of different algorithms. (a) PAN; (b) LP; (c) SWF.

Full size image

The analysis of the figure reveals that the edges in the original PAN image are distinctly pronounced; however, the low-pass filtered image in Fig. 2(b) suffers from considerable blurring, resulting in a lower similarity to the original PAN image and a reduction in visible edge details. In contrast, the SWF filtered image in Fig. 2(c) exhibits a strong similarity to the original PAN image, particularly regarding global edge representation. Notably, even in areas where edges are relatively subtle, the SWF method effectively highlights these edges and maintains detail. The comparison between Figs. 2(b) and 2(c) clearly demonstrates that the SWF filtered image in Fig. 2(c) shows a marked enhancement in edge information extraction compared to the low-pass filtered image in Fig. 2(b).

New injection gain matrices

As noted in the literature, the traditional GS (Gram-Schmidt) method employs an injection gain matrix Gk only addresses the relationship between the upsampled multispectral image and the intensity component, neglecting the relationship between the PAN image and the intensity component. In this study, we enhance detail information and reduce information distortion by incorporating the relationship between the PAN image and the intensity component.

We introduce a novel injection gain strategy that considers a scheme to augment the spatial information of the PAN image. The calculation method is as follows:

$${\bf{G}}_{k} = g_{k} {\bf{1}} = \frac{{{\text{cov}} \left( {\widetilde{{{\bf{MS}}}}_{k} ,{\bf{I}}_{L} } \right)}}{{{\text{cov}} \left( {{\bf{P}},{\bf{I}}_{L} } \right)}}{\bf{1}}$$
(7)

In Eqs. (7), 1 refers to a matrix of ones, and cov(X, Y) represents the covariance between two images X and Y.

In the traditional Gram-Schmidt (GS) method, the injected gain matrix solely considers the relationship between the intensity component and the panchromatic (P) image. In contrast, the Gram-Schmidt Adaptive (GSA) method emphasizes the relationship between multispectral (MS) images and the intensity component. This paper presents an improved approach that incorporates the covariance between the panchromatic (PAN) image and the intensity component. This enhancement not only considers the relationship between the MS images and the intensity component but also expands the analysis to include the relationship between the PAN image and the intensity component. This improvement significantly enhances the representation of image details, thereby elevating the quality of the fused image.

Experimental results and discussion

Experimental setup and dataset

A systematic evaluation of performance was conducted. All experiments were performed under the following configuration: the hardware used included an Intel(R) Core(TM) i5-8300 H CPU @ 2.30 GHz processor with 16GB of RAM; the software environment was Windows 10 (64-bit), and the experimental platform was MATLAB R2021A.

This study employed three sets of image datasets, performing two types of experiments on the IKONOS32GeoEye-133, and WorldView-334 datasets, including downscaling and full-size comparison experiments. We use ENVI 5.035 software for image registration and segmentation. In all experiments, the resolution of the multispectral (MS) images prior to fusion was 256 × 256, while the resolution of the panchromatic (PAN) images was 1024 × 1024, resulting in a resolution ratio R of 4. In the downscaling experiment, we filtered the original PAN and MS images according to Wald protocol36 and downsampled them by a resolution ratio of 4.

This paper compares nine representative fusion methods with the proposed approach, including Interpolated MS image with a 23-tap interpolation kernel (EXP)37Principal Component Analysis (PCA)10Smoothing Filter-based Intensity Modulation (SFIM)16PCA/wavelet model-based fusion (PWMBF)15Pansharpening Neural Network (PNN)21Advanced Pansharpening Neural Network (A-PNN)22FusionNet23Gram–Schmidt adaptive (GSA )12and GSA with Clustering (C-GSA)13. All comparison methods utilized in this study are based on open-source code provided by the respective authors. Seven evaluation metrics38,39 were employed to assess the performance of the fused image results obtained by the different methods, with detailed descriptions of these metrics provided in Table 1. To ensure the reproducibility and transparency of the research, the code used in this study will be made publicly available after the article’s publication, allowing other researchers to reference and utilize it.

Table 1 The quantitative evaluation index.
Full size table

Experimental results

To evaluate the fused images more effectively, we selected a small region (highlighted by the green small box) from each fused image for 4x magnification. The magnified area was then placed in the lower right corner of the fused image (indicated by the green large box).

The fusion effects of different algorithms tested on the IKONOS dataset are illustrated in Fig. 3. Figure 3(a) displays the ground truth image, while Fig. 3(b) shows the panchromatic image. Figures 3(c) to 3(l) present the corresponding fusion results obtained from various fusion methods. From the fusion results of this set of images, it is evident that the traditional EXP algorithm performs the worst, producing a blurry image. The fusion results from the PCA, SFIM, and PWMBF algorithms also exhibit localized areas of ghosting and loss of detail in certain regions. The PNN algorithm suffers from spectral distortion issues, leading to color deviations and poor spatial quality. The APNN algorithm produces blurry images. The FusionNet algorithm yields relatively satisfactory results. In contrast, the GSA and C-GSA algorithms produce clear image outputs. The algorithm proposed in this paper effectively preserves image details, resulting in high-quality images.

Fig. 3
figure 3

Fusion results of IKONOS dataset. (a) Ground truth. (b) PAN image. (c) EXP; (d) PCA; (d) SFIM; (f) PWMBF; (g) PNN; (h) A-PNN; (i) FusionNet; (j) GSA; (k) C-GSA; (l) Proposed method.

Full size image

Table 2 presents a comparison of the objective evaluation metrics results obtained by various algorithms on the IKONOS dataset. The optimal results for each metric are highlighted in bold, while the best results among the GSA-related methods are italics. From Table 2, it can be seen that for the Dλ index, the results from the proposed algorithm are only slightly lower than those of the SFIM algorithm, indicating a significant improvement over the GSA and C-GSA algorithms. For the Ds index and ERGAS index, the proposed algorithm achieves the smallest numerical values, showcasing a clear advantage. In terms of RQNR, Q4, and SSIM metrics, the proposed algorithm produces the highest values, reflecting a notable enhancement compared to the second-best results. For the PIQE index, the results from the proposed algorithm are second only to those of the SFIM algorithm. Among the GSA-related methods, both the C-GSA and GSA algorithms exhibit minimal differences across the various metrics. In contrast, the proposed algorithm achieves optimal results across all metrics, demonstrating improvements over both the GSA and C-GSA algorithms.

Table 2 Quantitative evaluation results for IKONOS.
Full size table

The fusion effects of different algorithms tested on the GeoEye-1 dataset are illustrated in Fig. 4. Figure 4(a) displays the ground truth image, while Fig. 4(b) shows the panchromatic image. Figures 4(c) to 4(l) present the corresponding fusion results obtained from various fusion methods. From the fusion results of this set of images, it is clear that the traditional EXP algorithm still performs the worst, exhibiting significant spatial distortion and overall blurriness. The PCA algorithm suffers from color distortion. The SFIM and PWMBF algorithms demonstrate oversharpening, resulting in unclear edges. The results from both the PNN and APNN algorithms show blurriness in the enlarged areas, indicating subpar quality. The FusionNet algorithm presents slightly blurred results in the enlarged regions. The GSA and C-GSA algorithms exhibit overexposure in the grayscale of the white roof areas. In contrast, the results from the proposed algorithm demonstrate good clarity and detail in the images.

Fig. 4
figure 4

Fusion results of GeoEye-1 dataset. (a) Ground truth. (b) PAN image. (c) EXP; (d) PCA; (e) SFIM; (f) PWMBF; (g) PNN; (h) A-PNN; (i) FusionNet; (j) GSA; (k) C-GSA; (l) Proposed method.

Full size image

Table 3 presents a comparison of the objective evaluation metrics results obtained by various algorithms on the GeoEye-1 dataset. The optimal results for each metric are highlighted in bold, while the best results among the GSA-related methods are italics. It is clear from the table that the proposed algorithm achieves the best results in the Ds, RQNR, SSIM, and PIQE metrics. For the Dλ index, the results from the proposed algorithm are only surpassed by those of the SFIM and PNN algorithms. In terms of the Q4 index, the PNN algorithm achieves the best result, while the PWMBF algorithm excels in the ERGAS index. Among the GSA-related methods, the C-GSA algorithm shows only marginal improvements over the GSA algorithm, with minimal differences in their performance. In contrast, the proposed algorithm demonstrates improvements over both the GSA and C-GSA algorithms in the Ds, Dλ, RQNR, SSIM, PIQE, and ERGAS metrics, although it performs relatively poorly in the Q4 index.

Table 3 Quantitative evaluation results for GeoEye-1.
Full size table

The fusion effects of different algorithms tested on the WorldView-3 dataset are illustrated in Fig. 5. Figure 5(a) displays the ground truth image, while Fig. 5(b) shows the panchromatic image. Figures 5(c) to 5(l) present the corresponding fusion results obtained from various fusion methods. From the fusion results of this set of images, it is clear that the EXP algorithm performs poorly, resulting in a blurred image. The SFIM algorithm shows blurriness in the enlarged regions of the fusion results. The PCA algorithm produces blurred enlarged images with poor spatial quality. The PWMBF algorithm suffers from oversharpening and color distortion. The results from both the PNN and APNN algorithms are generally subpar, exhibiting color deviations and blurriness, leading to poor quality. The FusionNet algorithm presents enlarged regions that are not very clear. The GSA and C-GSA algorithms yield images with decent brightness but suffer from excessive smoothing. In contrast, the results from the proposed algorithm do not show overexposure and maintain good clarity.

Fig. 5
figure 5

Fusion results of WorldView-3 dataset. (a) Ground truth. (b) PAN image. (c) EXP; (d) PCA; (e) SFIM; (f) PWMBF; (g) PNN; (h) A-PNN; (i) FusionNet; (j) GSA; (k) C-GSA; (l) Proposed method.

Full size image

Table 4 presents a comparison of the objective evaluation metrics results obtained by various algorithms on the WorldView-3 dataset. The optimal results for each metric are highlighted in bold, while the best results among the GSA-related methods are italics. It is clear from the table that the proposed algorithm achieves the best results in the Ds, RQNR, SSIM, and PIQE metrics. For the Dλ index, the SFIM algorithm shows the best results, followed by the APNN algorithm. In terms of the Q8 index, the SFIM algorithm again achieves the best results, with the proposed algorithm ranking just behind the SFIM and PWMBF algorithms. Regarding the ERGAS index, the PWMBF algorithm obtains the best results, with the proposed algorithm placing just below the SFIM, PWMBF, and FusionNet algorithms. Among the GSA-related methods, the C-GSA algorithm exhibits negative optimization in several metrics compared to the GSA algorithm, showing limited improvement. In contrast, the proposed algorithm demonstrates enhancements over both the GSA and C-GSA algorithms across all metrics, achieving the optimal results.

Table 4 Quantitative evaluation results for WorldView-3.
Full size table

A key aspect of this study is the analysis and comparison of the computational complexity of the algorithms. By measuring the runtime of different methods on the IKONOS, GeoEye-1, and WorldView-3 datasets, we evaluate the computational complexity of the panchromatic sharpening algorithms and conduct an in-depth analysis of their effectiveness. As shown in Table 5, the optimal results for each metric are highlighted in bold, while the best results among the GSA-related methods are italics. The component replacement and multi-resolution analysis methods generate the final products in a shorter time, while variational optimization and deep learning methods are characterized by longer execution times, which is inherent to the algorithms themselves. The runtime of the proposed algorithm is only slightly higher than that of the PCA and SFIM algorithms, but it demonstrates a significant reduction compared to the GSA and C-GSA algorithms. The average runtime of the proposed algorithm across the three datasets is only two-thirds of that of the GSA algorithm and just 6.8% of that of the C-GSA algorithm.

Table 5 Comparison of running times for different methods(s).
Full size table

Discussion

Based on the image fusion results from the IKONOS, GeoEye-1, and WorldView-3 datasets, the proposed algorithm demonstrates superior performance across four evaluation metrics (Ds, RQNR, SSIM, and PIQE). However, its performance on the Dλ and Q4 metrics is relatively weak. The reasons for the suboptimal performance in these two metrics can be attributed to several factors: First, to enhance the spatial details of the panchromatic image, the SWF filtering method is employed during the sharpening process, which can lead to some distortion of the spectral information, ultimately resulting in a decline in the Dλ metric. Second, while the proposed method uses SWF filtering, which is effective at preserving edges and details, it may, in certain cases, cause excessive enhancement of image edges, leading to unnatural transitions in some areas that negatively affect the Q4 metric. Additionally, the images in the three datasets contain complex textures and rich details. Although the proposed method comprehensively considers the relationships between the multispectral images and the principal component (PAN) images with the intensity component, this approach may lead to some duplication of image details, thereby impacting the evaluation of the Dλ and Q4 metrics.

Although the proposed algorithm performs relatively poorly on the Dλ and Q4 metrics, it shows improvements across all performance indicators when compared to the GSA and C-GSA algorithms. This optimization effect primarily stems from the different filtering techniques and the injected gain matrix used in this study. Since the injected gain matrices of the GSA and C-GSA algorithms are identical, the differences in their performance across various metrics are relatively minor, resulting in insignificant variations in the processing outcomes. The side window filter employed in this study not only effectively reduces computational load but also preserves the edges and details of the image while eliminating noise. Furthermore, the newly introduced injected gain matrix considers not only the relationship between the multispectral (MS) images and the intensity component but also fully accounts for the relationship between the principal component (PAN) image and the intensity component. This enhancement significantly improves the representation of image details and boosts the overall quality of the fused image.

In summary, based on the image fusion results from the three datasets, the proposed algorithm outperforms both the GSA and C-GSA algorithms across all metrics and achieves the best results in several key indicators, including Ds, RQNR, SSIM, and PIQE. The proposed method exhibits lower computational complexity and can deliver excellent image quality and optimal performance across multiple evaluation metrics within a shorter runtime. Further comprehensive subjective and objective evaluations, along with performance analyses, indicate that the method proposed in this study has clear advantages and can effectively enhance the quality of multispectral image fusion.

Conclusions

This paper presents a multispectral image fusion method based on side window filtering and a novel injected gain, termed the improved adaptive GS method based on SWF (SWGSA). The side window filtering technique facilitates denoising while enhancing edge preservation in the images. By modifying the injected gain and incorporating the panchromatic (PAN) image as a reference, further enhancement of image details is achieved. The proposed method’s performance is evaluated on three image datasets using nine comparison methods and seven quantitative metrics. The results confirm that the proposed method effectively enhances spatial details and spectral information, leading to improved quality in the fused images.