Multi-band frequency selective metasurface based filter for WLAN and X-band EMI shielding applications

Abstract

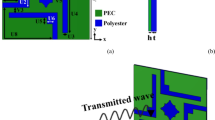
In this paper, a double-sided planar frequency selective metasurface (FSMS) has been presented for airborne electromagnetic interference (EMI) shielding applications. The proposed structure uniquely combines two narrow bands of WLAN (2.4 and 5.8 GHz) and the entire bandwidth of the X-band (8–12 GHz) spectrum. The proposed FSMS unit element (UE) is designed on a double-sided Rogers 5870 substrate with a total dimension of 11.4 × 11.4 mm². The proposed UE design has a compact and symmetric layout. It is polarization-independent and has a stable angular response for up to 45^o oblique angle of incidence. In addition, the low profile of the FSMS makes it appropriate for conformal surfaces. The proposed design has been backed by detailed explanations of the physical phenomena of current and field distribution and equivalent circuit models. For experimental validation, a 20 × 13 element FSMS with a total footprint of 229 × 152 mm² is fabricated and experimentally validated. The simulated and measured characteristics and the equivalent circuit model predictions are well-aligned, which corroborates the high performance of the proposed design. The proposed FSMS features a novel and straightforward structure with multiband operation, stable incident angle output, polarization insensitivity, and scalability, making it a potentially attractive candidate for WLAN and X-band EMI shielding applications.

Introduction

A frequency selective metasurface surface (FSMS) is a planar periodic structure. It consists of unit cells having a reflective or transmissive response at particular frequencies¹. Metamaterial properties such as negative permittivity or negative permeability determine the FSMSs’ filter features. Metamaterial provides an optimal way to generate cost-effective and low-profile 2D surfaces due to their exotic properties of manipulating the electromagnetic wavefront within a subwavelength scale. The FSMSs are being given special consideration in many domains, including military applications, antennas, reflectors, and electromagnetic interference (EMI) shields¹ Recent advancements have demonstrated the potential of metamaterial-based FSMS designs in diverse applications. For instance, a metamaterial lens was developed using a CAD-based model to enhance antenna performance for Traffic Collision Avoidance Systems (TCAS) applications². Additionally, novel methods for permeability extraction, such as neurospace mapping techniques, have been applied to Omega unit cells to improve equivalent circuit modeling accuracy³. Furthermore, radar cross-section (RCS) reduction techniques using reflecting metasurfaces, incorporating hexagonal supercells with modified Jerusalem Cross meta-cells, have shown significant improvements in electromagnetic wave manipulation⁴. These developments highlight the versatility of FSMSs in multiband filtering and wavefront control.

The literature proposed several FSMS designs, which cover multiple bands. Notwithstanding, they offer a narrow bandwidth. Other designs are a single band but cover wide bandwidth. The structures offering wide stopband implemented through multiple transmission zeros are characterized based on the number of layers that constitute the unit cell. In the first type, the physical structure utilizes only one side of the laminate and has only one transmission zero, as in the case of^5,6, and⁷. In⁵ a convoluted loop is realized to have a stopband for the entire X-band from 8 to 12 GHz with 10 dB isolation, but it only exhibits one transmission zero at 10 GHz. Similarly, another convoluted loop is realized in⁶ operating in the X-band and has a stopband from 8.5 to 11.3 GHz having only one transmission zero at 10 GHz. A tunable one-sided surface is reported in⁷, having a wideband response with a single transmission zero. The structures that utilize both sides of the laminate usually have two transmission zeros and higher bandwidth is achieved as compared to single side designs. In⁸, a Jerusalem cross on one side and a fan-type structure on the other side is reported. It has a wide stopband from 40 to 70 GHz. In^9,10 similar topologies have been adopted that use a cross on one side and a loop on the other side of the laminate. Both these structures have wideband responses with two transmission zeros. In¹¹ a wideband design is proposed that utilizes both sides of the substrate with square loops to achieve the desired bandwidth. Generally, wideband shielding surfaces offer certain advantages, but application-specific bands are often desired to be suppressed, such as WLAN bands or ISM bands, etc. Likewise, in^12,13,14, multiband structures have been proposed which offer suppression for specific application frequency bands. A triple-band structure shielding WiMAX, Wi-Fi, and X-band is reported in¹⁵. The structure offers wideband shielding for 5 GHz Wi-Fi and X-band but with angular stability up to 30˚. The multifunctional operation can be performed by multiple stopband and passband FSMSs^16,17. Besides, the proximity of resonant peaks generates broadband FSMSs for multiple-frequency applications. The planar FSMS structure can only be utilized on flat surfaces; as a result, pointed or curved structures such as cones or cylinders cannot be shielded. These applications require conformal FSMSs, which maintain performance when installed around the chosen conformal object^16,18,19. Different miniaturized microwave FSMSs are presented with single or multiple stopband applications in^{16] and [18}. Although the designs have shown promising results, the multi-layer structure and large unit cell dimensions are detrimental to its usefulness. In this research work, a novel dual-layer FSMS-based filter design has been proposed capable of suppressing the two narrow bands of WLAN along with a wide band suppression of the complete X-band spectrum.

In contrast to the published literature, to cater to the bandwidth constraints and multiband requirements, a novel FSMS-based filter design is proposed here that works with the help of four transmission zeros, two for both Wi-Fi bands and two for rejecting the entire X-band. Similarly to the unique characteristics of the proposed design, the application of this FSMS is also different from conventional FSMSs. The proposed design is useful in indoor Wi-Fi applications, but it has additional applications for passenger airplanes offering in-flight Wi-Fi, where various radars are also operational, thereby safeguarding the sensitive plane equipment within both bands. Furthermore, the presented shield can be used as a wrapping surface.

The unit cell design achieves a high grazing angle of incidence stability up to 45 degrees and a stable response for TE and TM polarization. The key contributions of this work are detailed as follows:

• 1. The design and implementation of a double-layer, low profile, and compact FSMS unit-cell structure for dual-band WLAN and whole X-band shielding applications.

• 2. The proposed FSMS unit cell structure is symmetric, which offers a stable response for both TE and TM polarization and for oblique angles of incidence up to 45⁰.

• 3. To the author’s knowledge, this is the first ultra-compact dual-sided FSMS based filter design with four transmission zeros, covering the dual bands of WLAN and complete X-band reported in the literature.

• 4. The compact and symmetric layout of the proposed unit cell allows for accommodating a large number of cells in a small footprint which enhances the EMI shielding effects.

• 5. Single substrate design incorporates multiple resonating structures, making our design compact, low cost, and easy to fabricate and integrate.

• 6. The proposed design has the potential to be used on conformal surfaces due to thin and flexible substrate.

The rest of the paper is organized as follows. Section II covers the suggested FSMS unit cell design, geometry evolution, parametric analysis, and the equivalent circuit model. Section III elaborates implementation and measurements of the proposed FSMS. Section IV concludes the work.

Unit element design overview

A novel unit element has been designed to provide effective shielding across multiple frequency bands. There are several potential approaches to achieving this goal. Here, we have selected a 4-pole design complemented by stubs of varying lengths. Introducing these stubs at different lengths induces resonances at distinct frequencies, which allows the design to effectively cover the desired frequency ranges and achieve the required shielding response. Additionally, we enhance the performance of this design by coupling it with a square loop placed on the opposite side of the substrate. This strategic coupling further improves the shielding effectiveness, enabling broadband coverage across the X-band and both Wi-Fi bands.

The unit element (UE) design and its geometrical parameters are shown in Fig. 1. The top layer comprises a cross-shape structure loaded with stubs. The bottom layer comprises a simple square loop. a is the total length and width of the UE, W₁ and W₂ are the thicknesses of the stubs of the upper layer cross structure, g₁ and g₁₂ are the gaps between stubs, and l₁ is the dimension of the upper layer cross structure. L₂ and W₃ are the length and thickness of the bottom layer square ring structure, respectively. The structure is symmetric with respect to TE and TM polarizations. Therefore, the S-parameter response in both modes is the same. The design is realized on Roger 5870 high-frequency laminate with a thickness of 1.575 mm. CST Microwave Studio is used to simulate and optimize the proposed design. Periodic boundary conditions were assigned along the xy-plane, and the incident wave along the z-axis.

Fig. 1

UE geometry, dimensions are: a = 11.4 mm, l₁ = 5.4 mm, w₁ = 0.45 mm, w₂ = 0.3 mm, w₃ = 1.1 mm, g = 0.4 mm, g₁₂ = 0.35 mm, l₂ = 8 mm, s = 0.3 mm.

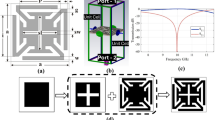
Stepwise design evolution

The step-by-step design process of the proposed UE and the transmission response are presented in Fig. 2. Figure 2(a) shows the transmission response of a cross-shape design. Two notches can be observed at 2.4 GHz and 10 GHz. In the second step, each arm of the cross is loaded with a stub. In the transmission response shown in Fig. 2(b), an additional notch appears around 5 GHz. The last notch is shifted to 11 GHz. The cross-shape stub loaded structure is designed on the top layer, whereas a planar square loop has been added to the bottom layer. The isolated planar square loop alone has a single stopband response at 10 GHz, as shown in Fig. 2(c). When both layers are simulated together, the three transmission zeros of the top layer and one transmission zero of the bottom layer produce four operating bands in total, as shown in Fig. 2(d). The first two transmission zeros, at 2.4 GHz and 5 GHz, offer stopband characteristics at both Wi-Fi bands. The next two transmission zeros are at 8.3 GHz and 11.83 GHz which completely suppress the X band from 8 GHz to 13.4 GHz. The bottom square loop in the design directly relates to the third resonance at 8 GHz. Also, by adding the third transmission zero, the bandwidth of the second transmission zero is reduced.

Fig. 2

Stepwise transmission response of the proposed dual-sided FSMS.

The transmission response of the design concerning different incident angles is shown in Fig. 3. The angular stability of the transmission response up to 45^o corroborated through simulations. The transmission response remains stable for notches at both Wi-Fi bands. A variation in the transmission response above 10 GHz is observed, caused by impedance variation and generation of undesired current modes in the structure. Despite this instability at higher frequencies, the stopband transmission for the entire X-band remains below − 10 dB.

Fig. 3

Simulated transmission response against incident angles up to 45^o.

Parametric analysis

Parametric analysis is carried out regarding the key parameters having the major effects on the transmission response. l₁ is the main parameter that controls the overall size of the UE. The unit element design is symmetrical. Therefore, l₁ represents the distance from the center to the edge on all sides, maintaining the symmetry of the FSMS design. Variation in l₁ directly affects the first, second, and fourth transmission zero as shown in Fig. 4(a). With the increase in l₁, the frequency of transmission zeros is lowered. The third transmission zero is unaffected by the change in l₁. Variation in the second and fourth transmission zero is large as compared to the first resonance as closely depicted in Fig. 4(b).

Fig. 4

Transmission response for the parametric analysis of l₁.

The parameter g₁₂ is the gap between the cross-shape structure and the loaded stubs. Increasing g₁₂ decreases the length of the loaded stub. As shown in Fig. 5(a), this significantly impacts the second transmission zero. The first resonance is unaffected by the changing g₁₂, but slight variation is observed in the third and fourth resonance as shown in Fig. 5(b). Increase g₁₂ also increased the second resonant frequency.

Fig. 5

Transmission response for the parametric analysis of g₁₂.

The parameter l₂ controls the bottom layer loop. The transmission response for l₂ variation can be seen in Fig. 6(a). The impact of l₂ is quite evident on the third transmission zero: increasing l₂ decreases the third transmission zero as shown in Fig. 6(b). The first two resonances are not affected by l₂, whereas a slight decrease in the resonance of fourth transmission zero is observed with increasing l₂ showing the mutual coupling effects between the two sides.

Fig. 6

Transmission response for the parametric analysis of l₂.

The inter-element spacing is represented by the parameter s. Since s is defined concerning the upper layer structure the impact can be judged accordingly. The variation in the inter-element spacing affects the fourth resonance the most, as shown in Fig. 7(a). Increases s leads to decreasing the fourth resonant frequency. A slight variation in the first two resonances can also be observed; however, the third resonance remains intact as seen in Fig. 7(b).

Fig. 7

Transmission response concerning the variation in s.

Substrate thickness plays a vital role in realizing wideband responses as reported in²⁰. The thickness variation effect on the transmission response is analyzed in Fig. 8(a). Since the substrate thickness changes the coupling between the two layers, the second and third resonance frequencies are mostly affected as shown in Fig. 8(b). After revisiting the design, it is observed that if the proposed UE is realized on the laminate of thicker substrate, the stability in the response can be improved but that would make the design unsuitable for conformal surfaces. Figure 9 shows that the transmission response simulated for the substrate thickness of 3.5 mm against varying incidence angles is greatly improved as compared to the response shown in Fig. 3.

Fig. 8

Transmission response for the parametric analysis of substrate thickness.

Fig. 9

Transmission response for the design using thick substrate.

Simulations were also carried out to analyze the stability of the transmission response of the conformed structure. The simulated transmission response for flat (R_c = ∞) and conformal scenario (R_c = 300 mm) are shown in Fig. 10. For the normal incident angle with this conformation, there is no significant difference between the responses. The E-field distribution on the top and bottom layers for all transmission zeros can be seen in Fig. 11. The fields on the top layer are stronger for all frequencies as depicted in Figs. 11(a), 11(b), and 11(d), whereas the fields at the bottom layer are only significant for the third transmission zero as shown in Fig. 11(c).

Fig. 10

Transmission response comparison of flat and conformal FSMS.

Fig. 11

Electric field distribution on UE surfaces at (a) 2.4 GHz, (b) 5.0 GHz, (c) 8.3 GHz, (d) 11.8 GHz.

Equivalent circuit modelling

The working mechanism of the proposed FSMS can be clearly understood through an equivalent circuit model (ECM) shown in Fig. 12. The parametric analysis and UE design modeling can be used effectively to implement the equivalent circuit model. The proposed design is a multi-resonant structure. As the top layer is composed of crossed dipole arms, it behaves predominantly as inductive elements, while the gaps between the arms and the edges contribute to capacitive coupling, thus forming a resonant LC structure. The top layer offers three resonances; they can be modeled with three LC networks as shown in Fig. 12(a) and Fig. 12(b). The bottom layer, a square loop, acts as an inductive element and supports capacitive effects at the edges and corners, again forming a resonant LC circuit. The impact of the bottom layer square loop on the three resonances of the upper layer structure in terms of equivalent structure is also shown in Fig. 12(c).

The equivalent circuit shown in Fig. 13(a) represents the impact of the bottom layer structure on all resonances resulting from the top layer. The self-resonance of the bottom layer structure in the X-band is represented by L_LC_L. Consequently, its impact on the first two resonances of the top layer structure is negligible, as shown in Fig. 13(b). The stopband of the second resonance is narrowed with the introduction of the bottom layer square loop, but there is a negligible shift in resonance. This effect is modelled by the transmission line inductor L_t1 and capacitor C_t1. The bottom layer significantly impacts the third resonance of the cross structure, which results in a wide stopband for the X-band. The transmission zeros in the X-band are represented by L_L, C_L, and L₃, C₃. The final equivalent circuit of the proposed FSMS is shown in Fig. 13(c).

Fig. 12

Step-by-step representations of the unit element, their respective transmission responses, and equivalent circuits.

Fig. 13

Equivalent circuit modelling of the proposed multi-band FSMS.

In the equivalent circuit shown in Fig. 13(c), Z₁, Z₂ and $\:{f}_{r1}$, $\:{f}_{r2}$ represent the impedances and resonant frequencies of the first two resonators, respectively. The third ($\:{f}_{r3}$) and fourth ($\:{f}_{r4}$) transmission zeros are represented by their respective impedances Z₃ and Z₄. The dielectric slab separating the top and bottom layers is represented by a short transmission line. The characteristic impedance of the transmission line is $\:{Z}_{d}={Z}_{0}/\sqrt{{\epsilon\:}_{r}}$, where Z₀ is the free space impedance. The complete expression for the frequency response at Wi-Fi and X-band is given as $\:{Z}_{WiFi}$ and Z_X, respectively:

$$\:{Z}_{1}={j\omega\:L}_{1}+\frac{1}{{j\omega\:C}_{1}};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{r1}=\frac{1}{2\pi\:\sqrt{{L}_{1}{C}_{1}}}$$

(1)

$$\:{Z}_{2}={j\omega\:L}_{2}+\frac{1}{{j\omega\:C}_{2}};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{r2}=\frac{1}{2\pi\:\sqrt{{L}_{2}{C}_{2}}}$$

(2)

$$\:{Z}_{WiFi}={Z}_{1}\parallel{Z}_{2}\parallel\left({j\omega\:L}_{t1}+j\omega\:{C}_{t1}\right)$$

(3)

$$\:{Z}_{3}={j\omega\:L}_{{L}^{{\prime\:}}}+\frac{1}{{j\omega\:C}_{{L}^{{\prime\:}}}}\:;\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{r3}=\frac{1}{2\pi\:\sqrt{{L}_{L{\prime\:}}{C}_{L{\prime\:}}}}\:$$

(4)

$$\:{Z}_{4}={j\omega\:L}_{{3}^{{\prime\:}}}+\frac{1}{{j\omega\:C}_{{3}^{{\prime\:}}}}\:;\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{r4}=\frac{1}{2\pi\:\sqrt{{L}_{3{\prime\:}}{C}_{3{\prime\:}}}}$$

(5)

$$\:{Z}_{X}={Z}_{3}\parallel\left({j\omega\:L}_{t2}+\left(\frac{1}{{j\omega\:C}_{t2}}\parallel{Z}_{4}\right)\right)$$

(6)

$$\:{Z}_{X}=\frac{{Z}_{3}\left[{Z}_{4}\left(1-{\omega\:}^{2}{L}_{t2}{C}_{t2}\right)+j\omega\:{L}_{t2}\right]}{{Z}_{3}\left(1+{Z}_{4}j\omega\:{C}_{t2}\right)+{Z}_{4}\left(1-{\omega\:}^{2}{L}_{t2}{C}_{t2}\right)+j\omega\:{L}_{t2}}$$

(7)

The next step is to map the equivalent circuit LC components shown in Fig. 13 to the physical design parameters of the proposed FSMS UE structure illustrated in Fig. 1. The structural components responsible for each resonance are highlighted in Fig. 14. It is worth mentioning, although previously discussed in the parametric analysis and field plots that the first, second, and fourth resonances originate from the top layer, while the third resonance is primarily contributed by the bottom layer. Based on the surface current distributions shown in Fig. 11, one can deduce which parts of the geometry correspond to each resonance. However, this relationship is further clarified in Fig. 14, where each resonating section of the structure is separately marked in terms of its inductive length and the associated capacitance.

Fig. 14

Equivalent LC circuit models of the proposed FSMS unit cell featuring inductances and capacitances, representing the electromagnetic behavior of the structure.

In Fig. 14(a), the inductive and capacitive elements contributing to the first resonance are denoted as L₁ and C₁, respectively. The inductive length L₁ corresponds approximately to 8l₁​ in terms of geometrical parameters. Similarly, Figs. 14(b-d) show the structure sections responsible for the second, third, and fourth resonances. The inductive lengths for the second and fourth resonances are approximately 4l₁​ and $\:\frac{5}{2}{l}_{1}$​, respectively. For the third resonance, which arises from the bottom layer, the inductive length is approximately 4l₂​. The closed-form relationships of lumped components forming the first, second, and the fourth resonance originating from the top layer are adopted from²¹, which are simplified forms of the expressions in²²:

$$\:{L}_{1}\approx\:8{l}_{1}{X}_{1}/\omega\:a$$

(8)

$$\:{C}_{1}\approx\:{{\epsilon\:}_{r}l}_{1}{B}_{1}/\omega\:a$$

(9)

$$\:{L}_{2}\approx\:{4l}_{1}{X}_{1}{X}_{2}/\left[\omega\:a\left({X}_{1}+{X}_{2}\right)\right]$$

(10)

$$\:{C}_{2}\approx\:{\epsilon\:}_{r}{B}_{1}{B}_{2}/\left[\omega\:a\left({X}_{1}+{X}_{2}\right)\right]$$

(11)

$$\:{L}_{{3}^{{\prime\:}}}\approx\:\frac{5}{2}{l}_{1}{X}_{1}/\omega\:a$$

(12)

$$\:{C}_{{3}^{{\prime\:}}}\approx\:2{\epsilon\:}_{r}{l}_{1}{B}_{2}{B}_{4}/\left[\omega\:a\left(B2+B4\right)\right]$$

(13)

where $\:{X}_{1}=F\left(a,2{w}_{1},\lambda\:\right)$, $\:{X}_{2}=F\left(a,{w}_{1}+{w}_{2},\lambda\:\right)$, $\:{B}_{1}=4F\left(a,s,\lambda\:\right)$, $\:{B}_{2}=4F\left(a,{g}_{12},\lambda\:\right)$ and $\:{B}_{4}=4F\left(a,g,\lambda\:\right)$. λ is the wavelength of corresponding resonant frequency, a represents the period among unit cells, rest of the terms used can be refer to the geometry of the structure shown in Fig. 1. The closed-form relationship for the bottom layer contributing to the third resonance is similar to the one used in^21,23,24.

$$\:{L}_{{L}^{{\prime\:}}}\approx\:{4l}_{2}{X}_{3}/\left(\omega\:a\right)$$

(14)

$$\:{C}_{{L}^{{\prime\:}}}\approx\:{\epsilon\:}_{r}{B}_{3}{l}_{2}/\omega\:a$$

(15)

where $\:{X}_{3}=F\left(a,2{w}_{3},\lambda\:\right)$ and $\:{B}_{3}=4F\left(a,a-({l}_{2}+{w}_{3}),\lambda\:\right)$. Additionally, the factor F represents the normalized inductance or capacitance of the strip grating²⁴.

$$\:F\left(a,s,\lambda\:\right)=\:\frac{a}{\lambda\:}\left[\text{ln}\left(csc\frac{\pi\:s}{2a}\right)+G\left(a,s,\lambda\:\right)\right]$$

(16)

In (16), G represents the correction term. Equations (8)-(15) illustrate the connection between the physical parameters of the proposed FSMS structure and the ECM parameters. Nevertheless, these formulas might not produce accurate circuit element values because of the coupling effect within the multilayer structure. According to these approximate mapping relationships, we can quickly estimate the mapped FSMS structural parameters and guide the structural design based on the circuit parameters. The values calculated using the closed-form expressions from Eq. (8) to (15) are listed in Table I. The equivalent circuit model was implemented in ADS, and its response is compared with that of the simulated prototype in Fig. 15. A good agreement is observed between the full-wave electromagnetic simulation and the equivalent circuit model. A limitation of this model is that it only addresses normal incidence conditions. While the interaction between electromagnetic waves and FSMS elements remains largely unchanged up to an incidence angle of 45 degrees, as shown in Fig. 3, angles beyond this may require additional correction factors to maintain reliability of the model.

Table 1 Equivalent circuit parameters (LC) corresponding to the proposed FSMS unit cell designs.

Fig. 15

Transmission responses according to full-wave EM simulation and ECM.

Prototype fabrication and measurements

The designed prototype was realized on Rogers 5870 laminate with the relative permittivity of 2.33, loss tangent of 0.0012, and thickness of 1.575 mm. The laminate measures 229 × 152 mm and encapsulates 20 × 13 unit elements. The FSMS is fabricated through chemical etching. In this process, the mask of the desired pattern is pasted on the light-sensitive dry-film-coated substrate. The substrate with the mask is exposed to collimated UV light. The substrate is then developed and etched to finalize the fabrication process. Since the FSMS structure is two-sided, precise alignment is crucial to ensure that the patterns on both sides of the substrate match accurately. This is achieved through a careful alignment process using fiducial markers before exposing each side to UV light. The entire fabrication process is conducted in a semi-clean room environment to minimize contamination and ensure the integrity of the design. The fabricated prototype with the top and bottom view is shown in Figs. 16(a) and 16(b), respectively. Figure 16(c) illustrates the actual experimental setup to measure the transmission response of the proposed FSMS prototype for TE/TM polarization. The measurements were carried out in the anechoic chamber. The measurement setup comprised of two standard gain horn antennas (transmitting and receiving antennas), connected to the Vector Network Analyzer (VNA) using coaxial cables. The FSMS is positioned between the antennas. To operate in the far-field region, the horn antennas were positioned 100 cm apart. FSMS measurements were conducted at 0^o, 15°, 30°, and 45° angles of incident and comparison between the simulated and measured transmission response is shown in Fig. 17. The agreement is satisfactory. As discussed earlier, the response for oblique incidence at higher frequencies is slightly deteriorated. Nevertheless, the entire X-band is blocked as confirmed by the measurements. The FSMS is partially unstable at high frequencies above 10 GHz. The FSMS was conformed assuming R_c = 300 mm, and the measured results for various incident angles are presented in comparison with the normal incident conformed response shown in Fig. 18. The comparison shows good agreement at frequencies below 10 GHz. At higher frequencies, a partial instability in response can be observed as the surface was initially designed for the planar scenario. The developed prototype is compared with the recently reported benchmark structures in Table II.

Fig. 16

Fabricated prototype of proposed FSMS (a) top layer, (b) bottom layer, (c) measurement setup.

Fig. 17

Transmission response comparison for simulated and fabricated prototype.

Fig. 18

Transmission response comparison at various incident angles in the conformal scenario for R_C = 300 mm.

Table II compares the proposed work with the state-of-the-art designs reported in the recent literature. In²⁵, a compact FSS is presented only for dual-band WLAN applications with the UE size of 0.072λ₀ × 0.072λ₀. However, the results are not completely stable for both TE and TM polarization. In²⁶, a miniaturized single-band FSS is proposed for 2.45 ISM band EMI shielding applications. The overall dimension of the UE is 0.12λ₀ × 0.12λ₀. Although the design is compact and exhibits polarization insensitivity, its drawback is the single-band operation. In²⁷, a compact single-layer reflective metasurface is proposed for polarization conversion applications in the C and X-bands. The overall size of this UE is 0.22λ₀ × 0.22λ₀ with an asymmetric design, which leads to polarization sensitivity and stability issues. In another work²⁸, a tunable broadband FSMS-based EMI absorber is presented for 1.6 GHz to 8 GHz applications. The tunability is realized using PIN diodes, which makes the design complex. In²⁹, a compact multilayer complementary structure‑based tri‑band FSMS is presented, operating at 3.7 GHz, 8.3 GHz, and 12.5 GHz. The tri-band operation was achieved using three layers of substrate. A flexible convoluted-ring-shaped FSS for X-band screening applications, and a symmetrical square-shaped metamaterial design for microwave frequency applications were presented in^{6] and [30}, respectively. The size of the UEs is larger than the design proposed here while operating over the same frequency bands. The proposed unit cell geometry is ultra-compact compared to the benchmark structures presented in Table II. The incident angle stability of the proposed FSMS is up to 45° with polarization insensitivity, which is better than most of the works reported in Table II.

Conclusion

An innovative structure of a dual-sided conformal FSMS has been proposed, which suppresses both Wi-Fi bands and the entire X band. Compared to the state-of-the-art, the suggested FSMS is compact and polarization insensitive, and it has demonstrated high performance at both bands of Wi-Fi and the X-band with oblique incidence angles of up to 45^o. The fabricated and measured prototype consists of 20 × 13 UEs with a total size of 229 × 152 mm². For the transmission coefficient below − 10 dB, the design resonates at both Wi-Fi (2.4 and 5.8 GHz) bands and complete X-band (8.3 GHz to 12 GHz). An excellent alignment between the simulated and measured FSMS characteristics has been demonstrated. Due to its superior performance overall, the presented FSMS-based filter is a viable choice for WLAN and X-band EMI shielding applications.

Table 2 Comparison of proposed FSMS with state-of-the-art designs.