Introduction

In mechanical engineering, stress-strength (S-S) reliability models serve as a cornerstone for quantifying the failure probability of structural components under stochastic loading conditions. These models mathematically characterize system reliability through the relationship \(R=P(X<Y)\), where X (stress variable) and Y (strength variable) are random variables representing intrinsic material resistance and external operational loads, respectively. The failure mechanism arises when transient stress exceeds instantaneous strength, a phenomenon critical to predicting component lifespan and structural integrity. The S-S reliability models have become pivotal analytical tools in modern reliability engineering, particularly for lifetime testing scenarios where X and Y represent the failure times of dual-component systems (e.g., redundant circuits in avionics or parallel hydraulic actuators in heavy machinery). These models enable the probabilistic prediction of sequential failure events through the indicator R, which quantifies the likelihood of one component (strength Y) outperforming another (stress X) under operational loads. Let Y be the strength of a system subject to the stress X, then \(R=P(X<Y)\) can be seen as a measure of system performance. If the stress surpasses the strength, i.e., \(X>Y\), the system breaks down; otherwise, the system is still working.

Over several decades, the estimation of the system reliability in the S-S model has caused widespread concern. Researchers focused on the estimation of R when X and Y are two random variables from Normal1, Burr2, Generalized Exponential3, Weibull4, Generalized Pareto5, Lindley6, Power Lindley7, Generalized Lindley type 5 distributions8, separately. In a word, the above literature mainly considers the estimation of the system reliability under the assumption that X and Y are two simple random samples from certain distributions. Actually, collecting the information in the samples regarding the variable of interest is usually time-consuming and expensive. Therefore, some efficient sampling designs may be more suitable than the traditional simple random sampling (SRS) in terms of measuring system reliability.

Ranked set sampling (RSS) proposed by McIntyre9 has been confirmed as a more efficient sampling method compared to SRS and extended to various improved versions, such as extreme ranked set sampling (ERSS)10, median ranked set sampling (MRSS)11, double ranked set sampling (DRSS)12, imperfect Z ranked set sampling (IZRSS)13 and so on. In fact, the RSS methods have been applied in reliability testing in mission-critical systems, software reliability validation, and quality control in manufacturing processes within reliability engineering. Compared to SRS, the RSS methods have the following strengths. The RSS methods demonstrate superior statistical efficiency compared to SRS by leveraging auxiliary ranking information to reduce variability and improve estimation accuracy, particularly for population mean estimation. The methods achieves higher precision with smaller sample sizes by strategically selecting extreme or balanced subsets, which enhances regression coefficient estimation efficiency in linear models. These advantages make RSS particularly effective for symmetric distributions and nonparametric inference.

Recently, estimating R based on ranked set sampling designs for different distributions has aroused much attention. Studies have considered the estimation for R based on RSS when X and Y are two independent random variables from Exponential14, Weibull15, Lindley16, Exponentiated Pareto17, Inverse Lomax18, Burr Type X19, Inverted Topp-Leone20, Generalized Inverted Exponential21, Generalized Exponential22, Unit Gompertz23,24, Inverted Kumaraswamy25,26 distributions, respectively. Up to now, the Power-Lindley (PL) distribution was not considered in the S-S model based on RSS designs. Actually, PL distribution plays a critical role in system reliability estimation due to its enhanced flexibility in modeling lifetime data and failure patterns, particularly in scenarios involving censored or interval-truncated observations common in reliability engineering. By extending the classical Lindley distribution with an additional shape parameter, the PL distribution provides improved adaptability to asymmetric and multimodal failure datasets, enabling more accurate reliability predictions under diverse operational conditions. Consequently, it is imperative to incorporate the PL distribution into the estimation of R in the S-S model based on ranked set sampling methodologies.

Besides, right-censored data are common in actual life because some measurements are usually below the limit of detection. In recent years, some research has been focused on the estimation of reliability in the context of right-censored data. Krishna and Kumar27 considered the estimation of reliability under the assumption of one parameter Lindley distribution with progressively type II right-censored data. Later, Krishna and Kumar28 suggested the Generalized Inverted Exponential distribution as the lifetime model to estimate reliability based on type II progressively right-censored sampling scheme. Jia29 proposed the nonlinear method and transformation-based least-squares methods to obtain the estimates of reliability when X and Y are two independent random variables from Weibull distributions based on right-censored data. Although scholars have achieved notable progress in system reliability estimation under right-censored data, they predominantly focus on simple sampling method such as SRS and neglect the importance of RSS methods.

Therefore, this paper mainly focuses on the estimation of R in the S-S model based on ranked set sampling designs for the PL distribution with uncensored and right-censored data. To our knowledge, no one has investigated this problem so far. The purpose of this paper is to estimate system reliability R based on SRS, RSS and ERSS under the assumption that stress and strength are independent random variables from the PL distributions with uncensored and right-censored data. Potential applications of this study include enhancing reliability estimation accuracy in multi-component systems under both uncensored and right-censored failure data scenarios, and optimizing industrial quality control protocols through efficient lifetime testing frameworks. We first obtain the ML estimates based on SRS, RSS and ERSS for the PL distribution. Then Monte Carlo simulations considering perfect and imperfect ranking with uncensored data and perfect ranking with right-censored data, are carried out to evaluate the performance on the estimation of reliability based on different sampling designs for the PL distributions. Finally, applications to two real datasets are used to illustrate the effectiveness of our proposed methodologies. Simulation studies and empirical analyses demonstrate that RSS and ERSS designs outperform SRS in estimating system reliability R. The proposed methodologies achieve enhanced precision across both perfect and imperfect ranking scenarios with uncensored data, while maintaining their superiority in right-censored data under perfect ranking conditions.

The remaining contents of this paper are organized as follows. In Section 1, we introduce the RSS and ERSS methods briefly. The system reliability for the PL distribution is given in Section 2. And in Section 3, we present the ML estimates based on SRS, RSS and ERSS under perfect and imperfect ranking with uncensored data and perfect ranking with right-censored data. The Monte Carlo study is arranged in Section 4 to compare the performance of SRS, RSS and ERSS on the estimation of reliability under various cases. In Section 5, we present two real data applications. Finally, some conclusions are drawn in Section 6.

Ranked set sampling designs

In this section, the brief introductions of RSS and ERSS are made.

Ranked set sampling

The classical RSS scheme can be described as follows:

Step 1: Collect a random sample of size \(k^2\) from a certain population and then divide it randomly into k sets of size k.

Step 2: Rank the units of the k sets from the smallest to the largest without measuring them.

Step 3: Measure just the ith smallest ranked unit from the ith set, for \(i=1,2,\cdots ,k\).

Step 4: Steps 1-3 are repeated m times to obtain a RSS sample of size \(n=mk\).

Here, k and m denote the ranked set size and times of cycle, separately. For the sake of brevity, let \(x_{i,j}\) be the ranked unit in position i from set i in jth cycle, then the RSS sample can be denoted by \(\left\{ x_{i,j},i=1,2,\cdots ,k,j=1,2,\cdots ,m\right\}\). If there is no errors in the process of ranking, the probability density function (pdf) of \(x_{i,j}\)9,30 can be written as

$$\begin{aligned} f_{i:k}(x_{i,j})=\frac{k!}{(i-1)!(k-i)!}f_X (x_{i,j})\left[ F_X (x_{i,j})\right] ^{i-1}\left[ 1-F_X (x_{i,j})\right] ^{k-1}, \end{aligned}$$
(1)

where \(f_X(\cdot )\) and \(F_X(\cdot )\) represent the pdf and cumulative density function (cdf) of the population. Besides, the probability of imperfect ranking increases when the set size k is large.

Extreme ranked set sampling

To reduce the impact of imperfect ranking, Samawi, Ahmed and Abu-Dayyeh10 proposed ERSS, which measures the extreme units in sets. The ERSS scheme can be described as follows:

Step 1: Collect a random sample of size \(k^2\) from a certain population and then divide it randomly into k sets of size k.

Step 2: Rank the units of the k sets from the smallest to the largest without measuring them.

Step 3: If k is odd, measure the smallest units from the first \(\frac{k-1}{2}\) sets, the median unit from the \(\frac{k+1}{2}\) set, and the largest units from the last \(\frac{k-1}{2}\) sets. If k is even, measure the smallest units from the first \(\frac{k}{2}\) sets and the largest units from the last \(\frac{k}{2}\) sets.

Step 4: Steps 1-3 are repeated m times to obtain a ERSS sample of size \(n=mk\).

Let \(x_{s,t,v}\) be the sth smallest unit in the tth set at vth cycle, then the ERSS sample can be denoted as

$$\begin{aligned} \bigcup _{j=1}^{m}((\bigcup _{i=1}^{\frac{k-1}{2}}x_{1,i,j})\bigcup x_{\frac{k+1}{2},\frac{k+1}{2},j}\bigcup (\bigcup _{i=\frac{k+3}{2}}^{k}x_{k,i,j})),\quad \text {if { k} is odd}, \end{aligned}$$

otherwise,

$$\begin{aligned} \bigcup _{j=1}^{m}((\bigcup _{i=1}^{\frac{k}{2}}x_{1,i,j})\bigcup (\bigcup _{i=\frac{k+2}{2}}^{k}x_{k,i,j})). \end{aligned}$$

For any element of the ERSS sample, its pdf can also be easily obtained by Eq. (1).

System reliability for the power Lindely distribution

Ghitany, Al-Mutairi, and Al-Enezi31 proposed the PL distribution and discussed its important properties. Due to its flexible characteristic, it has been widely used in various areas7,32,33,34. Therefore, in this paper, we discuss the estimation of system reliability based on different sampling designs with uncensored and right-censored data when both stress and strength are random variables from different PL distributions.

The pdf and cdf of PL distribution are written as follows

$$\begin{aligned} f(x;\alpha ,\theta )=\frac{\alpha \theta ^2}{\theta +1} (1+x^\alpha ) x^{\alpha -1} e^{-\theta x^\alpha }\quad x>0,\quad \alpha ,\theta >0, \end{aligned}$$
(2)

and

$$\begin{aligned} F(x;\alpha ,\theta )=1-(1+\frac{\theta }{\theta +1}x^\alpha ) e^{-\theta x^\alpha }\quad x>0,\quad \alpha ,\theta >0, \end{aligned}$$
(3)

where \(\alpha\) and \(\theta\) denote the scale and shape parameters, respectively. If a random variable X follows the PL distribution with the scale papameter \(\alpha\) and the shape paramter \(\theta\), then it can be denoted by \(X\sim PL(\alpha ,\theta )\).

Consider stress X and strength Y be two independent random variables from \(PL(\alpha _1,\theta _1)\) and \(PL(\alpha _2,\theta _2)\), individually. Then the system reliability for the distributions can be obtained as follows

$$\begin{aligned} R&=P(X<Y)=\int _{0}^{+\infty }f(y;\alpha _2,\theta _2)\left[ \int _{0}^{y}f(x;\alpha _1,\theta _1)dx\right] dy\nonumber \\&=\frac{\theta _2^2}{\theta _2+1}\left\{ \int _{0}^{+\infty }(1+u^{\frac{1}{\alpha _2}})^{\alpha _2} e^{-\theta _2 u}du-\int _{0}^{+\infty }(1+\frac{\theta _1}{\theta _1+1}u^{\frac{1}{\alpha _2}})(1+u)e^{-\theta _1 u^{\frac{\alpha _1}{\alpha _2}}-\theta _2 u}du\right\} \nonumber \\&=\delta (\alpha _1,\theta _1,\alpha _2,\theta _2), \end{aligned}$$
(4)

where we use the transformation \(u=y^{\alpha _2}\). It should be noted that the closed form expression of \(\delta (\alpha _1,\theta _1,\alpha _2,\theta _2)\) cannot be obtained owing to the unavailability of the solution of the integral in Eq. (4). So we compute the system reliability through the free statistical software R.

ML estimates of R based on different sampling designs with uncensored and right-censored data

In this section, we present the ML estimates based on three sampling methods for the PL distribution with uncensored and right-censored data.

ML estimates of R with uncensored data

Estimation of R based on SRS

Consider \(\left\{ x_i,i=1,2,\cdots ,n_x\right\}\) and \(\left\{ y_j,j=1,2,\cdots ,n_y\right\}\) to be two independent SRS samples from \(PL(\alpha _1,\theta _1)\) and \(PL(\alpha _2,\theta _2)\), separately. Then the log-likelihood function can be written as

$$\begin{aligned} L_{SRS}&=n_x \left\{ \ln \alpha _1+2\ln \theta _1-\ln (\theta _1+1)\right\} +\sum _{i=1}^{n_x}\left\{ \alpha _1 \ln (1+x_i)+(\alpha _1-1)\ln x_i-\theta _1 x_i^{\alpha _1} \right\} \nonumber \\&\quad +n_y \left\{ \ln \alpha _2+2\ln \theta _2-\ln (\theta _2+1)\right\} +\sum _{i=1}^{n_y}\left\{ \alpha _2 \ln (1+y_i)+(\alpha _2-1)\ln y_i-\theta _2 y_i^{\alpha _2} \right\} \end{aligned}$$
(5)

The likelihood equations can be obtained by taking the derivatives of the log-likelihood with respect to the unknown parameters. The numerical method is used to obtain the solutions of the equations, which can be seen as the ML estimates of the unknown parameters of interest. According to the invariance property of the ML estimates, we can easily get the ML estimate of reliability based on SRS, denoted by \(\hat{R}_{SRS}\), namely \(\hat{R}_{SRS}=\delta (\hat{\alpha }_1,\hat{\theta }_1,\hat{\alpha }_2,\hat{\theta }_2)\), where \(\hat{\alpha }_1\), \(\hat{\theta }_1\), \(\hat{\alpha }_2\) and \(\hat{\theta }_2\) are the ML estimates of the unknown parameters based on SRS.

Estimation of R based on RSS

Consider \(\left\{ x_{i,j},i=1,2,\cdots ,k_x,j=1,2,\cdots ,m_x\right\}\) and \(\left\{ y_{i,j},i=1,2,\cdots ,k_y,j=1,2,\cdots ,m_y\right\}\) to be two independent RSS samples from \(PL(\alpha _1,\theta _1)\) and \(PL(\alpha _2,\theta _2)\), separately. Here, the sample sizes \(n_x=k_x m_x\) and \(n_y=k_y m_y\), where \(k_x\) and \(k_y\) denote the set sizes and \(m_x\) and \(m_y\) represent the times of cycles, individually.

According to Eq. (1), the log-likelihood function for the RSS samples is written as follows

$$\begin{aligned} L_{RSS}&=\sum _{j=1}^{m_x}\sum _{i=1}^{k_x}\ln f_{i:{k_x},x}(x_{i,j})+\sum _{j=1}^{m_y}\sum _{i=1}^{k_y}\ln f_{i:{k_y},y}(y_{i,j})\nonumber \\&=\sum _{j=1}^{m_x}\sum _{i=1}^{k_x}\ln {\frac{k_x !}{(i-1)!(k_x -i)!}}+\sum _{j=1}^{m_y}\sum _{i=1}^{k_y}\ln {\frac{k_y !}{(i-1)!(k_y -i)!}}\nonumber \\&\quad +\sum _{j=1}^{m_x}\sum _{i=1}^{k_x}\left\{ \ln f_x (x_{i,j})+(i-1)\ln F_x (x_{i,j})+(k_x -i)\ln (1-F_x (x_{i,j}))\right\} \nonumber \\&\quad +\sum _{j=1}^{m_y}\sum _{i=1}^{k_y}\left\{ \ln f_y (y_{i,j})+(i-1)\ln F_y (y_{i,j})+(k_y -i)\ln (1-F_y (y_{i,j}))\right\} , \end{aligned}$$
(6)

where \(f_x(\cdot )\) and \(F_x (\cdot )\) are the pdf and cdf of \(PL(\alpha _1,\theta _1)\), \(f_y(\cdot )\) and \(F_y(\cdot )\) are the pdf and cdf of \(PL(\alpha _2,\theta _2)\), \(f_{i:{k_x},x}(\cdot )\) and \(f_{i:{k_y},y}(\cdot )\) are the pdfs of the ith smallest unit in the random samples with sizes \(k_x\) and \(k_y\) from \(PL(\alpha _1,\theta _1)\) and \(PL(\alpha _2,\theta _2)\), respectively.

Then we can obtain the ML estimates of \(\alpha _1\), \(\theta _1\), \(\alpha _2\) and \(\theta _2\) by taking the derivatives with the unknown paramters and solving the likelihood equations. Finally, the estimator of R based on RSS, namely \(\hat{R}_{RSS}\), can be obtained by incorporating the ML estimates of parameters into Eq. (4).

Estimation of R based on ERSS

Consider the ERSS sample of stress X to be \(\bigcup _{j=1}^{m_x} ((\bigcup _{i=1}^{\frac{k_x-1}{2}}x_{1,i,j})\bigcup x_{\frac{k_x+1}{2},\frac{k_x+1}{2},j}\bigcup (\bigcup _{i=\frac{k_x+3}{2}}^{k_x}x_{k_x,i,j}))\) if \(k_x\) is odd, otherwise, \(\bigcup _{j=1}^{m_x} ((\bigcup _{i=1}^{\frac{k_x}{2}}x_{1,i,j})\bigcup (\bigcup _{i=\frac{k_x+2}{2}}^{k_x}x_{k_x,i,j}))\). Additionally, the ERSS sample of strength Y is defined in a similar form as that of stress X.

If \(k_x\) is odd, then the log-likelihood function of the ERSS sample for X is

$$\begin{aligned} L_{ERSS,X}=\sum _{j=1}^{m_x}\sum _{i=1}^{\frac{k_x-1}{2}}\ln f_{1:k_x,x}(x_{1,i,j})+\sum _{j=1}^{m_x}\ln f_{\frac{k_x+1}{2}:k_x,x}(x_{\frac{k_x+1}{2},\frac{k_x+1}{2},j})+\sum _{j=1}^{m_x}\sum _{i=\frac{k_x+3}{2}}^{k_x}\ln f_{k_x:k_x,x}(x_{k_x,i,j}), \end{aligned}$$

otherwise,

$$\begin{aligned} L_{ERSS,X}=\sum _{j=1}^{m_x}\sum _{i=1}^{\frac{k_x}{2}}\ln f_{1:k_x,x}(x_{1,i,j})+\sum _{j=1}^{m_x}\sum _{i=\frac{k_x+2}{2}}^{k_x}\ln f_{k_x:k_x,x}(x_{k_x,i,j}). \end{aligned}$$

The log-likelihood function of the ERSS sample for Y, \(L_{ERSS,Y}\), also has a similar representation. Since the ERSS samples of X and Y are independent, then the joint log-likelihood function \(L_{ERSS}=L_{ERSS,X}+L_{ERSS,Y}\). Therefore, the ML estimate of R based on ERSS, namely \(\hat{R}_{ERSS}\), can be obtained in the same way.

ML estimates of R with righted-censored data

In this subsection, we mainly discuss the ML estimates of R in the S-S model with righted-censored data under various sampling designs. Firstly, the joint log-likelihood function based on SRS with right-censored data can be written as

$$\begin{aligned} L_{SRS}&=\sum _{i=1}^{m_x\times k_x}\delta _{i}\ln f_x(x_i)+\sum _{i=1}^{m_x\times k_x}(1-\delta _{i})\ln (1-F_x(x_i))+\sum _{j=1}^{m_y\times k_y}\delta _{j}\ln f_y(y_j)+\sum _{j=1}^{m_y\times k_y}(1-\delta _{j})\ln (1-F_y(y_j)), \end{aligned}$$
(7)

where \(\delta _{i}=0\) when \(x_{i}\) is a right-censored observation, otherwise, \(\delta _{i}=1\). And \(\delta _{j}\) is also defined in a similar manner. Then we present the joint log-likelihood function based on RSS with right-censored data, which is given by

$$\begin{aligned} L_{RSS}&=\sum _{j=1}^{m_x}\sum _{i=1}^{k_x}\zeta _{i,j}\ln f_{i:{k_x},x}(x_{i,j})+\sum _{j=1}^{m_x}\sum _{i=1}^{k_x}(1-\zeta _{i,j})\ln (1-F_{i:{k_x},x}(x_{i,j}))\nonumber \\&\quad +\sum _{j=1}^{m_y}\sum _{i=1}^{k_y}\eta _{i,j}\ln f_{i:{k_y},y}(y_{i,j})+\sum _{j=1}^{m_y}\sum _{i=1}^{k_y}(1-\eta _{i,j})\ln (1-F_{i:{k_y},y}(y_{i,j})), \end{aligned}$$
(8)

where \(\zeta _{i,j}=0\) when \(x_{i,j}\) is a right-censored observation, otherwise, \(\zeta _{i,j}=1\). \(f_{i:{k_x},x}(\cdot )\) and \(F_{i:{k_x},x}(\cdot )\) denote the pdf and cdf of the ith order statistic of the random sample with size \(k_x\) drawn from \(PL(\alpha _1,\theta _1)\), respectively. \(\eta _{i,j}\) and \(F_{i:{k_y},y}(\cdot )\) are defined in a similar manner as above. For simplicity, the joint log-likelihood function based on ERSS with right-censored data is not presented. The estimates of the parameters which maximize the log-likelihood function are also obtained through numerical optimization in computing softwares. Then, we can calculate the estimator of R with right-censored data using Eq. (4).

It should be stated that we use the Optim function in R software to obtain all ML estimates of parameters based on different sampling designs under various cases in this paper. Then all estimators of reliability are obtained according to Eq. (4).

Monte Carlo simulation

In this section, the extensive Monte Carlo simulations are carried out to observe the efficiency of the ML estimates of R based on SRS, RSS and ERSS under perfect and imperfect ranking with uncensored data and perfect ranking with righted-censored data. The mean, bias and mean squares error (MSE) criteria for evaluating the performance of the ML estimates of reliability are given as follows,

$$\begin{aligned} Mean(\hat{R})=\sum _{i=1}^{M}\hat{R}_i/M,\quad MSE(\hat{R})=\sum _{i=1}^{M}(\hat{R}_i-R)^2/M,\quad \text {and} \quad MSE(\hat{R})=\sum _{i=1}^{M}(\hat{R}_i-R)^2/M,\quad \text {respectively}, \end{aligned}$$

where R is the true reliability. Here M denotes the number of the simulation, which is set to 10000. Additionally, we also calculate the relative efficiencies (REs) of the estimates of reliability, which are written as follows

$$\begin{aligned} RE_1=\frac{MSE(\hat{R}_{SRS})}{MSE(\hat{R}_{RSS})}, RE_2=\frac{MSE(\hat{R}_{SRS})}{MSE(\hat{R}_{ERSS})}. \end{aligned}$$

It is obvious that the estimator in the denominator is superior to that in the numerator if \(RE>1\).

Besides, for both RSS and ERSS, the following simulations are conducted with various ranked set sizes and number of cycles. For set sizes, \((k_x,k_y)=(2,2),(2,3),(3,3),(3,4),(4,4)\) and (4, 5) are assumed. The times of cycles are all taken as 10. Therefore, the sample sizes are takn to be \((n_x,n_y)=(20,20),(20,30),(30,30),(30,40),(40,40)\) and (40, 50). It should be stated that the paramter vectors \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(0.5,1,0.5,1),(0.5,1,1,2)\) and (1, 2, 0.5, 1) are consided. Consequently, the true values of reliability corresponding to the above parameter settings can be computed as 0.5, 0.3313 and 0.6687, separately.

Perfect ranking with uncensored data

For simplicity, Table 1 presents the estimated results of the reliability based on different sampling designs, including means, biases, MSEs, and REs. It is evident from Table 1 that three sampling designs provide accurate estimates in all cases according to the mean and bias criterion. Besides, the MSE values tend to decrease with the increase of \(n_x\) and \(n_y\), which indicates that the ML method with a larger sample size produces a more precise estimator. It should also be noted that all \(RE_1\) and \(RE_2\) values are greater than 1, which confirms that the ML estimates of R based on RSS and ERSS are more efficient than the counterparts based on SRS for each of all cases.

Table 1 Means, Biases, MSEs and REs of the ML estimates of R based on SRS, RSS and ERSS.
Full size table

In addition, we can observe that the \(RE_1\) values are larger than the \(RE_2\) values in most cases, indicating that RSS provides more precise estimators of R compared to ERSS when both stress and strength are independent random variables from PL distributions.

Imperfect ranking with uncensored data

The above simulations are conducted under the assumption of perfect ranking. It cannot be neglected that there are some judgment ranking errors caused by some subjective factors in the ranking process, especially for large set sizes. So, in this section, the performance of SRS, RSS and ERSS on the estimation of R under imperfect ranking is also investigated via Monte Carlo simulations. It should be stated that ranking error creates no impact on the ML estimates based on SRS for all given cases.

Up to now, there are many models to simulate data with imperfect ranking, such as the fraction of neighbors model and the concomitant variable model35,36,37. Here the concomitant variable model of Dell and Clutter35 is used to generate data with imperfect ranking. First of all, the SRS samples of X and Y with sizes \(k_x^2 m_x\) and \(k_y^2 m_y\), denoted by \(x_{i,i,j}\) \((i=1,2,\cdots ,k_x,j=1,2,\cdots ,m_x)\) and \(y_{i,i,j}\) \((i=1,2,\cdots ,k_y,j=1,2,\cdots ,m_y)\), are generated from \(PL(\alpha _1,\theta _1)\) and \(PL(\alpha _2,\theta _2)\), respectively. Then the independent random errors \(\epsilon _{1,i,i,j}\) \((i=1,2,\cdots ,k_x,j=1,2,\cdots ,m_x)\) and \(\epsilon _{2,i,i,j}\) \((i=1,2,\cdots ,k_y,j=1,2,\cdots ,m_y)\) with the same sizes \(n_x\) and \(n_y\) are drawn from \(N(0,\sigma ^2)\). Next, compute \(x_{i,i,j}^*=x_{i,i,j}+\epsilon _{1,i,i,j}\) \((i=1,2,\cdots ,k_x,j=1,2,\cdots ,m_x)\) and \(y_{i,i,j}^*=y_{i,i,j}+\epsilon _{2,i,i,j}\) \((i=1,2,\cdots ,k_y,j=1,2,\cdots ,m_y)\), then sort them from the smallest to the largest without any certain measurement. The corresponding values of \(x_{i,i,j}\) and \(x_{i,i,j}\) can be called the concomitants of \(x_{i,i,j}^*\) and \(x_{i,i,j}^*\). According to the sampling procedures of RSS and ERSS, we can use the concmitants to obtain the RSS and ERSS samples with imperfect ranking. Finally, the obtained RSS and ERSS samples are used to calculate the ML estimates of R under imperfect ranking.

Furthermore, \(\sigma\) controls the quality of imperfect ranking. When \(\sigma =0\), then the concomitant variable model becomes a perfect ranking model. when \(\sigma\) increases, the quality of ranking tends to decrease and the ranking error becomes more serious. In addition, \(\sigma\) is set to 0, 0.25, 0.5, 0.75 and 1 in the simulation study.

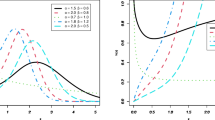
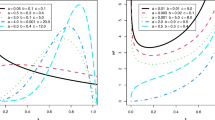
Figures 1, 2, 3 display the MSEs of the ML estimates based on various sampling designs under several levels \(\sigma\) of imperfect ranking. As expected, it is obvious that the MSEs based on RSS and ERSS gradually increase with the raise of \(\sigma\), which points to the fact that the estimators based on RSS-based designs become less efficient when the ranking error becomes more serious. However, the ML estimates based on ranking set samplings are still more effective than competitors based on SRS for each of parameter settings and levels of imperfect ranking. Besides, the estimates based on RSS are superior to the estimates based on ERSS in most cases.

Fig. 1
figure 1

MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(0.5,1,0.5,1)\) under different levels \(\sigma\) of imperfect ranking.

Full size image
Fig. 2
figure 2

MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(0.5,1,1,2)\) under different levels \(\sigma\) of imperfect ranking.

Full size image
Fig. 3
figure 3

MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(1,2,0.5,1)\) under different levels \(\sigma\) of imperfect ranking.

Full size image

Perfect ranking with righted-censored data

Actually, in survival data, the event time of interest is not always entirely recorded due to a series of subjective and objective factors. In this section, we mainly investigate the performance of SRS, RSS and ERSS on estimation of reliability with righted-censored data via simulations. For convenience, we assume that there is no error in the ranking process. Here we use the method of Taconeli and Giolo38 to simulate the righted-censored samples with censorship percentage p, where p is taken as 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45 and 0.5. The number of righted-censored observations gradually increases with the raise of p.

Figures 4, 5, 6 display the MSEs based on three sampling designs under perfect ranking with righted-censored data for four parameter settings. From the four figures, we can observe that RSS and ERSS produce lower MSE values than SRS for each of censorship percentages. And gradual increases in the MSE values for three sampling designs can be seen for all parameter settings and set sizes as the percentage of censorship increases.

Fig. 4
figure 4

Estimated MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(0.5,1,0.5,1)\) under different censorship percentages p.

Full size image
Fig. 5
figure 5

Estimated MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(0.5,1,1,2)\) under different censorship percentages p.

Full size image
Fig. 6
figure 6

Estimated MSEs of the ML estimates based on different sampling designs for \((\alpha _1,\theta _1,\alpha _2,\theta _2)=(1,2,0.5,1)\) under different censorship percentages p.

Full size image

Finally, it is obvious that the traditional RSS design usually produces the most accurate estimates. Therefore, RSS can be considered as the suggested design to estimate system reliability of the righted-censored stress and strength data from the PL distributions under perfect ranking.

Applications to real data sets

In this section, we firstly use the homeostasis model assessment (HOMA) index in the insulin resistance data39 to illustrate the effectiveness of our proposed procedure. The HOMA index for the healthy controls, denoted by X, contains 52 observations and the HOMA index for breast cancer patients, denoted by Y, contains 64 observations. Notably, the data set has been used by Akgul et al.40 to compare the insulin resistance of healthy individuals and patients using a stress-strength model based on ranked sampling designs for the generalized inverse Lindley distributions.

Before evaluating the performance of SRS, RSS, and ERSS on the estimation of reliability for the real data set, we use the PL distribution to fit the X and Y observations, respectively. The estimated results are presented in Table 2, which contains the estimates of parameters, the log-likelihood function and the p-values of the Kolmogorov-Simirnov (KS) tests. And the nonparametric plots of the datasets are given in Fig. 7.

Table 2 Estimated results for X and Y.
Full size table
Fig. 7
figure 7

The nonparametric plots of the HOMA index datasets.

Full size image

We can see from Table 2 that the p-values of the KS tests for X and Y are greater than 0.05, which shows that the PL distribution provides good empirical fits to the X and Y data. Besides, we can calculate the estimate of R based on the estimated parameters as 0.6698.

The following simulations under various situations are conducted to assess the performance of three sampling designs on estimation of R when stress X and strength Y are two independent random variables from the PL(1.2894, 0.8092) and PL(0.8243, 0.6058) distributions, respectively.

With respect to the RSS and ERSS samples, the set sizes are taken to be \((k_x,k_y)=(4,4)\). And the number of cycles \((m_x,m_y)=(6,9)\) are considered. Therefore, the sample sizes of the RSS and ERSS samples are \((n_x,n_y)=(24,36)\). Apparently, the sizes of the SRS samples for X and Y are also set to 24 and 36, respectively. The Monte Carlo simulations are also repeated 10000 times to obtain the ML estimates based on each sampling design under perfect and imperfect ranking with uncensored data, and perfect ranking with right-censored data. Here \(\sigma\) which controls the quality of imperfect ranking is also set to 0.25, 0.5, 0.75 and 1. Besides, the percentage of censorship p is also taken as 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45 and 0.5.

Table 3 presents the estimated results of the ML estimates based on three sampling designs under perfect and imperfect ranking, including average estimate (AE), bias and mean square error (MSE). And the corresponding results of the ML estimates under perfect ranking with uncensored and righted-censored data are reported in Table 4. According to Tables 3 and 4, all sampling designs produce the ML estimates close to 0.6698. Besides, gradual decreases in the MSEs of RSS and ERSS can be observed as \(\sigma\) decreases. Furthermore, the estimators for all sampling designs deviate more from the true value as p increases. More importantly, we can observe that the MSE values of RSS and ERSS are usually lower than that of SRS for each of all considered cases, which shows that RSS and ERSS provide more efficient estimators of reliability compared to SRS for the real data set.

Table 3 Estimated results of the ML estimates based on three sampling designs under perfect and imperfect ranking.
Full size table
Table 4 Estimated results of the ML estimates based on three sampling designs under perfect ranking with uncensored and righted-censored data.
Full size table

Then we use the PL distribution to fit two datasets41 on failure stresses of single carbon fibers of lengths 20 mm and 50 mm, denoted by X and Y, respectively. Table 5 presents the estimated results. Figure 8 shows the nonparametric plots of the datasets.

Table 5 Estimated results for X and Y.
Full size table
Fig. 8
figure 8

The nonparametric plots of the failure stresses of single carbon fibers of lengths 20 mm and 50 mm.

Full size image

We can see from Table 5 that the p-values of the KS tests for X and Y are much greater than 0.05, which shows that the PL distribution provides accurate empirical fits to the X and Y data. According to the estimated parameters in Table 5, the estimate of R for the two datasets can be obtained, which is 0.3739.

Next, we conduct simulation 10000 times under various cases to assess the performance of several sampling designs on estimation of R when stress X and strength Y are two independent random variables from the PL(3.8678, 0.0497) and PL(4.2212, 0.0521) distributions, respectively. Table 6 presents the estimated results of the ML estimates based on three sampling designs under perfect and imperfect ranking. And the corresponding results of the ML estimates under perfect ranking with uncensored and righted-censored data are reported in Table 7.

Table 6 Estimated results of the ML estimates based on three sampling designs under perfect and imperfect ranking.
Full size table
Table 7 Estimated results of the ML estimates based on three sampling designs under perfect ranking with uncensored and righted-censored data.
Full size table

We can see from Table 6 that all ML estimates of R are close to 0.3739. The increases in the MSEs of SRS, RSS and ERSS can be obviously observed as \(\sigma\) increases. In Table 7, the ML estimates of R under three sampling designs deviates significantly from 0.3739 when p is large. More importantly, the MSE values of RSS and ERSS are much lower than that of SRS for any considered cases, which also shows that the RSS and ERSS produce more accurate estimates of reliability R than SRS for these datasets.

Conclusion

This study proposes a ranked sampling-based stress-strength reliability model, where the stress variable X and strength variable Y follow independent PL distributions. We systematically evaluate the comparative performance of SRS, RSS, and ERSS through Monte Carlo experiments and two real datasets under three conditions: (i) perfect ranking with uncensored data, (ii) imperfect ranking with uncensored data, (iii) perfect ranking with right-censored data. Finally, we find that the ML estimates based on RSS and ERSS are superior to the competitors based on SRS for all considered scenarios.

In fact, our study also has certain limitations. First of all, this paper focuses solely on system reliability estimation based on various ranked set sampling methods under right-censoring scenarios. However, in actual life, collected data often involves left-censoring and interval-censoring due to various subjective and objective factors. How to derive system reliability based on ranked set sampling methods under these censoring mechanisms remains a significant challenge. Besides, we neglect the the presence of the fuzziness in our proposed stress-strength model. Actually, The Bayesian estimation of system reliability based on ranked set sampling methods under such scenarios also remains a critical research topic. We leave these for future research.