Introduction

As coal resources in China’s central and eastern regions become depleted, mining has gradually shifted to the resource-rich northwest, including Xinjiang, Inner Mongolia, and Ningxia1. These regions are characterized by the widespread distribution of weakly cemented rock layers. Excavating roadways in such formations often leads to roof falls, sidewall spalling, and collapse of the shaft walls. Hence, conducting an elastoplastic analysis of the surrounding rock in these roadways is crucial for safely extracting coal resources in the western mining areas.

Liu et al.2 conducted shear tests on weakly cemented soft rock to examine the effects of principal stress rotation on the rock’s stress, strain, and shear strength. Their findings provide theoretical and scientific guidance for roadway stability control and disaster prevention in such geological conditions. Liu et al.3 analyzed the mechanical properties and mineral composition of the roadway roofs and floors in weakly cemented soft rock within the Shanghai Temple mining area. They revealed the deterioration mechanisms of the surrounding rock, proposed instability criteria for the floors, and optimized support designs under actual operational conditions, effectively controlling the deformation of the surrounding rock. Song4 combined field measurements and numerical simulations to show the deformation mechanism of weakly cemented soft rock roadways influenced by alkaline water, investigated the expansion law of the plastic zone in the surrounding rock, and the load-bearing characteristics of the support structure, proposing an effective support scheme for such conditions. Li et al.5 employed numerical simulation methods to explore the impact of softening and expansion of weakly cemented soft rock on the stability of the roadway surrounding rock. They proposed a support scheme of “routing + anchor cable mesh + bottom arch” that effectively reduces the deformation and depth of the plastic zone of the roadway surrounding rock based on the failure mechanism and corresponding support principles of weakly cemented soft rock roadways.

Ma et al.6 explored the deformation patterns of floor heave in weakly cemented soft rock roadways in western mining areas affected by mining activities. They proposed a combined control technology of “floor slotting in the middle + pressure relief holes on the sides” that achieved good results. Reppas et al.7 developed a thermal-water-mechanical coupled model to describe fractured rocks, achieving the coupling of the THM process with plastic deformation and damage mechanics in dual porous media. Zhang et al.8 derived a mathematical expression for the radius of the plastic zone and developed a mechanical model for loose soft rock roadways. They indicated that increasing the strength of the surrounding rock can significantly reduce the plastic zone radius. Fan et al.9 investigated the plastic zone and stress distribution laws in weakly cemented soft rock mining roadways with various coal pillar sizes. They proposed differentiated support schemes to control large deformations, ensuring roadway stability and safety.

Zhao et al.10 considered the impact of water environments and non-uniform stress fields, establishing a mechanical model for weakly cemented surrounding rock. They revealed the influence of humidity fields and lateral pressure coefficients on the principal deviatoric stress and plastic zone of weakly cemented roadways. Tan et al.11 analyzed weakly cemented mudstone’s mineral composition and mechanical characteristics. They proposed a high pre-tensioned bolt-surrounding rock deformation collaborative support control technology, achieving the expected results. Zhou et al.12 proposed support schemes such as anchor and anchor cable reinforcement optimization, grouting, and combination reinforcement of anchors and beams and conducted tests. They reported that these support schemes can effectively control roof subsidence and achieve good application results. Ranjbarnia et al.13 proposed a method to determine rock softening parameters and their critical values. Wang et al.14 developed an elastoplastic model for the surrounding rock of weakly cemented soft rock roadways using damage theory, considering strain softening and plastic dilation. The research presents stress and displacement formulas for the surrounding rock in the presence of elastic, plastic softening, and plastic flow zones, providing theoretical support for controlling such roadways.

Zhou et al.15 utilized a combination of field measurements and numerical simulations to investigate the deformation characteristics and stress features of support structures in weakly cemented soft rock roadways, providing a reference for controlling the surrounding rock. Zhao et al.16 developed a FLAC 3D numerical simulation model to analyze the stability of the surrounding rock of weakly cemented soft rock roadways under varying moisture conditions through mechanical tests, mineral XRD diffraction, and determinations of liquid and plastic limits. Yu et al.17 explored the mineral composition, mechanical properties, and hydraulic properties of weakly cemented siltstone. They proposed a grouting reinforcement combined support plan that can control the deformation of the surrounding rock in a weakly cemented siltstone roadway. Cai et al.18 revealed the deformation mechanism of weakly cemented soft rock recovery roadways through laboratory tests, field measurements, and physical simulations. They proposed a coupled support technology of “high-strength anchor-net-cable-beam + comprehensive grouting,” which ensures the stability of the roadways and yields positive outcomes.

These studies provide ideas for the establishment of mechanical models of weakly cemented soft rock roadways, scientific guidance, and a decision-making basis for the stability control of the surrounding rock of such roadways. Weakly cemented soft rocks are prone to large deformation or even collapse after tunnel excavation due to their poor cement strength and easy softening upon contact with water. The entire failure process actually gradually evolves from the elastic zone to the softening zone to the fracture zone19,20,21. In addition, weakly cemented soft rocks also exhibit significant post-peak strain softening and plastic expansion characteristics. Combining softening (strength attenuation) and shear expansion (volume expansion) into a unified analysis framework is more consistent with its actual failure process. Most existing models consider the softening or shear dilation effect separately, lacking a description of their combined influence, and often underestimate the extent of the softening zone and fragmentation zone. The softening affects the extent of the plastic zone, while the shear dilation impact accelerates the deterioration of the surrounding rock and expands the displacement field. Both control the stability of the surrounding rock. Therefore, this study focuses on the mechanical properties of weakly cemented soft rock to comprehensively examine the softening and dilatancy effects in the plastic zone of the surrounding rock. It develops an elastic-soft-fractured mechanical model for the surrounding rock of weakly cemented soft rock roadways and derives analytical solutions for the stress and displacement fields of the roadway surrounding rock based on the Mohr–Coulomb strength criterion. In addition, this research indicates the deformation mechanism of the three zones of the surrounding rock. It discusses the influence laws of initial cohesion and internal friction angle on the stress distribution, deformation, and radius of the plastic zone of the surrounding rock using specific case studies. It proposes a grouting-centered “anchor-net-cable-grout” support scheme, which achieves good results and ensures roadway construction safety. The results provide a theoretical basis and scientific guidance for the bearing capacity assessment and stability control of the surrounding rock in weakly cemented soft rock roadways.

Project overview

The Talahao mining field is located in the eastern part of the Dongsheng Coalfield. Its structural morphology aligns with that of the regional coal-bearing strata. Generally, it features a monocline structure that dips southwestward, with a dip direction ranging from 220° to 260° and a stratum dip of approximately 1°. Although the occurrence of the strata varies along the strike and dip, the changes are not significant. In the same direction, the strata display broad and gentle wavy undulations. No fold or fault structures have been found in the area, and no igneous rock intrusions are present. The structure is, therefore, classified as simple. The in-situ stress of the auxiliary transport channel in the 3205 working face of the Coal Mine was measured using the hollow core package method, and the results are listed in Table 1. The in-situ stress field in this area is characterized as a horizontal tectonic stress field. The direction of the maximum principal stress is 244.09°, with a magnitude of 10.31 MPa, which is approximately 1.69 times greater than the vertical stress. The Angle between the principal stress direction and the auxiliary transport channel of the 3205 working face is approximately 2°, indicating a relatively minor impact on the stability of the mining roadway in this area. The intermediate horizontal principal stress measures 9.14 MPa, which is approximately 1.5 times the vertical stress. This stress is nearly perpendicular to the mining roadway and significantly affects its stability.

Table 1 Measured in-situ stress values of the auxiliary transport channel in the 3205 working face.
Full size table

In the 3205 auxiliary transportation roadways of the Talahao Coal Mine, the immediate roof consists of sandy mudstone with a thickness ranging from 3.5 to 14.7 m and an average thickness of 7.3 m. The main roof comprises siltstone and fine sandstone, with a thickness ranging from 3.1 to 13.6 m and an average thickness of 6.5 m. The immediate floor is composed of sandy mudstone and mudstone, with a thickness ranging from 1.2 to 16.9 m and an average thickness of 6.8 m. The main floor consists of fine sandstone and siltstone, with a thickness ranging from 4.9 to 14.4 m and an average thickness of 8.1 m. The coal seam is stable and structurally simple, with a thickness ranging from 2.8 to 4.89 m and an average thickness of 3.6 m. The roof and floor conditions of the coal seam are detailed in Table 2. The maximum burial depth of the auxiliary transport channel in the 3205 working face is 244 m. This roadway adopts a rectangular cross-section with clear dimensions of 5200 × 3400 mm. A 200 mm top coal excavation is retained to prevent direct exposure of the roof and subsequent weathering.

Table 2 The roof and floor conditions of the three coal seams.
Full size table

Through X-ray diffraction testing of the sandy mudstone in the roof (Fig. 1), the mineral composition mainly includes quartz, illite, kaolinite, and chlorite, with illite, kaolinite, and chlorite being clay minerals accounting for approximately 85%. Scanning electron microscopy (SEM) of the sandy mudstone (Fig. 2) reveals a disordered distribution of detrital particles within the rock, with a relatively loose structure and brittle fractures. The mineral composition leads to poor bonding at the interface between the roof and floor, with low cohesion, resulting in low strength and susceptibility to failure.

Fig. 1
figure 1

Sandy mudstone XRD test.

Full size image
Fig. 2
figure 2

Sandy mudstone SEM images.

Full size image

Basic assumptions and surrounding rock mechanical model

Basic assumptions and mechanical model

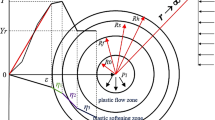
This study establishes an elastic-soft-fractured mechanical model for the surrounding rock of weakly cemented soft rock roadways by focusing on the mechanical properties of weakly cemented soft rock and the deformation and failure characteristics of the surrounding rock, as shown in Fig. 3. In addition, the following assumptions are made for the surrounding rock of the roadway:

  1. (1)

    The surrounding rock is considered a homogeneous, isotropic elastoplastic material that follows the Mohr–Coulomb yield criterion within the plastic zone.

  2. (2)

    The roadway’s cross-section is circular, with isotropic stress impacting the surrounding rock.

  3. (3)

    The roadway is treated as infinitely long, categorizing it as a plane strain problem.

Fig. 3
figure 3

Elastic-soft-fractured mechanical model for the surrounding rock of weakly cemented soft rock roadways. p0—support resistance, pw—the contact stress at the interface between the plastic softening zones and plastic fracture zone, ps—the contact stress at the interface between the elastic and plastic softening zones, p1—original rock stress, r0—the radius of roadway, rw—the radius of the plastic fracture zone, rs—the radius of the plastic softening zone, r1—the radius of elastic zone.

Full size image

Softening model

After the surrounding rock enters the post-peak state, the change in its internal friction angle becomes minimal and can be approximately regarded as constant, while the cohesive force decreases significantly22. In view of this, a softening model of the surrounding rock in the plastic zone is developed, as illustrated in Fig. 4. In the elastic zone, the cohesion of the surrounding rock, denoted as c0, remains constant. When entering the plastic softening zone, the cohesion cs of the surrounding rock in this zone reduces, with a softening coefficient denoted by Mc. In the plastic fractured zone, the cohesion of the surrounding rock is represented as cw.

$$c_{s} = \left\{ \begin{gathered} c_{o} ,\varepsilon_{\theta } \le \left( {\varepsilon_{\theta } } \right)_{{r_{s} }} \hfill \\ c_{o} - M_{c} \left[ {\left( {\varepsilon_{\theta } } \right)_{{r_{s} }} - \left( {\varepsilon_{\theta } } \right)} \right],\,\left( {\varepsilon_{\theta } } \right)_{{r_{s} }} < \left( {\varepsilon_{\theta } } \right) \le \left( {\varepsilon_{\theta } } \right)_{{r_{w} }} \hfill \\ c_{w} ,\left( {\varepsilon_{\theta } } \right)_{{r_{w} }} < \varepsilon_{\theta } \hfill \\ \end{gathered} \right.,$$
(1)
$$M_{c} = \frac{{c_{o} - c_{w} }}{{\left( {\varepsilon_{\theta } } \right)_{{r_{s} }} - \left( {\varepsilon_{\theta } } \right)_{{r_{w} }} }}.$$
(2)
Fig. 4
figure 4

Softening model of surrounding rock in the plastic zone.

Full size image

Stress field analysis

Elastic zone stress and displacement solution

The surrounding rock of a roadway typically undergoes elastoplastic deformation under the influence of in-situ stress. It can derive the stress and displacement field expressions in the elastic region using Lamé’s equations by treating the contact stress at the elastoplastic interface as a support force acting on the inner side of the elastic region. The stress expression for the elastic region of the surrounding rock is detailed in the literature23.

$$\left\{ \begin{gathered} \sigma_{r}^{e} = \left( {1 - \frac{{r_{s}^{2} }}{{r^{2} }}} \right)p_{1} + \frac{{r_{s}^{2} }}{{r^{2} }}p_{s} \hfill \\ \sigma_{\theta }^{e} = \left( {1 + \frac{{r_{s}^{2} }}{{r^{2} }}} \right)p_{1} - \frac{{r_{s}^{2} }}{{r^{2} }}p_{s} \hfill \\ \end{gathered} \right.,$$
(3)

where \(\sigma_{r}^{e}\) is the radial stress in elastic zone; \(\sigma_{\theta }^{e}\) is the hoop stress in elastic zone.

The circumferential strain can be expressed for plane strain problems as follows:

$$\varepsilon_{\theta } = \frac{{1 - \mu^{2} }}{E}\left( {\sigma_{\theta } - \frac{\mu }{1 - \mu }\sigma_{r} } \right),$$
(4)

where E is the elastic modulus; μ is the Poisson’s ratio.

The displacement in the elastic region can be obtained by substituting Eq. (3) into (4).

$$u_{e} = r\varepsilon_{\theta } = \frac{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}{E}p_{1} r + \frac{1 + \mu }{{Er}}r_{s}^{2} \left( {p_{1} - p_{s} } \right).$$
(5)

Plastic zone stress solution

The plastic zone is divided into the plastic softening and the plastic fracture zones, satisfying the equilibrium differential, geometric, and constitutive equations.

Differential Equations:

$$\frac{{{\text{d}}\sigma_{r} }}{{d_{r} }} + \frac{{(\sigma_{r} - \sigma_{\theta } )}}{r} = 0.$$
(6)

Geometric Equations:

$$\varepsilon_{r} = \frac{du}{{dr}},\,\varepsilon_{\theta } = \frac{u}{r}.$$
(7)

Constitutive Equations:

$$\left\{ \begin{gathered} \varepsilon_{r} = \frac{{1 - \mu^{2} }}{E}\left( {\sigma_{r} - \frac{\mu }{1 - \mu }\sigma_{\theta } } \right) \hfill \\ \varepsilon_{\theta } = \frac{{1 - \mu^{2} }}{E}\left( {\sigma_{\theta } - \frac{\mu }{1 - \mu }\sigma_{r} } \right) \hfill \\ \end{gathered} \right..$$
(8)

The M–C (Mohr–Coulomb) strength criterion can effectively represent the behavior of surrounding rock in the plastic zone, satisfying the M–C24 strength criterion.

$$F({\text{c,}}\varphi ) = \sigma_{\theta } - \alpha \sigma_{r} - k,$$
(9)

where \(\alpha = \frac{1 + \sin \varphi }{{1 - \sin \varphi }}\); \(k = \frac{2c\cos \varphi }{{1 - \sin \varphi }}\); c and φ are cohesion and internal friction angles, respectively.

The circumferential and radial stresses in the plastic softening zone satisfy the equilibrium differential equations and the M–C criterion. Combining these two equations yields:

$$\frac{{d\sigma_{r} }}{dr} + \frac{{(1 - \alpha )\sigma_{r} }}{r} - \frac{k}{r} = 0.$$
(10)

Solving this differential equation yields the general solution for the radial stress as follows:

$$\sigma_{r} = C_{1} r^{\alpha - 1} + \frac{k}{1 - \alpha }.$$
(11)

Plastic zone softening stress solution

The radial stress and circumferential stress of the plastic softening zone can be determined by considering the stress boundary conditions \(\sigma_{r}^{{p_{s} }} |_{{r = r_{s} }} = p_{s}\) for the plastic softening zone as follows:

$$\left\{ \begin{gathered} \sigma_{r}^{{p_{s} }} = \left( {p_{s} - \frac{{k_{s} }}{1 - \alpha }} \right)\left( {\frac{r}{{r_{s} }}} \right)^{\alpha - 1} + \frac{{k_{s} }}{1 - \alpha } \hfill \\ \sigma_{\theta }^{{p_{s} }} = \alpha \left( {p_{s} - \frac{{k_{s} }}{1 - \alpha }} \right)\left( {\frac{r}{{r_{s} }}} \right)^{\alpha - 1} + \frac{{k_{s} }}{1 - \alpha } \hfill \\ \end{gathered} \right.,$$
(12)

where \(\sigma_{r}^{{p_{s} }}\) is the radial stress in plastic softening zone; \(\sigma_{\theta }^{{p_{s} }}\) is the hoop stress in plastic softening zone; \(k_{s} = \frac{{2c_{s} \cos \varphi }}{1 - \sin \varphi }\); \(c_{s}\) is the cohesion in plastic softening zone.

The inner radial stress of the surrounding rock plastic softening zone is \(\left. {\sigma_{r}^{{p_{s} }} } \right|_{{r = r_{w} }} = p_{w}\). It yields the relationship between the yield stress and the plastic radius.

$$r_{s} = r_{w} \left( {\frac{{p_{w} \left( {1 - \alpha } \right) - k_{s} }}{{p_{s} \left( {1 - \alpha } \right) - k_{s} }}} \right)^{{\frac{1}{1 - \alpha }}} .$$
(13)

At the interface between the elastic and plastic zones of the surrounding rock, the radial and circumferential stresses are continuous, satisfying the Mohr–Coulomb yield criterion. The following can be derived by substituting \(\sigma_{r}^{{p_{s} }} |_{{r = r_{s} }}\) and \(\sigma_{\theta }^{{p_{s} }} |_{{r = r_{s} }}\) into the yield criterion:

$$p_{s} = \frac{{2p_{1} - k_{s} }}{{\left( {1 + \alpha } \right)}}.$$
(14)

Stress solution in the plastic fracture zone

The radial and circumferential stresses of the plastic fracture zone can be determined in the surrounding rock plastic fracture zone by considering the stress boundary conditions \(\sigma_{r}^{{p_{w} }} |_{{r = r_{w} }} = p_{w}\) as follows:

$$\left\{ \begin{gathered} \sigma_{r}^{{p_{w} }} = \left( {p_{w} - \frac{{k_{w} }}{1 - \alpha }} \right)\left( {\frac{r}{{r_{w} }}} \right)^{\alpha - 1} + \frac{{k_{w} }}{1 - \alpha } \hfill \\ \sigma_{\theta }^{{p_{w} }} = \alpha \left( {p_{w} - \frac{{k_{w} }}{1 - \alpha }} \right)\left( {\frac{r}{{r_{w} }}} \right)^{\alpha - 1} + \frac{{k_{w} }}{1 - \alpha } \hfill \\ \end{gathered} \right.,$$
(15)

where \(\sigma_{r}^{{p_{w} }}\) is the radial stress in plastic fracture zone; \(\sigma_{\theta }^{{p_{w} }}\) is the hoop stress in plastic fracture zone; \(k_{w} = \frac{{2c_{w} \cos \varphi }}{1 - \sin \varphi }\); \(c_{w}\) is the cohesion force in plastic fracture zone.

The inner radial stress of the surrounding rock plastic zone is \(\sigma_{r}^{{p_{w} }} |_{{r = r_{{0}} }} { = }p_{0}\), which yields the radius of the plastic fracture zone.

$$r_{w} = r_{0} \left( {\frac{{p_{0} \left( {1 - \alpha } \right) - k_{w} }}{{p_{w} \left( {1 - \alpha } \right) - k_{w} }}} \right)^{{\frac{1}{1 - \alpha }}} .$$
(16)

Displacement solution in the plastic zone

Dilation model

Rock materials show significant volume expansion upon entering the plastic phase, characterized by post-peak dilation. The following equations are satisfied based on the non-associated flow rule of rock dilation in the plastic softening zone and plastic fracture zone25,26:

$${\Delta }\varepsilon_{r}^{{p_{s} }} + \eta_{s} {\Delta }\varepsilon_{\theta }^{{p_{s} }} = 0,$$
(17)
$${\Delta }\varepsilon_{r}^{{p_{w} }} + \eta_{w} {\Delta }\varepsilon_{\theta }^{{p_{w} }} = 0,$$
(18)

where \({\Delta }\varepsilon_{r}^{{p_{s} }}\) and \(\Delta \varepsilon_{\theta }^{{p_{s} }}\) are the radial and circumferential strain increments in the plastic softening zone, respectively; \(\eta_{s} = \tan^{2} \left( {\varphi /2} \right)\) is the dilation coefficient for the plastic softening zone; \({\Delta }\varepsilon_{r}^{{p_{w} }}\) and \(\Delta \varepsilon_{\theta }^{{p_{w} }}\) are the radial and circumferential strain increments in the plastic fracture zone, respectively; \(\eta_{w} { = 1 + }\varphi\) is the dilation coefficient for the plastic fracture zone, typically considered 1.3 for weak surrounding rock.

Displacement solution in the plastic softening zone

Strain in the plastic softening zone is composed of both elastic and plastic strains, satisfying the following formula27:

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{r}^{{p_{s} }} = \varepsilon_{r}^{e} |_{{r = r_{s} }} + \Delta \varepsilon_{r}^{{p_{s} }} } \hfill \\ {\varepsilon_{\theta }^{{p_{s} }} = \varepsilon_{\theta }^{e} |_{{r = r_{s} }} + \Delta \varepsilon_{\theta }^{{p_{s} }} } \hfill \\ \end{array} } \right.,$$
(19)

where \(\varepsilon_{r}^{{p_{s} }}\) is the radial strain in plastic softening zone; \(\varepsilon_{\theta }^{{p_{s} }}\) is the hoop strain in plastic softening zone; \(\varepsilon_{r}^{e}\) is the radial strain in elastic zone; \(\varepsilon_{\theta }^{e}\) is the hoop strain in elastic zone.

The following can be obtained by combining the stress relationship in the plastic softening zone (19), the plastic flow rule (17), and the geometric Eq. (7).

$$\frac{du}{{dr}} + \eta_{s} \frac{u}{r} = \left. {\varepsilon_{r}^{e} } \right|_{{r = r_{s} }} + \eta_{s} \left. {\varepsilon_{\theta }^{e} } \right|_{{r = r_{s} }} ,$$
(20)
$$u_{{p_{s} }} = C_{1} r^{{ - \eta_{s} }} + T_{1} p_{1} r + \frac{{(\eta_{s} - 1)T_{2} \left( {p_{1} - p_{s} } \right)}}{{\eta_{s} + 1}}r,$$
(21)

where

$$T_{1} = \frac{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}{E},\,T_{2} = \frac{{\left( {1 + \mu } \right)}}{E}.$$

The displacement is continuous between the elastic zone and the plastic softening zone. The undetermined coefficients are determined by incorporating boundary conditions \(u_{e} |_{{r = r_{s} }} = u_{{p_{s} }} |_{{r = r_{s} }}\), thus deriving the displacement in the plastic softening zone.

$$u_{{p_{s} }} = \left[ {2r_{s}^{{1 + \eta_{s} }} r^{{ - \eta_{s} }} + (\eta_{s} - 1)r} \right]\frac{{T_{2} \left( {p_{1} - p_{s} } \right)}}{{\eta_{s} + 1}} + T_{1} p_{1} r.$$
(22)

Displacement solution in the plastic fracture zone

The deformation generated in the plastic fracture zone is irreversible, and the strain in the fracture zone is plastic strain:

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{r}^{{p_{w} }} = \Delta \varepsilon_{r}^{{p_{w} }} } \hfill \\ {\varepsilon_{\theta }^{{p_{w} }} = \Delta \varepsilon_{\theta }^{{p_{w} }} } \hfill \\ \end{array} } \right.,$$
(23)

where \(\varepsilon_{r}^{{p_{w} }}\) and \(\varepsilon_{\theta }^{{p_{w} }}\) are the radial and circumferential strain in the plastic fracture zone.

The following can be obtained by combining the strain relationship in the plastic fracture zone (23), the plastic flow rule (18), and the geometric Eq. (7):

$$\frac{du}{{dr}}{ + }\eta_{w} \frac{u}{r}{ = }0.$$
(24)

The general solution for the displacement in the plastic fracture zone can be derived by solving the differential equation as follows:

$$u_{{p_{w} }} = C_{2} r^{{ - \eta_{w} }} .$$
(25)

At the interface between the plastic softening zone and the plastic fracture zone, satisfying the continuity of displacement condition \(u_{{p_{s} |r = r_{w} }} = u_{{p_{w} |r = r_{w} }}\) allows computing the undetermined coefficients and thus obtaining the displacement equation in the plastic fracture zone.

$$u_{{p_{w} }} = \left[ {T_{1} p_{1} r_{w}^{{1 + \eta_{w} }} + \frac{{T_{2} \left( {p_{1} - p_{s} } \right)}}{{\eta_{s} + 1}}\left[ {2r_{s}^{{\eta_{s} + 1}} r_{w}^{{\eta_{w} - \eta_{s} }} + \left( {\eta_{s} - 1} \right)r_{w}^{{1 + \eta_{w} }} } \right]} \right]r^{{ - \eta_{w} }} .$$
(26)

The following formula can be obtained at the interface between the plastic softening and plastic fracture zones, satisfying the continuity of strain condition \(\varepsilon_{{p_{s} |r = r_{w} }} = \varepsilon_{{p_{w} |r = r_{w} }}\), substituting Eqs. (22) and (26) into the geometric equation.

$$\frac{{r_{s}^{{1 + \eta_{s} }} }}{{r_{w}^{{1 + \eta_{s} }} }}{ = }\frac{{T_{1} p_{1} \left( {\eta_{s} + 1} \right)\left( {\eta_{w} + 1} \right)}}{{2T_{2} \left( {\eta_{s} - \eta_{w} } \right)\left( {p_{1} - p_{s} } \right)}}{ + }\frac{{\left( {\eta_{w} + 1} \right)\left( {\eta_{s} - 1} \right)}}{{2\left( {\eta_{s} - \eta_{w} } \right)}}.$$
(27)

Analysis of roadway surrounding rock in elastic–plastic state

The excavation equivalent radius \(r_{0}\) of the auxiliary transport groove at the working face is 2.6 m. The initial rock stress \(p_{1}\) is approximately 5.5 MPa, while the support force \(p_{0}\) is 0 MPa. The internal friction angle \(\varphi\) is 31.4°, the initial cohesion is 0.84 MPa, the residual cohesion is 0.28 MPa, the elastic modulus (E) is 2.56 GPa, and Poisson’s ratio is 0.29. Since the stress and displacement solutions in the elastic, softening, and fractured zones are continuous piecewise functions, substituting the relevant parameters allows for determining the effects of initial cohesion and internal friction angle on the stress field, displacement field, and radius of the plastic zone.

The influence of initial cohesion and internal friction angle on the stress field

This study conducts a sensitivity analysis on initial cohesion and internal friction angle to assess their impact on the stress field using a controlled variable method. Although the internal friction angle is fixed at 31.4°, cohesion levels are adjusted to 0.4, 0.6, 0.8, 1.0, and 1.2 MPa to evaluate their effects on radial and tangential stresses, as illustrated in Fig. 5. With cohesion maintained at 0.84 MPa, variations in the internal friction angles 28°, 30°, 32°, 34°, and 36° are explored to determine their influence on radial and tangential stresses, as depicted in Fig. 6.

Fig. 5
figure 5

Effect of cohesion on stress field.

Full size image
Fig. 6
figure 6

Influence of internal friction angle on force field.

Full size image

Accordingly, the radial stress diminishes progressively from infinity towards the excavation face, whereas tangential stress initially rises before declining. The peak tangential stress, observed accurately at the elastoplastic interface, demonstrates that increasing initial cohesion and internal friction angle move the elastoplastic interface nearer to the excavation face, reducing the radius of the plastic zone. The peak tangential stress value also increases, indicating a decrease in the plastic zone. This pattern shows that higher values of initial cohesion and internal friction angle augment the rock mass’s load-bearing capacity, delaying the onset and development of the plastic zone.

The influence of initial cohesion and internal friction angle on the displacement field

Figure 7 demonstrate that the initial cohesion and internal friction angle significantly affect displacement. It indicates that displacement exhibits a “spoon-shaped” profile, with larger displacements occurring on the excavation face of the surrounding rock and smaller displacements in the elastic–plastic transition zone. In the far-field elastic zone, distance from the excavation face, the displacement is primarily governed by the elastic modulus and Poisson’s ratio, while the effects of cohesion and internal friction angle on the displacement are negligible. The difference between displacement curves resulting from varying cohesion and internal friction angles is minimal and remains nearly constant. In the near-field elastic zone, which is closer to the excavation face, the slope of the displacement curve decreases, and inflection points begin to appear. In this region, cohesion and internal friction angle gradually become the dominant factors influencing the displacement. Under varying cohesion and internal friction angles, the differences between the displacement curves start to increase. Upon entering the plastic zone, the influence of cohesion c and the internal friction angle φ reaches the maximum.

Fig. 7
figure 7

Effect of cohesion and internal friction angle on the displacement field.

Full size image

As cohesion and internal friction angle increase, the displacement decrease becomes more significant in the plastic softening and fracturing zones. The impact of cohesion and internal friction angle on different zones of the surrounding rock is as follows: fracture plastic zone radius > plastic softening zone > elastic zone. When cohesion increases from 0.4 to 1.2 MPa, the displacement within the surrounding rock decreases from 0.03 to 0.015 m, representing a reduction of 50%. Similarly, when the internal friction angle grows from 28° to 36°, the displacement within the surrounding rock decreases from 0.035 to 0.018 m, representing a reduction of 56.7%. These results confirm that higher cohesion and internal friction angle contribute to enhanced stability of the surrounding rock, decelerating the development of displacements in the plastic zones.

The effect of initial cohesion and internal friction angle on the radius of the plastic zone

Figure 8 illustrates the influence of initial cohesion and internal friction angle on the radius of the plastic zone. It indicates that as initial cohesion and internal friction angle increase, the radius of the plastic zone demonstrates a non-linear decreasing trend, with the plastic fracturing zone progressively contracting until it vanishes. Both initial cohesion and internal friction angle significantly impact the radius of the plastic fracturing zone. When cohesion reaches 0.8 MPa or the internal friction angle surpasses 34°, the plastic fracturing zone disappears, leaving only the elastic and plastic softening zones. An increase in cohesion from 0.4 to 1.2 MPa reduces the plastic softening zone radius from 7.28 to 5.07 m, representing a 30.4% decrease. Similarly, elevating the internal friction angle from 28° to 36° diminishes the radius of the plastic softening zone from 7.33 to 4.79 m, a decline of 34.7%.

Fig. 8
figure 8

Influence of cohesion and internal friction angle on the radius of the plastic zone.

Full size image

Supporting schemes and their effectiveness

Supporting scheme

The previous elastoplastic analysis indicates that in weakly cemented soft rock roadways, enhancing the surrounding rock’s cohesion and internal friction angle can significantly reduce the radius of the plastic zone. Therefore, a support scheme based on grouting, referred to as “anchor net and cable injection” is proposed to fundamentally improve the structural and mechanical properties of the surrounding rock and fully utilize its self-supporting capacity, as illustrated in Fig. 9.

Fig. 9
figure 9

Support design diagram for auxiliary transportation roadway of workface 3205 (mm).

Full size image

Support parameters

  1. (1)

    Thin spray sealing: Mudstone on the roof and sides was sealed using thin spray materials, with a layer thickness ranging from 2 to 5 mm.

  2. (2)

    Roof anchoring: SKZ22-1/1860 high-strength, high-prestress grouted anchor cables with specifications of Φ22 × 7300 mm were employed, arranged in a 3 + 2 + 3 pattern at intervals of 1900 × 1800 mm. High-strength trays measuring 300 × 300 × 14 mm and TS anchor rod spherical washers and corresponding fittings were installed. The grouting material consists of ordinary Portland cement with additives. The cement used is #525 ordinary Portland cement, and the water-cement ratio is 1:1.5. The dosage of the additive is 4% to 6% of the cement weight, serving as an accelerator. The grouting pressure is maintained between 3 to 5 MPa, and the grouting rate is controlled within the range of 5 to 10 L/min. During the grouting process, the air pressure control valve of the grouting pump should be opened gradually, and the grouting pressure must be monitored continuously. If the pressure suddenly exceeds 5 MPa, grouting should be halted.

  3. (3)

    Roof anchor rods: MG500 high-strength, high-prestress expansion anchor rods made of threaded steel, with specifications of Φ18 × 2500 mm, were placed at intervals of 950 × 900 mm. High-strength steel strap trays measuring 300 × 300 × 2.5 mm were used, accompanied by flanged damping nuts, TS anchor rod spherical washers, plastic pads, and iron pads. Metal mesh surface support measures 5200 × 1100 mm, with a mesh size of 50 × 50 mm and a diameter of 3 mm.

  4. (4)

    Coal pillar side anchoring: MG500 high-strength, high-prestress expansion anchor rods made of threaded steel, with specifications of Φ18 × 2000 mm, were located at intervals of 800 × 1000 mm. High-strength butterfly-shaped trays with 150 × 150 × 8 mm were installed, along with ordinary damping nuts, TS anchor rod spherical washers, and plastic pads. Metal mesh surface support measures 3400 × 1200 mm, with a mesh size of 50 × 50 mm and a diameter of 3 mm. Anchor rods near the roof and floor were installed at an angle of 15° relative to the horizontal.

  5. (5)

    Recovery side anchoring: Fiberglass anchor rods with specifications of Φ27 × 2100 mm were used, arranged at intervals of 1000 × 1000 mm. High-strength, plastic-overlaid trays with Φ170 × 10 mm were installed. Diamond weave mesh surface support measures 2700 × 1100 mm, with a mesh size of 50 × 50 mm and a diameter of 3 mm. Anchor rods near the roof and floor were also installed at an angle of 15° relative to the horizontal.

Numerical simulation and analysis

Model establishment

This study utilizes ANSYS software to establish a three-dimensional model with dimensions of X × Y × Z = 60 × 51 × 1 m. The model is then imported into FLAC3D numerical software for calculation, as shown in Fig. 10. The boundary conditions are as follows: fixed constraints were applied to the model base plate; forward and backward displacement constraints were imposed; self-weight of the overlying rock layer was applied at the top; and horizontal tectonic stress was applied on both sides. The maximum burial depth of the auxiliary transport channel in the 3205 working face is 244 m. The thickness of the rock layer above the coal seam in the model is 24 m. Therefore, the overlying rock layer load applied at the top of the model is 6.09 MPa-25 kN/m3 × 24 m ≈ 5.5 MPa. Based on this, the self-weight of the overlying rock layer applied at the top of the model is approximately 5.5 MPa, and the horizontal tectonic stress applied on both sides of the model is 9.14 MPa. The constitutive relations of the rock masses involved in the model all adopt the Mohr–Coulomb yield criterion. The mechanical parameters of the rock strata in the model are shown in Table 3. When applying the physical and mechanical parameters of each rock layer, corresponding reductions were made according to the integrity coefficient n to ensure that they were as close as possible to the actual engineering properties.

$$n = \left( {\frac{{V_{ml} }}{{V_{cl} }}} \right)^{2} .$$
(28)
Fig. 10
figure 10

Numerical simulation calculation model.

Full size image
Table 3 Mechanical parameters of rock strata.
Full size table

Among them: \(V_{m1}\) is the propagation speed of the elastic longitudinal wave in the rock mass, m/s; \(V_{c1}\) represents the propagation speed of elastic longitudinal waves in rock blocks, in m/s.

According to the “Classification Standard for Engineering Rock Masses”, since the coal seam and its top, bottom and surrounding rock masses are relatively complete, n = 0.8. The mechanical parameters of the rock mass after reduction are shown in the following table.

Analysis of simulation results

Damage to the surrounding rock in the roadway under unsupported conditions

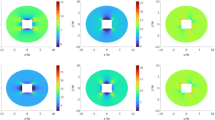
In unsupported conditions, the auxiliary haulage roadway of panel 3205 experiences extensive damage, as illustrated in Fig. 11. The roof damage extends to 8.6 m, floor damage up to 8.2 m, and the maximum damage on both the left and right sides reaches 5.5 m each. The surrounding rock deformation in the auxiliary transport channel is significant, with a maximum roof subsidence of 361.47 mm, a maximum floor heave of 284.42 mm, and horizontal displacement on the left and right sides reaching 462.61 mm.

Fig. 11
figure 11

Failure range, deformation, and displacement of the surrounding rock under unsupported conditions.

Full size image
Damage and deformation of surrounding rock after the “anchor net and cable injection” support

Figure 12 displays the extent of damage and deformation conditions of the auxiliary haulage roadway in panel 3205 following the implementation of the “anchor net and cable injection” support scheme.

Fig. 12
figure 12

Damage, deformation, and displacement of the surrounding rock under unsupported conditions.

Full size image

After adopting this support scheme, the overall integrity of the surrounding rock significantly improved, effectively limiting the expansion of the damage. Shear failure became the predominant form of damage. A shear failure zone is formed within approximately 1 m of the roof, floor, and surrounding rock on both sides of the auxiliary transport road, which is significantly reduced compared with the plastic failure zone observed without support. Specifically, the failure zone in the roof is reduced by 88.37%, on the floor by 87.80%, and on both sides by 81.82. The maximum roof subsidence of the auxiliary transport road is 10.02 mm, the maximum floor heave is 8.23 mm, and the horizontal movement of the left and right sides is 8.31 mm, all of which are markedly lower than the deformation values of the surrounding rock without support. In detail, the roof subsidence is reduced by 97.23%, the floor heaves by 97.11%, and the lateral movement on both sides by 98.20%. These observations confirm the effectiveness of the “anchor mesh grouting” support scheme in controlling the deformation of the surrounding rock.

Discussion

In this paper, addressing the mechanical characteristics of weakly cemented soft rock and comprehensively considering the softening effect and shear dilation effect of the surrounding rock in the plastic zone, an elastic-soft-fracture mechanical model of the roadway surrounding rock in weakly cemented soft rock is established. This model further refines the plastic zone and facilitates analysis and discussion in combination with specific cases. The analysis of the mechanical model indicates that, with the increase in internal friction angle and cohesive force, the resistance capacity of the surrounding rock gradually increases. In contrast, the displacements and radii of the softening zone and the fracture zone within the plastic zone of the surrounding rock both exhibit a decreasing trend.

The “anchor net and cable injection” support technology proposed in this paper represents an effective method of reinforcing the surrounding rock. It enhances the integrity and strength of the surrounding rock by improving the cohesion and internal friction angle through the combined use of anchor rods, anchor nets, and anchor cable grouting. Numerical simulation results demonstrate that this support scheme can significantly reduce the deformation of the surrounding rock and the depth of the plastic zone, which aligns with the deformation and failure patterns of the surrounding rock, as revealed by the mechanical model.

On-site support effectiveness

Three monitoring stations were arranged at intervals of 100 m in the auxiliary transport channel of the 3205 working faces to monitor the surrounding rock deformation and roof separation of the test section to verify the surrounding rock control effect of the support scheme on weakly cemented soft rock roadways.

The surface displacement of the roadway was monitored using the “cross” point arrangement method to measure the convergence of the top and bottom slabs and the two sides. The variation in the convergence of the surrounding rock over time was analyzed to determine its initial stability time and overall stability, as shown in Fig. 13. Roof subsidence and sidewall convergence increased in a generally linear trend. Roadway deformation primarily underwent two stages: deformation (0–30 days) and stabilization (after 30 days). During the tunneling period, the maximum roof subsidence was 51 mm, the convergence of both sides was 16.5 mm, the deformation of the surrounding rock remained relatively low, and the roadway’s resistance to deformation increased.

Fig. 13
figure 13

Surface displacement of the roadway.

Full size image

Shallow base points (not less than 3 m) and deep base points (not less than 8 m) were arranged on the roof of three monitoring stations in the roadway based on the geological conditions at the site, engineering experience, and the results of numerical simulation. The monitoring results of roof delamination are shown in Fig. 14.

Fig. 14
figure 14

Strata detachment of the surrounding rock.

Full size image

Roof delamination mainly occurs within the range of top coal, sandy mudstone, and siltstone. The delamination amount ranges from 0 to 15 mm, with the maximum delamination amount being 15 mm, which is within the allowable range, as shown in Fig. 14. The on-site performance of the “anchor net and cable injection” support scheme is shown in Fig. 15. The results demonstrate that the “ anchor net and cable injection” support scheme enhances the self-supporting capacity of the roadway’s surrounding rock, effectively controls deformation and strata detachment, and ensures smooth construction progress.

Fig. 15
figure 15

On-site support effect drawing.

Full size image

Conclusion

  1. (1)

    This study develops an elastic–plastic mechanical model of a roadway surrounding rock under uniformly distributed stress. This model considers softening and shear dilation effects and effectively represents the deformation characteristics of the elastic-softening-fracture zones in the roadway surrounding rock.

  2. (2)

    Increased initial cohesion and internal friction angle enhance the resistance of the surrounding rock against loads, delaying the onset and development of plastic zones. As the initial cohesion and internal friction angle increase, the elastic–plastic interface moves toward the excavation face. The circumferential stress values at this interface gradually increase, reducing the radius of the plastic zone.

  3. (3)

    As initial cohesion and internal friction angle increase, the radius of the plastic zone exhibits a non-linear decrease, with the plastic fracture zone disappearing first. The impact of initial cohesion and internal friction angle varies across different zones of the surrounding rock: fracture plastic zone radius > plastic softening zone > elastic zone.

  4. (4)

    The support scheme of “anchor net and cable injection” improves the self-supporting capacity of roadway surrounding rock, effectively controlling deformation and strata detachment in weakly cemented soft rock roadways. This method can be adopted for roadway excavation under similar conditions.