Introduction

Breast cancer (BC) is caused by particular kinds of cells growing out of control, similar to many other types of cancer1. Any breast tissue can gradually accumulate random cell mutations, and when the right mutations are combined, this morphological process results in the cells’ transformation into tumor cells2,3. This type of lesion developed in the breast may have an impact on the patient’s quality of life.

Because the focus of this research is the combination of image features and exploration of AI technologies, many new and repetitive terminology is introduced. To save space, a list of abbreviations used in this study has been included below. The integral letter symbols of frequently occurring words are displayed in Abbreviations section.

There are more organizations throughout the world that gather population health data. One of these is the World Health Organization (WHO), which specified that 2,261,419 cases of BC worldwide in 2020, and 684,996 deaths from the disease4. Two significant years of data about the spread of BC in the United States were 2018 (268,670 new cases recorded) and 2017 (252,710 new cancer cases)3. Additionally, a study performed in nine countries in Eastern Europe showed that 19,726 BC deaths were reported in 20195.

Patients who follow innovative treatments and therapies can survive and even lead normal lives, despite troubling statistics. Early detection of the disease and the timely administration of appropriate treatment are essential.

Artificial intelligence algorithms are typically found in equipment that scan the human body to establish a diagnosis. These have combined ML with neural networks, CNN or ensemble learning approaches, which are highly effective in improving the accuracy of disease categorization.

Breast ultrasound images are used by physicians to inspect the shape and texture of lesions in order to establish a diagnosis. The proposed study performs the same procedure combining textural and shape features into hybrid features. In an original concept textural and shape features are corroborated into a polynomial regression.

Previously, the most common features for BC classification have been extracted from US images. The MLs have been supplied with a large variety of features as various radius, smoothness, compactness geometric features and texture6 uniformity of cell size, bland chromatin, mitoses, clump thickness7, radius, perimeter, area, smoothness, compactness, concavity, concave points, symmetry fractal dimension8, statistical features9,10, multi-model features11, textural features12 and radiomics features13,14.

The feature sets have a null value if they are not analysed and classified. AI techniques are becoming indispensable in procedures such as regression or classification. This field includes AutoML, which can quickly automate the selection of the best classifiers and optimal hyperparameters. Experts believe that creating an ML classifier manually and using default hyperparameters is a trial-and-error process15. It was the reason of choosing two different types AutoML, PyCaret and TPOT16,17.

Prior to the validation process, the AutoMLs choose the optimal ML algorithm and its hyperparameters to provide a greater classification accuracy. Three techniques for collaborative learning: bagging, boosting, and stacking18,19 can be used for validating the obtained results.

Recently, researchers proposed other approaches to classify human tissue using pre-trained CNNs with deep features for kidneys20, brains21,22, and breast23. These papers leverage the power of convolutional neural networks (CNNs) to extract deep features that enhance the accuracy of tissue classification.

This paper presents a novel approach to combining textural and geometric features to derive HF, in contrast to the methods described in papers 6,7,8,9,10,11,12,13,14,15,16,17, which relied solely on one type of feature for classifying BC types. Once HFs are extracted, these serving as a pivotal element in the classification process. Relying on a single ML algorithm may result in suboptimal outcomes; thus, we propose fine-tuning both the ML model and its hyperparameters. A significant number of studies provide unvalidated results; therefore, this study advances by incorporating validation through three EML techniques. The pipeline illustrated in Fig. 1 distinguishes itself from other scientific literature by integrating the previously described elements. This integration not only enhances the robustness of the classification process but also ensures that the model’s performance is consistently reliable across various datasets. By leveraging these advanced techniques, we aim to provide a comprehensive framework that can be adapted for future research in this domain.

Fig. 1
figure 1

Schematic diagram of study methodology.

Full size image

Motivation and contributions

The analysis of BC statistics motivated the authors to try to identify how doctors analyse breast ultrasound images to make a diagnosis. Moreover, the textural and geometric features were combined in order to obtain the useful information only in the region of interest.

The motivation for this study arises from the concerning statistics regarding BC. After analyzing the data, we propose the primary goal of this work: to develop a study that implements features relevant to shape and texture, classification, and validates them. We aim to enhance the accuracy of classification methods in this field. By integrating advanced IA algorithms and comprehensive feature analysis, we believe this study will contribute significantly to the understanding and application of shape and texture in relevant contexts.

Finding adequate HFs is what will enable the most accurate classification of benign and malignant BC. In addition to achieving this goal, this study emphasizes innovative aspects in contrast to references7,8,9,10,11,12,13,14,17,24,25,26,27, where researches are centred solely on basic features.

In order to achieve this goal, the primary contributions were made, as follows:

  1. (1)

    The images were overlapped so as to contain only the texture of the breast lesion;

  2. (2)

    The proposed HF computation supports both geometric and textural methodologies;

  3. (3)

    Employing violin graphs to evaluate the raw data collected for the malignant and benign classes;

  4. (4)

    Labelling the data and supply PyCaret and TPOT AutoMLs with obtained data;

  5. (5)

    The optimal classifier based on the higher metrics computed from the confusion matrix was determined.

  6. (6)

    The results were validated using bagging, stacking, and boosting EML techniques.

The proposed mechanism stands out from others because it supports HFs, which are classified using two AutoML methods and validated through three EML techniques. The results demonstrate a robust performance in accurately categorizing the HFs, highlighting the effectiveness of the proposed mechanism. Furthermore, the integration of AutoML and EML methods streamlines the classification process and enhances the reliability of the outcomes.

Related work

This section presents a comparison with the references based on the use of simple ML, CNN, NN classifiers and AutoML tools for the classification of different type features. The studies are restricted to features obtained from breast US images. The following studies10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30 were established in occurrence using information collected over the last 50 years from the Google Scholar and PubMed platforms. A summary of the issues listed in Table 1 is kept.

Table 1 A list of previous works, features, IA algorithms and limitations.
Full size table

Three machine learning tools were employed by Viswanath et al.10 to get statistical features and the accuracy of classification was met. Therefore, this study was integrated in a Computer-Aided Diagnosis (CAD)—a system for diagnosing and classifying the three types of lesions: malignant, benign and normal. Also, Kayode et al.12 created a CAD system for facilitating breast cancer diagnosis by radiologists and the textural features extracted from GLCM were used for the feeding of the SVM classifier.

Arefan et al.13 calculated radionics features from an area of interest (ROI) using semi-automated image segmentation performed by an experienced radiologist. Five classifiers were used for the binary classification of benign versus malignant, and the bootstrap test method was used to validate the best classifier. In a recent study, Naranjo et al.14 coupled radiomics features analysis and ML, allowing the authors to eliminate unnecessary biopsies in benign breast tumours and enhance the evaluation of disturbing BC.

According to the statistical analysis, Ghiasi and Zendehboudi7 proposed a method able to classify the type of BC accurately. The modelling of the RF and ET employed nine features. The methods used to validate benign and malignant breast cancer included bagging, boosting, and stacking ensemble methods.

Sharma et al.8 proposed several methods for early cancer prediction. The authors used the neural network and ET classifiers for a binary classification while the geometrical features were used for empirical results and statistical analyses.

Ozcan et al.9 made a comparison of the classification of different ML algorithms for the diagnosis of BC. In this study, thirty features were classified using eleven classifiers. The classifiers were compared with both classification accuracy and matrix complexity, and GBC provided the best results.

Reshan et al.11 used EML approaches and multi-model features to study and predict BC, in an automated manner. In addition, a recursive feature elimination method is proposed to identify the most crucial features for usage in classification and detection.

AutoMLs models, Pycaret25,26,27 and TPOT17,24 were employed in multiple investigations17,18,19,20,21,22,23,24,25,26,27. To distinguish benign breast tumors Radzi et al.24 utilized advanced ensemble techniques like voting, bagging, stacking, and boosting as combination strategies. The primary goal of Labilloy et al. study25 was to identify features related to the care given to women who had been diagnosed with BC. The PyCaret Python package was used to compare fifteen models from an extensive data set.

Zhuang26 presented a traditional investigation with the main objective of identifying clinical risk and genetic factors. It classified genetic features and compared them using ML algortithms and hyperparameter tuning.

To assess the effectiveness of seven AutoML approaches in terms of classification accuracy, Rashed et al.17 supplied them with eight distinct datasets. The effective approach helped identify the optimum ML model for each AutoML technique, and it was necessary to use several BC datasets for an accurate data interpretation.

The latest studies proposed by Laghmati et al.28, Atrey et al.29, and Del Corso et al.30 deal with the classification of anatomical, fusions, and radiomic features, respectively. A small number of MLs is proposed, and their fine tuning is missing.

Classification of BC type is a difficult task, as it is shown in Table 1. The studies combine different features with MLs or AutoMLs, and a comprehensive literature review of state-of-the-art studies with their drawbacks is also provided by the authors. The main drawbacks of state-of-the-art studies that used MLs or AutoMLs supplied with extracted features from breast US images were divided into the following categories: small number of images12, a big time consuming11,13,17, extraction of features from whole images avoiding region of interest so the segmentation stage is missed12,24,26, the papers risk of underfitting for machine learning models not using validation stages10,25,27,28,29, detailed analysis of the model hyperparameters7,8,9,12,13,28,29,30.

After conducting extensive research in the scientific literature, we discovered that HFs have not been proposed at this time. An analysis of Table 1 indicates that these features are only recognized as a distinct category, specifically features7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35. We suggest that the optimal combination of key Haralick features and Hu moments, which encompasses both textural and geometric aspects, should extend beyond merely having separate categories of features. This approach would allow for a more holistic representation of the data, integrating the strengths of both feature categories. By merging these elements, we can enhance the accuracy and effectiveness of data analyses, ultimately leading to more robust predictive models.

Methodology

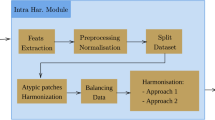
The methodology consists of five key components: the BUSI database, image pre-processing, HFs, statistical algorithms and feature classification, and validation. The first component includes the proposed dataset, which addresses the study’s requirements by incorporating the grey levels of breast US and ground truth images for both malignant and benign classes. Since the hybrid features were extracted solely from the region of interest (ROI), the image processing stage was implemented. The hybrid features block presents the original features—specifically, Haralick’s features and Hu moments—utilized then in polynomial regression. The originality of these features requires a pre-analysis, which was conducted using a violin plot to compute the mean and median values for each HF. The study progressed with the classification of features and performance validation; in this context, two AutoML methods were proposed, and following a tuning process, performance metrics were calculated. The validation stage, particularly regarding accuracy, were highlighted using three ensemble machine learning (EML) methods.

Results and discussion

Personal results from previously published studies prompted a shift from one type of feature to HF. Anghelache Nastase et al.36 proposed a solution based on the Hu moments extracted from ground truth images, achieving a medium accuracy of 81.7% for the first moment. Tăbăcaru et al.37 analyzed and classified textural features extracted from ultrasound breast images, obtaining an accuracy of 89.8% using the XGBoost classifier. The search for a solution for the same database utilized in earlier research continued with the combination of features in a regression approach. The results were improved, demonstrating the potential of integrating various feature extraction techniques and classifiers. This advancement not only enhances diagnostic accuracy but also paves the way for more robust methodologies in medical image analysis.

The proposed AutoML models are appropriate for features classification extracted from medical US images11,17,24,25,26,27. An AutoML tool determines the optimal architecture of the ML algorithm for the classification of features and, in addition, sets up the optimal hyperparameters for the right classifier. The selected classifiers by PyCaret and TPOT with their hyperparameters are stored in Table 2. In addition, it should be highlighted that for each individual hybrid feature noted with y1, y2, y3, y4, y5 and y6, the selection process was applied. Non-optimization of hyperparameters affects the performance of a model, so this aspect should not be neglected in studies where ML are applied.

Table 2 The best classifier selected by PyCaret, TPOT, and their hyperparameter.
Full size table

From experimentation purposes, for each classifier selected by PyCaret and TPOT and the features extracted from the US images that belong to the BUSI database, we evaluated the classification of the HFs with ACC, AUC, Recall, Precision, F1-score and MCC. Tables 3 and 4 store the computed metrics for a binary classification of the best classifier selected by AutoMLs PyCaret and TPOT, respectively. The feature with the higher values of proposed metrics is highlighted in bold in Tables 3 and 4.

Table 3 Performance comparison of the PyCaret AutoML.
Full size table
Table 4 Performance comparison of the TPOT AutoML.
Full size table

The present study continues with the last stage, called validation results. In Table 5, the validated values of accuracy obtained with bagging, boosting, stacking techniques. The boosting algorithm estimate the accuracy provided by the classifier in terms of the selection of the statistical regression models. Also, the accuracy computed by the stacking ensemble model consisting of MLR and RF is optimized by the SVR, and the bagging meta-estimator aggregates individual predictions of random subsets in order to form a final prediction. The EML is computed using both features of PyCaret and TPOT AutoMLs.

Table 5 Validation accuracy results with bagging, boosting, and stacking.
Full size table

The risk of overfitting was eliminated using the cross-validation method for each feature. The final accuracy was verified by averaging accuracies for applying a tenfold cross-validation method.

The stacking EML method had better accuracy than bagging and boosting for any individual feature. The AI method proposed in this paper is a novel approach for improving the classification of benign and malignant BC. According to Table 5, the best average accuracy was found for y1 feature, moreover, being confirmed by each AutoML.

The misclassifications of samples presented in Tables 3, 4, and 5 are influenced by the geometric shapes of BC. The shapes associated with malignant tumors closely resemble those of benign tumors, and the dataset includes similar shapes for both types. This resemblance can create difficulties in accurately distinguishing between the two cancer types when using automated classification methods. Therefore, it is essential to enhance the algorithms to better identify subtle differences in geometric features, which is vital for improving diagnostic accuracy.

Additionally, the highest ACC, AUC, Recall, Precision, F1-score and MCC metrics are obtained using the best model PyCaret (ADB classifier), and was confirmed by the model TPOT (MLPClassifier).

As there is no standard protocol for calculating the performance of HFs available in the literature, the authors have compared the studies of the last 5 years of the proposed work with a state-of-the-art method that deals with AutoMLs and their results only for the classification of BC, the collected data being shown in Table 6.

Table 6 Comparing with state-of-the-art papers.
Full size table

From metric prediction and the results obtained in previous works, an improvement in the classification is noticed. For all combinations, the hybrid features computed from EN and Hu moments yield the best results.

The proposed features are original, so a previously performed analysis of data with violin graphs was performed, and the distribution of features was verified. This step is necessary because the quality of data is very important in the classification process.

Corroborating the graphs from Fig. 2 and the results stored in Tables 3 and 4, a uniform distribution of data for y1 and y2 features is noticed. The first two selected features, y1 and y2, have the median value for benign classes of 0.18 and for malignant classes of 0.14, respectively. Also, the metrics computed for these two features give the best classification. The distribution of y3, y4, y5, and y6 features is chaotic, which led to a loss of information and inconsistencies; this is reflected by the metric values stored in the same tables.

Fig. 2
figure 2

Image samples (a) Original image; (b) Mask of ROI. (c) Gray scale of ROI;

Full size image

Out of fourteen classifiers for PyCaret and eleven for TPOT, there are candidates for the best classifiers that give the highest accuracy in BC classification. The PyCaret AutoML selected the optimal ADB classifier, which provided an accuracy of 0.914 for the y1 feature; this is the best accuracy in comparison with the other ones. Also, the second TPOT AutoML selected the optimal MLP classifier for the same feature, given an accuracy of 0.906. Both classifiers have the best hyperparameters stored in Table 2.

In addition, the proposed results with bagging, stacking, and boosting EML techniques were validated. In Table 5, the stacking method with averaging accuracy for applying a tenfold cross-validation method provides for PyCaret 0.928 and TPOT 0.922. Moreover, feature y1 was validated by all EML techniques with the highest accuracy.

The limitations of the presented results may be influenced by image quality, the type of segmentation method for ground truth detection, and the number of images used. Other limitations refer to the disease classes of breast cancer, malignant and benign.

Conclusion and future directions

The proposed paper contains original hybrid features computed from textural and shape features in a polynomial regressive way. Out of six created features, the hybrid feature y1, as a compassion from energy Haralick textural feature, and first Hu moments were validated by PyCaret (ADB classifier) and TPOT AutoML (MLP classifier), with accuracy of 0.914 and 0.906, respectively. From a set of three EML methods (bagging, boosting, and stacking), the y1 features are validated by stacking EML method, in an averaging of 10-cross validations of 0.928 by PyCaret and of 0.922 by TPOT, respectively. As a result, the energy features extracted from ROI and the first Hu moment expressed in the y1 hybrid feature can be used with success in BC classification.

For future research, the innovative features based on fractal dimensions and textural features and will be proposed to supply different AI algorithms, and the results will be validated by EML techniques. Other future directions consist of integrating handcraft and deep features for classifying different cancer types. This integration could enhance the accuracy of cancer diagnostics by leveraging both traditional handcraft techniques and advanced deep learning algorithms.

Methods

Dataset, hardware and software

In this study, the Breast Ultrasound Images Dataset medical data sets (BUSI)38 is used, and it is publicly available for academic and research purposes through open-access repositories. The images were collected in 2018 from 600 female patients. The dataset holds benign 487 records, malignant 210 and normal 133, respectively. The images are in PNG format with a resolution of 500 × 500 pixels. The advantage of BUSI is that each image is followed by a binary mask of the lesion’s ground truth. In the proposed study, only benign and malignant classes were used because the HFs are derived from texture and binary mask. The AutoMLs were supplied a dataset splited into 70% (487 samples/images) for train, and 30% (210 samples/images) for testing.

The hardware environment had the following architecture: Processor Intel(R) Core (TM) i7-1065G7 CPU @1.30–1.50 GHz, RAM 16.0 GB, and Windows 11 operating system, 64-bit, × 64-based processor. The environments programming Matlab R2019 with Image processing toolbox for computing of features and Python (version 3.9), PyCaret (version 3.0.4), and TPOT (version 0.12) versions, respectively, were used.

Hybrid image features

Computed features are called hybrid features, because they are extracted both from texture and shape of the object in an image. Different textural, geometric, fractal, statistical, or other measures could be used to calculate the features.

Their particular characteristics depend on texture information and shape and are interpreted by the dictionary of BC type expressed in US images. Additionally, a reliable analysis of the lesion is ensured by the computation of textual information from pixel arrangements within the BC lesion. The HFs go through three primary stages: (i) extracting Haralick’ features from the BC lesions only; (ii) computing Hu moments from the mask of the lesions; and (iii) obtaining complex HF through integrating the first two features type in a polynomial regression; this approach was proposed because hybrid features are interpreted as dependent variables, in which the coefficients are given by Hu moments and independent variable by Haralick’ features, respectively.

Haralick’ features

An intuitive idea in distinguishing between breast lesions with Haralick’ features is that these show the pixel arrangements, which vary in the presence of microcalcifications, branching patterns, or smoothing breast lesion textures39,40.

In order to avoid redundant information, only the breast lesions were analysed; for this, the ground truth images (Fig. 1, column b) were overlapped in the original images (Fig. 1, column a), thus resulting the region of interest (Fig. 1, column c).

The texture features of a grayscale image are associated with Gray Level Co-Occurrence Matrix (GLCM)41. The important Haralick features as energy (EN), entropy (ENT) homogeneity (H), contrast (C), correlation (CR) and dissimilarity (D) in Eqs. (1–6) are expressed.

$$EN = \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} p\left( {i, j} \right)^{2}$$
(1)
$$ENT = - \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} p\left( {i,j} \right)\log p\left( {i,j} \right)$$
(2)
$${\text{H}} = \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} \frac{{p\left( {i,j} \right)}}{{1 + \left( {i - j} \right)^{2} }}$$
(3)
$$C = \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} \left( {i - j} \right)^{2} p\left( {i,j} \right)$$
(4)
$$CR = \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} p\left( {i,j} \right)\left( {\frac{{1 - \mu_{x} }}{{\sigma_{x} }}} \right)\left( {\frac{{1 - \mu_{y} }}{{\sigma_{y} }}} \right)$$
(5)
$$D = \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = 1}^{N - 1} \left| {i - j} \right|p\left( {i,j} \right)$$
(6)

N is the number of gray levels, μx, μy and σx, σy are the means and standard deviations in Oy and Oy directions, and \(p\left( {i,j} \right)\) is the probability density of the pixels located at established distance41,42. From features expressed by (1–6) equations, it was built the set \(x_{fi} \in \left\{ {EN, ENT, H, C, CR, D} \right\}\).

The mentioned texture features showed significant differences in BC lesions and presented some of the most crucial image texture properties39.These were computed from all the images for prediction43, monitoring44 and classification45 of BC.

Hu moments

Hu Moments are descriptors that are used to describe shape objects in an image. They begin with a shape’s regular moment in a binary image.

In the analysis of BC, a critical parameter is the shape of the lesion, because it suggests the type of cancer. Figure 1b1 and b2 display a sample from the BUSI dataset, which contains ground truth for each lesion. In computer vision, the invariant Hu moments are commonly used as global form descriptors36, so that their capacity in analysing shape is explored. The shape of benign BC is well circumscribed; meanwhile, malignant BC is ill-defined in borders and has a non-uniform shape36. The BC types have different characteristics of shapes; thus, the Hu moments are viewed as shape descriptors, because they are invariant to translation, scale, rotation, and reflection36,46. In this context, only first six moments were proposed as coefficients in a polynomial regression, and their mathematical approaches are shown below:

$$M_{ij} = \mathop \sum \limits_{x} \mathop \sum \limits_{y} x^{i} y^{j} I\left( {i,j} \right)$$
(7)

where \(I\left( {i,j} \right)\) is the pixel intensity value located at the coordinates \(\left( {i,j} \right)\).

The centroid of the shape, is also called the geometric centre as it is a point that fixes the centre of gravity of a particular shape.

$$\overline{x} = \frac{{M_{10} }}{{M_{00} }}\;{\text{and}}\;\overline{y} = \frac{{M_{01} }}{{M_{00} }}$$
(8)

The centroid shape coordinates can be used to calculate the relative moments in the following way:

$$\mu_{pq} = \mathop \sum \limits_{x} \mathop \sum \limits_{y} \left( {x - \overline{x}} \right)^{p} \left( {y - \overline{y}} \right)^{q} I\left( {i,j} \right)$$
(9)

Taking into account that seven separate invariant moments for shape discrimination can be built44, they can be expressed by equations as follows (10)-(16).

$$\eta_{1} = \mu_{20} + \mu_{02}$$
(10)
$$\eta_{2} = \left( {\mu_{20} - \mu_{02} } \right)^{2} + 4\mu_{11}^{2}$$
(11)
$$\eta_{3} = \left( {\mu_{30} - 3\mu_{12} } \right)^{2} + \left( {3\mu_{21} - \mu_{03} } \right)^{2}$$
(12)
$$\eta_{4} = \left( {\mu_{30} + \mu_{12} } \right)^{2} + \left( {\mu_{21} + \mu_{30} } \right)^{2}$$
(13)
$$\begin{aligned} \eta_{5} & = \left( {\mu_{30} - 3\mu_{12} } \right)\left( {\mu_{30} + \mu_{12} } \right)\left( {\left( {\mu_{30} + \mu_{12} } \right)^{2} - 3\left( {\mu_{21} + \mu_{03} } \right)^{2} } \right) \\ & \quad + \left( {3\mu_{21} - \mu_{03} } \right)\left( {\mu_{21} + \mu_{03} } \right)\left( {3\left( {\mu_{30} + \mu_{12} } \right)^{2} - \left( {\mu_{21} + \mu_{03} } \right)^{2} } \right) \\ \end{aligned}$$
(14)
$$\eta_{6} = \left( {\mu_{20} - \mu_{02} } \right)\left( {\left( {\mu_{30} + \mu_{12} } \right)^{2} - \left( {\mu_{21} + \mu_{03} } \right)^{2} } \right) + 4\mu_{11} \left( {\mu_{30} + 3\mu_{12} } \right)\left( {\mu_{21} + \mu_{03} } \right)$$
(15)

Polynomial regression and feature computing

A polynomial regression refers to a nonlinear combination of coefficients and independent variables. The proposed method adapts a polynomial regression of degree six, obtaining the \(y_{i}\) (i = 1,2,3…,6) HFs through a nonlinear combination of the polynomial regression’s coefficients \(\eta_{j}\)(j = 1,2,3…,6) (Hu moments) and the independent variable \(x_{fi} \in \left\{ {EN, ENT,H,C,CR,D} \right\}\) Haralick’s features.

The general form of a polynomial regression of degrees six is given by the following equation46,47.

$$y_{i} = \eta_{1} x_{fi}^{5} + \eta_{2} x_{fi}^{4} + \cdots + \eta_{5} x_{fi} + \eta_{6} \;\left( {{\text{i}} = {1},{2}, \ldots ,{6}} \right)$$
(16)

Equation (17), which expresses Eq. (16) in detail using matrices, shows hybrid features in the first column matrix, independent variables in the main matrix, and coefficients in the last column matrix.

$$\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {y_{3} } \\ {y_{4} } \\ {y_{5} } \\ {y_{6} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{f1}^{5} } & {x_{f1}^{4} } & {x_{f1}^{3} } & {x_{f1}^{2} } & {x_{f1} } & 1 \\ {x_{f2}^{5} } & {x_{f2}^{4} } & {x_{f2}^{3} } & {x_{f2}^{2} } & {x_{f2} } & 1 \\ {x_{f3}^{5} } & {x_{f3}^{4} } & {x_{f3}^{3} } & {x_{f3}^{2} } & {x_{f3} } & 1 \\ {x_{f4}^{5} } & {x_{f3}^{4} } & {x_{f4}^{3} } & {x_{f4}^{2} } & {x_{f4} } & 1 \\ {x_{f5}^{5} } & {x_{f3}^{4} } & {x_{f5}^{3} } & {x_{f5}^{2} } & {x_{f5} } & 1 \\ {x_{f6}^{5} } & {x_{f3}^{4} } & {x_{f6}^{3} } & {x_{f6}^{2} } & {x_{f6} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\eta_{1} } \\ {\eta_{2} } \\ {\eta_{3} } \\ {\eta_{4} } \\ {\eta_{5} } \\ {\eta_{6} } \\ \end{array} } \right]$$
(17)

The polynomial regression was used to the detriment of linear regression because the last one is a linear combination between features, and in fact the HF can be interpreted as a product between two types of features; instead, the polynomial regression reinforces the contribution of Hu moments in the final value of HF, giving decreasing weights in order of importance of Hu moments. For example, the first moment is the most important moment because it expresses the area of the lesion36.

The Fig. 2 displays the processed image types. The original images for benign and malignant conditions are displayed in first column, the binary mask of ROIs is displayed in column two, and the overlap of the first two is displayed in column three. Because only evaluating the texture of the ROI is relevant, the images presented in column three were used to compute textural features. The binary image was used to calculate the Hu moment. The first line indicates a benign lesion, while the second line indicates a malignant lesion, images from BUSI dataset. The images shown in column (a) and (b) belong BUSI dataset and column (c) depicts the images obtained in a pre-processed process.

There is a strong association between the morphology of the breast tumour and the tumour diagnostic outcome48. Because segmented lesions include enough shape information to distinguish between benign and malignant tumours, it is important to consider these aspects49. Additionally, distinct types of tissue can be identified using textural properties50. Together form hybrid features \(y_{1} ,y_{2,} y_{3} ,y_{4,} y_{{5,{ }}}\) and \({ }y_{6}\) supplied the AutoMLs tools.

A pre-analysis of data was necessary, because the justification of classification is necessary. In this way, the probability distributions of the hybrid features \(y_{1} ,{ }y_{2} , y_{3} ,{ }y_{4} , y_{{5,{ }}}\) and \({ }y_{6}\) with violin plot was plotted.

AutoML and ensemble model learning

An ensemble strategy for classifying benign and malignant classes is presented in this work. This procedure has been divided into three phases: (i) collecting and annotating data for the AutoMLs; (ii) automated machine learning, or AutoML for short, is a new discipline where building ML models from data is done automatically. In the proposed study, two distinct AutoMLs as PyCaret and TPOT were suggested while (iii) validating the data was done by using ensemble bagging, boosting, and stacking techniques. This type of classifier is proposed because PyCaret optimizes model hyperparameters and boosts ML productivity. The GA, which the TPOT uses, gives answers for finding and optimizing issues in ML.

The Hfs had to be annotated because a binary classification was used, and the data was collected from the BUSI image database, which included both benign and malignant classes.

PyCaret is an open-source machine learning library in Python and this tool automates, evaluates and compares ML classifiers, having integrated the fourteen classifiers: LightGBM, GBC, KNN, ADA, LR, RF, SVM, VM, ET, DT, Ridge, LDA, QDA and NB. Moreover, it is a method for hyperparameter tuning. Model training, explainability, data preprocessing, and exploratory data analysis are all supported by PyCaret. Additionally, PyCaret offers data scaling and transformation methods to change the shape of the distribution and reduce the magnitude of variation of image classification23.

The pipeline optimization tool (TPOT) based on GA uses Python automated ML system. It offers the optimal pipeline that was discovered. Moreover, it allows modifying the pipeline deeper17. The top-performing models from each generation are provided by TPOT and combined to produce a new generation of models that produces the best results in a classification task18. The proposed TPOT version consisted of the following classifiers: BNB, MNB, DT, ET, RF, GBC, KNN, SVC, LR, XGB, and MLP.

An EML technique called bootstrap aggregation, often known as bagging, is used to overcome overfitting issues in regression and classification. Only the predicted set that the classifiers provide is used for BA; the training set is divided into subsets using bootstrap and cross-validation. The model’s base prediction is constructed by merging the forecast outcomes for every subset. In this work, the KNN classifier is used; typically, this technique is applied using DT, NB, or KNN classifiers51,52.

A significant benefit of utilizing the EML technique is its integrated k-fold cross-validation option. The results obtained are computed for both bagging and stacking using tenfold cross-validation. This method not only enhances the reliability of the model’s performance estimates but also aids in reducing overfitting by validating the model on multiple data subsets.

The logistic regression method is used for stacking in the classification process. In contrast to bagging, stacking increases the final forecast’s interpretability by confirming each prediction. The procedure may be divided into two parts: first, baseline models are used to forecast test dataset results, and then, a meta-classifier is used to create new predictions by using all of the baseline models’ predictions as input51,52,53.

An EML technique called “boosting” is used to evaluate the performance of a group of weak classifiers and turn them into strong classifiers. This approach was first created for classification when a predictor’s average accuracy was measured.

Boosting deals with the sequential learning of the predictors is used in the EML process where each classifier is trained using the entire data set, and subsequent classifiers are trained using the sets that performed the best in previous runs. To create a powerful classifier by linearly combining weak classifiers, the XGB classifier was chosen, which is recognized as the most popular boosting technique50.

Dataset collection and performance evaluation

Breast US images are in grayscale and the BUSI dataset, also it provides the ground truth of lesion considered binary mask, where the shape and the size of the breast lesion is given. Figure 1 illustrates samples of the original scanned images and the ROI and its binary mask. The features \({ }y_{1} ,y_{2,} y_{3} ,y_{4,} y_{{5,{ }}}\) and \({ }y_{6}\) are computed for the entire image database: benign 487, malignant 210 images. The BUSI dataset includes one, two, or three masks for the same ROI; in this instance, only the larger mask was retained. Figure 3 shows a graph for each HF obtained with Eq. (16). The resulting values for the benign and malignant classifications are interpreted using the violin graph. The data was grouped around the median value and this type of graph was selected because it shows the mean (black line) and median (red line) values for each grouping.

Fig. 3
figure 3

Violin plot for each HF; (a) y1, (b) y2, (c) y3, (d) y4, (e) y5, (f) y6.

Full size image

The main objective of the binary classification method is to identify a model and the relationship between the input dataset, which includes HFs. Hence, at first, in this research, the confusion matrix is considered as one of the common performance indicators for determining the model prediction. In addition, in terms of accuracy, F1-score, Matthews correlation coefficient and area under the curve, the performance of classification was evaluated, and computed from the basic confusion matrices \(\left[ {\begin{array}{*{20}c} {TP} & {FP} \\ {FN} & {TN} \\ \end{array} } \right]\), where TP and TN are the numbers of samples whose prediction results in accordance with the observation class. FP and FN are the numbers of the samples predicted to be the opposite class.

The MCC is a standard measure for analyse of imbalanced data. It generates a value in the [− 1; + 1] a high value for all the four basic rates of the CM and low value otherwise. Imbalanced classes can lead to misleading accuracy metrics; using MCC, a more comprehensive view of how well a classifier is performing across both classes can be performed. ACC, AUC and F1-score can range from 0 (worst result) to 1 (perfect result), ACC and F1-score the most used metrics in evaluation, that express the ratio of TP and TN over all the elements and the mean of precision and recall. AUC gives information about precision or negative predictive value obtained by a classifier54.

$$ACC = \frac{TP + TN}{{TP + TN + FP + FN}}$$
(18)
$$AUC = 1 - \frac{1}{2}\left( {\frac{FP}{{FP + TN}} + \frac{FN}{{FN + TP}}} \right)$$
(19)
$$F1 - score = \frac{{2{*}precision{*}recall}}{precision + recall}$$
(20)
$$precision = \frac{TP}{{TP + FP}}$$
(21)
$$recall = \frac{TP}{{TP + FN}}$$
(22)
$$MCC = \frac{TP \cdot TN - FP \cdot FN}{{\sqrt {\left( {TP + FP} \right) \cdot \left( {TP + FN} \right) \cdot \left( {TN + FP} \right) \cdot \left( {TN + FN} \right)} }}$$
(23)

The BUSI free and public image database was used for this study. The ethics committee of the Baheya Hospital for Early Detection & Treatment of Women’s Cancer, Cairo, Egypt, approved all experimental protocols, and patient protection is discussed in chapter “2.4. Ethical Considerations” of the reference38. In this context, all methods were carried out in accordance with relevant guidelines and regulations, and all experimental protocols were approved.