Optical soliton solutions, dynamical and sensitivity analysis for fractional perturbed Gerdjikov–Ivanov equation

Abstract

This work constructs the distinct type of solitons solutions to the nonlinear Perturbed Gerdjikov-Ivanov (PGI) equation with Atangana’s derivative. It interprets its optical soliton solutions in the existence of high-order dispersion. For this purpose, a wave transformation is applied to convert the fractional PGI Equation to a non-linear ODE. Solitons solutions and further solutions of the obtained model are sorted out by using the Sardar sub-equation (SSE) method and the generalized unified method. The different types of soliton solutions such as bright, kink, periodic, and exact dark solitons are achieved. Dynamical and sensitivity analysis is carried out for the obtained results. 3D, 2D, and contour graphs of attained solutions are presented for elaboration. Nonlinear model have played an important role in optic fibber, optical communications and optical sensing.

Introduction

An optical soliton is a self-reinforcing and self-sustaining wave packet that maintains its shape while propagating through a nonlinear medium. It was first observed in the context of nonlinear optics in the 1970s and has since been studied extensively due to its unique properties and potential applications¹. Chen et al.² provides an overview of the principles, fabrication techniques, and applications of FMF-LPFGs in mode division multiplexing optical communications and optical sensing. Optical solitons arise because of the balance between the dispersive and nonlinear effects in a medium. Dispersion causes different frequencies of light to travel at different speeds, leading to broadening of the pulse over time. However, non-linearity causes the pulse to self-focus, which counteracts the dispersion and allows the pulse to maintain its shape^3,4,5. Eslamifar et al.⁶ explore that copper nanoparticles exhibit strong nonlinear absorption and refraction, with optical nonlinearities, highlighting their potential for nonlinear optics applications.

Numerous efficient approaches have been employed to attain soliton solutions of nonlinear partial differential equations. The breather, one-soliton, two-soliton, lump, and interaction soliton solutions of the (2+1)-dimensional Kadomtsev-Petviashvili-Sawada-Kotera-Ramani equation have been examined by utilizing the Hirota bilinear method⁷. The one-soliton, two-soliton, lump, and traveling wave solutions of the (3+1)-dimensional Kadomtsev-Petviashvili-Boussinesq-like equation have also been investigated by using the Hirota method⁸. Exact solutions of the fractional Hirota-Satsuma coupled KdV equation were explored by utilizing the logistic function method, accompanied by a dynamical analysis⁹. Lump and novel interaction solutions, along with a chaotic analysis, were attained for the (3+1)-dimensional generalized shallow water-like equation¹⁰. Dark, bright, combined dark-bright, and singular periodic soliton solutions of the (3+1)-dimensional nonlinear Schrödinger equation were achieved by using the extended sinh-Gordon equation expansion technique¹¹. Furthermore, the extended auxiliary equation scheme and the extended Kudryashov technnique were applied to the nonlinear Schrödinger equation to derive dark, singular, and periodic solitary wave solutions¹². Chirped optical soliton solutions of the nonlinear Schrödinger equation with nonlinear chromatic dispersion and a quadratic-cubic refractive index law were attained via the new extended auxiliary equation technique¹³. Solitary wave solutions of the integrable Kuralay equation were studied by utilizing both the modified F-expansion method and the new extended auxiliary equation method¹⁴. AL-Taie and Salim Jasim attained the bright and dark soliton solutions of the nonlinear Schrödinger equation through the application of the split-step Fourier method¹⁵.

Recently researchers have applied the SSE method and the generalized unified method on many nonlinear model. Optical soliton solution of nonlinear fractional Schrödinger equation was attained by utilizing the SSE method¹⁶. In¹⁷, the optical solitary wave solution of the perturbed Fokas-Lenells equation was attained by using the SSE method. The ion-acoustic waves of the nonlinear plasma fluid model were attained in¹⁸. Traveling waves solution of fractional Schrödinger equation by employing generalized Unified method¹⁹. Asjad et al.²⁰ achieved the traveling wave solutions to the Boussinesq equation via SSE technique. The exact solution of the Kundu-Mukherjee-Naskar equation was attained in²¹. Bifurcation analysis in optical fibers involves studying how the qualitative behavior of optical solitons and wave propagation changes as system parameters, such as dispersion, nonlinearity, and input power, are varied. These changes can lead to different dynamical regimes, including the formation of stable or unstable solitons, periodic oscillations, or chaotic behavior. Common bifurcations in optical systems include pitchfork, Hopf, and saddle-node bifurcations, which determine the stability and transition of solutions. For example, in a fiber with varying dispersion, a critical bifurcation point may cause a transition from bright to dark solitons. Such analysis is essential for understanding pulse stability, soliton interactions, and the onset of optical instabilities, enabling better control of optical communication systems and nonlinear devices^22,23,24.

Nonlinear partial differential equations(NLPDEs) are very useful for their omnivorous portions in physical systems, fluid dynamics, quantum mechanics, control theory, nonlinear optics, plasma physics, and other numerous fields of science and engineering^{25,26,27,28,29}. However, an identical and worthy example of NLPDEs is the PGI equation^{30,31,32,33,34,35}.

$$\begin{aligned} i \psi _t+a_1\psi _{xx}+a_2\mid \psi \mid ^4\psi +i a_3\psi ^2\psi _x^*-i(a_4\psi _x+a_5(\mid \psi \mid ^2\psi )_x +a_6(\mid \psi \mid ^2)_x\psi )=0. \end{aligned}$$

(1)

The Eq. (1) plays an important role in optical fibers. Nonetheless this research goals to investigate the PGI Eq. (1) with Atangana’s conformable derivative³⁶ i.e.

$$\begin{aligned} i D_t^\alpha \psi +a_1 D_z^{2\alpha }\psi +a_2 \mid \psi \mid ^4\psi +i a_3\psi ^2 D_z^\alpha \psi ^*-i(a_4 D_z^\alpha \psi +a_5 D_z^\alpha (\mid \psi \mid ^2\psi )+a_6 D_z^\alpha (\mid \psi \mid ^2)\psi )=0. \end{aligned}$$

(2)

The different kinds of fractional derivatives have been used in the past, such as Caputo fractional³⁸, Reimann-Liouville³⁷, conformable fractional derivative³⁹, beta derivative⁴⁰, truncated M-fractional derivative^41,42, Atangana-Baleanu fractional derivative in Caputo sense^43,44. Atangana et al.⁴⁵ awarded few of the latest properties to the conformable derivative. Many applications of Atangana’s conformable derivatives have been used previously. For example, Modifled Korteweg de-Vries system⁴⁶, Schrodinger equation⁴⁷, Zakharov-Kuznetsov equation⁴⁸, Caudrey-Dodd-Gibbon equation⁴⁹.

The PGI equation has been observed by many efficient methods. For instance, Biswas and Alqahtani³⁰ draw out the soliton solutions of the PGI equation by utilizing the Semi-Inverse technique. By applying the Sine-Gorden technique, the optical solitons solution of the PGI equation³² were obtained. Similarly, by applying the Sine-Cosine formula technique, the dark and bright solitons solution of the PGI equation is achieved³³. The study investigates the gap in existing literature on the PGI equation by exploring new soliton solutions incorporating Atangana’s conformable derivative, using the Sardar sub-equation method and generalized unified method. While distinct technique like the Semi-Inverse technique and Sine-Gordon method have been applied, the effects of non-locality and higher-order dispersion on soliton dynamics remain under explored. This research contributes novel insights into these effects, advancing both theoretical understanding and potential applications in optical communication systems.

The primary contributions of this study are as follows:

• It introduces a new class of soliton solutions to the PGI equation, incorporating Atangana’s conformable derivative, by employing the Sardar sub-equation method and generalized unified method.

• A novel traveling wave transformation is applied, which distinguishes this study from previous works, such as⁵⁰, where different transformations were used.

• It provides new insights into the effects of non-locality and high-order dispersion on soliton dynamics, offering a deeper understanding of how these factors influence soliton behavior. This research not only extends theoretical knowledge of the PGI equation but also paves the way for potential future applications in optical communication systems.

The remaining paper is divided into different sections. In “Atangana’s-conformable derivative”, we discussed the fractional derivative. In “Methods and their objective”, we mentioned the description of methods. In “ Analysis of equation”, we analyze the equation with soliton solutions. In “ Graphically discussion” discussed the graphical representation. In “ Dynamical analysis”, the dynamical analysis is discussed in details. At the end, the conclusion is presented in “Conclusion”.

Atangana’s-conformable derivative

Atangana’s conformal derivative is a novel extension of the traditional derivative, purposed to capture non-local effects and long-range interactions in systems showing memory or scaling behaviors, making it especially important in fractional calculus and mathematical physics. Unlike classical derivatives, which concentrated on local changes at a single point, and fractional derivatives such as Riemann–Liouville or Caputo derivatives, which generalize the idea of differentiation to non-integer orders, Atangana’s conformal derivative contain a flexible kernel function that allows for more complex modeling of physical systems with long-range dependencies. This non-locality and the utilize of a power-law term for interaction distances make it appropriate for depicting phenomena like anomalous diffusion and complex dynamical systems, presenting a versatile alternative to more traditional derivative idea that are limited in modeling systems with memory or hereditary effects.

Definition 1

Let $f(\varrho )$ be a function defined for all non-negative $\varrho$. The Atangana-conformable derivative of $f(\varrho )$³⁶ as given below,

$$\begin{aligned} D_t^\alpha \{f(\varrho )\}=\lim _{\epsilon \rightarrow 0}{\frac{f\left( \varrho +\epsilon \left( \varrho +\frac{1}{\Gamma (\alpha )}\right) ^{1-\alpha }\right) - f(\varrho )}{\epsilon }}. \end{aligned}$$

(3)

Properties

Let f and g be any two function, $f\ne 0$, and $\alpha \in (0;1]$ then

1: $D_\varrho ^\alpha \{af(\varrho )+bg(\varrho )\}=aD_\varrho ^\alpha f(\varrho )+bD_\varrho ^\alpha g(\varrho )$,

where $a,b\in \Re$

2: $D_\varrho ^\alpha \{f(\varrho ).g(\varrho )\}=f(\varrho )D_\varrho ^\alpha \{g(\varrho )\}+g(\varrho )D_\varrho ^\alpha \{f(\varrho )\}$,

3: $D_\varrho ^\alpha (\frac{f(\varrho )}{g(\varrho )})=\frac{g(\varrho ) D_\varrho ^\alpha \{f(\varrho )\}-f(\varrho ) D_\varrho ^\alpha \{g(\varrho )\}}{g(\varrho )^2}$,

4: $D_\varrho ^\alpha \{f(\varrho )\}=(\varrho +\frac{1}{\Gamma (\alpha )})^{1-\alpha }\frac{df(\varrho )}{d\varrho }$,

5: $D_\varrho ^\alpha f(\eta )=I\frac{df(\eta )}{d\eta }$, Here, I is constant and $\eta =\frac{I}{\alpha }(\varrho +\frac{1}{\Gamma (\alpha )})^\alpha .$

Methods and their objective

In this section, we explore the basic steps of the SSE method and the generalized uniform method. Consider the following NPDE,

$$\begin{aligned} \Psi \left( \zeta , \frac{\partial \zeta }{\partial x}, \frac{\partial \zeta }{\partial t},...\right) =0. \end{aligned}$$

(4)

Using the transformation,

$$\begin{aligned} \zeta (x,t)=V(\eta ),~~~ \text {where},~~ \eta =x+vt. \end{aligned}$$

(5)

The Eq. (4) become,

$$\begin{aligned} O(V, V^{'}, V^{''}... )=0. \end{aligned}$$

(6)

Sardar sub-equation method

The main steps of this method²⁰ are given below,

Step:1

solution of the above equation is,

$$\begin{aligned} V(\eta )=\sum _{n=0}^{N}\lambda _n\phi (\eta )^{n}, \end{aligned}$$

(7)

where, $\lambda _n$, $n=1,2,...,n$ are non-zero parameters to be found later.

Step:2 We apply the homogeneous balance technique to achieve the value of N in Eq. (7).

$$\begin{aligned} \left( \frac{d\phi (\eta )}{d\eta }\right) ^2=a_0+a_2\phi (\eta )^2+\phi (\eta )^4. \end{aligned}$$

(8)

The solution of the above equation is given below,

Family 1: If $a_2>0$ and $a_0=0$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _1(\eta )=\pm \sqrt{-pqa_2}{{\,\textrm{sech}\,}}_{pq}(\sqrt{a_2}\eta ),\\ \phi _2(\eta )=\pm \sqrt{pqa_2}{{\,\textrm{csch}\,}}_{pq}(\sqrt{a_2}\eta ),\\ \end{array}\right. } \end{aligned}$$

(9)

where, ${{\,\textrm{sech}\,}}_{pq}(\eta )=\frac{2}{pe^{\eta }+qe^{-\eta }}$, ${{\,\textrm{csch}\,}}_{pq}(\eta )=\frac{2}{pe^{\eta }-qe^{-\eta }}$.

Family 2: If $a_2<0$ and $a_0=0$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _3(\eta )=\pm \sqrt{-pqa_2}\sec _{pq}(\sqrt{-a_2}\eta ),\\ \phi _4(\eta )=\pm \sqrt{-pqa_2}\csc _{pq}(\sqrt{-a_2}\eta ),\\ \end{array}\right. } \end{aligned}$$

(10)

where, $\sec _{pq}(\eta )=\frac{2}{pe^{i\eta }+qe^{-i\eta }}$, $\csc _{pq}(\eta )=\frac{2i}{pe^{i\eta }-qe^{-i\eta }}$.

Family 3: If $a_2<0$ and $a_0=\frac{a^2_2}{4}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _5(\eta )=\pm \sqrt{\frac{-a_2}{2}}\tanh _{pq}\left( \sqrt{-\frac{a_2}{2}}\eta \right) ,\\ \phi _6(\eta )=\pm \sqrt{\frac{-a_2}{2}}\coth _{pq}\left( \sqrt{-\frac{a_2}{2}}\eta \right) ,\\ \phi _7(\eta )=\pm \sqrt{\frac{-a_2}{2}}\left( \tanh _{pq}(\sqrt{-2a_2}\eta )\pm i\sqrt{pq}{{\,\textrm{sech}\,}}_{pq}(\sqrt{-2a_2}\eta )\right) ,\\ \phi _8(\eta )=\pm \sqrt{\frac{-a_2}{2}}\left( \coth _{pq}(\sqrt{-2a_2}\eta )\pm \sqrt{pq}{{\,\textrm{csch}\,}}_{pq}(\sqrt{-2a_2}\eta )\right) ,\\ \phi _9(\eta )=\pm \sqrt{\frac{-a_2}{8}}\left( \coth _{pq}\left( \sqrt{-\frac{a_2}{8}}\eta \right) +\tanh _{pq}\left( \sqrt{\frac{-a_2}{8}}\eta \right) \right) , \end{array}\right. } \end{aligned}$$

(11)

where, $\tanh _{pq}(\eta )=\frac{pe^{\eta }-qe^{-\eta }}{pe^{\eta }+qe^{-\eta }}$,  $\coth _{pq}(\eta )=\frac{pe^{\eta }+qe^{-\eta }}{pe^{\eta }-qe^{-\eta }}.$

Family 4: If $a_2>0$ and $a_0=\frac{a^2_2}{4}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _{10}(\eta )=\pm \sqrt{\frac{a_2}{2}}\tan _{pq}\left( \sqrt{\frac{a_2}{2}}\eta \right) ,\\ \phi _{11}(\eta )=\pm \sqrt{\frac{a_2}{2}}\cot _{pq}\left( \sqrt{\frac{a_2}{2}}\eta \right) ,\\ \phi _{12}(\eta )=\pm \sqrt{\frac{a_2}{2}}\left( \tan _{pq}(\sqrt{2a_2}\eta )\pm \sqrt{pq}\sec _{pq}(\sqrt{2a_2}\eta )\right) ,\\ \phi _{13}(\eta )=\pm \sqrt{\frac{a_2}{2}}\left( \cot _{pq}(\sqrt{2a_2}\eta )\pm \sqrt{pq}\csc _{pq}(\sqrt{2a_2}\eta )\right) ,\\ \phi _{14}(\eta )=\pm \sqrt{\frac{a_2}{8}}\left( \tan _{pq}\left( \sqrt{\frac{a_2}{8}}\eta \right) +\cot _{pq}\left( \sqrt{\frac{a_2}{8}}\eta \right) \right) , \end{array}\right. } \end{aligned}$$

(12)

$\tan _{pq}(\eta )=i\frac{pe^{i\eta }-qe^{-i\eta }}{pe^{\eta }+qe^{-i\eta }}$,  $\cot _{pq}(\eta )=i\frac{pe^{i\eta } +qe^{-i\eta }}{pe^{i\eta }-qe^{-i\eta }},$

where p and q are known parameters.

Step:3

Putting Eq. (7) into Eq. (6) with Eq. (8), then we get the system of algebraic equations. The system is solved by using Mathematica software, and then the solution of Eq. (7) is substituted into Eq. (7) by utilizing Eq. (5). Finally, the solution of Eq. (4) is attained.

Generalized unified method

The main steps of this method²¹ are given below,

Step:1: Consider the equation,

$$\begin{aligned} V(\eta )=a_0+\sum _{n=1}^{N}a_n\phi (\eta )^{n}+b_n\phi (\eta )^{-n}. \end{aligned}$$

(13)

In which $a_n$, $b_n$ are unknown and determined later.

$$\begin{aligned} \phi ^{'}(\eta )=\phi ^{2}(\eta )-\mu ^2. \end{aligned}$$

(14)

Here, $\mu$ is the unknown parameter.

The general solution of Eq. (14) as follows:

$$\begin{aligned} \phi (\eta )= {\left\{ \begin{array}{ll} \phi _1=\frac{\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}, \\ \phi _2=\frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))},\\ \phi _3=\frac{\mu (-A_1+e^{-2\mu (\eta +\eta _0)})}{A_1+e^{-2\mu (\eta +\eta _0)}},\\ \phi _4=\frac{-\mu (-A_1+e^{2\mu (\eta +\eta _0)})}{A_1+e^{2\mu (\eta +\eta _0)}},\\ \phi _5=-\frac{1}{\eta +\eta _0}. \end{array}\right. } \end{aligned}$$

(15)

where $A_1, B_1$ and $C_1$ are the unknown parameters.

Step:2 We apply the homogeneous balance technique to attain the value of N on Eq. (13).

Step:3 Substituting Eq. (13) with Eq. (14) into Eq. (6) and obtained the results in the form of an algebraic system, which solving it by Mathematica software gives the optical solitons of the Eq. (3).

Analysis of equation

To achieve the optical solitons solutions of the PGI Equation with the Atangana conformable derivative, we adopt the following wave transformation,

$$\begin{aligned} \psi (z,t)=F(\eta )e^{(i\xi )}, \end{aligned}$$

(16)

where,

$$\begin{aligned} \eta =\frac{K}{\alpha }\left[ \left( z+\frac{1}{\Gamma (\alpha )}\right) ^\alpha +\upsilon \left( t+\frac{1}{\Gamma (\alpha )}\right) ^\alpha \right] , \xi =-\frac{\kappa }{\alpha }\left[ \left( z+\frac{1}{\Gamma (\alpha )}\right) ^\alpha +\omega \left( t+\frac{1}{\Gamma (\alpha )}\right) ^\alpha \right] , \end{aligned}$$

(17)

where $\upsilon$ indicates the velocity, $\kappa$ represents the wave number, $\phi$ is the phase component, $\omega$ represents the frequency, and K is the width of the soliton. Substituting the wave transformation Eq. (16) and Eq. (17) into Eq. (2) and separates the real and imaginary parts. The real part is

$$\begin{aligned} \alpha _1K^2\frac{d^2F(\eta )}{d\eta ^2}+(\kappa \omega -\alpha _1\kappa ^2-\alpha _4\kappa )F(\eta )-(\alpha _3\kappa +\alpha _5\kappa )F^3(\eta )+\alpha _2F^5(\eta )=0. \end{aligned}$$

(18)

and the imaginary part is

$$\begin{aligned} (\upsilon -2\alpha _1\kappa -\alpha _4)+(\alpha _3-3\alpha _5-2\alpha _6)F^2(\eta )=0. \end{aligned}$$

(19)

From Eq. (19)

$$\begin{aligned} \upsilon =(2\alpha _1\kappa +\alpha _4), \alpha _3=3\alpha _5+2\alpha _6. \end{aligned}$$

(20)

Substituting Eq. (20) into Eq. (18). After this setting $F(\eta )=\sqrt{V(\eta )}$ into Eq. (18), then we have

$$\begin{aligned} \begin{aligned}&\alpha _1K^2\left( \frac{dV(\eta )}{d\eta }\right) ^2-2\alpha _1K^2V(\eta )\frac{d^2V(\eta )}{d\eta ^2}-4(\kappa \omega -\alpha _1\kappa ^2-\alpha _4\kappa )V(\eta )^2\\ &+8(2\alpha _5\kappa +\alpha _6\kappa )V(\eta )^3-4\alpha _2V(\eta )^4=0. \end{aligned} \end{aligned}$$

(21)

Application of sub-Sardar equation method

Applying the balance technique on terms $(\frac{dV(\eta )}{d\eta })^2$ with $V(\eta )^4$ of Eq. (21), then we get $N=1$. Putting this value of N into Eq. (7).

$$\begin{aligned} V(\eta )=\lambda _0+\lambda _1\phi (\eta ). \end{aligned}$$

(22)

Substituting Eq. (22) into Eq. (21), then we get following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi (\eta )^{0}: & \quad a_0 \alpha _1 K^2 \lambda _1^2 - 4 \alpha _1 \kappa ^2 \lambda _0^2 + 16 \alpha _5 \kappa \lambda _0^3 + 8 \alpha _6 \kappa \lambda _0^3 - 4 \alpha _4 \kappa \lambda _0^2 \\ & \quad - 4 \alpha _2 \lambda _0^4 + \kappa \lambda _0^2 \omega =0, \\[10pt] \phi (\eta )^{1}: & \quad -2 a_2 \alpha _1 K^2 \lambda _1 \lambda _0 - 8 \alpha _1 \kappa ^2 \lambda _1 \lambda _0 + 48 \alpha _5 \kappa \lambda _1 \lambda _0^2 \\ & \quad + 24 \alpha _6 \kappa \lambda _1 \lambda _0^2 - 8 \alpha _4 \kappa \lambda _1 \lambda _0 - 16 \alpha _2 \lambda _1 \lambda _0^3 + 8 \kappa \lambda _1 \lambda _0 \omega =0, \\[10pt] \phi (\eta )^{2}: & \quad -a_2 \alpha _1 K^2 \lambda _1^2 - 4 \alpha _1 \kappa ^2 \lambda _1^2 - 4 \alpha _4 \kappa \lambda _1^2 + 48 \alpha _5 \kappa \lambda _0 \lambda _1^2 \\ & \quad + 24 \alpha _6 \kappa \lambda _0 \lambda _1^2 - 24 \alpha _2 \lambda _0^2 \lambda _1^2 + 4 \kappa \lambda _1^2 \omega =0, \\[10pt] \phi (\eta )^{3}: & \quad 16 \alpha _5 \kappa \lambda _1^3 + 8 \alpha _6 \kappa \lambda _1^3 - 4 \alpha _1 K^2 \lambda _0 \lambda _1 - 16 \alpha _2 \lambda _0 \lambda _1^3=0, \\[10pt] \phi (\eta )^{4}: & \quad -3 \alpha _1 K^2 \lambda _1^2 - 4 \alpha _2 \lambda _1^4=0. \end{array}\right. } \end{aligned}$$

(23)

Solving above system, we get

$$\begin{aligned} \small \begin{aligned} \omega =&\frac{256\alpha _1 \alpha _2^3 \lambda _0^4 + 192\alpha _4 \alpha _2^2 \lambda _0^3 (2\alpha _5 + \alpha _6) + (240\alpha _2^2 \lambda _0^4 - 27a_0 \alpha _2^1 K^4)(2\alpha _5 + \alpha _6)^2}{192\alpha _2^2 \lambda _0^3 (2\alpha _5 + \alpha _6)},\\ &\lambda _0=\lambda _0,\lambda _1=\pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}},\kappa =\frac{4 \alpha _2 \lambda _0}{3 \left( 2 \alpha _5+\alpha _6\right) }, a_2=\frac{9 a_0 \alpha _1^2 K^4+16 \alpha _2^2 \lambda _0^4}{12 \alpha _1 \alpha _2 K^2 \lambda _0^2}. \end{aligned} \end{aligned}$$

(24)

Eq. (22) become,

$$\begin{aligned} V(\eta )=\lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \phi (\eta ). \end{aligned}$$

(25)

Solution of Eq. (2) are written as:

Family 1: If $a_2>0$ and $a_0=0$,

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{-pqa_2}{{\,\textrm{sech}\,}}_{pq}(\sqrt{a_2}\eta )\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(26)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{-pqa_2}{{\,\textrm{csch}\,}}_{pq}(\sqrt{a_2}\eta )\right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(27)

Where, $\eta =\frac{k}{\alpha }[(z+\frac{1}{\Gamma (\alpha )})^\alpha +\upsilon (t+\frac{1}{\Gamma (\alpha )})^\alpha ], \xi =-\frac{\kappa }{\alpha }[(z+\frac{1}{\Gamma (\alpha )})^\alpha +\omega (t+\frac{1}{\Gamma (\alpha )})^\alpha ].$

Family 2: If $a_2<0$ and $a_0=0$,

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{-pqa_2}\sec _{pq}(\sqrt{-a_2}\eta )\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(28)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{-pqa_2}\csc _{pq}(\sqrt{-a_2}\eta )\right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(29)

Family 3: If $a_2<0$ and $a_0=\frac{a^2_2}{4}$,

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{-a_2}{2}}\tanh _{pq}\left( \sqrt{-\frac{a_2}{2}}\eta \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(30)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{-a_2}{2}}\coth _{pq}\left( \sqrt{-\frac{a_2}{2}}\eta \right) )\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(31)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{-a_2}{2}}\left( \tanh _{pq}(\sqrt{-2a_2}\eta )\pm i \sqrt{pq}{{\,\textrm{sech}\,}}_{pq}(\sqrt{-2a_2}\eta )\right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(32)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{-a_2}{2}}\left( \coth _{pq}(\sqrt{-2a_2}\eta )\pm \sqrt{pq}{{\,\textrm{csch}\,}}_{pq}(\sqrt{-2a_2}\eta )\right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(33)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{-a_2}{8}}\left( \coth _{pq}\left( \sqrt{-\frac{a_2}{8}}\eta \right) +\tanh _{pq}\left( \sqrt{\frac{-b_2}{8}}\eta \right) \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(34)

Family 4: If $a_2>0$ and $a_0=\frac{a^2_2}{4}$,

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{a_2}{2}}\tan _{pq}\left( \sqrt{\frac{a_2}{2}}\eta \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(35)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{a_2}{2}}\cot _{pq}\left( \sqrt{\frac{a_2}{2}}\eta \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(36)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{a_2}{8}}\left( \tan _{pq}\left( \sqrt{2a_2}\eta \right) \pm \sec _{pq}\left( \sqrt{2a_2}\eta \right) \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(37)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{a_2}{8}}\left( \cot _{pq}\left( \sqrt{2a_2}\eta \right) \pm \csc _{pq}\left( \sqrt{2a_2}\eta \right) \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(38)

$$\begin{aligned} & \psi (z,t)=\left[ \lambda _0+\left( \pm \frac{i \sqrt{3} \sqrt{\alpha _1} K}{2 \sqrt{\alpha _2}}\right) \left( \pm \sqrt{\frac{a_2}{8}}\left( \tan _{pq}\left( \sqrt{\frac{a_2}{8}}\eta \right) +\cot _{pq}\left( \sqrt{\frac{a_2}{8}}\eta \right) \right) \right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(39)

Application of generalized unified method

Applying the balance technique on Eq. (21), then we get $N=1$. Putting this value of N into Eq. (7).

$$\begin{aligned} V(\eta )=a_0+a_1\phi (\eta )+b_1\phi (\eta )^{-1}. \end{aligned}$$

(40)

Putting Eq. (40) into Eq. (21), then we get following system

$$\begin{aligned} \phi (\eta )^{0}:&\quad -4 a_0^2 \alpha _1 \kappa ^2 + a_1^2 \alpha _1 K^2 \mu ^4 - 4 a_0^2 \alpha _4 \kappa + 16 a_0^3 \alpha _5 \kappa + 8 a_0^3 \alpha _6 \kappa - 4 a_0^4 \alpha _2 \\&\quad - 8 a_1 \alpha _1 b_1 \kappa ^2 + 12 a_1 \alpha _1 b_1 K^2 \mu ^2 - 8 a_1 \alpha _4 b_1 \kappa + 96 a_0 a_1 \alpha _5 b_1 \kappa + 48 a_0 a_1 \alpha _6 b_1 \kappa \\&\quad - 24 a_1^2 \alpha _2 b_1^2 - 48 a_0^2 a_1 \alpha _2 b_1 + 8 a_1 b_1 \kappa \omega + 4 a_0^2 \kappa \omega + \alpha _1 b_1^2 K^2, \\ \phi (\eta )^{1}:&\quad -8 a_1 \alpha _1 a_0 \kappa ^2 + 4 a_1 \alpha _1 a_0 K^2 \mu ^2 + 48 a_1 \alpha _5 a_0^2 \kappa + 24 a_1 \alpha _6 a_0^2 \kappa - 8 a_1 \alpha _4 a_0 \kappa \\&\quad - 16 a_1 \alpha _2 a_0^3 + 48 a_1^2 \alpha _5 b_1 \kappa + 24 a_1^2 \alpha _6 b_1 \kappa - 48 a_1^2 \alpha _2 a_0 b_1 + 8 a_1 a_0 \kappa \omega =0, \\ \phi (\eta )^{2}:&\quad -4 \alpha _1 a_1^2 \kappa ^2 + 2 \alpha _1 a_1^2 K^2 \mu ^2 - 4 \alpha _4 a_1^2 \kappa + 48 a_0 \alpha _5 a_1^2 \kappa + 24 a_0 \alpha _6 a_1^2 \kappa \\&\quad - 24 a_0^2 \alpha _2 a_1^2 - 6 \alpha _1 a_1 b_1 K^2 - 16 \alpha _2 a_1^3 b_1 + 4 a_1^2 \kappa \omega =0, \\ \phi (\eta )^{3}:&\quad 16 \alpha _5 a_1^3 \kappa + 8 \alpha _6 a_1^3 \kappa - 4 a_0 \alpha _1 a_1 K^2 - 16 a_0 \alpha _2 a_1^3=0, \\ \phi (\eta )^{4}:&\quad -3 \alpha _1 a_1^2 K^2 - 4 \alpha _2 a_1^4=0, \\ \phi (\eta )^{-1}:&\quad -8 \alpha _1 a_0 b_1 \kappa ^2 + 4 \alpha _1 a_0 b_1 K^2 \mu ^2 + 48 \alpha _5 a_0^2 b_1 \kappa + 24 \alpha _6 a_0^2 b_1 \kappa - 8 \alpha _4 a_0 b_1 \kappa \\&\quad + 48 a_1 \alpha _5 b_1^2 \kappa + 24 a_1 \alpha _6 b_1^2 \kappa - 16 \alpha _2 a_0^3 b_1 - 48 a_1 \alpha _2 a_0 b_1^2 + 8 a_0 b_1 \kappa \omega =0, \\ \phi (\eta )^{-2}:&\quad -6 a_1 \alpha _1 b_1 K^2 \mu ^4 + 48 a_0 \alpha _5 b_1^2 \kappa + 24 a_0 \alpha _6 b_1^2 \kappa - 16 a_1 \alpha _2 b_1^3 - 24 a_0^2 \alpha _2 b_1^2 \\&\quad - 4 \alpha _1 b_1^2 \kappa ^2 + 2 \alpha _1 b_1^2 K^2 \mu ^2 - 4 \alpha _4 b_1^2 \kappa + 4 b_1^2 \kappa \omega =0, \\ \phi (\eta )^{-3}:&\quad -4 a_0 \alpha _1 b_1 K^2 \mu ^4 - 16 a_0 \alpha _2 b_1^3 + 16 \alpha _5 b_1^3 \kappa + 8 \alpha _6 b_1^3 \kappa =0, \\ \phi (\eta )^{-4}:&\quad -3 \alpha _1 b_1^2 K^2 \mu ^4 - 4 \alpha _2 b_1^4=0. \end{aligned}$$

Solving the above system, then we get

Set 1:

$$\begin{aligned} \begin{aligned}&\omega =\frac{1}{12} \left( -2 \alpha _5-\alpha _6\right) \left( \frac{144 \alpha _5 a_0}{2 \alpha _5+\alpha _6}+\frac{72 \alpha _6 a_0}{2 \alpha _5+\alpha _6}-\frac{16 \alpha _1 \alpha _2 a_0}{\left( 2 \alpha _5+\alpha _6\right) ^2}-60 a_0-\frac{12 \alpha _4}{2 \alpha _5+\alpha _6}\right) ,\\ &a_0=a_0, a_1=0,b_1=\pm a_0 \mu ,\kappa =\frac{4 a_0 \alpha _2}{3 \left( 2 \alpha _5+\alpha _6\right) }, K=\frac{2 a_0 \sqrt{-\alpha _2}}{\sqrt{3} \sqrt{\alpha _1} \mu }. \end{aligned} \end{aligned}$$

(41)

Solutions for Eq. (2) are obtain as follows,

$$\begin{aligned} \begin{aligned} \psi (z,t)=\left[ a_0+(\pm a_0 \mu )\left( \frac{\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}\right) ^{-1}\right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned} \end{aligned}$$

(42)

where, $\eta =\frac{k}{\alpha }[(z+\frac{1}{\Gamma (\alpha )})^\alpha +\upsilon (t+\frac{1}{\Gamma (\alpha )})^\alpha ], \xi =-\frac{\kappa }{\alpha }[(z+\frac{1}{\Gamma (\alpha )})^\alpha +\omega (t+\frac{1}{\Gamma (\alpha )})^\alpha ].$

$$\begin{aligned} & \psi (z,t)=\left[ a_0+(\pm a_0 \mu )\left( \frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A \sinh (2\mu (\eta +\eta _0))}\right) ^{-1}\right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(43)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+(\pm a_0 \mu )\left( \frac{\mu (-A_1+e^{-2\mu (\eta +\eta _0)})}{A_1+e^{-2\mu (\eta +\eta _0)}}\right) ^{-1}\right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(44)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+(\pm a_0 \mu )\left( \frac{-\mu (-A_1+e^{2\mu (\eta +\eta _0)})}{A_1+e^{2\mu (\eta +\eta _0)}}\right) ^{-1}\right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(45)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+(\pm a_0 \mu )\left( -\frac{1}{\eta +\eta _0}\right) ^{-1}\right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(46)

Set 2:

$$\begin{aligned} \begin{aligned}&\omega =\frac{1}{12} \left( -2 \alpha _5-\alpha _6\right) \left( \frac{144 \alpha _5 a_0}{2 \alpha _5+\alpha _6}+\frac{72 \alpha _6 a_0}{2 \alpha _5+\alpha _6}-\frac{16 \alpha _1 \alpha _2 a_0}{\left( 2 \alpha _5+\alpha _6\right) ^2}-60 a_0-\frac{12 \alpha _4}{2 \alpha _5+\alpha _6}\right) ,\\ &a_0=a_0, a_1=\frac{a_0}{\mu },b_1=0,\kappa =\frac{4 a_0 \alpha _2}{3 \left( 2 \alpha _5+\alpha _6\right) },K=\pm \frac{2 a_0 \sqrt{-\alpha _2}}{\sqrt{3} \sqrt{\alpha _1} \mu }. \end{aligned} \end{aligned}$$

(47)

Solutions for Eq. (2) are obtain as follows,

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( \frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(48)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( \frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(49)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( \frac{\mu (-A_1+e^{-2\mu (\eta +\eta _0)})}{A_1+e^{-2\mu (\eta +\eta _0)}}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(50)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( \frac{-\mu (-A_1+e^{2\mu (\eta +\eta _0)})}{A_1+e^{2\mu (\eta +\eta _0)}}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(51)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( -\frac{1}{\eta +\eta _0}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(52)

Set 3:

$$\begin{aligned} \begin{aligned}&\omega =\frac{1}{12} \left( -2 \alpha _5-\alpha _6\right) \left( \frac{144 \alpha _5 a_0}{2 \alpha _5+\alpha _6}+\frac{72 \alpha _6 a_0}{2 \alpha _5+\alpha _6}-\frac{16 \alpha _1 \alpha _2 a_0}{\left( 2 \alpha _5+\alpha _6\right) ^2}-60 a_0-\frac{12 \alpha _4}{2 \alpha _5+\alpha _6}\right) ,\\ &a_0=a_0, a_1=-\frac{a_0}{\mu },b_1=0,\kappa =\frac{4 a_0 \alpha _2}{3 \left( 2 \alpha _5+\alpha _6\right) },K=\pm \frac{2 a_0 \sqrt{-\alpha _2}}{\sqrt{3} \sqrt{\alpha _1} \mu }. \end{aligned} \end{aligned}$$

(53)

Solutions for Eq. (2) are obtain as follows,

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( \frac{a_0}{\mu }\right) \left( \frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(54)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( -\frac{a_0}{\mu }\right) \left( \frac{-\mu \sqrt{A_1^2+(B_1+i C_1)^2}-A_1 \mu \cosh (2\mu (\eta +\eta _0))}{(B_1+i C_1)+A_1 \sinh (2\mu (\eta +\eta _0))}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(55)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( -\frac{a_0}{\mu }\right) \left( \frac{\mu (-A_1+e^{-2\mu (\eta +\eta _0)})}{A_1+e^{-2\mu (\eta +\eta _0)}}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(56)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( -\frac{a_0}{\mu }\right) \left( \frac{-\mu (-A_1+e^{2\mu (\eta +\eta _0)})}{A_1+e^{2\mu (\eta +\eta _0)}}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }, \end{aligned}$$

(57)

$$\begin{aligned} & \psi (z,t)=\left[ a_0+\left( -\frac{a_0}{\mu }\right) \left( -\frac{1}{\eta +\eta _0}\right) \right] ^{\frac{1}{2}}\times e^{i\xi }. \end{aligned}$$

(58)

Graphically discussion

In this section, we present the graphical discussion of the attained solutions to the PGI equation to gain deeper knowledge into the physical nature and dynamic behavior of the nonlinear optical model. The solutions were illustrated by allocating suitable values to the arbitrary constants by utilizing Mathematica 11. These visualizations serve to present the emergence of different types of optical solitons governed by the equation under study.

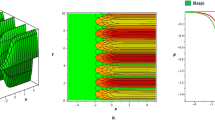
The Fig. 1 depict the graphical solutions of Eq. (26) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =-0.5, \alpha _5=0.1, a_0=0, \alpha _6=0.5, \lambda _0=-0.2, K=0.02, p=0.4, q=4$, presenting W-type soliton profiles for varying fractional parameters $\alpha$. The 2D and contour plots shows the characteristic multi-peaked“W” shape of these solitons and their evolution over time, while the 3D surface plots display how changes in $\alpha$ impact the soliton’s amplitude, width, and oscillatory behavior. W-type solitons are important in optical fiber because their multi-lobed structure makes the transmission of complex pulse shapes that keep stability over long distances despite dispersive and nonlinear effects. The inclusion of fractional dynamics, modeled by the parameter $\alpha$, presents memory and anomalous dispersion effects that can be leveraged to tailor pulse propagation, potentially improving the performance and resilience of optical communication systems.

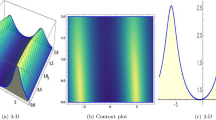
The Fig. 2 shows the bright optical soliton with parametric value $\alpha _1=-0.8, \alpha _2=0.04, \nu =0.5, \alpha _4=0.5, \alpha _5=0.1, a_0=0, \alpha _6=0.5, \lambda _0=2, K=0.02, p=1, q=0.1$. Fig. 2 shows distinct graphical visualizations of the solution $|\psi (z,t)|$ to the PGI equation, analyzing its behavior with respect to space z, time t, and the fractional parameter $\alpha$. Figure 2a, b depict 2D plots of the wave amplitude over space for distinct times and fractional orders, respectively, showing that the wave shape remains localized and stable over time but varies with $\alpha$. The 3D surface plots d–f shows how the solution evolves in both space and time for increasing values of $\alpha = 0.5, 0.8,$ and 1.0, respectively, exposing that higher fractional orders yield to more complex oscillatory patterns and increased wave activity. Bright optical solitons are stable, localized wave packets in optical fibers formed by a balance between anomalous dispersion and nonlinear effects. These solitons are crucial in optical communications and ultrafast pulse generation.

The Figs. 3, 4 and 5 represents the periodic optical soliton. Periodic optical solitons are repetitive, wave-like structures in optical fibers that result from a stable balance between nonlinearity and periodic modulation of dispersion or nonlinearity. Unlike isolated solitons, they exhibit periodic intensity peaks. These solitons have applications in fiber-optic communication and pulse train generation for mode-locked lasers. In each figure, subplots a, b shows 2D graphs indicating the amplitude $|\psi (z,t)|$ as a function of the spatial coordinate z at different time instants t and for distinct fractional parameters $\alpha$. These graphs show the periodic intensity peaks, a hallmark of periodic solitons, and present how the wave profiles evolve both temporally and with changes in fractional order. The contour plots c in each figure present a two-dimensional visualization of constant amplitude levels over the spatial-temporal plane, clearly emphasizing the periodic repetition of wave maxima and minima along both axes. Subplots d–f provide 3D surface plots for $\alpha =0.5, 0.8,$ and 1.0, respectively, highlighting the full spatiotemporal dynamics of the periodic solitons. These 3D visualizations shows how the fractional parameter $\alpha$ affect the shape, frequency, and amplitude modulation of the soliton trains. Increasing $\alpha$ typically results in more complex oscillatory patterns and finer wave structures.

Figure 6 indicates the graphical solution of Eq. (46) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =-0.5, \alpha _5=0.1, a_0=2, \alpha _6=0.5, \mu =-0.3,\eta _0 =-0.2$ illustrating the behavior of dark optical solitons. The 2D graphs display the amplitude $|\psi (z,t)|$ as a function of the spatial variable z for different times $t=0,1,2$ and varying fractional parameters $\alpha = 0.6, 0.8, 1.0$, respectively. These graphs shows localized intensity dips against a continuous-wave background, features of dark solitons. The contour plot c shows a spatial-temporal map of constant amplitude levels, highlighting the persistent dip structure throughout propagation. The 3D surface plots d–f shows the evolution of the dark soliton profile in space and time for fractional orders $\alpha = 0.5, 0.8,$ and 1.0. As $\alpha$ increases, the number of oscillatory wave patterns also increases, showing that fractional derivatives affect the complexity and modulation of the dark soliton structures. In this investigation, we compare the solutions attained through the methods described with those presented in⁵¹. The various types of soliton solutions are presented in Table 1, which shows the successful achievement of distinct soliton solutions.

Table 1 Comparison of soliton types and methods.

Fig. 1

Graphical solution of Eq. (26) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =-0.5, \alpha _5=0.1, a_0=0, \alpha _6=0.5, \lambda _0=-0.2, K=0.02, p=0.4, q=4$.

Fig. 2

Graphical solution of Eq. (28) with parameters $\alpha _1=-0.8, \alpha _2=0.04, \nu =0.5, \alpha _4=0.5, \alpha _5=0.1, a_0=0, \alpha _6=0.5, \lambda _0=2, K=0.02, p=1, q=0.1$.

Fig. 3

Graphical solution of Eq. (42) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5,\nu =0.2, \alpha _5=0.1, a_0=0.3, \alpha _6=0.5, a_0=0.2, A_1=0.1, B_1=0.2, C_1=0.3, \mu =0.2,\eta _0 =-0.2$.

Fig. 4

Graphical solution of Eq. (43) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =0.04, \alpha _5=0.1, a_0=0.3, \alpha _6=0.5, a_0=0.2, A_1=0.1, B_1=0.2, C_1=0.3, \mu =-0.2,\eta _0 =-0.2$.

Fig. 5

Graphical solution of Eq. (44) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =0.5, \alpha _5=0.1, a_0=0.2, \alpha _6=0.5, A_1=0.1, B_1=0.2, C_1=0.3, \mu =-0.2,\eta _0 =-0.2$.

Fig. 6

Graphical solution of Eq. (46) with parameters $\alpha _1=0.8, \alpha _2=0.4, \alpha _4=0.5, \nu =-0.5, \alpha _5=0.1, a_0=2, \alpha _6=0.5, \mu =-0.3,\eta _0 =-0.2$.

Dynamical analysis

In this section, we will discuss the dynamical behavior through bifurcation and sensitivity.

Bifurcation analysis

From (18), we can write as

$$\begin{aligned} F^{''}=\frac{\alpha _1\kappa ^2+\alpha _4\kappa -\kappa \omega }{\alpha _1K^2}F+\frac{\alpha _3\kappa +\alpha _5\kappa }{\alpha _1K^2}F^3-\frac{\alpha _2}{\alpha _1K^2}F^5. \end{aligned}$$

(59)

Let $\frac{\alpha _1\kappa ^2+\alpha _4\kappa -\kappa \omega }{\alpha _1K^2}=A$, $\frac{\alpha _3\kappa +\alpha _5\kappa }{\alpha _1K^2}=B$ and $\frac{\alpha _2}{\alpha _1K^2}=C$, then we get

$$\begin{aligned} F^{''}=AF+BF^3-CF^5. \end{aligned}$$

(60)

Using the Galilean transformation on (60), then we get dynamical system

$$\begin{aligned} {\left\{ \begin{array}{ll} F^{'}=H, \\ H^{'}=AF+BF^3-CF^5. \end{array}\right. } \end{aligned}$$

(61)

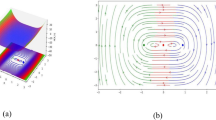
Case 1: $A>0$, $B>0$, and $C>0$.

We take different values of parameters $\alpha _1 = 0.3$, $\alpha _2 = 0.5$, $\alpha _3 = 0.4$, $\alpha _4 = 0.2$, $\alpha _5 = 0.1$, $\omega = 0.1$, $K = 0.5$, and $\kappa = 0.4$, then get five equilibrium points (0, 0), (0.81, 0), $(-0.81,0)$, (0.51i, 0), and $(-0.51 i,0)$. As we see in Fig. 7 (0, 0) is the saddle and (0.81, 0), $(-0.81,0)$ are center points.

Fig. 7

Phase portrait diagram when $A>0$, $B>0$, and $C>0$.

Case 2: $A<0$, $B<0$, and $C<0$.

We take different values of parameters $\alpha _1 = 0.3$, $\alpha _2 = -5$, $\alpha _3 = 0.2$, $\alpha _4 = 1$, $\alpha _5 = 0.3$, $\omega = -5$, $K = 2$, and $\kappa = -1.5$, then we get five equilibrium points (0, 0), (0.17, 0), $(-0.17,0)$, (0.10i, 0), and $(-0.10 i,0)$. As we analyze in Fig. 8, (0, 0) is the center point.

Fig. 8

Phase portrait diagram when $A<0$, $B<0$, and $C<0$.

Case 3: $A<0$, $B>0$, and $C>0$.

We take different values of parameters $\alpha _1 = 0.5$, $\alpha _2 =2$, $\alpha _3 = 0.6$, $\alpha _4 = -3$, $\alpha _5 = 0.4$, $\omega = 5$, $K = 1$, and $\kappa = 0.8$, then we get five equilibrium points (0, 0), $(1-0.89 i,0)$, $(-1+0.89 i,0)$, $(1+0.88 i,0)$, and $(-1-0.88 i,0)$. As we see in Fig. 9 (0, 0) is the center point.

Fig. 9

Phase portrait diagram when $A<0$, $B>0$, and $C>0$.

Case 4: $A>0$, $B<0$, and $C>0$.

We take various values of parameters $\alpha _1 = 0.5$, $\alpha _2 =2$, $\alpha _3 = -1$, $\alpha _4 = 3.0$, $\alpha _5 = -0.5$, $\omega = 1.0$, $K = 1$, and $\kappa = 1.2$, then we get five equilibrium points (0, 0), (1.43i, 0), $(-1.43 i,0)$, (1.06, 0), and $(-1.06 i,0)$. As we see in Fig. 10 (0, 0) is the saddle point and (1.06, 0), $(-1.06,0)$ are the center points.

Fig. 10

Phase portrait diagram when $A>0$, $B<0$, and $C>0$.

Case 5: $A>0$, $B>0$, and $C<0$.

We take diverse values of parameters $\alpha _1 = 0.5$, $\alpha _2 =-2$, $\alpha _3 = 1.0$, $\alpha _4 = 3.0$, $\alpha _5 = 0.5$, $\omega = 1.0$, $K = 1.0$, and $\kappa = 1.2$, then get five equilibrium points (0, 0), $(0.63-0.92 i,0)$, $(-0.63+0.92 i,0)$, $(0.63+0.92 i,0)$, and $(-0.63-0.92 i,0)$. As we analyze in Fig. 11, (0, 0) is the saddle point.

Fig. 11

Phase portrait diagram when $A>0$, $B>0$, and $C<0$.

Case 6: $A<0$, $B<0$, and $C>0$.

We take various values of parameters $\alpha _1 = 1$, $\alpha _2 =3$, $\alpha _3 = -2$, $\alpha _4 = -4$, $\alpha _5 = -1$, $\omega = 8.0$, $K = 0.8$, and $\kappa = 1.0$, then we get five equilibrium points (0, 0), $(0.81-1.03 i,0)$, $(-0.81+1.03 i,0)$, $(0.81+1.03 i,0)$, and $(-0.81-1.03 i,0)$. As we see in Fig. 12, (0, 0) is the center point.

Fig. 12

Phase portrait diagram when $A<0$, $B<0$, and $C>0$.

Case 7: $A<0$, $B>0$, and $C<0$.

We take various values of parameters $\alpha _1 = 1.0$, $\alpha _2 =-5.21$, $\alpha _3 = 1.5$, $\alpha _4 = 22.69$, $\alpha _5 = 3.57$, $\omega = 10.0$, $K = 1.0$, and $\kappa = 1.2$, then we get five equilibrium points (0, 0), (1.57i, 0), $(-1.57 i,0)$, (1.14, 0), and $(-1.14,0)$. As we see in Fig. 13, (0, 0) is the center point and (1.14, 0), $(-1.14,0)$ are the saddle points.

Fig. 13

Phase portrait diagram when $A<0$, $B>0$, and $C<0$.

Case 8: $A>0$, $B<0$, and $C<0$.

We take various values of parameters $\alpha _1 = 0.5$, $\alpha _2 =-3.0$, $\alpha _3 = -1.0$, $\alpha _4 = 4.0$, $\alpha _5 = -0.5$, $\omega = 1.0$, $K = 1.0$, and $\kappa = 1.2$, then we get five equilibrium points (0, 0), $(0.86-0.67 i,0)$, $(-0.86+0.67 i,0)$, $(0.86+0.67 i,0)$, and $(-0.86-0.67 i,0)$. As we see in Fig. 14, (0, 0) is the saddle point.

Fig. 14

Phase portrait diagram when $A>0$, $B<0$, and $C<0$.

Sensitivity analysis

For sensitivity analysis we will decompose the Eq. (60) into dynamical system as,

$$\begin{aligned} {\left\{ \begin{array}{ll} F^{'} = H, \\ H^{'} = AF + BF^3 - CF^5. \end{array}\right. } \end{aligned}$$

(62)

The system (62) explores how variations in initial conditions and parameters $\alpha _1 = 0.8$, $\kappa = 2$, $\alpha _2 = 0.4$, $K = 3$, $\alpha _3 = 0.3$, $\alpha _4 = 0.5$, $\alpha _5 = 0.1$, and $\alpha _6 = 0.5$ influence the system’s behavior. The system is governed by nonlinear terms that can yield to complex dynamics, making it highly sensitive to small variation in initial conditions. In Fig. 15a, where the system starts with (0.40, 0) and a slight perturbation is introduced by changing the initial conditions to (0.45, 0.01), there is a significant divergence between the two trajectories. This shows the system’s high sensitivity to initial conditions, characteristic of unstable or chaotic systems where small changes lead to large variations in the results.

In contrast, Fig. 15b present the system with different initial conditions (1.60, 1.02) and a slight changes in the initial values. The two curves in this plot show much less divergence, showing that the system is less sensitive to changes in initial conditions. This present that the system is operating in a more stable region, where minor variations do not significantly affect its trajectory. Thus, the comparison between the two figures indicates the system shows sensitive.

Fig. 15

Sensitivity behavior of perturbed system (42) assuming the initial condition (a) (0.40, 0) for blue solid line and (0.45,0.01) for red dotted curve, (b)(1.60, 1.02) for blue solid line and (1.75, 1.4) red dotted curve.

Conclusion

In this research work, we successfully applied the Sardar sub-equation (SSE) method and the generalized unified method to solve the Perturbed Gerdjikov-Ivanov (PGI) equation. Through these two approaches, we achieved a variety of soliton solutions, including bright, dark, and singular solitons, identifying the versatility of the approaches in solving complex nonlinear equations. The novelty of this work lies in the application of fractional derivatives, particularly Atangana’s derivative, to the PGI equation, which introduces non-local effects and high-order dispersion. Moreover, the study provides a thorough dynamical and sensitivity analysis, presenting deeper understanding of the stability and behavior of the solutions under different conditions. The results of this research not only extend theoretical knowledge of nonlinear wave phenomena but also have significant implications for the nonlinear propagation of solitons in optical fibers, with potential applications in telecommunication system and other areas of nonlinear mathematical physics. The methods employed here exhibit their effectiveness and versatility in tackling a broad range of nonlinear problems, opening new ideas for future research in related fields.