Thermal study of Fe₃O₄/blood and CoFe₂O₄/blood magneto nanofluids study over an exponential surface inspired by convective heating and radiations

Abstract

This work examines the role of Fe₃O₄/blood and CoFe₂O₄/blood nanofluids across an exponential surface associated to magnetic field, thermal radiation, and convective heating. It provides better thermal conductivity, biomedical application (such as drug targeting for treatment), and excellent efficiency of heat transfer, significant for the hyperthermia treatment and new hemodynamic systems. Thus, a bionanofluid model under mentioned physical constraints through an exponential surface is modeled. The formulation leads to a nonlinear mathematical model with enhanced characteristics of bionanofluid which then investigated numerically for physical responses of the parameters. It is examined that thermal efficiency of Fe₃O₄/blood is higher than CoFe₂O₄/blood due to strengthening the concentration and radiation effects. Intensive magnetic field and convective heating provided considerable thermal improvement in Fe₃O₄/blood and CoFe₂O₄/blood which point towards the use of Fe₃O₄ as a reliable option for magnetic hyperthermia and controlled thermal treatment in biomedical systems. Further, the shear drag in CoFe₂O₄/blood diminishes rapidly than Fe₃O₄/blood due to enhanced magnetic field and stretching of the surface. The outcomes demonstrate the applicability of Fe₃O₄ to areas where efficient heat transfer is demanded in biomedical or thermal applications.

Introduction

Three-dimensional blood-based nanofluid flow over an exponentially stretching surface is of vital significance in biomedical as well as engineering applications. This research is particularly valuable in the realm of drug delivery systems, where nanoparticles suspended in blood can enhance therapeutic effects by allowing for better targeting and controlled drug release. The way the surface stretches exponentially alters the dynamic characteristics of biological tissues and membranes, creating a realistic environment to study how blood flow interacts with nanoparticle transport. A study by Khan et al.¹ showcases the improved thermal and mass transfer properties of nanofluids, which are essential for optimizing biomedical devices like hyperthermia treatments and cancer therapies. Additionally, Nadeem and Ijaz² emphasize the role of magnetic fields in managing flow dynamics, which is vital for developing advanced medical devices. The three-dimensional aspects of this flow also contribute to creating more efficient cooling systems for electronics by using nanofluids to manage heat transfer. The insights gained from this research, as highlighted by Sheikholeslami and Ganji³, play a significant role in the broader field of fluid dynamics, paving the way for more effective and innovative solutions in both healthcare and technology sectors.

The investigation of heat transfer along stretching surfaces has gained a lot of attention lately, mainly due to its importance in various industrial applications such as polymer extrusion, glass fiber drawing, and metal spinning. Recent research by Ali et al.⁴ looked into how thermal radiation and viscous dissipation affect the heat transfer behavior of nanofluids on an exponentially stretching surface. They found that adding nanoparticles significantly boosts thermal conductivity and heat transfer rates. Similarly, Gireesha et al.⁵ explored the impact of magnetohydrodynamics (MHD) on heat transfer in boundary layer flow over a stretching sheet, focusing on how magnetic fields can control flow dynamics and temperature distribution. Additionally, Reddy et al.⁶ examined the combined effects of thermal stratification and chemical reactions on heat and mass transfer over a stretching surface, providing valuable insights for optimizing industrial processes that involve heat exchange. Together, these studies highlight the importance of understanding heat transfer processes on stretching surfaces, as they play a crucial role in developing more efficient cooling systems, energy-saving technologies, and innovative manufacturing methods. The integration of nanofluids, magnetic fields, and radiation in this research showcases the rich variety of heat transfer applications in modern engineering.

The impacts of magnetic fields on the three dimensional heat transfer study of cooling or heating surfaces with the use of nanofluids is becoming a popular area of interest for researchers because of the potential applications in micro electromechanical systems, biomedical devices, and emerging energy technologies. New studies have shown what many have claimed for years: that applying a magnetic field can greatly affect the flow and thermal behavior of nanofluids, thus giving better control over the heat transfer rate. For instance, Waini et al.⁷ investigated dual solutions and stability analysis of hybrid nanofluid flow over permeable stretching/shrinking surface in a magnetic field and observed that the application of the magnetic parameter enhances the heat transfer while reducing the skin friction. It can be said from the findings that one of the most important factors when it comes to thermal performance is the magnetic effects. Likewise, the study by Zainal et al.⁸ considered the three dimensional flow and heat transfer of Cu-Al₂O₃/ water hybrid nanofluids through a radiation assisted stretching/ shrinking sheet and focused on the effect of nanoparticle volume fractions in the thermal conductivity enhancement. This work will greatly assist in the design of the thermal management system to operate at maximum efficiency. Furthermore, Lund et al.⁹ focused on MHD of a nanofluid model while illustrating viscous dissipation and Joule heating. They looked at the combined effects of these two features on the flow above a stretched sheet.

The gravity effects on the nanofluids performance is highly affected and physical mixed convection presents these influences. Thus, Kumar et al.¹⁰ analyzed the mixed convective effects using machine approach along with ternary NPs influence. The data obtained using ODE45 algorithm and suggested that ANN approach is good tool to acquire accurate heat transfer. Further, studies on nanofluids using new Lie symmetries approach have been used in the Refs¹¹. , and¹², to investigate the contribution of NPs structure and MHD with hybrid NPs. Govindarajulu et al.¹³ discussed $\:F{e}_{3}{O}_{4}/Blood$ features associated to radiation and Joule heating. The study focuses on the entropy trends while the MHD influenced in the model. The positive impacts of radiation are inspected for entropy performance.

Three-dimensional thermal conduction analysis of nanofluids flowing over stretching/shrinking surfaces subject to convective heat has attracted immense focus owing to its significance in cutting-edge thermal management systems, energy efficiency, and industrial processes. Recent research has investigated the critical interaction between convective boundary layer conditions, behavior of nanoparticles, and surface geometry, shedding valuable insights into the optimization of heat transfer efficiency. The study by Ghadikolaei et al.¹⁴ examined the impact of convective heat transfer on the flow of hybrid nanofluids over a stretching/shrinking surface, highlighting the influence of nanoparticle concentration and thermal radiation on increasing the heat transfer rates. In a similar context, the study by Animasaun et al.¹⁵ also explored the influence of convective boundary conditions on the three-dimensional nanofluid flow, emphasizing the role of buoyancy forces and viscous dissipation in thermal performance. In addition, the study by Tlili et al.¹⁶ investigated the connected influence of convective heating and magnetic fields on nanofluid flow, which showed that convective conditions effectively impact temperature gradients and flow stability. Moreover, the study of Mahanthesh et al.¹⁷ investigated the hydrodynamic and thermal characteristics of nanofluids under convective heat transfer, presenting a thorough analysis of nanoparticle shape and size effects. Finally, the study of Khan et al.¹⁸ examined the effect of convective boundary conditions on the heat transfer behavior of nanofluids on a stretching surface, showing that convective heating increases thermal efficiency in industrial cooling systems. These researches cumulatively highlight the significance of convective heat conditions in the optimization of nanofluid-based thermal systems for various engineering applications. Some most recent investigations supporting the nanofluids applications from multiple scenarios have been deeply discussed in the Refs.^19,20,21 and²².

Exploring Fe₃O₄ and CoFe₂O₄ bio-nanofluid when considering magnetic field influence, thermal radiation, and convective heat effects, across an exponential surface has considerable potential. Although considerable advances have been achieved in the thermophysical properties of nanofluids and their applications to enhance heat transfer, there exists an acute deficiency in evaluating the combined influence of magnetic fields, thermal radiation, and convective boundary conditions on the hemodynamic and thermal behavior of blood-based nanofluids. Current research tends to consider simpler geometries or one-factor analysis and ignores the intricate interaction between such multiphysical phenomena in realistic biological and industrial applications. The particular contribution of hybrid nanoparticles such as Fe₃O₄ and CoFe₂O₄ to changing blood flow behavior, heat transfer rates, and thermal stability under such conditions has not been studied extensively. In addition, the effects of exponentially stretching surfaces that better replicate physiological and industrial situations on the flow and temperature profiles of blood-based nanofluids have yet to be extensively investigated.

Model formulation

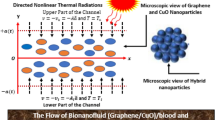
This investigation deals with 3D boundary layer flow (Fig. 1) of two types of bio-nanofluids (Fe₃O₄/blood, and CoFe₂O₄/blood) over an exponential surface. The surface is subject to uniform stretching with velocities (${U_w}=\frac{{{U_o}}}{{{e^{ - \left( {x+y} \right)/L}}}},~and~{V_w}=\frac{{{V_o}}}{{{e^{ - \left( {x+y} \right)/L}}}}$), along x and y directions, respectively. The fluids flow in the $xy$ plane while z axis is taken normal to this region. Further, the magnetic field ($B=\frac{{{B_o}}}{{{e^{ - \left( {\frac{{x+y}}{{2L}}} \right)}}}}$) is also considered at the surface which is important for the flow control and also contributes in the heat performance of the bio-nanofluids. Moreover, the temperature with exponential variations is taken at the surface as ${T_w}={T_\infty }+\frac{{{T_o}}}{{{e^{ - 2\left( {x+y} \right)/2L}}}}$. The fluid over the surface is heated due to thermal radiations and convection from the surface. The analysis is subject to the below assumptions.

• Both types of homogenously saturated in the base fluid.

• The boundary layer flow is laminar.

• The surface is subject to the convective heat phenomena.

• Thermal radiations and magnetic field applied externally.

• The bionanofluid flow is incompressible.

• The study is limited to laminar flow type.

Fig. 1

Schematic of the flow of Fe₃O₄/Blood and CoFe₂O₄/Blood.

The above assumptions yields the following mathematical models by taking the effects of magnetic field, thermal radiations and convective conditions. The three primary laws are expressed in Eqs. (1–4) and then flow confinements are given in Eq. (5). It is worth to reference that Eqs. (1–4) describing the conservation of mass, momentum, and energy along with body force and radiation source.

$${u_x}+{v_y}+{w_z}=0,$$

(1)

$${\rho _{nf}}\left[ {u\left( {{u_x}} \right)+v\left( {{u_y}} \right)+w\left( {{u_z}} \right)} \right]={\mu _{nf}}\left[ {{u_{zz}}} \right] - {\sigma _{nf}}B_{o}^{2}\left[ u \right],$$

(2)

$${\rho _{nf}}\left[ {u\left( {{v_x}} \right)+v\left( {{v_y}} \right)+w\left( {{v_z}} \right)} \right]={\mu _{nf}}\left[ {{v_{zz}}} \right] - {\sigma _{nf}}B_{o}^{2}\left[ v \right],$$

(3)

$$u\left( {{T_x}} \right)+v\left( {{T_y}} \right)+w\left( {{T_z}} \right)=\frac{{{k_{nf}}}}{{{{\left( {\rho {c_p}} \right)}_{nf}}}}\left[ {{T_{zz}}} \right]+\frac{{16{\sigma ^*}T_{\infty }^{3}}}{{3{k^*}{{\left( {\rho {c_p}} \right)}_{nf}}}}\left[ {{T_{zz}}} \right],$$

(4)

$$- {k_{nf}}\left[ {{T_y}} \right]={h_f}\left[ {{T_f} - T} \right],~w=0,~v={V_w},~u={U_w},~at~z=0,$$

(5)

$$T \to {T_\infty },~v \to 0,~u \to 0,~as~z \to \infty ,$$

(6)

The transformations²³ for further formulation of the problem are expressed in Eqs. (7, 8) for the temperature and velocity where $\:\:\eta\:$designates the similarity variable. The effective characteristics of NPs and blood are specified in Table 1. These attributes are very crucial in developing the thermal efficiency and applicability of the problem. Further, Fig. 2 presenting the specific values of the components Fe₃O_4, CoFe₂O₄, and blood. While, Fig. 3a-c depicting the variations of bionanofluids characteristics for different concentrations of the Fe₃O_4, CoFe₂O₄, respectively. These changes are helpful in improving the efficiency of the model. As, the concentration enhances it provides significant augmentation in the effective features which improves the model output. Enhanced thermal and electrical conductivities positively affect the heat transport and flow controlling over the surface in which increasing concentration plays central role. Further, the tri velocity components ($u,v,w$), temperature T, and similarity variable expressed in Eqs. (7, 8). The expression ${\mu _{nf}}$ (dynamic viscosity), ${\left( {\rho {c_p}} \right)_{nf}}$ (effective heat capacity), ${k_{nf}}$ (thermal conductivity), ${\rho _{nf}}$ (density), and ${\sigma _{nf}}$ (electrical conductivity) are included in Table 1.

$$\eta =\sqrt {\frac{{{U_o}}}{{2yL}}~} {e^{\left( {x+y} \right)/L}}z,~T={T_\infty }+{T_o}{e^{A\left( {x+y} \right)/2L}}\beta ,~u={U_o}{e^{\left( {x+y} \right)/L}}F^{\prime},~v={V_o}{e^{\left( {x+y} \right)/L}}G^{\prime},$$

(7)

$$w=\sqrt {\frac{{{\nu _f}{U_o}}}{{2L}}} ~{e^{\left( {x+y} \right)/L}}\left[ {F+\eta F^{\prime}+G+\eta G^{\prime}} \right],~$$

(8)

Table 1 Characteristics of bio-nanofluids.

Fig. 2

The specific values of the NPs and blood.

Fig. 3

Behaviour of the nanofluid properties versus concentration.

The 3D bionanofluid model is obtained after carrying the mathematical operations and reduction of the basic laws using transformations and effective attributes. The final form of the nonlinear problem incorporating the additional constraints is given below.

$$F^{\prime\prime\prime}+\frac{{{\rho _{nf}}}}{{{\rho _{blood}}}}{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)^{ - 1}}\left[ {\left( {G+F} \right)F^{\prime\prime} - 2\left( {G^{\prime}+F'} \right)F'} \right] - \frac{{{\sigma _{nf}}}}{{{\sigma _{blood}}}}{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)^{ - 1}}MF^{\prime}=0,$$

(9)

$$G^{\prime\prime\prime}+\frac{{{\rho _{nf}}}}{{{\rho _{blood}}}}{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)^{ - 1}}\left[ {\left( {G+F} \right)G^{\prime\prime} - 2\left( {G^{\prime}+F'} \right)G'} \right] - \frac{{{\sigma _{nf}}}}{{{\sigma _{blood}}}}{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)^{ - 1}}MG^{\prime}=0,$$

(10)

$$\left( {1+\frac{4}{3}Rd\frac{{{k_{blood}}}}{{{k_{nf}}}}} \right)\beta ^{\prime\prime}+Pr\frac{{{{\left( {\rho {c_p}} \right)}_{nf}}}}{{{{\left( {\rho {c_p}} \right)}_{blood}}}}\left( {\frac{{{k_{blood}}}}{{{k_{nf}}}}} \right)\left[ {\left( {G+F} \right)\beta ^{\prime} - A\left( {G^{\prime}+F^{\prime}} \right)\beta } \right]=0,$$

(11)

The problem is confined to the following flow and temperature controls at the surface and the bionanofluid at the freestream, respectively. The constraints are Hartmann number ($M=\frac{{2{\sigma _f}LB_{o}^{2}}}{{{U_o}{\rho _f}}}$), radiation number ($Rd=\frac{{16{\sigma ^*}T_{\infty }^{3}}}{{3{k^*}{k_f}}}$), Prandtl ($Pr=\frac{{{\mu _f}{{\left( {{c_p}} \right)}_f}}}{{{k_f}}}$) number, stretching ($\alpha ={V_o}U_{o}^{{ - 1}}$) number.

$$\beta ^{\prime}\left( 0 \right)= - {B_i}\left( {1 - \beta \left( 0 \right)} \right),~G\left( 0 \right)=0,G^{\prime}\left( 0 \right)=\alpha ,~F\left( 0 \right)=0,~F^{\prime}\left( 0 \right)=1,$$

(12)

$$\beta \left( \infty \right) \to 0,G\left( \infty \right) \to 0,and~F\left( \infty \right) \to 0,$$

(13)

The SFC and Nu are key factors in the analysis of an exponential surface flow under thermal radiation of bionanofluid. The SFC measures the shear stress on the surface, which is vital in determining the drag force and momentum transfer rate of the bionanofluid. This is especially critical in engineering and biomedical applications where energy loss due to friction is of utmost importance. Conversely, the Nu is the measure of convective to conductive heat transfer, and it offers information on the thermal efficiency of the system. In thermal radiation, the Nu is even more important since it assists in the assessment of the effect of radiation on the rate of heat transfer, which is crucial for maximizing thermal management in applications like hyperthermia treatment, drug delivery, and cooling systems. All these parameters together provide a holistic idea of the hydrodynamic as well as the thermal properties of bionanofluids, which can lead to designing more efficient and optimum systems. Thus, these quantities are formulate in the following for the current bionanofluid problem.

$$\begin{aligned} {C_f} & =\frac{1}{2}\frac{{{\mu _{nf}}}}{{{\rho _f}U_{o}^{2}}}{\left( {\frac{{\partial u}}{{\partial z}}} \right)_{z=0}},~{C_{fy}}=\frac{1}{2}\frac{{{\mu _{nf}}}}{{{\rho _f}U_{o}^{2}}}{\left( {\frac{{\partial v}}{{\partial z}}} \right)_{z=0}},~ \\ {N_{ux}} & = - \frac{{x{k_{nf}}}}{{{k_f}\left( {{T_w} - {T_\infty }} \right)}}\left( {{k_{nf}}+\frac{{16}}{3}\frac{{{\sigma ^*}T_{\infty }^{3}}}{{3{k^*}{k_f}}}} \right){\left( {\frac{{\partial T}}{{\partial z}}} \right)_{z=0}}, \\ \end{aligned}$$

(14)

$$Re_{x}^{{\frac{1}{2}}}\left( {{C_{fx}}} \right){\left( {2{e^{\frac{{3\left( {x+y} \right)}}{{2L}}}}} \right)^{ - 1}}=\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}F^{\prime\prime}\left( 0 \right),~Re_{x}^{{\frac{1}{2}}}\left( {{C_{fy}}} \right){\left( {2{e^{\frac{{3\left( {x+y} \right)}}{{2L}}}}} \right)^{ - 1}}=\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}G^{\prime\prime}\left( 0 \right),~$$

(15)

$$Re_{x}^{{\frac{{ - 1}}{2}}}\left( {{N_{ux}}} \right){\left( {{e^{\frac{{\left( {x+y} \right)}}{{2L}}}}} \right)^{ - 1}}\left( {\frac{L}{x}} \right)= - \left( {\frac{{{k_{nf}}}}{{{k_{blood}}}}+\frac{4}{3}Rd} \right)\beta ^{\prime}\left( 0 \right),$$

(16)

Mathematical investigation

The comparative bionanofluid problem investigated through numerical approach termed as bvp4c. This scheme is helpful to analyze the solution of the first order system. Thus, firstly the system arranged in the reduced model. For this, essential functions are expressed as below.

$$\check{\Theta }_{{1i}} = F,~\check{\Theta }_{{2i}} = F^{\prime},~\check{\Theta }_{{3i}} = F^{\prime\prime},~\check{\Theta }^{\prime}_{{3i}} = F^{\prime\prime\prime},$$

(17)

$$\check{\Theta }_{{4i}} = G,~\check{\Theta }_{{5i}} = G^{\prime},~\check{\Theta }_{{6i}} = G^{\prime\prime},\check{\Theta }^{\prime}_{{6i}} = G^{\prime\prime\prime},$$

(18)

$$\check{\Theta }_{{7i}} = \beta ~,\check{\Theta }_{{8i}} = \beta ^{\prime},~\check{\Theta }^{\prime}_{{8i}} = \beta ^{\prime\prime},$$

(19)

Now, express the original problem in the following pattern.

$$F^{\prime\prime\prime}= - \left[ {\frac{{{\rho _{nf}}}}{{{\rho _{blood}}}}{{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)}^{ - 1}}\left[ {\left( {G+F} \right)F^{\prime\prime} - 2\left( {G^{\prime}+F'} \right)F'} \right] - \frac{{{\sigma _{nf}}}}{{{\sigma _{blood}}}}{{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)}^{ - 1}}MF^{\prime}} \right],$$

(20)

$$G^{\prime\prime\prime}= - \left[ {\frac{{{\rho _{nf}}}}{{{\rho _{blood}}}}{{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)}^{ - 1}}\left[ {\left( {G+F} \right)G^{\prime\prime} - 2\left( {G^{\prime}+F'} \right)G'} \right] - \frac{{{\sigma _{nf}}}}{{{\sigma _{blood}}}}{{\left( {\frac{{{\mu _{nf}}}}{{{\mu _{blood}}}}} \right)}^{ - 1}}MG^{\prime}} \right],$$

(21)

$$\beta ^{\prime\prime}= - {\left( {1+\frac{4}{3}Rd\frac{{{k_{blood}}}}{{{k_{nf}}}}} \right)^{ - 1}}\left[ {Pr\frac{{{{\left( {\rho {c_p}} \right)}_{nf}}}}{{{{\left( {\rho {c_p}} \right)}_{blood}}}}\left( {\frac{{{k_{blood}}}}{{{k_{nf}}}}} \right)\left[ {\left( {G+F} \right)\beta ^{\prime} - A\left( {G^{\prime}+F^{\prime}} \right)\beta } \right]} \right],$$

(22)

Integrating the expressions from Eqs. (17–19), yields the subsequent first order form of the problem.

$$\check{\Theta }^{\prime}_{{3i}} = - \left[ {\frac{{\rho _{{nf}} }}{{\rho _{{blood}} }}\left( {\frac{{\mu _{{nf}} }}{{\mu _{{blood}} }}} \right)^{{ - 1}} \left[ {\left( {\check{\Theta }_{{4i}} + \check{\Theta }_{{1i}} } \right)\check{\Theta }_{{3i}} - 2\left( {\check{\Theta }_{{5i}} + \check{\Theta }_{{2i}} } \right)\check{\Theta }_{{2i}} } \right] - \frac{{\sigma _{{nf}} }}{{\sigma _{{blood}} }}\left( {\frac{{\mu _{{nf}} }}{{\mu _{{blood}} }}} \right)^{{ - 1}} M\check{\Theta }_{{2i}} } \right],$$

(23)

$$\check{\Theta }^{\prime}_{{6i}} = - \left[ {\frac{{\rho _{{nf}} }}{{\rho _{{blood}} }}\left( {\frac{{\mu _{{nf}} }}{{\mu _{{blood}} }}} \right)^{{ - 1}} \left[ {\left( {\check{\Theta }_{{4i}} + \check{\Theta }_{{1i}} } \right)\check{\Theta }_{{6i}} - 2\left( {\check{\Theta }_{{5i}} + \check{\Theta }_{{2i}} } \right)\check{\Theta }_{{5i}} } \right] - \frac{{\sigma _{{nf}} }}{{\sigma _{{blood}} }}\left( {\frac{{\mu _{{nf}} }}{{\mu _{{blood}} }}} \right)^{{ - 1}} M\check{\Theta }_{{5i}} } \right],$$

(24)

$$\check{\Theta }^{\prime}_{{8i}} = - \left( {1 + \frac{4}{3}Rd\frac{{k_{{blood}} }}{{k_{{nf}} }}} \right)^{{ - 1}} \left[ {\Pr \frac{{\left( {\rho c_{p} } \right)_{{nf}} }}{{\left( {\rho c_{p} } \right)_{{blood}} }}\left( {\frac{{k_{{blood}} }}{{k_{{nf}} }}} \right)\left[ {\left( {\check{\Theta }_{{4i}} + \check{\Theta }_{{1i}} } \right)\check{\Theta }_{{8i}} - A\left( {\check{\Theta }_{{5i}} + \check{\Theta }_{{2i}} } \right)\check{\Theta }_{{7i}} } \right]} \right],$$

(25)

The associated conditions transformed in the following pattern for the reduced system of nanofluids.

$$\check{\Theta }_{{8ia}} = - B_{i} \left( {1 - \check{\Theta }_{{7ia}} } \right),~\check{\Theta }_{{4ia}} = 0,\check{\Theta }_{{5ia}} = \alpha ,~\check{\Theta }_{{1ia}} = 0,~\check{\Theta }_{{2ia}} = 1,$$

(26)

$$\check{\Theta }_{{7ib}} \to 0,\check{\Theta }_{{4ib}} \to 0,\;and~\;\check{\Theta }_{{1ib}} \to 0,$$

(27)

Accuracy of the scheme is settled up to ${10^{ - 7}}$ by setting the $\infty$ condition as $2.5$ for the velocity and temperature numerical outcomes and operated the bvp4c scheme in MATLAB. The comparative solutions for $F{e_3}{O_4}/Blood$, and $CoF{e_2}{O_4}/Blood$ are enlisted in Table 2. This computation provides the difference between the two nanofluid solutions and the information is sufficient to replicate the output in future. These solution values accurately followed the imposed conditions and calculated for default ranges $\alpha =0.1,~\phi =0.1,~M=5.0,~Rd=0.2,~$and ${B_i}=0.2.$

Table 2 Solutions difference for $F{e_3}{O_4}/Blood$, and $Co{F_2}{O_4}/Blood$

Results and discussion

The involve parameters have vibrant effects on the movement, thermal behavior, surface shear drag and heat transport rate of bionanofluid through an exponential surface. Thus, this section explores these important aspects on the model over the feasible ranges. For this, Figs. 4, 5 and 6 are organized along with the pertinent quantities.

Figure 4a-f demonstrating the velocities output ($F^{\prime},~and~G'$) versus considered magnetic, concentration and elongating number $\alpha$. The output plotted for comparative behavior of Fe₃O₄/blood and CoFe₂O₄/blood bionanofluids. The results reveal that the bionanofluids lost the movement as the strength of $M,~\phi ,~$and $\alpha$ enhances. Physically, strengthening the magnetic effects promotes the Lorentz forces inside the bionanofluids which produces resistance. As a consequence, the bionanofluid velocities drops over the region. Moreover, increasing the NPs concentration promotes the density which ultimately responsible for higher resistance among the bionanofluid layers. Because of this reason, the $\phi =0.01,0.02,0.03,0.04$ causes considerable decrease in the velocities $F^{\prime},$ and $G'$, respectively. On contrary, it is noticed that Fe₃O₄/blood has quite abrupt decrease than CoFe₂O₄/blood. For this, densities difference between the Fe₃O₄ and CoFe₂O₄ playing significant part. Higher density of ferro nanoparticles compact the bionanofluid particles and produces much resistive forces than cobalt ferrite NPs. Thus, the observed changes occur for both bionanofluids with velocities variances. Further, the stretching effects of the surface observed excellent to acquire the optimum velocity of the fluid. The fluid molecules freely flow over the surface which enhances the particles momentum thus, the velocity upsurges rapidly near the surface.

Fig. 4

The bionanofluid velocity $F^{\prime},~and~G'$ for $M,~\phi ,~$and $\alpha$.

Figure 5a-f demonstrate the thermal performance of Fe₃O₄/blood and CoFe₂O₄/blood versus the pertinent quantities as mentioned in the results. It is observed that the thermal behaviour can be augmented for higher concentration and radiation number $Rd$. These two quantities are critical in optimizing the effectiveness of Al₂O₃/blood and CoFe₂O₄/blood bionanofluids. Physically, inclusion of Al₂O₃ and CoFe₂O₄ NPs in blood augments the blood TC which directly affects the temperature. The bionanofluid temperature observed increasing because addition of NPs enhances the thermal capability while externally acting radiation provide extra thermal energy to the system; as a consequence over all the performance augmented. High increase in Fe₃O₄/blood is obvious due to strong TC than CoFe₂O₄/blood. Hence, the bionanofluid becomes more efficient for Fe₃O₄ nanomaterial. Further, the increasing radiation factor is advantageous to reduce the TBL than varying concentration case. The stretching and thermal ratio number $\:A$ declines the temperature and control the TBL however, low efficiency is noticed for CoFe₂O₄/blood. Magnetic field and convective transport are critical phenomena in the heat mechanism of bionanofluids. These trends are furnished in Fig. 5e-f along with other fixed quantities. Increase in Biot number improves the effectiveness of bionanofluid due to strong heat transfer to the neighboring layers at the surface. This gradual phenomena positively enhances the temperature of the successive layers as a result overall performance of the bionanofluidic system increases. Physically, this add the energy to the system which play critical role in the thermal management.

Fig. 5

The bionanofluid performance $\beta$ for $~\phi ,~Rd,~\alpha ,~A,~M$and ${B_i}$.

The shear drag exertion and heat transport rate at the surface in bionanofluids has potential applications in biomedical engineering. Thus, to examine the behaviour of these two quantities in Fe₃O₄/blood and CoFe₂O₄/blood, Fig. 6e-f is organized. The shear drags minimizes as the strong magnetic field and stretching parameters apply on the system. However, these trends are dominant for CoFe₂O₄/blood. The high density of CoFe₂O₄/blood is responsible for such dominating behavior. Thus, imposing high magnetic and stretching effects, the shear drag can be minimized over the surface. The convective and thermal ratio number influences on the Nu are demonstrated in Fig. 6c-f, respectively. As noted that increase in Biot effects provided considerable transport when A and $Rd$ varies horizontally. Physically, convective phenomena from the surface to near the nanofluid particles make them more energetic and transmits the heat. As a consequence, the rapid rate of heat transport is observed at the surface. However, these effects are examined quite slowly for stretching of the surface. Thus, addition of convective heat is a good tool to optimize the Nu values. Additionally, better TC of Fe₃O₄ NPs make the Fe₃O₄/blood for quick thermal response.

Fig. 6

The bionanofluid SFC and Nu performance for $~~\alpha ,~M,~{B_i},~A,~$and ${R_d}$.

Conclusions

This investigation provided detailed thermal analysis in two bionanofluids (Fe₃O₄/blood, and CoFe₂O₄/blood) through an exponentially enlarging surface along with constraints of practical interest. The comparative investigation reveals that:

• The velocity of Fe₃O₄/blood nanofluid reduces faster than that of CoFe₂O₄/blood along the surface, which reflects greater viscous effects or interaction forces in Fe₃O₄-based nanofluids.

• Dominant behaviour due to CoFe₂O₄ nanoparticles have improved stability or reduced resistance in blood flow than Fe₃O₄. The results emphasize the significance of nanoparticle composition in enhancing nanofluid behavior for biomedical applications.

• Temperature of Fe₃O₄/blood nanofluid is observed higher than CoFe₂O₄/blood with elevated nanoparticle concentration and thermal radiation, reflecting higher thermal improvement in Fe₃O₄-based nanofluids.

• The heat transfer of Fe₃O₄/blood is slow compared to CoFe₂O₄/blood under more intense magnetic fields and larger Biot numbers, signifying higher thermal responsiveness of Fe₃O₄ nanoparticles.

• The shear drag for CoFe₂O₄/blood diminishes rapidly than Fe₃O₄/blood under augmented magnetic field and stretching surface influences, implying greater flow improvement with CoFe₂O₄ nanoparticles. Such behavior reflects that CoFe₂O₄ has superior shear-thinning or lower viscous resistance than Fe₃O₄ under dynamic flow conditions. The findings underscore CoFe₂O₄ as a suitable option for use in applications that demand reduced drag in magnetically regulated biofluidic systems.

The investigation of Fe₃O₄/blood and CoFe₂O₄/blood nanofluids along an exponential surface under magnetic fields, thermal radiation, convective heating, and stretching forces provides a number of opportunities for future research. Firstly, the exploration of the effects of hybrid nanoparticles (e.g., Fe₃O₄-CoFe₂O₄ composites) would improve thermal and hydrodynamic performance with reduced shear stress in biomedicine applications like targeted drug delivery or hyperthermia. Secondly, high-fidelity computational analysis with machine learning or multi-objective optimization might optimize predictive nanofluid behavior models so that these designs can be custom-made for enhanced thermal applications in biomedical engineering.