Introduction

Oceanic internal waves are gravity waves oscillating at stratified ocean interfaces, with frequencies between the buoyancy frequency and inertial frequency. As a distinct category, internal solitary waves (ISWs) whose crest lengths and amplitudes can reach 150 km and 240 m1,2 respectively, are extremely dynamic phenomena that frequently occur in the tropical and subtropical oceans3. Mainly generated by tide-topography interactions4,5,6,7,8 ISWs can propagate for great distances with nearly unchanged waveforms while carrying substantial energy9,10. Due to their strong velocity shear, ISWs are likely to trigger shear instability11 and induce enhanced mixing12,13,14which can provide favorable conditions for coral reef growth and phytoplankton communities through uplifting cooler and nutrient-rich subsurface water into surface15,16. Moreover, owing to their strong vertical velocity and rapid thermocline displacements, ISWs are considerable threats to submarines17.

Besides their great impact on the ocean interior, ISWs also significantly modulate sea surface conditions18,19. Alpers demonstrated that sea surface capillary gravity waves are modulated by sea surface convergence (divergence) induced by ISW front (rear), forming obvious alternating belts of rough and smooth water at the sea surface20. These belts are distinct enough to be observed from nearby ships21. Furthermore, because signal intensities received by radar or optical sensors are often determined by sea surface roughness, these rough and smooth belts could appear as bright and dark stripes in the remote sensing images acquired by satellites or aircraft22,23,24,25. Recent studies show that ISWs can increase the effective wave height and further induce sea surface wave fragmentation21,26.

Fig. 1
figure 1

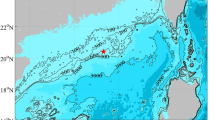
(a) MODIS/Terra RGB image acquired on 22 August 2020 at 12:10 UTC+8. The yellow arrows mark the crest lines of ISWs. The red dashed lines highlight the area around the Dongsha Island. The red star marks Station IW1, which water depth is 3000 m. The green star marks mooring Station IW6, which water depth is 323 m. The yellow arrow marks the crest lines of ISWs. Satellite imagery courtesy of the NASA Worldview application (https://worldview.earthdata.nasa.gov), part of the NASA Earth Observing System Data and Information System (EOSDIS). Geospatial axes and all scientific annotations were subsequently added using MATLAB R2024b (http://www.mathworks.com/). (b) Background water temperature profile measured by CTD. The red triangle marked the background SST. (c) Velocity components profiles of the background velocity \({\mathbf{u}}_{{\mathbf{b}}}\). The current velocity from −20 m to 0 m is supplemented by nearest interpolation. (d) Schematic diagram of the relative position of the data analysis area of WaMoS II system (three red rectangles) to the ISW front (blue shadow). \(\theta\) is the propagation direction of the ISW. \(\varphi\) is the angle between \(\theta\) and the ship heading. The orange arrows denote the directions along and across the propagation direction of the ISW. At 12:10 a.m., the wind speed (\(\left| {{\mathbf{U}}_{{\mathbf{a}}} } \right|\)), ship heading, and wind direction (\(Dir_{a}\)) are 8.95 m·s−1, 305°, and 215° (0° pointing east), respectively. (e) Drift trajectory and drift speed of R/V DFH3 during the experiment

Full size image

Sea surface is the primary location where the exchange of mass and energy between the ocean and atmosphere occurs27,28,29,30,31,32. ISWs are expected to modulate air-sea interactions due to their obvious impact on sea surface conditions. However, research on air-sea interactions under ISW processes remains highly limited. The only existing study have found that mean wind velocity, Reynolds stress components, humidity variance, and gradients exhibit direct responses to roughness variability induced by small-amplitude nonlinear internal waves, yet air temperature showed no direct response33. More recently, high-resolution satellite observations have identified distinct sea skin temperature (SST) cold anomalies associated with ISWs34. Currently, critical evidence remains lacking to determine: (1) the response of sea skin temperature to ISWs and the impact ISWs have on air temperature, (2) the quantification of these responses, and (3) whether observed perturbations occur predominantly in rough or smooth zones along crest lines of ISWs. Understanding the response of both SST and near-surface air temperatures to ISWs is crucial for clarifying the air-sea heat flux variability during ISW processes. Moreover, the mechanism by which ISWs modulate air-sea interactions remains inadequately understood.

Fig. 2
figure 2

(a) Backscatter intensity of seawater. The white dashed line represents the theoretical waveform of the ISW calculated by Eq. (2). (b) Along-wave velocity component \({u_f}\). (c) Horizontal gradient of \({u_f}\) scaled by 104. (d).\({u_f}\). at −20 m and its horizontal gradient scaled by 104. The horizontal gradient value is 0 s−1 along the blue dashed line. (e) Surface effective wave height \({H_s}\) and the angle \(\varphi\). (f) Sea surface roughness \({z_0}\) scaled by 104. The gray shadows represent 95% confidence intervals derived from 5,000 Monte Carlo simulations. (g) Sea skin temperature \({T_s}\) and air temperature \({T_a}\). (h) Air pressure \({P_a}\) and relative humidity. (i) Wind speed \(\left| {{{\mathbf{U}}_{\mathbf{a}}}} \right|\) and wind direction. The blue shadows represent the sea surface convergence area ranging from − 5.3 km to 0 km.

Full size image

ISWs are active in the northern South China Sea (SCS)23,35,36 characterized by large wave amplitudes, intense current velocities, and striking sea surface signatures37. By using simultaneous ship-board air-sea observations of a typical ISW process in the northern SCS, we found that when the ISW front passed, SST, air temperature and wind speed decreased notably accompanied by significant changes in the estimated air-sea heat flux. The elevated surface waves at the ISW front are proposed to account for the skin temperature variations. This paper is arranged in the following manner. The results are presented in three parts. First, the ISW properties are presented. Second, the observed changes in the sea surface and near-surface air are described. Third, the air-sea heat flux and wind stress variabilities are evaluated. Next, we discuss the mechanism with which ISWs modulate SST and address the potential role ISWs play in regional seas. Subsequently, we present our conclusions. The experiment, data and processing methods are introduced in the final section.

Results

Properties of the ISW

On 22 August 2020, an ISW event was captured by R/V DFH3 at IW1 station in the northern SCS (Fig. 1). The maximum vertical displacement of isopycnals, which can be closely tracked by the seawater echo backscatter intensity9, was 80 m (Fig. 2a). The along-wave velocity \({u_f}\) increased significantly and peaked at −1.55 m·s−1 when the wave trough approached (Fig. 2b). Figure 2c shows substantial horizontal convergence (divergence) of seawater in the wave front (rear). Figure 2d shows that the greatest near surface flow convergence (divergence) was as high as −4.2 × 10−4 s−1 (4.6 × 10−4 s−1) and appeared at −1.3 km (1.0 km) position.

The mode-1 linear phase speed \({c_0}\) was obtained by solving the Taylor-Goldstein Eq. 5:

$$\begin{gathered} {d^2}\hat {w}/d{z^2} - \mathcal{[}{U_{zz}}/\left( {U - {c_0}} \right) - {N^2}/{\left( {U - {c_0}} \right)^2}\mathcal{]}\hat {w}=0 \hfill \\ \alpha =3\int_{{ - h}}^{0} {{{\mathcal{(}{c_0} - U\mathcal{)}}^2}{{\hat {w}}^3}_{z}dz} /\mathcal{[}2\int_{{ - h}}^{0} {\mathcal{(}{c_0} - U\mathcal{)}} {{\hat {w}}^2}_{z}dz\mathcal{]} \hfill \\ \beta =\int_{{ - h}}^{0} {{{\mathcal{(}{c_0} - U\mathcal{)}}^2}{{\hat {w}}^2}dz} /\mathcal{[}2\int_{{ - h}}^{0} {\mathcal{(}{c_0} - U\mathcal{)}} {{\hat {w}}^2}_{z}dz\mathcal{]} \hfill \\ \end{gathered}$$
(1)

with boundary conditions at the surface and bottom defined as: \(\hat {w}\mathcal{(0)}=\hat {w}\mathcal{(-}h\mathcal{)}=0\). Here, \(\hat {w}\) is the eigenfunction of wave vertical displacement; \(h\) is the water depth; \(U\) is the along-wave background current velocity; \({U_{zz}}\) is its vertical second derivative; \(N\) is the Brunt–Väisälä frequency calculated from the CTD profile in the upper 500 m and supplemented by the seasonal WOA data in the lower layer; \(\alpha\) is the nonlinear coefficient, \(\beta\) is the dispersion coefficient. The theoretical waveform \(\eta \mathcal{(}x,t\mathcal{)}\), phase speed \({c_p}\) and half wave width \(l\) of this ISW were calculated from the solutions to the Korteweg-de Veries (KdV) equation:

$$\begin{gathered} \eta \mathcal{(}x,t\mathcal{)}= \pm {\eta _0}{\operatorname{sech} ^2}\left[ {\mathcal{(}x - {c_p}t\mathcal{)}/l} \right], \hfill \\ {c_p}={c_0}+\alpha {\eta _0}/3, \hfill \\ l=\sqrt {12\beta /\mathcal{(}\alpha {\eta _0}\mathcal{)}} . \hfill \\ \end{gathered}$$
(2)

Here, the wave amplitude \({\eta _0}\) is 80 m; These calculation results showed that the ISW with an amplitude of 80 m and a half-wave width of 2,180 m and propagated at a speed of 2.84 m·s−1 during the observational period. Moreover, the theoretical waveform defined with the following equation: \(\eta \mathcal{(}x\mathcal{)=} - 80{\operatorname{sech} ^2}\mathcal{(}x/2,108\mathcal{)}\) was consistent with the observed waveform (Fig. 2a).

Changes in sea surface and near-surface air

Sea surface waves and roughness were significantly impacted by the ISW. In the wave front, the effective wave height \({H_s}\) increased from 1.34 m to 1.75 m peaking at the − 1.4 km position, where the strongest sea surface current convergence occurred (Fig. 2e). Then, following the decreased convergence effect, \({H_s}\) rapidly decreased to 1.31 m at the wave trough and remained at approximately 1.4 m in the wave rear. It should be noted that the measured \({H_s}\) are spatial average values (Fig. 1d), and thus, the peak value of \({H_s}\) in the wave front is probably underestimated. Furthermore, we estimated the sea surface roughness \({z_0}\) by using the Coupled Ocean-Atmosphere Response Experiment (COARE) 3.5 algorithm: \({z_0}=1,200{H_s}{\mathcal{(}{H_s}/{L_p}\mathcal{)}^{0.45}}+\gamma \nu /{u_*}\)38,39,40,41. Here, \({L_p}\) is the measured dominant wavelength; \(\gamma\) is the roughness Reynolds number (0.11 in this case); \(\nu\) is the kinetic air viscosity; and \({u_*}\) is the friction velocity. \({z_0}\) increased from 0.46 × 10−4 m to 1.75 × 10−4 m in the wave front and then rapidly decreased to 0.46 × 10−4 m at the wave trough (Fig. 2f). The maximum \({z_0}\) increased by 152.2% compared with the background value (mean value between − 8 km and − 5.3 km in this case), which also peaked at the − 1.4 km position.

Notable changes were also observed in sea skin temperature \({T_s}\) during the passage of the ISW (Fig. 2g). Before the ISW arrived, the background \({T_s}\) was 30.6℃. When the ISW passed, \({T_s}\) decreased to a low of 29.7℃ at the − 1.4 km position and then returned to the background value at the wave trough. This resulted in remarkable sea skin temperature fronts with a maximum horizontal temperature gradient of 0.9℃·km−1. The ship-board CTD profile showed that the bulk water temperature, traditionally measured at depths of a few centimeters to a few meters below the surface, was approximately 29.6℃ before the ISW arrived (Fig. 1b). As can be seen, \({T_s}\) almost decreased to the bulk water temperature as the ISW approached.

Before the ISW, the air temperature \({T_a}\) was 29.7℃, which was 0.9℃ lower than \({T_s}\). As the ISW approached, \({T_a}\) underwent similar changes as \({T_s}\). At −1.4 km position, \({T_a}\) reached the lowest temperature of 29.3℃ and then returned to the background temperature at the wave trough. The correlation between \({T_a}\) and \({T_s}\) was as high as 0.9. In addition, in the wave front, the relative humidity \(f\) increased from 76 to 82% within ~ 0.9 km, and the maximum also \(f\) occurred at −1.4 km position (Fig. 2h).

Striking changes in the near-surface wind speed \({{\mathbf{U}}_{\mathbf{a}}}\) were observed in the wave front. Figure 2i shows that \(\left| {{{\mathbf{U}}_{\mathbf{a}}}} \right|\) dropped by up to 3.1 m·s−1 compared to the background value (8.6 m·s−1), with little changes in wind direction \(Di{r_a}\) of only ~ 10 degrees. The minimum wind speed of 5.5 m·s−1 occurred in the region of −1.4 km ~ −0.9 km. Similar drops in wind speed at 6 m above the sea surface were observed by Ortiz-Suslow et al., which also occurred over the rough surface associated with small-amplitude nonlinear internal waves33.

Fig. 3
figure 3

(a) Temperature difference between sea skin temperature \({T_s}\) and air potential temperature \({\theta _a}\). (b) Latent heat flux \({Q_{LH}}\). (c) Specific humidity difference (\({q_s} - {q_a}\)). (d) Sensible heat flux \({Q_{SH}}\). (e) Relative wind speed over the sea surface \(\left| {{{\mathbf{U}}_{\mathbf{a}}} - {{\mathbf{U}}_{\mathbf{s}}}} \right|\). (f) The magnitude of wind stress \(\left| {\mathbf{\tau }} \right|\). The blue shadows represent the sea surface convergence area ranging from − 5.3 km to 0 km. The gray shaded areas in subfigures (b), (d), and (f) represent 95% confidence intervals derived from 5000 Monte Carlo simulations.

Full size image

Changes in surface heat flux and wind stress

We estimated sensible heat flux \({Q_{SH}}\), latent heat flux \({Q_{LH}}\) and wind stress \({\mathbf{\tau }}\) by using the COARE 3.5 algorithm:

$$\begin{gathered} {Q_{SH}}=c{\rho _a}{C_s}\left| {{{\mathbf{U}}_{{\mathbf{10}}}} - {{\mathbf{U}}_{\mathbf{s}}}} \right|\mathcal{(}{T_s} - {\theta _{10}}\mathcal{),} \hfill \\ {Q_{LH}}={\rho _a}{L_e}{C_e}\left| {{{\mathbf{U}}_{{\mathbf{10}}}} - {{\mathbf{U}}_{\mathbf{s}}}} \right|\mathcal{(}{q_s} - {q_{10}}\mathcal{),} \hfill \\ {\mathbf{\tau }}\mathcal{=}{\rho _a}{C_D}\mathcal{(}{{\mathbf{U}}_{{\mathbf{10}}}} - {{\mathbf{U}}_{\mathbf{s}}}\mathcal{)}\left| {{{\mathbf{U}}_{{\mathbf{10}}}} - {{\mathbf{U}}_{\mathbf{s}}}} \right|. \hfill \\ \end{gathered}$$
(3)

Here, \({C_s}\), \({C_e}\) and \({C_D}\) are the sensible heat transfer coefficient, latent heat transfer coefficient and drag coefficient, respectively; \({L_e}\) is the latent heat of evaporation; \({q_s}\) is the sea surface specific humidity; \({{\mathbf{U}}_{\mathbf{s}}}\) is the sea surface current velocity, and here we assume it equals the velocity at a depth of −20 m;.\({\theta _{10}}\)., \({q_{10}}\) and \({{\mathbf{U}}_{{\mathbf{10}}}}\) are the air potential temperature, specific humidity and wind speed at 10 m, respectively; \(c\) is the isobaric specific heat of air; and \({\rho _a}\) is the air density.

Heat was always transferred from the sea surface to the atmosphere during the experiment. Both the specific humidity difference (\({q_s} - {q_a}\)) and the temperature difference (\({T_s} - {\theta _a}\)) exhibited lows around the position of −1.2 km (Fig. 3a and c). Near the same location, the latent heat flux \({Q_{LH}}\) and the sensible heat flux \({Q_{SH}}\) were reduced by up to 49.8% and 50.6%, respectively (Fig. 3b and d), with a maximum reduction of 104 W·m−2 in latent heat flux. In addition, relative wind speed over the sea surface \(\left| {{{\mathbf{U}}_{\mathbf{a}}} - {{\mathbf{U}}_{\mathbf{s}}}} \right|\) dropped by 2.5 m·s−1 at −1.2 km position compared to the background value (9.0 m·s−1) (Fig. 3e). Correspondingly, the wind stress \(\left| {\mathbf{\tau }} \right|\) also exhibited a low at about − 1.2 km position, which decreased by 36.8% (Fig. 3f).

Fig. 4
figure 4

(a) Schematic of air-sea interactions modulated by the ISW. (b) Photo of one ISW front in the northern SCS taken on R/V DFH3. (c) MODIS image in gray covering the area around the Dongsha Island, which is circled in red in Fig. 1a. (d) Proportion of ISW fronts (red) and rears (blue) along the zonal red dashed lines in Fig. 4c, and their means are indicated by dashed lines and numbers.

Full size image

Discussion

Our observations revealed a near-surface current velocity gradient of up to −4.2 × 10⁻⁴ s⁻¹ in the wave front (~ −1.4 km position), accompanied by concurrent peaks in significant wave height and sea surface roughness. Concurrently, the SST was observed to decrease to 29.7 °C, approximating the bulk water temperature (Fig. 4a). Based on the distinct results, we propose a possible mechanism for SST modulation by ISWs: The considerable surface flow convergence in the wave front of ISWs might lead to the accumulation of sea surface waves25. Small-scale waves (e.g., short-gravity and capillary waves) attached to these accumulated waves would steepen and break26 as evidenced by the whitecaps shown in Fig. 4b. This sea surface perturbation and the resulting enhanced near-surface mixing42 likely cause the SST to approach the bulk water temperature. Recently, the backscatter signals received by SAR across ISW crest lines show that the peak region of their backscatter signals (the sea surface roughness zone induced by ISWs) is consistent with the SST cold anomaly region34. This spatial correlation demonstrates that the observed SST depression within ISW wave fronts constitutes a reproducible physical phenomenon, not merely an isolated occurrence in our case study.

Fig. 5
figure 5

(a) A typical ISW event captured at IW6 on 19 May 2013. Background shadings indicate the temperatures measured by the thermistor chains, and the black line shows indicative of fluctuations in the 20 °C isotherm. The white shading highlights the waveforms counted in the ISW duration statistics. (b) Temporal distribution of ISW wave front (red fill) and wave rear (blue fill) observed at station IW6 in May 2013.

Full size image

ISWs are widely distributed in the northern SCS. Zhao et al. reported that the crest line of ISWs covered the northern SCS in remote sensing images1. For depression ISWs, the sea surface is rougher (smoother) in the wave fronts (rears) because of the intense sea surface flow convergence (divergence). To quantify the extent of ISW impacts on the sea surface spatially, we selected sea surface around the Dongsha Island as a study area (red rectangle in Fig. 1a) and estimated the spatiotemporal prevalence of ISW processes. During our observational period, the study area was cloud-free and located within the non-sunglint area, where the ISW fronts reflected more sunlight to the remote sensors mounted on satellites23 and manifested as bright stripes visible in the MODIS image (Fig. 1a). To minimize interference from broken cloud cover, we extracted the gray values of pixels along the 20 zonal red dashed lines in Fig. 4c. Through careful manual inspections, the regions of the wave front and rear were distinguished. The wave fronts (rears) were calculated to occupy 13.4% (11.3%) of the sea surface around the Dongsha Island (Fig. 4d).

ISW occurs extremely frequently in SCS. A 415-day mooring observation (IW6) deliver critical time-series ISW data for quantifying the temporal effects of ISWs in the study region. A total of 555 ISW packets were captured during this period. Figure 5a shows a typical wave packet, whose leading wave rapidly depressed the 20 °C isotherm by 130 m in 13 min, indicating significant surface responses. Notably, this packet contained 12 trailing waves exceeding 20-meter amplitudes, markedly extending the ISW-induced sea surface response duration. Figure 5b depicts daily durations of wave fronts (red) and rears (blue) in May 2013, demarcated by wave troughs. The results reveal that wave front and rear processes represented 6.2% each of the 415-day observation period, reaching 10.2% and 10.7% respectively in May 2013.

Thus, although ISWs are short period oceanic processes, their spatiotemporal accumulation reveals them as a significant phenomenon in the ocean area around Dongsha Island, which was expected to have a potential role in the regional air-sea interactions. Furthermore, both as case study within ~ O(1) km scale, our case results revealed that the average reduction in latent heat flux within the wave front was 24.2 Wm⁻² and the maximum reduction reached 104 Wm⁻². These estimated suppressions markedly exceeded the latent heat flux loss caused by a sub-mesoscale process reported by Song et al. (mean: 14.3 Wm⁻²; peak: 18.3 Wm⁻²)43. Notably, as high-frequency phenomena, ISWs during spring tide conditions—when they are particularly active—may exert non-negligible impacts on air-sea interactions across their regions of occurrence.

Conclusions

In this study, air-sea observations during the passage of one ISW were conducted in the northern SCS. Before the ISW arrived, we used a ship-board CTD to acquire the background water temperature profile. When the ISW passed, the current velocity, seawater backscatter intensity, surface wave conditions, SST, air temperature, air relative humidity and near-surface wind were monitored. The observations showed intense surface flow convergence in the wave front, accompanied by an increase in sea surface effective wave height. Additionally, in the wave front, skin temperature, air temperature, and wind speed decreased by 0.9℃, 0.72℃, and 3.1 m·s−1, respectively, which was accompanied by a sudden increase in air relative humidity. We noticed that the skin temperature in the wave front almost dropped to the bulk water temperature. The following possible mechanism for SST changes is proposed: due to the strong convergence of surface flow in the ISW front, the effective wave height increased, and the small-scale surface waves became steeper (or even broken), which could enhance the disturbance in sea surface and decrease the skin temperature to the bulk water temperature. Both latent and sensible heat fluxes were estimated to change by up to 50% in comparison with the background values ahead of the wave front.

Based on MODIS imagery during the experiment, we estimated that ISW fronts covered 13.4% of the sea surface around Dongsha Island. Long-term mooring records further indicated a temporal proportion of 6.2% for ISW fronts in this area. Given such substantial spatial and temporal prevalence, combined with observed significant modifications of air-sea interface elements (including heat flux and wind stress) during ISW events, these findings collectively suggest ISW may act as a potential modulator of regional air-sea interactions. Nevertheless, ISW structures exhibit substantial variability during their evolution and may manifest differently at the sea surface. Moreover, Huang et al. reported that ISWs varied significantly from hourly to inter-annual timescales35. Thus, more comprehensive and long-term observations coupled with modeling studies are necessary for the future to fully elucidate the mechanisms and magnitude of ISW modulation on air-sea interactions, to assess its significance relative to other processes, and to quantify its time-varying impact.

The conclusions presented in this study are subject to the following limitations: (1) It should be noted that the observed perturbations in sea surface properties and subsequent flux estimations are derived exclusively from an ISW event at a single location; (2) Although the latest satellite observations34 bolster confidence in our proposed ISW-SST modulation mechanism — wherein perturbations generated by ISW-induced surface convergence modify SST — the universality of this mechanism remains to be validated under diverse background conditions (such as warm bulk temperature under the cold skin layer, low wind speed and suppressed surface waves, etc.) and across multiple case studies. Moreover, the dynamic linkages between air temperature anomalies, turbulent heat fluxes, wind stress anomalies, and ISW processes are yet to be quantitatively established. (3) Using the current velocity at a depth of −20 m to represent the sea surface current velocity introduces certain errors. However, given that ISWs generate horizontally dominant currents within the ocean upper layer, where vertical shear (~ 0.01 cm s⁻¹ m⁻¹) remains statistically insignificant above the pycnocline threshold, the resultant velocity discrepancy falls within instrumental uncertainty margins (~ 0.4 cm s⁻¹) and thus constitutes a negligible systematic error; (4) Table 1 exhaustively documents the Accuracies (measurement errors) for all observed variables. Considering the propagation of observational errors, the estimation of sea surface roughness, air-sea heat flux, and wind stress inherently incorporates some degree of uncertainty. Consequently, 95% confidence level intervals are explicitly indicated for respective estimates in their corresponding figures.

Table 1 Instrument settings and observed variables.
Full size table

Experiment, data and processing methods

Field experiment

The observations presented here were collected as part of the Large Solitons Tracking Experiment (LSTE) conducted in the northern SCS in August 2020. According to the prediction results of the Internal Wave Prediction System, R/V DFH3 arrived at Station IW1 (20.7 °N, 119.6 °E) at 12:05 on August 22th, 64 min before the arrival of the wave trough of one depression ISW. Between 12:25 and 12:49, the background water temperature profile in the upper 500 m was measured by using the ship-board Sea-Bird SBE 911 plus CTD before the ISW arrived. As the ISW passed, we collected comprehensive measurements of the ocean interior, sea surface and near-surface air. Current velocities were measured by a 75 kHz ADCP with sampling intervals of 10 s. Vertical displacements of isopycnals were determined by the seawater scattering intensity signal detected by a 38 kHz echosounder. Wind speed (\({\mathbf{U}_\mathbf{a}}\)), air temperature (\({T_a}\)), relative humidity (\(f\)), air pressure (\({P_a}\)), and SST (\({T_s}\)) were measured by an automatic weather station secured to the front deck, which had sampling intervals of 1 min for each variable except \({\mathbf{U}_\mathbf{a}}\) (which were 3 s instead). The sea surface effective wave height \({H_s}\) and the dominant wavelength \({L_p}\) were measured by an X-band radar belonging to the Wave and Surface Current Monitoring System (WaMoS II), which was installed on the front deck. Details of the instruments and variables are shown in Table 1. Moreover, to investigate ISWs’ activities in the experimental area, we utilized a satellite remote sensing image with a spatial resolution of 250 m acquired by the MODIS sensor equipped on NASA’s Terra satellite at 12:10 on August 22th (Fig. 1a). Furthermore, comprehensive documentation of the IW6 mooring and the corresponding ISW identification methodology are detailed in Zhang et al. (2018)44.

Preliminary data processing

The current profile of the ISW [\({{\mathbf{u}}_{{\mathbf{ISW}}}}=\mathcal{(}{u_{ISW}},{v_{ISW}}\mathcal{)}\)] was obtained by subtracting the background current [\({{\mathbf{u}}_{\mathbf{b}}}=\mathcal{(}{u_b},{v_b}\mathcal{)}\)] from the ADCP observations [\({\mathbf{u}}=\mathcal{(}u,v\mathcal{)}\)], where \({\mathbf{u}_\mathbf{b}}\) was the average current velocity 40 to 60 min before the arrival of the wave trough. The propagation direction \(\theta\) of this ISW was estimated to be 170.1° (0° pointing east) from the mean current direction in the upper layer around the wave trough. Then, we decomposed \({\varvec{u}_{\varvec{ISW}}}\) into the along-wave component \({u_f}\) and the across-wave component \({u_a}\) by: \(({u_f},{u_a})=({u_{ISW}}\cos \theta +{v_{ISW}}\sin \theta , - {u_{ISW}}\sin \theta - {v_{ISW}}\cos \theta )\). Background current velocity \({\mathbf{u}_\mathbf{b}}\), ship drift speed \({\varvec{c}_{\varvec{ship}}}\) and wind speed \({\mathbf{U}_\mathbf{a}}\) were also decomposed in this way.

All the time series data and navigation information for the R/V DFH3 were uniformly interpolated into 1-minute intervals for unified processing. Then, we spatially transformed the data by: \(\Delta x= - V \times \Delta t\). Here, \(V\) is obtained by subtracting the along-wave ship speed \({c_{shi{p_f}}}\) from the 2.84 m·s−1 phase speed \({c_p}\). In this way, the spatial distortions in the ship-board measurements due to ship movements are removed45.

Figure 1c xshows that both \({H_s}\) and \({L_p}\) are the spatial mean values of the data analysis area obtained by spectral analysis. The earliest sea surface wave signal associated with the ISW was detected at a mean distance of 2160 m from the ship, so we delayed the wave data by: \(dt=2,160/V=875\) s to synchronize it with the ocean interior and near-surface air data.