Introduction

Friction reducer, as a key component of slick-water, is widely used in hydraulic fracturing to stimulate unconventional reservoirs1,2,3. Most common friction reducers are polyacrylamide-based polymers, which are primarily used to reduce flow friction in pipelines2,4 and to transport proppant sands. Gas shale micro-fractures and pores have a much larger contact area with the shale matrix, and therefore, the characterization of shale pore structure has attracted significant attention from many scholars5.

The characterization of shale pore structure has garnered considerable interest among researchers6,7,8 The techniques published in current literature can be broadly categorized into three types: direct imaging methods9,10, fluid invasion methods11,12, and non-invasive methods13. For example, He et al.14 utilized X-ray computed tomography (CT) and focused ion beam-scanning electron microscopy (FIB-SEM) to investigate the geometric and topological characteristics of multiscale pore systems in shale. HPMI is a typical method for characterizing PSD15. Mercury, as a non - wetting phase, is injected into the pores of a rock sample under different pressures. The relationship between pore size and injection pressure can be derived from the Washburn equation15, which assumes that all pores are cylindrical. NMR T2 relaxation time can also reflect the PSD in rock samples. Therefore, the pore radius can be described through the combined characterization of HPMI and NMR16. Huang et al.17 estimated PSD based on NMR and HPMI. Furthermore, some researchers have combined two or three fluid invasion methods to identify continuous pore structure parameters18,19,20. Furthermore, characterizing the shale pore structure is crucial for understanding shale gas adsorption8, shale gas recovery21, fracturing fluid imbibition22, and fracturing fluid flowback23. However, the specific influence of friction reducers on pore evolution and permeability changes remains unclear.

This study hypothesizes that friction reducers modify shale pore connectivity, leading to dynamic permeability changes over time. The gas shale samples were obtained from the Longmaxi Formation in an exploration well located in the northeast of Chongqing Municipality, China. Two gas shale samples were collected from the same block; one was used for HPMI testing, while the other was subjected to NMR testing under different immersion time conditions. PSDs were derived from NMR T2 spectra under various immersion times by integrating the HPMI data. Additionally, the effects of the friction reducer on PSD and permeability were analyzed. The results of this study may enhance the understanding of the interaction mechanisms between friction reducer and gas shale, and optimize the composition of slick-water for hydraulic fracturing in gas shale reservoirs.

Experiments

Materials

Core samples

In this study, the rock samples were selected from a depth of 1072 m in the Longmaxi Formation in the Northeast Sichuan Basin, China24. Following ASTM D4543-19 standards, we prepared: (1) Φ25.0 ± 0.2 mm × 30 mm cylindrical specimens for high-pressure mercury intrusion (HPMI) analysis, and (2) irregular block specimens (≈ 20 × 20 × 20 mm2) for nuclear magnetic resonance (NMR) measurements. All samples were dried to constant mass at 60 ± 2 °C.

Sulfonate polyacrylamide

A sulfonate polyacrylamide (SPAM) with a molecular weight of 12 million and a hydrolysis degree of 30% was used as the friction reducer in the slick-water for fracturing the shale formation25. The SPAM was used to reduce friction and enhance the sand-carrying capacity. An aqueous solution of SPAM with a concentration of 0.1 wt% was prepared using distilled water for testing.

Apparatus and procedures

High pressure mercury intrusion

PoreMaster-60 mercury porosimeter was used to obtain the distribution of connected pores in the rock samples as a classical analytical method26. Maximum test pressure is 414 MPa (60,000 psi) and pore size range is 0.003–500 μm. The test was in accordance with the ASTM D4404-10 testing standard.

The shape of the mercury intrusion curve indicates the diameter of the throat and the connectivity of the pores27. The mercury will intrude into progressively narrow pores for constant values of surface tension (\(\:{\gamma\:}_{Hg}\)) and contact angle (\(\:\theta\:\)) of mercury, with the pressure increasing28, and the surface tension equals to 0.480 N/m and the contact angle is generally 140°. The relationship between pore radius (\(\:{r}_{p}\)) and pressure (P) is given by Young-Laplace law for the case of cylindrical pores as following6.

$$\:{r}_{p}=\frac{2{\gamma\:}_{Hg}cos{\theta\:}_{Hg}}{{P}_{w}}$$
(1)

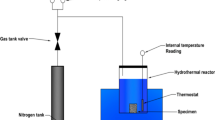
The experimental procedure was and designed as follows and shown in (Fig. 1),

  1. (1)

    Cylindrical samples are dried at 60 °C for 24 h and then cooled at room temperature.

  2. (2)

    Place the dried cylindrical core in an airtight high-pressure chamber under vacuum conditions.

  3. (3)

    Sequentially increase mercury injection pressure to stable values while monitoring pressure changes.

  4. (4)

    Measure and log the cumulative mercury volume (cm³/g) intruded at each stabilized pressure.

Fig. 1
figure 1

Flowchart of HPMI test.

Full size image

Nuclear magnetic resonance

As a non-destructive method, NMR has been extensively applied in the exploration and development of oil and gas fields29. The experiments were performed using a MacroMR12-150 H-1 low-field NMR analyzer (Shanghai Niumai Corporation) operating at a resonance frequency of 12 MHz. The instrument was set with an echo number of 8000, 32 scanning repetitions, a waiting time (TW) of 8000 ms, and an echo spacing (TE) of 0.2 ms, while the receiver gain was maintained at 50. To investigate the impact of the friction reducer (SPAM aqueous solution) on shale pore structure, NMR experiments were conducted under different soaking time conditions following the SY/T 5336 − 2006 testing standard, the experimental procedure was designed as follows:

  1. (1)

    The bulk shale sample was placed in a vacuum system. After being heated in an oven until its weight remained constant, the sample was evacuated to a vacuum state using a vacuum pump to expel the air within it.

  2. (2)

    After the vacuum treatment, the sample was saturated with an aqueous solution of SPAM to ensure that the pores were fully infiltrated.

  3. (3)

    After removing the sample from the liquid, the surface of the bulk sample was dried using moisture-absorbent paper, and then its T2 spectra were measured.

  4. (4)

    The sample was immersed back into the liquid.

  5. (5)

    The T2 spectra of the bulk sample were acquired under different immersion time conditions (0, 1, 5, 10, and 30 days).

Method

In this study, block and cylindrical shale rocks from the same sample were separately subjected to HPMI and NMR testing. Additionally, NMR tests were conducted under different immersion time conditions (0 day, 1 day, 5 days, 10 days, and 30 days) and combined with HPMI tests to illustrate the impact of a friction reducer on the microstructure of gas shale. The specific data processing procedure is as follows: (1) The cubic spline difference between the cumulative PSD curve obtained from the HPMI test and the cumulative distribution curves of T2 obtained from the NMR test under different immersion - time conditions was used to establish a one - to - one correspondence between T2 values and pore radius (r) for each immersion - time condition; (2) The transformation from T2 values to pore radius (r) was achieved by fitting the interpolated pore radius to T2 values under different immersion - time conditions using linear least - squares regression. Subsequently, the parameters C’ and n were determined for each immersion - time condition30. The specific process is shown in (Fig. 2).

Fig. 2
figure 2

Workflow for pore-throat radius correlation between NMR and HPMI.

Full size image

For NMR tests, the pore structure information of rock samples can be inferred from the transverse relaxation time (T2) of the fluid saturated within the pores. T2 can be expressed by the following equation31.

$$\:\frac{1}{{T}_{2}}=\frac{1}{{T}_{2bulk}}+\frac{1}{{T}_{2diffusion}}+\frac{1}{{T}_{2surface}}$$
(2)

Where \(\:{T}_{2bulk}\) is the transverse volume relaxation, \(\:{T}_{2diffusion}\) is diffusion induction time, \(\:{T}_{2surface}\) is transverse surface relaxation.

In this actual application, the shale rock surface relaxation can be depicted as Eq. (3) as the previous publications11,32.

$$\:\frac{1}{{T}_{2}}={\rho\:}_{2}\frac{S}{V}$$
(3)

Where \(\:{\rho\:}_{2}\) is the relaxation rate, µm/ms; \(\:S/V\) is the pore specific surface area, µm.

Then, Eq. (3) can be expressed as Eq. (4) because the pore specific surface equals to the ratio of pore shape factor (\(\:{F}_{s}\)) to pore radius (r)33.

$$\:r={T}_{2}{\rho\:}_{2}{F}_{s}$$
(4)

Furthermore, Eq. (4) can be expressed as Eq. (5) because it has been demonstrated that there is a power exponential relationship between T2 and r in previous articles31,34.

$$\:{T}_{2}=\frac{{r}^{n}}{{\rho\:}_{2}{F}_{s}}$$
(5)

Where n is the power exponent.

Finally, the equation between r and T2 can be expressed in Eq. (6).

$$\:r=({\rho\:}_{2}{F}_{s}{)}^{\frac{1}{n}}{{T}_{2}}^{\frac{1}{n}}=C{{T}_{2}}^{\frac{1}{n}}$$
(6)

Take the logarithm of both sides of Eq. (6), the result can be expressed as following,

$$\:{ln}\left(r\right)={ln}C+\frac{1}{n}{ln}\left({T}_{2}\right)$$
(7)

To establish a one-to-one correspondence between the T₂ distribution (from NMR) and cumulative PSD (from HPMI), cubic spline interpolation was applied to match their cumulative distribution curves. The cubic spline function used is defined as35,

$$\:{P}_{i}\left(x\right)={a}_{i}{(x-{x}_{i})}^{3}+{b}_{i}{(x-{x}_{i})}^{2}+{c}_{i}\left(x-{x}_{i}\right)+{d}_{i}$$
(8)

Where \(\:{a}_{i}\), \(\:{b}_{i}\), \(\:{c}_{i}\), \(\:{d}_{i}\)(i = 1, 2,3…,n-1)are the constant coefficients to be found.

Once T₂–r were established via interpolation, least squares fitting was performed to determine the parameters \(\:C\) and n in the power-law relationship, Least squares method was expressed as follows36:

$$\:S\left(\theta\:\right)={{\sum\:}_{i=1}^{m}\left({y}_{i}-f({x}_{i},\theta\:)\:\:\right)}^{2}$$
(9)

Based on the assumption that the rock is composed of a bundle of capillary tubes of varying diameters and equal lengths37, the permeability of the core is calculated as follows38,

$$\:K=\frac{\varphi\:{r}^{2}}{8{\tau\:}^{2}}$$
(10)

Where r is Mean capillary radius, um; ϕ is porosity, %; \(\:\tau\:\) is capillary tortuosity, generally \(\:\tau\:=1\sim1.4\).

Result and discussion

PSD by HPMI experiments

Mercury intake - withdrawal curves obtained via the HPMI method on the cylindrical sample are depicted in (Fig. 3). The intake curve reaches a plateau as the injection pressure reaches 411.59 MPa, indicating a maximum injection pressure of 411.59 MPa and a maximum mercury saturation of 39.87%. The results reveal that mercury cannot be completely discharged from the rock sample even when the mercury pressure is reduced to 4.45 MPa, suggesting that approximately 30% of the mercury remains trapped within the pores. Furthermore, the maximum mercury saturation is significantly lower than 100%, demonstrating that the micro-pores in this shale sample are inaccessible through mercury injection experiments18. Figure 4 shows the PSD curve derived from the HPMI data. The curve displays one main peak and two secondary peaks, indicating that mesopores (2 nm < r < 50 nm) are the dominant pore size class in this sample.

Fig. 3
figure 3

Intake-withdrawal curves by HPMI experiments.

Full size image
Fig. 4
figure 4

PSD by HPMI experiments.

Full size image

PSD by NMR experiments

Figure 5 illustrates the NMR T2 relaxation time spectra of shale sample immersed in the friction reducer solution for different immersion time (0, 1, 5, 10, and 30 days). The T2 spectra consistently show two peaks, labeled as the left and right peaks. As immersion time increases, the left peak shifts to shorter relaxation time and increases in magnitude before stabilizing, a trend similar to that reported by Sun et al.39.

Fig. 5
figure 5

T2 relaxation time spectra of shale samples after immersion in friction reducer solution for different durations.

Full size image

Figure 6 presents the cumulative frequency curves of T2 relaxation time and mercury saturation obtained from HPMI. When the cumulative frequency is below the maximum mercury saturation (SHgmax), a strong correspondence is observed between the pore-throat radius (rti) and the cumulative mercury saturation (SHgi). Using SHgi as interpolation targets, the corresponding T2i values were determined via cubic spline interpolation (Eq. 8), resulting in paired data sets of rti and T2i.

Fig. 6
figure 6

Transforming from T2 to pore radius.

Full size image

Furthermore, the least square method is used to fit the interpolated T2i and pore radius rti by using Eq. (9), and the parameters C’ and n are obtained. The transformation from T2 to pore diameter is completed by substituting into Eq. (6), and the results can be shown as (Fig. 7). Meanwhile, the fitting equations, parameters C’ and n at different immersion time are shown in (Table 1). The parameter C’ firstly increases, then decreases, finally increases, which is contrary to the parameter n, but the turning points are 1 and 5 days.

Fig. 7
figure 7

Numerical fitting curves of pore radius versus T2.

Full size image
Table 1 Fitting parameters and equations for the relationship between pore radius and T2.
Full size table

The relationship between pore radius and proportion was depicted as (Fig. 8). It can be obviously seen that there are two peaks on these curves, and these curves move as time extends, which is a little different from the T2 curves shown in (Fig. 5). This is mainly attributed to the method of transforming the T2 to pore radius in this study.

Fig. 8
figure 8

PSD by combining HPMI and NMR.

Full size image

Effects on pore structure

Effect on micro-pore

The proportion of micro-pores under different time conditions after the core sample was immersed in the friction reducer aqueous solution was calculated using the data from Fig. 8 and is shown in (Fig. 9). It can be clearly seen that the proportion of micro-pores initially increases, then decreases, and subsequently increases again as the immersion time grows. This indicates that the friction reducer can alter the micro-pore ratio. Similarly, Changbao et al. stated that cyclic liquid N2 treatment can change the pore structure due to increase pore volume40. This result is mainly due to interactions between the shale and friction reducer solution, where micro-cracks from hydration connect previously isolated micro-pores.

Fig. 9
figure 9

Variation of micro-pore proportion with immersion time.

Full size image

Effects on meso-pore

Figure 10 illustrates the relationship between the proportion of meso-pores and immersion time. It is evident that the proportion of meso-pores first decreases, then increases, and finally decreases again as the immersion time extends, with the turning points occurring at 5 days. These results indicate that the friction reducer can enhance the proportion of meso-pores when the immersion time is less than 30 days, with the maximum proportion of meso-pores achieved at 5 days. This phenomenon can be attributed to the interaction between the gas shale sample and the friction reducer aqueous solution. Specifically, the micro-cracks produced by hydration first connect more disconnected micro-pores and subsequently connect more disconnected meso-pores41. This finding can be used to optimize the flowback time for shale gas wells, as the highest proportion of meso-pores is achieved at 5 days.

Fig. 10
figure 10

Variation of meso-pore proportion with immersion time.

Full size image

Effect on macro-pore

Figure 11 presents the variation in the proportion of macro-pores in gas shale immersed in a 0.1 wt % friction reducer aqueous solution. It is distinctly observed that the proportion of macro-pores initially increases, then decreases, and stabilizes afterward, with the maximum value occurring at 1 day. These results are primarily due to the interaction between the gas shale sample and the friction reducer aqueous solution. Specifically, the micro-cracks produced by hydration initially connect more disconnected macro-pores, and the subsequent dissolution of water further increases the proportion of macro-pores, which has been Jiaxin et al. discussed to investigate the effect of slickwater on shale pore structure42. This finding can also be applied to guide the design of flowback time for shale gas wells to achieve the highest proportion of macro-pores.

Fig. 11
figure 11

Variation of macro-pore proportion with immersion time.

Full size image

Effect on permeability

The permeability of the core sample under different immersion time conditions was calculated using Eq. (10), and the results are plotted in (Fig. 12). The permeability first increases, then decreases, and finally increases again as the immersion time extends, which corresponds to the changes in the proportions of micro- and macro-pores. Meanwhile, the permeability at an immersion time of 5 days is higher than the initial permeability, which is different from the change trends of the micro- and macro-pore proportions. Therefore, the change trend of permeability is primarily influenced by the change trend of macro-pores before the immersion time reaches 5 days.

Furthermore, to illustrate the change in permeability with increasing immersion time, the permeability ratio was defined as the ratio of the permeability at different immersion times to the initial permeability. It is clearly seen that the permeability ratios are all greater than 1.0, indicating that the friction reducer aqueous solution has the function of increasing the permeability of the shale sample.

Fig. 12
figure 12

Permeability variation with immersion time.

Full size image

At last, average pore radius and permeability at different immersion time are summarized in (Table 2). Obviously seen that the average pore radius and permeability all firstly increase at 1 day then decrease at 5 days, finally increase at 10 and 30 days. Furthermore, the relationship between permeability and average pore radius is plotted in (Fig. 13). Clearly seen that there is a linear positive correlation relationship between permeability and average pore radius, revealing that the soaking of slickwater can increase the permeability of shale sample and the permeability increases linearly with average pore radius43.

Table 2 Average pore radius and permeability at different immersion time.
Full size table
Fig. 13
figure 13

The relationship between permeability and average pore radius.

Full size image

Conclusion

The method that combines NMR with HPMI can be effectively applied to illustrate the impact of the friction reducer on the microstructure and permeability of gas shale under different immersion time conditions.

The proportions of both micro- and macro-pores initially increase, then decrease, and stabilize afterward, with the maximum value occurring at 1 day and 30 days respectively. Meanwhile, the proportion of meso-pores first decreases, then increases, and decreases, finally stabilize as the immersion time extends, with the turning points occurring at 5 days.

The proportions of micro- meso- and macro-pores all stabilizes after 10 days of soaking, indicating that the interaction between friction reducer aqueous solution and shale nearly ceased at 10 days. This finding implies that the optimal shut-in time should be within 10 days.

The permeability first increases, then decreases, and finally stabilizes as the immersion time extends, which corresponds to the changes in the proportions of micro- and macro-pores. The permeability ratio is always greater than 1.0, indicating that the friction reducer aqueous solution has the function of increasing the permeability of the shale sample. The types and concentrations of the friction reducer should be taken into account and indoor experimental studies should be carried out to optimize the slickwater formulation.