Incentive mechanism of foundation model enabled cross-silo federated learning

Abstract

The integration of foundation models (FMs) into cross-silo federated learning (FL) introduces transformative capabilities but also exacerbates strategic client behaviors, such as knowledge hoarding and free-riding, which degrade global model performance and system sustainability. Existing incentive mechanisms fail to address the knowledge hoarding and free-riding in FM-enabled FL. This paper proposes a novel incentive framework to harmonize client-server interests while suppressing adversarial behaviors. First, we propose a dynamic participant screening mechanism including pre-screening mechanism and confidence attenuation monitoring to filter low-quality updates and penalize intermittent participation. Second, we propose a cost-benefit balanced contribution metric to quantify clients’ impacts by jointly evaluating accuracy gains, cost, and participation patterns. Third, we model the incentive mechanism as a two-stage Stackelberg game to establish symbiotic incentives, where the server adaptively adjust pricing strategy while clients optimize participation strategies. Simulation results demonstrate that our method can achieve up to 21.9% higher model accuracy and effectively filter malicious clients compared to existing benchmarks.

Introduction

The exponential growth of artificial intelligence (AI) has precipitated an unprecedented surge in data generation, with global data volumes projected to exceed 175 zettabytes by 2025¹. However, increasing regulatory constraints (e.g., GDPR, CCPA) and organizational privacy concerns have fundamentally reshaped data utilization paradigms, propelling federated learning (FL) as a pivotal distributed machine learning framework that enables collaborative model training without raw data sharing².

Cross-silo FL has emerged as a predominant paradigm for institutional collaboration in federated learning architectures, particularly in healthcare³, financial services⁴, and industrial IoT⁵, where multiple organizations jointly train models under a central server’s coordination. Compared with conventional cross-device FL scenarios with numerous edge devices, cross-silo FL typically involves fewer but more sophisticated participants who actively initiate training processes and engage in model aggregation⁶.

In traditional cross-silo federated learning, the server only aggregates the uploaded local model of clients. However, the advent of foundation models (FMs) has introduced transformative capabilities through efficient adaptation techniques. Specifically, the server maintains a cloud-based FM and broadcasts only low-rank adapters which are compressed representations of model updates to requesting clients. Clients freeze all pre-trained model parameters during local training, updating the low-rank matrices of their adapters. After domain-specific adaptation, clients submit these lightweight adapter parameters to the server, which performs weighted aggregation to update the FM of the server.

However, the combination of FM and federated learning brings new challenges to the traditional incentive mechanism of federated learning⁷. Unlike traditional FL systems where model updates are typically homogeneity⁸, FM-enabled FL creates asymmetric knowledge distribution. Specifically, clients’ personalized models encapsulate their domain insights refined through iterative adaptations, which brings two challenges to the incentive mechanism of federated learning which will pose deterioration to the performance of federated learning:

Definition 1

(Knowledge Hoarding) Clients may intentionally degrade update quality to prevent competitors from benefiting from their specialized features⁹.

Definition 2

(Free-Riding) Rational clients can strategically alternate between active contribution phases (to steer evolution) and passive phases (to minimize computational expenditures). Free-riding is a widely studied behavior pattern on incentive mechanism in federated learning⁶.

Furthermore, the server incurs computation costs for local adaptions aggregation and FM updating (e.g., GPU cluster utilization, energy consumption). Without appropriate compensation mechanisms, the server lacks economic incentives to sustain FM updates, particularly when client contributions are sparse or inconsistent.

To tackle the aforementioned challenges, in this paper, we propose an incentive mechanism for foundation model enabled cross-silo federated learning. Specifically, the incentive mechanism includes three components: 1) A dynamic participant screening mechanism that combines pre-screening mechanism and confidence attenuation monitoring to suppress knowledge hoarding and free-riding behaviors; 2) A cost-benefit balanced contribution valuation metric that quantifies clients’ contributions while considering clients’ costs and update continuity; 3) A two-stage Stackelberg game formulation that establishes symbiotic incentives between the server and clients. We summarize our main contributions as follows.

• Novel Incentive Mechanism in FM-enabled Cross-Silo Federated Learning: To the best of our knowledge, this is the first paper that designs incentive mechanism for FM-enabled cross-silo federated learning which suppresses knowledge hoarding and free-riding behaviors and establishes symbiotic incentives between the server and clients.

• Adaptive Participation Control: We design a pre-screening mechanism that employs dynamic base accuracy thresholds and a confidence attenuation monitoring mechanism that detect abnormal behaviors to ensure that clients maintain active participation and progressive performance improvements.

• Two-Stage Stackelberg Game Mechanism: We design a novel contribution valuation mechanism that integrates accuracy gains, the cost of clients, and the participation pattern of clients to metric the contribution of clients. Then we formulate a two-stage Stackelberg game which designs the server’s pricing strategy and clients’ participation strategy to create symbiotic incentives between the server and clients. We design differentiated incentives for high-quality clients, overcoming the linear reward limitations in existing mechanisms.

• Simulation Results: We conduct extensive simulations on three datasets. Simulation results show that our method achieves better model accuracy and can effectively filter knowledge hoarding and free-riding clients. We also conduct sensitivity analysis and ablation study to show the effectiveness of our method.

Related work

In this section, we discuss related work regarding cross-silo federated learning, incentive mechanism, and foundation model enabled federated learning.

Cross-silo federated learning

Cross-silo FL has emerged as a critical paradigm in federated learning, especially in healthcare, finance, and IoT. Existing works usually assume a central server dedicated to simply aggregating model updates⁶. Tang et al. propose an incentive mechanism in cross-silo federated learning to maximize social welfare in distributed manner¹⁰. Bao et al. propose to cluster clients with similar distribution to mitigate negative transfer¹¹. Huang et al. propose FedAMP to facilitate pairwise collaboration between clients with similar data¹². Huang et al. provide an overview of cross-silo federated learning and discuss future directions⁴. However, none of the above papers consider a server that operates as a foundation model provider, which brings new directions to cross-silo federated learning.

Incentive mechanism

Incentive mechanisms are crucial for maintaining sustainable FL training. Auction-based approaches¹³ and contract theory¹⁴ have been applied to cross-device FL, but their assumption of homogeneous client capabilities becomes invalid in cross-silo contexts. Shapley value based methods¹⁵ struggle with exponential computation costs for FM-scale models. Game-theoretic solutions^16,17 provide convergence guarantees for federated learning on heterogeneous data, but usually only consider the game between clients. Li et al. investigate FL in Industrial IoT scenarios with meta-computing integration, designing a satisfaction function balancing data size, AoI, and latency to optimize system utility through a Stackelberg game and deep reinforcement learning¹⁸. Few researchers consider the incentive mechanism in cross-silo federated learning. Li et al. propose a repeated game based incentive mechanism for cross-silo federated learning in MEC to motivate active and long-term participation of high quality clients¹⁹. Mao et al. propose a multi-stage game based incentive mechanism to achieve approximate social efficiency²⁰. Our work advances prior arts by considering incentive mechanism in cross-silo federated learning and considering the game between the server and clients.

Foundation model enabled federated learning

The integration of foundation models with FL creates new research frontiers. Parameter-efficient fine-tuning techniques like LoRA²¹ enable lightweight FM adaptation, while²² develops federated prompt tuning for NLP tasks. However, current works focus on technical feasibility⁷ rather than incentive structures. The closest work²³ propose a data quality-aware incentive mechanism to encourage participation. However, their method only applies to cross-device federated learning. We are the first to design incentive mechanism for FM-enabled cross-silo federated learning.

System model

In this section, we first introduces the architecture of FM-enabled cross-silo federated learning. Then we characterize the utility of clients and the server.

Foundation model enabled cross-silo federated learning

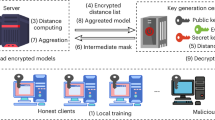
In this subsection, we introduce the architecture of FM-enabled cross-silo federated learning. We consider a set $\mathcal {N} = \{1,2, \cdots , N\}$ of clients. These clients may be small companies or organizations which have computation capabilities and local datasets. The local dataset of each client $n \in \mathcal {N}$ is $\mathcal {D}_n$ with size $D_n$. The server has its own dataset $\mathcal {D}_s$ with size $D_s$. The server trains the foundation model $\varvec{\omega }$ in the cloud. The server can also aggregate the uploaded local updates and utilize the aggregated updates to update the foundation model.

Low-Rank Adaptation (LoRA)²¹ is a efficient method to fine-tune the pre-trained model. LoRA adds a low-rank adapter with the same output dimension with the pre-trained model, which achieves efficient computation and storage.

The architecture of LoRA-based FM-enabled cross-silo federated learning is illustrated in Fig. 1. At the beginning of federated learning round t, clients first initiate a request to the server for the foundation model. The server broadcasts the global low-rank adapter $\mathbb {A}(\theta ^{t-1})$ which is an inherently “dimension-reduced ” version of the foundation model to clients ($\mathbb {A}(\cdot )$ is the adapter structure, and $\theta ^t$ is the adapter parameters). Clients replace their local adapters with the received global adapter. For a pre-trained weight matrix $\mathbb {R}^{d \times h}$, the global adapter is a combination of two small matrices $A \in \mathbb {R}^{d \times r}$ which is initialized with a Gaussian distribution and $B \in \mathbb {R}^{r \times h}$ which is initialized with a zero matrix, where r is the rank and $r \ll \min (d, h)$. The adapter and the pre-trained model have the same output dimension for the same input.

During local training, the client freezes all parameters of the local pre-trained model and only updates the low-rank matrices A and B. Specifically, in each iteration of training, the local pre-trained model is frozen. A sample is input into the frozen local pre-trained model and the adapter synchronously. Then the output of two models are summed as the final output for loss calculation to update the adapter by gradient descent.

After local training, the local models are stored in clients and the updated adapter $\theta _n^{t}$ are uploaded to the server for weighted aggregation by the size of local dataset

$$\begin{aligned} \theta ^t = \sum \limits _{n=1}^{N}\frac{D_n}{\sum \limits _{n=1}^{N}D_n}\theta _n^{t}. \end{aligned}$$

As only the small adapter is trained and uploaded, the computation and communication resource consumption is largely reduced. The server updates the global adapter according to the updated local adapters and update the FM model. Then the server broadcasts the new global adapter to clients in the next round.

Fig. 1

LoRA-based FM-enabled cross-silo federated learning.

Utility of clients

In FM-enabled cross-silo federated learning, the utility of clients includes: benefits from improved model accuracy, computation cost, communication cost, and the payment to the server.

Benefits from improved model accuracy

The clients initiate the cross-silo federated learning process for achieving higher local model accuracy. The model accuracy can be represented by the difference between the current model loss function and the theoretical optimal model accuracy loss, i.e., the model accuracy loss⁶. The model accuracy loss before local training is $L(\omega _{n}) - L(\omega ^*)$ and the model accuracy loss after local training is $L(\omega _{r,n}) - L(\omega ^*)$, where $L(\omega _n)$, $L(\omega _{r,n})$, and $L(\omega ^*)$ are the loss function under parameter $\omega _n$, $\omega _{r,n}$, and $\omega ^*$ respectively. Thus the model accuracy improvement can be denoted by $L(\omega _n) - L(\omega _{r,n})$. In this paper, we denote the benefit of client n in round r from improved model accuracy as $B_{r,n}$. Assume the benefit of each unit of model accuracy loss improvement for client n is $\alpha _n$, then the benefits from improved model accuracy can be calculated as follows:

$$\begin{aligned} B_{r,n} = \alpha _n(L(\omega _n) - L(\omega _{r,n})). \end{aligned}$$

(1)

Computation cost

Clients perform local model training and thus incur computation cost. Local computing consumes a lot of computing resources, and each client has different computing power, so the computational cost is heterogeneous and cannot be ignored. According to²⁴, the computation cost of client n at round r can be calculated as follows:

$$\begin{aligned} E_{r,n} = \frac{\zeta _n}{2}\mu _n\theta _n^2D_n, \end{aligned}$$

(2)

where $\zeta _n$ is a computational capability coefficient depending on the computing chip, $\mu _n$ is the CPU operation cycles for training one data sample, and $\theta _n$ is CPU processing speed coefficient. For convenience, we denote $\beta _n = \frac{\zeta _n}{2}\mu _n\theta _n^2$ as the computation coefficient of client n, which is a coefficient depending on the hardware of client n. Thus the computation cost of client n at round r can be calculated as:

$$\begin{aligned} E_{r,n} = \beta _n D_n. \end{aligned}$$

(3)

Communication cost

Clients incur communication cost in the process clients communicate with the server²⁵. Clients communicate with the server and request for the foundation model. The server broadcasts the global low-rank adapter to clients. After local training, clients upload the local adapter to the server. Since clients may be companies, the communication takes up large bandwidth and can be improved by communication technologies such as multi-criteria path finding, load balancing, and congestion control²⁶. The communication capability of clients may be heterogeneous, but the communication pattern of each client does not change much in each round, the communication loss also does not change much. Thus we denote the communication cost of client n as heterogeneous constant $C_n$ as in⁶.

Payment to the server

The payment clients give to the server are related to their contributions. The payment is related to the performance of clients, the higher the local update quality and the more active participation of clients, the less the payment will be. On the contrary, the client’s knowledge hoarding, free-riding and other behaviors will affect the model quality, and the payment will increase. Assume that the contribution of client n is $\Phi _n$, then the payment to the server is:

$$\begin{aligned} p_n^r = H(\Phi _n^r), \end{aligned}$$

(4)

where $p_n^r$ is the payment client n give to the server, and $H(\cdot )$ is the payment function formulated by the server.

Utility of the server

The utility of the server includes: The payment from the clients, and the cost for updating foundation model.

Payment from the clients

The server collects payment from all clients participating in federated learning. The server sets the payment function according to the local model quality of clients and the participation status of clients. Thus the payment from the clients is:

$$\begin{aligned} p_s^r = \sum _{n \in \mathcal {N}} p_n^r \end{aligned}$$

(5)

Cost for updating foundation model

After receiving the local adapters of clients, the server updates the foundation model based on the current foundation model. The training loss of the server is related to its compute resources, which can be assumed to be $C_{FM}^r = \xi \Vert \varvec{\omega }_r - \varvec{\omega }_{r-1} \Vert _2^2$, where $\xi$ is the coefficient to convert the model update to the cost.

Thus the server’s utility is

$$\begin{aligned} U_{server} = \sum _{n \in \mathcal {N}} p_n^r - C_{FM}^r \end{aligned}$$

(6)

Proposed method

In this section, we propose an incentive mechanism algorithm for the training process. The incentive mechanism includes three parts: the participant screening mechanism, the contribution valuation mechanism, and the two-stage Stackelberg game mechanism.

Participant screening mechanism

Although clients initiate the federated learning process in cross-silo federated learning, low quality participants have a negative effect on the overall model performance. As illustrated in²⁷, clients have two behaviors that only consider their own interests: knowledge hoarding and free-riding.

In order to prevent these speculative behaviors, we propose to dynamically screen clients participating in cross-silo federated learning. The participant screening mechanism is conducted after clients request for FM and before the server distributes global adapter to clients, including pre-screening mechanism and confidence attenuation monitoring.

The purpose of pre-screening mechanism is to prevent the phenomenon of knowledge hoarding. When clients request for FM, clients should upload the local validation set accuracy $A_{local,n}^{r-1}$. The server will set a dynamic base accuracy $\theta _{base}^{r}$, which is calculated as follow:

$$\begin{aligned} \theta _{base}^{r} = \frac{1}{|\mathcal {S}_{active}^{r-1}|} \sum _{n \in S_{active}^{r-1}} A_{local,n}^{r-1} - \delta \sqrt{\frac{\log r}{|S_{active}^{r-1}|}}, \end{aligned}$$

(7)

where $S_{active}^{r-1}$ is the set of clients the server select in the last round, and $\delta$ is the robustness factor which we define as 1.96 which corresponds to 95% confidence interval. The first term in (7) is the group benchmark and the second term in (7) is the robust correction. If the local validation accuracy is smaller than the base accuracy, then the server will reject the client’s request. The base accuracy initially takes 80% accuracy of the foundation model. The pre-screening mechanism prevents clients from intentionally degrade update quality to compromise the overall training quality by preventing clients from participating in cross-silo federated learning.

The confidence attenuation monitoring aims at reducing free-riding behavior. We define a decay factor to detect the abnormal behavior of clients. Specifically, when clients have free-riding behaviors, clients perform little or no local training and thus the gradient vector has large deviation. We define the decay factor as

$$\begin{aligned} \beta _n^{r} = \frac{A_{local,n}^{r-1}}{\theta _{base}^{r}} \times \cos (\textbf{g}_n, \textbf{g}_{global}) \times e^{-\lambda (r - r_n^{last})}, \end{aligned}$$

(8)

where $\textbf{g}_n$ is the gradient vector of client n and $\textbf{g}_{global}$ is the average gradient of all participants. The first term in (8) is the capability factor which reflects the contribution ability of the client. If the behavior of the high ability client is abnormal, its credibility attenuation is more significant, which has a greater impact on the global model. Low capability clients have lower attenuation even if their performance fluctuates. Since the second and third terms in (8) are in the range of (0,1), the larger the capability factor is, any abnormal behavior will make the decay factor decrease faster. The second term in (8) is the gradient consistency, which reflects the deviation of the client’s update from the global gradient, the larger the deviation, then the smaller the gradient consistency, and the decay factor is smaller. Gradient consistency can identify potentially malicious clients or low-quality updates. The third term in (8) is the time penalty term, which is used to punish the free-riding behavior. If only participating in a specific round, then the difference from the last participating round is larger, the time penalty term is smaller, and the decay factor is smaller. The term $\lambda$ in the third term is the decay rate. We set a threshold $\beta _{thres}$ and a punishment mechanism. If the decay factor of client n in round r is smaller than the threshold, then the server suspends the client from participating in one round. If the decay factor still smaller than the threshold in the next round, then the server suspends client from participation. The dynamic threshold adapts to the collective progress of participants. Clients temporarily excluded due to performance dips can re-qualify by improving their local models to surpass the updated baseline.

Contribution valuation mechanism

Through the participant screening mechanism, the server selects high-quality clients to participate in the training. However, due to the heterogeneity among clients, the contribution of clients to the global model are different, so it is necessary to evaluate the contribution of clients.

In this paper, considering the utility of clients and the training performance, we propose a cost-benefit balanced contribution metric, which is calculated by:

$$\begin{aligned} \Phi _n^r = \gamma _1(\frac{B_{r,n}}{E_{r,n} + C_n}) \times \gamma _2\left( \max \left( 0, \frac{A_{local,n}^r - \theta _{base}^{r}}{\theta _{base}^{r}}\right) \right) \times \gamma _3\left( \frac{1}{1 + \lambda (r - r_n^{last})}\right) , \end{aligned}$$

(9)

where $\gamma _1, \gamma _2,\gamma _3$ are tunable coefficients to support domain-specific tuning through parameter adaption, and we set as 1 in our paper empirically. The first term in (9) is the cost-benefit ratio which measures the benefit per unit cost, which rewards resource efficiency rather than absolute capabilities. This metric ensures that low-resource but efficient clients can achieve high contribution scores if they deliver strong accuracy improvements relative to their limited computation/communication costs, while high-resource but inefficient clients are penalized if their massive resource expenditure fails to produce proportional accuracy gains. The second term in (9) is the quality factor which filter low-quality updates via local validation accuracy. When $A_{local,n}^r < \theta _{base}^{r}$, the contribution is set to 0 to prevent knowledge hoarding. Clients must continuously improve their local models to outpace the progressing baseline, as static performance would eventually fall below the dynamic base threshold. The third term in (9) is the continuity factor to inhibit intermittent participation. The more rounds the client skips, the smaller the continuity factor, and thus can reduce free-riding behaviors.

Two-stage Stackelberg game mechanism

Game formulation

We model the incentive interaction between the server and clients as a two-stage Stackelberg game with complete information:

• Leader: The server acts first by announcing the pricing strategy $\{p_n^r\}_{n=1}^N$ based on contribution metrics $\{\Phi _n^r\}_{n=1}^N$

• Followers: Clients subsequently decide their participation strategies $\{x_n^r\}_{n=1}^N$, where $x_n^r \in \{0,1\}$ and $x_n^r= 1$ denotes active participation.

The game repeats iteratively over FL rounds, with the server updating pricing strategy according to clients’ historical behaviors.

Stage 1: Server’s pricing strategy

The server’s pricing strategy is designed as a dual-component function that balances cost recovery and contribution-based incentives:

$$\begin{aligned} p_n^r = \frac{C_{FM}^r}{|\mathcal {S}_{active}^r|} + \frac{p_{\max } - p_{\min }}{1 + e^{-\kappa \Phi _n^{r}}} \end{aligned}$$

(10)

where $C_{FM}^r = \xi \Vert \varvec{\omega }^r - \varvec{\omega }^{r-1} \Vert _2^2$ represents the server’s FM update cost, $\Phi _n^{r}$ is client n’s contribution score, and $\kappa$ controls price sensitivity to contribution changes $(\kappa > 0)$.

The first term in (10) is the cost allocation term $\frac{C_{FM}^r}{|\mathcal {S}_{active}^r|}$ which distributes the server’s computation cost equally among all clients and ensures basic cost recovery regardless of participation status. The second term in (10) is the contribution-sensitive incentive term which creates exponential discounting for high contributors, i.e.,

$$\begin{aligned} \lim _{\Phi _n^{r} \rightarrow \infty } \frac{p_{\max } - p_{\min }}{1 + e^{-\kappa \Phi _n^{r}}} = p_{\min }, \end{aligned}$$

and penalizes low contributors through progressive pricing, i.e.,

$$\begin{aligned} \lim _{\Phi _n^{r} \rightarrow 0} \frac{p_{\max } - p_{\min }}{1 + e^{-\kappa \Phi _n^{r}}} = \frac{p_{\max } - p_{\min }}{2}. \end{aligned}$$

$p_{\max }$ and $p_{\min }$ are the maximum and minimum payment clients pay to the server in the last round. The sigmoid shape ensures smooth transitions between pricing tiers.

The server’s pricing strategy aims to punish knowledge hoarding and free-riding behaviors. Specifically, clients with declining $\Phi _n^{r-1}$ face price increases:

$$\begin{aligned} \frac{\partial p_n^r}{\partial \Phi _n^{r}} = -\frac{\kappa (p_{\max } - p_{\min })e^{-\kappa \Phi _n^{r}}}{(1 + e^{-\kappa \Phi _n^{r}})^2}. \end{aligned}$$

(11)

The negative gradient forces clients to maintain or improve contributions to avoid payment increase. Furthermore, free riders have small contribution metric $\Phi _n^{r}$ due to large continuity factor as in (9). Thus clients have incentive to participate continuously to reduce the payment.

Stage 2: Client participation strategy

Clients engage in non-cooperative game with utility functions:

$$\begin{aligned} U_n^r = \alpha _n(L(\omega _n) - L(\omega _{r,n})) - (\beta _n D_n + C_n) - p_n^r \end{aligned}$$

(12)

Thus the decision of clients should be:

$$\begin{aligned} x_n^r = {\left\{ \begin{array}{ll} 1 & \text {if } \alpha _n\Delta L_{r,n} \ge \beta _n D_n + C_n + p_n^r, \\ 0 & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(13)

Where $\Delta L_{r,n} = L(\omega _n) - L(\omega _{r,n})$ represents local model improvement, $\alpha _n$ converts accuracy gains to monetary value, $\beta _n D_n$ captures computation costs proportional to dataset size, and $C_n$ is fixed communication cost.

The game satisfies Rosen’s conditions for concave N-person games²⁸ when the server’s strategy space forms a convex set, client’s utility is concave, and server’s utility is continuous. Under these conditions, the hierarchical game admits a Stackelberg Equilibrium. Clients reach pure-strategy Nash equilibrium in participation decisions given server’s pricing. Server optimizes pricing against this equilibrium response. The equilibrium becomes unique when the pricing is monotonic $\frac{\partial ^2p_n^r}{\partial (\Phi _n^r)^2} < 0$ and the client utility is submodular $\frac{\partial ^2U_n^r}{\partial x_n^r \partial x_m^r} \le 0$ for $m \ne n$²⁹.

Iterative implementation

Algorithm 1

Incentive mechanism algorithm

In summary, we design an incentive mechanism algorithm for the training process as in Algorithm 1. In each round, clients initiate a request for FM and meanwhile upload the local validation set accuracy and gradient vector of the previous round. The server selects client based on the participation screening mechanism according to (7) and (8). Then the server distributes the FM to clients. Clients perform local personalized training and upload the local model updates. The server aggregates the local updates and update the FM. Then the server evaluates the contribution of clients according to (9) and decides the pricing strategy $p_n^r$ of each client according to (10). Clients pay to the server and compute their utility function according to (13) and decide whether to participate in the next round.

Performance evaluation

In this section, we conduct simulations to study the performance of our incentive mechanism in FM-enabled cross-silo federated learning. We first show the experimental setting of our paper. Then we evaluate the performance of our incentive mechanism compared with several benchmarks. Finally, we conduct ablation study to analyze the effectiveness of the components of the incentive mechanism.

Experimental setup

We simulate a cross-silo FL environment with 50 institutional clients using two benchmark datasets which are widely used in federated learning: CIFAR-10 and MNIST³⁰. Each dataset is partitioned following Dirichlet distribution ($\alpha =0.3$) to create non-IID data silos³¹. We employ the pre-trained model in³² as the foundation model as in²³. We assume that the communication rounds $R = 300$, and each client perform 10 steps of local training in each communication round. The learning rate is 0.01. The communication costs $C_n$ are random constants in [1, 10]. The computation coefficient $\beta _n$ are random constants in [0.001, 0.002]. The robustness factor $\delta = 1.96$ which corresponds to 95% confidence interval. The decay rate $\lambda = 0.2$ to punish free-riding behaviors and the threshold $\beta _{thres} = 0.2$. The price sensitivity to contribution changes $\kappa = 0.5$.

Furthermore, to further validate the scalability of our method to large foundation models, we conduct additional experiments using ViT-Base/16 model pretrained on ImageNet-21k and fine-tuned on CIFAR-100 via LoRA (rank=8). The federated learning settings remain consistent with the main experiments, including 50 clients and non-IID data distribution.

Table 1 Comparison with three methods under three datasets.

Comparison with existing methods

In this subsection, we compare our proposed incentive mechanism against three state-of-the-art incentive mechanisms. We first introduce these existing methods which are common methods of incentive mechanism in federated learning. Then we compare the performance between our incentive mechanism and the existing methods.

Fig. 2

The number of common clients and malicious clients in our method and the three existing methods.

The three existing methods of incentive mechanism in federated learning as follows:

• Repeated game based method ⁶: a repeated game based incentive mechanism to encourage long-term cooperation and reduce free rider.

• Auction mechanism based method ¹⁰: an incentive mechanism for cross-silo FL considering social welfare maximum problem.

• Contract theory based method ¹⁴: a contract based incentive mechanism considering clients’ multi-dimensional private information.

In order to compare our incentive mechanism and existing methods in reducing knowledge hoarding and free-riding, we set part of clients as common clients while others as malicious clients. Specifically, we set 30% of clients gradually reduce local training steps (from 10 to 2) over rounds. We also set 20% of clients follow a periodic participation pattern, i.e., active for 2 rounds then idle for 2 rounds.

We conduct simulations and make comparisons in terms of two important metrics: the model accuracy and the number of malicious clients. We first show the model accuracy achieved by our method and that achieved by the three existing methods in Table 1. We can see that our methods achieves 88.0% final test accuracy on MNIST, 85.5% final test accuracy on CIFAR-10, and 76.3% final test accuracy on CIFAR-100, outperforming Auction mechanism based method (74.4% on MNIST, 71.5% on CIFAR-10, and 68.1% on CIFAR-100), Contract theory based method (66.1% on MNIST, 64.7% on CIFAR-10, and 63.7% on CIFAR-100), and Repeated game based method (77.9% on MNIST, 76.1% on CIFAR-10, and 67.7% on CIFAR-100). The results show that our method can improve the model accuracy even under large foundation models. The performance improvement is mainly due to that the dynamic screening mechanism effectively filters most low-quality updates, which may even degrade the performance in the three existing methods. The repeated game based method outperforms the auction mechanism based method and the contract theory based method because it filters most free riders. However, the repeated game based method cannot filter knowledge hoarding behaviors.

Then we show the number of malicious clients after training. We can see that the number of malicious clients after training varies significantly across methods. In our approach as shown in Fig. 2a, only 1 malicious client (1 knowledge-hoarding client with 0 free-riding clients) remains alongside 22 common clients, demonstrating that our method can effectively filter malicious clients. In contrast, the repeated game based method retains 15 malicious clients (14 knowledge-hoarding and 1 free-riding) despite maintaining 22 common clients as shown in Fig. 2b, the reason is that this method aims to reduce the number of free rider but can hardly address knowledge hoarding. Meanwhile, auction mechanism and contract theory based methods can hardly filter malicious clients as shown in Fig. 2c and 2d: the former has 20 common clients and 16 malicious clients (10 knowledge-hoarding, 6 free-riding), while the latter has 18 common clients and 20 malicious clients (13 knowledge-hoarding, 9 free-riding). Our method can effectively filter malicious clients and thus can improve both training stability and final model performance.

Sensitivity analysis

In this subsection, we conduct sensitivity simulations to show the impact of parameters.

First we conduct sensitivity tests on CIFAR-100 via LoRa to analyze the influence of the number of rank on the model accuracy and communication cost, the results are shown as follow in Table 2.

Table 2 Number of rank sensitivity analysis.

Table 3 Coefficient Sensitivity Analysis.

The result demonstrate that higher rank (16) slightly improves accuracy (76.5%) but increases communication cost by 37%, while lower rank (4) reduces accuracy by 2.2% with only 18% communication cost saving. Therefore, we choose rank=8 as the default setting.

Then we conduct sensitivity tests on CIFAR-10 dataset to analyze the influence of coefficients in (9) on the model accuracy and the results are shown as follow in Table 3.

The results demonstrate asymmetric sensitivity where quality factor changes produce the largest impacts, followed by cost-benefit ratios, with continuity having more moderate effects. This empirically verifies that the components naturally create differentiated weighting through their operational ranges rather than requiring explicit coefficients. These coefficients can be adjusted to emphasize specific factor priorities while preserving the core multiplicative logic.

Then we conduct experiments to systematically evaluate how varying proportions of malicious clients impact model performance in Table 4. Specifically, we compare the model accuracy under two datasets in different proportions of knowledge hoarding (denoted by K-H for simplicity) and free-riding (denoted by F-R for simplicity) behaviors.

Table 4 Proportion analysis.

The results shows that knowledge hoarding causes accuracy reduction when dominant. Our method can maintain 80% accuracy even with 50% knowledge hoarding clients, demonstrating the effectiveness of our dynamic screening mechanism. When free-riding behavior dominants, our method can effectively filter free riders and maintain high accuracy.

Finally, we conduct sensitivity analysis to evaluate how hyperparameter variations impact system performance in Table 5.

Table 5 Hyperparameter sensitivity analysis.

The decay rate $\lambda$ controls the penalty for intermittent participation. At $\lambda =0.2$, the framework achieves optimal accuracy with a balanced participation rate and malicious client filtration. Lower $\lambda$ values reduce penalties for free-riders, allowing more intermittent clients to participate but compromising accuracy. Conversely, higher $\lambda$ aggressively filters inactive clients, decreasing participation and causing lack of diverse updates. This highlights a critical trade-off, i.e., moderate $\lambda$ values effectively suppress free-riding while preserving sufficient client diversity for robust federated training.

The price sensitivity parameter $\kappa$ governs how payment adapts to contribution changes. Higher $\kappa$ increases average contribution score by 5.6% through stronger rewards for high contributors, but over-penalization reduces participation. Lower $\kappa$ reduces payment differentiation, leading insufficient suppression of low-quality updates. The optimal $\kappa$ balances contribution-based pricing while preserving client engagement.

The robustness factor parameter $\delta$ in the pre-screening mechanism determines baseline accuracy thresholds. Loose screening is insufficient to suppress malicious clients, which leads to the decline of model accuracy. Although strict screening eliminates malicious clients, the model accuracy also declines due to excessive client exclusion which leads to lacking of diverse updates.

Ablation study

In this subsection, we conduct ablation study to analyze the impact of participant screening mechanism. We compare the model accuracy in three scenarios under the two datasets, i.e., without pre-screening mechanism only, without confidence attenuation monitoring only, and with both pre-screening mechanism and confidence attenuation monitoring. We show the results in Fig. 3.

Fig. 3

Ablation study of our method.

• 1. The effectiveness of pre-screening mechanism. Compared with the result of accuracy of our method with both pre-screening mechanism and confidence attenuation monitoring, removing pre-screening mechanism reduces accuracy by 9.3% under MNIST and 9.7% under CIFAR-10. Pre-screening mechanism prevents clients from degrading update quality. Knowledge hoarding clients may have negative effect on the overall training performance.

• 2. The effectiveness of confidence attenuation monitoring. Compared with the result of accuracy of our method with both pre-screening mechanism and confidence attenuation monitoring, we further disable the confidence attenuation monitoring and the model accuracy decreases by 7.6% under MNIST and 7.8% under CIFAR-10. The confidence attenuation monitoring can effectively filter free riders and thus can keep high quality updating.

Conclusion

This paper proposes a novel incentive mechanism for foundation model enabled cross-silo federated learning, addressing critical challenges of knowledge hoarding and free-riding. We propose a dynamic participant screening mechanism which filters malicious clients, effectively suppressing low-quality updates. We also propose a cost-benefit balanced contribution metric to quantify the contribution of clients. Finally, we model the incentive mechanism as a two-stage Stackelberg game and propose the incentive mechanism algorithm. Experimental results demonstrate that our method can achieve 85.5% accuracy on CIFAR-10 and 88.0% accuracy on MNIST, outperforming the performance of existing incentive mechanisms. Our method can filter malicious clients by up to 96% while other incentive mechanisms cannot effectively filter malicious clients. The ablation study validates the effectiveness of our method. For future work, it is interesting to analyze the incentive mechanism of foundation model enabled cross-silo federated learning in incomplete information scenario.