Introduction

Decomposition of soil organic carbon (SOC) is fundamental for regenerating nutrients by plants and microbes1,2. To proceed with the decomposition process, soil microbes such as bacteria and fungi secrete a wide range of extracellular hydrolases that catalyze the release of nutrients and break down polymerized soil organic matter (SOM) into assimilable small molecules (i.e., sugars, amino acids, etc.)3. The hydrolases are involved in carbon (C), nitrogen (N), and phosphorus (P) turnover in soils4,5,6. Despite recent progress, knowledge of hydrolases’ activities such as their responses to N fertilization in bioenergy croplands is scarce7. Furthermore, due to the large difference of bioenergy crops in physiology, morphology and chemistry8,9,10it is imperative to elucidate the responses of hydrolases’ activities under N fertilization in different bioenergy croplands.

Extracellular hydrolases catalyze hydrolytic reactions and typically cleave C-O and C-N bonds11,12. The N-acquisition hydrolases include N-acetylglucosaminidase (NAG), urease (UREA), and peptidase leucine amino peptidase (LAP)13. NAG targets chitin and the hydrolysis of terminal, non-reducing β-N-acetylglucosamine residues14UREA catalyzes the hydrolysis of urea ((NH2)2CO) into carbon dioxide and ammonia15,16and LAP targets protein and catalyzes the hydrolysis of leucine residues17. The acid phosphatase (AP) and alkaline phosphatase are involved in P cycling and AP cleaves PO43− from organic phosphates at an acid pH18,19.

N fertilization generally increased the hydrolases associated with C and P acquisitions7. Reports showed that invasion of an N-fixing tree species dramatically increased the activity of AP20. However, the effects of N fertilization on hydrolases associated with N-acquisition were statistically insignificant7and this meta-analysis suggested highly varied responses of hydrolases associated with N-acquisition across different ecosystems. For instance, N addition depressed proteolytic hydrolase activities (i.e., LAP) in a semiarid grassland soil21 and NAG activities in a boreal forest soil in Alaska, USA22. But NAG activities were stimulated by 14% in a temperate hardwood forest17.

Plot-level spatial heterogeneity refers to the degree of variation in specific soil properties across different locations within a research plot. Areas with sharply contrasting values among scattered points indicate high spatial heterogeneity, while a uniform distribution of values signified low spatial heterogeneity23. The spatial heterogeneity and spatial variability or variation are interchangeable in this study. Besides the typical geostatistical methods (e.g., kriging map and surface trend), the coefficient of variation (CV) and the derived sample size requirement (SSR) provided a simple way to describe spatial heterogeneity in this study (see Methods for details).

N fertilization could increase spatial heterogeneity of hydrolases associated with C acquisition in bioenergy croplands24but little is known about hydrolases associated with N and P acquisitions. Studies also reported that high N deposition homogenized the spatial pattern of soil hydrolases25. However, multiple studies reported that N fertilization could increase spatial heterogeneity of soil microbial biomass, given the strong influence of soil pH, nutrient availability, and soil organic matter, particularly driven by the intensified fine-scale distributions of these variables under N fertilization26,27,28. Given the expected positive relationship between microbial biomass and soil extracellular enzyme activities29N fertilization is projected to re-establish spatial heterogeneity of soil enzyme activities. Thus, knowledge of the spatial pattern of hydrolases will further our understanding of nutrient cycling in soil and help refine best management practices for fertilization. For instance, from manually applying fertilizer to a well-controlled stratified fertilization via seed/fertilizer dispenser may help diminish sharp gradients or hot spots of nutrients, facilitate uniform nutrient supply, and likely enhance soil quality and carbon sequestration. Especially in physiologically contrasting bioenergy croplands such as switchgrass (SG: Panicum virgatum L.) and gamagrass (GG: Tripsacum dactyloides L.)8,9SG root has a smaller molecular weight and less complex molecular structure of dissolved organic matter (DOM), higher percent tyrosine-like DOM, and lower percent tryptophan-like DOM than GG root8. Understanding the spatiotemporal patterns of hydrolases under N fertilization can shed insights into the enzymatic control of soil C and N sequestration in bioenergy croplands.

A three-year N fertilization experiment was initiated at Tennessee State University’s campus farm in Nashville, TN. Three fertilization rates (i.e., no input, low input, and high input) and two bioenergy croplands (SG and GG) were implemented in the experiment using a complete random block design. The activities of soil hydrolases associated with N and P cycling (LAP, NAG, UREA, and AP) were assayed. This study aims to examine how N fertilization affects the central tendency and spatial distribution of hydrolases associated with N and P acquisition. We hypothesized that N fertilization would increase the activities of hydrolases catalyzing P acquisition and decrease the activities of hydrolases catalyzing N acquisition. Second, we hypothesized that the effects of N fertilization would be more pronounced in SG than in GG, that is, there would be significant interactions between N fertilization and crop types on hydrolases’ activities given the contrasting plant characteristics and root morphology, chemistry, and physiology8,9,10; Third, we hypothesized that N fertilization would result in soils with more apparent spatial heterogeneity of all hydrolases given the increased spatial variability of microbial biomass and the positive relationship between hydrolases and microbial biomass. It is also expected that N fertilization effects on central tendency and spatial heterogeneity vary with enzyme type (e.g. LAP, NAG, AP, and UREA) due to the unique characteristics of each enzyme.

Materials and methods

Site characteristics and field experiment design

The site condition and experimental design were described in detail in Duan, et al.30. Seeds of “Alamo” switchgrass and gamagrass were planted (6.9 kg pure live seed ha− 1) in a field plot in spring 2011, and these stands were established in 2012. In 2011, N fertilization of 67 kg N ha− 1, the typical recommended application rate, was applied to improve the stand establishment. In 2012, a bioenergy crop field fertilization experiment was established at the Tennessee State University (TSU) Main Campus Agriculture Research and Education Center (AREC) in Nashville, TN, USA. Before the croplands, the land was mowed grassland for several decades with no amendment of fertilizer, and the indigenous variations are assumed to be similar before bioenergy croplands were established. During 2011–2012, the two crops were planted and maintained to secure the plant establishment evenly and across the experimental area before any treatment deployment. Although there was no formal quantification of spatial distribution and heterogeneity before the experiment, the perennial bioenergy crops were successfully established, uniformly managed, and experienced the same climate conditions before the start of the N fertilization treatment in the experimental area. Nevertheless, the establishment of crops further altered the original spatial patterns of grassland soils. These changes were presumably distributed homogenously in all treatment plots, given the uniform and standard management practices during the crop planting and maintenance toward successful establishment. Each year, switchgrass was harvested once to ~ 15 cm height in December, following the first killing frost, and the harvested biomass was removed out of the research plot.

In a randomized block design, two perennial bioenergy grass crops, Alamo SG (Panicum virgatum L.) and GG (Tripsacum dactyloides L.) and three N levels including no N fertilizer input (NN), low N fertilizer input (LN: 84 kg N ha− 1 yr− 1 as urea), and high N fertilizer input (HN: 168 kg N ha− 1 yr− 1 as urea) were replicated four times. A total of 24 plots were established for the original experiment (i.e., 2 crop × 3 N × 4 replicates) as depicted in Fig. 1. The experimental site was located in a warm, humid temperate climate with an average annual temperature of 15.1 °C, and total annual precipitation of 1200 mm31. The fertilizer was manually applied in June or July each year after cutting the grass. The soil series for the plots is Armour silt loam soil (fine-silty, mixed, thermic Ultic Hapludalfs) with acidic soil pH (i.e., 5.97) and intermediate organic matter content of 2.4%32,33,34.

Fig. 1
figure 1

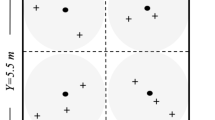
Illustration of experimental plots and layout (above) and an efficient stratified and clustered random sampling design within a plot (bottom; 5.5 m × 2.75 m). Twelve of 24 plots in the experiment were selected for this study by choosing two of four replicated plots under each N fertilization and crop type (i.e., P1 and P2). Each plot was divided into eight subplots (grey zone) and there was a centroid (dark solid circle) in each subplot (1.375 m × 1.375 m), where three soil sampling points (diamonds) were determined from random directions and distances from a centroid in each sampling region (grey area). The extent of an interpolation map was thus determined by the minimum and maximum values at horizontal and vertical axes, and each map can attain its extent less than or equivalent to a plot area. NN, LN and HN denote no fertilization, low and high fertilization treatments; SG: switchgrass; and GG: gamagrass.

Full size image

Soil sampling and chemical analysis

Details of soil collection can be found in Duan, et al.30 and here is a brief description. For the current study, two replicated plots were identified to conduct intensive soil sampling in each plot (Fig. 1), which was not an ideal experimental design. Given the high demands for labor and resources in each plot, the current sampling density was required to detect the plot-level spatial distribution. The relevant issue of statistical analysis was addressed in the next section. For each N treatment and crop type, two of four replicated plots (i.e., P1 and P2) were selected randomly from the original experiment plots (Fig. 1). Twenty-four cores were collected from each plot, yielding 288 soil cores in 12 plots. The soil samples were collected using a stratified and clustered sampling method during the growing season before the fertilization in September. On June 6th, 2015, soil cores were collected from 0 to 15 cm depth using a soil auger (Thermo Fisher Scientific, Waltham, Massachusetts, USA) from 12 plots (2 crop × 3 N × 2 replicates). Within each plot, a sampling area of 2.75-m × 5.5-m rectangle was determined, and the southwestern corner point was identified as the origin. Each plot was divided into two-square subplots, and within each subplot, four centroids were determined, and three cores were collected randomly, given random direction and distance relative to each centroid (Fig. 1). When a soil core was collected, we recorded its location in reference to the origin taken as the southwestern corner, i.e., each sampling point had a unique x, y coordinates. Soil samples were stored at 4 ˚C for chemical analysis after roots and rocks were removed and passing through a 2 mm soil sieve.

Using soil fluorimetric enzymatic assay methods17four hydrolytic activities associated with N and P acquisitions were quantified. They include leucine aminopeptidase (LAP), β-N-acetylglucosaminidase (NAG), acid phosphatase (AP) and urease (UREA). Substrates were L-Leucine-7-amido-4-methylcoumarin hydrochloride, 4-Methylumbelliferyl N-acetyl-β-D- glucosaminide, 4-Methylumbelliferyl phosphate and urea each with the concentration of 200mmol/L. Fluorescence was measured using a Molecular Devices (Multi-Mode Microplate Reader, FilterMaxF5), with excitation set to 365 nm and emission set to 460 nm for LAP, NAG and AP and absorbance set to 610 nm for UREA. All enzyme activities were calculated as µmol activity h− 1 g soil− 1. The activities of N-acquisition enzymes LAP and NAG were summed as Nacq.

Descriptive and statistical analyses

A two-way analysis of variance (ANOVA) was used to test whether N fertilization, crop species and their interaction significantly affected each enzyme. To avoid the pseudo-replication impacts, the plot means were used in the two-way ANOVA test8. Using plot level means (i.e., 24 samples in each plot) satisfied the underlying statistical assumptions of the normality and the homogeneity of variance tests based on the Shapiro-Wilk test and chi-Square statistics (p-value > 0.05). The significance level for the ANOVA test was set at P < 0.05 and the analysis was conducted using R project35. Post-hoc tests were conducted to compare group means using the Tukey HSD method when the main or interactive terms were significant.

The within-plot variation was explored by Cochran’s C test and sampling size requirement. The former was performed to test the assumption of variance homogeneity, and the latter a quantitative estimate of the sample number required under a given desired sampling error. The details of the relevant method, formula, and calculation can be found in our former publications30,36. Briefly, the Cochran’s C test is used to test the assumption of variance homogeneity. The test statistic is a ratio that relates the largest empirical variance of a particular treatment to the sum of the variances of the remaining treatments. The theoretical distribution with the corresponding critical values can be specified37,38,39. Soil properties that exhibited non-normal distributions were log-transformed to better conform to the normality assumption of the Cochran’s C test36.

The study also derived the sample size requirement (\(\:N\)) in each plot, given specified relative errors (\(\:{\upgamma\:}\), 0 ~ 100%) in order to evaluate how within-plot variances (i.e.,sample size requirements) are altered by N fertilization or crop types at a certain relative error.

$$\:\text{C}\text{I}=\:\overline{X}\pm\:\:{t}_{0.975}\times\:\frac{s}{\sqrt{n}}$$
(1)
$${\upgamma } = {\text{~}}\frac{{t_{{0.975}} \times \frac{s}{{\sqrt N }}~}}{{\overline{X}}} = ~t_{{0.975}} \times \frac{{CV}}{{\sqrt N }}$$
(2)
$$\:\text{ln}\left(\text{N}\right)=2\times\:\text{ln}\left({t}_{0.975}\times\:\text{C}\text{V}\right)-2\times\:\text{l}\text{n}\left({\upgamma\:}\right)$$
(3)

Where \(\:\text{C}\text{I},\) \(\:\overline{X,}\) \(\:s,\:\) \(\:n,\) \(\:N,\:\) \(\:CV,\) and \(\:{\upgamma\:}\) denote confidence interval, plot mean, plot standard deviation, sample number (n = 24), sample size requirement, coefficient of variation, and relative error, respectively. \(\:{t}_{0.975}\) = 1.96. The log transformed sample size requirement (\(\:N\)) has a negative linear relationship (i.e., slope = 2) with the log transformed relative error (\(\:{\upgamma\:}\)). To note, the coefficient of variation (CV) precisely describes the contrasting quantity of certain features at the sampling locations only, and though it could be an indicator of spatial variability, but not necessarily reflect the plot-level spatial heterogeneity. For instance, under a specific practice (e.g., N fertilization), a declining CV could be achieved because of the similar values at the sampling locations, but these locations could just represent a part of a more scattered distribution of locations with similar low or high values relative to other locations seen from the plot level, possibly creating more fine-scale spatial heterogeneity. Precisely, the larger CV, the greater number of SSR.

Geostatistical analyses

The spatial distributions of each enzyme within each plot were derived using three geostatistical methods including the trend surface analysis (TSA), the Moran’s I index, and the inverse distance weighting (IDW) interpolation, as previously described30,36. A brief description of each method was presented below.

First, using the trend surface analysis (TSA), all sample points in a plot fit a model that accounts for the linear and non-linear variation of an enzyme. The relationships between the soil properties and the x and y coordinates of their measurement location within the sampling plots are estimated with the trend surface model:

$${\text{Soil }}\,{\text{property}}\,{\text{ value}} = b_{0} + b_{1} x{\text{ }} + b_{2} y{\text{ }} + b_{3} xy{\text{ }} + b_{4} x^{2} + b_{5} y^{2}$$
(4)

The presence of a trend in the data was determined by the significance of any of the parameters β1 to β5, while the β0 term modeled the intercept40,41. Linear gradients in the x or y directions were indicated by significance of the β1 or β2 parameters. A significant β3 term indicated a significant diagonal trend across a plot. Significant β4 and β5 parameters indicated more complex, polynomial spatial structure such as substantial humps or depressions. Trend surface regressions were estimated using R version 4.4.2 program35. Model parameters were determined to be significant at a level of P < 0.05. The significant TSA coefficients represented detectable spatial heterogeneity either as continuous changes in certain directions or as scattered high or low value of patches in a plot. The larger number of significant coefficients indicated the high spatial heterogeneity.

Second, residuals from the trend surface regressions were subjected to spatial analysis using a Moran’s I index41. The Moran’s I analysis42,43,44 quantifies the degree of spatial autocorrelation that existed among all soil cores taken from each plot. The resulting local Moran’s I statistic ranges from − 1 to 1. Positive Moran’s I value indicates similar values (either high or low) are spatially clustered. Negative Moran’s I value indicates neighboring values are dissimilar. Moran’s I values of 0 indicates no spatial autocorrelation or spatial randomness. A significant autocorrelation is determined if the observed Moran’s I value is beyond the projected 95% confidence interval at a certain distance. Correlograms for local Moran indices were estimated for each soil enzyme in each plot in a range of 0–5.5 m with 0.25-meter incremental interval. The larger number of significant Moran’s I values indicated the high spatial heterogeneity.

Third, we used inverse distance weighting (IDW) interpolation rather than ordinary kriging to derive spatial distribution maps due to relatively small sample sizes (n = 24) per plot45. The weights for each observation are inversely proportional to a power of its distance from the location being estimated. Exponents between 1 and 3 are typically used for IDW, with 2 being the most common46. Tests with different IDW exponents indicated that 2 was optimal with these data, as estimated values generated with an exponent of 2.0 showed the best fit with actual data in cross-validation tests. The maps produced by IDW offered direct and visual assessments to compare the spatial distributions of soil enzymes among the plots. ArcGIS 9.0 (ESRI, USA) was used to generate IDW maps and perform cross-validation. If the IDW maps showed more scattered high or low value patches in a plot, it indicated high spatial heterogeneity; the more smaller size patches, the higher spatial heterogeneity.

Results

Fertilization and crop type effects on N- and P-hydrolases

Across all treatments, significant main effect of N fertilization and interactive effects of N fertilization and crop species were identified for LAP (P < 0.05; Table 1). Post hoc tests showed that HN significantly escalated LAP activities by 54% in SG but not in GG (P < 0.05; Table 2). Significant crop type effects were identified for NAG and Nacq (P < 0.05; Table 1) such that these enzymes’ activities in GG were higher than in SG by 26% and 22%, respectively (Table 2).

Table 1 P-values of two-way ANOVA tests for the main and interactive effects of N fertilization and crop species on LAP, NAG, Nacq, AP and UREA (µmol g−1 soil h−1).
Full size table
Table 2 Means (±SE) of LAP, NAG, Nacq, AP and UREA (µmol g−1soil h−1) under three N fertilization treatments (NN, LN and HN) in two bioenergy croplands (SG and GG).
Full size table

Plot-level variance

Despite the large plot-to-plot variations within each treatment for both crops, Cochran’s C tests showed there were significant differences in homogeneity between treatments in each crop type (Table 3). The within-plot CVs of both N- and P-hydrolases ranged from 15 to 50%, but it was always beyond 20% for UREA (Fig. 2). Except for UREA, the CVs of all enzymes under NN were generally higher than LN and HN in SG plots, but not in GG plots (Fig. 2). Accordingly, the sample size requirement for most hydrolases was higher for NN than LN or HN in SG cropland, but not in GG (Table 4; Figure S1). Comparing two crops, a larger number of samples was required for SG than for GG under the same N fertilization treatment given the same desired relative error, e.g., 10%, except UREA (Table 4). In general, the sample sizes varied with different enzyme types, and given the 10% relative error, the number of samples needed ranged from less than 10 to more than 100, depending on the enzyme type, crop type, or N fertilization treatment (Figure S1).

Table 3 Comparison of the variances and cochran’s C test results for LAP, NAG, Nacq, AP and UREA (µmol g− 1soil h− 1) under three N fertilization treatments (NN, LN and HN) in two bioenergy croplands (SG and GG).
Full size table
Fig. 2
figure 2

Within-plot CVs of LAP, NAG, Nacq, AP and UREA under three N fertilization treatments (NN, LN and HN) in two bioenergy croplands (SG and GG). The dashed lines represent a CV of 20% and 40%. The abbreviations are referred to the Methods section.

Full size image

The abbreviations are referred to in the Methods section.

Table 4 Sample size requirement for LAP, NAG, Nacq, AP and UREA (µmol g− 1 soil h− 1) under the relative error of 10% under three N fertilization treatments (NN, LN and HN) in two bioenergy croplands (SG and GG).
Full size table

Spatial distribution of hydrolases

Trend surface analysis (TSA) results showed significant linear or nonlinear trends only in some plots for some enzymes (Table S1) and the sum of number of significant linear or nonlinear trends varied between the two replicated plots (P < 0.05; Table 5). In SG, there were more significant linear or nonlinear surface trends of hydrolases in NN plots than LN and HN plots. Whereas in GG, there was no distinct pattern among different N treatments (Table 5). As for the spatial autocorrelation (i.e., Moran’s I), there were overall a greater number of significant autocorrelations in SG than GG and the number of significant autocorrelations varied from plot to plot in each cropland (Table S2). Compared to NN, fertilized treatments (LN or HN) had a higher number of significant spatial autocorrelations of LAP, NAG, Nacq, and AP in SG, and of NAG, Nacq, and AP in GG (P < 0.05; Table 5). The distances in which the significant spatial autocorrelations ranged from − 5.25 m to 5 m across all enzymes (Figure S2 ~ 6).

Table 5 The number of significant regression coefficients of trend-surface analysis and moran’s I for LAP, NAG, Nacq, AP and UREA (µmol g− 1soil h− 1) under three N fertilization treatments (NN, LN and HN) in two bioenergy croplands (SG and GG).
Full size table

The IDW maps of AP and LAP exhibited higher activities (e.g., darker color) in GG than those in SG (Figs. 3 and 4). In SG, the IDW maps for most glycosidases exhibited low to high activities (e.g., shallower and gradually darker colors) from NN, through LN, to HN plots (Fig. 3). In GG, the color regimes appeared different in spatial distribution and pattern, but the plot-level heterogeneity seemed comparable among all plots for each enzyme (Fig. 4).

Fig. 3
figure 3

Spatial distributions of LAP, NAG, LAP, UREA, AP and Nacq activity in soils under three N fertilization treatments (i.e. NN, LN and HN) in SG. The interpolation maps were produced by inverse distance weighting (IDW) method using ArcGIS software by Esri (version 10.2.1, http://www.esri.com). The abbreviations are referred to Method section.

Full size image
Fig. 4
figure 4

Spatial distributions of LAP, NAG, LAP, UREA, AP and Nacq activity in soils under three N fertilization treatments (i.e. NN, LN and HN) in GG. The interpolation maps were produced by inverse distance weighting (IDW) method using ArcGIS software by Esri (version 10.2.1, http://www.esri.com). The abbreviations are referred to Method section.

Full size image

Discussions

Little responses to N fertilization of most hydrolases associated with N and P acquisitions

The first hypothesis of hydrolases’ activities in response to N fertilization was not exclusively supported. Rather than a decrease, LAP was significantly increased under HN in SG. Also, NAG, UREA, and AP elicited insignificant responses to N fertilization. These suggested little effects of N fertilization on average activities of most hydrolases associated with N and P acquisitions. The increased LAP with N fertilization, a pattern like a C-acquisition enzyme β-xylosidase (BX) in diverse terrestrial ecosystems7,24,47is likely a result of reduced allocations of energy and resource to enzymes that function to acquire organic N given the readily available N, thus stimulating C-acquisition glycosidases48. Strikingly, we suspect that the N fertilizer type may control the response of LAP. In these studies with significantly decreased LAP activities under N fertilization, the N fertilizer used were either ammonium nitrate (NH4NO3)22,47,49,50 or sodium nitrate (NaNO3 )17,51. In our study, urea (e.g., CH4N2O) was employed. The bulk of organic N in soil is thought to be in amide (CO-NH) form, either as peptide or non-peptide C–N bonds52. Nitrate (NO3− ) is the form of N that can be absorbed directly by plants53. Yet for urea to be absorbed by plants, it first needs to be converted by soil enzymes to ammonia54. Therefore, it is possible that when urea was applied in soil, LAP, as an N-acquisition enzyme was stimulated to fill the gap during the N conversion from organic to inorganic form. That is, the organic N input may override the allocation theory which is valid under the inorganic N input. Given the sampling date in June and fertilization amended in the previous September, the N availability may remain relatively low due to N leaching, plant uptake, and N-containing gas emission.

NAG, as another N-acquisition enzyme, was not affected by either LN or HN fertilization. The contrasting sensitivities of LAP and NAG may be due to the different microbes that produce them, chemical structure and substrate preference, and edaphic conditions. The decreased NAG activities under N fertilization was attributed to the depressed ectomycorrhizal taxa Cortinariaceae22which were known to produce extracellular enzymes that facilitate organic N decomposition55,56. Due to the nature of chemical structure, LAP targets on protein and NAG on chitin57. As a result, different substrates require enzymes to cleave different bonds thus demanding variable energy costs14. Last, Saiya-Cork, et al.17 found increased LAP activity and decreased NAG in litter layer, along with an opposing pattern for the two enzymes in soil. The two enzymes’ opposite responses, particularly variable NAG response to N fertilization across studies may lie in a high interaction of climatic, physiological, and edaphic conditions.

LAP responses to N fertilization were evident in switchgrass plots

Supporting our second hypothesis, the activities of LAP were significantly elevated by N fertilization only in SG plots, suggesting differential response mechanisms of hydrolases in SG and GG bioenergy crops. Despite limited research in bioenergy croplands, the influence of plant litter and root exudates on soil microbial communities has been widely verified in other ecosystems58,59,60,61,62. It has been reported that plant tissue quality determined hydrolase activity in response to N additions63,64,65. Compared to GG, SG root has smaller molecular weight and less complex molecular structure of dissolved organic matter (DOM), higher percent tyrosine-like DOM and lower percent tryptophan-like DOM8. Thus, relatively labile C and N through root input might be found in SG soil, whereas more recalcitrant substrates in GG soil, consistent with higher SOC and TN contents in GG than SG soil8. Given the close relationship between agriculturally relevant microbial taxa and crop type66we speculate that microbes targeting labile substrates might dominate in SG relative to GG. When N fertilizer was applied and provided readily available N, microbes in SG could elicit responses to a greater extent.

N fertilization reestablished spatial distribution of hydrolases but had mixed effects on their abundance

In support of our third hypothesis, more apparent spatial heterogeneity of N- and P-hydrolase activities (except UREA) was evident with either low or high N fertilization. This is consistent with the effects of N fertilization on microbial biomass C and N33 and SOC and TN68but was distinct from that on the oxidases30. The concerted responses of N- and P-hydrolases with microbial biomass and bulk soil C and N stocks suggested that hotspots created by manual fertilization alter and restructure these key microbial and ecosystem characteristics. At the locations of receiving N input in a plot, the high responsiveness of soil microbial community features (e.g., abundance and activity) could have potentially neutralized the general prediction of plot level homogenization under N fertilizations36,69,70. On the other hand, the stimulated hydrolases may have been accompanied by less microbial demand for oxidases based on the allocation theory17,71,72. As a result, the depressed spatial heterogeneity of oxidases in SG, as revealed in our former study30appeared to be the reciprocal reflection of the influence of N fertilizers on hydrolases. This reconciliation of opposing responses of spatial distribution in multiple soil enzymes corroborated the key influence of fertilization management in determining soil nutrients status and their supply.

Based on an adjacent field experiment with biochar and N fertilization amendments, there was no significant effect of N fertilization on SG biomass73. At the same research farm, a microcosm study with fly ash and poultry litter amendment, however, indicated higher proportional biomass accretion of GG than SG relative to their respective controls67. The same study also revealed consistently higher root/shoot ratios for GG than SG (1.6 ~ 2.1 vs. 0.9 ~ 1.2)67. These suggested that both crops’ biomass was most likely unresponsive to N fertilization due to compounded mixed effects of soil, time, and climate variability. The slight acidity at the site (soil pH = 5.97) rendered soil microbial communities unable to thrive below an optimal pH range of 6.2–7.574,75. This acidity not only reduced most nutrient availability but also induced less efficient nutrient uptake by microbes and plant roots76. Despite the silt loam soil texture and soil moisture and temperature at the sampling date (e.g., June) favored soil microbial activities, soil pH may override the impacts of soil type and climate. Because both crops grow in a clustered manner, that is, multiple plant stems sharing a massive root volume, it appeared plausible for both crops’ root development that tended to restructure the spatial distribution of most soil enzymes, resulting in large plot-to-plot variations. The biomass harvested without residue retention in the plots can potentially stimulate root development for nutrient acquisition at deeper soil depths and larger soil volumes.

Given the history of land use of the study site, a similar extent of spatial heterogeneity was believed to remain valid across all treatments when the experiment was deployed. Overall, this study revealed large plot-to-plot spatial variations and the escalated variation in soil hydrolyses with N fertilization in these bioenergy croplands, particularly in SG. NAG and Nacq were significantly more abundant in GG than in SG soils. LAP appeared to be highly responsive to N fertilization, and was marked with a 54% increase in SG soils. Overall, this study suggested greater sensitivity and responsiveness of spatiotemporal dynamics to N fertilization in SG cropland. Taken together, a specific peptidase (i.e., LAP) shall receive more studies under intensive fertilization in SG soil. Future research should explore the relationships between hydrolase activities and soil organic C and N, particularly by integrating root morphology, chemistry, and physiology with soil and ecosystem processes to enhance soil C and N sequestration in bioenergy croplands. To improve experimental rigor, future studies should also prioritize increasing field replications and the frequency of soil and plant sampling. Limited by the number of field replicates and the single soil sampling in this study, cautious interpretation and application are anticipated.