PolSAR image classification using shallow to deep feature fusion network with complex valued attention

Abstract

Polarimetric Synthetic Aperture Radar (PolSAR) images encompass valuable information that can facilitate extensive land cover interpretation and generate diverse output products. Extracting meaningful features from PolSAR data poses challenges distinct from those encountered in optical imagery. Deep Learning (DL) methods offer effective solutions for overcoming these challenges in PolSAR feature extraction. Convolutional Neural Networks (CNNs) play a crucial role in capturing PolSAR image characteristics by exploiting kernel capabilities to consider local information and the complex-valued nature of PolSAR data. In this study, a novel three-branch fusion of Complex-Valued CNN named (CV-ASDF2Net) is proposed for PolSAR image classification. To validate the performance of the proposed method, classification results are compared against multiple state-of-the-art approaches using the Airborne Synthetic Aperture Radar (AIRSAR) datasets of Flevoland, San Francisco, and ESAR Oberpfaffenhofen dataset. Moreover, quantitative and qualitative evaluation measures are conducted to assess the classification performance. The results indicate that the proposed approach achieves notable improvements in Overall Accuracy (OA), with enhancements of 1.30% and 0.80% for the AIRSAR datasets, and 0.50% for the ESAR dataset. However, the most remarkable performance of the CV-ASDF2Net model is observed with the Flevoland dataset; the model achieves an impressive OA of 96.01% with only a 1% sampling ratio. The source code is available at: https://github.com/mqalkhatib/CV-ASDF2Net

Introduction

Polarimetric Synthetic Aperture Radar (PolSAR) images offer a specialized perspective in microwave remote sensing by capturing the polarization properties of radar waves, which provides detailed insights into Earth’s surface features, such as vegetation¹, water bodies², and man-made structures³. PolSAR images tackle the limitations of optical remote sensing images, which are susceptible to changes in illumination and weather conditions. Unlike optical systems, PolSAR is capable of functioning under all weather conditions and possesses a robust penetrating capability⁴. Moreover, PolSAR outperforms conventional SAR systems by comprehensively capturing extensive scattering information through four different modes. This enables the extraction of a wide range of target details, including scattering echo amplitude, phase, frequency characteristics, and polarization attributes⁵. Nowadays, PolSAR imagery has numerous applications in environmental monitoring⁶, disaster management⁷, military monitoring^8,9, crop prediction^10,11, and land cover classification¹².

PolSAR image classification is the task of classifying pixels into specific terrain categories. It involves analyzing the polarization properties of radar waves reflected from the Earth’s surface. This classification helps automate the identification and mapping of land cover for many applications. Conventional approaches to PolSAR image classification primarily rely on extracting distinctive features through the application of target decomposition theory¹³. The Krogager decomposition model, for instance, segregates the scattering matrix into three components: helix, diplane, and sphere scattering mechanisms¹⁴. Another widely used method is the Freeman decomposition¹⁵, which dissects the polarimetric covariance matrix into double-bounce, surface, and canopy scattering components. Yamaguchi et al.¹⁶ enhanced the Freeman decomposition by introducing a fourth scattering component known as helix scattering power, which proves more advantageous in the classification of PolSAR images. Additionally, the Cloude decomposition¹⁷ stands as a common algorithm for PolSAR image analysis. Despite the popularity of traditional classifiers like Support Vector Machine (SVM)¹⁸ and Decision Trees¹⁹ for PolSAR classification, challenges arise when dealing with PolSAR targets characterized by complex imaging mechanisms. This complexity often leads to inadequacies in representing these targets using conventional features, which leads to a decline in classification accuracy.

Recently, Deep Learning (DL) technology has shown remarkable effectiveness in PolSAR image classification^20,21. Specifically, Convolutional Neural Networks (CNNs) have exhibited impressive performance in this domain^4,22. For example, Chen and Tao²³ successfully applied the roll-invariant features of PolSAR targets and the concealed attributes within the rotation domain to train a deep CNN model. This approach contributed to an enhanced classification performance. Zhou et al.²² derived high-level features from the coherency matrix using a deep neural network comprising two convolutional and two fully connected layers, specifically tailored for the analysis of PolSAR images. Radman et al.²⁴ discussed the fusion of mini Graph Convolutional Network (miniGCN) and CNN for PolSAR image analysis. Spatial features from Pauli RGB and Yamaguchi were fed into CNN, and polarimetric features were utilized in miniGCN. The study aims to address the limitations of traditional PolSAR image classification methods and presents a dual-branch architecture using miniGCN and CNN models. Dong et al.²⁵ introduced two lightweight 3D-CNN architectures for fast PolSAR interpretation during testing. It applies two lightweight 3D convolution operations and global average pooling (GAP) to reduce redundancy and computational complexity. The focus of this study is on improving the fully connected layer, which occupies over 90% of model parameters in CNNs. The proposed architectures use spatial global average pooling to address the computational difficulties and over-fitting risks associated with a large number of parameters.

Phase information, a distinctive feature of SAR imagery, is crucial for applications such as object classification and recognition²⁶. Complex-Valued CNNs (CV-CNNs) have been explored for PolSAR data classification to address challenges unique to this domain^5,27,28,29. Unlike traditional CNNs, CV-CNNs employ complex-valued filters and activation functions, enabling the simultaneous processing of phase and amplitude information, which is essential for accurate classification. However, training CNNs requires substantial data, and the limited availability of high-quality ground reference data often leads to overfitting and unreliable parameters, making it critical to achieve high performance with minimal training samples. Handling complex-valued PolSAR data further complicates this task, as directly applying such data to real-valued networks typically discards the imaginary component. Approaches like transforming PolSAR data into real-valued vectors³⁰ or utilizing feature descriptors to generate real-valued feature maps^31,32 aim to preserve essential information during this transformation. To address these challenges, this paper proposes a novel Complex-Valued (CV) Module that combines a multi-branch fusion block to extract features at multiple depths, a CV Attention module for feature refinement. By utilizing phase information and employing multi-depth convolutions, the model achieves a balance between discriminative feature extraction and reduced complexity, resulting in enhanced classification performance.

Shallow networks excel at capturing simple features but struggle when confronted with more complex ones; hence, they are ideal for scenarios with limited datasets and computational constraints³³. These networks are highly interpretable and well-suited for applications where straightforward variable relationships prevail. However, Deep Neural Network structures can capture more complex features, excelling at extracting intricate patterns from vast datasets. The integration of information from various depths within a deep network facilitates efficient learning, which greatly improves the network’s ability to unravel the complex details of the dataset, even when working with a limited number of training samples³⁴. While shallow learning methods are effective for small datasets and problems with simple structure, DL expands the scope of Machine Learning (ML) by offering unparalleled accuracy in complex variable relationships. The trade-offs between shallow and DL approaches have been extensively studied in various fields, including anomaly detection, classification, and medical imaging³⁵. For instance, brain tumor classification and anomaly detection have demonstrated the capacity of shallow networks to offer quick, interpretable solutions with limited data, while DL models provide more detailed insights at the cost of higher computational requirements and reduced interpretability. The selection between shallow and DL methods often depends on specific problem characteristics, data availability, and computational resources, requiring careful consideration of the advantages and limitations of each approach.

In recent years, Attention-based techniques have also been widely employed in PolSAR image classification³⁶ to enhance the model’s ability to emphasize informative features and suppress less relevant ones by allocating more Attention to the most important features rather than treating the entire input uniformly, which in turn improves the overall classification performance³⁷. While attention mechanisms enhance feature selectivity in PolSAR classification, their effectiveness depends on optimal placement within the network. Many existing methods lack systematic analysis on attention placement, potentially leading to premature suppression of useful features. Additionally, most approaches operate in a real-valued space, limiting their ability to fully utilize complex-valued polarimetric information.

The motivation behind our work is to develop a PolSAR image classification model that performs effectively, even with a very small number of training samples. To address this challenge, we focus on enhancing the model performance by integrating shallow features with deep features. This approach utilizes the strengths of both shallow and DL layers, allowing for more robust classification despite limited data availability. Unlike most existing methods that rely on real-valued representations, our approach operates in a complex-valued space, which preserves critical polarimetric phase information that is essential for PolSAR classification. Additionally, by incorporating an Attention mechanism, we aim to further boost the model’s performance by enabling it to focus on the most relevant features and improve its ability to generalize. Furthermore, we introduce a multi-scale spatial-polarimetric integration strategy to effectively capture both local structures and global context, addressing a common limitation in existing deep learning-based PolSAR classification approaches. This integrated approach of feature fusion and Attention-driven refinement aims to significantly advance PolSAR image classification capabilities. To further enhance feature refinement, we propose a novel complex-valued attention mechanism, specifically designed for PolSAR processing, and strategically implement it after feature fusion to maximize its impact in refining discriminative features.

The main contributions of this research paper are demonstrated as follows:

• 1. A feature-learning network with multiple depths and varying layers in each stream is developed. This design enables filters to simultaneously capture shallow, medium, and deep properties, enhancing the utilization of complex information in PolSAR. Experimental results indicate that the proposed model exhibits superior feature-learning capabilities compared to the existing models in use.

• 2. Development and implementation of a Complex-Valued (CV) Attention mechanism that extends traditional real-valued attention by utilizing both amplitude and phase information, preserving the full complex structure of PolSAR data. This approach enhances feature discrimination and ensures a more effective representation of intricate polarimetric characteristics, leading to improved classification performance compared to conventional magnitude-based attention mechanisms.

• 3. Utilization of a median filter for post-processing, which enhances the final classification results by reducing noise and improving the overall quality of the output.

• 4. The proposed model surpasses current methods not only when dealing with a limited number of samples but also attains higher accuracy with an ample training dataset. This conclusion is drawn from statistical outcomes obtained through thorough trials on three PolSAR datasets (AIRSAR, ESAR, and Flevoland), which will be further elaborated and discussed in the subsequent sections.

Related work

This section offers a concise examination of the relevant literature on CNNs and Attention mechanisms, with a particular emphasis on the Squeeze-and-Excitation module.

Overview of CNNs

A standard CNN consists of an input layer, convolutional layers, activation layer, and an output layer. The initial input layer receives features from the image. Subsequently, convolutional layers employ convolutional kernels (illustrated in Fig. 1) to extract the input features. These kernels operate by taking into account neighboring pixels, considering spatially correlated pixels within a close range (as depicted by the $3\times 3$ grid in Fig. 1a). This approach enhances the network’s ability to capture spatially related features. However, 2D-CNNs process each band individually and fail to extract the polarimetric information provided by PolSAR images. To better process PolSAR images, researchers often turn to more advanced architectures, such as three-dimensional CNNs (3D-CNNs).

Figure 1

Illustration of different types of convolution on images with multiple channels.³⁸ (a) 2D convolution; (b) 3D convolution; (c) complex valued 3D convolution.

The application of convolution operations can be expanded into three dimensions, wherein calculations are conducted across all channels concurrently instead of handling each channel separately. Figure 1b visually depicts the concept of 3D convolution. In 3D convolution, the process encompasses height, width, and channels, making it a suitable approach for incorporating channel context. For an image represented as X with dimensions $N \times N \times B$ and a kernel denoted as K with dimensions $M \times M \times C$, the expression for 3D convolution at position (x, y, z) is given by Eq. (1).

$$\begin{aligned} F_{(x,y,z)} = \sum ^M_{i=1}\sum ^M_{j=1}\sum ^C_{k=1} K_{(i,j,k)}X_{(x+i,y+j, z+k)} + b, \end{aligned}$$

(1)

where b denotes the bias term, and the indices i, j, k iterate over the spatial and channel dimensions of the kernel. This operation enables the network to capture contextual information in both spatial and spectral domains simultaneously.

Although 3D-CNNs can capture features in a better fashion when compared to 2D-CNNs^39,40, the complex nature of PolSAR images, represented by complex-valued data, adds an extra layer of complexity when considering the use of 3D-CNNs for their processing. Compared to traditional CNNs, CV-CNNs have proven their superiority in PolSAR classification tasks^41,42. To fully explore the complex values in PolSAR data, we utilized CV-3D-CNN. For an image $X = \Re {(X)} + i\Im {(X)}$ and a kernel $k = \Re {(K)} + i\Im {(K)}$, the result of the complex convolution Y can be expressed in Eq. (2).

$$\begin{aligned} Y = X *K = \Re {(X)} *\Re {(K)} - \Im {(X)} *\Im {(K)} + i.(\Re {(X)} *\Im {(K)}) + i.(\Im {(X)} *\Re {(K)}), \end{aligned}$$

(2)

where $\Re {(.)}$ and $\Im {(.)}$ represent the real and the imaginary parts of a CV number, respectively, i is the imaginary number $\sqrt{-1}$, and Y can be expressed as $\Re {(Y)} + i.\Im {(Y)}$. This is also illustrated in Fig. 1c.

Attention mechanism for complex-valued PolSAR image classification

While CNNs have shown promising results in classifying PolSAR images, research on enhancing input identifiability during CNN development remains limited. To tackle this challenge, Dong et al.⁴³ proposed the integration of the Squeeze-and-Excitation (SE) module⁴⁴, which enhances CNN performance by selectively emphasizing critical features within the input data⁴⁵. Additionally, the SE module improves channel interdependencies with minimal computational overhead.

Most Attention mechanisms are primarily designed for real-valued data, which limits their effectiveness in processing PolSAR images. For example, Dong et al.⁴³ applied the SE block to real-valued features extracted from PolSAR data for classification tasks. On the other hand, researchers in³⁶ took a different approach by using coordinate Attention⁴⁶ to handle both the real and imaginary parts, separately, of PolSAR complex data for their classification efforts. This contrast underscores the need for developing Attention mechanisms that can fully utilize the distinct properties of complex-valued data in PolSAR image processing. Unlike real-valued attention mechanisms, which operate only on magnitude-based features, the proposed complex-valued attention mechanism uses both amplitude and phase information, enabling more effective feature discrimination in complex-valued data. Specifically, it preserves the full complex structure of PolSAR data, allowing it to capture more informative representations while maintaining consistency with the inherent properties of the data. This is a key improvement over real-valued attention blocks, which typically extract only magnitude-based features or require separate processing of real and imaginary components, potentially leading to information loss.

Given a transformation $F_{tr}$, which maps the complex-valued input $X \in \mathbb {C}^{H\times W\times C}$ to complex-valued feature maps $u_{c} \in \mathbb {C}^{H\times W}$, where $u_{c}$ represents the c-th $H \times W$ feature map and C denotes the number of channels. The SE module is modified to operate on complex-valued feature maps by separating them into real and imaginary components, such that $u_{c} = u_{c}^{Re} + j u_{c}^{Im}$, where $u_{c}^{Re}$ and $u_{c}^{Im}$ represent the real and imaginary parts, respectively.

During the Squeeze operation, GAP is applied to both real and imaginary components independently, transforming each $H \times W \times C$ feature map into a $1 \times 1 \times C$ output. The Squeeze function for the real and imaginary components is defined as follows:

$$\begin{aligned} & z_{c}^{Re} = F_{sq}(u_{c}^{Re}) = \frac{1}{H \times W} \sum _{i=1}^{H} \sum _{j=1}^{W} u_{c}^{Re}(i,j), \end{aligned}$$

(3)

$$\begin{aligned} & z_{c}^{Im} = F_{sq}(u_{c}^{Im}) = \frac{1}{H \times W} \sum _{i=1}^{H} \sum _{j=1}^{W} u_{c}^{Im}(i,j). \end{aligned}$$

(4)

The outputs $z_{c}^{Re}$ and $z_{c}^{Im}$ are then concatenated to form a complex-valued column vector $z_{c}$, where $z_{c} = z_{c}^{Re} + j z_{c}^{Im}$. This complex-valued vector serves as the input to the subsequent excitation operation.

The excitation operation exploits Complex-Valued Fully Connected (CV-FC) layers to model channel interdependencies in the complex domain. The CV-FC layers are designed to maintain both amplitude and phase information, ensuring that the complex nature of the PolSAR data is preserved. The complex excitation function is defined as:

$$\begin{aligned} s = F_{ex}(z, W) = \sigma (g(z, W)) = \sigma (W_{2} \cdot \text {ReLU}(W_{1} \cdot z)), \end{aligned}$$

(5)

where $\sigma$ denotes the complex-valued sigmoid activation function, and $W_1 \in \mathbb {C}^{\frac{C}{r} \times C}$ and $W_2 \in \mathbb {C}^{C \times \frac{C}{r}}$ are complex-valued weight matrices used in the two consecutive CV-FC layers. Here, C represents the number of input channels, and r is the reduction ratio used to control the dimensionality of the intermediate representation. The function g(z, W) refers to the intermediate transformation applied to the complex-valued input vector $z \in \mathbb {C}^C$ before activation. The CV-FC layers apply linear transformations to both the real and imaginary components of z and are defined as:

$$\begin{aligned} W \cdot z = W^{Re} \cdot z^{Re} - W^{Im} \cdot z^{Im} + i.(W^{Re} \cdot z^{Im} + W^{Im} \cdot z^{Re}), \end{aligned}$$

(6)

where $W^{Re}$ and $W^{Im}$ denote the real and imaginary parts of the complex weights, respectively, and $z^{Re}$ and $z^{Im}$ are the real and imaginary components of the input vector z.

After passing through the CV-FC layers, the output is processed by a complex-valued ReLU activation function, which independently activates the real and imaginary components. This complex-valued excitation function captures channel interdependencies in both amplitude and phase, yielding a complex-valued Attention vector s that modulates the feature channels of $u_{c}$. Figure 2 shows the block diagram of CV-SE block utilized in this research.

This Attention mechanism for complex-valued PolSAR data provides a powerful means to enhance feature representation by focusing on significant channels and suppressing less relevant ones, ultimately improving classification accuracy for PolSAR images.

Figure 2

Complex-valued squeeze-and-excitation block.

Methodology

Within this section, a comprehensive description of the CV-ASDF2Net architecture is provided. Initially, the processing of polarimetric data from PolSAR images is showcased, followed by an exposition of the CV-ASDF2Net network architecture.

PolSAR data preprocessing

The construction of a polarimetric feature vector serves as a fundamental step in PolSAR imagery classification process. In PolSAR imagery, the description of each pixel is defined by a $2 \times 2$ complex scattering matrix, denoted as S, as given in Eq. (7)⁴⁷.

$$\begin{aligned} S = \begin{bmatrix} S_{HH} & S_{HV} \\ S_{VH} & S_{VV} \end{bmatrix} , \end{aligned}$$

(7)

where $S_{AB}(A,B \in {H,V})$ represents the backscattering coefficient of the polarized electromagnetic wave in emitting A direction and receiving B direction. H and V represent the horizontal and vertical polarization channels, respectively. In the context of the data acquired by a monostatic PolSAR radar system, the assumption $S_{VH}$=$S_{HV}$ holds, indicating that the scattering matrix S is symmetric. This enables the simplification and reduction of the matrix to the polarization scattering vector $\vec {k}$. Employing the Pauli decomposition method, the expression for t$\vec {k}$ can be represented as⁵.

$$\begin{aligned} \vec {k} = \frac{1}{\sqrt{2}} [S_{HH} + S_{VV} , S_{HH} - S_{VV}, 2S_{HV}]^T. \end{aligned}$$

(8)

In general, multi-look processing is essential for PolSAR data. Following the processing step, the obtained coherency matrix serves as the most commonly used representation for PolSAR data, as given in Eq. (9)⁵.

$$\begin{aligned} T = \frac{1}{n}\sum _{j = 1}^n \vec {k_j}{\vec {k_j}}^H= \begin{bmatrix} T_{11} & T_{12}& T_{13} \\ T_{21} & T_{22}& T_{23}\\ T_{31} & T_{32}& T_{33} \end{bmatrix}, \end{aligned}$$

(9)

where the operator $(.)^H$ stands for complex conjugate operation and n is the number of looks. It is worth mentioning that T is a Hermitian matrix with real-valued elements on the diagonal and complex-valued elements off-diagonal. As a result, the three real-valued and three complex-valued elements of the upper triangle of the coherency matrix (i.e. T11, T12, T13, T22, T23, T33) are used as the input features of the models.

Data pre-processing is an essential step for achieving higher classification accuracy. Initially, the mean $\overline{T}$ and standard deviation $T_{std}$ of each channel are computed. Subsequently, normalization is applied to each channel, ensuring optimal data preparation for classification. By taking $T_{11}$ as an example, each channel will be normalized as in Eq. (10).

$$\begin{aligned} T_{11} = \frac{T_{11} - {\overline{T}}_{11}}{T_{{11}_{std}}}. \end{aligned}$$

(10)

Feature extraction using CV-3D-CNN

As explained in “Overview of CNNs” section, CV-3D-CNNs are more suitable to process PolSAR data due to their complex nature. Each layer of CV-3D-CNN is followed by a ReLU activation function, and since the output features are complex, we propose the use of Complex Valued ReLu ($\mathbb {C}$ReLU(.)). It is obtained by applying the well-known ReLU(.) to both the real and imaginary parts separately, such that $\mathbb {C}$ReLU(x) = ReLU($\Re$(x)) + i.ReLU($\Im$(x)).

Feature fusion block

The feature fusion block plays a critical role in integrating multi-scale features extracted at different depths, enhancing the overall classification performance. In PolSAR classification, effective discrimination of land cover types requires capturing both local and global dependencies. While shallow features capture fine textures and edges, medium and deep features encode increasingly abstract representations. The fusion of these hierarchical features allows the model to employ rich spatial-polarimetric dependencies.

Mathematically, let $\textbf{X}$ denote the input PolSAR image representation. The extracted features from the three branches–shallow, medium, and deep–are denoted as:

$$\begin{aligned} \textbf{F}_s = f_s(\textbf{X}), \quad \textbf{F}_m = f_m(\textbf{X}), \quad \textbf{F}_d = f_d(\textbf{X}), \end{aligned}$$

(11)

where:

• $f_s(\cdot )$ represents the shallow feature extractor, which consists of a single 3D complex convolutional layer capturing fine-grained spatial-polarimetric structures.

• $f_m(\cdot )$ represents the medium feature extractor, which applies two consecutive 3D complex convolutions to capture regional patterns.

• $f_d(\cdot )$ represents the deep feature extractor, which applies three stacked 3D complex convolutions, extracting high-level abstract features.

The outputs from the three branches are concatenated along the channel dimension to form a fused feature representation:

$$\begin{aligned} \textbf{F}_{\text {fusion}} = \text {Concat}(\textbf{F}_s, \textbf{F}_m, \textbf{F}_d), \end{aligned}$$

(12)

where $\text {Concat}(\cdot )$ denotes the concatenation operation, merging feature maps along the channel axis.

Finally, the fused representation $\textbf{F}_{\text {fusion}}$ is passed to the subsequent complex-valued attention module, enhancing the most informative feature channels before the final classification. The motivation behind this hierarchical feature fusion stems from the need to balance fine-grained and global information in PolSAR classification:

• Shallow features preserve high spatial resolution and capture textural differences, which are useful for differentiating small-scale structures.

• Medium features integrate regional scattering patterns, improving discrimination in areas where similar land cover types may overlap.

• Deep features provide high-level semantic understanding, capturing broader class dependencies and improving robustness against noise.

By integrating these three different levels of feature representation, the model gains a comprehensive understanding of the PolSAR image, reducing misclassification and improving accuracy.

Architecture of the proposed CV-ASDF2Net

Currently, the predominant approach in PolSAR classification tasks involves the utilization of 2D-CNN architectures. While 2D-CNNs effectively capture spatial information, they fail in exploiting the intricate interchannel dependencies inherent in PolSAR images. On the other hand, a 3D-CNN exhibits superior feature extraction capabilities when compared to 2D-CNN architecture³⁹.

Figure 3 shows the comprehensive framework of the complete process of the proposed methodology. The model processes the data through a three-branch network, extracting features at different levels (shallow, medium, and deep), which are later concatenated. The concatenated features then pass through the Attention block to enhance the channel dependencies. The flattening layer is employed to transform the concatenated features into a one-dimensional vector. For the final classification, two fully-connected layers are employed, incorporating dropout to mitigate overfitting and a softmax layer for generating the final prediction. The detailed distribution of parameters of each layer is shown in Fig. 3. The first branch incorporates a single layer of complex CV-3D-CNN with 16 filters, employing a 3$\times$3$\times$3 kernel size to capture shallow features. In contrast, the second branch focuses on medium features with two CV-3D-CNN layers, each maintaining a 3$\times$3$\times$3 kernel size. Meanwhile, the third branch is tailored to extract deep features through the utilization of three layers of CV-3D-CNN, employing 16 filters at each layer, and configuring the kernel size of each filter as 3$\times$3$\times$3. Due to the information loss caused by the pooling layer, it has not been utilized in this network architecture.

The selection of the kernel size, number of filters, and layer depth was guided by both empirical results and practical considerations. A kernel size of $3 \times 3 \times 3$ was chosen as it effectively captures spatial-polarimetric context while maintaining computational efficiency and preserving spatial resolution through zero-padding. Larger kernels would increase the parameter count and risk over-smoothing, whereas smaller ones might miss important features. Each convolutional layer uses 16 filters, which provided a good trade-off between model capacity and complexity; increasing the number of filters did not yield significant performance gains, while fewer filters degraded feature representation. The three-branch structure–with one, two, and three layers respectively–was designed to extract shallow, medium, and deep features, enabling the model to learn a rich hierarchy of representations suitable for PolSAR image classification with limited training data.

Figure 3

Block diagram of the proposed CV-ASDF2Net.

Loss function

The proposed CV-ASDF2Net is trained and optimized by calculating the Cross-entropy (CE) loss on the training samples. A softmax classifier is utilized to produce the predicted probability matrix for the samples, as shown in Eq. (13).

$$\begin{aligned} \hat{y}_l^m = Softmax(|\textbf{x}_{out}|), \end{aligned}$$

(13)

where $\textbf{x}_{out}$ is the output of the last fully connected layer, and |.| is the magnitude operator. It is worth noting that $\textbf{x}_{out}$ is complex, while the value of $|\textbf{x}_{out}| = \sqrt{(\Re {(\textbf{x}_{out})})^2 + (\Im {(\textbf{x}_{out})})^2}$ is real, and hence the value of $\hat{y}_l^m$ will also be real. Subsequently, the presentation of the loss $Loss_{CE}$ is depicted as given in Eq. (14).

$$\begin{aligned} Loss_{CE} = -\sum _{m = 1}^M \sum _{l = 1}^L y_l^m \log (\hat{y}_l^m), \end{aligned}$$

(14)

where $y_l^m$ and $\hat{y}_l^m$ are the reference and predicted labels, respectively, and L and M are the land cover categories and the overall number of small batch samples, respectively.

Alternative loss functions, such as hinge loss⁴⁸, are often used in margin-based classifiers like Support Vector Machines (SVMs) and can be beneficial for imbalanced datasets. However, CE loss naturally accounts for class probabilities and can be extended to handle class imbalance by introducing weighting factors based on inverse class frequencies. In our case, while class imbalance was present due to the use of only 1% of samples for training, the selection process was conducted in a stratified manner, ensuring that the proportion of samples from each category was maintained across both the training and testing sets. This approach provided a balanced representation of all classes, mitigating the effects of imbalance. Consequently, standard CE loss remained an appropriate choice. However, if more severe imbalance were present, a weighted CE loss formulation could be employed to further balance learning across different classes.

Experiments and results

In this section, three prevalent datasets in PolSAR classification, namely Flevoland, San Francisco, and Oberpfaffenhofen have been used in our experiments to validate the effectiveness of the proposed approach under various experimental configurations of the suggested framework. For a comprehensive demonstration, both visualized classification results and quantitative performance metrics are reported, in addition to comparisons with existing state-of-the-art approaches.

Polarimetric SAR datasets

• 1. Flevoland Dataset: The dataset consists of L-band four-look PolSAR data with dimensions 750 $\times$ 1024 pixels with 12 meters. It was acquired by the NASA/JPL AIRSAR system on August 16, 1989 for Flevoland area in the Netherland. It has 15 distinct classes: stem beans, peas, forest, lucerne, wheat, beet, potatoes, bare soil, grass, rapeseed, barley, wheat 2, wheat 3, water, and buildings⁴⁹. Figure 5a shows the Pauli pseudo-color image and ground truth map is shown in Fig. 5b. Table 4 shows the number of pixels used for training and testing per each class in the dataset.

• 2. San Francisco Dataset: The San Francisco dataset, obtained from the L-band AIRSAR, covers the San Francisco area in 1989. The image size is 900 $\times$ 1024 pixels and has a spatial resolution of 10 meters. It comprises of five categorized terrain classes: mountain, water, urban, vegetation and bare soil⁵⁰. Figure 6a shows a colored image formed by PauliRGB decomposition, and the reference class map is shown in Fig. 6b. Table 5 shows the number of pixels used for training and testing per each class in the dataset.

• 3. Oberpfaffenhofen Dataset: The Oberpfaffenhofen dataset is captured by L-band ESAR sensor in 2002, encompassing the area of Oberpfaffenhofen in Germany. It includes a PolSAR image with dimensions of 1300 $\times$ 1200 pixels and a spatial resolution of 3 meters, annotated with three land cover classes: Built-up Areas, Wood Land, and Open Areas⁵¹. Figure 7a shows the PauliRGB composite and Fig. 7b shows the reference class map. Table 6 shows the number of pixels used for training and testing per each class in the dataset.

The three PolSAR datasets used in this study present distinct classification challenges due to differences in spatial resolution and land cover complexity. The Flevoland dataset (12m resolution) consists mainly of agricultural fields with spectrally similar crops, making discrimination difficult, especially along narrow field boundaries. The San Francisco dataset (10m resolution) contains a mix of urban, water, and vegetation classes, where overlapping regions and strong corner reflectors in urban areas increase classification difficulty. The Oberpfaffenhofen dataset (3m resolution) offers finer spatial details, aiding the distinction of built-up areas, but the variability in urban structures and volume scattering in forests pose challenges. Higher-resolution datasets introduce greater intra-class variation, while lower-resolution datasets make classification more reliant on polarimetric features rather than spatial details.

Evaluation metrics

Assessing the effectiveness of classification results involves comparing predicted class maps with the provided reference or ground truth data. Depending solely on visual or qualitative inspection for confirming pixel accuracy in the image is subjective and may lack comprehensiveness. Therefore, adopting a quantitative evaluation approach is more reliable. In this context, three various metrics are employed: Overall Accuracy (OA), Average Accuracy (AA) and the Kappa score (k). Additionally, training will be performed 10 times to obtain statistical measures such as the T-statistic, which quantifies the difference between models relative to variability, and the P-value, which determines whether this difference is statistically significant or due to chance.

OA calculates the ratio of correctly assigned pixels to the total number of samples. AA computes the mean classification accuracy across all categories or classes. The Kappa score assesses the agreement between the predicted classified map and the ground truth, with values ranging from 0 to 1. A value of 1 indicates perfect agreement, while 0 suggests complete disagreement. Typically, a Kappa value equal to or greater than 0.80 signifies substantial agreement, whereas a value below 0.4 indicates poor model’s performance⁵². The T-statistic quantifies the difference between two sample means in relation to the variability within the data. A higher absolute T-value suggests a greater distinction between the two compared groups. The P-value, on the other hand, represents the probability of obtaining an effect at least as extreme as the observed one, assuming the null hypothesis is true. A low p-value (typically < 0.05) indicates that the difference is statistically significant, meaning it is unlikely to have occurred by random chance. Conversely, a high p-value suggests insufficient evidence to reject the null hypothesis, implying that any observed differences might be due to random variation rather than a true effect.

Experimental configuration

All the tests were conducted utilizing Python 3.9 compiler and TensorFlow 2.10.0 framework. Adam optimizer is adopted with a learning rate of $1 \times 10^{-3}$, the batch size is 64, and the training epoch is set to 250. In the course of model training, an early stopping strategy is implemented. Specifically, if there is no improvement in the model’s performance over a consecutive span of 10 epochs, the training process halts, and the model reverts to its optimal weights. The network configuration of the proposed model using Flevoland dataset is shown in Table 1. The number of samples used for training the model is set to $1\%$ for all three datasets to ensure a fair comparison. While using such a small amount of data for training is uncommon in optical image classification, it is a widely recognized practice in hyperspectral and PolSAR image classification tasks^25,42.

Table 1 Parameter settings of CV-ASDF2Net on each dataset with N classes.

Experimental results

In this section, we assess the classification performance of the suggested model both quantitatively and qualitatively, utilizing the three previously mentioned datasets: Flevoland, San Francisco, and Oberpfaffenhofen. To mitigate the impact of sample selection randomness on classification outcomes, the experiments were iterated 10 times, and the final result is presented as the average value of these repetitions. Furthermore, detailed classification outcomes for each category are provided.

Determining optimal window size

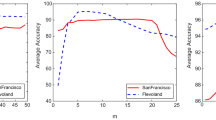
In this part, we investigate how the spatial characteristics of different PolSAR datasets influence the proposed model’s ability to categorize PolSAR data and determine the optimal window size for feature extraction. The window size represents the extent of retrieved spatial information from the 3D patch used for assigning a label to the extracted feature representation. A larger window may capture a broader spatial context but risks introducing information from neighboring classes, which can degrade classification performance due to mixed class boundaries. Conversely, a window that is too small may lead to a loss of critical spatial dependencies, limiting the model’s ability to utilize contextual information for classification.

To systematically assess the impact of window size, we conducted experiments using spatial sizes of {$5\times 5$, $7\times 7$, $9\times 9$, $11\times 11$, $13\times 13$, $15\times 15$, and $17\times 17$}. The results, presented in Fig. 4, indicate that the optimal window size varies across datasets: $13\times 13$ for Flevoland, $15\times 15$ for San Francisco, and $13\times 13$ for Oberpfaffenhofen. This variability can be attributed to differences in spatial resolution and scene complexity. Higher-resolution datasets, such as Oberpfaffenhofen (3m), require relatively smaller windows since fine-grained spatial details are available. Conversely, lower-resolution datasets, such as Flevoland (12m), benefit from larger windows to compensate for reduced spatial detail.

While these findings are dataset-specific, the observed trends suggest generalization to other PolSAR scenarios. In datasets with higher noise levels or finer spatial resolution, smaller windows may be preferable to prevent the inclusion of irrelevant information from surrounding pixels. In contrast, datasets with lower resolution or large-scale homogeneous regions may benefit from larger windows to incorporate sufficient spatial context for classification. These insights highlight the importance of selecting an optimal window size based on the dataset’s resolution, class distribution, and scene complexity, ensuring a balance between spatial context and classification accuracy.

Figure 4

Overall accuracy (OA) of the proposed model employing varying window sizes across the three datasets.

Ablation study

This section is divided into two parts for the ablation study. The initial part focuses on assessing the influence of diverse combinations of network components. We conducted comprehensive experiments on the Flevoland dataset, as outlined in Table 2. The results demonstrate that our proposed fusion technique outperforms other combinations or fusion methods, such as Shallow (S), Medium (M), Deep (D), Shallow and Medium (S+M), Shallow and Deep (S+D), and Medium and Deep (M+D), in terms of AA, OA, and Kappa metrics.

The results in Table 2 further illustrate that the combination of Medium (M) and Deep (D) features achieves higher accuracy than individual components and even some other combinations (e.g., S+M). This can be explained by the role of each feature type: M features capture regional scattering patterns, which are crucial for distinguishing spectrally similar classes, while (D) features provide high-level semantic abstraction, reducing confusion between classes with overlapping textures. The fusion of (M) and (D) effectively balances spatial and abstract representations to maximize both mid-level contextual cues and deep feature hierarchies. In contrast, the (S+M) combination, while incorporating local and regional details, lacks the global abstraction provided by (D), leading to slightly lower performance. These results highlight the necessity of integrating multi-scale features to enhance classification robustness in PolSAR imagery.

Table 2 Results of ablation studies on different combination of model branches over the Flevoland dataset.

The second part of the ablation study examines the impact of incorporating the Attention mechanism. Initially, we experimented with the model without any Attention mechanism, followed by placing Attention at each stream before feature fusion, and finally applying Attention after feature fusion. The results in Table 3 indicate that applying attention after feature fusion yields the highest classification accuracy, primarily because this placement allows the model to operate on a richer and more informative representation. By fusing shallow, medium, and deep features first, the network captures both fine-grained spatial details and high-level semantic structures, providing a comprehensive understanding of the data. Applying attention at this stage enables the model to selectively emphasize the most discriminative features while suppressing noise and redundant information, which is particularly beneficial for PolSAR data that often suffers from speckle noise and complex scene variations. In contrast, placing attention earlier in the pipeline might filter out potentially useful features prematurely, limiting the model’s ability to utilize both local and global information effectively. Furthermore, attention after fusion ensures better balancing between low- and high-level features, preventing dominance by either shallow or deep representations. This placement ultimately enhances class separability and improves overall classification performance.

Table 3 Impact of attention mechanism over the Flevoland dataset.

Comparison with other methods

Several techniques have been chosen for comparison with the CV-ASDF2Net model, such as SVM⁵³, ResNet⁵⁴, VGG19⁵⁵, 2D-CVNN⁵⁶, 3D-CVNN⁵⁷, Wavelet CNN³¹, and our previously proposed method in⁵⁸, namely CV-CNN-SE. The specific experimental configurations for these methods are outlined below:

• SVM: The SVM employs the Radial Basis Function (RBF) kernel, with the parameter $\gamma$ set to 0.001 to regulate the local scope of the RBF kernel.

• ResNet⁵⁴: A deep learning architecture that employs residual connections to enable the training of extremely deep networks, improving performance and mitigating vanishing gradient problem. The model was pre-trained on ImageNet and we applied transfer learning approach.

• VGG19⁵⁵: A widely used model for image classification tasks, the model consists of 19 layers and was trained on ImageNet, transfer learning approach was also applied to this model.

• 2D-CVNN: The model consists of two Complex-Valued CNN layers, with 6 and 12 kernels of size $3\times 3$ in each layer, and two fully connected layers. The input patch size is specified as $12\times 12$ in⁵⁶.

• Wavelet CNN: The proposed model utilizes the Haar wavelet transform for feature extraction to improve the classification accuracy of PolSAR imagery. It consists of three branches, each utilizing different concepts and advantages of CNNs. The model parameters were configured based on the values given in³¹

• CV-CNN-SE: This model utilizes the use of 2D-CVNNs at different scales to extract features from PolSAR data. Extracted features are then fused and passed to SE block to enhance the classification performance.

• 3D-CVNN: In this model, four Complex-Valued convolutional layers, with 16, 16, 32 and 32 kernels of size $3\times 3\times 3$ in each layer, and one fully connected layer. The input patch size is specified as $12\times 12$ in⁵⁷.

ResNet and VGG19 were included in this study as they are well-established deep learning models widely referenced in the literature. However, their application has predominantly been in optical image processing, with limited exploration in PolSAR imagery. Investigating their performance on PolSAR data is expected to provide valuable insights.

As previously noted, the experiments were performed over 10 iterations, and the results are reported as the mean values of these repetitions. The quantitative evaluation of the compared methods is summarized in Tables 4, 5 and 6, with the best-performing values in each table highlighted in bold.

Table 4 Experimental results of different methods on flevoland dataset.

Figure 5

Classification results of the Flevoland dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) ResNet; (e) VGG19; (f) 2D-CVNN; (g) Wavelet CNN; (h) CV-CNN-SE; (i) 3D-CVNN; (j) Proposed CV-ASDF2Net.

Based on the findings presented in Tables 4, 5 and 6, it is evident that the proposed CV-ASDF2Net model surpasses other methods in performance. Examining the datasets utilized in this study, the Flevoland dataset is composed of 207,832 labeled samples, with 1% (2,078 samples) reserved for training, spanning across 15 classes. In contrast, the San Francisco dataset boasts a larger pool of labeled samples, with 8,023 allocated for training, explaining the higher classification performance observed in San Francisco.

The results on Flevoland dataset are reported in Table 4, SVM demonstrated the least OA, primarily because it heavily depends on 1-dimensional information. Additionally, classes with a low number of training samples, such as Grass, Bare Soil, Wheat 2, Barley, and Buildings, were hardly detected by SVM. This suggests that SVM is an unsuitable option for datasets with a limited number of training samples, a limitation evident in the quantitative metrics associated with each class. ResNet and VGG19 showed slight improvements over SVM, with ResNet achieving 69.80% OA and VGG19 achieving 66.86% OA. The metrics of the 2D-CVNN exhibited an enhancement, approximately 10% greater than that of SVM. Unlike SVM, the 2D-CVNN utilizes 2D filters for spatial information extraction, resulting in a moderate increase in accuracy. Nevertheless, certain classes with a limited number of training samples, like Grass and Bare Soil, recorded lower accuracy metrics, influencing the overall performance of the model. The Wavelet CNN achieved substantial improvement to the accuracy with 91.73%, utilizing Wavelet decomposition for feature extraction, thereby enhancing classification accuracy. CV-CNN-SE, employing three parallel branches of two-dimensional kernels, demonstrated an improvement over Wavelet CNN. The 3D-CVNN, using 3D filters for three-dimensional information extraction, did not surpass CV-CNN-SE in accuracy, but did outperform other methods used in this research. Our proposed CV-ASDF2Net method outperformed CV-CNN-SE by approximately 1.5% in OA and outperformed other methods in seven categories, as detailed in the Table 4. While the model performs well overall, it may struggle with some classes due to overlapping features, indistinct boundaries, or inherent complexities. Deep learning models often face interpretability challenges, acting as black boxes that obscure performance reasons. Furthermore, our model may be limited by factors such as data imbalance, noise, or insufficient class representation.

For a visual representation, Fig. 5 illustrates the classification results for the eight approaches alongside the reference map. It is clearly shown from Fig. 5c that SVM had numerous incorrectly assigned pixels, while the classification map generated by CV-ASDF2Net closely aligned with the reference map, showcasing superior performance.

Table 5 Experimental results of different methods on San Francisco dataset.

Figure 6

Classification results of the San Francisco dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) ResNet; (e) VGG19; (f) 2D-CVNN; (g) Wavelet CNN; (h) CV-CNN-SE; (i) 3D-CVNN; (j) Proposed CV-ASDF2Net.

To validate the effectiveness of the proposed CV-ASDF2Net model, we conducted a paired t-test comparing its classification performance against the chosen baseline deep learning architectures on the Flevoland dataset. The last two rows in Table 4 present the T-Statistic and P-Value for each comparison. The results demonstrate that CV-ASDF2Net significantly outperforms SVM, ResNet, VGG19, and 2D-CVNN, with P-Values of 0.0000, indicating strong statistical significance. Additionally, the comparison with Wavelet CNN shows a statistically significant difference (P = 0.0230), while the difference between CV-ASDF2Net and CV-CNN-SE is also statistically significant (P = 0.0168). The large T-Statistic values for SVM (35.9061), ResNet (26.3495), and VGG19 (28.3225) further support the substantial performance gap between these models and the proposed approach.

For the San Francisco dataset, Table 5 displays the classification performance metrics for various models. Unlike the Flevoland dataset, this dataset consists of only five target categories. SVM yields relatively poor classification results, suggesting that the original polarimetric features lack effective discrimination. The 2D-CVNN and CV-CNN-SE models show unsatisfactory performance, particularly in the Bare Soil category, whereas the Wavelet CNN and 3D-CVNN methods handle the intricate polarimetric features more effectively. CV-ASDF2Net achieves the highest OA at 97.13%, Average Accuracy (AA) at 91.31%, and Kappa coefficient at 95.50%. Figure 6 further confirms that the classification maps produced by our method closely align with the ground truth, particularly in the Urban class (Blue). The table also shows the T-statistic and P-values, demonstrating that CV-ASDF2Net consistently outperforms all baseline methods, as indicated by positive T-statistic values across all comparisons. The P-values for all comparisons remain below the 0.05 threshold, confirming the statistical significance of the improvements at a 95% confidence level. The large T-statistic values for SVM (113.8885), ResNet (23.1007), and VGG19 (11.6937) further highlight the substantial performance gap, reinforcing the effectiveness of CV-ASDF2Net on the San Francisco dataset.

Table 6 Experimental results of different methods on Oberpfaffenhofen dataset.

Figure 7

Classification results of the Oberpfaffenhofen dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) ResNet; (e) VGG19; (f) 2D-CVNN; (g) Wavelet CNN; (h) CV-CNN-SE; (i) 3D-CVNN; (j) Proposed CV-ASDF2Net.

The classification results of the Oberpfaffenhofen dataset are shown in Table 6, where CV-ASDF2Net achieves the highest performance in terms of OA, AA, and Kappa metrics, as well as the best accuracy in two out of three classes. Figure 7 further confirms that our proposed method produces the closest classification map to the ground truth. The table also shows the T-statistic and P-values, demonstrating that CV-ASDF2Net consistently outperforms all baseline models, as indicated by positive T-statistic values across all comparisons. The P-values for all comparisons remain below 0.05, confirming the statistical significance of the improvements at a 95% confidence level. The large T-statistic values for SVM (36.3087), ResNet (11.2273), and VGG19 (19.8394) further highlight the substantial performance gap, reinforcing the effectiveness of CV-ASDF2Net on the Oberpfaffenhofen dataset.

According to the experimental findings discussed above, CV-ASDF2Net outperforms other classification methods, achieving superior results across all three datasets. Although the improvement in OA ranges between 1% and 2%, it holds significance in PolSAR image classification, where even small gains contribute to better land cover differentiation and enhanced classification reliability. The inherent complexity of PolSAR data and challenges in feature extraction make these gains a strong indicator of improved feature representation and classification robustness. To ensure the reliability of these improvements, multiple experimental runs were conducted, with the reported results representing the average value of these trials, and standard deviations, as presented in the tables, were computed to assess the stability of the proposed method. SVM exhibits the weakest performance due to its reliance on 1-dimensional features, leading to a loss of spatial information. While ResNet and VGG19 perform better than SVM by integrating spatial information, their architectures are designed for real-valued data, limiting their effectiveness in complex-valued PolSAR classification. Models such as 2D-CVNN, Wavelet CNN, and CV-CNN-SE employs complex-valued information, which results in higher OA compared to SVM, ResNet, and VGG19. The 3D-CVNN method further enhances classification by extracting hierarchical features in both spatial and scattering dimensions through 3D complex-valued convolutions, effectively capturing physical properties from polarimetric adjacent resolution cells. CV-ASDF2Net exploits the strengths of each branch to extract multilevel features, ultimately improving overall classification performance and demonstrating its effectiveness in complex land cover classification tasks.

Networks complexity

The complexity analysis of each model is presented in Table 7, detailing the number of parameters, FLOPs, and MACs. While models like ResNet and WaveletCNN exhibit high computational demands–WaveletCNN, for instance, requires 4,714,043 parameters and 195,928,265 FLOPs–the lightweight 2D-CVNN model offers a more efficient alternative with only 28,794 parameters and 383,568 FLOPs. In comparison, CV-ASDF2Net achieves a balance between computational efficiency and performance, with 5,241,002 parameters, 5,242,600 FLOPs, and 2,611,136 MACs. The number of parameters reflects memory requirements, while FLOPs and MACs indicate computational complexity. Although CV-ASDF2Net incurs a higher computational cost than some baseline models, this is justified by its ability to extract more informative features through complex-valued layers and attention mechanisms.

In PolSAR classification tasks, achieving higher accuracy is often prioritized over minimizing computational complexity, as the ability to capture fine-grained spatial-polarimetric dependencies is essential for reliable results. While CV-ASDF2Net introduces a higher computational load compared to some baseline models, this trade-off is justified by its superior feature extraction capability enabled through complex-valued operations and attention mechanisms. To better assess the practical feasibility of this added complexity, Table 8 presents the inference time required to classify all 768,000 samples in the Flevoland dataset. The experiments were conducted on a Windows 10 machine with 64 GB of RAM and an NVIDIA GeForce RTX 2080 GPU (8 GB VRAM). The results show that while the SVM model incurred the longest inference time–primarily due to the lack of GPU utilization–deep architectures like ResNet and VGG19 also required considerable time because of their large number of parameters. On the other hand, models such as 2D-CVNN, WaveletCNN, and CV-CNN-SE achieved faster inference owing to their reliance on efficient 2D convolutional operations. In contrast, the 3D-CVNN model exhibited longer inference times due to the higher computational cost of 3D convolutions. The proposed CV-ASDF2Net achieved a moderate inference time, which is reasonable considering its consistent superiority in classification performance. This confirms that the model strikes a good balance between accuracy and efficiency, and that the added computational complexity represents a necessary and worthwhile trade-off to achieve a more discriminative feature representation.

Table 7 Parameters, FLOPs, and MACs of each model used in the research.

Table 8 inference time of different models used in this research when applied to Flevoland dataset.

Post-processing with median filtering

To further boost the classification accuracy, an additional spatial post-processing strategy employs a $3\times 3$ median filter to eliminate isolated misclassified pixels within the assigned class. The underlying assumption is that information classes tend to occupy spatial regions of relatively uniform characteristics, typically larger than a few pixels⁵⁹. While a $3\times 3$ kernel effectively removes small misclassified regions while preserving spatial coherence, larger kernels (e.g., $5\times 5$ or $7\times 7$) may introduce pixels from different classes, potentially degrading classification performance. The selected kernel size was empirically determined to balance the removal of isolated noise with the preservation of class boundaries. The application of median filtering yields a more refined version of the class map with smoother transitions. To showcase the effectiveness of this process, the smoothed classification map is compared with the reference map through the confusion matrix. For illustrative purposes, the Oberpfaffenhofen dataset will be utilized as an exemplar.

Figure 8

Oberpfaffenhofen Image: (a) classification map resulted from the proposed model; (b) classification map after applying median filtering; (c) reference data classification map.

Table 9 Confusion matrix between reference and generated classification maps for Oberpfaffenhofen dataset.

Table 10 Confusion matrix between reference and filtered classification maps for Oberpfaffenhofen dataset.

Table 11 Impact of Median Filtering on the classification maps produced by CV-ASFD2Net of different datasets.

Figure 8 displays classification maps for Oberpfaffenhofen. In Fig. 8a, the map is generated using the proposed model. Figure 8b depicts the same map after smoothing with a median filter. Figure 8c represents the reference data classification map. Table 9 exhibits the confusion matrix comparing the generated classification map with the reference, while Table 10 shows the confusion matrix for the filtered generated classification map in comparison to the reference one.

The diagonal of the confusion matrix demonstrates the agreement between the predicted class map and the reference class map, while discrepancies are indicated by the non-diagonal elements. Tables 9 and 10 display a decline in the values of these non-diagonal components, signaling a decrease in the number of misclassified pixels. As a result, there is an enhancement in OA. This improvement is noticeable, particularly in the Build-Up Areas class (depicted in red). Figure 8a highlights numerous pixels initially classified as Open Areas. However, a substantial correction is observed after applying the median filter. This correction is corroborated by Tables 9 and 10, revealing an initial misclassification of 22,640 Build-Up Areas pixels as Open Areas, which reduces to 15,780 after the application of the median filter. In fact, the reduction appears on all non-diagonal values. Table 11 provides a summary of the enhancement achieved by applying the median filter to the resulting class map of each dataset.

Table 12 provides a detailed summary of the impact of median filtering on the classification performance of various models when applied to the output class maps on the Flevoland dataset. The table highlights the performance metrics before and after the application of median filters across different models, including SVM, 2D-CVNN, ResNet, VGG19, Wavelet CNN, CV-CNN-SE, and 3D-CVNN.

The results clearly indicate that median filtering significantly enhances the performance of each model. For instance, the OA of the SVM model improved from 63.22% to 71.49%, while the ResNet model saw an increase from 69.80 to 72.75%. Similarly, the kappa coefficient for the CV-CNN-SE model improved from 93.92 to 94.86 after applying the median filter.

Overall, the data shows that median filtering as a post-processing step leads to a consistent improvement in performance, with increases of at least 1–2% for each metric across all models. This demonstrates the effectiveness of median filtering in enhancing the accuracy and reliability of classification results in remote sensing applications.

Table 12 Impact of median filtering on classification performance of different models on Flevoland dataset.

Performance of different models at different percentages of training data

The model’s performance can be effectively assessed by examining the classification accuracy across different percentages of training data. We randomly chose 1%, 2%, 3%, 4%, and 5% of labeled samples for training, using the remaining samples for testing the model’s performance. The classification results for each dataset are depicted in Fig. 9. It is evident that, across all methods employed in this study, the classification accuracy shows improvement with an increase in the number of training samples. Notably, the proposed model consistently outperforms others across all proportions of training samples on the three datasets.

Figure 9

Classification accuracy at different percentages of training data for (a) Flevoland; (b) San Francisco and (c) Oberpfaffenhofen.

Conclusion

This paper introduces a novel model called CV-ASDF2Net designed for PolSAR image classification. The model addresses existing challenges in PolSAR classification by incorporating a three-branch feature fusion structure and optimizing the creation of a complex-valued CNN-based model. The data is processed through three branches of CV-3D-CNN, and the generated features from each branch are combined. Then, the fused features undergo enhancement through an Attention SE block to improve the model performance, followed by the application of fully connected and dropout layers to yield the final classification result. Experimental results demonstrate the effectiveness of the proposed model in terms of OA, AA, and Kappa metrics. Notably, even with a limited number of training samples, the model produces classification results almost identical to the reference or ground truth data.

As part of future work, we plan to explore a lightweight architecture with fewer training parameters to reduce computational complexity without compromising model performance. Furthermore, our objective is to explore the potential of integrating Real-Valued CNNs and CV-CNNs to enhance the classification accuracy across various datasets. Additionally, we aim to incorporate explainability techniques, such as Grad-CAM and SHAP, to improve model interpretability by highlighting the most influential features in classification decisions. This will provide deeper insights into how the model utilizes spatial-polarimetric dependencies in PolSAR data. We also aim to seek the possibility of testing the model on data from other SAR sensors, such as RADARSAT-2 and Sentinel-1. This will allow us to assess the model’s adaptability to different sensor characteristics, acquisition modes, and polarization settings, thereby evaluating its generalization potential beyond the datasets used in this study.