Introduction

Modern societies rely on finite and unevenly allocated fossil resources to meet the rising demand for electrical energy. This reliance incurs significant costs—anthropogenic global warming—necessitating the pursuit of cleaner and more sustainable energy alternatives1. Polymers are essential in numerous aspects of human life, primarily attributed to their beneficial characteristics, including low weight, chemical stability, and ease of processing, as well as economical production2,3. Moreover, polymers are controllable and exhibit several degrees of freedom for evaluating their chemical and physical characteristics. Additional improvement in their performance4. Polymers are extensive macromolecules formed from the assembly of smaller units referred to as monomers5. The forces that hold the components of a polymer together are intermolecular covalent bonds. The Polymer’s backbone is constituted by these links, creating a chainlike structure3. Polymers have resistivity’s that are approximately \(\:{10}^{18}\:\)times higher than metals, making them effective electrical insulators6. It encompasses various attributes that can be monitored and controlled. These features exhibit low weight, mechanical flexibility, high dielectric strength, fracture resistance, excellent chemical resistance, ease of processing, and low production costs. These materials also have the potential to be molded into nearly any imaginable shape, and their properties can be customized to suit a wide range of applications7.

Major synthetic polymers generated from petrochemicals are widely employed throughot various industries, including packaging, appliances, and construction. In the global polymer market, approximately 42% of polymers are utilized for packaging applications, including food, chemicals, cosmetics, and pharmaceuticals, with an annual growth rate of 5%. The extensive use of synthetic polymers, including polystyrene (PS), polyethylene terephthalate (PET), polyvinyl chloride (PVC), polyamide (PA), polyethylene (PE), and polypropylene (PP) in packaging since the mid-20th century can be attributed to their remarkable mechanical properties, effective barrier capabilities, ease of fabrication, economic viability, and abundant supply8. Polystyrene (PS) is a thermoplastic composed primarily of the aromatic monomer styrene. It is synthesized from ethylene and benzene via a gas-phase process utilizing zeolite or through Friedel–Crafts catalysis employing aluminum chloride9. (PS) is a robust glassy substance at ambient temperature and undergoes melting when subjected to temperatures beyond its glass transition temperature10. PS is a clear, glass-like substance that does not break down in acids, bases, or alcohol. However, it may dissolve in certain organic solvents, such as benzene, chloroform, tetrahydrofuran, toluene, and esters. The melting point is 239 °C, and the glass transition temperature is 100 °C. It has a density of 1.05 g/cm³ and tends to crystallize in strange ways11. PS is a versatile polymer12, extensively utilized in various goods due to its cost-effectiveness, favorable chemical properties, durability, transparency, excellent electrical insulation, rigidity, and low water absorption. Food packaging and components for optical and electrical equipment are particularly essential. It is a rigid glass substance at ambient temperatures and liquefies when subjected to temperatures exceeding its glass transition temperature13,14. Polymers are versatile materials commonly utilized in several fields, including optoelectronic and photonic applications15,16. Therefore, polymers are essential in human being life and are environmentally friendly materials that could be considered as a replacement for other metals. A polymer composite can be created by mixing polymers with fillers. The composite’s constituent components are held together by physical or chemical interactions while preserving their distinct identities and demonstrating enhanced properties compared to their pristine states17. Composite materials are now typically referred to as reinforcing arrangements, also known as fillers, that are embedded within a matrix. The matrix and reinforcement can be made of metallic, ceramic, or plastic materials, allowing for numerous combinations18. The current study employs a novel advanced method to reduce the optical band gap of synthetic polymers to the level of small optical band gap polymers, which are crucial for optoelectronics and photonics applications. The aforementioned approaches to building up polymer composites are traditional procedures. The new, free carbon material, enriched with hydrocarbons and N/O elements containing hybridized orbitals, could be obtained from mountains in Kurdistan and was used in this investigation. Carbon is one of nature’s most abundant elements and the fundamental component of organic chemistry. Consequently, direct conversion reactions represent a straightforward and cost-effective method for synthesizing carbon molecules. Carbon-based materials have long been used as electrodes in various battery technologies because of their exceptional electrical conductivity, distinct porosity, high specific surface area, and exceptional chemical stability19. Carbon and electricity have a historical relationship spanning two centuries. In 1800, Humphry Davy exhibited the inaugural electric light, the carbon arc lamp. Subsequently, in the 1870 s, Thomas Edison and Joseph Swan created incandescent electric lamps employing carbon filaments. Graphite functions as an anode in most batteries and is essential in power generation as a neutron moderator in nuclear reactors. Notable carbon science progress in recent decades includes the large-scale synthesis of \(\:{C}_{60}\) by arc discharge in \(\:1990\) and the ensuing production of multi-walled carbon nanotubes the subsequent year utilizing a similar technique20. The present work establishes that in addition to above applications of carbon; it is possible to produce polymer/bitumen composites with controlled optical characteristics for various technologies from the viewpoint of optics, photonics and optoelectronics. Disordered and nanostructured carbons comprise a diverse range of materials. These materials include amorphous carbons, microcrystalline graphite, graphite fibers, whiskers, and innovative carbon structures obtained from the regulated pyrolysis of molecular precursors. A prevalent feature of these materials is the substantial presence of hydrocarbons and N/O elements containing hybridized orbital, organized as fragments or (islands). These structural characteristics can be correlated, both their spatial configuration and Raman spectrum attributes, with an optimal two-dimensional graphite crystal, specifically (graphene)21.

Diamondlike structures exhibit a covalently bound face-centered cubic lattice comprised of fully saturated sp³-hybridized carbon atoms, with a density of 3.515 g/cm³. Density Conversely, graphite displays a hexagonal configuration of sp²-hybridized carbon atoms with a density reduction of 2.267 \(\:\frac{g}{c{m}^{3}}\). The layers of graphite are bound by weak van der Waals forces enabled by \(\:\pi\:\) orbitals. The extensive surface area of graphene layers and the \(\:\pi\:-\pi\:\) interactions make stacking these layers unavoidable1. Disordered carbon is abundant in the Earth’s crust, and its technological applications are expected to be more economical and environmentally sustainable than those of synthetic structural counterparts. Moreover, the natural origin provides a spectrum of antecedents and physicochemical qualities linked to formation processes in various geological contexts, thereby facilitating a reduction in the laboratory production costs of specific carbon materials for studying the effects of variations in structural and chemical parameters during experimentation.

The excellent electrical conductivity of disordered carbon materials, combined with their thermal and chemical resilience, presents considerable potential for industrial applications. This study’s findings indicate that economic carbon compounds can proficiently alter the optical characteristics of synthetic insulating polymers for various applications. Polymer composites with improved optical properties have been widely applied in numerous fields, and the fusion of technologies such as optical networking, biomedical applications, laser switching, sensors, polarizers, laser attenuation, solar cells, data storage, and light-emitting diodes is essential. The results of the current project are actually evidence that carbon material-doped bitumen, which is soluble in organic solvents, is a novel strategy for the reduction of the optical band gap of organic soluble polymers and their application to various photonics and optoelectronics applications. The achievements of this study demonstrate that bitumen is likely to replace conventional methods in reducing the optical band gap of synthetic polymers. Conventional methods, which use ceramic fillers or metal nanoparticles, are highly costly, and the results of optical improvement for the polymer composite are not favorable compared to those achieved in the present study.

Experimental and investigation details

Experimental methodology

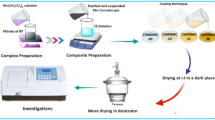
This work collected glassy black rocks composed of carbon materials from the mountains surrounding the Surdash area in Sulaimani Governorate, the Kurdistan Region of Iraq. The people in the area used the black rocks to build short streets and for heating in winter. The rock can easily be fired. This indicates that rocks are enriched with hydrocarbons. During migratory processes, Bitumen and hydrocarbon mixtures are produced in hydrothermal mineral deposits and sedimentary or metasedimentary rocks. These Bitumen are initially liquid, but they may later harden due to several alteration processes, including fluid movement, oxidation, and thermal modification. Usually occurring in rock or mineral fissures and fractures, accumulations can also infrequently form vein-like deposits22. The production of disordered carbon materials often involves significant energy consumption and environmental impact. However, previous studies have revealed that disordered graphite-like carbon, in its naturally “finished” form, exists in the near-surface layers of the Earth’s crust. This naturally occurring material is not only easily extractable but also more cost-effective compared to synthetic alternatives. Recently, there has been growing interest in disordered \(\:s{p}^{2}\) carbon material with a glassy carbon structure. Glassy carbon is notable for its hardness, isotropic properties, and lower density compared to traditional graphitic materials23. Some steps should be taken to prepare PS doped with BT. Firstly, 5 g of glassy carbon material was powdered and dissolved at room temperature in 80 mL of chloroform using a magnetic stirrer. Following that, the mixture was stirred for more than 5 h to obtain a homogeneous solution. It should be noted that the color of the dissolved carbon material is completely black, and no precipitants could be found, indicating that the rocks are entirely composed of carbon and do not contain any clay or sediments. Secondly, for purifying carbon materials, a separation funnel and distilled water were used to remove a small number of polar materials mixed with the distilled water. Thirdly, 5 g of PS was liquified separately in 60 \(\:mL\) of chloroform. The solution was stirred for\(\:\:2\) hours to obtain a homogeneous, translucent polymer solution.To synthesize PS/BT, different concentrations (\(\:0.5,\:1,\:1.5,\) and 2 \(\:mL\)) of dissolved glassy carbons enriched with sp2 hybridized π-orbitals were added to the dissolved PS solutions under stirring for 2 h. The alteration of color of the PS solution to black color indicated a good interaction between the polymer and BT. No precipitates at the bottom of the beakers are evidence for the interaction between the polymer’s and the disordered carbon materials. Finally, the solution was transferred to a clean glass petri dish and located on a level table to produce smooth films of PS/BT materials. The dried film was then removed easily using a tweezers clamp, and the films of polystyrene composites were obtained after thoroughly drying (see Fig. 1). The film thicknesses were quantified using Vernier Micrometers. The codes were assigned to the samples in such a way that PSBT0, PSBT1, PSBT2, PSBT3 and PSBT4 represents pure PS with 0, 0.5, 1, 1.5 and 2mL of dissolved disordered BT materials, respectively.

Fig. 1
figure 1

Schematic diagram of composite film preparation.

Full size image

Characterization techniques

Well-known techniques, such as Fourier-transform infrared (FTIR) analysis, X-ray diffraction (XRD), and UV-visible absorption spectroscopy, were employed to investigate the structural and optical properties of the polymer composite. The samples were structurally analyzed utilizing an XRD with\(\:\:CuK\alpha\:\) radiation (\(\:{k}_{\propto\:}\) = 1.54178 Å), operating at an acceleration voltage of \(\:25\:kV\) and a current of 400 \(\:\mu\:A\). The diffraction angle \(\:2\theta\:\:\)was varied from 10° to 80°. This apparatus determines the kind of crystal lattice and quantifies the intensities of the diffraction peaks. Next, the FTIRA Perkin Elmer Nicolet iS10 spectrophotometer was employed to perform (FTIR) analysis. The analysis was conducted with a spectral resolution of cm⁻¹ over a range of 400 cm⁻¹ to 4000 cm⁻¹. The synthetic series of samples’ UV-visible spectra were obtained using a UV–Vis spectrophotometer (PerkinElmer double-beam UV–Vis–NIR spectrometer, Lambda \(\:25\) absorption). The aforementioned techniques facilitate thorough structure and optical investigation of the polymer films. In particular, absorption spectroscopy, which utilizes absorbance and transmittance information, lays the groundwork for understanding and measuring substantial optical properties, such as the band gap, dielectric constant, refractive index, absorption coefficient, and localized density. The microstructure image of the material can be obtained using advanced field-emission scanning electron microscopy (FE-SEM) technology. FE-SEM (TESCAN MIRA3 model, Czechia) is generally performed in a vacuum to prevent gas molecules from disrupting the electron beam and the secondary and backscattered electrons produced during imaging. FT-Raman spectra were obtained using a Bruker IFS \(\:88\) spectrometer with an FRA 106 Raman attachment. The excitation source was an air-cooled, diode-pumped Nd: YAG laser (\(\:\lambda\:=1.064\:mm;\:v=9394\:{cm}^{-1}\)), operating at a power output of \(\:160\:mW\). The materials were housed in 5-mm cuvettes, and the scattered light was collected using a backscattering geometry.

Results and discussion

X-ray diffraction (XRD) analysis

The atomic arrangement and uniformity of the sample combination were assessed using the diffraction pattern acquired via (XRD). This non-invasive analytical method is used to determine the crystalline phases in materials. The diffraction pattern generated by atomic scattering elucidates details regarding the substance’s atomic configuration24. XRD of polystyrene, illustrated in Fig. 2a, reveals that the principal diffraction peak at 2θ between \(\:15^\circ\:\:and\:20^\circ\:\).Prior research25,26,27, showed that the significant peak of pure PS appeared at approximately \(\:15^\circ\:-20^\circ\:,\) which signifies the amorphous nature of pure polystyrene. On the other hand, Fig. 2b reveals the XRD pattern of BT powder. The pattern shows a prominent band at approximately 2θ = 20.44°, identified as the gamma (γ) band. This is overlaid on a peak located at 2θ = 24.64°, commonly mentioned as the graphene (002) band, along with a weaker band at 2θ = 42.89°, identified as the (100) band. The previously discussed γ-band is attributed to the spatial configuration of aliphatic chains or layers composed of condensed saturated rings. In contrast, the graphene band is formed by stacking aromatic molecules, whereas the (100) band is linked to the in-plane arrangement of the aromatic rings28,29.

Fig. 2
figure 2

XRD Pattern for (a) pure PS and (b) bitumen powder.

Full size image

Figure 3 exhibits the XRD pattern for neat PS and PS: BT composites. The pattern illustrates a modification in the polystyrene structure, evidenced by variations in peak intensities when the volume of BT escalates from 0.5 to 2. The doped polystyrene pattern demonstrates that the incorporation of BT altered the structure of the polystyrene samples. The alteration was evident in the firm peaks identified in the XRD pattern of BT-doped polystyrene. This alteration transformed the structure of pure polystyrene from an amorphous to a crystalline state. As the BT ratio increases, the intensities rise, indicating a structural alteration resulting from the incorporation of BT into the polystyrene. This outcome parallels findings by Ezeonu, S.O. et al.25, which indicated that augmenting the weight% of MWCNT in pure PS transformed the structure of pure polystyrene from amorphous to crystalline. The crystallite size (D) for the main peak has been measured via the Debey Scherrer equation as follows:

$$\:D\:=\:\:k\lambda\:/\beta\:cos\theta\:$$
(1)

Where \(\:D\) is the crystallite size (Å), \(\:K\) = constant (usually\(\:\:k\:=\:0.89\)),\(\:\:\lambda\:\:\)= The incident X-ray beam’s wavelength (\(\:{\lambda\:}_{Cu\:K\alpha\:}\) = 1.5418 Å), \(\:\beta\:\) = width of the X-ray diffraction peaks at half maximum (rad),\(\:\:\theta\:\) = Bragg angle of XRD peak. As it is clear from Eq. 1, to evaluate the crystallite size, the θ and full width at half maximum (FWHM) of the composite films are required. The results are displayed in Table 1. The data indicate changes in the crystallinity of the composite materials, with the crystallite size generally increasing as the BT concentration increases. The crystalline size escalated from 12.375 Å in the PABT0 sample to 15.40 Å in the PSBT2 sample (maximum BT concentration). Adding BT could improve the composite’s crystallinity or change its microstructural characteristics according to this pattern.

Fig. 3
figure 3

Showed adiffraction pattern of BTdoped polystyrene at varying concentrations.

Full size image
Table 1 Structural parameters for the polystyrene-natural bitumen composite.
Full size table

Study of fourier transform infrared (FTIR) spectroscopy

FTIR spectroscopy is an excellent method for identifying functional groups. By analyzing the infrared absorption bands in the spectrum and considering their positions in wave numbers, it becomes possible to identify specific chemical constituents that may not be apparent in X-ray photoelectron spectroscopy. This method applies to both qualitative and quantitative studies and can be used across various materials and situations30. Fig. 4 shows the IR spectra of powder Bitumen, emphasizing the distinctive absorption peaks corresponding to its functional groups. At peak 3431.68 \(\:{cm}^{-1}\:\), the \(\:OH\) functional group is observed. The \(\:C-H\:\)alkane chain is seen at peaks 2922 \(\:{cm}^{-1}\) and 2851 \(\:{cm}^{-1}\). The \(\:C=C\) alkane chain is found at a peak of 1600 \(\:{cm}^{-1}\). The \(\:CH3\) chain is present at peaks 1455.55\(\:{cm}^{-1}\:\) and 1375 \(\:{cm}^{-1}\). Peak 1029.49 \(\:{cm}^{-1}\)displays the carboxylic functional group \(\:C=O\) (Table 2). This result has similarities to the findings of by Yuanita, E. et al.33.

Table 2 Shows the peaks in the FTIR spectrum of natural bitumen.
Full size table
Fig. 4
figure 4

FTIR Spectra of Powder Bitumen.

Full size image

Figure 5a illustrates the infrared absorption spectra of pure polystyrene alone, highlighting the characteristic peaks associated with its molecular vibrations. Figure 6b shows the ATR spectra for clean and doped samples with various amounts of bitumen. Several absorption peaks occur within the specified wavenumber range. The absorption peak at 3025.61 \(\:c{m}^{-1}\)is ascribed to the stretching vibration of aromatic \(\:C-H\) bonds inside the benzene rings of polystyrene. A peak at 2850.68\(\:cm\)⁻¹ and 2920\(\:\:cm\)⁻¹ indicates the stretching vibration of aliphatic \(\:C-H\) bonds from the polymer backbone, and there are two absorption peaks at the wave numbers \(\:of\:1593.09\:c{m}^{-1}\)and 1490.2 \(\:c{m}^{-1}\) are ascribed to the stretching vibrations of \(\:C=C\) bonds. These absorption peaks indicate the existence of benzene rings. The summit at \(\:1447.75\:c{m}^{-1}\) is allocated to the bending vibrations of \(\:C{H}^{2}\) or \(\:{CH}_{3}\) groups. The absorption peaks at the wave numbers of 1025.71 \(\:c{m}^{-1}\) are due to in-plane bending vibrations of \(\:aromatic\:C-H\) bonds. A prominent peak at 693.98 \(\:c{m}^{-1}\)is related to the out-of-plane bending of aromatic \(\:C-H\) bonds. These findings were consistent with previous research conducted by others31,32. It can be seen that in doped PS films, the bands changed weakly, and some broadness occurred in the doped films (Fig. 5b).

Fig. 5
figure 5

FTIR Spectra for (a) pure polystyrene and (b) doped PS films.

Full size image

Study of field emission scanning electron microscopy (FESEM)

The morphology of the generated samples was analyzed utilizing the SEM technique. The morphology and dimensions of the synthesized PS, as assessed by FESEM, are demonstrated in Fig. 6 (\(\:a\)), (\(\:b\)), (\(\:c\)), (\(\:d\)), and (\(\:e\)), correspondingly. The surface of synthesized PS: bitumen sheets displayed smooth and aggregated spherical forms with consistent distribution. It is significant that the photos obtained at 135 K, despite the great magnification, reveal that the surfaces of the films are not too rough. Spherical particles with elevated concentrations of BT are depicted in Figs. 8d-e, exhibiting both tiny and large sizes. These may be attributed to the carbon constituents of the incorporated bitumen. The morphological appearance suggests a substantial interaction between BT and PS, and phase separation is not observed. Previous studies34,35 have shown that carbon black, graphene oxides, and carbon nanotubes cannot be mixed well, and their morphology results revealed many particle leakages and phase separations. Thus, to our knowledge, dissolved bitumen enriched with hydrocarbons and N/O atoms is the most effective methodology for synthesizing polymer composites with nearly homogeneous phases.

Fig. 6
figure 6

FESEM for (a) PSBT0 pure PS and (b) PSBT1(c) PSBT2 (d) PSBT3 and (e) PSBT4 composite films.

Full size image

Raman spectra characterization

Figure 7 illustrates the primary vibrational modes of pure bitumen as identified in the Raman spectrum. Multiple research groups have validated the effectiveness of Raman spectroscopy in characterizing fuels, particularly with the advent of Fourier Transform Raman (FT-Raman) technology. A significant advantage of Raman spectroscopy is its enhanced sensitivity to aromatic compounds, which are crucial components in fuels derived from bitumen and heavy oils36. Atoms within a molecule are linked by chemical bonds, resulting in periodic movements. Concerning one another, these motions are superpositions of normal mode vibrations that exhibit identical phases and normal frequencies. Infrared and Raman spectroscopy are the most effective methods for analyzing vibrational spectra as indicators of specific chemical substances. Research has shown that Raman spectroscopy can be effectively employed for the qualitative assessment of the chemical properties of organic materials, particularly in relation to Rock-Eval parameters. Substantial fluorescence background noise in immature shale granules hinders Raman spectroscopy; however, applying solvent extraction in conjunction with focused signal processing techniques may mitigate this fluorescence interference37. High-quality spectra are obtained for the bitumen. The two prominent features in the bitumen spectra are the band at around 1380 \(\:c{m}^{-1}.\) and the broad band ranging from 1580 to 1610 \(\:c{m}^{-1}.\) The latter band seems to be a doublet, exhibiting overlapping bands at 1586 and 1610 \(\:c{m}^{-1}.\) at the specified resolution. The 1380 \(\:c{m}^{-1}.\) band is ascribed to the ring stretching of bi-cyclic and higher aromatic hydrocarbons, whereas the broad 1600 \(\:c{m}^{-1}.\) feature corresponds to the \(\:C=C\) stretching of all aromatic and other unsaturated molecules38. A prior study confirmed that the \(\:D\) band shifts toward lower wavenumbers, while the G band appears at higher wavenumbers38. They established that the D and G bands cannot be separated clearly if the bitumen rock was enriched with maturity, which means that \(\:\frac{H}{C}\) and \(\:\frac{O}{C}\) ratios reduction and the final composition of the organic materials rock approaches the pure carbon (graphite), which can be reflected by minor separation in the D and G bands39. The bands determined in the current work are quite closing sufficient to those detected by other researchers for natural bitumen found in China40. The above results indicate that our bitumen is augmented with hydrocarbons and O/N functional groups. Furthermore, the results demonstrate that the hydrocarbons are pure crystalline substances, as the D and G bands are exclusively observable in crystalline materials. This phenomenon is attributed to the Stokes phonon energy shift induced by laser excitation, which generates two primary peaks in the Raman spectrum: G (\(\:\approx\:1580\) \(\:c{m}^{-1}\)), a fundamental in-plane vibrational mode, and \(\:2D\) (\(\:\approx\:2690\) \(\:c{m}^{-1}\)), a second-order overtone of a distinct in-plane vibration, \(\:D\) \(\:(\approx\:1350\) \(\:c{m}^{-1}\)). Phonons are identified as the quantum of lattice vibration. Previous research indicated that these two modes are the only observable features in the Raman spectrum of high-quality single crystals41. The\(\:\:D\) band, also known as the \(\:D1\) band, arises from vibrations of the disordered structure of carbonaceous material. The \(\:G\) band corresponds to vibrations of the ordered (graphitic) structure40. The G-band is the dominant spectral feature commonly detected in graphene and graphite materials, reflecting the planar arrangement of \(\:sp2\)-hybridized carbon atoms that constitute graphene. Conversely, the \(\:D\)-band indicates the presence of defects within the graphitic framework, which result from vibrations occurring out of the plane. In Fig. 8, the \(\:D\) and \(\:G\) bands are linked to the crystalline characteristics of bitumen. Graphite is characterized by a layered structure, with its crystal arrangement being hexagonal; the prominent G band is detected at 1585 \(\:c{m}^{-1}\). This G band is specifically associated with the graphite lattice’s zone-center longitudinal optical (LO) phonon mode. Alongside the two phonon modes related to the G band, the Raman spectrum of high-quality single crystals reveals a notable feature known as the D band (disorder band), which is present in polycrystalline graphite. This band was first identified at 1355 \(\:c{m}^{-1}\)when the Raman spectrum was excited using the \(\:488\:nm\) line from an \(\:Ar-ion\) laser. Although its initial detection occurred some time ago, the precise origin of this peak remains elusive. It has been proposed that the D band results from a zone-center phonon mode in single crystalline graphite; however, this mode does not exhibit Raman activity at symmetric sites. Conversely, the disorder found in polycrystalline samples permits this mode to become Raman active41.

Fig. 7
figure 7

Raman spectra for pure bitumen.

Full size image

Optical properties

The optical properties of composites represent a crucial aspect, comprising absorbance (A), transmittance (\(\:T\)), optical refractive index (\(\:n\)), dielectric constant (\(\:\epsilon\:\)), absorption coefficient (\(\:\alpha\:\)), and optical band gap (\(\:Eg\)). Ongoing research focuses on the optical attributes of PS/BT as influenced by different concentration levels.

Absorbance and transmission studies

The UV–Vis–NIR spectrophotometer recorded the transmittance and absorption spectra for the polymer films (PSBT) in the wavelength range of 190–1190 nm, as shown in Figs. 8 and 9, respectively. According to the analysis, absorbance increased as BT concentrations increased at wavelengths longer than 400 nm and remained constant as wavelength increased. The absorption of light or photon energy by polymeric materials in the UV and vis spectrum regions entails the excitation of electrons from the ground state to elevated-energy molecular orbitals, particularly within the \(\:\sigma\:,\:\pi\:,\) and \(\:n\) orbital42. The electronic shifts in the \(\:UV\) area (\(\:160-260\:nm\)) are classified as \(\:n\:\to\:\:{\sigma\:}^{*}\)38, In contrast, the transitions →∗ and →∗ need relatively lower energy, leading to longer wavelengths, as depicted in Fig. 10. The absorption peaks detected at higher wavelengths (\(\:400-700nm\)) in the PS-doped samples are attributed to the presence of \(\:\pi\:\)electrons43. Conjugated systems having alternating dual bonds have been recognized as a vital category of materials for optoelectronic applications owing to their \(\:\pi\:-\)rich characteristics44. The transition to longer wavelengths signifies the reduced band gap of the doped sample. Low-bandgap semiconducting or π-conjugated polymers are widely employed in various commercial applications, including molecular electronics, organic solar cells (OSCs), organic light-emitting diodes (OLEDs), nonlinear optical devices, memory devices, organic field-effect transistors (OFETs), and energy storage systems45. Substantial transitions to longer wavelengths are ascribed \(\:to\:\pi\:-\)delocalization across the polymer chain. The lack of unique absorption characteristics in the spectra of the unaltered PS polymer further corroborates this observation44. The basis of π-delocalization across the polymer chain in the doped samples is associated with the configuration of the included \(\:s{p}^{2}\) carbons.

Amorphous carbon \(\:(a-C\))films are often harder, more transparent, and thermally stable than hydrogenated amorphous carbon (\(\:a-C:H\)) films. The rocks used in the current study can be easily fired, establishing the a-C: H structure rather than the a-C structure, which is similar to the cloud of fired tiers built up from synthetic rubbers enriched with hydrocarbons. A previous study, using Raman analysis and theoretical modeling, showed that the stretching modes exhibit no dispersion in the -bonded chains of poly para-phenylene benzene rings. The electrons are restricted to individual benzene rings and do not delocalize throughout the chain. Incorporating a heteroatom or disorder is crucial for π delocalization and consequent dispersion46. However, the findings of the present investigation indicate that π-electrons are not restricted to individual benzene rings but are largely delocalized throughout the chain in polymer composite films. An increasing BT content, A reduction in the gap occurs, as theoretically established by Ferrari and Robertson, even in the absence of a structured\(\:{sp}^{2}\)matrix47. The findings demonstrate that a wide range of solar energy may be efficiently absorbed, making these samples suitable as raw materials for producing optoelectronic devices and organic solar cells. The broadening of the absorption band in the PSBT composite beyond 290 nm can be attributed to an increased electron density, which enhances interactions among neighboring phenyl groups within the polymer, thereby promoting energy absorption at higher wavelengths48. Figure 10 illustrates the transmittance spectra for neat PS and PS films doped with various Materials. Between the samples, Pure PS almost transparent between the samples for all incident light of visible spectrum, while at UV region declines. Furthermore, there is a drop in the transmittance spectrum with the increased weight of BT. This is because the energy of the incident photon was necessary to interact with the atoms and elevate an electron from the VB to the CB, resulting in the absorption of the photons. This shift can be ascribed to the establishment of many conjugated double bonds.

Fig. 8
figure 8

Absorbance spectra of both pure and doped materials.

Full size image
Fig. 9
figure 9

Transmittance spectra of both doped and clean samples.

Full size image

Study of the absorption coefficient (\(\:\varvec{\alpha\:}\))

The optical absorption spectra are crucial for elucidating the band structure and energy band gap of both crystalline and non-crystalline materials. A key characteristic of the absorption spectra for these materials is the fundamental absorption edge. The absorption coefficient measures the degree to which a material absorbs light, defined as the ratio of absorbed incoming radiant energy to the thickness of the absorbing medium49. The absorption coefficient (\(\:\alpha\:\)) of pure PS and \(\:{sp}^{2}\) carbon doped PS films are exposed in Fig. 10. \(\:\alpha\:\)has been determined using the subsequent Eqs50.,

$$\:\propto\:=2.303\times\:\left(\:\frac{\varvec{A}}{\varvec{t}}\:\right)$$
(2)

\(\:A\) denotes the absorbance, whereas \(\:t\) denotes the sample thickness. The absorption peak at\(\:\:250\) \(\:nm\) results from a \(\:\pi\:\to\:\:{\pi\:}^{*}\) electron transition linked to double bonds in carbon. Pure PS exhibits a distinct absence of absorption peaks within the visible spectrum. The polymer film displays transparency in this range, as the incoming light does not induce any electronic transitions. The \(\:\alpha\:\) of the films improved with higher photon energy and greater \(\:{sp}^{2}\) carbon concentrations. The absorption edge of\(\:{sp}^{2}\) carbon-doped PS films changed to lower photon energy as the \(\:{sp}^{2}\) carbon volume percent increased. This shows that the \(\:{E}_{g}\:\)of the doped PS sample is decreasing. The alteration in molecular configuration, which shows the distribution of \(\:\pi\:-\)electrons along the chains of the polymer composites, is responsible for the increment of (\(\:\alpha\:\)) with increasing \(\:{sp}^{2}\)carbon content.

The absorption edge was determined by extending the linear section of the curves until it reached the point of minimum absorption. Table 3 indicates that the absorption edge of clean PS markedly falls from \(\:4.31\) \(\:eV\) to \(\:1.37\:eV\) with the incorporation of \(\:2\:mL\) of a solution containing dissolved \(\:s{p}^{2}\) carbon compounds. The current study’s findings align well with previous publications, indicating that the energy band gap of the amorphous carbon sheet diminishes as the percentage increases51,52. A notable shift in the absorption edge signifies a substantial change in the band structure of polymer composites, resulting from the emergence of new localized states within the mobility gap53.

Table 3 Value of absorption edge of PSBT films.
Full size table
Fig. 10
figure 10

Absorption coefficient and photon energy for PS and PSBT films.

Full size image

Refractive index (\(\:\varvec{n}\)) and extinction coefficient (\(\:\varvec{k}\)) studies

Figure 11 illustrates the variation of the extinction coefficient \(\:\left(k\right)\) variation about wavelength \(\:\left(\lambda\:\right)\) for all films in clean and doped forms. \(\:k\:\)represents the imaginary part of the complex refractive index.\(\:(\)n*\(\:\:=\:n+ik)\) is determined for clean PS and PSBT composites using the following relations54,

$$\:k=\frac{\alpha\:\lambda\:}{4\pi\:}$$
(3)

The absorption coefficient (\(\:\alpha\:\)) signifies the interaction between light and the substance, whereas λ indicates the wavelength. \(\:k\) calculates the proportion of electromagnetic energy lost due to absorption and scattering per unit of material thickness.\(\:k\) rises with a rise in concentration; however, it remains significantly lower than the refractive index. The low \(\:k\) \(\:{\approx\:10}^{-4}\)) signifies that the samples remain clear55. The \(\:k\) is essential for assessing optical losses within the system56. Our prior research indicated that the extinction coefficient rises at elevated wavelengths. The results of \(\:k\) which decreases to the lowest amount at high wavelengths, as presented in Fig. 12, are completely different compared to our previous extinction coefficient results57,58.

Fig. 11
figure 11

Extinction coefficient versus λ for pure PS and PS: \(\:BT\) composite films.

Full size image

Figure 12 displays the distinction of the refractive index against wavelength for all films of\(\:\:PS\) prior to and after doping. The refractive index (\(\:n\)) of optical materials is a fundamental property that indicates the amount of alteration in light speed while transitioning between different media59. n for the films is ascertained from the extinction coefficients (\(\:k\)) and reflectance (\(\:R\)) through the application of certain equations60;

$$\:n=\frac{\left(1+R\right)}{\left(1-R\right)}+\sqrt{\frac{4R}{{\left(1-R\right)}^{2}}-{k}^{2}}$$
(4)

The \(\:k\) was determined using the formula \(\:k\:=\frac{\alpha\:\lambda\:}{4\pi\:}\). The \(\:n\) of unfilled PS film almost plateaued, while the PS-filled with BT began to exhibit dispersion. The incorporation of BT elevated the \(\:n\) from 1.17 to 1.61. Polymers characterized by an increased refractive index offer significant benefits in optics and photonics, primarily due to their ability to reduce reflection losses at material interfaces. Additionally, polymer nanocomposites exhibiting high refractive indices further enhance these advantageous properties. (RI) have attracted significant research interest due to the widespread application of optical materials in devices such as glass lenses, camera lenses, optical reflectors and optical waveguides. Organic materials offer numerous benefits, such as transparency, lightweight characteristics, ease of fabrication, and economic efficiency. Nevertheless, the frequently low refractive index of organic materials is a significant constraint61. Polymers have been recognized as effective dielectric materials and function as superior host matrices for nanoparticles. Nanoparticles benefit from their role as reducing and capping agents, enhancing their production and stability. This dual capability contributes to the environmental and chemical stability of the resulting nanocomposites62,63. The incorporation of a small percentage of nanoparticles into the polymer matrix influences the chemical, optical, electrical, and mechanical characteristics of the host polymers64,65. The size of \(\:{sp}^{2}\)carbon materials that enrich with \(\:\pi\:\)-delocalzed electrons, almost in nano size as calculated from Debye-Schere equation. Thus, carbon nano-materials are essential to build up polymer composites with improved optical performance.

Fig. 12
figure 12

n versus λ for pure PS and PSBT composite films.

Full size image

Study of dielectric constant

The real (\(\:{\epsilon\:}_{r}={n}^{2}-{k}^{2}\)) and imaginary components (\(\:{\epsilon\:}_{i}=2nk\)) of the optical dielectric constant are also computed. In this research, these elements are directly linked to states’ energy density within the samples’ optical band gap66. The dielectric function is not easily accessible through measurements obtained via optical spectroscopy. The available functions comprise absorbance, reflectance, extinction coefficient and refractive index. Figure 13 displays the optical dielectric constant of pure PS and PS-doped films versus wavelength. The Spitzer-Fan model predicts that the material’s dielectric constant at low frequencies (short wavelengths) \(\:{\epsilon\:}_{\infty\:}\), can be derived from relationships among wavelength and refractive index14;

$$\:{\epsilon\:}_{r}={\epsilon\:}_{\infty\:}-D\:\left(\frac{N}{{m}^{*}}\right){\lambda\:}^{2}\:\:,D=\left(\frac{{e}^{2}}{{4\pi\:}^{2}{c}^{2}{\epsilon\:}_{o}}\right)\:$$
(5)

Where\(\:\:e\) represents the charge of the electron\(\:,\:\:\:c\) denotes the light speed, \(\:{\epsilon\:}_{o}\) signifies the dielectric constant of free space, N indicates the charge concentration carriers, and\(\:\:{m}^{*}\) is the effective mass, estimated to be 1.1\(\:{m}_{e}\). The PS film denotes the existence of an increased number of charge carriers, resulting in the development of a novel density of states inside

the polymer3. The material’s band structure significantly influences the dielectric function, and optical spectroscopy studies of the dielectric function are essential for forecasting the material’s comprehensive band structure67. Figure 15 illustrates that the result is a straight line when the values are plotted against the visible wavelength area. The values of \(\:{\epsilon\:}_{\infty\:}\)and \(\:\frac{N}{{m}^{*}}\) were ascertained from the slope and intercept of the line with the y-axis correspondingly. This value is reported in Table 5. Based on the information provided in Table 4, the value of \(\:{\epsilon\:}_{\infty\:}\:\)increased from 1.38 to 3.6 as the concentration reached 2 mL.

The augmentation of the dielectric constant indicates a greater energy density of states, resulting in improved polarization and, consequently, a larger dielectric constant value. The dielectric constants exhibit a dispersion region at shorter wavelengths, whereas they tend to maintain a relatively stable value at longer wavelengths (Fig. 14). When a material is exposed to incident electromagnetic radiation, The internal charge distribution undergoes time-dependent pressures as a result of the electric field component of the incident wave. This dispersion region is significantly broad. The fluctuations in the dielectric constant spectrum are crucial for practical applications, particularly in the design of optical communication systems and devices50.

Fig. 13
figure 13

depicts the (\(\:\epsilon\:r\)) versus wavelength for both clean and PS-doped films.

Full size image
Fig. 14
figure 14

Dielectric constant for both clean and doped samples as a function of \(\:{\lambda\:}^{2}\).

Full size image
Table 4 Estimated the optical dielectric parameters values for PS BT composites.
Full size table

The dielectric loss spectra indicate that the loss in the \(\:UV\) range (\(\:200\:to,\:400\:nm\)) shifts to longer wavelengths with the incorporation of BT materials. The observed changes show that the optical relaxation time (\(\:\tau\:\)) diminishes with a rise in the concentration of charge carrier68. Previous studies14,69 confirmed that the localized electronic state density inside the forbidden \(\:\left({E}_{g}\right)\) of composite films is closely associated with the optical dielectric functions \(\:{\epsilon\:}_{r}\) and \(\:{\epsilon\:}_{i}\).

Figure 15a, b Illustrates the fluctuation of \(\:\epsilon\:i\) with \(\:{\lambda\:}^{3}\) for clean PS films and various concentrations. By applying the values of \(\:\frac{N}{m}*\) derived from Eq. (5) and the slope of \(\:\epsilon\:i\:\)vs. \(\:{\lambda\:}^{3}\) the values of relaxation time \(\:\left(\tau\:\right)\) were calculated

$$\:{\epsilon\:}_{i}=2nk=\frac{1}{4{\pi\:}^{3}{\epsilon\:}_{o}}\:\frac{{e}^{2}}{{c}^{3}}\:\left(\frac{{N}_{c}}{{m}^{*}}\right)\:\left(\frac{1}{\tau\:}\right)\:{\lambda\:}^{3}$$
(6)

Thus, from the above equation, it is crucial to notice that relaxation time (\(\:\varvec{\tau\:}\)) has a direct correlation with the density of state \(\:\varvec{N}/{\varvec{m}}^{\varvec{*}}\:\)of polymer composite materials. The results demonstrate that the optical relaxation time \(\:(\tau\:\)) reduces with increased concentration of charge carriers, indicating an inverse correlation between \(\:\epsilon\:i\) and\(\:\:\tau\:\)68. Table 5 demonstrates that the relaxation time (\(\:\tau\:\)) of pure PS decreased with the incorporation of BT, signifying that the relaxation response of the composites to the applied electric field happened more rapidly than that of the empty polymer.

Table 5 Values of optical dielectric parameters estimated for PS composites.
Full size table
Fig. 15
figure 15

a-b Plots of;i versus λ3 for clean PS and PSBT composites.

Full size image

Band gap study

Electronic transitions and charge transport in complex systems remain inadequately understood in semiconducting and conducting polymers. Transitions are facilitated by supplying the necessary energy and momentum obtained from the incoming photon and phonon70. Previous research indicated that a comparison analysis of optical dielectric loss and Tauc’s model is necessary for identifying the \(\:{E}_{g}\:\)and forms of electronic transitions53,71,72.The optical dielectric function is largely independent of the band structure of the materials. As a result, A more detailed description of this relationship necessitates thoroughly comprehending the quantum physics governing complex dielectric functions. The complex dielectric function \(\:\epsilon\:*\) describes the response of a material’s electron density to an electromagnetic wave. It has been noted that determining whether the band structure is direct or indirect poses significant challenges when considering Tauc’s equation73. A real transition between occupied and unoccupied states, denoted by the wave functions\(\:({\varPsi\:}_{k}^{v}\)and \(\:{\varPsi\:}_{k}^{c}\), respectively) can be characterized by the imaginary component \(\:({\epsilon\:}_{2}\)) of complex dielectric function (\(\:\varepsilon\:\)) using74,

$$\epsilon_{2}=\frac{4{\pi\:}^{2}{e}^{2}}{{m}^{2}{\omega\:}^{2}V}{\sum\:}_{v,c,k}\left|\langle {\varPsi\:}_{k}^{v}\left|{p}_{i}^{\to\:}\right|{\varPsi\:}_{k}^{c}\rangle\right|\delta\:\left({E}_{{\varPsi\:}_{k}^{c}}-{E}_{{\varPsi\:}_{k}^{v}}-\hslash\:\omega\:\right)$$
(7)

It is evident from Eq. (7) that the optical dielectric loss is linked to the material’s band structure. Numerous simple equations can be employed to determine the complex dielectric function, which is related to various specific optical parameters, including the refractive index and the extinction coefficient.

Figure 16 displays the optical dielectric loss as a function of the applied photon energy for all samples. Each sample demonstrates distinct linear segments. Furthermore, previous studies have shown that the linear segments observed in the spectra are closely related to interband transitions53,72,75. Thus, the intersection of the linear segments (see Fig. 16) with the photon energy axis represents the actual band gap. To determine the category of electron transition in each system; the results of energy band gap from optical dielectric loss could be comapared with those derived from Taucs approach as can be seen in later sections.

Fig. 16
figure 16

The dielectric loss against \(\:h\upsilon\:\) for both virgin and doped samples.

Full size image

The optical band gap describes the quantity of optical energy required to transfer the electrons from the top of the VB to the bottom of the CB. Thus the band structure of solids consists of VB, CB and the band gap which separated the VB from the CB. Based on the band structure of solids varios models has been developed to explore and analize the materials optical and electrical properties. It is the principal criterion for classifying insulating and semiconducting materials into direct and indirect band gap materials. The maximum valence and lowest conduction bands occur at identical wave vectors for direct band gap materials, while for indirect band gap materials, the lowest point of the conduction band does not coincide with zero crystal momentum. This misalignment requires the participation of a phonon possessing a particular crystal momentum to facilitate the transition from the VB to the CB76.

Figure 17 illustrates the various types of electronic transitions between the VB and the CB based on Tauc’s approach. The inter-band absorption theory suggested by Tauc’s relation is helpful to assess the nature of transitions within the solid materials, as demonstrated in Eq. 877;

$$\:\left(\alpha\:h\nu\:\right)={B\left(hv-{E}_{g}\right)}^{n}$$
(8)

In this context, the parameter takesvarious categories of electronic transitions: n = 1/2 for direct band gap transitions, 

\(\:n\:=\:2\) for indirect band gap transitions, n = 3/2 for direct prohibited transitions, and \(\:n\:=\:3\) for indirect forbidden transitions78,79. In the previous investigation, \(\:{E}_{g}\)values were ascertained from the junction of the linear section and the horizontal axis \(\:\left(h\upsilon\:\right)\) of the dielectric loss \(\:{\epsilon\:}_{2}\) spectra displayed in Fig. 16.

Fig. 17
figure 17

Transitions type for (a) direct allowed, (b) direct forbidden, (c) indirect allowed, (d) indirect forbidden.

Full size image

The linear extrapolation of the \(\:\frac{{\left(\alpha\:hv\right)}^{1}}{n}\) curve to the x-axis in Figs. 18 (a-d) was utilized to ascertain the value of \(\:Eg\) for each form of transition. Table 6 presents the Tauc model for all transition types. Table 6 demonstrates that the\(\:\:Eg\) of PSBT composites diminished from 4.34 \(\:eV\) for pure PS to 1.14 \(\:eV\) for doped PS films, signifying an increase of localized density of states in the band gap of PS polymer and thus a drop in the optical energy gap. The characteristics of the electronic transition can be determined based on εi plot and the plots drawn based on Taucs model. According to the results of \(\:{\epsilon\:}_{i}\:\:\)and Tauc’s approach, the electron transfer in pure PS and PS doped with 0.5 mL of bitumen is classified as a direct transition. On the other hand, the films of PS doped with 1 mL, 1.5 mL, and 2 mL of bitumen followed a direct prohibited transition type based on the Tauc model.

Fig. 18
figure 18figure 18

Calculation of \(\:Eg\) value of each form of transition by plotting (a) \(\:{\left(\alpha\:hv\right)}^{1/2}\) \(\:\frac{{\left(\alpha\:hv\right)}^{1}}{n}\) vs. \(\:\left(h\upsilon\:\right)\) (b) \(\:{\left(\alpha\:hv\right)}^{2}\) vs. \(\:\left(h\upsilon\:\right)\), (c) \(\:{\left(\alpha\:hv\right)}^{1/3}\) vs. \(\:\left(h\upsilon\:\right)\) and (d) \(\:{\left(\alpha\:hv\right)}^{2/3}\) vs. \(\:\left(h\upsilon\:\right)\) for pristine PS and doped samples.

Full size image
Table 6 Displays the band gap and absorption edge values derived from the \(\:{\epsilon\:}_{i}\) plot and tauc’s approach.
Full size table

Various metals, fillers, and nanomaterials are utilized in conjunction with polymers to develop polymer composites that exhibit unique physical properties. A huge number of research studies have confirmed that the integration of nanomaterials, metal, and ceramic fillers results in a moderate reduction of the optical band gap of PS, as demonstrated in Table 7. The optical band gap is more significantly affected by bitumen (BT) than by ceramic fillers, metal powders, or nanomaterials. Thus, the results of this work are novel in that a small amount of bitumen is sufficient to improve the optical properties of PS.

Table 7 Various used materials for reducing band gap energy.
Full size table

Study of wemple and DiDomenico (\(\:\varvec{W}\varvec{D}\varvec{D}\)) model

The variation in refractive index across different wavelengths is crucial in optical communication and is a key consideration in designing devices for spectral dispersion management85. \(\:WDD\) single oscillator model was employed to examine the dispersion characteristics of the refractive index within the energy range of \(\:hv<Eg\)86. This model presents two essential parameters: the dispersion energy \(\:(Ed\)) and the oscillator energy (\(\:{E}_{0}\)). The \(\:Ed\) parameter represents the average intensity of interband optical transitions and is intricately related to the charge distribution in the unit cell as well as the nature of the chemical bonding87. In contrast, the \(\:{E}_{0}\) parameter represents an average energy band gap88. The subsequent empirical equation expresses the correlation between the refractive index and photon energy,

$$\:{\varvec{n}}^{2}=1+\frac{{\varvec{E}}_{\varvec{o}}{\varvec{E}}_{\varvec{d}}}{{\varvec{E}}_{\varvec{o}}^{2}-(\varvec{h}\varvec{\upsilon\:}{)}^{2}}$$
(9)

The following form can be obtained by rearranging Eq. (9):

$$\:\left[{\varvec{E}}_{\varvec{o}}^{2}-(\varvec{h}\varvec{\nu\:}{)}^{2}\right]=\frac{{\varvec{E}}_{\varvec{o}}{\varvec{E}}_{\varvec{d}}}{\left({\varvec{n}}^{2}-1\right)}\to\:\frac{{\varvec{E}}_{\varvec{o}}^{2}}{{\varvec{E}}_{\varvec{o}}{\varvec{E}}_{\varvec{d}}}-\frac{(\varvec{h}\varvec{\nu\:}{)}^{2}}{{\varvec{E}}_{\varvec{o}}{\varvec{E}}_{\varvec{d}}}=\frac{1}{\left({\varvec{n}}^{2}-1\right)}$$
(10)

Consequently, Eq. (9) gives us:

$$\:\frac{1}{\left({\varvec{n}}^{2}-1\right)}\hspace{0.33em}=\hspace{0.33em}\left(\frac{{\varvec{E}}_{\varvec{o}}}{{\varvec{E}}_{\varvec{d}}}\right)-\frac{{\left(\varvec{h}\varvec{\nu\:}\right)}^{2}}{\left({\varvec{E}}_{\varvec{o}}\hspace{0.33em}{\varvec{E}}_{\varvec{d}}\right)}$$
(11)

The \(\:{E}_{o}\:\)and \(\:{E}_{d}\) parameters can be found by plotting the 1/(n2−1) against (hν)2 using Eq. (11).

In Fig. 19, the linear equation for the linear lines is;

$$\:\varvec{y}=-\varvec{a}\varvec{x}+\varvec{b}$$
(12)

The determination of the \(\:\frac{{E}_{o}}{{E}_{d}}\) ratio can be achieved by comparing Eqs. (11) and (12) from the intersection of the graph with the y-axis. Additionally, from the graph, the slope of the linear portion can be used to obtain the \(\:\frac{1}{{E}_{d}{E}_{o}}\) values, i.e.,

$$\:\varvec{b}=\frac{{\varvec{E}}_{\varvec{o}}}{{\varvec{E}}_{\varvec{d}}}\:,\:\varvec{a}\varvec{n}\varvec{d}\:\varvec{a}=\frac{1}{{\varvec{E}}_{\varvec{d}}{\varvec{E}}_{\varvec{o}}}$$

So, 

$$\:{{\varvec{E}}_{\varvec{d}}=\frac{{\varvec{E}}_{\varvec{o}}}{\varvec{b}}\:,\:\mathbf{a}\mathbf{n}\mathbf{d}\:\varvec{E}}_{\varvec{o}=}\sqrt{\frac{\varvec{b}}{\varvec{a}}\:}$$
(13)

The variable “a” and “b” represent pure numbers derived from Fig. 18a, b. The oscillation parameters \(\:{E}_{0}\) and \(\:{E}_{d}\) values were found by calculating the intercept and slope of the linear part of the \(\:\frac{1}{{n}^{2}-1}\) plot against\(\:{\left(hv\right)}^{2}\) at the absorption edge. The slope of the line denotes (\(\:-1\)/\(\:{E}_{0}{E}_{d}\)), whereas Conversely, (\(\:{E}_{0}\)/\(\:{E}_{d})\) is ascertained from the intersection of the line with the vertical axis, the dispersion parameters (\(\:{E}_{0}\) and \(\:{E}_{d}\)). The oscillator energy value (\(\:{E}_{0}\)), as shown in Table 7, has a compositional dependence similar to that of the direct (\(\:Eg\)) determined using Tauc’s relation. The band gap energy computed using the \(\:WDD\) model nearly aligns with those obtained from Tauc’s relationship. Furthermore. Both models indicate that \(\:Eg\) diminishes as BT concentration increases. Table 7 indicates that the dispersion energy (\(\:{E}_{d}\))) rises with the increased amount of different of BT. \(\:{E}_{d}\) relates to the mean intensity of interband optical transitions88. The enhancement of\(\:\:{E}_{d}\) with the addition of BT indicates the development of a charge transfer complex between PS molecules and BT, leading to an enhancement in the degree of disorder. The \(\:n\:\)at zero frequency derived from the \(\:WDD\) model closely resemble the samples’ refractive indexes at long wavelengths, as demonstrated in Fig. 19a, b.

Fig. 19
figure 19

illustrates the graphs of \(\:\frac{1}{{n}^{2}-1}\) against \(\:{\left(hv\right)}^{2}\) for (a)pure PS and (b) PS-doped films.

Full size image
Table 7 Analyzing \(\:\varvec{E}\varvec{g}\) using an empirical WDD single oscillator model.
Full size table

Conclusions

In conclusion, films consisting solely of polystyrene (PS) and those with varying levels of bitumen (BT) (0, 1, 2, 3, and 4 mL) were created through the solution casting technique, exhibiting enhanced UV-vis absorption properties. The results from IR spectroscopy indicated that the addition of BT enhanced the transmission regions related to hydroxyl (3500 \(\:c{m}^{-}\)¹) and carbonyl (1700 \(\:cm\)⁻¹) functional groups, suggesting the occurrence of chemical interactions between the PS matrix and BT, likely through hydrogen bonding mechanisms. Furthermore, UV-visible spectroscopy revealed that the presence of BT led to a reduction in the films’ transparency while simultaneously improving their absorption properties. It was found that the optical parameters of PS improved significantly, which is crucial from the technological viewpoint, including photonics and optoelectronics. The XRD pattern establishes that adding BT to PS improved the crystalline phase structure in the composite films. The D and G bands related to order and disorder structures were distinguished in Raman spectra of the bitumen and support the XRD pattern of pure bitumen. The FESEM images revealed rough surfaces in the composite films, and spherical white spots may be related to carbon dots. Optical characterizations reveal that integrating BT into PS films shifts the absorption edge to lower photon energies. The optical parameters, such as the refractive index () and dielectric constant encompassing both the real () and imaginary () parts, were analyzed and found to increase with increasing bitumen concentrations. The optical energy gap dropped from 4.34 to 1.14 as the BT doping concentration upgraded to 2 mL. The band edge width, which characterizes the tail-localized states, increases with higher BT concentration. The dispersion energy obtained from the W-D model reveals that, with increasing bitumen concentration, the rate of interaction between the PS polymer and bitumen carbon materials also increases.