Abstract
Imaging with X-rays poses fundamental limits due to radiation damage of the highly energetic photons. This becomes problematic for sensitive biological systems such as subcellular structures. Lowering the radiation dose, without sacrificing the signal-to-noise ratio, would be desirable for any kind of imaging modalities involving X-rays. To achieve this goal, quantum imaging with entangled X-ray photons constitutes a promising route. Production of biphotons have been demonstrated in the X-ray regime by the process of Spontaneous Parametric Down-Conversion (SPDC). However, compared to SPDC in the regime of visible light, the production rate for X-ray biphotons is extremely low. With the introduction of new high average brightness X-ray sources, such as 4th generation synchrotrons and high repetition rate Free-Electron X-ray Lasers (XFEL), quantum imaging may become practical. We introduce a ray tracing approach using Monte-Carlo sampling, specifically designed for quantum imaging with entangled X-ray photons generated by SPDC. By simulation, the superior image quality of quantum over classical imaging methods is demonstrated using realistic experimental conditions available at high repetition rate XFELs. With these simulations, we can efficiently assist the design of future experiments at beam lines, which can substantially accelerate the advancement of X-ray quantum imaging and reduce costs.
Similar content being viewed by others
1. Introduction
X-rays can, in principle, achieve atomic resolution due to their short wavelength. However, being ionizing radiation, X-rays break bonds and destroy the sample’s structure. Hence, in X-ray microscopy the maximum tolerable dose for a biological system is typically much lower than the required dose for reaching the diffraction limit1,2,3. Lowering the dose results in a reduction of the signal-to-noise ratio (SNR) which ultimately limits the resolution of imaging, ‘Rose Criterium’4. Studies show that damage-free resolution is about 10 nm at best both experimentally as well as theoretically1. By distributing the dose over multiple identical copies of the same molecular structure the resolution can be improved significantly, as done for example in X-ray crystallography. However, this practice is not always desirable or cannot be realized in many samples, as for example in subcellular structures5,6,7.
Several techniques have been suggested to address damage-related image quality reduction. Such techniques include for example, phase contrast imaging8 as well as computational techniques for noise reduction including compressive sensing9 and artificial intelligence10,11. In this paper we focus on quantum imaging with entangled X-ray photons (XQI) as the preferred technique. XQI can be employed to reduce the dose without sacrificing the SNR12,13,14,15,16. The principle of XQI is analogous to the well-established quantum imaging in the visible regime12,17,18,19,20. Similarly, as with visible light, X-ray biphotons can be produced by the process of Spontaneous Parametric Down-Conversion (SPDC). SPDC is a nonlinear phenomenon that converts an incoming pump photon into two outgoing biphotons. Both the visible and X-ray processes of SPDC generating biphotons obeys the principles of energy and momentum conservations21,22.
In practice, generation of biphotons in the X-ray regime is challenging as the conversion rate is only about one biphoton for every 1010 – 1011 pump photons23,24. It took Eisenberger and McCall roughly one year to collect enough biphotons to demonstrate the SPDC phenomenon with an X-ray tube22. The X-ray biphoton production rate has been recently improved to ~ 6000 biphotons per hour with the increasing brightness of 4th generation synchrotrons24. Despite this progress, such a rate is still not satisfactory to make quantum imaging practical.
The introduction of the new generation of X-ray Free Electron Lasers (XFEL) might provide the solution for the efficiency problem as such a source generate pulses up to about 1011 photons/pulse and up to 1 million pulses/sec25. This type of a source can provide about 4 orders of magnitude more biphotons than a synchrotron.
X-ray experiments at the XFEL are expensive and access to such facilities is limited. Thus, each experiment needs to be carefully prepared. Quantum imaging is affected by multiple experimental parameters such as biphotons’ degree of entanglement, quantum efficiency of the detector, beam bandwidth, divergence and width, as well as sample properties such as absorption and refractive index. It is essential for the success of the project to establish a conceptual framework which can incorporate all these experimental factors into the entire process of image formation and data collection. This will enable us to explore the method’s potential while tweaking the mentioned parameters. For this purpose, this paper introduces a simulation method that enables the investigation of XQI in silico. The presented simulations provide guidance in evaluating different imaging modalities and allows for refining the associated critical experimental parameters. It also enables feasibility studies to develop and establish such experiments within XFEL facilities without the need for spending valuable beam time on trial-and-error measurements. Additionally, this allows to identify the fundamental limits of XQI under ideal conditions.
The presented simulation technique is based on a combination of ray-tracing algorithms and a Monte-Carlo sampling method. The Monte-Carlo simulations were implemented in a module that simulates SPDC. We also present the data analysis methodology developed for this study. This methodology can also be used to analyze experimental data. Through this analysis we show that quantum imaging is highly advantageous over that of classical methods as it allows to significantly reduce the dose and thus the radiation damage.
The paper is organized as follows; Sect. 2 presents the results.Sect. 3 discusses the results from the analysis of the simulations output. Sect. 4 describe the algorithms developed for this study, and Sect. 5 summarizes the paper.
2. Results
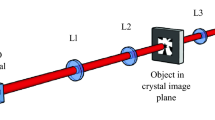
All the results presented in this paper were obtained from simulations using the setup depicted in Fig. 1A. An X-ray laser pump beam is hitting a diamond crystal detuned slightly away from the Bragg condition of the (400) reflection. The nonlinear crystal down-converts the incoming photons into biphotons, which travel along concentric conical surfaces and appear on the detector as rings with different energies (see inset in Fig. 1A). A sample is placed in the biphotons’ path near the detector to obtain X-ray quantum images. Figure 1B shows the momentum space representation of the setup, where a photon with a wave vector \(\:{\mathbf{K}}_{p}\) transforms into two photons with wave vectors \(\:{\mathbf{K}}_{s}\) and \(\:{\mathbf{K}}_{i}\), conserving energy and momentum.
The setup parameters were as follows. The distance between the 9.83 keV X-ray laser source and the crystal was 100 m. For the detector we assumed the ePix100, a pixelated area detector with single-photon resolution capability used at XFELs. The detector, comprising 704 × 768 pixels (50 μm x 50 μm each), was placed 0.5 m downstream of the crystal. A sample with 80% transmittance was positioned 1 mm in front of the detector.
The resulting energy spectrum from SPDC is presented in Sect. 2.1. X-ray classical, ghost, and quantum images, obtained by an ideal source (IDL), are presented in Sect. 2.2. Comparison between classical images and quantum images with non-ideal sources are presented in Sect. 2.3. These include a source with a divergence of 2.15 µrad (DVG), one with a width of 200 μm (WDT), and a combination of the two (MIX).
To simulate SPDC and XQI, the ray tracing toolkit described in Sect. 4.1 was utilized. The simulation output was analyzed using the toolkit described in Sect. 4.2. A detailed specification of all the setup parameters is given in Sect. 4.3.
(A) Schematic representation of the optical setup used for the generation of SPDC and XQI. An X-ray beam (red line) travels through two slits before hitting a diamond crystal which splits the photon into two photons. The biphotons propagate towards the detector (pink and yellow cones and dots). Some of the photons hit the sample while others go directly to the detector. A circular beam stop (BS) centered at the Bragg angle was used in front of the detector. (B) A schematic representation of the momentum space for the down-conversion process. \(\:{\mathbf{K}}_{p}\), \(\:{\mathbf{K}}_{s}\), and \(\:{\mathbf{K}}_{i}\) are the pump, signal, and idler wave vectors, respectively. \(\:\mathbf{G}\) is the reciprocal lattice vector, and \(\:{\alpha}_{s}\) / \(\:{\alpha}_{i}\) are the angles between signal/idler photon wave vectors and \(\:{\mathbf{K}}_{p}+\mathbf{G}\) (dark green arrow). \(\:{\theta}_{B}\) and \(\:{\Delta}\theta\:\) are the Bragg and detuning angles, respectively. The inset shows the detected image of the SPDC with circles representing the biphoton probable location at a fixed energy ratio with dot presenting an example of such photon pair. The biphotons are collinear with the beam center and positioned diametrically opposite.
2.1. Energy spectrum
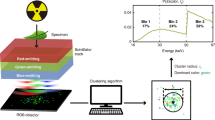
The photon energy spectrum is derived from the cross section of the SPDC, as discussed in Supplementary Information (SI) sections S2 and S3. The simulated energy spectra for the IDL source and the DVG source, along with the theoretical calculation of the energy probability distribution are depicted in Fig. 2.
In both IDL and DVG cases the curves follow each other closely, although the curve for DVG is noisier than the one for IDL. The theoretical line matches the simulated data. The curve is nearly flat between 4 keV and 7 keV, with the lowest value at half the source (pump) photon energy (4.9 keV). Figure 2 also shows an increase between 2.8 keV to 4 keV which relates to the finite detector size. Photons down to 4 keV are still detected as they fall fully within the detector area. For energies below 4 keV, however, some photons fall outside of the detector area. Hence, the probability of having lower energies decreases as the photon energy get lower. For energies above 7 keV, photons are blocked out by the beam stop. Both observations are discussed in detail in SI section S3.
While the energy spectrum in Fig. 2 is nearly uniform, the photon density captured by the detector drops as a function of distance from the center (inset in Fig. 1A). This results in a non-uniform sample illumination.
2.2. X-ray quantum image for an ideal source
Figure 3 presents the results for simulated classical, ghost and quantum images of a sample shaped like a πK using the IDL source. For all images, the setup from Fig. 1A was used with the parameters defined above. The classical image was obtained by accumulating all the photons ignoring their correlation (see Sect. 4.1). The ghost image was composed by summing up the photons which lost their partner due to absorption in the sample (see Sect. 4.2.4). The quantum image was assembled by calculating the positions of the absorbed photons from their pairs (Sect. 4.2.5). In each case, the accumulation of the photons was solely by counting photons ignoring their energy. The πK image clearly appears in the quantum image (Fig. 3C), less so in the ghost image (Fig. 3B), and with much lower contrast in the classical image (Fig. 3A). Additionally, the ghost image is also warped, because the idler and signal photon fall on circles of different sizes and are opposite to each other as shown in Fig. 1A. The lower contrast in the classical image can be attributed to the large background surrounding the image while such a background is absent in the ghost image and quantum image.
2.3. X-ray quantum image for source with divergence and/or width
While Fig. 3 provides valuable information about the advantage of quantum imaging over classical imaging, it is not realistic. The source does not diverge, and the beam size is infinitely small. To explore more realistic configurations, we examined three additional cases. The first, described in Sect. 2.1, introduces divergence. The second features a source with a width of 200 μm and the third modeled a source which combined both characteristics. The summary of the results, analyzed from these cases, are presented in Fig. 4.
The classical images of the four cases are shown in panels 4A-4D, while the corresponding quantum images are presented in panels 4E-4H. The πK is clearly visible in the quantum image in panel 4E, while its contrast is lower in the corresponding classical image in panel 4A. However, in the other cases, while the πK is more blurred in the quantum images (panels 4F-4H), it has completely disappeared in the corresponding classical images (panels 4B-4D).
(A–D) Classical image of a πK with uniform transmittance \(\:T=0.8\). The image was obtained by summing up all the imaged frames. The panels represent different illuminations conditions: (A) a point source with a single beam direction (IDL), (B) illumination with half angle divergence of 2.15 µrad (DVG), (C) illumination with a beam size of 200 μm (WDT) and (D) illumination with both half angle divergence of 2.15 µrad and beam size of 200 μm (MIX). (E-H) Quantum image of the same sample under the corresponding illumination conditions. The slits sizes used are 100 μm for the first one and 125 μm for the second. Simulations were performed with 4 million source rays.
To quantify the signal to noise ratio for both the quantum and the classical images, we used the calculations outlined in Sect. 4.4. A more detailed discussion about the superior image quality of the quantum image over the classical image is provided in next section.
3. Discussion
3.1. Quantum advantage
The quantum image appears with a better contrast compared to the classical image as seen in Figs. 3 and 4. This can be traded with a lower illumination dose to protect the sample from irradiation damage. In this subsection we provide a quantitative formalism to determine the level of improvement of the quantum image over the classical one. In the attempt to quantify the quantum advantage, we used the following definition,
.
where \(\:{\sigma}_{c}^{2}\) and \(\:{\sigma}_{q}^{2}\) are the variances of the classical and quantum images respectively. Equation (1) is further explained in Sect. 4.4. The comparison between the classical image and the quantum image is found in Table 1. The theoretical value of the quantum advantage equals 1/absorbance, which corresponds to a fivefold improvement over the classical image for a sample with a uniform transmittance of 0.8 (see Sect. 4.4). However, when it comes to the more realistic cases, this advantage may change.
The increase in image quality for quantum imaging is attributed to the fact that the number of photons incident on the sample directly correlates to the number of idler photons. In contrast, this information is missing in the classical image, as such information is not available.
3.2. Using simulations to help designing XFEL experiments
The setups studied in this paper included two sets of slits. This configuration option has improved the image quality when compared with a setup with no slits. The comparison is presented in Fig. S.6 in the SI. With slits the πK image is clear and has a high contrast. Without the slits, due to the divergence of the X-ray source, the image is severely blurred when using DVG source and completely indistinguishable for the WDT and MIX sources. This result highlights the critical role of adding slits, or other collimation elements, to the optical setup for optimizing image quality, even at the cost of reduced source intensity.
The simulation can also help optimize the detector position for an experimental setup. For example, Fig. 2 shows a drop in photon number for energies in the range of 2.8 keV to 4 keV, and a complete extinction of photons’ energies below 2.8 keV. Placing the detector closer to the diamond crystal will retain the ability to detect low energy photons at the cost of resolution. On the contrary, placing it farther enhances resolution at the expense of losing low energy photons.
The size and placement of the beam stop and its relation to the object can also be optimized by the simulations. A beam stop is used to block pump photons scattered from the crystal concentrated at the beam center. If too large, it eliminates information needed for quantum imaging as it can block idler photons that leads to removing parts of the quantum image.
The quality of the diamond crystal is also important. Crystal with higher mosaicity will add blur to the image. As mentioned in the results section, the SPDC illumination is composed of concentric conical surfaces where each cone corresponds to a different photon energy. Mosaicity introduces a blurring of these cones. For higher mosaicity (i.e. lower crystal quality) the blurring of the illuminating cones increases, which leads to a reduction in image contrast. A possible solution for reducing this effect is to increase the detuning angle. Increasing the detuning angle will increase illumination spread and will separate the circles more. Such a change will provide a sharper image.
Optimizing an optical system to achieve high quality image requires multi-parameter optimization to find ideal balance. For example, increasing the detuning angle to address mosaicity also increases converted photon dispersion which may necessitate placing the detector closer to the crystal to capture lower energy photons. However, this adjustment can reduce image resolution. Multi-parameter tuning, when performed at X-ray facilities like synchrotrons or XFELs, risks inefficient resource utilization. Conducting simulations as a first step can significantly reduce the cost and increase the success rate of achieving a high-quality quantum image in such facilities.
4. Methods
This section includes descriptions for algorithms used in the two essential software packages developed in this study. Section 4.1 describes the algorithms for simulating the SPDC and interaction with the object. Section 4.2 describes the data analysis algorithms for imaging. Section 4.3 provide a full account of the optical system setting parameters and Sect. 4.4 describes the procedure to quantify the quantum advantage.
The symbols used in this manuscript are defined in Table 2.
4.1. Simulations using ray tracing
The acquisition of the X-ray quantum images was simulated using ray tracing with a modular toolkit developed for this study. The toolkit consists of functions simulating X-ray source, free space propagation, mirrors, detectors, and spontaneous parametric down-conversion (SPDC). A description of the SPDC module can be found in Sect. 4.1.1 and with more details in section S4 of the SI. The simulation is performed by sequentially executing the different modules in a pipeline as they appear in the simulated optical setup. A typical pipeline starts with the source generating an X-ray beam with multiple rays positioned in 3D each directed using three angles. The rays propagate to a crystal, with a pair of slits just upstream of the crystal. In our model the slits were located 4.7 m and 1.1 m away from the diamond crystal. The crystal converts each ray into two rays determined by SPDC cross section. The sum of energies of the two down-converted rays, generated by the crystal, is equal to the source ray, i.e., energy is conserved. The sum of momenta of the two down-converted rays equals to the momentum of the source photon plus the momentum transfer from the crystal, \(\:\mathbf{G}\)21. The resulting down-converted photons will propagate to the sample plane. One of the photons will interact with the sample (signal photon) and the other will continue undisturbed to the detector (idler photon). The signal photon will be either absorbed or transmitted by the sample. If the signal photon is transmitted through the sample, it will continue to the detector plane. An example of such an optical setup is presented in Fig. 1A. The setup is simulated, and the analysis of these simulations are presented in the results section. The output of each module is a binary file listing the ray’s properties including ray number, position coordinates, direction, wavelength, pathlength, intensity, and polarization. The photon pairs generated by the crystal are sequential to one another on the list created by the SPDC module.
Once the photons reach the detector, they will be partitioned into frames, corresponding to an XFEL snapshot. In this process the information of the correlation between the biphotons is lost. In the following, photon pairs need to be identified from the position and energy measured on the detector as described in Sect. 4.2.
4.1.1. Description of SPDC module
For each ray the magnitude of the sum of the pump’s wave vector, \(\:{\mathbf{K}}_{p}\), and the crystal’s reciprocal lattice vector, \(\:\mathbf{G}\), is compared to the magnitude of the pump wave vector, \(\:{k}_{p}\). If \(\:\left|{\:\mathbf{K}}_{p}+\mathbf{G}\right|<{k}_{p}\), two additional rays are created with wave vectors \(\:{\mathbf{K}}_{s}\) for a signal photon and \(\:{\mathbf{K}}_{i}\) for the idler photon. The creation of these vectors requires a draw of random number for the angle between \(\:{\mathbf{K}}_{s}\) and \(\:{\mathbf{K}}_{G}\), i.e. \(\:{\alpha}_{s}\) (see Fig. 1B). \(\:{\alpha}_{s}\) is drawn randomly from a distribution with a certain range as described in the SI section S4. The probability distribution was derived from Freund and Levine21. \(\:{\alpha}_{s}\) and \(\:{k}_{s}\) will determine the direction and magnitude of \(\:{\mathbf{K}}_{s}\). \(\:{\mathbf{K}}_{i}\) is calculated based on momentum and energy conservation laws (see SI section S1 and Fig. 1B). The angle of propagation along the azimuthal direction of the cone is also drawn randomly from a uniform distribution function with values between 0 and 2π.
To add mosaicity to the module a rocking curve is introduced. The rocking curve is represented by a Gaussian distribution graph with a selected width from which random values are drawn for angles added to the tilt of the crystal lattice vector \(\:\mathbf{G}\). A detailed study of this part of the toolkit is out of the scope of this paper.
4.2. Analysis of X-ray quantum imaging simulation/experimental data
The toolkit used for the analysis of the simulations conducted in the method described in Sect. 4.1, includes several modules. Subsection 4.2.1 describes the extraction of the beam center (see Fig. 5B). Subsection 4.2.2 describes the extraction of the photon position within the frame (see Fig. 5A). Subsection 4.2.3 describes the algorithm for finding pairs of photons among the photon list generated by the algorithm in subsection 4.2.2 (see Fig. 5C). The fourth module is used to find the unpaired photons within the list of photons generated by the second module. These photons are unpaired as their pair was absorbed by the sample or did not hit the detector. The fifth module is used for calculating the position of the absorbed photon if it would have hit the detector. Additional functions are included in the toolkit to visualize the classical image generated when no biphotons are created or the quantum image as well as the ghost image (see Fig. 3). Description of each module is elaborated below.
(A) Four frames with single or pair of photons circled by blue circle indicating the identification of the positions of photons. A white arrow points to the locations of the photons. The red circle in the first frame panel indicates the center of the SPDC illuminating cone (Bragg spot). (B) An image generated by accumulating all the photons though out the simulation. The red circle in the center indicates the center of the SPDC illuminating cone as identified using the watershed algorithm from Sect. 4.2.1. (C) An image of several frames integrated on the detector. The red circles indicate the position of the photons, and the green line connects a pair of biphotons indicated using the algorithm in Sect. 4.2.3.
4.2.1. Extracting center of beam
Finding the center of the beam is important as there is correlation between photon momentum and distance from the center of the beam (see example in Fig. 5B and SI sections S1 and S9). To find the center we use a segmentation procedure that includes watershed algorithm26 followed by the calculation of center of mass of a central segment. The watershed algorithm is applied to the classical image when no sample is introduced. Classical image is generated by summing all the frames of an experiment or a simulation. The calculation of center of mass is done by calculating the average x and y coordinates of all the pixels within the central segment.
4.2.2. Identifying photon position within a frame
The distance between the position of a photon and the beam center is correlated to its momentum (see SI sections S1 and S9). Photons coordinates within a frame is needed for (i) checking energy conservation22 and (ii) calculating the location of the absorbed photon as if it had been detected by the camera. Identifying the location for the absorbed photon is required for quantum image generation. The algorithm for this module is written as follows:
-
1.
Collect the frames from an experiment or a simulation into a 3D stack.
-
2.
The stack of frames is shifted x pixels left and right in the frame’s horizontal direction as well as, up and down along the frame’s vertical direction to create four new stacks.
-
3.
The 5 stacks are compared, and a minimum value is calculated for each pixel to generate a stack of frames with minima values.
-
4.
The 5 stacks are compared again, and the maximum values are recorded for each pixel. This step creates a stack of frames with maxima values.
-
5.
If a pixel in the original stack equals to the corresponding pixel in the maxima stack, its coordinates are added to a maxima list.
-
6.
If the difference between the maxima pixels value and the corresponding minima pixels values is smaller than a threshold, remove the pixel from the maxima pixels list.
4.2.3. Identify photon pairs in a frame
Finding photon pairs requires frames to record at least two photons. Identifying the two photons as a pair requires two tests. First, the line connecting the position of the photon pairs needs to go through the beam center. Second, energy must be conserved, i.e., the sum of energies of the photon pair equals the energy of the source photon. The photon energy can be calculated from either the distance of the photon from the beam center (see section S9) or measured by the detector.
The pair identification function is simply checking the two mentioned tests. if both tests are passed the pair is added to a list. The function follows different pairs within the frame if more than one exists. If no pairs left to check, the function goes to the next frame.
4.2.4. Identify idler photons without their signal pair
The pairs of photons generated by the down-conversion mechanism travel through the sample plane. The signal photon is the one hitting the sample and being absorbed or transmitted, and the idler photon is the one traveling directly to the detector. If the signal photon is transmitted the detector will detect a pair of photons, however, if the signal photon is absorbed by the sample the detector will detect an unpaired photon.
Two methods have been developed to find unpaired photons. First method extracts the unpaired photons by removing the photon pairs identified using the algorithm in Sect. 4.2.3. from the complete list of the photons identified using the algorithm in Sect. 4.2.2. The remaining photons are assumed to be idler photons with their pairs being absorbed. The second method simply looks for frames that have only one photon identified. The advantage of the second method lies in its ability to reduce noise, particularly in experimental settings. The first method, however, might falsely identify photons as idlers.
4.2.5. The assessed position of absorbed photon on detector plane
The absorbed signal photon cannot be detected by the camera. However, the estimated position of the photon on the camera can be calculated. The quantum image is constructed by adding up the calculated absorbed signal photon for each pixel. This calculation increases SNR as the background is removed. The algorithm to calculate the position of the absorbed photons uses the coordinates of its idler photon pair extracted using the algorithm in Sect. 4.2.4. The coordinates of the signal photon are calculated as follows:
-
1.
Calculate the energy of the idler photons using their distance from the Beam center (see Eqs. S9.11 or S9.13) or the actual energy measured by the detector.
-
2.
Subtract the idler photon energy from the source photon energy.
-
3.
Convert the energy resulting from step 2 to distance from beam center.
-
4.
Calculate the direction of the line connecting the idler coordinate and the beam center.
-
5.
The position of the signal photon would be x pixels away from the beam center as calculated in step 3, in the direction calculated in step 4.
-
6.
Add the coordinates of the absorbed photon to a list of absorbed photons.
-
7.
Repeat steps 1–6 for all unpaired idler photons.
4.3. Simulated optical setup description
The simulations are executed by utilizing the ray-tracing toolbox described in Sect. 4.1. The toolbox contains modules for all the components used in a typical x-ray setup. Each module requires input parameters such as element size and position. In this subsection we provide all the required parameters for each module.
-
(i)
Source module: Sect. 2 describes four different sources (IDL, DVG, WDT, and MIX). The divergence in the DVG and MIX sources is simulated by randomly drawing ray direction values from a Gaussian distribution with a zero mean and a standard deviation of 2.15 × 10− 6. The beam size in the WDT and MIX sources is simulated by randomly choosing ray position from a Gaussian distribution with a zero mean and a standard deviation of 200 × 10− 6. Each source produces 4 million rays unless noted otherwise. The optical axis is parallel to the z direction and the source was placed 100 m away from the crystal.
-
(ii)
Slit module: The first/second set of two slits oriented along x and y directions are positioned 4.7 m/1.1 m away from the crystal with an opening of 100 μm/125 µm each.
-
(iii)
SPDC module: The diamond crystal is tilted 0.022\(^\circ\:\) away from the Bragg angle related to the (400) lattice plane.
-
(iv)
Sample module: The down-converted illumination from the crystal propagates towards the sample plane positioned 1 mm away from the detector.
-
(v)
Detector module: The idler photons and the transmitted signal photons continue to propagate to the detector which is positioned 0.5 m away from the crystal. The detector is an array of \(\:704\times\:768\) pixels with size of 50 μm each. The black circle in the middle of the inset of Fig. 1A, resulted from energy filtering of the photons hitting the detector (simulation of beam block). The allowed energy range after filtering is between 2.8 keV and 7 keV.
4.4. Quantum advantage
The advantage of quantum imaging over classical imaging lies in its better SNR. For homogenous objects, such an advantage is theoretically calculated as the ratio of the classical image variance, \(\:{\sigma}_{c}^{2}\), to the quantum image variance, \(\:{\sigma}_{q}^{2}\), i.e.
where T is the ground truth sample transmittance. Classical and quantum transmittance are defined as
and
where \(\:{N}_{s}\) and \(\:{N}_{i}\) are the number of photons transmitted through the sample (signal photons) and the pairs of the signal photons (idler photons), respectively.\(\:\:\langle N \rangle\) is the average number of incoming photons. The classical image variance can be calculated as:
where \(\:{\sigma}_{{N}_{s}}^{2}\) is the measured variance of the transmitted photons. For \(\:{N}_{s}\) we can assume a Poissonian distribution and thus \(\:{\sigma}_{{N}_{s}}^{2}=\langle {N}_{s} \rangle\), where \(\:\langle \rangle\) represents the mean value, hence
The variance of the quantum image can be calculated as:
where \(\:{\sigma}_{{N}_{I}}^{2}\) is the variance of the idler photons. Dividing Eq. (6) by Eq. (7) leads to Eq. (1), which indicates that for a quantum image to have a similar quality as a classical image, the number of photons illuminating the sample is reduced by a factor of \(\:\frac{1}{1-T}\). While the presented calculation of quantum advantage can only be accurate for an IDL source, it does provide a formula connecting advantage with transmission of the sample. Empirical methods to calculate the quantum advantage from simulated data are presented in SI section S7.
5. Summary
We have shown the quantum advantage of XQI is highest for highly transparent objects. Given most biological samples are highly transparent in the X-ray regime this could enable damage-free high-resolution imaging beyond 10 nm resolution.
To advance quantum imaging with X-rays, we developed and employed ray-tracing simulations with Monte-Carlo sampling for the SPDC process. Results from realistic optical setups, that can be used at an XFEL facility, were presented. At first, we studied the formation of SPDC, showing that the energy spectrum of the biphotons is mostly uniform, however, radially the density of photons increases as their position gets closer to the beam center.
To evaluate quantum imaging advantage, four distinct source configurations were studied. These configurations introduce a source emitting photon along a single ray, source with divergence of 2.15 µrad, one with 200 μm beam width, and one combining divergence and beam size. While the non-diverging point source is not feasible, it does provide insight into quantum imaging. Such a case can confirm the theoretical calculations of, e.g., the quantum image advantage over the classical image. The other scenarios are more realistic. We have shown that the quantum image has a higher quality than the classical image.
Besides the effects of beam divergence and finite beam size studied in this work, there are additional nuisance parameters that need to be addressed. Such parameters include detector quantum efficiency, detector noise, and background signals from various contributions along the optical setup such as fluorescence and Compton scattering. These parameters will be addressed in the future. In addition, our method is not limited to the different cases presented in this paper, it can be extended equally well to other modalities such as diffraction and ptychography27.
Our results presented in this paper demonstrate the potential of simulations as an efficient design tool for planning experiments at XFEL beamlines and synchrotrons. These simulations can drastically reduce potential risks and save valuable beam time for future XQI experiments. We expect that this will have a positive impact on advancing Quantum Imaging with X-rays.
Data availability
For this study we used the simulation software package MCXQI v1.0, developed by the authors of this paper. The source code is publicly available from GitHub released under the GNU General Public License v 3.0 via the URL: https://github.com/gabbiener/MCXQI-Simulation-Package.
References
Howells, M. R. et al. An assessment of the resolution limitation due to radiation-damage in X-ray diffraction microscopy. J. Electron. Spectros Relat. Phenom. 170, 4–12 (2009).
Henderson, R. The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological molecules. Q. Rev. Biophys. 28, 171–193 (1995).
Noh, D. Y., Kim, C., Kim, Y. & Song, C. Enhancing resolution in coherent x-ray diffraction imaging. J. Phys.: Condens. Matter. 28, 493001 (2016).
Rose, A. Television pickup tubes and the problem of vision. in (ed. Marton, L. B. et al.) vol. 1 131–166 (Academic Press, 1948).
Nass, K. et al. Indications of radiation damage in ferredoxin microcrystals using high-intensity X-FEL beams. J. Synchrotron Radiat. 22, 225–238 (2015).
Lomb, L. et al. Radiation damage in protein serial femtosecond crystallography using an x-ray free-electron laser. Phys. Rev. B. 84, 214111 (2011).
Quiney, H. M. & Nugent, K. A. Biomolecular imaging and electronic damage using X-ray free-electron lasers. Nat. Phys. 7, 142–146 (2011).
Kitchen, M. J. et al. CT dose reduction factors in the thousands using X-ray phase contrast. Sci. Rep. 7, 15953 (2017).
Zhang, C. et al. A model of regularization parameter determination in Low-Dose X-Ray CT reconstruction based on dictionary learning. Comput. Math. Methods Med. 2015, 831790 (2015).
Shan, H. et al. 3-D convolutional Encoder-Decoder network for Low-Dose CT via transfer learning from a 2-D trained network. IEEE Trans. Med. Imaging. 37, 1522–1534 (2018).
Yang, Q. et al. Low-Dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Trans. Med. Imaging. 37, 1348–1357 (2018).
Morris, P. A., Aspden, R. S., Bell, J. E. C., Boyd, R. W. & Padgett, M. J. Imaging with a small number of photons. Nat. Commun. 6, 5913 (2015).
Yanoff, B. D. et al. SPIE,. Quantum x-ray imaging for medical and industrial applications. in Optical and Quantum Sensing and Precision Metrology (eds. Shahriar, S. M. & Scheuer, J.) vol. 11700 117003H (2021).
Schneider, R. et al. Quantum imaging with incoherently scattered light from a free-electron laser. Nat. Phys. 14, 126–129 (2018).
Schori, A., Borodin, D., Tamasaku, K. & Shwartz, S. Ghost imaging with paired x-ray photons. Phys. Rev. A. 97, 063804 (2018).
Yu, H. et al. Fourier-Transform ghost imaging with hard X rays. Phys. Rev. Lett. 117, 113901 (2016).
Brida, G. et al. Measurement of sub-shot-noise Spatial correlations without background Subtraction. Phys. Rev. Lett. 102, 213602 (2009).
Brida, G., Genovese, M. & Berchera, I. R. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics. 4, 227–230 (2010).
Gregory, T., Moreau, P. A., Toninelli, E. & Padgett, M. J. Imaging through noise with quantum illumination. Sci. Adv. 6, 2652 (2020).
Shapiro, J. H. & Boyd, R. W. The physics of ghost imaging. Quantum Inf. Process. 11, 949–993 (2012).
Freund, I. & Levine, B. F. Parametric conversion of X rays. Phys. Rev. Lett. 23, 854–857 (1969).
Eisenberger, P. & McCall, S. L. X-ray parametric conversion. Phys. Rev. Lett. 26, 684–688 (1971).
Hartley, N. J. et al. Confirming X-ray parametric down conversion by time–energy correlation. Results Phys. 57, 107328 (2024).
Goodrich, J. C. et al. Quantum imaging with X-rays. Preprint At. (2024). https://arxiv.org/abs/2412.09833
Schoenlein, R. W. et al. LCLS-II High Energy (LCLS-II-HE): A Transformative X-Ray Laser for Science. https://www.osti.gov/biblio/1634206 (2016). https://doi.org/10.2172/1634206
Najman, L. & Schmitt, M. Geodesic saliency of watershed contours and hierarchical segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 18, 1163–1173 (1996).
Pfeiffer, F. X-ray ptychography. Nat. Photonics. 12, 9–17 (2018).
Funding
P.S., P.E., G.B., A.A. and J.B. are supported by the US Department of Energy, Office of Science, Biological and Environmental Research under award DE-SC0023170. A.A. and J. B. are also supported by the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
P.E. and G.B. performed analytic calculations, implemented software, carried out numerical simulations, and analyzed the results, each with equal contribution. A.A. co-designed the study, provided software code, and helped analyzing the results. J.B. helped analyzing the results. P.E., G.B. and P.S. wrote the paper with contributions from A.A. and J.B. P.S. designed the study, developed the theoretical framework, analyzed the results, and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Espoukeh, P., Biener, G., Baxter, J. et al. Advancing X-ray quantum imaging through Monte-Carlo simulations. Sci Rep 15, 25359 (2025). https://doi.org/10.1038/s41598-025-10495-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-10495-z