Grid-connected PV inverter system control optimization using Grey Wolf optimized PID controller

Abstract

This paper introduces a robust and adaptive control framework that integrates a Proportional–Integral–Derivative (PID) controller with the bio-inspired Grey Wolf Optimization (GWO) algorithm for real-time tuning of controller parameters in grid-connected photovoltaic (PV) inverter systems. Conventional controllers such as P and PI are widely used in PV applications due to their simplicity, but they exhibit notable limitations in dynamic environments, including increased Total Harmonic Distortion (THD), slower transient response, and poor voltage regulation—particularly under variable irradiance conditions. The proposed GWO-PID method overcomes these limitations by leveraging the GWO algorithm’s global search capability to dynamically optimize the PID gains (K_p, K_i, K_d) based on a composite fitness function that minimizes Mean Squared Error (MSE) and THD. The system architecture, simulated in MATLAB/Simulink, comprises a 50 kW PV array with a boost converter employing an Incremental Conductance (INC) Maximum Power Point Tracking (MPPT) algorithm, a three-phase voltage source inverter, RLC filters, and a dual-loop (voltage and current) control system synchronized with the utility grid through a Phase-Locked Loop (PLL). The GWO algorithm iteratively refines PID parameters to achieve real-time adaptation to environmental fluctuations. Under standard irradiance (1000 W/m²), the GWO-PID controller achieved a rise time of 0.025 s, settling time of 0.035 s, THD of 3.7%, and MSE of 0.25 kW², while maintaining a stable DC-link voltage of 500 V, thereby ensuring compliance with IEEE 519–2014 power quality standards. Across irradiance levels ranging from 400 W/m² to 1000 W/m², the GWO-PID controller consistently maintained DC-link voltage stability and minimized oscillations in PV voltage and current. Compared to traditional PI and P controllers, the proposed method reduced settling time by over 45%, improved power tracking accuracy, and significantly lowered harmonic distortion. Furthermore, it ensured a power factor close to unity and exhibited excellent frequency stability under transient disturbances. Simulation results also confirm the superior performance of the GWO-PID controller in managing active and reactive power exchange, minimizing overshoot, and maintaining synchronization with the grid, even during rapid environmental transitions. By embedding intelligent metaheuristic optimization into a classical PID framework, this work advances the state of inverter control strategies for PV systems. The proposed GWO-PID technique provides a scalable, efficient, and real-time solution that enhances grid compliance, energy quality, and system stability, marking a key advancement in adaptive control for smart grid and microgrid applications.

Introduction

Today, we are confronted with urgent challenges such as rising temperatures, poor air quality, environmental degradations, all of which are adversely impacting our health and the planets ecology. Addressing these issues is crucial for safeguarding both our well-being and the environment. The Long-term economic costs of failing to address these concerns far outweigh the initial capital investment needed to prevent them. As a result, the transition to renewable energy systems (RES), such as PV energy, is essential in mitigating these negative impacts¹.

PV energy presents a sustainable solution for meeting current and future energy demands while simultaneously reducing greenhouse gases and air pollution. This energy shift not only offers significant environmental benefits but also long-term economic gains by preventing healthcare costs and ecological losses due to pollution and climate change. This widespread adoption of PV installations further supports this transition, with cumulative global PV capacity expected to exceed approximately 1.2 terawatts (TW) by 2025^2,3.

PV systems, now a pillar of modern power production, are increasingly integrating distributed generation (DG) technologies. This integration allows PV systems to operate autonomously from the central electricity grid, a practice that has been successfully adopted by nations like Japan, Germany, Spain, and the United States⁴. However, challenges related to power quality, stability, and power output mismatches arise when PV systems are connected to the grid via inverters. Inverters, being pivotal power electronic converters, convert the DC from RES to AC, enabling the supply of electricity to AC loads or the utility grid⁵.

PV systems use various types of inverters, ranging from the single-phase inverter for small residential loads to the $\:3\:\%$ inverter for large, utility-scale loads⁶. Effective Inverter control is vital for optimizing PV power usage, especially in off-grid applications.

Proper inverter management in grid-connected PV systems ensures the stability and quality of the electricity supplied to the grid. An appropriate control strategy is necessary to ensure reliable performance over diverse system configurations and fluctuating environmental conditions. Grid-connected PV systems are particularly play a critical role in addressing the growing global demand for clean, renewable energy⁷.

Grid connection of PV systems poses a series of problems, primarily due to fluctuations in power generated as a function of temperature, irradiance, as well as non-linear characteristics of the PV panels and power electronics equipment like inverters and converters. Such a risk will compromise system stability and reliability, especially when there are grid faults, e.g., voltage sag due to an abrupt change of load⁸. Such disturbances decide whether the PV system remains grid connected or goes off-line. To combat such challenges, grid codes have been developed to specify connection and disconnection requirements of PV systems during fault conditions. These codes typically provide permissible voltage levels during faults and establish trip and connection areas in terms of the PCC voltage level⁹. These regulations are very important in facilitating Fault Ride Through (FRT) and Low Voltage Ride Through (LVRT) capabilities, in such a way that the PV system sustains the grid fault without disconnection. In grid-connected system, DC-DC choppers and DC-AC inverters are utilized to facilitate energy conversion¹⁰. Authors in recent research¹¹, present hybrid MPPT technique with 5 level inverters to control the variability and fluctuation in the performance of grid connected PV. The MPPT is utilized in the DC-DC chopper to ensure maximum energy harvesting from the PV system under variable environmental conditions. Despite the advantages, there are still issues with regulating the power exchange between the grid and the PV system, especially under abnormal operating conditions. To improve this regulation, a number of control techniques have been suggested¹². Recently, a hybrid WOADE-based MPPT algorithm was introduced for wind energy conversion systems (WECS) used in water pumping, combining Whale Optimization and Differential Evolution to ensure fast, oscillation-free power tracking under dynamic conditions. A modified Ćuk converter and PMSG-driven pump validated its effectiveness experimentally. Similarly, an improved improved differential evolution particle swarm optimization (IDEPSO)-based MPPT was proposed for PV-powered water pumping systems leveraging a high-gain boost-Ćuk converter and a switched reluctance motor (SRM) with a mid-point converter to achieve accurate GMPP tracking and efficient performance under varying solar conditions^13,14. DC-AC inverter control techniques, on the other hand, improve PCC voltage grid connection performance while operating under fault conditions by means of controlling active and reactive power exchanges between the grid and the PV system. Control techniques contribute significantly to stabilizing PCC voltage as well as proper synchronization with the grid. Several methods have been proposed in managing active power exchange and voltage quality improvement at PCC for effective grid integration¹⁵.

Proportional (P) control widely used in grid-connected PV systems. P control adjusts the output proportionally to the error signal, which represents the difference between the desired setpoint (e.g., target voltage or current) and the current system value. P control gives a quick response to the deviations and is employed for voltage and current regulation in PV inverters¹⁶. It is easy to apply and requires fewer computational resources, making it suitable for rapid correction in renewable energy systems. However, P control alone does not remove steady-state error, which can lead to persistent offsets between desired and actual system output. This limitation is relevant, particularly in grid-connected PV systems, where external conditions such as solar irradiance or temperature can alter over time¹⁷. The Proportional-Integral (PI) controller is a commonly used and simple control algorithm which have the ability to control both short- and long-term system behavior. It is often used due to its simplicity of structure, rendering it easy for implementation in a variety of real-world applications¹⁸. The tuning of the PI controller could be challenging, especially in dynamic systems where the environment causes variability. There has been the use of traditional approaches, like the Ziegler-Nichols method, in tuning PI controllers, but it has led to suboptimal performance. Other newer approaches target better performance by adjusting the system’s damping and control properties more precisely, giving better overall performance in practical situations^19,20. In²¹, Authors proposed and investigated a novel control strategy using PSO for tuning of PI controller in real-time to enhance power quality and transient response hence, setting a benchmark in optimization of controllers in 3 phase grid connected PV systems.

Several recent studies have underscored the critical role of advanced metaheuristic optimization and robust control strategies in enhancing the performance of grid-connected PV systems and other dynamic control applications. For example, Altawil et al.²² applied a slap swarm algorithm to optimize fractional-order PI controllers, demonstrating significant improvements in regulating grid voltage under varying PV conditions, a challenge also addressed in the present study through GWO-tuned PID gains. Izci et al.²³ proposed a fractional-order PID plus double-derivative controller optimized via the mountain gazelle algorithm for automatic voltage regulation, highlighting how combining fractional calculus with bio-inspired optimizers yields improved dynamic stability—a parallel to the adaptive capabilities targeted in this work. Similarly, Abualigah et al.²⁴ showcased the effectiveness of the sinh cosh optimizer in designing filtered PID controllers for precise aircraft pitch control, further confirming that enhanced search mechanisms can improve controller performance across diverse domains. Beyond algorithmic innovations, robust control frameworks for PV integration have been advanced through sliding mode and fractional-order methods. Mohapatra et al.²⁵ implemented super-twisting sliding mode controllers to achieve real-time power management in PV systems, achieving superior tracking and stability compared to conventional techniques. Goud et al.²⁶ developed a gravitational search algorithm-tuned fractional-order PID current control strategy to mitigate power quality issues in PV systems, demonstrating reduced harmonics and improved dynamic response—objectives similarly addressed by the GWO-PID scheme proposed here. Babu et al.²⁷ provided comprehensive modeling and performance analysis of PV-grid interfaces incorporating advanced controllers under fluctuating environmental conditions, emphasizing the need for adaptive control solutions to maintain grid compliance and energy quality. Further, Mohapatra et al.²⁸ validated an offset hysteresis band current controller based on an improved Aquila optimizer (IAOA), confirming the feasibility of real-time deployment of metaheuristic-based controllers in grid-tied PV environments. Lastly, Pachauri et al.²⁹ introduced a robust fractional-order control approach tailored for PV-integrated microgrids, showcasing enhanced resilience to uncertainties and disturbances, and reinforcing the importance of controller adaptability—a key contribution of the present GWO-based PID tuning framework. Collectively, these studies demonstrate that integrating intelligent optimization techniques with advanced control architectures significantly enhances power quality, stability, and tracking performance in grid-connected renewable energy systems, aligning closely with the objectives and outcomes of this research.

In recent researches, the power quality of injected electrical power from grid-connected PV systems has been a major issue. These researches focus on regulating the injected voltage and current at the PCC. The proposed model includes current and voltage cascade control loops, utilizing conventional PI controllers, to control the voltage at the PCC on the AC side of the inverter and ensure precise synchronization of the injected current with the grid voltage. The model was evaluated using MATLAB/Simulink simulations, demonstrating its to deliver optimal power to the grid with a unity power factor and maintain a stable PCC voltage under both steady-state and transient conditions³⁰. In other experiment, A two-stage power converter, commonly used in $\:3\:\varnothing\:$ grid-connected PV systems, was tested. The converters regulate the DC link voltage to control the power injected into the grid. The focus of the study was on designing PI controllers for the outer voltage loop and the inner current loop of the converter. The findings suggested that optimal decoupling of the two loops occur when the inner loop’s bandwidth is ten times larger than that of the outer loop. The approach was validated through simulations, which demonstrated that the controllers performed effectively even under rapid changes in irradiance^31,32. The increasing integration of RES into power systems has created a need for effective control mechanisms and high-power quality in microgrids. to optimize solar power utilization and ensure a high-quality power supply, an efficient control mechanism is proposed in³³. The FOPI controller employed within the inverter employs voltage-oriented control (VOC). Fractional-order proportional integral controllers possess a unique advantage due to the additional degree of freedom, which allows a wider range of parameters and more precise control. The PSO algorithm optimizes the FOPI and traditional PI controller parameters, and the results indicate the superior performance of the PSO-FOPI controller in response time, stability, accuracy, and reduction of THD in the injected current into the grid, even under varying solar irradiance conditions and are investigated in^34,35.

In¹, the Z-source inverter (ZSI) topology is introduced as a promising solution for single-phase grid-connected PV systems, simplifying the power conversion process by consolidating multiple stages into a single stage. The paper discusses various Z-source topologies and proposes a PI controlled bridged grid-connected PV network for electric vehicle (EV) charging. The study also investigates different modulation techniques used in these topologies. The system’s parameters fluctuate depending on operational modes, such as when PV generation is connected to the grid or when EVs are charging, with simultaneous grid and PV system connection also considered. The simulation results, analyzed using Pulse Width Modulation (PWM) techniques, assess battery voltage, grid voltage, and evaluate system performance based on THD and Fast Fourier Transform (FFT) results².

In³, the design and performance of an adaptive PI controller using an Artificial Neural Network (ANN) are explored, applied to a single-phase, single-stage, transformer less grid-connected PV system. A Feed Forward Neural Network (FFNN) dynamically adjusts the PI parameters to address the system’s sensitivity to parameter variations. The adaptive PI controller outperforms the traditional PI controller in terms of power quality, grid synchronization, and reference tracking, particularly by reducing THD in the injected current, especially under low solar irradiance conditions⁴.

The PI controller parameters must be carefully chosen to ensure optimal function and robust control. Common tuning methods, such as Ziegler-Nichols, Cohen-Coon, and self-tuning fuzzy PI-based M-constrained integral gain optimization (MIGO), are widely used to identify optimal values for PI controller parameters. However, challenges arise from insufficient process information and reliance on trial-and-error methods, which can reduce robustness and lead to suboptimal performance^5,7. Sliding Mode Controllers (SMC) have been introduced to address periodic errors in inverter output voltage under varying load conditions. These controllers are effective in reducing THD for both linear and non-linear loads⁸. Furthermore, optimization techniques like Genetic Algorithm (GA), PSO, Differential Evaluation (DE), Ant Colony Optimization, and neural-fuzzy logic have been employed to improve PI controller performance and fine-tune its parameters. For instance, one study used GA in a backpropagation neural network to optimize the initial weights and minimize DC current, thus improving controller performance⁹.

In¹⁰, the voltage-oriented PI control of three-phase grid-connected PWM rectifiers with LCL filters is discussed. Although LCL filters require resonance damping, and active resonance damping is widely used, the PI control method remains a simpler alternative, especially for systems using L filters. The paper investigates the limitations of PI control, particularly its inability to maintain system stability with varying LCL filter resonance and control frequencies. Experimental results validate the theoretical analysis, showing that voltage-oriented PI control provides stable performance within specific frequency ratios but fails to maintain stability outside this range.

In¹¹, a PID-Fuzzy Logic hybrid controller is introduced to improve the dynamic response of active and reactive power in grid-connected PV inverters. By combining the PID controller with fuzzy logic, the hybrid approach provides more effective and adaptable control for nonlinear systems. Simulation comparisons between a standalone PID controller and the PID-Fuzzy controller show that the latter offers better time response, overshoot, and stability. The PID-Fuzzy controller maintains more consistent and stable performance, even when grid parameters change during operation and for power reference change¹².

In³⁶, an adaptive PID controller derived from an Artificial Neural Network (ANN-PID) is utilized to regulate the grid-integrated PV network’s a three-phase inverter currents that output and boost converter output voltage. ANN-PID methodology enhances the reference tracking of DC link voltage with a maximum overshoot of merely 3.16% and provides better robustness than conventional PID controllers with a THD of 0.96%. The conventional PID controllers are surpassed by the proposed methodology with larger THD, proving its ability to enhance the system performance.

The study presented in¹³, proposed the design and performance of an optimized PID controller for a PV system integrated into a microgrid, addressing the limitations of conventional PI controllers during fault conditions. The paper introduces an optimized PID regulator to enhance system constancy and response time under DC and AC faults, varying load demands, and transmission line lengths.

In¹⁴, For grid-tied PV systems, the authors suggest a transformer-less seven-level inverter with a buck-boost regulator and an improved PID regulator. For optimization, the system employs a hybrid metaheuristic algorithm that combines the Equilibrium Optimization Algorithm (EOA) and Honey Badger Algorithm (HBA). In a combination of PV and battery system, MATLAB/Simulink simulations verify the system’s effectiveness by reducing switching losses and guaranteeing ideal power quality.

In order to better tune PI controllers and shed light on the properties of an indirect field-oriented controlled induction motor drive, metaheuristic optimization methods are used in³⁷. Another study compares the benchmark algorithm PSO for controller’s parameter optimization with the Grey Wolf Optimization and Teaching-Learning-Based Optimizing algorithms. The performance is experimented based on the ITAE, ZLG, and MSE objective functions, which are outperformed by GWO than TLBO and PSO in terms of minimizing the objective function values and achieving a faster convergence. The results show that the system performance tuned with GWO delivers the best outcomes with less settling and rise time related to the PSO-tuned system, particularly by employing the ZLG objective function³⁸.

In³⁹, PSO and GWO algorithms are compared in simulating a lithium-ion battery in terms of voltage behavior and delivery of current. Both algorithms have been employed for optimizing the parameters of model and reducing the root mean square error between simulated and experimental responses. Using MATLAB/Simulink implementation, the model optimized using GWO performed better with a reduction in RMSE by 42% compared to the PSO-optimized model with polynomial complexity behavior. The Proportional-Integral-Derivative controller is very well known to be simple yet effective⁴⁰. For reasonable reference signal changes, PID controllers will generally suffice, with no discernible benefit in employing more advanced controllers. Yet they possess some disadvantages, like integral wind-up and actuator wear due to the derivative action, particularly when confronted with large reference changes or large disturbances. In situations where systems are subjected to harsh operating conditions, nonlinear zones, or instability problems, the PID controller’s limitations are realized, calling for more advanced control methods⁴¹.

Despite considerable advancements in control strategies for grid-connected PV systems, existing literature reveals persistent challenges in achieving robust and adaptive performance under dynamic environmental conditions. Conventional controllers such as P, PI, and even classical PID, while widely adopted for their simplicity and ease of implementation, exhibit significant limitations—particularly in maintaining voltage stability, minimizing THD, and ensuring fast dynamic response during fluctuating solar irradiance. Prior attempts to improve controller performance using tuning heuristics like Ziegler-Nichols, ANN-based adaptation, and soft computing approaches such as Genetic Algorithms (GA) o have shown improvements, but often at the cost of increased computational complexity or slow convergence. Additionally, most methods lack real-time adaptability and are not rigorously validated under full-load transient and varying irradiance conditions. Furthermore, limited integration exists between optimization techniques and real-time inverter control loops that simultaneously manage both active and reactive power. These gaps highlight the need for an intelligent, computationally efficient, and real-time compatible PID tuning approach that ensures grid-code compliance, enhanced power quality, and stability across diverse operating conditions in PV systems.

The key technical contributions of this work are as follows:

• I. Design and implementation of a GWO-PID control strategy that automatically and adaptively tunes the PID parameters in real time, enabling superior regulation of DC-link voltage, inverter output current, and grid power injection in a three-phase grid-connected PV inverter system.

• II. Development of a computationally efficient optimization framework using Grey Wolf Optimization that ensures global search capability with fast convergence and low overhead, thereby making the control scheme suitable for real-time embedded implementation in dynamic PV environments.

• III. Comprehensive simulation and validation under variable irradiance conditions (ranging from 400 W/m² to 1000 W/m²), demonstrating substantial improvements over conventional PI and P controllers in terms of reduced THD (3.7%), lower MSE (0.25 kW²), and faster settling and rise times (0.035s and 0.025s, respectively), all while maintaining a constant DC-link voltage of 500 V and a power factor close to unity.

• IV. Demonstration of robustness and adaptability of the proposed GWO-PID framework in managing transient conditions, frequency oscillations, and load disturbances, thereby ensuring seamless and stable operation of the PV system with full compliance to IEEE 519–2014 grid standards.

Simulation Outcomes:

• I. Contribution 1: Achieved real-time optimization with fast convergence in Figs. 15, 16, 17, 18 and 19, where the GWO-PID controller demonstrated a faster settling time and lower THD compared to PI and P controllers.

• II. Contribution 2: The computational efficiency of GWO was validated by the fitness evaluation shown in Fig. 14, where the GWO algorithm converged faster than other optimization methods, resulting in optimized PID gains.

• III. Contribution 3: Simulation results, including the DC-link voltage, power output, and THD, confirmed the controller’s superior performance, especially under dynamic irradiance conditions (Fig. 15).

• IV. Contribution 4: The robustness of the system in transient conditions was demonstrated in Figs. 15, 16, 17, 18 and 19, where rapid voltage corrections and minimal power oscillations were achieved.

The grid-integrated PV system’s description

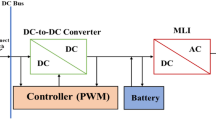
In this study, a 3-phase voltage source inverter (VSI) is used in the grid-tied photovoltaic system depicted in Fig. 1 and its corresponding simulation in Fig. 2. The PV array, inverter, boost converter, RLC filter, load, and MPPT algorithm are all part of the system. Located on the PV array’s output terminal, the DC link capacitors carry the voltage that is output to the inverter. The IC MPPT algorithm, that regulates system performance based on real-time temperature and sun irradiation fluctuations, helps the boost converter to extract the most power possible. The PV array’s DC output is converted to AC power using a three-phase VSI, and the RLC filter is employed to guarantee power quality. The system has a 50-kW capacity and supplies the grid with the filtered AC electricity. The inverter control strategy ensures the grid-connected system ensures required grid compliance standards, with a unit power factor, voltage stability, and reducing harmonic distortions. In the next sections, the dynamic characteristics of grid-linked photovoltaic system is investigated, with special emphasis placed on the control mechanisms and power quality performance.

Fig. 1

A representation of the grid-tied photovoltaic system.

Fig. 2

Simulation of the grid-tied photovoltaic system under investigation.

PV model

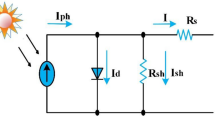
The solar cell is the main part of a PV system. A PV module is formed when multiple solar cells are joined in series. Figure 3 displays the comparable circuit that corresponds to a PV module.

Fig. 3

PV module equivalent circuit.

The connection between the equivalent circuit’s output voltage V_pv and the current I_PV in the equivalent circuit is governed by the following equation for (ideal Conditions):

I_PV=$\:{\varvec{I}}_{\varvec{p}\varvec{h}}-{\varvec{I}}_{\varvec{s}\varvec{h}}\mathbf{exp}\left(\frac{{\varvec{V}}_{\varvec{p}\varvec{v}}+{\varvec{I}\varvec{R}}_{\varvec{s}}}{\varvec{n}{\varvec{V}}_{\varvec{t}}}\right)-\:\left(\frac{{\varvec{V}}_{\varvec{p}\varvec{v}}+{\varvec{I}\varvec{R}}_{\varvec{s}}}{{\varvec{R}}_{\varvec{s}\varvec{h}}}\right)\:$ (1)

where $\:{\varvec{I}}_{\varvec{p}\varvec{h}}$ is the photocurrent, $\:{\varvec{I}}_{\varvec{s}\varvec{h}}$ is the diode’s saturation current, $\:{\varvec{V}}_{\varvec{p}\varvec{v}}\:$ is output voltage, $\:{\varvec{R}}_{\varvec{s}}$is resistance connected in series, $\:{\varvec{R}}_{\varvec{s}\varvec{h}}$k is resistance connected in shunt, $\:\varvec{n}\:$is the diode’s ideality factor.

The solar cell’s photocurrent ($\:{\varvec{I}}_{\varvec{p}\varvec{h}}$) which is influenced by temperature and sun irradiation, is determined by:

$$\:{\varvec{I}}_{\varvec{p}\varvec{h}}=\:\frac{G}{{G}_{ref}}\:({\varvec{I}}_{\varvec{s}\varvec{c}}+\:{\varvec{K}}_{\varvec{i}}(\varvec{T}-\:{\varvec{T}}_{\varvec{r}\varvec{e}\varvec{f}})$$

(2)

.

where $\:G$ is the real amount of solar radiation, $\:{G}_{ref}$ is the solar radiation’s nominal value, $\:{\varvec{I}}_{\varvec{s}\varvec{c}}$ is the current in the short circuit under normal test conditions, $\:{\varvec{K}}_{\varvec{i}}$ is the short-circuit current temperature coefficient, $\:\varvec{T}$ is the temperature, $\:{\varvec{T}}_{\varvec{r}\varvec{e}\varvec{f}}$ is the temperature that is referred to usually 25 °C.

The saturation current (I$\:{\varvec{I}}_{\varvec{s}\varvec{a}\varvec{t}}$) and other variables are also determined by the following equations:

$$\:{\varvec{I}}_{\varvec{s}\varvec{a}\varvec{t}}=({\varvec{I}}_{\varvec{s}\varvec{c},\varvec{r}\varvec{e}\varvec{f}}+\:{\varvec{K}}_{\varvec{i}}\left(\varvec{T}-\:{\varvec{T}}_{\varvec{r}\varvec{e}\varvec{f}}\right)\left(\frac{{\varvec{V}}_{\varvec{o}\varvec{c},\varvec{r}\varvec{e}\varvec{f}}+{\varvec{A}\varvec{N}}_{\varvec{s}}\varvec{K}\varvec{T}}{\varvec{q}}\right)-1$$

(3)

.

Where $\:{\varvec{I}}_{\varvec{s}\varvec{c},\varvec{r}\varvec{e}\varvec{f}}$and $\:{\varvec{V}}_{\varvec{o}\varvec{c},\varvec{r}\varvec{e}\varvec{f}}$ are the open-circuit voltage and short-circuit current under typical test circumstances, $\:{\varvec{K}}_{\varvec{i}}$ is temperature coefficient of $\:{\varvec{I}}_{\varvec{s}\varvec{c}}$, A is the diode’s ideality factor. $\:{\varvec{N}}_{\varvec{s}}$ is the number of cells in series, k is the Boltzmann constant, T, $\:{\varvec{T}}_{\varvec{r}\varvec{e}\varvec{f}}$ is the temperature and reference temperature, Q is elementary charge.

Table 1 below lists the PV module parameters that were employed based on these model equations.

Table 1 Characteristics of the PV model.

The PV module parameters used in the model are listed above, and these values were utilized to simulate characteristic curves for the module’s P-V and I-V under STC. Figure 4 illustrates these settings, which include an irradiance of $\:{G}_{ref}$=1000 W/m² and a module temperature of $\:{\varvec{T}}_{\varvec{r}\varvec{e}\varvec{f}}$=25 °C as shown in Fig. 3.

Fig. 4

PV module characteristic curves.

System configuration

The proposed system is designed for a 5 kW grid-connected PV configuration. The PV array is composed of multiple series-connected modules arranged in parallel strings to achieve a total output of 360 V and 320 A under standard irradiance conditions (1000 W/m²). A high-gain boost converter, operating at a 20 kHz switching frequency, is used to raise the PV voltage to the regulated DC-link level of 500 V. The boost converter is controlled using a maximum power point tracking (MPPT) algorithm based on the Incremental Conductance (INC) method. This technique dynamically adjusts the PWM duty cycle by monitoring the (V_pv) and PV current (I_pv), and incrementally modifying the voltage to identify the direction of maximum power. The three-phase PWM inverter, operating around 500 V and 50 Hz, interfaces with the grid using d–q axis control and a PLL for synchronization. System control is implemented using the proposed GWO-PID algorithm for adaptive and real-time performance under varying conditions.

MPPT and boost converter algorithm

The PV system runs at its MPP due to the INC MPPT technology, which regulates the DC-DC converter’s duty cycle. As illustrated in Fig. 5a and b, the INC MPPT controller uses the instantaneous power supplied by the PV system to determine the duty cycle modulation ∆D. It receives two inputs, V_pv and I_pv. The updated duty cycle is then given as an input to the PWM. For initial stage, the duty cycle is kept at 0.35 and is dynamically controlled depending of environmental conditions. By using this technique, the efficacy of PV system is enhanced and outcomes in better outputs for grid integration.

Fig. 5

(a) Simulation of INC MPPT method. (b) MPPT control block diagram.

Among the photovoltaic system and the inverter, the DC link is essential for maintaining voltage stability and reducing current ripple. The following equation governs how the boost converter functions:

$$\:{\varvec{V}}_{\varvec{dc}}=\left(\frac{{\varvec{V}}_{\varvec{p}\varvec{v}}}{1-\varvec{D}}\right)\:$$

(4)

.

where $\:{\varvec{V}}_{\varvec{p}\varvec{v}}\:$ is the PV array’s input voltage, $\:{\varvec{V}}_{\varvec{d}\varvec{c}}$ is the DC link output voltage, $\:\varvec{D}$ is the PWM signal’s duty cycle that regulates the boost converter.

The boost converter ensures effective power transfers to the inverter by raising the PV voltage to meet the voltage at the DC link (V_dc) by varying the duty cycle (D).

DC–AC inverter

An essential part of a photovoltaic system is a DC-AC inverter, which transforms DC electricity produced by the array through AC power that can be fed into the grid. The inverter helps the PV system supply electricity to the grid by coordinating its AC output with the frequency and voltage of the grid. One of the key elements during this conversion procedure is the introduction of an AC filter, that rejects high-frequency harmonics while allowing only clear, high-grade power to feed into the supply to the grid. Figure 6 below illustrates the control mechanism of the inverter. The 1200 µF DC link capacitor has the function to smooth voltage ripple, thus resulting in an efficient and stable system. For allowing minimal high-frequency harmonic distortion as well as compliance with the grid, the AC filter supplies the inverter. Both the voltage control circuit and the inner current loop serve as the foundation for the inverter’s control. Even under load-varying situations, steady operation is made possible by the inner loop of the PID controller, which regulates grid current and the voltage at the DC link (V_dc). In order to send as much power as possible to the grid, the voltage loop regulates the voltage at the DC link to the setpoint.

Fig. 6

Block diagram of the grid-connected PV system’s inverter control system.

Inverter control strategy

An essential component of grids-connected PV systems, the DC-AC inverter transforms the DC electricity from PV arrays into AC power that is compatible with the utility grid. Using a Phase-Locked Loop (PLL) in inverters synchronization with the grid is one of the steps used to accomplish it. PLL provides inverter phase angle synchronization and grid phase angle to provide smooth power transmission and stable power transmission. PLL uses d-q reference frame, which is Park’s Transformation-based. This makes regulation easier as revolving reference frame allows for the regulation of both active and reactive power. In three-phase grid voltages (V_{(g, abc)}) and the grid current (I_{(g, abc)}), the phase angle θ of PLL is utilized to their corresponding d-q components transformation equations may be expressed as:

$$\:\begin{array}{c}{\varvec{V}}_{\varvec{a}}\\\:{\varvec{V}}_{\varvec{b}}\\\:{\varvec{V}}_{\varvec{c}}\end{array}=\sqrt{3}\:V\begin{array}{c}{\varvec{V}}_{\varvec{d}}\\\:{\varvec{V}}_{\varvec{q}}\end{array}{\left[\begin{array}{c}Cos\left(\theta\:\right)\\\:Cos\left(\theta\:-\frac{2}{3}\right)\\\:Cos(\theta\:+\frac{2}{3})\end{array}\right]}_{m*n}$$

(5)

.

The pulse width modulation signal generator uses the generated voltages (V_abc) to regulate the VSI’s switching. To ensure that the necessary voltage and frequency are achieved, the PWM signal controls the inverters by varying the duty cycle to regulate the electricity pumped into the grid.

The following formulas are used to determine the reactive and active powers that are transferred between the grid and the inverter in the d-q referencing frame:

$$\:P\:=\:\frac{3}{2}\:({V}_{ad}.{i}_{ad}+{V}_{aq}{i}_{aq})$$

(6)

$$\:Q\:=\:\frac{3}{2}\:({V}_{aq}.{i}_{aq}+{V}_{ad}{i}_{aq})$$

(7)

.

where $\:{V}_{ad},{V}_{aq}$ are voltage components of d-q frame, $\:{I}_{ad},{I}_{aq}$ are current components.

The PID controller in the inner loop adjusts the voltage references to ensure optimal inverter efficiency. The controller compensates for transient conditions and disturbances, such as short-circuit currents, ensuring high power excellence and system steadiness. A modulated pulse from the controller’s output powers the inverter switching, regulating the quantity of power fed into the grid. Controlling both the reactive and active power in the synchronous references frame is made easier by the control system’s ABC to d-q transformation block. The transformation allows for better voltage regulation and power flow control, particularly under the dynamic grid or irradiance change scenarios. The use of this advanced transformation technique improves the system’s characteristics and efficacy,

Major components of the control system

Phase-lock loop (PLL)

The utility network and the grid-connected inverter must be synchronized, and this requires the PLL structure, as seen in Fig. 6. It makes it possible to quickly and accurately determine the utility angle of phase, which is essential for the inverter to operate correctly while supplying power to the grid. It also guarantees that the inverters output electricity with the appropriate phase and frequency, avoiding instability or problems with power quality.

As illustrated in Fig. 7, a A PID regulator is employed to power the $\:{V}_{oq}*$ component to zero, minimizing any phase error and ensuring the correct rotation frequency of the grid reference. Integrating an angular frequency (ω) yields the phase angle (θ) over time, allowing the system to track the changes in the grid’s phase continuously. This dynamic phase synchronization is essential for maintaining the system’s overall stability.The relationship for calculating the angular frequency is expressed by the following equation:

ω = $\:{K}_{{PLL}_{p}}.{V}_{oq}+{K}_{{PLL}_{I}}.{\int\:}_{0}^{t}{V}_{oq}.dt$ (8)

where $\:{K}_{{PLL}_{p}}$, $\:{K}_{{PLL}_{q}}$ are proportional and integral gains of PLL controller, $\:{V}_{oq}$is the output of quadrature axis.

Fig. 7

Block diagram of the implemented PLL.

Voltage regulation controller (VRC)

In a grid-dependent PV system, the DC-link is crucial as it serves as a bridge between the inverter and the boost converter, ensuring smooth power transfer between the system components. In addition to improving power quality, it helps maintain system stability and compliance with grid integration standards. By minimizing voltage fluctuations, the DC-link capacitor plays a vital role in enhancing overall system reliability and preserving power quality. Moreover, a DC-link regulator ensures efficient control of the power flow into the grid, maintaining consistency and synchronization with the utility. The simulation block for the Voltage Regulation Controller (VRC), which governs the DC-link voltage, is illustrated below in Fig. 8.

A controller with a PID algorithm is used to control the voltage and produce the grid’s reference maximum current (I_d) in order to preserve the consistency of the voltage across the DC link. The DC link voltage is kept constant during system operation by feeding the voltage controller’s output into the inside current control loop.

The following equation provides the formula for controlling the DC link voltage:

$$\:{{I}^{*}}_{d}\:=\:e\:({K}_{pdv}+\:{RK}_{idv+}\:{K}_{d}.{e}^{*})$$

(9)

.

where “e” represents the error signal, $\:{K}_{pdv}$, $\:{K}_{idv}$ and $\:{K}_{d}$ are proportional and integral gains of PID, $\:{e}^{*}$ is derivative of error signal, compensates sudden change in error to ensure fast response, R is resistance factor.

Any fluctuation in the voltage of DC link can lead to increased THD, whereas negatively impacts power quality and can destabilize the grid system. Therefore, maintaining a stable voltage is essential to ensure efficient power delivery while complying with the grid’s regulatory standards.

Fig. 8

Simulation of the implemented VRC.

Current controller

By controlling the current transferred between the inverter and the grid, the current controller plays a vital role in ensuring excellent power quality in grid-connected PV systems. Figure 9 illustrates that the controller operates using a feed-forward decoupling strategy, which effectively separates current error from voltage fluctuations, leading to more precise current regulation. This strategy allows the inverter to maintain synchronization with the grid, minimizing deviations in the grid current and ensuring stable power quality.

The current regulator works in d-q frame to regulate both the active current ($\:{{I}^{*}}_{d}$) and the reactive current ($\:{{I}^{*}}_{q}$). The PID controller in the inner loop generates the reference voltages $\:{V}_{d}$, $\:{V}_{q}$ for the grid. The d-q to abc conversion is then used to convert these voltage components back into the abc frame before being fed into the PWM switching technique to control the inverter’s switching transistors as show in in Fig. 9 below.

Mathematically model for the current control strategy implemented are written as,

$$\:{V*}_{d}\:=\:{K}_{pd}({{I}^{*}}_{d}-{I}_{od})+{K}_{id}\int\:{{(I}^{*}}_{d}-{I}_{od})\:.dt$$

(10)

$$\:{V*}_{q}\:=\:{K}_{pq}({{I}^{*}}_{q}-{I}_{oq})+{K}_{iq}\int\:{{(I}^{*}}_{q}-{I}_{oq})\:.dt$$

(11)

.

where $\:{{\text{I}}^{\text{*}}}_{\text{d}}$, $\:{{\text{I}}^{\text{*}}}_{\text{q}}$ are reference current components, $\:{\text{I}}_{\text{o}\text{d}}$and $\:{\text{I}}_{\text{o}\text{q}}\:\text{a}\text{r}\text{e}\:\text{a}\text{c}\text{t}\text{u}\text{a}\text{l}\:\text{c}\text{u}\text{r}\text{r}\text{e}\text{n}\text{t}\:\text{c}\text{o}\text{m}\text{p}\text{o}\text{n}\text{e}\text{n}\text{t}\text{s}\:,\:{\text{K}}_{\text{p}\text{d}}$, $\:{\text{K}}_{\text{i}\text{d}}\:,\:$ $\:{\text{K}}_{\text{p}\text{q}}$, $\:{\text{K}}_{\text{i}\text{q}}$ are proportional and integral gains for the current regulation of the active and reactive currents .

Fig. 9

Block diagram of the current control system.

GWO & PID based control system

The GWO + PID algorithm integrates GWO with a PID controller to optimize the PID parameters (K_p, K_i, K_d) for grid-connected PV systems. This combination enhances the system’s ability to adapt to fluctuating environmental conditions, such as varying irradiance, by dynamically optimizing the controller’s performance.

GWO algorithm

The GWO method was first presented by⁴⁰ and was motivated by the hunting techniques and social structure of grey wolves. The effectiveness of GWO in resolving intricate, nonlinear optimization issues has been demonstrated. Recent advancements in GWO-based strategies have further established the algorithm’s adaptability across domains, such as hierarchical multi-step optimization for energy systems⁴², augmented clustering⁴³, frequency response enhancement of virtual synchronous generators⁴⁴, accurate parameter identification in PV models⁴⁵, improved localization in 3D wireless sensor networks⁴⁶, and hybrid schemes for malware detection⁴⁷, highlighting GWO’s effectiveness in both engineering and data-driven contexts. The algorithm replicates the α, β, δ and ω wolves’ hierarchical pack structure. While the β and △ wolves direct the optimization process, the alpha wolf is the best option among them, and the omega wolves keep the pack in order without having a big impact on the search.

As seen in the Fig. 10 below, the hierarchy of the wolves in the GWO algorithm is divided into four roles: α, β, δ and ω wolves. While the β and δ wolves direct the search, the alpha wolf symbolizes the best solution discovered. The omega wolves sustain the social framework without actively influencing the quest. Each wolf in the search space represents a possible solution, and the algorithm models this social behavior.

Fig. 10

Dominance levels.

The optimization process in GWO is divided into different phases that mirror the natural hunting behaviours of wolves: attacking, chasing, and encircling the target. Using mathematical models, the wolves’ locations within the search space are iteratively updated in each step.

The method helps the search progress toward the global optimum by dynamically modifying the weight of inertia (ω), social coefficients (C₁), and cognitive coefficients (C₂), so striking an equilibrium between exploration and exploitation.

The following formula controls how each wolf’s position changes in search space throughout each iteration:

$$\:{{V}_{i}}^{n+1}=\omega\:{{V}_{i}}^{n}+\:{C}_{1}{r}_{1}({{P}_{i}}^{n}-{{X}_{i}}^{n})+\:{C}_{2}{r}_{2}{{(P}_{g}}^{n}-{{X}_{i}}^{n})$$

(12)

.

$\:{V}_{i}$ is the Velocity of the $\:{i}^{th}$ wolf, $\:{X}_{i}$ is where the $\:{i}^{th}$wolf located, $\:{P}_{i}$is where the $\:{i}^{th}$ wolf best position, $\:{P}_{g}\:$is the Global best position (the best solution), $\:{C}_{1}$, $\:{C}_{2}$ are the elements of learning that direct exploitation and exploitation. $\:{r}_{1}$, $\:{r}_{2}$ are the random numbers in the range of 0 and 1. $\:\omega\:\:$ is inertia weight

The position update equation ensures that the wolves move towards the best solutions, while exploration and exploitation balance is managed by $\:{C}_{1}$ and $\:{C}_{2}.$

The updated position of the wolf can be written as:

$$\:{{X}_{i}}^{n+1}=\:{{X}_{i}}^{n}+\:{{V}_{i}}^{n+1}$$

(13)

.

The Eq. (13) ensures that the wolfs position is updated iteratively until the stopping criteria are met.

PID controller

In processes control systems and control applications, a PID regulator is frequently utilized where an output needs to be regulated at a desired setpoint irrespective of disturbances or changes in input. Three elements form the basis of its design: proportional (K_p), derivative integral (K_i), and (K_d) gains. By reducing the discrepancy between the intended threshold and the actual result, these benefits enable the controller to improve response time, stability, and system performance. The simplicity, reliability, and effective operation of the PID controller make it the best choice for inverter system control in grid-connected PV systems. Mathematically the PID controller can be expressed as:

$${\text{U}}\left( {\text{t}} \right) = {\text{~}}K_{p} e\left( t \right) + K_{i} ~\mathop \smallint \limits_{0}^{T} e\left( \tau \right)d\left( \tau \right) + ~{\text{~}}K_{d} \frac{d}{{dt}}~e\left( t \right)$$

(14)

where U(t) is the system input, $\:e\left(\tau\:\right)$ is the error signal.

Each term in the PID equation addresses a different aspect of the error:

• $\:{K}_{p}$ adjusts the control input w.r.t to the error.

• $\:{K}_{i}$ sums up past errors to eliminate steady state error.

• $\:{K}_{d}$ considers the rate of change of the error to predict future trends, reducing overshoot and improving stability.

Fitness function

In the proposed GWO-PID optimization algorithm, the most crucial element is the fitness function in defining the performance of every candidate solution throughout the optimization process. In grid-connected inverter systems, the fitness function is designed to minimize two most significant performance indices: MSE and THD. These indices are significant to ensure high performance, efficient grid synchronization, and maintain the inverter operating under various grid conditions.

Since dynamic in nature, grid-connected PV systems require a PID controller to be fast and efficient in countering voltage, current, and temperature changes, with little distortion and error in the system output. The subsequent fitness function therefore aims to optimize the harmonic distortion and steady-state error, which affect the standard of electricity supplied to the grid.

and the inverter system’s stability.

The fitness function is given by:

$$\:F\left(x\right)={C}_{1}{\int\:}_{0}^{Tmax}\left|e\left(t\right)\right|dt\:+\:{C}_{2}{\int\:}_{0}^{Tmax}{THD}_{v}dt$$

(15)

.

Where $\:e\left(t\right)$ is the error signal, $\:{THD}_{v}\:$ refers to THD of output signal.

GWO PID

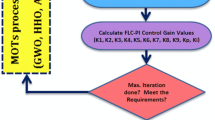
The steps of optimization process for combining the GWO and PID controller is described in Fig. 11. It starts with the initialization of the key parameters, i.e., population size (N), number of iterations (L), and limits of PID values K_p, K_i, and K_d. These parameters set search space, and the GWO algorithm searches over meaningful and feasible solutions within limits. The PID controller parameters are subjected to upper and lower limits so that the optimal solution meets physical constraints. Once the parameters are initialized, the GWO algorithm creates random solutions for each “wolf” (optimal solution) of the population and illustrates potential sets of PID parameters. The next step is to find the fitness function for each wolf, which attempts to minimize important performance measures such as the MSE and THD. These measures are of vital importance in maintaining high power quality as well as ensuring synchronization with the grid. Based on fitness evaluations, the global best solution, represented by g_best, and the best solution, represented by p_best, are updated.

The algorithm adjusts each wolf’s position in the search space upon the completion of the fitness evaluation. The wolves’ hierarchical positions serve as the basis for the position update calculation: α, β and δ wolves. These positions, which regulate the search process, are incorporated in the position update formula:

$$X_{i} ^{{\left( {t + 1} \right)}} = ~X_{i} ^{t} + ~\alpha \left( {\alpha X_{{best}} - ~X_{i} ^{t} } \right) + \beta \left( {\beta X_{{best}} - ~X_{i} ^{t} } \right) + \delta \left( {\delta X_{{best}} - ~X_{i} ^{t} } \right)$$

(16)

where $\:{{X}_{i}}^{(t+1)}$ is the updated position, $\:{{X}_{i}}^{t}\:$ is current position, $\:{X}_{best}\:$ is best known solution (optimum solution), $\:\alpha\:$, $\:\beta\:$, $\:\delta\:\:$are weight coefficients.

The algorithm goes through the population repeatedly, shifting the positions and re-evaluating the fitness function. The iteration goes on until the stopping condition is reached, either the iterations or when an acceptable fitness has been reached. The best set of PID values Kp, Ki, and K_d is the final output of optimizing process in the sense that the inverter system is performing maximally under dynamic conditions.

Fig. 11

Flowchart of GWO + PID.

The incorporation of the PID controller with the GWO algorithm provides dynamic tuning of both grid current and DC link voltage, ensuring high performance and grid-connected inverter system stability, as illustrated in Fig. 12 below. This diagram shows how the GWO optimization technique dynamically adjusts the PID gains K_p, K_i, and K_d in real-time, optimizing the system for faster convergence, zero steady-state error, and improved transient response.

The system topology integrates a GWO-PID controller that tunes the PID gains for efficient power conversion, ensuring minimal harmonic distortion and stable operation during dynamic changes in irradiance and grid conditions. The DC–DC boost converter, regulated by the Incremental Conductance (INC) MPPT method, extracts the maximum power from the PV array regardless of environmental changes, maintaining a stable DC output voltage that feeds the inverter.

The inverter uses a PWM switching technique, where pulse width modulation signals are generated from the outer voltage loop and inner current control loops. The current reference values $\:{{\text{I}}^{\text{*}}}_{\text{d}}\:$ and $\:{{\text{I}}^{\text{*}}}_{\text{q}}\:$are derived from the voltage regulator, stabilizing the DC-link voltage and improving system performance. To simplify active and reactive power control, Park’s Transformation is applied, converting the three-phase grid currents and voltages (I_abc, V_abc) into a d-q synchronous reference frame (I_dq, V_dq). A Phase-Locked Loop (PLL) ensures phase synchronization, aligning the inverter’s output with the grid’s voltage to maintain a unity power factor.

The PID controllers within the system are optimized through the GWO algorithm, where real-time feedback, including the error between reference and actual outputs, is passed to a fitness computation module. This module evaluates the controller’s performance, and the GWO optimizer iteratively updates the PID parameters, ensuring optimal tuning throughout the system’s operation. The resulting control signals are used to generate the PWM pulses, which control the IGBT switches (S1–S6) of the inverter.

To ensure high-quality energy supply to the grid, the system is equipped with AC filters and line impedance units. These filters suppress high-frequency harmonics, while the control scheme guarantees that the current and voltage waveforms are sinusoidal and in-phase with the grid, adhering to grid standards such as IEEE 519. The system also includes a Circuit Breaker CB at the PCC for fault protection and isolation.

This system under the GWO-PID control framework achieves the optimal integration of real-time power quality, flexibility, and high grid synchronization robustness. Intelligent controller parameter optimization ensures minimal THD, fast response during dynamic operations, and efficient grid integration, enabling the reliable injection of PV energy into the power grid.

Fig. 12

Implementation of GWO-PID algorithm.

Results and discussion

In order to verify effectiveness of suggested optimization technique GWO + PID in modifying the PID controller characteristics to be utilized by the inverter control scheme, a 50-kW grid-connected solar power plant was simulated using MATLAB with stable irradiance and temperature parameters of 1,000 W/m² and 25 °C, respectively. The improvement in inverter control performance brought about by the application of the suggested optimization technique is demonstrated by simulation and practical test results. The THD test in output voltage, test experiment comparative findings without or with optimization, and optimized PI parameter values are the study work’s most notable outcomes. THD study demonstrates that the three-phase grid-feeding inverter’s power quality has improved as a result of using the suggested GWO + PID optimization algorithm, leading to more reliable and effective system operation.

Pseudocode for GWO based PID controller algorithm

Input:

• I (maximum no. of epochs),

• N (no. of population size),

• V_n (no. of variables),

• D (no. of dimensions),

• C1, C₂ (cognitive and social factors),

• LB (lower bounds),

• UB (upper bounds),

• a (convergence coefficient),

• A, C (GWO parameters).

• Fobj: Fitness function for PID evaluation.

Output:

• Global_Best: optimal PID parameters $\:{K}_{p}$, $\:{K}_{i}\:$, $\:{K}_{d}$

• fitness value: Value corresponding to optimal solution.

Algorithm:

Simulation scenario

Irradiance testing of the system begins at 1000 W/m² and is then gradually decreased to 500 W/m² over a period of 0.6 s with a ramp-down effect as illustrated in Fig. 13. Following this, returning to 500 W/m², the irradiance rises to 1000 W/m² over the remaining time, again with a ramp-up effect. The time axis spans from 0 to 1 s, with the changes occurring in 0.2-second intervals. Throughout this test, 25 °C is maintained as the constant temperature. The graph below illustrates how the irradiance of the PV system is subjected to these dynamic changes, representing real-world conditions where the sunlight intensity fluctuates over time. This variation in irradiance is essential for evaluating the system’s functionality, as it simulates system performance to changes in environmental conditions. Plot serves as a visual representation of how the irradiance varies over time, impacting the system’s power generation capacity.

Fig. 13

Input irradiance.

The plots in Fig. 14, are of fitness value on the y-axis vs. number of epochs on the x-axis, with the red curve representing the PSO algorithm, purple colour for EHO and the blue curve representing the GWO algorithm. Both algorithms begin at a relatively high fitness value of about 200. As iterations increase, both optimization algorithms lower the fitness value, indicating improvement in the optimization of the PID controller parameters. The GWO algorithm (blue curve) converges more quickly to a lower fitness value, plateauing at about 73 after about 50 iterations. The EHO algorithm (purple curve) demonstrates moderate convergence, plateauing at a higher fitness than GWO and stabilizes around 76 values slightly higher than GWO but better than PSO (red curve) which plateau around 80. The results are consistent with GWO converging to an optimal solution more quickly and more efficiently than EHO and PSO, exhibiting improved fitness performance. The figure below illustrates how well the these three algorithms perform in comparison, indicating that GWO provides better optimization efficiency^15,48,49.

Fig. 14

Fitness value.

The performance and optimisation of grid-tied photovoltaic system with various irradiance conditions were tested under three control schemes: GWO + PID, PI, and P controllers. Based on the figures, performance was evaluated in terms of DC-link voltage, PV voltage, current, and power output. A range of irradiance settings, between 1,000 W/m² to 400 W/m², were used to test the system. The results showed that the GWO + PID controller had a remarkable advantage over PI and in providing stable system operation as well as power quality enhancement. At 1000 W/m², PV voltage remained steady at 360 V with minimal oscillation, while current was steady at 320 A, and power output at 5 kW. Even at 800 W/m² irradiance, stability was maintained where PV voltage was at 320 V and power output at 3.48 kW with the DC-link voltage remaining steady around 485 V. The figure insets also showed that the GWO + PID controller minimised voltage and power oscillation to the lowest, with faster stabilisation compared to PI and P. The P controller-based model had large oscillation and slower stabilisation, while the traditional PI controller was better compared to the GWO + PID but was less efficient while maintaining uniform voltage as well as power output. During transient intervals (0.26 to 0.31 s), the GWO + PID controller responded with minimal overshoot and rapid voltage correction, demonstrating superior control under dynamic irradiance conditions.

This transient resilience is evident in Figs. 15c, 16, 17, 18 and 19, where DC-link voltage, power delivery, frequency, and d–q axis voltages quickly return to steady-state values. These simulation outcomes are displayed below in Fig. 15a–d clearly reveal the GWO + PID optimisation superiority in controlling PV system parameters and ensuring more efficient and stable operation, particularly in varying irradiance conditions. In addition, Table 2 is shown demonstrating the system performance under different irradiance levels further proving the efficiency of the GWO + PID controller in maximum power transfer and stability. The combination of GWO optimization and PID control is an efficient method for dynamic grid integration, ensuring fast and stable convergence in real-time PV system optimization.

Fig. 15

(a) PV voltage. (b) PV current. (c) DC link voltage. (d) PV power.

Table 2 Comparison of parameters.

As shown in Fig. 16, power from the grid and inverter power were monitored for a brief period of time (from 0.26 to 0.31 s) in order to examine the results of the PV system connected to the grid with the GWO + PID control strategy. The grid power (as indicated by the red line in the top graph) fluctuates before it takes a value of about 6000 W, as indicated by the dotted line. This indicates the capability of the GWO + PID controller to quasi-steady the system in just a few seconds, with very little oscillations and with a stable power delivery to the grid. The inverter power, also as indicated by the bottom graph with the blue line, also follows the same trend, with initial transient oscillations before settling to almost 6000 W. The inverter operation is in accordance with the grid, and this indicates that the GWO + PID controller can control the inverter output to fulfil grid requirement. The inverter power and power from the grid steady-state performance shows how well the GWO + PID control method works to guarantee a steady power supply under various operating conditions while maintaining the optimum efficiency for a grid-tied PV system.

Fig. 16

Grid power and inverter power.

The Power factor (PF) of the system under GWO + PID control strategy is shown in Fig. 17, where x-axis varies from 0 to 1 s and power factors on the y-axis. The power factor experiences minor oscillations during the initial stages before settling at a value of approximately 1, as shown by the magenta dashed line in the plot. GWO + PID control technique maintains the power factor in extremely close proximity to 1, which shows the effectiveness of the system to use maximum amount of power provided to the grid with zero reactive power loss. The plot shows the stability of the power factor throughout the simulation, it attests to the GWO + PID optimization method’s effectiveness in attaining high power quality by guaranteeing a small reactive power part and sending the grid the maximum amount of active power. In order to maximize the grid-connected PV system’s overall efficiency, the system guarantees a power factor that is close to unity.

Fig. 17

Power factor.

Reference frame control voltage for the d-q axis (V_d & V_q) is represented in the Fig. 18 below, where the V_d and V_g voltages are represented by the red and purple lines, respectively. The initial spike in the V_d and V_q is observed by the yellow dashed box at approximately 0.1 s, as there is a transient response in the system towards the beginning of the simulation. The initial voltage spike is reflection of response of the systems to abrupt changes in operating conditions. After a while, however, the V_d and V_q both attain a steady state, as observed by the blue dashed line towards the later stages of the plot. This is a reflection that the GWO + PID controller stabilizes the system effectively, with the direct and quadrature control voltages being in a very narrow range after the transient time. The system stabilizes very quickly, which reflects the ability of the GWO + PID controller to regulate and stabilize the voltage effectively and deliver seamless operation across a range of operating circumstances. The quick stabilization of the voltage in both axes reflects the strength of the GWO + PID control strategy in providing voltage regulation and removing oscillations under dynamic changes in system behavior.

Fig. 18

Control voltage.

The system’s frequency response under the GWO + PID control policy is shown in Fig. 19, from 0 to 1 s. The plot is a comparison between the system performance with and without the GWO optimization, with the system’s response under GWO is shown by the blue line, and its response without GWO is shown by the red line. In absence of GWO (red line), the frequency has large oscillations, from 49.85 Hz to 50.10 Hz. The system shows significant transient behavior, particularly around 0.2 s and 0.6 s, and shows instability in sustaining a constant frequency. The insets also reflect these oscillations, particularly the transient one. Under the GWO + PID controller (blue line), the oscillations are significantly reduced. The frequency returns quickly to 50 Hz following disturbances, as shown by the smooth and stable nature of the response in the inset plots. The system’s capacity to sustain a stable frequency of 50 Hz under dynamic conditions reflects the efficiency of the GWO + PID optimization in reducing frequency oscillations and enhancing system stability. The comparison shows that the GWO + PID controller outperforms the conventional approach in aspects of stability and quick frequency regulation, ensuring better overall performance of the grid-connected system.

Fig. 19

Frequency response.

The THD analysis of the system’s output frequency is shown below in Fig. 20, in the frequency spectrum display, where the frequency (Hz) is shown by the x-axis and the y-axis indicating the magnitude as a percentage of the fundamental frequency. The graph compares the THD for two control strategies: GWO + PID and only PID. The plot indicates that the PID controller (blue line) results in a THD of 3.67%, with significant harmonic spikes appearing in the higher frequency range (above 1000 Hz), as denoted by the orange arrows and the label “THD Spike above 10%”. These high-frequency spikes contribute to poor power quality and reduced system efficiency, which is not ideal for a grid-tied photovoltaic system.

In contrast, GWO + PID (magenta line) exhibits a much lower THD, below 5%, with a more controlled and uniform harmonic distribution across frequencies. This behavior is marked in the graph, where the “Proposed GWO + PID” shows a significant reduction in high-frequency harmonics, providing greater results in terms of power quality. The PI regulator (cyan line), while better than the PID controller, still presents some harmonic distortion above 10% at higher frequencies. These outcomes demonstrate how well the GWO + PID controller reduces harmonic distortion and improves the grid-connected PV system’s power quality. Reduction in THD demonstrates that GWO + PID is a highly effective strategy for improving system efficiency and stability, making it preferable over conventional control methods.

Fig. 20

THD response.

The evaluation of the several performance metrics between the GWO + PID, PI and P are being tabulated below in Table 3.

Table 3 Comparison of different performance metrics under different radiation settings.

The operation of the grid-integrated PV system underwent testing at different radiation levels, and the results confirm the advantages of the novel GWO + PID optimization method for PID controller tuning of inverter systems. The performance indicators like Rise Time, Setting Time, Peak Power, THD, and MSE were compared for the three control methods: GWO + PID, PI, and P controllers. The GWO + PID controller yielded a THD of 3.7% and MSE of 0.25 kW² at 1000 W/m² superior to the PI and P controllers. The results offered faster stabilization, a peak power value of 9.9 kW, and lower error measures for the GWO + PID method, confirming its superior performance. The GWO + PID controller also controlled power better at all irradiance levels, with stable voltage and current control, with MSE and THD experiencing drastic improvements compared to traditional controllers. This verifies the excellence of the GWO + PID optimization technique in enhancing power quality, dynamic performance, and having stable integration in grid-connected PV systems.

The performance of the proposed GWO-PID control approach is further validated by comparing its performance with some of the well-documented state-of-the-art controllers available in the literature. While Table 3 presents the internal benchmarking among P, PI, and GWO-PID for various irradiance, Table 4 below extends the same to some of the optimized techniques like PSO, ANN, Fuzzy Logic, TLBO-GWO, and PSO-FOPI.

Table 4 Comparative performance of GWO-PID with other controllers.

Conclusion

This study investigates the best grid-connected photovoltaic system with a focus on applying the GWO + PID control strategy for the optimization of PID parameters. Performance was experimented under different irradiance levels 1,000 W/m² to 400 W/m² at a fixed temperature of 25 °C. GWO + PID strategy was contrasted with conventional PI and P controllers. Results validate that the GWO + PID controller vastly performs better in terms of stability and quality of the system, particularly in having the shortest time of stabilization, minimum Total Harmonic Distortion THD (3.7%), and minimum MSE of 0.25 kW² at 1000 W/m². PI controller registered THD (4.6%) and MSE (0.33 kW²), and P controller had maximum THD and MSE, depicting the inferiority of lesser control techniques.

At high irradiance (1000 W/m²), the GWO + PID controller regulated the PV Voltage to 360 V, PV Current to 150 A, and generated 10.43 kW power with constant DC-Link Voltage of 500 V. At decreasing irradiance, the GWO + PID controller maintained constant DC-Link Voltage and minimized oscillations in PV Voltage and Current. The result also suggests that the GWO + PID controller minimizes oscillations and generates smoother transition under varying environmental conditions, and the system offers improved grid integration and performance.

Overall, the GWO + PID optimization technique is an economic means of enhancing overall characteristics of grid-tied photovoltaic systems. It offers faster response time, improved voltage regulation, reduced power fluctuation, and improved power quality compared to conventional techniques. The findings highlight the necessity of advanced optimization techniques like GWO + PID to meet the increasing demand for efficient and reliable renewable energy systems. Future research can explore the utilization of other advanced control techniques and real-time adaptability to environmental conditions to improve the robustness and effectiveness of the system.