A steady state micro genetic algorithm for hyper-heuristic generation in one-dimensional bin packing

Abstract

The one-dimensional bin packing problem (1DBPP) is a well-known NP-hard problem in computer science and operations research that involves many real-world applications. Its primary objective is to allocate items into bins while minimizing the number of bins used. Due to the complexity of the problem, exact algorithms are often impractical for large instances, which has led to a reliance on tailored heuristics that may perform well on some instances but poorly on others. In this study, we propose a method to automatically generate selection hyper-heuristics (HHs), which are then applied to solve 1DBPP instances by leveraging the strengths of simple heuristics while avoiding their drawbacks. Specifically, we introduce a steady-state $\mu$ Genetic Algorithm (SS$\mu$GA) to generate selection HHs, benefiting from the gradual population updates of steady-state GAs and the efficiency of $\mu$GAs with smaller populations for faster iterations. Our experimental results showcase the effectiveness of the SS$\mu$GA across multiple training and testing datasets for the 1DBPP. Compared to other evolutionary methodologies, also used as generative HH methods (i.e., generational GA, steady-state GA, and generational $\mu$GA), the SS$\mu$GA consistently achieves higher fitness values within the same number of evaluations, on the training set. Additionally, on both generated and literature 1DBPP instances for the testing set, the selection HHs generated by the SS$\mu$GA were highly competitive, often outperforming those produced by other methods. Furthermore, the SS$\mu$GA-generated HHs displayed both specialization for specific instance types and generalization across varied instances.

Introduction

The bin-packing problem (BPP) is a classical combinatorial optimization problem with diverse applications in supply chain management¹, manufacturing², aircraft arrangement³, among others. The goal of the problem is to find the minimum number ($N^* \in \mathbb {N}$) of bins, of a given capacity $B>0$, to store a set of n items $I=\{i_{1}, i_{2}, \dots , i_{n}\}$, each one of a size $s_i \in (0,B), i=1,2,\dots ,n$. Thus, the solution to the BPP is a partition $I=I_{1} \cup I_{2} \cup \cdots \cup I_{N^*}$. The BPP is present in many real-world situations, ranging from packing clothes in a suitcase before taking an airplane to loading the containers of a cargo ship or placing computer files of specified sizes into fixed-sized memory blocks. Consequently, producing high-quality solutions for this problem benefits many fields.

However, since the BPP is an NP-hard problem, finding exact solutions is impractical for many instances. Hence, it is common to rely on techniques that approximate its solution, such as heuristics ^4,5,6,7,8. Among the different algorithms, several greedy heuristics have been commonly utilized^4,5. The simplest greedy heuristic is the Next-Fit (NF) algorithm, where an item i is directly placed in the current opened bin $I_{j}$, if possible; otherwise, another bin $I_{j+1}$ is opened. On the other hand, the First-Fit (FF) heuristic places an item i in the first bin with enough capacity⁹. In addition to NF and FF, other heuristics have been proposed such as Best-Fit (BF)¹⁰, Worst-Fit (WF)¹¹, and Almost-Worst-Fit (AWF)¹¹. It is worth emphasizing that none of these approximation algorithms can achieve a performance ratio better than 3/2 unless $P = NP$⁴.

Despite the good theoretical results of greedy heuristics¹¹, Evolutionary Algorithms (EAs) have gained the attention of the community for tackling large BPP instances^6,12. EAs are stochastic population-based metaheuristics (MHs) that efficiently explore and exploit the search space. Among EAs, Genetic Algorithms (GAs) have extensively been applied on the BPP ^13,14,15. The core of all the GA-based approaches is the definition of an encoding of the BPP. Then, a GA evolves a population of solutions to optimize a fitness value (e.g., the average bin usage). A common aspect of most EA-based approaches is that they meet the problem directly. In other words, they evolve partitions of I. However, EAs may suffer from sparse search spaces for large-scale BPP instances. Thus, their behavior may resemble a random search¹⁶.

Instead of using EAs directly to solve a BPP instance, they can be used to design a high-level solver that takes advantage of low-level heuristics. This high-level solver is a hyper-heuristic (HH) that serves as an alternative for tackling the complexity of the BPP and other combinatorial optimization problems^7,17. An HH combines the strengths of low-level heuristics (e.g., FF, BF, WF, and AWF) using a set of rules that indicate which heuristic should be called depending on the problem state under exploration. In this regard, an EA should discover the best possible combination of rules to generate the so-called selection HHs in the space of heuristics. Regarding the BPP, GAs and Genetic Programming (GP) approaches have been extensively studied^7,8,18,19,20. Despite their promising results when tackling different BPP instances, a common drawback of all the EA-based approaches is the consumption of many function evaluations to find a good HH. As a result, EAs are time-consuming and exhibit a low convergence behavior when evolving populations of hundreds of HHs.

In this work, we focus on speeding up the convergence behavior of EAs to generate selection HHs for the one-dimensional BPP (1DBPP). To this aim, we propose a steady-state micro-GA ($\mu$GA), extending the work by⁸. The underlying idea of using a $\mu$GA²¹ as a search engine is due to using small populations and reinitialization strategies when nominal convergence is reached²². Hence, we can drastically reduce the number of function evaluations and the overall computational overhead. Furthermore, the selection of a steady-state approach is based on their proven theoretical advantages over generational EAs²³. Under this light, a steady-state $\mu$GA prevents stagnation and continuous reinitializations. Our approach leverages the combined qualities of both the steady-state approach and small-sized populations to produce high-quality HHs. As a result, two main contributions are derived from our work:

• The proposal of a steady-state $\mu$GA. All the previous works with $\mu$GAs opted for generational schemes. We proposed replacing only one individual in the population per generation, which seems beneficial for the search as it improved the results obtained by the generational $\mu$GA in this work.

• A steady-state $\mu$GA-based generative hyper-heuristic approach for producing selection hyper-heuristics that outperform those generated by other evolutionary methods in the literature for the 1DBPP (or similar problems), achieving superior performance in terms of average bin usage during the training stage, and competitive performance on unseen instances.

The remainder of this document is structured as follows. "Foundations" section provides a context of our work by providing relevant concepts related to the BPP, such as a formal definition and the description of some heuristics designed to address this problem. "Related work" section reviews the most relevant works related to our topic, including MHs and HHs for the BPP. In "Steady-state µGA as a hyper-heuristic generator" section, we provide details of our solution model and how we propose creating and testing HHs for the BPP through a steady-state $\mu$GA. Sect. 5 describes the experiments conducted and analyzes their main results. Finally, we provide our final remarks and potential paths for future work in "Conclusion and future work" section.

Foundations

The one-dimensional bin packing problem

1DBPP is a classic optimization problem in computer science where we aim to allocate n items of various sizes into the minimum number ($N^{*} \in \mathbb {N}$) of bins without exceeding their capacity ⁵. In the following, we formally define this problem. Let $I = \{i_1, i_2, \dots , i_n\}$ be a finite set of n items and $x_{ij}$ and $y_{j}$ be two binary variables. On the one hand, $x_{ij} = 1$ if item $i \in I$ is allocated in bin j; otherwise, $x_{ij} = 0$. On the other hand, $y_{j} = 1$ if bin $j \in \{1,\dots ,n\}$ is used; otherwise, it is zero. Each item $i \in I$ has a size $s_i \in (0, B)$, where $B > 0$ is the capacity of each bin j. Hence, 1DBPP is defined as follows:

$$\begin{aligned} \min \sum _{j = 1}^{n} y_{j} \end{aligned}$$

(1)

subject to:

$$\begin{aligned}&\sum _{i = 1}^{n} x_{ij}s_{i} \le y_{j}B,&\forall j \in \{1,\dots ,n\}, \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j = 1}^{n} x_{ij} = 1,&\forall i \in I. \end{aligned}$$

(3)

It is worth emphasizing that the constraints of the problem force each item not to exceed the capacity of each bin (Eq. 2), and allocate each item into exactly one bin (Eq. 3).

Note that this problem has some straightforward lower and upper bounds on the number of bins we can use. First, since bins can allocate at least a single item, the number of bins cannot exceed the number n of items. Second, the number of used bins cannot be less than the sum of the size of all the items divided by the bin capacity. Consequently, the optimal number of bins $N^{*}$ is bounded by the following inequality:

$$\begin{aligned} \frac{\sum \limits _{i \in I} s_{i}}{B} \le N^{*} \le n. \end{aligned}$$

(4)

Given $I=\{i_1, \dots , i_n\}$, an instance for the 1DBPP is a sequence $\pi = \, \ll i_{j_1}, \dots , i_{j_{k-1}}, i_{j_k}, i_{j_{k+1}}, \dots , i_{j_n} \gg$, where $i_{j_k}$ is the current item to pack. In other words, $\pi$ is an n-permutation of I. An algorithm for the 1DBPP consumes $\pi$ in order from item $i_{j_1}$ until $i_{j_n}$. Furthermore, let $\pi _{j_k} = \, \ll i_{j_k}, i_{j_{k+1}}, \dots , i_{j_n} \gg$ be a subsequence of $\pi$ starting from $i_{j_k}$. $\pi _{j_k}$ indicates the sequence of items that remain to be processed by an iterative algorithm. From this point onwards, let us call $\pi _{j_k}$ as a problem state.

Classic heuristics for the 1DBPP

Typically, heuristic approaches for the BPP are categorized into two types: online and offline⁴. Online approaches assume that items arrive in a specific sequence $\pi$, and must be packed as soon as received. Even when some statistics about the set of items are known in advance, the order in which they arrive is unknown and cannot be altered. Conversely, offline approaches may assume that the ordering of the items in $\pi$ is either known in advance or can be rearranged before deciding which bin to pack. In this study, we will mainly focus on heuristic approaches for the online version of the problem. Some classical heuristics for the online 1DBPP are described as follows:

• First Fit (FF) FF selects the first bin with enough capacity to pack the current item. The bins are revised following a FIFO strategy, where the first open bins are revised first⁹.

• Best Fit (BF) BF selects the bin where packing the current item minimizes the waste¹⁰.

• Worst Fit (WF) WF selects the bin where packing the current item maximizes the waste¹¹.

• Almost Worst Fit (AWF) AWF selects the bin where packing the current item produces the second largest waste¹¹.

In the event of ties, the first bin that meets the heuristic’s criterion is preferred. If the item cannot be packed given the current open bins, the system opens a new bin to pack such an item. Since no item is larger than the bin’s capacity, opening a new bin guarantees that such an item will be packed. It is essential to mention that, although these heuristics were defined many years ago, they remain helpful and have been used in many recent works^8,24,25.

For clarity, we will briefly outline how these heuristics operate, using a small instance as an example. Let $I = \{i_{1}, \cdots , i_{5}\}$ be a set of five items arriving at the order defined by the sequence $\pi = \, \ll i_{1}, i_{2}, i_{3}, i_{4}, i_{5} \gg$. The sizes of each item $i \in I$ are given by the set $\{s_{1} = 4, s_{2} = 7, s_{3} = 2, s_{4} = 6, s_{5} = 5\}$, where $s_{k}$ represents the size of item $i_{k}$, and the bin capacity is $B = 10$. Let us also informally define a configuration of the system in our example as the tuple $(\pi _{j_k} = \, \ll i_{j_k}, i_{j_{k+1}}, \dots , i_{j_5} \gg ,([~]_{1}^{0},\dots ,[~]_{5}^{0}))$, where the subsequence $\pi _{j_k}$ in the tuple represents the remaining items to be processed. On the other hand, the second component represents the items in each bin that have already been packed (the empty brackets $[~]^{s}_u$ represent an empty bin, the underscript (u) represents the index of the bin, and the superscript (s) represents the contents of the bin). Using any heuristic H (denoted by $\vdash _{{\mathbf {H}}}$) over a configuration would yield the system to another configuration. Then, starting with empty bins, using FF repeatedly for each item arriving in the sequence given by $\pi$, it would work like this:

$$\begin{aligned} (\ll i_{1}, i_{2}, i_{3}, i_{4}, i_{5} \gg , ([~]_{1}^{0}, \dots , [~]_{5}^{0}))&\vdash _{\mathbf {FF}} (\ll i_{2}, i_{3}, i_{4}, i_{5} \gg , ([i_{1}]_{1}^{4}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {FF}} (\ll i_{3}, i_{4}, i_{5}\gg , ([i_{1}]_{1}^{4}, [i_{2}]_{2}^{7}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {FF}} (\ll i_{4}, i_{5} \gg , ([i_{1}, i_{3}]_{1}^{6}, [i_{2}]_{2}^{7}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {FF}} (\ll i_{5} \gg , ([i_{1}, i_{3}]_{1}^{6}, [i_{2}]_{2}^{7}, [i_{4}]_{3}^{6}, [~]_{4}^{0}, [~]_{5}^{0})) \\&\vdash _{\mathbf {FF}} (\ll ~ \gg , ([i_{1}, i_{3}]_{1}^{6}, [i_{2}]_{2}^{7}, [i_{4}]_{3}^{6}, [i_{5}]_{4}^{5}, [~]_{5}^{0})). \end{aligned}$$

Similarly, using BF heuristic on the same example would work like this:

$$\begin{aligned} (\ll i_{1}, i_{2}, i_{3}, i_{4}, i_{5} \gg , ([~]_{1}^{0}, \dots , [~]_{5}^{0}))&\vdash _{\mathbf {BF}} (\ll i_{2}, i_{3}, i_{4}, i_{5} \gg , ([i_{1}]_{1}^{4}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {BF}} (\ll i_{3}, i_{4}, i_{5}\gg , ([i_{1}]_{1}^{4}, [i_{2}]_{2}^{7}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {BF}} (\ll i_{4}, i_{5} \gg , ([i_1]_{1}^{4}, [i_{2}, I_{3}]_{2}^{9}, \dots , [~]_{5}^{0})) \\&\vdash _{\mathbf {BF}} (\ll i_{5} \gg , ([i_1]_{1}^{4}, [i_{2}, i_{3}]_{2}^{9}, [i_4]_{3}^{6}, [~]_{4}^{0}, [~]_{5}^{0})) \\&\vdash _{\mathbf {BF}} (\ll ~ \gg , ([i_{1}]_{1}^{4}, [i_{2}, i_{3}]_{2}^{9}, [i_{4}]_{3}^{6}, [i_{5}]_{4}^{5}, [~]_{5}^{0})). \end{aligned}$$

Coincidentally, for this example, WF heuristic would have an identical behavior as FF, and AWF heuristic would have an identical behavior as BF.

Related work

The BPP is NP-hard, and its corresponding decision version is NP-Complete, which means that computing an optimal solution in a reasonable time is out of the reach of current algorithms⁵. This calls for alternative approaches that focus on producing near-optimal solutions in polynomial time. Many early heuristics developed for the BPP are frequently described as online approaches. In these methods, the order of arriving items is not known beforehand and cannot be altered. Despite this limitation, they were relatively effective. Notably, heuristics such as BF and FF were shown to produce solutions at most 1.7 times the optimal number of bins, rounded down^26,27. The potential for improving these methods, plus their simplicity, led to efforts to integrate them with other strategies, including MHs and HHs.

In the following subsections, we will briefly review relevant approaches, with particular emphasis on those that harness the synergy between MHs, HHs, and classic heuristic methods.

Metaheuristic approaches

MHs are a family of stochastic algorithms designed to explore wide search spaces in optimization problems efficiently. Often considered general-purpose optimization methods due to their problem domain independence, MHs have been one of the most popular off-the-shelf algorithms for dealing with complex combinatorial optimization problems¹², including 1DBPP.

Most MH implementations for the 1DBPP, as found in the literature, focus on the offline version of the problem^6,28, where the arriving items are known in advance and can be rearranged before packing. In these cases, many MHs employ permutation-based encodings representing the order in which items should arrive or be processed. This sequence is then decoded using classic online heuristics, typically BF or FF.

Early MHs that utilized permutation-based item representations and heuristic decoding were mainly typical nature-inspired algorithms^29,30.³⁰, for instance, proposed a simple genetic algorithm to optimize the item sequence, with decoding performed by a bin-packing heuristic to minimize the number of bins used. Later, an ant colony optimization algorithm was adapted to solve instances of the BPP³¹. In this approach, ants build a tour among items, filling bins one at a time. The decision of each ant to move from one item to another is partly based on a variant of FF and the previous pheromone trails. The solution is represented as a sequence of items packed according to NF.¹⁵ proposed a biased random-keys GA for the two and three-dimensional BPP. Since a direct chromosome representation of bin packing would be too complex, they used an indirect representation where the chromosome encodes the order of items, their orientation, and a placement heuristic that is used to decode it into a solution. More recently, a survey of 1DBPP reviewed and compared swarm-based MHs, including the firefly algorithm, cuckoo search, and artificial bee colony, which utilize permutation-based item representations combined with classic heuristic decoding techniques²⁸. Additionally, a modified squirrel search algorithm was introduced in³², incorporating a BF variation for the population initialization mechanism.

Other MHs for the 1DBPP employ a more direct representation, such as group-based representations for grouping problems (like the BPP). In these approaches, the correspondence between items and bins is explicitly encoded within the chromosome³³. In other words, there is no need for an additional heuristic to reconstruct the solutions from their representations, whether at the end of the optimization process or during fitness evaluation. However, since these representations are pretty specific and the variation process might break some constraints, classic heuristics like FF are still often used during recombination operations or as a kind of repair mechanisms^14,34.

Overall, these studies help to emphasize that classic heuristics, even within modern MHs, remain instrumental at various stages of the optimization process —whether initializing solutions, decoding permutation-based representations, assisting in crossover operations, or repairing infeasible solutions.

Hyper-heuristic approaches

HHs are high-level strategies designed to select, combine, or generate low-level heuristics to address computational search or optimization problems¹⁷. HHs are typically categorized into two main types: selection-based and generation-based approaches. In the context of the BPP and other related combinatorial problems, HHs frequently use traditional heuristics as a pool of low-level components and rely on mechanisms to guide their application. Many of these mechanisms have been optimized through genetic and evolutionary approaches.

The use of genetic programming as an HH was first introduced by¹⁸ to solve the BPP considering an online environment. Their approach was to evolve functions to assist the decision of whether or not to pack a current item in a current bin. Although their approach does not rely on existing packing heuristics, this work laid the foundations for subsequent research on HHs in this domain.

Pillay took a different approach by evolving disposable heuristics for the BPP in offline environments⁷. The evolved heuristics were sequences of low-level heuristics particular for every problem instance, hence disposable. They explored the evolution of both a sequence of bin selection heuristics and a sequence of tuples of item selection and bin selection heuristics. A similar approach for a scheduling problem was proposed by³⁵. Both studies showcased the potential of these types of HHs to outperform low-level heuristics when applied in isolation.

Other HH approaches for the BPP operate on under a semi-online setting with full look-ahead information, that is, the item sequence remains fixed but full information about the items is available in advance. These approaches are often linked to the algorithm selection problem, where problem instances are mapped to heuristics. Once a heuristic is selected based on the instance, it is applied uniformly to all items in the sequence.³⁶ presented a recurrent neural network with long-short term memory model that predicts heuristics without the need for feature extraction, relying instead on the temporal sequence of items in the instance. The same authors later extender their work incorporating recurrent neural network with generated recurrent units³⁷. Recently, for the 3DBPP,³⁸ proposed a set of online low-level heuristics with complementary performance across a diverse set of instances. Using supervised learning models (a neural network, a support vector machine and k-nearest neighbors), they trained these models to predict which online heuristic to apply given the instance features of a full look-ahead environment.

In another direction, for a problem closely related to the BPP (the 2D-regular Cutting Stock Problem),¹⁹ proposed a messy GA to generate selection HHs, which sequentially select classic low-level online heuristics based on partial information that characterizes the remaining sequence of items to be processed (but not a full look-ahead of the sequence of items). This approach evolves (trains) a set of condition$\rightarrow$action rules that function as the selection HH in a semi-online environment. The generated HHs operate as constructive methods, generating a solution step-by-step from scratch, often changing the heuristic applied at each step. At each step, the current problem configuration—determined by the characterization of the remaining items—is matched to the closest predefined condition, which triggers the corresponding action and updating the problem configuration. This approach was later extended for the two-dimensional BPP (2DBPP)²⁰, the bi-objective 2DBPP³⁹, and constraint satisfaction problems⁴⁰. Most recently, inspired by these approaches,⁸ proposed using a $\mu$GA to evolve selection HHs in the form of condition$\rightarrow$action rule sets for the 1DBPP. To manage the computational overhead of evaluating large populations of HHs, their approach focuses on evolving a smaller population with multiple restarts upon stagnation.

Steady-state µGA as a hyper-heuristic generator

Since the 1DBPP is an NP-hard combinatorial problem, we need to use heuristics to approximate its solution. However, due to the No-Free Lunch theorem, no single heuristic performs well in every 1DBPP instance⁴¹. Consequently, we need an automatic method that decides which heuristic is the best suited for a given 1DBPP instance. In this section, we propose a methodology to generate well-performing selection HHs for the 1DBPP. This methodology relies on utilizing a steady-state $\mu$GA (SS$\mu$GA) that gradually updates a population of selection HHs and replaces one individual every generation. SS$\mu$GA explores the space of selection HHs to find one such HH with good generalization performance over different 1DBPP instances. In other words, our SS$\mu$GA behaves as a generation HH. Furthermore, it is worth noting that SS$\mu$GA represents an extension of the preliminary study by Ortiz-Bayliss et al.⁸.

The intuition behind using an SS$\mu$GA as an optimization engine is to leverage the combined qualities of both the steady-state approach and small-sized populations (typically denoted by the $\mu$ symbol). On the one hand, steady-state GAs introduce gradual changes to the population, preserving diversity, whilst replacing only the most unfit individuals⁴². On the other hand, $\mu$GAs operate with a small-sized population (typically five to ten individuals), allowing for faster iterations and less computational overhead⁴³. Furthermore, the potential diversity and stagnation issues of having a small population are balanced out with a population reinitialization mechanism. Hence, our SS$\mu$GA proposal weighs on the benefits of the $\mu$GA part while the steady-state nature delays stagnation and reinitializations, allowing for promising populations to be exploited further. In the following sections, we describe two main aspects of SS$\mu$GA: the encoding of each selection HH and the fitness assignment function. Then, we provide the complete description of SS$\mu$GA to evolve selection HHs for the 1DBPP.

Representation of a selection hyper-heuristic

Each selection HH is represented as a finite set of condition$\rightarrow$action rules. For each rule, the condition is a point $\pmb {\lambda } \in \mathbb {R}^m$, where m is the number of features that characterize a problem state $\pi _{j_k}$ (remember that $\pi _{j_k}$ is a tuple that represents the remaining items to be processed). On the other hand, an action represents a heuristic in the set $\mathcal {H} = \{{\mathbf {FF}}, {\mathbf {BF}}, {\mathbf {WF}}, {\mathbf {AWF}}\}$ to pack item $i_{j_k}$. In this article, we use a function $\sigma : \pi \rightarrow \mathbb {R}^{m}$ to quantitatively represent the problem state. Consequently, a selection HH behaves as an automaton that packs item $i_{j_k}$ using an heuristic $H_t \in \mathcal {H}$ if $|| \sigma (\pi _{j_k}) - \pmb {\lambda }_t||$ is minimum, where $|| \cdot ||$ represents the Euclidean distance, $t \in \{1, \dots , T\}$, and T is the number of rules that compose the given selection HH. It is worth emphasizing that the value of T may change from one selection HH to another.

Problem state features

Because we deal with the 1DBPP in this work, we can only represent a problem state using variations in the item length. Hence, given a problem state $\pi _{j_k}$, we propose the following five straightforward features to represent it.

• AVG The average length of the items within $\pi _{j_k}$.

• STD The standard deviation of the length of the items in $\pi _{j_k}$.

• SMALL The proportion of small items within $\pi _{j_k}$. Items are considered small if they have a length that is less or equal to 15% of the bin’s original capacity.

• MEDIUM The proportion of medium-length items within $\pi _{j_k}$. Items are considered of medium length if they have a length that is larger than 15% but less or equal to 30% of the bin’s original capacity.

• LARGE The proportion of large items within $\pi _{j_k}$. Items are considered large if they have a length that is greater than 30% of the bin’s original capacity.

For better performance, we normalize the values of AVG and STD by dividing them by the maximum length among the items considered (in this article, it is 64). Furthermore, we want to justify the boundaries between small, medium, and large instances. Because the instances we generated for this work have a maximum length of 64, half the bin’s capacity, there is no way for the instances to have a length larger than 50% of the bin’s original capacity. Hence, we only considered the first half of the bin’s capacity to classify the items according to their length.

Chromosome encoding and decoding

In our proposal, each individual (i.e., a selection HH) is encoded by a variable-length binary string chromosome. The total length T of a chromosome is determined by its number of genes, with each gene encoding a single condition$\rightarrow$action rule (see Fig. 1). The minimum number of genes per chromosome is 1, and the maximum can be derived from the number of iterations of SS$\mu$GA, the population size $\mu$, and the crossover operator employed.

Each rule is encoded as a binary string of fixed length $mk + \log _{2}(h)$, where m is the number of features that characterize a problem state, k is the number of bits used to code the value of each feature, and $h = |\mathcal {H}|$. Under this approach, we can map $2^{k}$ unique values for each feature. When decoding the value of a feature, we can calculate its corresponding 10-base value as

$$\frac{{\sum\nolimits_{{j = 0}}^{{k - 1}} {2^{j} \cdot b_{j} } }}{{2^{k} - 1}}$$

where $b_{j} = 1$ if the $j^\text {th}$ bit is equal to 1, or $b_{j}=0$, otherwise. In the case of the heuristics, decoding the corresponding string is straightforward since each unique string maps to a unique heuristic in $\mathcal {H}$. In our implementation, we use the five features ($m = 5$) described in "Representation of a selection hyper-heuristic" section, each represented using ten bits ($k = 10$), and the four heuristics ($h = 4$) described in Classic Heuristics for the 1DBPP" section represented using two bits. Consequently, each rule within the chromosome requires 52 bits for encoding.

Let us recall that each set of condition$\rightarrow$action rules, of each individual, acts as a selection constructive HH. The condition part of a rule corresponds to a problem state, defined by its feature values, while the action part specifies the heuristic to apply. Whenever an item arrives and is to be packed, the Euclidean distance between the current problem state and the condition in each rule is calculated. The condition closest to the problem state then triggers the corresponding heuristic. After applying the heuristic, the problem state is updated, and the process repeats until all the items have been packed.

Fig. 1

An example of a chromosome encoding three condition$\rightarrow$action rules. Each rule contains three artificial features ($f_{i1}, f_{i2}$, and $f_{i3}, i=1,2,3$, where i is the rule number) that characterize the problem state and four available heuristics to apply.

An encoding-decoding example

Let us use the chromosome depicted in Fig. 1 as a problem-independent example. Such a chromosome codes three condition$\rightarrow$action rules. The chromosome represents three features using four bits, then $m = 3$ and $k = 4$. Besides, we can choose from the four different heuristics in $\mathcal {H}$, so $h = 4$, thus, we can use four 2-bit strings to code such heuristics.

For example, in Fig. 1, Rule 1 (R1) condition$\rightarrow$action is encoded as follows. The feature values of the condition part are f₁₁ = 1110, f₁₂ = 1100, and f₁₃ = 0001. When we convert to their corresponding 10-base values, we obtain 0.9333, 0.8000, and 0.0667, respectively. For the action part we have h₁ = 11 which, assuming the following binary heuristic mapping (00:FF,01:BF,10:WF,11:AWF), corresponds to AWF. Thus, let us then say that R1: (0.9333, 0.8000, 0.0667)$\rightarrow$AWF. Similarly, we have that R2: (0.0667, 1.0000, 0.2667)$\rightarrow$FF and R3: (0.5333, 0.0667, 0.2000)$\rightarrow$BF.

Moreover, let us recycle our example from "Classic heuristics for the 1DBPP" section, where $I = \{i_1, \cdots , i_5\}$ arriving at the order defined by the sequence $\pi = \, \ll i_1, i_2, i_3, i_4, i_5 \gg )$, whose sizes are given by the set $\{s_1 = 4, s_2 = 7, s_3 = 2, s_4 = 6, s_5 = 5\}$, and the capacity of the bins is $B = 10$. In the beginning, the problem configuration would be described by $(\ll i_1, i_2, i_3, i_4, i_5\gg , ([~]_{1}^{0}, \cdots , [~]_{5}^{0}))$, with all items left to pack, and all the bins empty. To define our problem state, let us choose three features from "Representation of a selection hyper-heuristic" section, AVG, STD, and LARGE. Then, the problem state of the current configuration would be described by the following tuple (0.6857, 0.2457, 0.8000).

At this point, we are in the position to illustrate how the selection HH encoded in Fig. 1 operates. From the initial problem state described by (0.6857, 0.2457, 0.8000), using Euclidean distance, the closest condition would be that of R3, which indicates us to trigger action BF. Applying BF one time, would yield the following problem configuration $(\ll i_1, i_2, i_3, i_4, i_5\gg , ([~]_{1}^{0}, \cdots , [~]_{5}^{0})) \vdash _{\mathbf {BF}} (\ll i_2, i_3, i_4, i_5\gg , ([i_1]_{1}^{4}, \cdots , [~]_{5}^{0}))$, which in turn generates the following problem state (0.7142, 0.2672, 0.75). From the new current problem state, the closest condition would be again that of R3, triggering action BF. Applying BF once again would yield $(\ll i_2, i_3, i_4, i_5\gg ,$ $([i_1]_{1}^{4}, \cdots , [~]_{5}^{0})) \vdash _{\mathbf {BF}} (\ll i_3, i_4, i_5\gg , ([i_1]_{1}^{4}, [i_2]_{2}^{7}, \cdots , [~]_{5}^{0}))$, whose corresponding problem state is (0.7222, 0.2832, 0.6667). This process continues until no other items remain to be packed.

Fitness evaluation

The core idea of our proposal is that an SS$\mu$GA evolves a population of selection HHs for the 1DBPP, where the best-performing ones must survive according to a fitness function. Since each selection HH is a general problem solver for the 1DBPP, the fitness function should numerically characterize how well this HH generalizes the problem. At the level of the solution to the 1DBPP, a single heuristic is to minimize the number of bins used, thus reducing the waste. Thus, the number of bins used may represent a suitable measure to estimate the performance of a single heuristic. However, if SS$\mu$GA (which is a generator of selection HHs) uses the number of bins as a fitness function, this would lead to stagnation because many individuals are likely to have the same value¹³. Furthermore, SS$\mu$GG should have a fitness value that indicates if the selection HHs have a good generalization behavior, i.e., a selection HH should have a good performance over different 1DBPP instances. In other words, given a training set, a selection HH is expected to have good fitness values that encompass the performance over all the instances in the training set. In consequence, we use the average bin usage (ABU) as both an indicator of HH performance and a fitness value for SS$\mu$GA; similar to the fitness function used by¹⁸. The usage of a single bin is calculated as the sum of the lengths of the items contained in the bin divided by the bin’s capacity. Thus, the ABU is the average of the usage among all bins. The closer the ABU is to 1.0, the smaller the waste of space per bin, the fewer bins needed, and the better the solution. In this context, the ideal heuristic will always produce solutions that yield an ABU of 1.0. Note that ABU is a real number in [0, 1], thus, it provides a wider resolution than the bin usage, which is an integer number. Hence, this avoids stagnation of SS$\mu$GA.

Workflow of the steady-state $\mu$GA

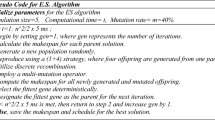
Figure 2 shows the overall sequence of actions followed to produce and test a selection HH using SS$\mu$GA. The process starts by creating a small random population of selection HHs represented by $\mu$ chromosomes. Each chromosome is randomly initialized with three to five coded condition$\rightarrow$action rules. Then, each chromosome is evaluated over all the training set instances to compute its ABU fitness value.

Fig. 2

A graphical depiction of SS$\mu$GA that searches for selection HHs to solve an instance of the 1DBPP.

Once the initial population is evaluated, we use tournament selection of size two and one-point crossover to produce a single offspring. Since our SS$\mu$GA uses variable-length chromosomes, the crossover point is calculated on the parent with the smallest chromosome. Once the offspring is generated, it is evaluated and added to the population. Now that the population has one additional chromosome, we can remove the one with the smallest fitness evaluation. If we reach the maximum number of fitness function evaluations, the search stops, and the best individual from the last population is returned. If the stop criteria are not met, we check if the population is stagnated (there is little difference between the fitness of the selection HHs in the population). If this is the case, we keep the best chromosome and replace the remaining ones in the population with randomly generated chromosomes. Then, the process is repeated from the population evaluation. When the termination criterion is reached, the best selection HH in the last population is returned as the selection HH produced by the model. Finally, we solve the instances in the test set using the selection HH produced with SS$\mu$GA.

Experimental setup, datasets and preliminary experimentation

This section describes the 1DBPP instances considered for this work, the experiments conducted, and their results and analysis. We implemented all the algorithms considered for this work using Java (SDK 11.0.24). The experiments (both preliminary and confirmatory) ran on a Linux-based machine (Linux Mint 21.2 Cinnamon) with 16 GB of RAM and Intel(R) Core(TM) i7-8650U CPU @ 1.90GHz $\times$ 4.

Problem instances (datasets)

In this article, we use three types of instances: (i) synthetically generated instances, (ii) well-known benchmark instances from the literature, and (iii) instances derived from real-world applications. The synthetic instances were generated using a modified implementation of the evolutionary-based method proposed by Plata et al.⁴⁴. The benchmark instances were recovered from the work by Delorme et al.⁴⁵, while the real-world instances were retrieved and adapted from Umetani et al. and Matsumoto et al.^46,47. Since our proposed SS$\mu$GA requires a training process, we required two separate sets of instances, one for training (evolving) the selection HHs, and another set for testing their performance.

Training instances: the synthetic instance generator

The instance generator used in this investigation is similar to the one proposed by Plata et al.⁴⁴. It uses a GA to evolve the structure of 1DBPP instances, guided by a specific fitness function. The GA modifies the length of the items until it finds a configuration where the heuristics exhibit the desired behavior. Our GA requires three input elements: the number of items in the instance, the maximum length per item ($l_{max}$), the bin capacity (C, which is the same for all the bins), and the fitness function ($f_{h\updownarrow }$), which varies according to the heuristic to benefit/harm. The evolutionary process within the GA starts with a population of randomly initialized binary strings that we will refer to as chromosomes. Each chromosome encodes a 1DBPP instance of n items. Each item in the encoded instance uses $\lceil \log _{2}(l) - 1 \rceil$ bits. Therefore, $n \times \lceil \log _{2}(l) - 1 \rceil$ gives the number of bits within the chromosome.

We proposed four categories of instances, one per heuristic in $\mathcal {H}$. We generated instances suitable for a particular heuristic using the method proposed by⁴⁴. While⁴⁴ originally designed their approach to generate Knapsack Problem instances, we adapted it to generate instances for the 1DBPP. Then, we have four categories of instances, and the category defines the heuristic that is the best choice. This strategy guarantees that each heuristic is the best performer in around 25% of the cases (its corresponding category). We generated 250 instances per category, totaling a thousand instances.

It is essential to highlight a critical difference between our training set and the one used for the $\mu$GA proposed by⁸. In the former approach, instances were generated to be pathological for each heuristic. For each heuristic, several instances were generated to represent a challenge for that particular heuristic. Consequently, a selection HH could overcome the drawback of a particular heuristic simply by avoiding it. In contrast, in our work, a selection HH must correctly identify and select the most suitable heuristic for each instance, posing a more challenging scenario.

The instance generator used in this work and the instances generated are freely available at https://bit.ly/3RWEmx9. The instance generator was implemented in Java (SDK 11.0.24) using Apache Netbeans IDE 24.

Testing instances: synthetic and real-world instances

For testing, we employed three different sets of problem instances: Benchmark Testing Suite I (BTS-I), BTS-II, and BTS-III. In the following, we describe each test suite.

BTS-I It consists of an additional set of 1000 synthetic instances, generated in the same manner as the training set. Specifically, 250 instances were created for each category. We refer to this instance set simply as the test set.

BTS-II Includes six families of well-established instance sets from the literature (freely available by⁴⁵ at https://site.unibo.it/operations-research/en/research/bpplib-a-bin-packing-problem-library), which are detailed as follows:

• FalkenauerU³³. This is a set of 80 instances with uniformly distributed item sizes, $n \in [120, 1000]$, and the bin capacity $B = 150$.

• Scholl⁴⁸. These are 1210 instances with uniformly distributed item sizes and $n \in [50, 500]$. The instances are divided into three subsets (Scholl1, Scholl2 and Scholl3) of 720, 480, and 10 instances, respectively. The bin capacity is $B \in [100, 150]$, $B=1000$, and $B=10^{5}$ for Scholl1, Scholl2, and Scholl3, respectively.

• Wäscher⁴⁹. These are 17 hard instances with $n \in [27, 239]$ and $B = 10^{5}$.

• Hard28⁵⁰. This is a set of 28 hard instances, with $n \in [160, 200]$ and $B = 1000$.

• Irnich⁵¹. This set is comprised of 240 instances with B either $5\times 10^{5}$ or $15\times 10^{5}$, with uniformly distributed item sizes between $[\frac{2}{15}B, \frac{2}{3}B]$ and $[\frac{1}{150}B, \frac{2}{3}B]$, and $n \in \{125, 250, 500\}$.

• Augmented Non IRUP and Augmented IRUP⁵². These benchmarks correspond to two hard-to-solve sets (IRUP and non-IRUP) of 250 instances each. Each benchmark is divided into five subsets of 50 instances with $n \in \{201, 402, 600, 801, 1002\}$ and $B \in \{2500, 10^4, 2\times 10^4, 4\times 10^4, 8\times 10^4\}$, respectively. That is, the first subset corresponds to 50 instances with $n = 201$ and $B = 2500$, and so on.

BTS-III This test suite comprises two benchmarks, featuring real-world instances (freely available at https://sites.google.com/view/umepon/benchmark), originally derived from the closely related one-dimensional cutting stock problem. The two benchmarks have been reformulated as 1DBPP instances.

• Tube⁴⁷. This set consists of six instances derived from a real-world application in a paper tube manufacturing company in Japan. The instances feature a number of items n ranging from 780 to 1500, and tube stock lengths (bin capacity B) ranging from 1800 to 2100.

• Fiber⁴⁶. These instances originate from a real-world application in a chemical fiber company in Japan. The dataset includes 39 instances (the authors report using 40 instances in their paper, but only 39 could be retrieved from the Web), with the number of product types ranging from 6 to 29 and a demand per product type varying between 2 and 264 units. Stock roll lengths (the bin sizes B in our case) are either 9080 or 5180 units, while the lengths of the individual product types range from 500 to 2000 units.

Parameter settings

The running parameters of SS$\mu$GA employed in our experiments are shown in Table 1. We decided to set the parameters for parent selection, crossover rate, and mutation rate to the values recommended on the original $\mu$GA⁴³. In addition, we set the offspring size and replacement to the values used in the original steady-state GA presented in⁴².

Table 1 Running parameters for SS$\mu$GA.

Other parameters such as population size and number of individual evaluations were determined through preliminary tests as presented in the following "Preliminary experiments" section.

Preliminary experiments

Our preliminary experiments aimed to explore the feasibility of the proposed approach: a SS$\mu$GA to produce HHs for the 1DBPP. To do so, we explored three scenarios related to configuring and justifying our approach. We briefly describe the preliminary experiments as follows.

• Effect of population size ("Preliminary experiments" section). We defined the population size through experimentation. Throughout this experiment, we produced 70 selection HHs using the proposed SS$\mu$GA, ten for each population size (ranging from four to ten individuals).

• Effect of the training set size ("Preliminary experiments" section). With this experiment, we estimated the effect on the performance of the resulting selection HHs when changing the number of instances used for training. We produced 30 selection HHs using the proposed approach, considering different training subsets (120, 400, and 1000 instances). We evaluated the performance of the selection HHs in both the complete training (1000 instances) and the test set from BTS-I.

• Effect of extending the problem characterization ("Preliminary experiments" section). In this experiment, we focused on the benefit of extending the set of features that characterize the instances. Thus, we generated 20 selection HHs using the proposed SS$\mu$GA; ten using AVG and STD as features and ten more considering AVG, STD, SMALL, MEDIUM, and LARGE, as described in "Representation of a Selection Hyper-Heuristic" section. We evaluated the performance of the selection HHs in both the training and test set from BTS-I.

All subsequent results in this section are primarily presented using 50% empirical attainment functions (EAFs)⁵³, computed from ten independent runs for each configuration. Although not intended for statistical significance testing, this representation highlights the median behavior—naturally excluding outliers—and is a common approach for visualizing performance dynamics during the evolutionary process. The 50% EAF curve indicates the boundary that is attained by at least half of the runs at each evaluation step, thus providing insight into the typical progress of the algorithm over time.

The effect of population size

To determine an appropriate population size and number of evaluations, we conducted a preliminary experiment. We performed ten independent runs of the $\mu$GA for each population size, ranging from four to ten individuals, over the training set and controlling for fitness function evaluations. In all cases, other parameters (i.e., selection, crossover, mutation) were set as outlined in Table 1.

Fig. 3

The 50% empirical attainment functions of ABU, corresponding to the best individual per number of evaluations of ten independent runs of SS$\mu$GA for various population sizes (four to ten).

Figure 3 shows the 50% EAFs among the ten independent runs for each configuration (population size). From this figure, we observe that no particular configuration outperforms the others. However, we can see that the configuration with six individuals strikes a good balance between population size and performance. Therefore, we will use this population size for the subsequent experiments in this section. Additionally, 1500 fitness function evaluations appear sufficient for any considered configuration to reach a point where further improvement is minimal. Based on this, we fixed the number of fitness function evaluations to 1500 for the remaining experiments.

The effect of the training set size

Now that we have empirically determined the parameters for SS$\mu$GA, we experimented to evaluate the effect of the training size on the learning process of our solution model. Let us recall that we are using a nominally more challenging training set than the one used by⁸ for the reasons explained in Sect. 5.1. In this spirit, we divided the training set into three sizes: 120, 400, and 1000 instances. We evaluated their performance evolution in each case based on the ABU and the number of function evaluations in the training set. Fig. 4 presents the 50% EAFs derived from this experiment.

Fig. 4

The 50% empirical attainment functions of ABU, corresponding to the best individual per number of evaluations of ten independent runs of SS$\mu$GA for various training set sizes (120, 400, and 1000 instances). The dotted lines represent the median ABU obtained on the test set (BTS-I) for each case.

Based on the results presented in Fig. 4, we observe that the fewer instances used for training, the better the performance of the evolved selection HHs over the training set. Specifically, the selection HHs that evolved with 120 instances achieved a higher ABU than those with 400 and 1000 instances. However, their performances behave differently when evaluating these selection HHs over the 1000-instance generated test set (the BTS-I presented in "Problem instances (datasets)" section). The dotted lines in Fig. 4 show the performance of the resulting selection HHs on BTS-I. Contrary to the performance of the selection HHs over the training set, in the test set, the best results are obtained by the selection HHs evolved with larger training sets. In other words, the results indicate that selection HHs evolved using a larger training set tend to generalize better than their counterparts trained on smaller sets.

The effect of extending the problem characterization

In this experiment, we explored the impact of extending the set of features that characterize 1DBPP instances so that the selection HHs can map instances to heuristics in such a way that we can improve the search and the results obtained. For this reason, we generated ten independent selection HHs using the two features originally proposed by⁸ and another ten using the extended set of features proposed in this work. In all the cases, we used the configuration depicted in Table 1.

Fig. 5

The 50% empirical attainment functions of ABU, corresponding to the best individual per number of evaluations of ten independent runs of SS$\mu$GA for two sets of features to characterize the problem state (AVG, STD) and (AVG, STD, SMALL, MEDIUM, LARGE). The dotted lines represent the median ABU obtained on the test set (BTS-I) for each case.

The results shown in Fig. 5 showcase the 50% EAFs on the effect of extending the set of features that characterize the problem state. By considering the additional three features proposed in this work (SMALL, MEDIUM, and LARGE) the performance of the selection HHs increases significantly, both in the training, shown with the continuous line, and the test set (BTS-I), represented by the dotted line.

Comparison of evolutionary approaches for hyper-heuristic generation

In this section, we aimed to show the benefits of using the proposed SS$\mu$GA in both the instances we artificially produced (BTS-I) and some others taken from the literature including real-world applications (BTS-II and BTS-III). The performance was measured in ABUs and the number of bins used, and compared against other evolutionary approaches for generating selection HHs for the 1DBPP in semi-online scenarios. For that, we conducted two main experiments as follows.

• Performance analysis I: Performance comparison on training set ("Performance comparison on training set" section). In this experiment, we compared and contrasted the efficacy of different evolutionary frameworks in generating selection HHs for the 1DBPP. For this task, we produced 40 selection HHs using four evolutionary approaches: generational GA (GA), generational $\mu$GA ($\mu$GA)⁸, steady-state GA (SSGA)⁴⁰, and our proposal, SS$\mu$GA; that is, ten HHs per approach. We compared these approaches on both the instances of the training set and BTS-I.

• Performance analysis II: Performance comparison on testing sets ("Performance comparison on testing sets" section). Aiming at estimating how well the selection HHs produced with each evolutionary framework generalize to unseen instances. We arbitrarily selected two selection HHs per approach from the previous experiment. We used them to solve the instances in BTS-I, BTS-II and BTS-III. For this experiment, we considered the ABU and the number of bins used.

Overview of comparative evolutionary approaches

State-of-the-art approaches for the 1DBPP vary depending on the problem-type scenario. The approaches designed for online and semi-online environments often do not perform as well compared to approaches designed for offline settings, where full instance information is available in advance, and items can be rearranged before processing. Consequently, a comparison between these approaches is not equitable. Similarly, comparisons among algorithms for the 1DBPP in semi-online environments characterized by full look-ahead information are not generally suitable for direct comparisons with algorithms for semi-online environments with partial look-ahead information. Thus, we compared and contrasted the efficacy of different evolutionary frameworks in generating selection HHs for the 1DBPP in semi-online scenarios with partial look-ahead item information.

We describe the models we used for comparison as follows.

• $\mu$GA This recent approach relies on a $\mu$GA to produce selection HHs for the 1DBPP⁸. The parameters used in this approach consist of a population size of five chromosomes, a crossover rate of 1.0, and no mutation. The crossover operator takes two parents and produces two offspring (using one-point crossover). The offspring replace each generation, the whole population, but the best chromosome. When the standard deviation of the fitness among the chromosomes is below 0.001, we restart and randomly regenerate all the chromosomes in the population, but the best one.

• GA Although we have no evidence that this model has been published before, it is simple to consider it a variation of the work by⁴⁰. This time, the GA is generational, allowing for the replacement of the entire population. This type of algorithm requires a larger population, so we used 100 chromosomes in the population, and all of them are replaced each generation. We keep a record of the best chromosome found so far, so we do not lose it if it disappears from the population. The remaining parameters are similar to those used by⁴⁰: tournament selection of size two, one-point crossover (takes two parents and produces two offspring), and mutation rate (flip mutation) of 1.0 and 0.1, respectively.

• SSGA It consists of a steady-state GA with dynamic-length chromosomes that evolves selection HHs for constraint satisfaction problems⁴⁰. This approach has not been applied to the 1DBPP, so we took the parameters as they appear in the corresponding publication: 25 chromosomes in the population, tournament selection of size two, replacement of only the two worst individuals in the population, one-point crossover (takes two parents and produces two offspring) and mutation rate (flip mutation) of 1.0 and 0.1, respectively. Their work used the number of generations, not the evaluations, as stopping criteria (250 generations, around 525 fitness function evaluations).

Performance comparison on training set

The intention with this experiment is to compare our SS$\mu$GA against three other GAs (from "Overview of comparative evolutionary approaches" section), acting as generation HHs. For each generation framework, we conducted ten independent runs using the training set instances, and evaluate the fitness evolution throughout the training of the models.

Fig. 6

The 50% empirical attainment functions of ABU, corresponding to GA, $\mu$GA, SSGA, and SS$\mu$GA. The dotted horizontal lines represent the median ABU obtained on the test set (BTS-I) for the resulting HH produced by each evolutionary framework. The dotted vertical line indicates the control point at which SS$\mu$GA outperforms the other approaches.

The comparison results from the training are illustrated in Fig. 6. The continuous colored lines represent the 50% attainment functions of ABU over the training set throughout the evolutionary process for each framework (one for each color). At 1500 function evaluations, the median of the best HHs produced by our approach, SS$\mu$GA, achieves the highest ABU compared to the median of the best HHs generated by other methods. Additionally, the vertical dotted line marks the point at 734 function evaluations, beyond which the ABU of the median of the best HHs produced by SS$\mu$GA is never exceeded by corresponding HHs from other methods. In other words, there is a certain point at which SS$\mu$GA yields higher-valued HHs with less number of function evaluations. Since a faster specialization on the train set may lead to reduced generalization, the horizontal dotted lines display the ABU values of the median of the best resulting HHs, when evaluated on the test set BTS-I. From this, we observe that SS$\mu$GA not only converges faster but also produces HHs with the highest ABU on BTS-I, showcasing superior performance on unseen instances.

Performance comparison on testing sets

While the previous section focused on comparing the overall performance of all the generated selection HHs, in this section, we compare the performance of specific resulting selection HHs for solving 1DBPP instances. Two selection HHs were selected from those generated by each method—GA (HHGA$_{1}$ and HHGA$_{2}$), $\mu$GA (HH$\mu$GA$_{1}$ and HH$\mu$GA$_{2}$), SSGA (HHSSGA$_{1}$ and HHSSGA$_{2}$), and SS$\mu$GA (HHSS$\mu$GA$_{1}$ and HHSS$\mu$GA$_{2}$). The eight selected HHs were employed to solve instances from both benchmark suites: the generated testing set, BTS-I (with instances similar to the ones used for training), six classic families of datasets from the literature, BTS-II, and two datasets derived from real-world applications, BTS-III. The quality of the produced 1DBPP solutions determines the HH’s performance. The ABU and the number of bins used assess the quality of a solution. It is important to recall that ABU is the fitness function that guided the evolutionary process in all cases. In contrast, the number of bins used corresponds to the objective function of the 1DBPP. The overall results for each selection HH are presented in terms of mean performance, standard deviation, cumulative error relative to the best-performing low-level heuristic, the number of solutions that are worse than the best-performing low-level heuristic, the number of solutions matching the best-performing low-level heuristic, and the number of results surpassing the best-performing low-level heuristic across each problem instance per dataset.

Results on BTS-I

Table 2 shows the performance of each selection HH regarding ABU across the instances of BTS-I, while Table 3 shows the performance regarding the number of bins used on the same dataset. In both tables, the results are organized by dataset. The first rows present the results for instances favorable to FF, followed by those favorable to BF, and so on. The rows labeled “Overall” present the aggregated results of all the instances from the benchmark. Additionally, the first set of columns corresponds to the performance of the low-level heuristics, followed by the results of the selection HHs. Finally, the best results among selection HHs are highlighted by boldface characters, while underlined characters correspond to the second-best values—zeros are not highlighted.

One of the first things to note in both Tables 2 and 3 is that they share almost identical positions in the top rankings of the selection HHs. From these tables, we can observe that the best-performing selection HHs are HHGA$_{1}$, HH$\mu$GA$_{1}$, HH$\mu$GA$_{2}$, HHSS$\mu$GA$_{1}$, HHSS$\mu$GA$_{2}$, consistently obtaining the best and second-best results. Moreover, note that these selection HHs specialize in one or two datasets. Specifically, observe that HH$\mu$GA$_1$ and HHGA$_1$ have specialized in FF-type of instances. HH$\mu$GA$_2$ shows specialization in both BF- and AWF-type instances, while HHSS$\mu$GA$_2$ in BF- and FF-type instances. Finally, HHSS$\mu$GA$_1$ is the only selection HH among the eight to show WF-type instances specialization. These results show that they all show competitive performances, with HH$\mu$GA$_{2}$ perhaps showing some of the best results. However, note that in the Overall dataset, both selection HHs produced from our approach, HHSS$\mu$GA$_{1}$ and HHSS$\mu$GA$_{2}$, share the top results among the mean and cumulative error performance values.

Table 2 Average Bin Usage (ABU) obtained by the heuristics and a few selected HHs on the test set (BTS-I).

Table 3 Number of bins used by the heuristics and a few selected HHs on the test set (BTS-I).

The one-sided Wilcoxon rank-sum tests presented in Supplementary Table SI-3 and Supplementary Table SI-4, conducted on the results shown in Tables 2 and 3, support many of the previous observations. Both HHGA$_1$ and HH$\mu$GA$_1$ achieved statistically better ABU values (p < 0.05) than all other HHs on the FF-type test subset. In contrast, HH$\mu$GA$_2$ showed statistically worse ABU values compared to all other HHs on this subset. Interestingly, HH$\mu$GA$_2$ was also the only method to achieve statistically better ABU values across all others on the BF-type test subset. For the WF-type, AWF-type, and overall test subsets, the best-performing methods in terms of ABU were HHSS$\mu$GA$_1$, HH$\mu$GA$_2$, and HHSS$\mu$GA$_1$, respectively. In terms of the number of bins used, only HH$\mu$GA$_1$ and HH$\mu$GA$_2$ showed statistically significant improvements, specifically on the WF-type and AWF-type subsets, respectively.

Results on BTS-II

Table 4 and Table 5 present the results of the selection HHs, on 1DBPP instances from the literature (BTS-II), reported in terms of bin usage and number of bins used, respectively. Similar to the previous tables, the best results are highlighted using boldface characters, and the second-best results are identified by characters with an underlined format.

From Table 4 we can observe that among the top performing selection HHs are HHGA$_1$, HHSSGA$_1$, HHSS$\mu$GA$_1$ and HHSS$\mu$GA$_2$, as they show one or more top values in at least six of the nine benchmark subsets. Interestingly, one of the best-performing HHs on BTS-I, HH$\mu$GA$_2$, is missing from this list—although if we only consider the last four benchmarks (Hard28, Irnich, IRUP and nonIRUP), it stands out as one of the best performing HHs. Conversely, HHSSGA$_1$ was not among the top-performing selection HHs on BTS-I, but it is now on BTS-II. One reason for that might be that, based on the results on BTS-I, HH$\mu$GA$_2$ showed an over-specialization on BF-type (and AWF-type) of instances along with an inefficiency for FF-type of instances, whereas HHSSGA$_1$ showed a balance of preference between BF-type of problems and FF-type of problems, which are both common between instances from the BTS-II datasets. Also, in a case-by-case analysis from this table, we observe that HHGA$_1$ is a top performer on the Wäscher dataset, HHGA$_2$ on FalkenauerU dataset, HH$\mu$GA$_2$ on Hard28, IRUP and nonIRUP datasets, HHSSGA$_1$ had some of the best results on Scholl02, Irnich, IRUP and nonIRUP datasets, HHSSGA$_2$ showed top results on Scholl01 and Hard28 datasets, and HHSS$\mu$GA$_2$ presented the best values on FalkenauerU, Scholl01 and Hard28 datasets. Overall, we can see that both HHSSGA$_1$ and HHSS$\mu$GA$_2$ were the most consistent top performers among all selection HHs. Remarkably, although HHSS$\mu$GA$_1$ is consistently among the worst-performing methods in terms of mean ABU values and error, it was consistently among the top two results in producing better results than the low-level heuristics. Overall, HHSS$\mu$GA$_1$ produced 49 solutions that have a better ABU value than the best-performing low-level heuristic.

From Table 5, we observe that the results are very similar among the methods. This was somewhat expected since the count of bins does not usually produce a lot of variance among methods. Nonetheless, we can see that HHSS$\mu$GA$_2$ is consistently among the best-performing methods overall. Furthermore, despite being among the worst-performing selection HHs overall, HHSS$\mu$GA$_1$ still found three solutions with a smaller number of bins than the best low-level heuristic.

Table 4 Average Bin Usage (ABU) obtained by the heuristics and a few selected HHs on the literature testing set (BTS-II).

Table 5 Number of bins used by the heuristics and a few selected HHs on the literature testing set (BTS-II).

The one-sided Wilcoxon rank-sum tests presented in Supplementary Tables SI-5 and SI-6, based on the results from Tables 4 and 5, suggest that there is generally little performance difference among all HHs. However, specific differences across certain datasets are noteworthy. For instance, HHSS$\mu$GA$_1$ appears to have over-specialized on BTS-I, as its ABU performance on several BTS-II benchmarks is statistically worse than that of all other HHs. Interestingly, on both the IRUP and non-IRUP benchmarks, HHSS$\mu$GA$_1$, HH$\mu$GA$_1$, HH$\mu$GA$_2$, and HHSSGA$_1$ achieved statistically better ABU values compared to HHGA$_1$, HHGA$_2$, HHSSGA$_2$, and HHSS$\mu$GA$_2$. Even more interesting, on these same benchmarks, both HHGA$_1$ and HHGA$_2$ were statistically worse than all other HHs in terms of both ABU and the number of bins used.

Results on BTS-III

Although a comparison was conducted using real-world derived instances, these turned out to be somewhat easy for the heuristics to solve, as most of them exhibited similar performance-with the exception of the WF heuristic. In this sense, the instances behaved similarly to pathological cases that disproportionately affect WF. That is, a good enough performance could generally be achieved as long as WF was avoided. This type of behavior was previously shown to be easily handled by the $\mu$GA-generated HHs⁸.

Given the above, the corresponding results were placed in the Supplementary Information. There, ABU performance and its statistical comparison are provided in Supplementary Tables SI-1 and SI-7, respectively, while the performance in terms of the number of bins used and its statistical comparison are presented in Supplementary Tables SI-2 and SI-8.

Understanding the impact of the SS$\mu$GA components

Aiming to understand the aspects within our approach that have the largest impact on its performance, we conducted a $2^{3}$ factorial design involving the following factors, each with two levels: type of GA (generational or steady state), population size (6 or 25 individuals), and minimum fitness standard deviation in the population to restart the population ($10^{-4}$ or $10^{-5}$). We conducted five independent runs for each combination of levels using the corresponding configuration. Then, we conducted a three-way factorial analysis of variance (ANOVA) with the data we gathered.

The results obtained from this analysis show that the type of GA has a statistically significant effect on the performance of the resulting hyper-heuristics (p-value = 0.00441). This means that changes in the type of GA (generational or steady state) lead to meaningful changes in the resulting performance. The other two main factors, population size (p = 0.57863) and minimum fitness standard deviation in the population to restart the population (p-value = 0.40936), do not have significant individual effects on the performance of the hyper-heuristics produced. None of the two-way or three-way interactions between the factors are statistically significant (all exhibit a p-value larger than 0.05), indicating that the effect of one factor does not depend significantly on the level of the others. However, the residuals capture a large portion of the variance, suggesting substantial unexplained variability exists in the data. To summarize, the statistical evidence suggests that replacing only a small fraction of the population at each iteration (using a steady state GA instead of a generational one) is the element within our model that impacts the performance of the hyper-heuristics produced most.

Potential bottlenecks

Although we recognize the results obtained by our model are competitive and promising, we understand that a more in-depth analysis of the underlying causes of any potential performance bottlenecks would be beneficial. For this reason, we have carefully revised our model, looking for potential elements that could lead to slower convergence or increased computational overhead. We identified two aspects that may represent a bottleneck in future scenarios:

• 1. textitRestarting the population Whenever we restart a population due to its low variance, the new population is randomly initialized (with only the best individual from the previous population preserved). Since the individuals in the new population are randomly initialized (this is the only way to add diversity since we lack a mutation operator in our model), such individuals likely exhibit a low quality. Then, solving the instances in the training set may take longer for the first generations than for the last ones (where the population has converged to a competent hyper-heuristic).

• 2. Updating the problem state In most instances, calculating the features’ values to characterize the problem state might not represent a significant overhead. However, we must recall invoking the hyper-heuristic whenever we pack an item. So, we calculate the problem state as many times as the number of bins in the instance. This might represent a problem when the number of bins or features increases drastically because it implies looping over the items repeatedly. In these cases, we expect the model to be slower for producing the hyper-heuristics and applying them once they have been trained.

We know these potential bottlenecks will likely appear when dealing with much larger instances than the ones studied in this work. Although we have not implemented any mechanisms to deal with these potentially undesirable situations, we have thought of some ideas to overcome these problems.

For example, a fraction of the population could be reinitialized using a mutation operator instead of doing this completely at random. This strategy would produce individuals that represent variations of the best one, increasing the probability of exhibiting a good performance, but at the price of reducing the exploratory nature of the population restart. Another way to deal with the restart process would be to use a heuristic approach to generate a fraction of the new population.

Concerning the problem of continually updating the problem state, we could implement a variation of a delta evaluation. Then, the evaluation of the problem will not need to be conducted from scratch every time we need it. Instead, it will be updated using fast operations and keeping a few additional variables related to the problem state. For example, the first time we calculate AVG (at $t = 0$), we can calculate it as $(w_{\sum , t = 0} \times n_{t = 0} ) / n_{t = 0}$. However, if we save the sum of the weights $w_{\sum , t = 0}$ and the number of items ($n_{t = 0}$) for future calculations, once we remove item j (with its correesponding weight, $w_{j}$), we can recalculate AVG at time $i + 1$ as $w_{\sum , t = i + 1} = (w_{\sum , t = i} \times n_{t = i} - w_{j}) / (n_{t = i} - 1)$. Finally, we would only need to update $n_{t = i + 1} = n_{t = i} - 1$. Using this strategy, we would avoid calculating the features from scratch, which would reduce computation time.

Discussion and scientific relevance

Collectively, the results presented in this section highlight the potential of the selection HHs for both specialization and generalization. Regarding the performance of the selection HHs produced by our proposed method, we observed that their effectiveness largely depends on the characteristics of the instances they were trained on. In this case, the training instances balanced features that allowed the selection HHs to generalize well on the BTS-I instances (similar to those from the training set). On BTS-II, the results were more varied, producing an overall competitive selection HH (HHSS$\mu$GA$_2$) and another HH (HHSS$\mu$GA$_1$), which performs poorly overall but occasionally produces better results than its composing low-level heuristics in isolation. On BTS-III (as shown in Supplementary Table SI-1 and Supplementary Table SI-2), the results from each method were very similar to each other. Nonetheless, this outcome was somewhat expected, as the instances were relatively easier than those from the other two benchmark test suites.

Overall, the contributions and scientific relevance of our proposed method are as follows. First, the steady-state selection scheme improves the diversity of HHs by delaying stagnation and controlling the number of population reinitializations. This is a critical point since the number of restarts has an impact on the quality of the generated selection HHs: too many restarts hinder convergence, while too few limit exploration. Therefore, the steady-state approach strikes a balance, improving both performance and stability. Second, we expanded the set of features used to describe a problem state from two to five (AVG, STD, SMALL, MEDIUM, and LARGE). As validated in "Preliminary experiments" section, this richer representation leads to the generation of higher-quality selection HHs. Third, in our previous work, we trained $\mu$GA on pathological 1DBPP instances (i.e., instances crafted to be difficult for a specific heuristic)⁸. In contrast, we trained SS$\mu$GA on 1DBPP instances where a specific heuristic is known to perform well. As a result, this requires SS$\mu$GA to generate selection HHs that accurately select the appropriate heuristic for each instance, rather than merely avoiding poor choices—thus posing a harder and more practical learning task (see "Problem instances (datasets)" section). Following this line, each selection HH was evaluated not only on a synthetic test set (BTS-I) resembling the properties of the training instances but also on well-established instance sets (FalkenauerU, Scholl, Wäscher, Hard28, Irnich, Augmented Non IRUP, and Augmented IRUP) as well as two real-world datasets adapted from the 1D Cutting Stock Problem (BTS-III). Finally, we extended the analysis in addition to ABU, we also report the number of bins used during testing, aligning our analysis with the actual objective of the 1DBPP. This dual reporting strengthens the empirical validity of our findings. Finally, it is worth emphasizing that SS$\mu$GA contributes to the scarcely explored field of generation HHs that construct selection HHs, highlighting its novelty and relevance in the state of the art⁵⁴.

Conclusion and future work

In this study, we presented a steady-state $\mu$GA methodology for generating selection HHs for the classic 1DBPP. This work improves the solution approach proposed by⁸. Our proposal introduces the integration of a steady-state selection scheme that improves population diversity and stability by effectively managing the number of reinitializations. We also enrich the problem state representation with five descriptive features (namely, AVG, STD, SMALL, MEDIUM, and LARGE), enhancing the quality of the generated selection HHs. Unlike prior work focused on pathological instances, our approach trains on instances where a specific heuristic is optimal, demanding more accurate and meaningful heuristic selection. The proposed method was validated on a wide range of synthetic, benchmark, and real-world datasets, and performance was assessed using both ABU and the number of bins used. Together, these elements underscore the novelty and practical relevance of our SS$\mu$GA in the context of generative HHs.

Our experimental results demonstrate the feasibility and advantages of the proposed approach across various training and testing datasets. First, preliminary experiments showed that a population size of six individuals for our SS$\mu$GA provided a good balance between resulting selection HH quality and computational resource consumption. Furthermore, our experiments also showed that increasing the training set size led to better generalization, as selection HHs trained on larger datasets performed better on unseen test instances. Additionally, including features beyond the simple statistical measures (average and standard deviation) improved the effectiveness of the mapping between instances and heuristics, leading to consistently better performance across both the training and test datasets.

Compared with other generative methodologies based on evolutionary approaches, our proposed SS$\mu$GA outperformed a generational GA, a steady-state GA, and a generational $\mu$GA, consistently reaching higher fitness values within the same number of evaluations, during training. During testing, our results on benchmark datasets (BTS-I, BTS-II and BTS-III) revealed that the selection HHs produced by SS$\mu$GA were highly competitive, often outperforming HHs generated by the other methods, particularly on the instances of BTS-I. Additionally, our SS$\mu$GA generated selection HHs with strong specialization for certain instance types and others with generalization capabilities. Unfortunately, a limitation in this work is that BF was the best-performing heuristic in almost all the cases of BTS-II and BTS-III. This behavior makes it challenging to produce an HH that does not include BF as one of the options. Since BF is the best option for many instances, the HHs tend to replicate its behavior. This phenomenon is similar to what happens in other learning approaches when the training set is biased. Although this does not mean a bad result since the HHs do learn, it opens a path for future work in which we should explore ways to overcome the problem of working with “unbalanced” sets of instances, where one of the heuristics is almost always the best performer.

As a natural continuation of this work, we plan to extend the application of SS$\mu$GA to more complex variants of the BPP, such as two- and three-dimensional BPPs. Furthermore, exploring its performance on additional problem domains and refining the instance characterization are promising directions to improve the generalization capabilities of the generated selection HHs. Lastly, we consider analyzing the cross-domain behavior of SS$\mu$GA, even if it requires incorporating heterogeneous feature representations.