Introduction

The water scheme’s continued existence cannot be the foundation for the society’s growth. The main causes of the deliberate environmental contamination in the river basin areas nowadays are human production and related activities1,2,3, which was not beneficial to ecological civilization construction in any watershed regions4. Dependable and accurate streamflow prediction was dynamic for the operative and optimal hydrological resources use and ancillary provision services through hydrological possessions5,6. Nevertheless, non-stationary and stochastic appearances of streamflow pose some encounters for its precise prediction7,8,9. Consequently, numerous examinations in current years absorbed on accurate stream flow prediction10,11,12,13. Their streamflow forecasting type models are observed are statistical, physical, and blended. The scaled models reflect the hydrological cycle methods14,15. Deep learning models (DLM) are the advanced version of ML that can now handle non-linear datasets because of their ability to learn sequential criteria7,9. The long short-term memory (LSTM) irregularity of the recurrent neural network (RNN) was the best DLM applied for streamflow prediction applications. Consequently, enlightening streamflow forecasting accuracy was a significant theme for hydrologists, and the investigation of streamflow prediction approaches has established considerable consideration. The river water level was divided into data-namely and process-driven approaches8,16. The Procedure-oriented approaches have a possible benefit in building physical empathy for hydrological procedures17,18,19.

The data-driven approaches usually comprise statistical-based approaches like multiple linear regression (MLR) and autoregressive moving average (ARMA)20, while AI-based approaches, like SVM, artificial neural network (ANN), with the tree based models21. Out of AI-based approaches, an extreme learning machine (ELM) method is the novel ML technique22. The ELM provides many advantages, such as excellent presentation and quick learning speed, and it does not require repetition for weight adjustment like older neural network techniques23. Compared to old neural network approaches, the ELM does not need repetition for weight alteration and suggests numerous benefits, like outstanding presentation and fast learning speed. Currently, the ELM has an extensively valuable in various scientific arenas. Researchers applied ELM to estimate the operative drought index in the eastern Australia. It has been reported that the ELM algorithm performs much well than the ANN in relations of training and learning speed24. The model leverages the superior signal decomposition capabilities of CEEMDAN and the capacity of GRU to capture nonlinear dynamic patterns in time series. The study employed precipitation data from January 1, 2019, to December 31, 2022, as a sample. With an R2 of 0.7915, MAE of 0.05382, and MSE of 0.09081, using an Adam optimizer with adaptive learning rate reduction results in improved convergence and dependable predictions25.

Consequently, the ELM was a progressive method for prediction and approximation. However, there have been some ELM applications for stream flow prediction. In this analysis, CEEMDAN with some ML models were applied for monthly stream flow prediction19. The previous literature specifies that the CEEMDAN model is highly beneficial for river water level prediction (Table 1). Conventionally, physical-based methods depend on prudently designed calculations were established to imitate complex precipitation-runoff procedures26. Many precise datasets were often obligatory for these approaches to control computational limitations. In repetition, it may be limited through specific unforeseen difficulties to acquire necessary datasets on time, which unavoidably take about poor prediction outcomes and high indecision7,10. To tackle this difficulty, famed statistical approaches based on linear relation assumptions were announced for the hydrological forecast, like MLR, auto regression, and step wise regression27.

Table 1 Summary of recent streamflow forecasting using ML and CEEMDAN.
Full size table

Based on the literature, one gets the impression that difficulties are accessible and that numerous models, upon standardization, can grip tasks and also deliver skilful predictions. Those are stark differences to working approaches that still deeply trust the time-proven took and empirical models established periods ago and additional highly on knowledge and local knowledge of human predictors28,44. Figure 1 indicates that the CEEMDAN applications are different sectors, which suggests that a limited study is observed in river water level estimation. It is similarly obvious how little has been recognized in the literature on the performance of the operation in real-time stream flow prediction31. The EEMD determined nearly mode mixing matters of the EMD; though, it was powerless to eliminate the EMD mode mixing issue, which led to the growth of the CEEMDAN4,39,40. It is possible to achieve nearly zero refurbishing errors with the CEEMDAN. White noise and reduced addition time are obtained at each stage of the CEEMDAN45. The effectiveness of the CEEMDAN approach in modified stream flow prediction applications has been demonstrated4. The CEEMDAN method has an established track for its viability in changed streamflow prediction applications4. However, the CEEMDAN still agonizes from the disadvantages of the modal residual noise, interruption in the signal info compared to the EEMD, and doubtful modes occurrence. Improved CEEMDAN, also called ICEEMDAN, was EMD-based on the latest varieties and resolutions of concerns about its forerunners29. The ICEEMDAN applies experiential in the signal for the IMF sifting to resolve the EEMD, and its different difficulties have been examined in the literature46 Some researchers developed the two-layer decay model to approximate the water quality limitations47.

Fig. 1
figure 1

CEEMDAN applications in different investigations (Based on Scopus database).

Full size image

The highest-frequency IMF1 is further broken down into the numerous IMFs using the VMD algorithm after the unique water quality stricture data series are first transformed into the multiple IMFs through the CEEMDAN48. This time–frequency domain analysis method, known as CEEMDAN, was commonly used to handle non-stationary and nonlinear signals. It eliminates modal effects through addition, has strong adaptive noise, and converges. Table 1‘s literature review section contains more information on the CEEMDAN-decomposed models than what was previously found45. This research’s important objective and goal is to create an advanced hydrological forecasting method. We have established four goals for this investigation; the CEEMDAN in treatment nonlinear datasets was used. Also, different ML models like random subspace, RF, SVM-RBF and SVM-linear are applied for predicting river water level in between 2014 to 2023 in Sg Muar at Buloh Kasap, Johor station. Compared with the other DL-based models, the future coupled model in this study proves higher correctness and better stability. Based on the decent decay effect of the CEEMDAN and the combination effect of the other ML models, a comprehensive knowledge to identify the autocorrelation function (ACF), Partial autocorrelation function (PACF), CEEMDAN-SVM (linear and RBF), CEEMDAN-RF, and CEEMDAN-RS have calculated which is help to understand the actual river water level in the examining area. The CEEMDAN pre-processing technique decomposes the data to improve prediction accuracy. The results showed the combined CEEMDAN-NAR model outperforms the single model in predictive accuracy, boasting a deterministic coefficient (DC) of 0.93. Our study also found improved performance of the developed models when integrated with the CEEMDAN technique. The proposed technique is better than the standalone models utilized.

Study area

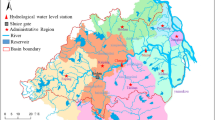
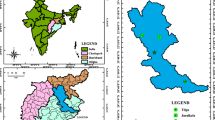
The Sg Muar, Buloh Kasap, Johor station was established along the Muar River in Segamat, Johor, in Malaysia. The stations is collected the monthly river water level datasets from 2014 to 2023. The total area of the catchment is 6,595 km2; this area is the entire states of Negeri Sembilan and Pahang. The critical source of Sg Muar is 310 km extended, and mean yearly discharge at its inlet is 140m3/s. The both essential population locations are Muar at the Sg Muar entrance in the basin area. The present region’s understanding is representative of humid equatorial weather, which has the highest temperature and humidity every year. The mean once-a-month lower temperature is 23 °C—24 °C and higher temperature is 31 °C—33 °C. The yearly precipitation in the catchment region is between 1,300 mm to 2,400 mm. The Southwest monsoon transports moderate precipitation to the study area from May to July. The river water level data is important for understanding the flood during heavy rain, so it is essential to know what level can reach the stream.

figure a

Methodology

Data collection and analysis

The monthly stream flow and water level data are collected from the station from 2014 to 2023, this datasets pre-processed before applied models. The prediction of river water level modeling was created using two scenarios to selection of best models for future condition of river water level. The first scenario divided into four input variables such as lags 1 to 3 and stream water flow using ACF and PACF methods, and the second scenario decomposition modeling was used for prediction of the river water level based on the five input variables such as IMF-1 to 5 and stream flow also included as an input variables. In this research, the three lags and monthly stream flow time series are utilized as predictors (inputs), and the actual/observed time series of river water level are used as the target (outputs) for decomposition ML modeling.

ML modeling development for predicting river water level

Estimating accurate river water levels is vital for flood and drought risk management, water resources planning, electrical energy production, urban infrastructure design, and irrigation planning. Machine learning algorithms are widely used in estimating river water levels because they provide helpful data. These models stand out and provide simple and promising inferences where physical models cannot be used or are too complex49,50. In this paper, we have been selected the one station for prediction of monthly river water level based on the eight ML and decomposition models. We have ensured the data quality, and regular, missing values were removed in the river water level datasets using the dropna() function from Pandas library. The outliers were removed in the datasets using interquartile range (IQR) method. Hence, we have developed multiple models to predict river water levels based on the nine-year datasets. The seasonal decompose (multiplicative) model was used for seasonal plots such as trend, residual, and seasonal based on river water level and stream flow datasets. The many input variables and feature selection is important steps to development of ML modeling to prediction of target variable for prediction modeling. In this study, we have used to best subset regression analysis was used to identify the best input variables combination for river water level prediction. The seasonal decompose modeling to analysis and to prepared the seasonal, Residual and trend plots for understand the datasets. The river water level datasets were divided into 80% training and 20% testing, which were used to prediction of river water level modeling. During the training phase, ML modeling used river water level data from 01–06-2014 to 20–07-2020 and testing modeling was used to this datasets, from 01–08-2020 to 31–12-2022, these datasets was developed the prediction modeling of monthly river water level. Finally, this research has been developed eight powerful models using different input combinations such as three lags and CEEMDAN (IMF 1 to 5) methods in two scenarios. The details information related to input and output variables adopted are presented in Table 2. Table 3 represented the ML and decomposition modeling structures during the first and second combination scenarios, these hyper-parameters of modeling were help to improve the model accuracy and correct prediction values. The detailed adopted methodology is shown in Fig. 2. The details information about the input variables of second combination is presented in Fig. 3. The entire prediction models have been used developed and processed the datasets on the python programming and packages.

Table 2 The Input–output structures adopted for model development.
Full size table
Table 3 Details of ML and decomposition models structures for predicting the river water level.
Full size table
Fig. 2
figure 2

Adopted methodology framework of river water level monthly forecasting of the river water level values.

Full size image
Fig. 3
figure 3

The workflow of CEEMDAN-ML model.

Full size image

SVM-linear

The SVM algorithm has been developed by51 with further refined by52, relies on operational danger minimization and arithmetical learning principles53. Its primary objective is to decrease both model difficulty and mistakes. SVM achieves this by projecting the data into a greater-dimensional feature space to identify a best separation hyperplane from training data54. In practice, SVM effectively captures the nonlinear relationships among variables by creating linear boundaries using a kernel function55. This algorithm constructs straightforward classifications by establishing hyperplanes. The kernel function mathematically represents this relationship55. By projecting a separation hyperplane from the origin between points belonging to two classes within a specified error threshold, SVM delineates the relationship between the xi parameters in the original space with n coordinates. Considering input and output variables as x and y, respectively, where xi belongs to the set Rn, yi belongs to the set {1, −1}, and the value of i ranges from 1 to n, the optimal separation hyperplane is expressed by the following equation53:

$$g(x)=\text{sgn}\left(\sum_{i=1}^{n} {y}_{i}{\alpha }_{i}K\left({x}_{i},{x}_{j}\right)+b\right)$$
(1)

Here n is the number of contribution variables, αi is the Lagrange multipliers, K(xi, xj) is the kernel function, and b is the offset of hyperplane from source.

It has several options: linear, polynomial, RBF, or sigmoidal. The linear kernel is used to linearly decompose the input data of the SVM and express it on a hyperplane. The efficacy of the linear kernel support vector machine is notable, particularly in belongings where the dataset exhibits linear separate. However, in belongings where dataset is not linearly separable and possesses a complex structure, it is recommended to employ the RBF kernel.

SVM-RBF

In contrast to linear, and RBF kernel facilitates the modeling of nonlinear relationships among class labels and features. The distinctive shape of RBF kernel’s demonstrated by56, underscores its effectiveness in capturing such nonlinearities. Additionally, the difficulty of model choice is influenced by the number of tuning parameters, with RBF kernel requiring less factors compared to polynomial and sigmoid kernels57. Moreover, RBF kernels demonstrate robust show under common smoothness assumptions58. Due to its easy plan, strong generalization capabilities, high tolerance to involvement noise, and efficient online learning capability, the RBF kernel is preferred. The RBF kernel function is defined by Eq. 355,59:

$$K\left({x}_{i},{x}_{j}\right)=\text{exp}{\left(-\gamma {x}_{i}-{x}_{j}\right)}^{2}$$
(2)

Here, the parameter γ governs the level of nonlinearity in the SVM model.

Random forest (RF)

The RF algorithm60 proposed is based on combining many decision trees. RF algorithm helps solve many engineering problems by performing prediction and inference operations. RFs have significant superiority in modeling complex structures with small samples and high-dimensional feature spaces61. The mathematical expression of RF is presented in Eq. 162.

$$T_{j} = \sum\limits_{i = 1}^{n} {g_{j} \left( {X_{ij} } \right)s\left( {Y_{i} } \right)}$$
(3)

The RF model operates under the assumption that s(Yi) ∈ R, where Yi ∈ {1, 2, 3, …, k}, signifies the ordinal response of observation i with covariates Xij. Here, j = {1, 2, 3, …, p} represents the index for the predictor variables. A test statistic is utilized to evaluate the association among the ordinal answer and the forecast variable Xj. The function gj: Xj → Rpj denotes a deterministic conversion of the forecast variable Xj, converting it from a one-dimensional space vector to a pj-dimensional vector space63.

Random subspace

In RS, sampling and combining methods similar to bagging are used to create a prediction model. In contrast to bagging, the RS algorithm employs bootstrapping from the feature space rather than from the training samples64. RS stands out in effectively solving both regression and classification problems. This algorithm comprises several elements, primarily including the training dataset x, quantity of subspaces L, the classifier or regressor w, and number of features ds65. In the RS model, a random number of subsets with ds features are generated and stored in the L subspace. During the second phase, a distinct regressor is created for each subset by training each base regressor. The combination of these elements results in the formation of an ensemble regressor E66.

Complete ensemble empirical mode decomposition adaptive noise (CEEMDAN) technique

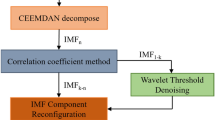
CEEMDAN is a spatiotemporal study method; the concept is an extra finite amplitude white sound in couples is regularly circulated in whole time–frequency space of novel signal, and space is combined with diverse scale mechanisms in various frequencies. The technique decreases residue mistake in rebuilding procedure by totaling white combined noise, which adds positive and negative signals and finds mechanisms with less noise and extra physical significance67,68. EMD and EEMD can decompose data into high-frequency signals, IMFs, over many iterations. However, it always causes a certain amount of white noise. To resolve this issue69, developed a novel data decomposition technique called CEEMDAN. Steps to implement CEEMDAN:

  1. (1)

    White noise, wi(t), with a noise standard deviation of ε, is included to the original signal, Xi(t), as explaned by the Eq. 4:

    $${X}^{i}(t)=X(t)+{\varepsilon }_{0}{\omega }^{i}(t),i=\text{1,2},\dots ,k$$
    (4)

    where k shows a real number.

  2. (2)

    The collection of signals undergoes an EMD decomposition, after which the components from every decomposition are averaged.

    $$\overline{{IMF_{1} }} \left( t \right) = K^{ - 1} \sum\limits_{i = 1}^{k} {IMF_{1}^{i} \left( t \right)}$$
    (5)
  3. (3)

    The residuals of the first stage are calculated:where EMDk(·) represents the k-th IMF mode decomposition by the EMD algorithm.

    $${r}_{1}(t)=X(t)-\overline{IM{F}_{1}}(t)$$
    (6)
  4. (4)

    The signal r1(t) + ε1 EMD1wi(n) is EMD-decomposition, and the second IMF mode is obtained as follows:where EMDk(·) represents the k-th IMF mode decomposition by the EMD algorithm.

    $$\overline{IM{F}_{2}}(t)={K}^{-1}\sum_{i=1}^{K} EM{D}_{1}\left({r}_{1}(t)+{\varepsilon }_{1}EM{D}_{1}\left({\omega }^{i}(t)\right)\right)$$
    (7)

    where EMDk(·) represents the k-th IMF mode decomposition by the EMD algorithm.

  5. (5)

    In the subsequent stages, the k + 1-th component and the k-th residual are measured according to following formula:where R(t) represents the final residual.

    $$\begin{array}{c}\overline{IM{F}_{k+1}}(t)={K}^{-1}\sum_{i=1}^{K} EM{D}_{1}\left({r}_{k}(t)+{\varepsilon }_{k}EM{D}_{k}\left({\omega }^{i}(t)\right)\right)\\ {r}_{k}(t)={r}_{k-1}(t)-\overline{IM{F}_{k}}(t)\end{array}$$
    (8)
  6. (6)

    Repeat Eqs. 7 and 8 until the residual component (rk) no longer sufficient the decomposition rules, and the decomposition process stops. Ultimately, the novel signal R can be represented by Eq. 9.

    $$X(t)=\sum_{i=1}^{K} \overline{IM{F}_{i}}(t)+R(t)$$
    (9)

    where R(t) represents the final residual.

It is utilized for data decomposition, denoising, and noise decomposition. The application of CEEMDAN to every model is crucial (Yan et al. 2023). Figure 3 shown the workflow of CEEMDAN.

Model comparison statistical analysis

In this research, assessing the model’s performance involved using three statistical performance metrics such as MSE, RMSE, and R2.The model’s prediction accuracy was evaluated from multiple perspectives, thus assessing its effectiveness. The evaluation of forecasting performance is conducted using various metrics. The calculation of these metrics required the application of the equations provided in the list below.

$${R}^{2}=\frac{\sum_{i=1}^{n} {\left({WL}_{i}-{WL}_{mean}\right)}^{2}-\sum_{i=1}^{n} {\left({WL}_{i}-{\text{PR}}_{i}\right)}^{2}}{\sum_{i=1}^{n} {\left({WL}_{i}-{WL}_{mean}\right)}^{2}}$$
$$MSE=\frac{1}{N}\sum_{i=1}^{N}{\left({WL}_{i}-{\text{PR}}_{i}\right)}^{2}$$
$$RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left({WL}_{i}-{\text{PR}}_{i}\right)}^{2}}$$

Here, PR is the forecast value and WL is the observed value of water levels, \(WL\)i and PRi are the observed and predicted ith value. When error values are near 0 and R2 values are close to 1, it signifies the utmost accuracy in prediction outcomes.

Results and discussion

In the initial phase of adopted methodology, the original river water level data was subjected to decomposition using CEEMDAN. Figure 1 illustrates the results of this decomposition. As depicted in Fig. 1, the CEEMDAN process sorted the frequency of each IMF from the uppermost frequency to the lowest. The first and second IMF (IMF 1 and IMF 2) components exhibited a highly irregular pattern, while IMF 3 and IMF 4 displayed periodic and more consistent patterns. The final IMF component (IMF 5) depicted the overall data trend. The five IMFs have been considered for predicting Monthly River water levels based on the decomposition modeling approach.

ACF and PCF analysis for river water level

The ACF and PACF graphs are presented in Fig. 4. Seasonal patterns are absent in the data for most of the years. The ACF showed a significant spike at lag 1, with no significant residual correlation after lag 1. However, the PACF is showed important spikes at lags 1, 14, and 16. Hence, the current research on the prediction of river water level considered the three lags as input variables in the first combination of ML modeling and second combination modeling based on IMFs input variables.

Fig. 4
figure 4

ACF and PACF lags of river water level.

Full size image

Trend analysis based on the seasonal decompose multiplicative model

In this section shown the outcomes of stream water flow and water level trend analysis based on the seasonal decompose multiplicative model method. Figure 5 is represented the valuable insights regarding the seasonal trend variability of the stream flow and water level during different years. The stream flow and water levels data series show high fluctuation by spiked lines, mostly during monsoon periods. The trend analysis can help understand the basin area input and output variables datasets before applied in the ML modeling.

Fig. 5
figure 5

Seasonal and trends of stream flow and water level.

Full size image

ML & decomposition ensemble model development and performance evaluation

The ML and decomposition models to development of river water level prediction was created by the univariate modeling approach, where individual accurate values of river water level were utilized as input variables for the ML model improvement. In this research, we have adopted two types of variables added into ML modeling. Hence, ACF and PACF were selected the three legs1-3 based times series datasets in the first combination modeling. The second combination of modeling five IMFs and original stream flow was used as input variables in the decomposition modeling based on the CEEMDAN approach. Both input combinations models performance metrics have been compared, which model can better predict river water level in the study area. This station performed inversely year to year climate change due to river features, drought, air pollution, and weather phenomena.

In the present study was to recommend various innovative ML and decomposition models and accepted their accuracy with various popular ML and advanced models in the literature for river water level and stream flow prediction. The performance of the first and second combination models performance was measured based on the statistical equations using various well-known like R2, RMSE, and MSE. For the selected the one station for prediction of river water level based on the two I/O (input–output) combinations variables, which is divided into training and testing phases given the results are shown in Tables 2 and 3, respectively. For the second I/O combination of the stations, based on the accomplished ML modeling outcomes for the training and testing phases, the second input–output combinations indicated higher predicting accuracy than the first input–output combination modeling (Table 4). Between the four ML models suggested (SVM-Linear, SVM-RBF, RF, and Random Subspace) with two input–output combinations, the SVM-Linear model, CEEMDAN-SVM (LINEAR) and CEEMDAN-RF observed excellent prediction performance results other than models in first and second input–output combinations in Table 4, respectively.

Table 4 Results of predication of water level for Sg Muar at Buloh Kasap Johor station.
Full size table

SVM-Linear model is achieved a superior ML model compared with other models in first combination, that results are represent based on the R2 = 0.93, RMSE = 0.17, and MSE = 0.03 in the testing phase. Whereas the RF model is showed better results compared with other models in the training phase, that model accuracy is R2 = 0.97, RMSE = 0.11, and MSE = 015 for the first input and output combination. During the testing phase, the suggested models have been showed the same results, with slightly better performance accurateness from the RF model with R2 = 0.97, RMSE = 0.11, and MSE = 0.15 for the similar in the first input–output combination modeling. Line and scatter graphs are shown in Fig. 6 (a to d) and Fig. 7 (a to d), so that this station can look closer at the performance of the created ML models. Line and scatter graphs provide a more perceptive visualization of the predicted data matched against the experiential river water level datasets.

Fig. 6
figure 6

Comparison Line plots of predicted and observed river water level for test and train period for (a) SVM-Linear, (b) SVM-RBF, (c) RF, (d) Random Subspace.

Full size image
Fig. 7
figure 7

Scatter plots of forecast and observed river water level for test and train period for (a) SVM-Linear, (b) SVM-RBF, (c) RF, (d) Random subspace.

Full size image

The prediction results of CEEMDAN-based models and their comparison with standalone models are displayed in Table 4, it is directly indicated the CEEMDAN method is improved the model accuracy. In the second combination, we have found the CEEMDAN–RF model is perform better compared with other seven models, that performance metrics such as R2 = 0.98, RMSE = 0.08 and MSE = 0.01, this values directly indicated the higher accuracy given as compared with the SVM-Linear (R2 = 0.84, RMSE = 0.27, MSE = 0.07), SVM-RBF (R2 = 0.87, RMSE = 0.24, MSE = 0.06), RF (R2 = 0.97, RMSE = 0.11, MSE = 0.015), Random Subspace (R2 = 0.86, RMSE = 0.25, MSE = 0.06), CEEMDAN-SVM-Linear ((R2 = 0.87, RMSE = 0.26, MSE = 0.07), CEEMDAN-SVM-RBF (R2 = 0.91, RMSE = 0.23, MSE = 0.01), and CEEMDAN-RS (R2 = 0.88, RMSE = 0.24, MSE = 0.06) during training phase. The CEEMDAN-RF model outperforms all the models during the testing phase are given higher accuracy values based on the R2 (0.94) and the lowest values of RMSE (0.13) and MSE (0.02), hence that models shows the better results compared with other models in the testing phase. Amongst all the developed models, the RS models performed lower during training and testing phases, indicating its inadequacy in understanding the pattern and behavior of the data and thus unsuitable for predicting the river water level. The decomposition of the river water levels has been improved the performance of the models. CEEMDAN with the combined the RF models significantly improved and that model performance metrics also shown the higher results based on the R2, RMSE, and MSE values in the training and testing phases, respectively, compared to the performance of the standalone RF model performance in predicting river water level. Therefore, other hybrid models based on CEEMDAN are more improved model performance in the training and testing compared with standalone model performance. Amongst all the standalone models, RF model is outperformed for prediction of river water level. The line diagrams and scattered plots of the standalone and CEEMDAN hybrid models are presented in Fig. 8 (a to d) and Fig. 9 (a to d). Actual and predicted river water level lines of the CEEMDAN-RF model performance are shown in Fig. 8c and 9c. The Fig. 9 (a to d) shown predicted model of river water level data are represented on the best-fit line, this plots are shown the four CEEMDAN models. This further confirms the superiority of the CEEMDAN-RF models in predicting river water levels. The hybrid models based on CEEMDAN method are visualized in Fig. 9 (a to d). Hence, the first and second ML and hybrid models were studied by using violin plots, which better understand the prediction model performance, which model can give better performance as per violin plots. Figure 10a and Fig 10b are shown the observed and predicted values for eight ML models, this plots can more helpful for understanding the model performance during first and second combination of input and output variables. Finally, result of violin plots are shown that the SVM-Linear and CEEMDAN-RF model simulated predictions values are most accurate during training and testing phases.

Fig. 8
figure 8

Comparison line plots of predicted and observed river water level for test and train period for (a) CEEMDAN-SVM-Linear, (b) CEEMDAN-SVM-RBF, (c) CEEMDAN-RF, (d) CEEMDAN-Random subspace.

Full size image
Fig. 9
figure 9

Scatter plots of forecast and observed river water level for test and train period for (a) CEEMDAN-SVM-Linear, (b) CEEMDAN-SVM-RBF, (c) CEEMDAN-RF, (d) CEEMDAN-Random subspace.

Full size image
Fig. 10
figure 10

Violin plots displaying the performance of ML models for (a) First I/O combination, and (b) First I/O combination.

Full size image

The best model selected based on the various statistics performance metrics; this process is standard for selection of best models. Based on the model performance metrics of CEEMDAN-RF significantly outperformed seven other models, It is reach the higher accuracy of R2 = 0.98; R2 = 0.94 and other performance metric also shown the lowest RMSE and MSE values during training and testing phases, respectively. This signs are shown higher predictive accurateness and generalization ability. In contrast, other standalone ML models such as SVM and Random Subspace have been indicated comparatively lower R2 and greater error metrics, mainly during the testing phase. The advantage of CEEMDAN-RF model is combined the both the models, it’s a hybrid structure-CEEMDAN is excellently decomposes the difficult and non-stationary stream flow time series into IMFs, every capturing different temporal trends. This decomposition mechanisms, when added into a RF model then these model is improve learning by decreasing noise and refining signal clarity.

We have compared with the another CEEMDAN-based models, CEEMDAN-RF is found the outperformed due to the ensemble strength of RF model, which efficiently handles non-linearity and avoids over-fitting issue using averaging across decision trees. The real-world implications for river basin management and hydrological forecasting are so important in the heavy rainy area. In this paper, higher accuracy hybrid model of CEEMDAN-RF will gives more reliable model and method for flood forecasting, river water level prediction, water resources development and reservoir management and planning. Its robustness ensures accurate policymaking support for governments and experts to critical situations of climate variability and extreme events. Hence, adopted the hybrid models can lead to more adaptive and data-driven sustainable water development and management policies.

Fig. 11 a to Fig. 11 d is presented the river water level prediction models such as SVM-Linear, SVM-RBF, RF, Random Subspace and hybrid models like CEEMDAN-SVM-Linear, CEEMDAN-SVM-RBF, CEEMDAN-RF, and CEEMDAN-Random Subspace performances are estimated by Taylor diagram. It is shown the model performance during training and testing, which model better performance based on the R2, RMSE and standard deviation values. In the testing phase of Taylor diagrams shows the SVM-Linear and CEEMDAN-RF best models in first and second input combinations, respectively. The different input combinations of ML models and CEEMDAN models performance are shown in Fig. 12; these plots better to understand the models accuracy, which model suitable for predication. Figure 13 showing the heat maps of ML models understanding the training and testing models accuracy in both combination of models.

Fig. 11
figure 11

visualization of Taylors diagram of Models: (a) Training data of first combination, (b) Testing data of first combination, (c) Training data of first combination, (d) Testing data of second combination.

Full size image
Fig. 12
figure 12

Visualization of radar plots: (a) Training Data of first combination, (b) Testing data of first combination, (c) Training data of first combination, (d) Testing data of second combination.

Full size image
Fig. 13
figure 13

Heat map showing of ML models: (a) Training, (b) Testing.

Full size image

Future work and limitations of CEEMDAN and ML models for river water level prediction

The river water level is most affected by outside features i.e. stream flow, rainfall and evaporation. The long historical datasets can important for the prediction of river water level ML modeling70. The CEEMDAN was applied to decomposition the observed data into various IMF components70. These methodology adopted addresses the limitations of traditional EEMD models and mitigates interference problems. While CEEMDAN-established hybrid models have been presented robust predictive abilities in the accurate prediction of river water levels, and flood risk is serious for water resource management, early warning systems, and sustainable surface water resources development71. The CEEMDAN model, while active in decomposing complex and non-stationary time series into IMFs, is computationally severe and may low-variance IMFs that contribute minimal prediction value. Without careful selection and preprocessing of these IMFs, they can familiarize noise and rise model difficulty. Standalone ML models such as SVM-Linear, SVM-RBF, RF, and RS are also constrained by good quality datasets and well arrangement. These models accuracy is affected due to missing datasets, errors, and outlier datasets, hence before apply in the ML models first priority seriously check the availability of datasets, clean, and high-resolution datasets, which is frequently not feasible in river monitoring systems plagued by missing values, well stations or instruments faults, and irregular collection datasets. Additionally, their completely data-driven nature limits physical interpretability and flexibility entire varying river basins area. These models many problems face during the extreme events for e.g. heavy rainfall or man-made influences such as dam operations and built-up runoff flow, which are not proper captured in historical datasets. Therefore, while hybrid methods like CEEMDAN-SVM and CEEMDAN-RF better improve better performance for river water level prediction; their practical established to need long time series datasets, deep learning models, rigorous datasets preprocessing, advanced level model tuning, and combination with climate and hydrological field knowledge for operational reliability. In future investigation, we aim to incorporate large datasets related with river basin system, and maximum years river water level datasets or include into deep learning models to improve both the accurateness and interpretability of river water level forecasting for operational work, this study area every time facing issues of flood risk and heavy rainfall and suddenly increase river water level problems.

Conclusion

The prediction of river water level is essential for real time understanding the flood, losses of crops and damaged the infrastructures due to raising the river water level. It gives a proper scientific basis for enhancing the planning, ecosystem safety polices and development for river basin management, to safeguarding their systematics operational and rational used of water resources. In this study used the CHEEMDAN technique to decompose datasets into numerous IMFs components at different instantaneous frequencies with lags method utilization. CEEMDAN models and standalone models were combined to develop the hybrid models to prediction of river water level. A complete decomposition modeling was used to 5-IMFs with different frequencies and residues for actual river water level data. The CEEMDAN has been successfully combined in the SVM-Linear, SVM-RBF, RF and RS to predict river water level. The aggregate of total predicted findings from IMFs and residue is a noteworthy success for the precise river water level prediction. In this research, SVM-Linear model is best model other than model in first combination, while the CEEMDAN-RF is outperformed with other models in second combination of model. Hence, both the models performance measured based on the higher value of R2 and lower values of RMSE and MSE during training and testing phases. The results of CEEMDAN-RF model was superior as per R2, RMSE and MSE values as 0.98, 0.08, 0.01 during training and 0.94, 0.13, and 0.02 during testing phases, respectively, which is compared with other than seven models. The study observed that the decomposition components (IMF5 and residue) in low frequencies act better than IMF-1 and IMF-2 in high frequencies in predication accuracy. The developed methodology exhibits the capability of the CEEMDAN-RF model to predict river water levels exactly. This improved performance could be due to CEEMDAN’s ability to effectively manage data that shows non-linear patterns and lacks stationarity. The CEEMDAN algorithm helped model different frequency levels separately by dividing the data sets into various sub-bands. This enables a better understanding of complex trends and changes. Therefore, it has been found that the CEEMDAN algorithm significantly increases the prediction performance of ML models. It has been determined that this algorithm improves the river water level prediction performance of the ML model by reducing the noise in the data set by separating the data set into different IMFs and residuals. In future studies, it is recommended to evaluate the performance of models established in different regions and to investigate the accuracy of river water level predictions by hybrid deep learning models with variational mode decomposition, non-negative matrix factorization, and multi-scale principal component analysis techniques12.