Introduction

Background and motivation

The Small Satellite (SmallSat) industry, encompassing mini, micro, nano, pico, and femto satellites, has experienced significant growth in recent years and continues to expand. This expansion is driven by advancements in SmallSat subsystem technologies, including digital signal processing (DSP), integrated circuits (ICs), microelectromechanical systems (MEMS), and additive manufacturing. Moreover, the integration of cost-effective and advanced Commercial-Off-The-Shelf (COTS) technologies has led to significant reductions in mass, volume, development time, and overall costs1,2. Future NanoSat applications are expected to include satellite constellations for space-based telecommunication networks, supporting mobile communications and global internet coverage3,4,5,6, contributing to continued market growth. A major factor fuelling interest in NanoSats is the increasing prominence of CubeSats. Since the first CubeSat launch in 2003, these satellites have gained attention from governments, educational institutions, scientists, and commercial organizations7. Named after their cubic structure, CubeSats are built from standardized units (U), each weighing 1.33 kg with a volume of one liter and dimensions of 10 × 10 × 10 cm8. To accommodate higher payload demands, CubeSats can be extended by stacking multiple units. While NanoSats are generally classified within the 1–10 kg range, CubeSats are not strictly confined to this weight limit. For instance, a 27U CubeSat, one of the heaviest reported, weighs 40 kg3. CubeSat classification based on mass and volume is presented in9, while spacecraft classification based on mass and cost is provided in10.

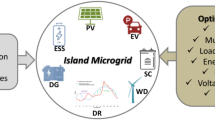
SmallSats, particularly those in the 1–10 kg range, commonly referred to as NanoSats, have garnered significant attention from various stakeholders, including academic institutions, government agencies, and private sector entities. Among these, CubeSats have witnessed rapid expansion due to their standardized design and modular scalability. A CubeSat, typically measuring 10 × 10 × 10 cm and weighing around 1.33 kg, represents a 1U configuration, which can be scaled up to larger sizes such as 2U, 3U, and more. These satellites serve a broad spectrum of applications, including Earth observation, space exploration, and technological demonstrations, primarily operating in Low Earth Orbit (LEO). NanoSats are typically equipped with essential subsystems, such as an Electrical Power System (EPS), Communication Transceiver System (COM), an Attitude Determination and Control System (ADCS), Onboard Data Handling (OBDH), and mission-specific payloads. Among these, the EPS plays a critical role in ensuring reliable power distribution across all subsystems, making it a cornerstone of successful satellite operation. Structurally, the EPS functions as a space microgrid (MG), integrating multiple distributed generators (DGs), an energy storage system (ESS), a controlled coordination mechanism, and various onboard loads11,12. A typical NanoSat DC MG architecture is depicted in Fig. 1.

Fig. 1
figure 1

A standard NanoSat DC microgrid architecture.

Full size image

While NanoSat DC MGs offer numerous advantages, their operation faces substantial challenges. These systems must function efficiently in both grid-connected and islanded modes, necessitating enhanced reliability and security in power delivery13,14,15. Furthermore, the increasing complexity of NanoSat DC MG subsystems, which often rely on the EPS, introduces stability concerns in the MG. Many of these subsystems act as constant power loads (CPLs), exhibiting incremental negative impedance (INI) properties that can destabilize the NanoSat DC MG if not properly managed. Addressing these challenges requires advanced power management strategies and robust control approaches to ensure the stability of NanoSat DC MGs16. In particular, CPLs can introduce instability in NanoSat DC MGs when inappropriate control strategies are applied. This instability often arises in configurations where two cascaded DC converters are employed, with one serving as a power source and the other as a load. CPLs exhibit nonlinear characteristics, behaving as INI loads. This behaviour manifests through an inverse relationship between output current and voltage—where an increase in output voltage results in a decrease in output current and vice versa17,18. While NanoSat DC MGs offer modularity and scalability, their dynamic operation—marked by transmission line transients, sensor nonidealities, and CPL-induced instability—necessitates novel control paradigms to ensure DC bus stabilization under varying load conditions.

Hierarchical control is widely used in NanoSat DC MGs to achieve various operational objectives. It includes three control levels: primary, secondary, and tertiary. The primary control level commonly employs the droop control method, a decentralized approach that enhances system reliability and flexibility by eliminating the need for communication links. This approach ensures system stability and facilitates effective load sharing among converters19,20.

The secondary and tertiary control approaches in MGs are generally grouped under centralized and distributed control architectures. In a centralized framework, secondary and tertiary adjustments are managed by a central controller, whereas in a distributed approach, these functions are executed across multiple controllers within the MG. However, implementing droop control involves a balance between optimal power sharing and voltage stability. Although it enhances load-sharing performance, it often causes notable DC bus voltage deviation15. To address these challenges, a secondary control strategy incorporating a compensation controller is introduced. This controller enhances the regulation of the DC bus, improves current-sharing accuracy, and ensures overall system stability. By detecting and processing voltage deviation errors, the system generates corrective control signals, which are then distributed to all DGs within the NanoSat DC MG. This mechanism effectively ensures the required DC bus voltage, reducing the negative impacts of CPLs and uncertain external inputs.

Literature review

Hierarchical control strategies for DC MGs have been extensively studied to address stability and performance challenges. Primary control, typically implemented through droop mechanisms, enables decentralized voltage regulation and current sharing but introduces steady-state deviations and sensitivity to line impedance mismatches. To mitigate these limitations, secondary control strategies are structured into centralized and distributed architectures.

In centralized secondary control, a master unit gathers system-wide data and transmits control signals to all DGs via real-time communication networks. While effective for voltage restoration, this approach risks single-point failures and modelling inaccuracies21,22,23,24,25. Distributed secondary control methods, such as voltage shifting26,27,28, slope adjustment29,30,31, and hybrid voltage/slope-compensation techniques32,33,34, enhance resilience by enabling peer-to-peer coordination. For example, studies in35,36 improve current sharing and voltage regulation by simultaneously applying voltage modulation and slope compensation. Cooperative strategies, such as the voltage/current regulator proposed in37, dynamically adjust voltage set points to maintain equilibrium. Plug-and-play (PnP) regulators38,39,40,41 further enhance adaptability and scalability, while event-triggered methods42,43,44,45,46,47 reduce communication overhead by activating control actions only during critical deviations. A degrading fault forecast for DC-Link capacitors in multistring-connected photovoltaic boost converters sensitive to cable uncertainties was presented online by the author in48. Based on hybrid numerical integration, the authors of49 presented an effective half-bridge modular multilevel converter model for electromagnetic transients program-type modelling. The authors of50 created a Bayesian optimization-based online optimization escape entrapment plan for planetary rovers. A solid-state DC circuit breaker with a three-winding coupled inductor based on a thyristor was proposed by the authors in51. A general modelling and study of the effects of unbalanced inductance on PWM methods for two-parallel interleaved power converters was reported by the authors in52. The fault-tolerant multi-parallel three-phase two-level converters with adaptive hardware reconfiguration were introduced by the authors in53. A new double-layer Helmholtz coil for wirelessly powering a capsule robot was created and refined by the authors in54. A feature-aware task offloading and scheduling strategy for vehicle edge computing environments was proposed by the author in55. A precise and ongoing reactive power control method for a three-terminal hybrid DC transmission system was proposed in56.

Recent advances focus on optimizing secondary control efficiency. The work in48 derives compensation signals from the average current of all DGs and integrates them into droop functions, while57 introduces an average voltage-sharing scheme to counteract primary control-induced deviations. Similarly,58 proposes a simplified control technique requiring only total load current and droop gain, reducing computational complexity.

Despite these advancements, the stability of DC MGs supplying CPLs remains a critical challenge. Dynamic interactions between hierarchical control layers, CPL nonlinearities (INI effects), and inherent system uncertainties complicate stability analysis. Furthermore, existing methods often incur efficiency losses due to supplementary resistive loads or oversimplified modelling assumptions. These unresolved issues underscore the need for advanced co-design strategies that integrate robust primary control with adaptive secondary mechanisms, ensuring stable operation under real-world conditions.

Research gaps and contributions

Building upon the existing literature, this work introduces a novel centralized secondary control strategy for a NanoSat DC MG. The proposed strategy aims to regulate the DC bus voltage to its reference value and maintain the power-sharing balance established by the primary control. Unlike previously reported methods, the proposed strategy relies on a single centralized controller to send compensation signals to all DGs. The dual-time-scale hierarchical control framework is designed to ensure system stability, with the primary control operating at a faster time scale than the secondary control. This centralized approach is implemented at a designated DG, with the control signal integrated into the droop control function. Remarkably, the proposed method achieves its objectives without requiring communication among the DGs, matching the performance of decentralized and distributed control architectures.

The principal contributions of this work are summarized as follows:

  1. 1.

    A novel primary control level based on nonsingular terminal sliding mode (NTSM) control is introduced to mitigate CPL effects without relying on passive loads.

  2. 2.

    A new centralized secondary control strategy for spinning flight scenarios is proposed, addressing power load variations, source dynamics, and PnP capability.

  3. 3.

    Validation of controller effectiveness through theoretical analysis, MATLAB/PSIM co-simulations, and experimental results.

Paper organization

The rest of this paper is organized as follows: “Problem formulation, objectives, and system description” outlines the problem formulation, objectives, design, and modelling of the NanoSat DC MG. “Proposed control strategy” details the design of the primary and secondary controllers. “Results and discussion” presents simulation results. “Experimental validation” provides experimental results. “Conclusion” concludes the paper and summarizes key findings.

Problem formulation, objectives, and system description

The EPS of a satellite comprises various components, including PV cells, switching converters, battery cells, voltage regulators, and distribution units. Its primary function is to supply sufficient power to the satellite loads, such as the payload and subsystems. To validate the effectiveness and operational performance of the proposed satellite design, a NanoSat DC MG is utilized as a case study.

Problem statement

Voltage imbalance between sources connected in parallel constitutes the primary cause of current load-sharing error and the emergence of circulating currents. To quantify these circulating currents, consider a simplified setup with three parallel sources, each with its cable resistance, supplying the same subsystems of the NanoSat DC MG, as shown in Fig. 2.

Fig. 2
figure 2

Circulating current phenomenon.

Full size image

Using the charge-and-energy conservation principles, the following equations are derived:

$$V_{o1} - Z_{1} I_{o1} - Z_{Load} I_{Load} = 0$$
(1)
$$V_{o2} - Z_{2} I_{o2} - Z_{Load} I_{Load} = 0$$
(2)
$$V_{o3} - Z_{3} I_{o3} - Z_{Load} I_{Load} = 0$$
(3)
$$I_{Load} = I_{o1} + I_{o2} + I_{o3}$$
(4)

and

$$P_{cpl} = V_{Bus} .I_{Load}$$
(5)

By replacing ILoad with its expressions given in Eqs. (1)–(3), we derive the branch currents Io1, Io2, and Io3 (each containing a source) and the inter-source circulating current Ic123 between these sources.

$$\left[ {\begin{array}{*{20}c} {I_{o1} } \\ {I_{o2} } \\ {I_{o3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Z_{1} + Z_{Load} } & {Z_{Load} } & {Z_{Load} } \\ {Z_{Load} } & {Z_{2} + Z_{Load} } & {Z_{Load} } \\ {Z_{Load} } & {Z_{Load} } & {Z_{3} + Z_{Load} } \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {V_{o1} } \\ {V_{o2} } \\ {V_{o3} } \\ \end{array} } \right]$$
(6)

and

$$I_{c123} = \frac{{\left( {V_{o1} - V_{o2} } \right)}}{{Z_{1} + Z_{2} }} + \frac{{\left( {V_{o2} - V_{o3} } \right)}}{{Z_{2} + Z_{3} }} + \frac{{\left( {V_{o3} - V_{o1} } \right)}}{{Z_{3} + Z_{1} }}$$
(7)

From Eq. (7), a mismatch in source voltages or differences in cable impedances causes circulating currents, leading to a voltage drop at the DC bus. Furthermore, assuming the source voltages Vo1, Vo2, and Vo3 are identical, differences in cable resistance values will lead to load-sharing errors. In other words, the current drawn from each source varies depending on the cable impedance.

Figure 2 shows that a source with lower cable impedance delivers higher current, with stress escalating as impedance disparities increase in the NanoSat DC MG. In a distributed power system—where each source corresponds to a DG and its power converter—load-sharing errors cause excessive current flow. This results in overheating, premature ageing, and potential converter failure. If one converter reaches its operational limit and fails, the remaining converters must compensate, increasing their load and risking cascading failures.

In addition, the interaction dynamics among subsystem loads of the NanoSat DC MG, such as the OBC, EPS, ADCS, and camera, can result in significant oscillations that compromise system stability. In CCM, when the frequency is below the NanoSat DC MG voltage loop cutoff frequency, its input impedance acts as a negative resistance. Above the cutoff frequency, it behaves inductively when supplying fixed-voltage loads such as the OBC, EPS, ADCS, and camera17,18.

For the subsystem loads of the NanoSat DC MG, the power absorbed within the controller bandwidth remains constant; these loads behave as CPLs, and their relationship is described by:

$$P_{cpl} = V_{Bus} .I_{Load} = c^{t}$$
(8)

where:

Pcpl represents the CPL demand, VBus represents the DC bus voltage, and ILoad represents the load current.

The incremental impedance of the CPL, defined as the inverse of the derivative of its load current with respect to DC bus voltage, is expressed as:

$$\frac{{dV_{Bus} }}{{dI_{Load} }} = - \frac{{V_{Bus} }}{{I_{Load} }} = - \frac{{P_{cpl} }}{{I_{Load}^{2} }} = - \frac{{V_{Bus}^{2} }}{{P_{cpl} }}$$
(9)

Thus

$$\frac{{dV_{Bus} }}{{dI_{Load} }} = - R_{cpl}$$
(10)

Since the CPL exhibits negative incremental impedance, it introduces a − π phase shift in the Bode diagram. Instability arises when cascaded with a NanoSat DC MG if the output impedance magnitude intersects the CPL’s input impedance magnitude and the system’s cutoff frequency is lower than the CPL’s cutoff frequency. Consequently, while CPL effects can severely destabilize the system, effective load control strategies play a critical role in mitigating these instabilities.

Figure 3 shows a conventional primary control architecture using cascaded PI controllers for a NanoSat DC MG supplying CPLs and resistive loads. Figure 4 illustrates the instability that arises when supplying only CPLs with this control methodology. The design specifications for the buck converter example include:

$$V_{in\_Ex} = 28V,V_{ref\_Ex} = 14V,L_{Ex} = 2.7mH,C_{Ex} = 470\mu F,D_{Ex} = 0.5,P_{cpl\_Ex} = 10W,R_{L} = 5\Omega$$
Fig. 3
figure 3

Cascaded PI control of a NanoSat DC MG supplying: (1) CPL and (2) CPL + R.

Full size image
Fig. 4
figure 4

Impact of Increased CPL demand on NanoSat DC MG performance with cascaded PI control.

Full size image

In addition, the PI parameters used for outer and inner loops to control output current and voltage are given as: \(k_{p\_v} = 0.08728018,k_{i\_v} = 5.491,k_{p\_I} = 27.5692,k_{i\_I} = 35540\).

Moreover, external fluctuations in both input voltage and CPL can significantly affect overshoot and settling time, as shown in Figs. 5 and 6.

Fig. 5
figure 5

Bode diagram of open-loop NanoSat DC MG with fluctuating CPL Pcpl = 10:10:200.

Full size image
Fig. 6
figure 6

Bode diagram analysis for an open-loop NanoSat DC MG supplying a CPL with input voltage variations.

Full size image

A passive load, typically a resistive load or stabilizer, is connected to the DC bus to mitigate the negative effects of the INI characteristic and improve system damping58,59. However, this approach introduces power loss, reducing overall system efficiency. Simulation results highlighting the impact of the INI characteristic on current and voltage, as well as the role of supplementary passive loads in reducing oscillations, are provided in60.

System description and modelling

Figure 7 depicts a detailed electrical schematic of the EPS architecture in a NanoSat DC MG. A step-up DC/DC converter is integrated with each PV cell, accompanied by a local controller. Solar panels are positioned on all six sides of the CubeSat and divided into three sections: X, Y, and Z. Each CubeSat face contains two PV cells connected in a series–parallel configuration to the input of the power converters. The converter output is connected to a DC bus, which is supplied by two GOMspace battery cells connected in series to achieve the required voltage. The DC bus links the communication receiver (COM RX) and transmitter (COM TX) modules, with the OBC, EPS), and ADCS acting as CPLs. Vref_(1,2,3) are set to 5 V or 3.3 V, aligned with the DC bus voltage requirements for NanoSat systems. Controllers are designed to regulate voltage, ensure proper power sharing, and adjust the output voltage according to load demands.

Fig. 7
figure 7

EPS architecture of the NanoSat DC MG CubeSat.

Full size image

DC/DC converters adjust voltage levels using components such as inductors, capacitors, diodes, and controlled switches. By modifying circuit connections and component values, they increase or decrease voltage and alter other electrical characteristics.

Figure 8 shows a simplified diagram of the NanoSat DC MG system, where a buck converter delivers power from the source to the CPLs. The system includes a PV supply source Vin, a PWM-driven switch device VT, a diode D, a filter inductor Li, a capacitor Ci, and a Pcpl. Dashed-line 1 and dashed-line 2 represent the ON and OFF states of the switch, respectively.

Fig. 8
figure 8

Typical NanoSat DC MG and its equivalent circuit.

Full size image

The averaged model of the buck converter operating in CCM, shown in Fig. 8, is expressed as:

$$\left\{ \begin{gathered} \frac{{di_{Li} }}{dt} = \frac{1}{{L_{i} }}\left( {V_{in} - V_{oi} } \right) \hfill \\ \frac{{dV_{oi} }}{dt} = \frac{1}{{C_{i} }}\left( {i_{Li} - \frac{{P_{cpl} }}{{V_{oi} }}} \right) \hfill \\ \end{gathered} \right.\quad For \, 0 \, < \, t \, < \, dT$$
(11)
$$\left\{ \begin{gathered} \frac{{di_{Li} }}{dt} = \frac{1}{{L_{i} }}\left( { - V_{oi} } \right) \hfill \\ \frac{{dV_{oi} }}{dt} = \frac{1}{{C_{i} }}\left( {i_{Li} - \frac{{P_{cpl} }}{{V_{oi} }}} \right) \hfill \\ \end{gathered} \right.\quad For \, dT \, < \, t \, < \, T$$
(12)

Using state-space averaging combined with Eqs. (11) and (12), the dynamic model is derived as follows:

$$\left\{ \begin{gathered} L_{i} \frac{{di_{Li} }}{dt} = V_{in} d_{i} - V_{oi} \hfill \\ C_{i} \frac{{dV_{oi} }}{dt} = i_{Li} - \frac{{P_{cpl} }}{{V_{oi} }} \hfill \\ \end{gathered} \right.$$
(13)

The objective is to regulate the output voltage Voi and maintain it at the reference value. The system exhibits nonlinear behavior, which is dependent on Voi.

To derive the state equations for NTSM control, the nonlinear system in Eq. (13) is linearized and expressed in controllable canonical form. The output voltage \(\dot{V}_{oi}\) and its time derivative \(\dot{V}_{oi}\) are selected as the state variables, as follows:

$$\left\{ \begin{gathered} x_{1} = V_{oi} \hfill \\ x_{2} = \frac{{dV_{oi} }}{dt} \hfill \\ \end{gathered} \right.$$
(14)

Substituting the state variables from Eq. (14) into Eq. (13) results in the updated state-space model, as shown below:

$$\left\{ \begin{gathered} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = \frac{1}{{C_{i} }}\left( {\frac{{V_{in} }}{{L_{i} }}d_{i} - \frac{{x_{1} }}{{L_{i} }} - \frac{{P_{cpl} x_{2} }}{{x_{1}^{2} }}} \right) \hfill \\ \end{gathered} \right.$$
(15)

Proposed control strategy

As shown in Fig. 8, DC/DC converters in NanoSat DC MGs act as controllable interfaces between loads and power sources. Primary control is implemented via inner loops to regulate current and voltage, along with droop control to enable power sharing. This section presents the local control strategies for DC/DC converters, introduces the centralized secondary control system, and details the design of CPLs.

Primary control

Figure 9 illustrates the local control design of a NanoSat DC MG connected to CPLs, linked through LC filters and line impedances.

Fig. 9
figure 9

Proposed control structure.

Full size image

The control scheme consists of two main components:

  • Virtual impedance control units—These units manage power sharing and stability among DGs.

  • Inner voltage controller based on NTSM control—This regulates the DC/DC converter’s output voltage to track its reference value.

NTSM-based single-loop inner controller

The proposed NTSM control enhances voltage regulation in the NanoSat DC MG by improving transient response, tracking accuracy, and efficiency while reducing steady-state error and energy consumption60,61. Figure 9 illustrates the NTSM control structure. To mitigate instability induced by CPLs, a Lyapunov-based NTSM control ensures system stability. The NTSM surface is defined as follows:

$$s = e + \frac{1}{\beta }\dot{e}^{\frac{p}{q}}$$
(16)

where:

\(\beta\) is a constant in this equation and p and q are odd integers greater than zero that satisfy: \(p > q\).

Let the tracking error \(e\left( t \right)\) and its derivative \(\dot{e}\left( t \right)\) be defined as follows:

$$e = x_{1} - V_{ref\_i}$$
(17)
$$\dot{e} = \dot{x}_{1} - \dot{V}_{ref\_i} = x_{2} - \dot{V}_{ref\_i}$$
(18)

The time derivative of Eq. (16) along the trajectories defined by Eq. (15) is given by:

$$\dot{s} = \dot{e} + \frac{1}{\beta }\frac{q}{p}\dot{e}^{{\frac{p}{q} - 1}} \ddot{e}$$
(19)

The first- and second-time derivatives of e(t) are defined as follows:

$$\dot{e} = \dot{x}_{1} - \dot{V}_{ref\_i}$$
(20)
$$\ddot{e} = \frac{{V_{in} }}{{C_{i} L_{i} }}d_{i} - \frac{{x_{1} }}{{C_{i} L_{i} }} - \frac{{P_{cpl} x_{2} }}{{C_{i} x_{1}^{2} }} - \ddot{V}_{ref\_i}$$
(21)

Substituting Eqs. (20) and (21) into Eq. (19), the time derivative of Eq. (16) is derived as:

$$\dot{s} = \left( {\dot{x}_{1} - \dot{V}_{ref\_i} } \right) + \frac{p}{\beta q}\left( {\dot{x}_{1} - \dot{V}_{ref\_i} } \right)^{{\frac{p}{q} - 1}} \left( {\frac{{V_{in} }}{{C_{i} L_{i} }}d_{i} - \frac{{x_{1} }}{{C_{i} L_{i} }} - \frac{{P_{cpl} x_{2} }}{{C_{i} x_{1}^{2} }} - \ddot{V}_{ref\_i} } \right)$$
(22)

Consider the candidate Lyapunov function V defined as follows:

$$V = \frac{1}{2}s^{2}$$
(23)

The time derivative of Eq. (23) is expressed as follows:

$$\dot{V} = s\dot{s} = s\left[ {\left( {\dot{x}_{1} - \dot{V}_{ref\_i} } \right) + \frac{p}{\beta q}\left( {\dot{x}_{1} - \dot{V}_{ref\_i} } \right)^{{\frac{p}{q} - 1}} \left( {\frac{{V_{in} }}{{C_{i} L_{i} }}d - \frac{{x_{1} }}{{C_{i} L_{i} }} - \frac{{P_{cpl} x_{2} }}{{C_{i} x_{1}^{2} }} - \ddot{V}_{ref\_i} } \right)} \right]$$
(24)

The control law u(t), expressed as follows, comprises two components: the equivalent control ueq(t), ensuring s = 0, and the discontinuous control usw(t):

$$u = u_{eq} + u_{sw}$$
(25)

The NTSM control law u(t) is derived from the SMC switching control law as follows:

$$u_{sw} = - k_{f} sat\left( {s\left( {x_{1} } \right)} \right) = \left\{ \begin{gathered} \dot{s} > 0\quad if\quad s < 0 \hfill \\ \dot{s} < 0\quad if\quad s > 0 \hfill \\ \end{gathered} \right.$$
(26)

where:

kf is the NTSM control gain satisfying kf > 0.

In a DC/DC converter, the control variable is the duty cycle (i.e., ui = di). Therefore, the control input d is derived from Eqs. (24) and (26) as follows:

$$d_{i} = u_{i} = - \frac{{L_{i} C_{i} }}{{V_{in} }}\left( { - \frac{{x_{1} }}{{C_{i} L_{i} }} - \frac{{P_{cpl} x_{2} }}{{C_{i} x_{1}^{2} }} - \ddot{V}_{ref\_i} + \beta \frac{p}{q}\left( {x_{2} - \dot{V}_{ref\_i} } \right)^{{2 - \frac{p}{q}}} - \left( { - k_{f} sat\left( {s(x_{1} } \right)} \right)} \right)$$
(27)

Substituting Eq. (27) into Eq. (24) yields the following result:

$$\dot{V} = - s\left( {\frac{p}{\beta q}\left( {x_{2} - \dot{V}_{ref\_i} } \right)^{{\frac{p}{q} - 1}} \left( {k_{f} sat\left( {s\left( {x_{1} } \right)} \right)} \right)} \right)$$
(28)

Knowing that

$$1 < \frac{p}{q} < 2$$
(29)

Thus

$$0 < \frac{p}{q} - 1 < 1$$
(30)

Therefore

$$\dot{V} < 0$$
(31)

Therefore, asymptotic stability is guaranteed via the Lyapunov criterion.

Droop control function

To improve load sharing among parallel-connected converters, droop control is employed, as load-sharing errors are inherent in systems with multiple distributed power sources. This method implements a virtual series impedance through a control loop to balance currents, as illustrated in Fig. 10. However, introducing virtual resistance results in a DC bus voltage drop15,62, necessitating a voltage restoration loop to compensate for the deviation. This approach eliminates the need for high-bandwidth communication, enhances system flexibility, and improves scalability. Instead of physical resistors, which increase power losses, virtual impedance Zd is integrated into the converter control via an outer droop gain loop.

Fig. 10
figure 10

Droop control mechanism.

Full size image

Then, the output voltage reference value Vref_i, seen by the i-th converter compensator, becomes:

$$V_{i}^{*} = V_{ref\_i} - Z_{d} I_{oi}$$
(32)

where:

Zd is the virtual output impedance.

The virtual impedance Zd is determined as follows:

$$Z_{d} = \frac{{\varepsilon_{v} }}{{I_{oi\_\max } }}$$
(33)

where:

εv denotes the maximum output voltage deviation,

Ioi_max represents the maximum output current of the i-th converter.

In Eq. (32), the output voltage reference is adjusted by subtracting the term Zd Ioi, leading to poor voltage regulation. To address this issue, a secondary control action is implemented. Here, a PI regulator calculates the DC bus voltage error and dynamically adjusts the output voltage reference as follows:

$$\delta V = \left( {k_{p} + \frac{{k_{i} }}{s}} \right)\left( {V_{Bus\_ref} - V_{Bus} } \right)$$
(34)

where:

δV represents the processed voltage deviation; the additional control action ensures power sharing and DC bus restoration.

Design of secondary control strategy

Model analysis

In DC MGs, voltage deviation occurs due to droop control, which distributes load current among parallel interface converters. Discrepancies in line impedances further degrade current-sharing accuracy. While increasing droop coefficients can improve current-sharing precision, this may result in larger voltage deviations from the reference value15. To mitigate this limitation of droop control, a centralized secondary control scheme is proposed, as shown in Fig. 7.

Figure 7 depicts a centralized secondary compensator with a voltage control loop for DC bus regulation in the NanoSat DC MG. A remote sensor measures the DC bus voltage and transmits control commands to the interface converters. The primary control of each converter, including voltage and current regulation loops with droop control, is described as follows:

$$V_{oi} = V_{ref\_i} - Z_{d} I_{oi} + \delta V$$
(35)

The superposition theorem is applied to derive the model of the proposed secondary control and determine the PI parameters. The full mathematical details and expressions are provided in63.

As shown in Fig. 2, the DC bus of the NanoSat DC MG is modelled as follows:

$$V_{Bus} = V_{oi} - Z_{i} I_{oi}$$
(36)

In the studied NanoSat DC MG, the local controllers provide identical output voltages (i.e., Voi = Vo_(i+t)). Therefore, the current Ioi is derived as follows:

$$I_{oi} = \frac{{V_{oi} }}{{Z_{eq} + Z_{i} }} - \frac{1}{{Z_{i} }}\frac{{V_{oi} \left( {n - 1} \right)}}{{Z_{eq} + Z_{i + t} + 1}}$$
(37)

where:

n denotes the number of DGs.

and

$$Z_{eq} = \left( {\sum\limits_{k = 0}^{n} {\frac{1}{{Z_{i + k} }} + \frac{1}{{\left| {R_{cpl} } \right|}} - \frac{1}{{Z_{i} }}} } \right)^{ - 1}$$
(38)

From Fig. 10, substituting Eq. (37) into Eq. (36) yields VBus as follows:

$$V_{Bus} = \left( {1 - \frac{{\left( {\left( {n - 1} \right) \cdot Y_{i} + \frac{1}{{\left| {R_{cpl} } \right|}}} \right) \cdot \left( {Z_{i} + Z_{d} } \right) - \left( {n - 1} \right)}}{{\left( {\left( {n - 1} \right) \cdot Y_{i} + \frac{1}{{\left| {R_{cpl} } \right|}}} \right) \cdot \left( {Z_{i} + Z_{d} } \right)^{2} + \left( {Z_{i} + Z_{d} } \right)}} \cdot \left( {Z_{i} + Z_{d} } \right)} \right) \cdot V_{oi}$$
(39)

where \(Y_{i} = \frac{1}{{\left( {Z_{i} + Z_{d} } \right)}}\) and \(V_{oi} = G_{NTSM} \cdot V_{i}^{*}\).

The transfer function \(G_{NTSM} (s)\), describing the open-loop voltage reference-to-output relation in Fig. 11, is obtained by substituting Eq. (27) into Eq. (15) and expressed as follows:

$$\left\{ \begin{gathered} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = \ddot{V}_{ref\_i} - \beta \frac{p}{q}\left( {x_{2} - \dot{V}_{ref\_i} } \right)^{{2 - \frac{p}{q}}} + k_{f} sat\left( {s\left( {x_{1} } \right)} \right) \hfill \\ \end{gathered} \right.$$
(40)
Fig. 11
figure 11

Block diagram of the corrective control-to-DC bus output transfer function.

Full size image

Using the Jacobian method, the transfer function \(G_{NTSM} (s)\) can be derived. Linearizing Eq. (40) simplifies its nonlinear dynamics, enabling streamlined secondary control analysis and design.

The system is defined as follows:

$$\dot{x} = f\left( {x,V_{ref} } \right)$$
(41)

where:

\(x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right]^{T}\) represents the state variable.

The Jacobian matrix at equilibrium is given by:

$$J = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1} }}{{\partial x_{1} }}} & {\frac{{\partial f_{1} }}{{\partial x_{2} }}} \\ {\frac{{\partial f_{2} }}{{\partial x_{1} }}} & {\frac{{\partial f_{2} }}{{\partial x_{2} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ {k_{f} C_{s} } & {C_{2} } \\ \end{array} } \right]$$
(42)

where:

Cs is the slope of the sliding surface chosen for the system, and is defined as:

$$\frac{{\partial f_{2} }}{{\partial x_{1} }} = \frac{{ds\left( {x_{1} } \right)}}{{dx_{1} }} = k_{f} C_{s}$$
(43)

and

$$\frac{{\partial f_{2} }}{{\partial x_{2} }} = C_{2} = - \beta \frac{p}{q}\left( {2 - \frac{p}{q}} \right)\left( {x_{2} - V_{ref\_i} } \right)^{{1 - \frac{p}{q}}}$$
(44)

Thus, the linearized system is given by:

$$\left[ \begin{gathered} \dot{x}_{1} \hfill \\ \dot{x}_{2} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ {k_{f} C_{s} } & {C_{2} } \\ \end{array} } \right]\left[ \begin{gathered} x_{1} \hfill \\ x_{2} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} 0 \hfill \\ 1 \hfill \\ \end{gathered} \right]V_{ref\_i}$$
(45)

Then, taking the Laplace transform allows derivation of the transfer function as follows:

$$G_{NTSM} \left( s \right) = \frac{{V_{o\_i} \left( s \right)}}{{V_{ref\_i} }} = \frac{{V_{M} }}{{s^{2} - C_{2} s - k_{f} C_{s} }}$$
(46)

where:

VM is the peak-to-peak voltage of the triangular wave voltage source.

From Figs. 10 and 11, the corrective control-to-output DC bus transfer function Gs(s) is derived by substituting Eq. (46) into Eq. (39) and expressed as follows:

$$G_{s} (s) = \left( {1 - \frac{{\left( {\frac{{\left( {n - 1} \right)}}{{\left( {Z_{d} + Z_{i} } \right)}} + \frac{1}{{\left| {R_{cpl} } \right|}}} \right) \cdot \left( {Z_{d} + Z_{i} } \right) - \left( {n - 1} \right)}}{{\left( {\frac{{\left( {n - 1} \right)}}{{\left( {Z_{d} + Z_{i} } \right)}} + \frac{1}{{\left| {R_{cpl} } \right|}}} \right) \cdot \left( {Z_{d} + Z_{i} } \right)^{2} + \left( {Z_{d} + Z_{i} } \right)}} \cdot \left( {Z_{d} + Z_{i} } \right)} \right) \cdot \left( {\frac{{V_{M} }}{{s^{2} - C_{2} s - k_{f} C_{s} }}} \right)$$
(47)

Note: All centralized secondary controllers employ the same control strategy, while DGs exhibit distinct line impedances and input voltages. To resolve this discrepancy, we propose the following assumptions:

  1. 1.

    All DGs supply identical input voltages: \(V_{in} = V_{in\_1} = V_{in\_2} = V_{in\_3}\).

  2. 2.

    All virtual impedances are identical:\(Z_{d1} = Z_{d2} = Z_{d3} = Z_{d}\) and must satisfy \(Z_{d(1,2,3)} \gg Z_{(1,2,3)}\), where \(Z_{1,2,3}\) represent the line impedances.

  3. 3.

    Based on these assumptions and Fig. 10, the term \(\left( {Z_{d} + Z_{i} } \right)\) becomes equivalent to \(\left( {Z_{d} } \right)\)64,65. Therefore, the transfer function Gs(s) is identical for all DGs, enabling the use of identical controllers.

Proportional-integral controller

A PI-based secondary control strategy is introduced to correct voltage deviations. The DC bus voltage (VBus) is sensed and compared to the reference voltage (VBus_ref), producing an error signal \(\left( {\Delta V = V_{Bus\_ref} - V_{Bus} } \right)\).This error is processed by the PI compensator to generate a correction term δV, which is uniformly applied to all units to restore the DC bus voltage.

This ensures δV directly represents the PI-compensated adjustment, aligning the formulation with the controller’s role. The PI compensator acts as a low-pass filter, reducing switching noise at the cost of bandwidth, which increases rise and settling times58,59,60. To maintain hierarchical stability, the crossover frequency of the secondary controller is designed to be lower than the primary control frequency, ensuring a slower but coordinated response.

At the desired crossover frequency, the magnitude of Gs (s) with the PI controller is expressed as:

$$\left| {T_{A} \left( {f_{c\_d} } \right)} \right| = \left| {G_{s} (f_{c\_d} )} \right|\left| {T_{c\_PI} (f_{c\_d} )} \right| = 1$$
(48)

where:

\(f_{c\_d}\) denotes the desired crossover frequency at which the loop-gain magnitude \(\left| {T_{A} \left( {f_{c\_d} } \right)} \right|\) equals unity.

Hence,

$$\left| {T_{c\_PI} (f_{c\_d} )} \right| = k_{p}$$
(49)

By using Eq. (47), the proportional part is given as:

$$k_{p} = \frac{1}{{\left| {G_{s} (f_{c\_d} )} \right|}} = \left| {\frac{{2\pi C_{2} f_{c\_d} - C_{s} k_{f} + 4\pi^{2} f_{c\_d}^{2} }}{{a_{1} + a_{2} }}} \right|$$
(50)

where

$$a_{1} = - Z_{d} \left( { - n + \left( {Z_{d} + Z_{i} } \right)\left( {\frac{1}{{\left| {R_{cpl} } \right|}} + \frac{n - 1}{{Z_{d} + Z_{i} }}} \right) + 1} \right)$$
(51)

and

$$a_{2} = \left( {Z_{d} + Z_{i} + \left( {Z_{d} + Z_{i} } \right)^{2} \left( {\frac{1}{{\left| {R_{cpl} } \right|}} + \frac{n - 1}{{Z_{d} + Z_{i} }}} \right)} \right)$$
(52)

Using Eq. (50), the integral component at the desired crossover frequency fc_d can be determined as:

$$k_{i} = \frac{{2\pi f_{c\_d} }}{10}k_{p} = \frac{{2\pi f_{c\_d} }}{10}\left| {\frac{{2\pi C_{2} f_{c\_d} - C_{s} k_{f} + 4\pi^{2} f_{c\_d}^{2} }}{{a_{1} + a_{2} }}} \right|$$
(53)

Design of CPLs

This study emulates a tightly voltage-controlled boost converter (Tb (s)) as a CPL, regulated by an integral-double-lead (IDL) compensator (Tc (s)). The converter supplies a resistive load, with the CPL power demand adjusted by varying the load resistance. The transfer functions of the boost converter and its controller are provided in66,67,68. The time response of the boost converter’s regulation must be faster than that of the local and secondary controllers. Table 1 summarizes the specifications of the DC/DC boost converter and its controller.

Table 1 Specifications of the DC/DC boost converter and its controller.
Full size table

Figure 12 presents the Bode plots of the IDL controller under varying resistive loads, illustrating changes in power demand. Figure 13 shows the Bode plot of the closed-loop boost converter with the designed controller,\(\left( {T = \frac{{T_{c} (s).T_{b} (s)}}{{1 + T_{c} (s).T_{b} (s)}}} \right)\), under the conditions specified in Table 1.

Fig. 12
figure 12

Bode plot of the voltage transfer function of the IDL compensator.

Full size image
Fig. 13
figure 13

Bode plot of the closed-loop boost converter with IDL compensator.

Full size image

Results and discussion

To evaluate the proposed hierarchical control approach, a simulation test system is implemented in PSIM under four case studies:

  1. 1.

    Performance validation under CPL fluctuations.

  2. 2.

    Performance evaluation under source variations.

  3. 3.

    Validation of islanding and connection modes.

  4. 4.

    Activation testing of the proposed hierarchical control.

Table 2 summarizes the hierarchical control parameters, while Table 3 provides the DC/DC buck converter specifications for the DGs.

Table 2 Specifications of DC MG and proposed control system.
Full size table
Table 3 Specifications of the DC/DC buck converters for the DGs.
Full size table

Case 1: Dynamic response of hierarchical control to load power fluctuations

The proposed hierarchical control strategy, integrating primary and secondary control levels, was validated through testing under CPL variations. The CPL power was increased in 10-W steps (from 10 to 40 W) and then decreased back to 10 W, as shown in Fig. 14. The DC bus voltage reference was set to 16 V. As depicted in Fig. 17, the DC bus voltage remains stable and accurately tracks the reference. The response time for each CPL increase is 0.02 s, while the settling time for decreases is 0.03 s. Similar trends are observed in the DG output voltages (Fig. 16). The DG output currents (Fig. 15) track their references with a 0.002-s response time. Figures 15, 16 and 17 illustrate the instantaneous DC output voltages, currents, and bus voltage. Table 4 summarizes the current distribution and DC bus regulation at different CPL levels.

Fig. 14
figure 14

Power load demand profile.

Full size image
Fig. 15
figure 15

Mean DC currents of DG1–DG3 under case 1.

Full size image
Fig. 16
figure 16

Mean DC voltage profiles of DG1, DG2, and DG3 during case 1 operation.

Full size image
Fig. 17
figure 17

Main DC bus voltage under case 1.

Full size image
Table 4 Current distribution and DC bus voltage under case 1.
Full size table

Table 4 demonstrates that despite CPL fluctuations, the DGs maintain proportional current sharing, and the DC bus voltage remains stable at 16 V, validating the proposed control method.

Case 2: Hierarchical control performance under input voltage variations

This case evaluates the proposed control under input voltage variations using a 15-V peak-to-peak square-wave perturbation at 0.5 Hz. With DG input voltages at 32 V, the 0.1-µs rise/fall times ensure a realistic disturbance test, as depicted in Fig. 18. As shown in Fig. 20, current sharing among the DGs remains proportional to their rated capacities despite input voltage variations. Figure 19 confirms that the DC bus voltage stabilizes near the reference value within 0.02 s. Table 5 summarizes the current distribution under these conditions.

Fig. 18
figure 18

Source variation profile: (a) DG1, (b) DG2, (c) DG3.

Full size image
Fig. 19
figure 19

DC bus voltage simulation results (Case 2).

Full size image
Table 5 DG current distribution and DC bus voltage regulation under case 2.
Full size table

Table 5 demonstrates that despite a 46% input voltage reduction, current sharing among DGs remains balanced, and the DC bus voltage is maintained at 16 V. Figure 21 illustrates that DG output voltages remain stable near their reference values despite input voltage variations. Figures 19, 20 and 21 show the instantaneous DC output voltages, currents, and DC bus voltage. These results indicate reduced transient voltage deviations and shorter settling times (0.02 s). Figures 19, 20 and 21 show the system response to input voltage (Vin) disturbances, treated as external perturbations. Reduced transient deviations and stable DC bus recovery demonstrate the controller mitigates disturbances without regulating Vin. Settling time reflects secondary control robustness in restoring voltage despite Vin variations.

Fig. 20
figure 20

DC output current simulation results (Case 2).

Full size image
Fig. 21
figure 21

Mean DC voltages for DG1, DG2, and DG3 (Case 2).

Full size image

Case 3: Hierarchical control evaluation with backup DG plug-and-play

System performance is evaluated during DG connections and disconnections to assess the effectiveness of the proposed secondary control method. As shown in Figs. 22, 23 and 24, only DG1 is connected to the DC bus from t = 0 s to t = 1.5 s. In the second stage, DG2 is connected in parallel with DG1 from t = 1.5 s to t = 5 s, during which the output currents equalize at 0.33A after a transient period of 0.017s. In the third stage, from t = 5 s to t = 7 s, DG3 is added in parallel with DG1 and DG2. Using the proposed hierarchical control, the output currents stabilize at 0.0833A after a settling time of 0.025 s. Using the proposed hierarchical control. Table 6 summarizes the current distribution during these connection stages.

Fig. 22
figure 22

DC bus voltage simulation results (Case 3).

Full size image
Fig. 23
figure 23

Mean DC voltages for DG1, DG2, and DG3 (Case 3).

Full size image
Fig. 24
figure 24

Mean DC currents for DG1, DG2, and DG3 (Case 3).

Full size image
Table 6 Current distribution and DC bus voltage regulation during case 3.
Full size table

Table 6 demonstrates that as additional DGs are integrated, the output current redistributes while maintaining a stable DC bus voltage at 16V. Figure 22 confirms that DG connections and disconnections do not adversely affect transient voltage regulation. After DG2 connects at t = 1.5 s, the DC bus voltage stabilizes within 0.04s. When DG3 connects at t = 5 s, the DC bus voltage remains at the reference value VBus_ref = 16V and recovers within 0.06s. Similar trends are observed in the DG output voltages (see Fig. 23). Figures 22, 23 and 24 illustrate the instantaneous DC output voltages, currents, and DC bus voltage. The proposed hierarchical approach ensures stability and enables PnP functionality.

Case 4: Resilient operation of NanoSat DC MG with activated hierarchical control

Three parallel converters forming the NanoSat DC MG are analysed to validate the proposed hierarchical control in a larger-scale system and assess its fault tolerance. Before the primary control is activated, Fig. 26 shows unequal output currents due to mismatched line impedances, which are exacerbated by increasing impedance differences. At t = 1.5 s, when primary control is activated, the output currents of the three converters equalize with a rapid settling time of 0.005 s. However, both the DG output voltages and the DC bus voltage exhibit deviations from their reference values. At t = 5 s, when the proposed secondary control is activated, the DC bus voltage is restored to its reference value with a response time of 0.01 s, as demonstrated in Figs. 25, 26 and 27. These figures illustrate the instantaneous DC output voltages of the DGs, output currents, and DC bus voltage. Table 7 quantifies the impact of hierarchical control on current distribution and DC bus voltage regulation.

Fig. 25
figure 25

Mean DC bus voltage simulation results (Case 4).

Full size image
Fig. 26
figure 26

DC currents simulation for DG1, DG2, DG3 (Case 4).

Full size image
Fig. 27
figure 27

Mean DC voltages simulation for DG1, DG2, DG3 (Case 4).

Full size image
Table 7 Current distribution and DC bus voltage regulation under case 4.
Full size table

Comparison with existing approaches

A comparative analysis of the proposed method and conventional centralized control approaches is detailed in Table 8. The results demonstrate that the proposed strategy achieves superior voltage regulation accuracy and precise power-sharing performance while significantly reducing communication requirements.

Table 8 Comparison of different voltage restoration methods.
Full size table

Experimental validation

A scaled-down NanoSat DC MG prototype with two DGs was implemented for experimental validation using PSIM-generated C code. The setup included a voltage-controlled boost converter (CPL) powered by two parallel buck converters, each modelled as an ideal 32 V source. Detailed configuration parameters, including component values and system settings of the boost converter and buck converters (1 and 2), are provided in Tables 1, 2, and 3. A DSP28335 microcontroller managed PWM signals at 25 kHz for synchronized control, using voltage sensors (LA25-NP, model 717087) and current sensors (LV25-P, model 714227). The experimental setup is depicted in Fig. 28.

Fig. 28
figure 28

The experimental setup.

Full size image

The effectiveness of the proposed controller was tested under three scenarios:

  1. 1.

    Response to sudden changes in CPL power demand.

  2. 2.

    Seamless integration and removal of DGs without destabilizing the system.

  3. 3.

    Performance during transitions between primary and secondary control layers.

These experimental scenarios were designed to evaluate the proposed control approach under real-world conditions and closely align with the simulation case studies, differing only in timing. The results of CPL load variations, input voltage variations, and hierarchical control activation are shown in Figs. 29, 30 and 31, which illustrate the dynamic response of the DC bus voltage, DG output voltages, and buck converter output currents. The following key observations are derived:

  • The DC bus voltage remains stable around 16 V despite CPL changes, indicating effective control.

  • Current distribution between sources adapts dynamically to CPL variations, demonstrating effective load-sharing.

  • The DC bus voltage remains stable (~ 16 V) when switching between DG configurations, confirming effective voltage regulation.

  • Current redistribution occurs when switching between DG1 + DG2 and DG1, reflecting system adaptability.

  • Improved DC bus voltage stability under secondary control suggests enhanced voltage regulation.

  • The output voltages \(V_{o1}\) and \(V_{o2}\) exhibit transient variations under different control stages.

  • The currents \(I_{o1}\) and \(I_{o2}\) indicate load distribution between sources.

  • Current imbalance is reduced progressively under Primary Control and eliminated under Secondary Control, demonstrating hierarchical efficacy.

  • Control stages transition from instability (unbalanced currents) to partial balancing (voltage drop) and finally full stability (balanced currents + precise voltage regulation).

Fig. 29
figure 29

Response to CPL variations: (a) Output voltages, (b) DC bus voltage, (c) Output currents, (d) Duty cycle.

Full size image
Fig. 30
figure 30

Response to PnP operation of DGs: (a) Output voltages, (b) DC bus voltage, (c,d) Output currents.

Full size image
Fig. 31
figure 31

Response under different control stages: (a) Output voltages, (b) DC bus voltage, (c,d) Output currents.

Full size image

Conclusion

This paper proposes a hierarchical control framework for islanded NanoSat DC MGs, addressing critical challenges in power allocation and voltage regulation. The primary control layer integrates I–V droop control for decentralized current sharing and a NTSM controller to achieve finite-time voltage stabilization, eliminating chattering effects and enhancing robustness against perturbations. The secondary control layer resolves voltage deviations caused by droop dynamics and ensures precise proportional current sharing, even under destabilizing CPLs. A stability analysis guides PI gain selection, ensuring adaptability to line impedance mismatches, unequal DG ratings, and dynamic load variations. Simulations in MATLAB/PSIM validate the framework under realistic NanoSat conditions, demonstrating ± 5% DC bus voltage regulation during input fluctuations and PnP operations, 98.5% current-sharing accuracy with mismatched DG capacities (surpassing conventional methods), and dynamic recovery of the nominal DC bus voltage within 0.02 s under step-load changes. Experimental results further validate the dual capability of the controller to maintain voltage stability and ensure proportional current sharing under real-world disturbances. The system exhibits resilience to communication delays, line impedance disparities, and variable CPLs. By addressing limitations of conventional secondary control in handling CPLs, the framework offers a scalable and reliable solution for aerospace applications, where transient performance, weight constraints, and fault tolerance are critical. Future work will integrate tertiary control for mission-specific energy optimization, advancing autonomous NanoSat operations. This study contributes a validated hierarchical strategy to enhance next-generation satellite power systems, bridging gaps in MG control for high-stakes aerospace environments.