Introduction

The mining of underground coal seams inevitably causes the movement of overlying strata, presenting certain regularities in the propulsion direction and vertical direction of the working face, such as the periodic rupture of the main roof and the formation of the Vertical Three Zones distribution1,2,3. Accurate understanding of the rupture law of the main roof, especially that of the main roof in long-wall faces, is conducive to carrying out the support design of the working face, improving the management level of mine pressure, and ensuring the safe production of the coal mining face4,5.

Many scholars have taken the plate model as the research object and analyzed the rupture law of the main roof. Zhao et al.6 started from the control equation of the thin plate bending problem and presented a unified symplectic analytical solution of the rectangular thin plate model under different boundary conditions. Yu7 analyzed the stress distribution characteristics and fracture mechanism of the main roof when the roof of the working face breaks. Xue et al.8 obtained the failure law of the roof through the distribution of tensile stress and bending moment. Yang et al.9 derived the calculation formulas for the fracture step distance of the roof under different face lengths and different propulsion speeds. Wang and Gao10 constructed five different roof mechanical models under different support boundary conditions by applying the elastic thin plate theory. Liu and Li11 established a mechanical model of main roof with two sides simply supported and two sides fixed, and three sides simply supported and one side fixed by means of theoretical analysis and numerical simulation. Pu et al.12 established an elastic thin plate mechanical model of the four-sided fixed roof and analyzed the generation mechanism of the roof fracture morphology using the Ritz method theory. Zhang et al.13 analyzed and calculated the stress distribution characteristics and fracture mechanism of the main roof during uphill and downhill mining with large dip angle by using the thin plate theory. Wang et al.14 established a mechanical model of the elastic foundation plate characterizing the main roof supported by the pillar in the goaf. Li et al.15 theoretically analyzed the internal force distribution law and fracture mechanism of the roof by using the displacement variational method. Wang et al.16 used the elastic thin plate theory to calculate the stress distribution inside the thin plate under different constraint boundary conditions. Tang and Ye17 analyzed the stress distribution law of the roof of the K13 coal seam in Bailaping Coal Mine by using the thin plate theory. He et al.18,19,20 analyzed the rupture law of the main roof with elastic foundation boundary based on the principal bending moment (PBM).

In addition to the theoretical analysis based on thin plate and beam models, experts and scholars have also adopted other methods to study the rupture law of the main roof. Zhou et al.21 explored the evolution of overlying strata structure and the ground pressure in the working face mining of close-distance coal seams were explored. Cheng et al.22 designed and conducted to investigate the deformation and failure mechanism of overlying rocks. Liu et al.23 used the dual-mode parallel electrical method for dynamic monitoring of overlying rock in shallow and large mining height working face. Zhang et al.24 investigated the failure law of weak overburden stratum underlying extra-thick alluvium. Lou et al.25 studied the evolution of the fracture tendency zone of the regenerated roof during the lower slice mining to solve the problem of safe fully-mechanized mining in steeply dipped thick soft coal seam. Cao et al.26 revealed the roof weighting characteristics during lower coal seam mining, combining with engineering statistics, physical simulation and theoretical analysis. Kong27 analyzed the structure form and movement law of large space overburden strata and its strata pressure mechanism of fully mechanized top-coal caving stope under extra-thick coal seam in extremely close goaf. Yang et al.28 analyzed the fracture migration laws and the dynamic evolution characteristics of “three zones” of overburden in thick coal seam mining under thick hard roofs. Yin et al.29 studied the spatial structure characteristics of the fully mechanized mixed mining coal face are systematically by means of theoretical analysis, physical similarity simulation and field measurement. Fu et al.30 investigated the roof collapse characteristics, fracture locations, and the development heights of the collapse zone and fracture zone in the fully mechanized mining face with a large mining height of 5.5 m. Yang31 studied the mechanical mechanism and asymmetric fracture conditions of a main roof with a large mining height and the first-weighting occurring in a shallow coal seam. Li et al.32 studied the working resistance of hydraulic supports in deep coal pillar working faces based on the composite mechanical model of “cantilever beam-masonry beam”.

Most of the existing studies adopted the bending moment to analyze the rupture law of the main roof with fixed support on all four sides. However, PBM and the bending moment are different concepts. PBM is converted from the bending moment and torque, reflecting the combined influence of the two. PBM is the maximum or minimum bending moment at a point. Therefore, it is necessary to analyze the rupture law of the main roof with fixed support on all four sides with the help of PBM. In this paper, PBM was taken as the rupture index. The main bending moment was visualized through MATLAB (Matrix Laboratory, 23.2.0.2515942 (R2023b) Update 7, URL link: https://software.ncut.edu.cn/index/product/index/?c_id=4) software. The rupture directions and sequences of each region of the main roof were analyzed, and the rupture law of the main roof was verified.

Visualization of PBM

Deflection surface equation

The 1304 working face of a certain coal mine of China Coal Group is the fourth working face of the 13th mining area. The working face length is 360 m, the propulsion length is 1110 m, and the burial depth reaches 1000 m. It belongs to a typical ultra-long working face in deep well. This working face mainly mines the 13-1 coal seam. The average thickness of the coal seam is 5.2 m and it is a nearly horizontal coal seam. The immediate roof of the 1304 working face is sandy mudstone with an average thickness of 6.7 m, and the main roof is fine sandstone with an average thickness of 5.0 m.

The coal mining face advances forward from the open-off cut. The immediate roof falls for the first time after reaching the maximum collapse distance. After that, the immediate roof falls off immediately with mining, and the exposed area of the main roof keeps increasing until it collapses for the first time. When the working face advances by 40 m, the thickness-to-width ratio of the main roof is 1/8, which satisfies the mechanical assumptions of elastic thin plates6,7,8,9,10,11,12,13,14,15,16,17. Therefore, the main roof can be regarded as a rectangular elastic thin plate.

Before the main roof collapses for the first time, the area around the mined area is all solid coal. Due to the relatively large thickness and high integrity of the solid coal and the immediate roof, the deflection and rotation angle of the main roof can be well restricted. Therefore, the boundary condition of the main roof is approximately regarded as constraint of fixed support.

Taking the propulsion direction of the working face as the x-axis, the length direction of the working face as the y-axis, and the vertical direction as the z-axis, a mechanical model of rectangular elastic thin plate with fixed support on all four sides was established, as shown in Fig. 1. In Fig. 1, s represents the propulsion distance of the working face and t represents the length of the working face. As the coal mining face is a long-wall face, before the main roof collapses for the first time, the propulsion distance of the working face is less than the length of the working face. Therefore, the side parallel to the propulsion direction of the working face is the short side, and the side parallel to the length direction of the working face is the long side. Points F1 and F2 are the midpoints of the long side, points G1 and G2 are the midpoints of the short side, and point O is the midpoint of the middle, located at the origin of the coordinate axis.

Fig. 1
figure 1

Mechanical model of rectangular elastic thin plate with fixed support on all four sides.

Full size image

According to the elastic thin plate theory33 the displacement boundary condition of the main roof is

$$\omega \left| {_{{x= \pm \frac{s}{2}}}} \right.=0,\frac{{\partial \omega }}{{\partial x}}\left| {_{{x= \pm \frac{s}{2}}}} \right.=0$$
(1)
$$\omega \left| {_{{y= \pm \frac{t}{2}}}} \right.=0,\frac{{\partial \omega }}{{\partial y}}\left| {_{{y= \pm \frac{t}{2}}}} \right.=0$$
(2)

Where ω represents the deflection of the thin plate (m).

The deflection surface equation that satisfies the above displacement boundary conditions is

$$\omega =C{\left ({x^2} - \frac{{{s^2}}}{4}\right) ^2}{\left({y^2} - \frac{{{t^2}}}{4}\right)^2}$$
(3)

Where C is an undetermined parameter.

Equation (3) satisfies the displacement boundary conditions listed in Eqs. (1) and (2) while also satisfying the internal force boundary conditions. According to the Galerkin method, then

$$C=\frac{{49q}}{{8(7{s^4}+4{s^2}{t^2}+7{t^4})D}}$$
(4)

Where D represents the flexural stiffness (GN·m).

Thus, the equation of the deflection surface of the main roof is

$$\omega =\frac{{49q}}{{8(7{s^4}+4{s^2}{t^2}+7{t^4})D}}{\left ({x^2} - \frac{{{s^2}}}{4}\right)^2}{\left ({y^2} - \frac{{{t^2}}}{4}\right)^2}.$$
(5)

Rupture index

According to the elastic thin plate theory33 the internal forces of the thin plate can all be represented by deflection ω. The bending moment and torque are respectively

$${M_x}= - D\left (\frac{{{\partial ^2}\omega }}{{\partial {x^2}}}+\nu \frac{{{\partial ^2}\omega }}{{\partial {y^2}}}\right)$$
(6)
$${M_y}= - D\left (\frac{{{\partial ^2}\omega }}{{\partial {y^2}}}+\nu \frac{{{\partial ^2}\omega }}{{\partial {x^2}}}\right)$$
(7)
$${M_{xy}}= - D(1 - \nu )\frac{{{\partial ^2}\omega }}{{\partial x\partial y}}$$
(8)

PBMs M1 and M2 can be represented by Mx, My and Mxy respectively, that is

$${M_1}=\frac{{{M_x}+{M_y}}}{2}+\sqrt {{{\left(\frac{{{M_x} - {M_y}}}{2}\right)}^2}+{M_{xy}}^{2}}$$
(9)
$${M_2}=\frac{{{M_x}+{M_y}}}{2} - \sqrt {{{\left(\frac{{{M_x} - {M_y}}}{2}\right)}^2}+{M_{xy}}^{2}}$$
(10)

The Angle α between the normal direction of the acting surface of M1 and the x-axis is

$$\alpha =\arctan \frac{{{M_1} - {M_x}}}{{{M_{xy}}}}$$
(11)

Substituting Eqs. (6), (7) and (8) into Eqs. (9) and (10), we can obtain

$${M_1}= - \frac{{D(1+\nu )}}{2}\left(\frac{{{\partial ^2}\omega }}{{\partial {x^2}}}+\frac{{{\partial ^2}\omega }}{{\partial {y^2}}}\right)+\frac{{D(1 - \nu )}}{2}\sqrt {{{\left(\frac{{{\partial ^2}\omega }}{{\partial {y^2}}} - \frac{{{\partial ^2}\omega }}{{\partial {x^2}}}\right)}^2}+4{{\left(\frac{{{\partial ^2}\omega }}{{\partial x\partial y}}\right)}^2}}$$
(12)
$${M_2}= - \frac{{D(1+\nu )}}{2}\left(\frac{{{\partial ^2}\omega }}{{\partial {x^2}}}+\frac{{{\partial ^2}\omega }}{{\partial {y^2}}}\right){\text{-}}\frac{{D(1 - \nu )}}{2}\sqrt {{{\left(\frac{{{\partial ^2}\omega }}{{\partial {y^2}}} - \frac{{{\partial ^2}\omega }}{{\partial {x^2}}}\right)}^2}+4{{\left(\frac{{{\partial ^2}\omega }}{{\partial x\partial y}}\right)}^2}}$$
(13)

The above-mentioned bending moment, torque and PBM are all internal forces acting on each unit width of the thin plate, with the dimension of LMT−2 and the unit of MN33.

Visualization of PBM

In order to visually analyze the rupture law of main roof, it was necessary to visualize PBM. The parameters of the working face were taken as follows: the propulsion distance of the working face s = 40 m, the length of the working face t = 360 m, the lateral load q = 0.25 MPa7,18 the elastic modulus E = 30 GPa, Poisson’s ratio ν = 0.2, and the thickness of main roof h = 5 m. Due to the boundary conditions of fixed support on all four sides, the thickness and lithology of the immediate roof, as well as the thickness and lithology of the coal seam, are no longer considered. The visualization results are shown in Fig. 2.

In Fig. 2, the points with the largest absolute value of PBM are located at points F1 and F2, which is the second main bending moment, with a value of −43.44 MN. Substituting − 43.44 MN into the calculation formula of the principal stress34,35 the tensile stress on the upper surface of the main roof can be calculated to be 7.24 MPa, which is of the same order of magnitude as the tensile strength of the rock. The propulsion distance of 40 m and the tensile stress of 7.24 MPa approach the initial collapse step distance and ultimate tensile stress of the main roof. The two have a good correspondence, which to a certain extent reflect the rationality of the model and parameter values.

Fig. 2
figure 2

Distribution of PBM: (a) the first PBM; and (b) the second PBM.

Full size image

As can be seen from Fig. 2, there are two PBMs at a point of the main roof, namely the first PBM and the second PBM. Numerically, the first PBM is greater than the second PBM. However, which PBM causes the rupture at a point of the main roof depends on the magnitudes of the absolute values of the first and second PBM.

Whether it is the first PBM or the second PBM, both have positive and negative values. The positive or negative of PBM determines the bending direction of the main roof. A positive PBM indicates that the main roof bends upward, with compression above the middle surface and tension below it. The rupture occurs on the lower surface of the main roof. A negative PBM indicates that the main roof bends downward, with tension above the middle surface and compression below it. The rupture occurs on the upper surface of the main roof33.

Rupture direction of each region of the main roof

In order to facilitate the analysis of the rupture law of the main roof, it is necessary to divide the main roof into regions. The main roof can be divided into the long-side region, the middle region and the short-side region, as shown in Fig. 3.

Fig. 3
figure 3

Regions division of main roof.

Full size image

The main bending moment that determines the rupture of each area is defined as the control bending moment. The control bending moment in the long-side region is the second PBM and is a negative bending moment, denoted as Mck. The control bending moment in the middle region is the first PBM and is also the positive bending moment, denoted as Mzk. The control bending moment in the short-side region is the second PBM and is a negative bending moment, denoted as Mdk.

Rupture direction of the long-side region

Starting from the midpoint of the long side, a direction angle β is set between the length direction of the working face and the propulsion direction of the working face, as shown in Fig. 4a. The distribution of the control bending moment in the long-side region is shown in Fig. 4b.

Fig. 4
figure 4

Distribution of Mck: (a) β; and (b) Mck.

Full size image

It can be known from Fig. 4b that the point with the smallest control bending moment in the long-side region is the midpoint of the long side. When the long-side region breaks, this point breaks first. In the length direction of the working face, the control bending moments when the distances from the midpoint of the long side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are − 43.43 MN, −43.43 MN, −43.41 MN, −43.40 MN, −43.37 MN and − 43.34 MN respectively. In the propulsion direction of the working face, the control bending moments when the distances from the midpoint of the long side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are − 37.08 MN, −30.06 MN, −25.35 MN, −19.97 MN, −14.92 MN and − 10.19 MN respectively. In other directions, the control bending moments when the distances from the midpoint of the long side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are between the control bending moments in the length direction of the working face and the control bending moments in the propulsion direction of the working face, indicating that the control bending moments in the length direction of the working face are smaller than those in other directions, especially smaller than those in the propulsion direction of the working face. Correspondingly, the absolute value of the control bending moment in the length direction of the working face is greater than that in other directions. Therefore, when the main roof breaks, it extends along the length direction of the working face starting from the midpoint of the long side.

The torque of the main roof is visualized, and the distribution of the torque is shown in Fig. 5.

Fig. 5
figure 5

Distribution of torque.

Full size image

The rupture of the long-side region is mainly caused by tensile failure. According to Eq. (11) and Fig. 5, the direction of the tensile failure is the propulsion direction of the working face, verifying that the rupture direction of the long-side region is the length direction of the working face.

Rupture direction of the middle region

Starting from the midpoint of the middle, a direction angle β is set between the length direction of the working face and the propulsion direction of the working face, as shown in Fig. 6a. The distribution of the control bending moment in the middle region is shown in Fig. 6b.

Fig. 6
figure 6

Distribution of Mzk: (a) β; and (b) Mzk.

Full size image

It can be known from Fig. 6b that the point with the maximum control bending moment in the middle region is the midpoint of the middle. When the middle region breaks, this point breaks first. In the length direction of the working face, the control bending moments at distances of 1 m, 2 m, 3 m, 4 m, 5 m and 6 m from the midpoint of the middle are 21.77 MN, 21.77 MN, 21.76 MN, 21.75 MN, 21.74 MN and 21.72 MN respectively. In the propulsion direction of the working face, the control bending moment at distances of 1 m, 2 m, 3 m, 4 m, 5 m and 6 m from the midpoint of the middle are 21.61 MN, 21.12 MN, 20.30 MN, 19.16 MN, 17.69 MN and 15.90 MN respectively. In other directions, the control bending moments at distances of 1 m, 2 m, 3 m, 4 m, 5 m and 6 m from the midpoint of the middle are between the control bending moments in the length direction of the working face and the control bending moments in the propulsion direction of the working face, indicating that the control bending moments in the length direction of the working face are greater than those in other directions, especially greater than those in the propulsion direction of the working face. Therefore, when the main roof breaks, it extends along the length direction of the working face starting from the midpoint of the middle.

The rupture of the middle region is mainly caused by tensile failure. According to Eq. (11) and Fig. 5, the direction of the tensile failure is the propulsion direction of the working face, verifying that the rupture direction of the middle region is the length direction of the working face.

Rupture direction of the short-side region

Starting from the midpoint of the short side, a direction angle β is set between the propulsion direction of the working face and the length direction of the working face, as shown in Fig. 7a. The distribution of the control bending moment in the short-side region is shown in Fig. 7b.

Fig. 7
figure 7

Distribution of Mdk: (a) β; and (b) Mdk.

Full size image

It can be known from Fig. 7b that the point with the smallest control bending moment in the short-side region is the midpoint of the short side. When the short-side region breaks, this point breaks first. In the propulsion direction of the working face, the control bending moments when the distances from the midpoint of the short side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are − 0.54MN, −0.53MN, −0.52MN, −0.50MN, −0.47MN and − 0.43MN respectively. In the length direction of the working face, the control bending moments when the distances from the midpoint of the short side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are − 0.49 MN, −0.44 MN, −0.39 MN, −0.34 MN, −0.29 MN and − 0.24 MN respectively. In other directions, the control bending moments when the distances from the midpoint of the short side are 1 m, 2 m, 3 m, 4 m, 5 m and 6 m respectively are between the control bending moments in the propulsion direction of the working face and those in the length direction of the working face, indicating that the control bending moments in the propulsion direction of the working face are smaller than those in other directions, especially smaller than those in the length direction of the working face. Correspondingly, the absolute value of the control bending moment in the propulsion direction of the working face is greater than that in other directions. Therefore, when the main roof breaks, it extends along the propulsion direction of the working face starting from the midpoint of the short side.

The rupture of the short-side region is mainly caused by tensile failure. According to Eq. (11) and Fig. 5, the direction of the tensile failure is the length direction of the working face, verifying that the rupture direction of the short-side region is the propulsion direction of the working face.

Rupture sequence of each region of the main roof

Substituting Eq. (5) into Eqs. (12) and (13) can yield the specific expressions of the first and second PBM, namely

$${M_1}=\frac{{49q(1+\nu )A - 49q(\nu - 1)\sqrt {{B^2}+64{x^2}{y^2}{{(\frac{{{s^2}}}{4} - {x^2})}^2}{{(\frac{{{t^2}}}{4} - {y^2})}^2}} }}{{28{s^4}+16{s^2}{t^2}+28{t^4}}}$$
(14)
$${M_2}=\frac{{49q(1+\nu )A{\text{+ }}49q(\nu - 1)\sqrt {{B^2}+64{x^2}{y^2}{{(\frac{{{s^2}}}{4} - {x^2})}^2}{{(\frac{{{t^2}}}{4} - {y^2})}^2}} }}{{28{s^4}+16{s^2}{t^2}+28{t^4}}}$$
(15)

Where \(A=(\frac{{{s^2}}}{4} - {x^2})(\frac{{{t^2}}}{4} - {y^2})(\frac{{{s^2}}}{4}+\frac{{{t^2}}}{4} - {x^2} - {y^2}) - 2{y^2}{(\frac{{{s^2}}}{4} - {x^2})^2} - 2{x^2}{(\frac{{{t^2}}}{4} - {y^2})^2}\),

\(B=(\frac{{{s^2}}}{4} - {x^2})(\frac{{{t^2}}}{4} - {y^2})(\frac{{{s^2}}}{4} - \frac{{{t^2}}}{4} - {x^2}+{y^2}) - 2{y^2}{(\frac{{{s^2}}}{4} - {x^2})^2}+2{x^2}{(\frac{{{t^2}}}{4} - {y^2})^2}\)

It can be seen from Eqs. (14) and (15) that PBM is affected by the propulsion distance of the working face, the length of the working face, the lateral load and the Poisson’s ratio.

The rupture sequence of each region of the main roof depends on the magnitude of the absolute value of the control bending moment at the midpoint of the long side, the middle and the short side. The absolute value of the control bending moment at the midpoint mentioned above is denoted as Mok. The following discusses the rupture sequence of each region in combination with the changes in the influencing factors of PBM.

Effect of the propulsion distance of the working face

Due to the influence of geological conditions, mining techniques and other factors, when the coal mining face is generally advanced to 30–60 m, the main roof breaks for the first time. The change curve of the absolute value of the control bending moment at the midpoint with the propulsion distance of the working face is shown in Fig. 8.

Fig. 8
figure 8

Change curve of Mok with s.

Full size image

Taking the long side as an example, the effect of the propulsion distance of the working face on the absolute value of the control bending moment at the midpoint is studied. It can be known from Fig. 8 that when the propulsion distance of the working face is 10 m, the absolute value of the control bending moment at the midpoint of the long side is 2.73 MN. When the propulsion distance of the working face is 60 m, the absolute value of the control bending moment at the midpoint of the long side is 96.83 MN, indicating that with the increase of the propulsion distance of the working face, the absolute value of the control bending moment at the midpoint of the long side increases significantly. The change curve of the absolute value of the control bending moment at the midpoint of the long side with the propulsion distance of the working face becomes steeper and steeper, meaning that the promoting effect of the propulsion distance of the working face on the absolute value of the control bending moment at the midpoint of the long side is constantly increasing. As the propulsion distance of the working face increases, the exposed area of the main roof becomes larger and larger. Under the action of self-weight and overlying load, the absolute value of the control bending moment at the midpoint of the long side increases accordingly.

Under the same propulsion distance of the working face, the absolute value of the control bending moment at the midpoint of the long side is the largest, and the absolute value of the control bending moment at the midpoint of the short side is the smallest, indicating the main roof breaks first from the midpoint of the long side. As the coal mining face advances, the midpoint of the middle and the midpoint of the short side break successively.

The absolute values of the control bending moments at the midpoint of long side and the middle vary greatly with the propulsion distance of the working face, indicating that the propulsion distance of the working face mainly affects the control bending moments at the midpoint of long side and the middle.

Effect of the working face length

The length of the long-wall face is generally over 80 m. With the emergence of high-yield and efficient mines and the requirements of intensive production of one shaft and one face, the length of coal mining faces has been continuously broken through. In some shallow-buried coal seams and mining areas with superior geological conditions, ultra-long working faces have even emerged. The length of the working face once reached more than 350 m, and new lengths of the working face are constantly being tried. The change curve of the absolute value of the control bending moment at the midpoint with the length of the working face is shown in Fig. 9.

Fig. 9
figure 9

Change curve of Mok with t.

Full size image

It can be known from Fig. 9 that when the length of the working face is 120 m, the absolute value of the control bending moment at the midpoint of the long side is 40.67 MN. When the length of the working face is 420 m, the absolute value of the control bending moment at the midpoint of the long side is 43.52 MN, indicating that as the length of the working face increases, the absolute value of the control bending moment at the midpoint of the long side keeps increasing. The change curve of the absolute value of the control bending moment at the midpoint of the long side with the length of the working face becomes increasingly gentle, indicating that the promoting effect of the length of the working face on the absolute value of the control bending moment at the midpoint of the long side is constantly decreasing. With the increase of the working face length, the newly exposed load of the main roof is borne by the newly exposed long side. Therefore, the absolute value of the control bending moment at the midpoint of the long side does not increase significantly. The absolute value of the control bending moment at the midpoint of the middle shows the same variation law.

It can be known from Fig. 9 that when the length of the working face is 120 m, the absolute value of the control bending moment at the midpoint of the short side is 4.52 MN. When the length of the working face is 420 m, the absolute value of the control bending moment at the midpoint of the short side is 0.39 MN, indicating that as the length of the working face increases, the absolute value of the control bending moment at the midpoint of the short side continuously decreases. The change curve of the absolute value of the control bending moment at the midpoint of the short side with the length of the working face becomes increasingly gentle, indicating that the inhibitory effect of the working face length on the absolute value of the control bending moment at the midpoint of the short side is constantly decreasing. As the length of the working face increases, the newly exposed load of the main roof is borne by the newly exposed long side, and the load originally allocated to the short side also partially migrates to the long side. Therefore, the absolute value of the control bending moment at the midpoint of the short side begins to decrease.

Under the same working face length, the absolute value of the control bending moment at the midpoint of the long side is the largest, and the absolute value of the control bending moment at the midpoint of the short side is the smallest, indicating the main roof breaks first from the midpoint of the long side. As the coal mining face advances, the midpoint of the middle and the midpoint of the short side break successively.

Although the absolute values of the control bending moments at the midpoint of the long side and the middle keep increasing with the length of the working face, the increase is limited, basically remaining unchanged from the initial values, which to a certain extent explains the reason for the continuous breakthroughs in the length of the working face.

Effect of lateral load

The lateral load of the main roof mainly come from the self-weight, the loads exerted by the overlying strata on the basic roof, etc. The change curve of the absolute value of the control bending moment at the midpoint with the lateral load is shown in Fig. 10.

Fig. 10
figure 10

Change curve of Mok with q.

Full size image

Taking the long side as an example, the effect of the lateral load on the absolute value of the control bending moment at the midpoint is studied. It can be known from Fig. 10 that when the lateral load is 0.25 MPa, the absolute value of the control bending moment at the midpoint of the long side is 43.44 MN. When the lateral load is 0.50 MPa, the absolute value of the control bending moment at the midpoint of the long side is 86.87 MN, indicating that with the increase of the lateral load, the absolute value of the control bending moment at the midpoint of the long side increases significantly. The absolute value of the control bending moment at the midpoint of the long side increases approximately linearly with the lateral load, meaning that the promoting effect of the lateral load on the absolute value of the control bending moment at the midpoint of the long side remains approximately constant. With the increase of the lateral load, in order to maintain mechanical balance, the internal force of the main roof increases accordingly.

Under the same lateral load, the absolute value of the control bending moment at the midpoint of the long side is the largest, and the absolute value of the control bending moment at the midpoint of the short side is the smallest, indicating the main roof breaks first from the midpoint of the long side. As the coal mining face advances, the midpoint of the middle and the midpoint of the short side break successively.

The absolute values of the control bending moments at the midpoint of long side and the middle vary greatly with the lateral load, indicating that the lateral load mainly affects the control bending moments at the midpoint of long side and the middle.

Effect of poisson’s ratio

Rocks of different strengths have different Poisson’s ratios. The greater the strength of the rock, the smaller the Poisson’s ratio. The main roof has greater strength than the immediate roof and the overlying strata, and the Poisson’s ratio is smaller. Therefore, the influence of the Poisson’s ratio on the absolute value of control bending moment at the midpoint is discussed within the range of 0.20–0.30. The change curve of the absolute value of the control bending moment at the midpoint with the Poisson’s ratio is shown in Fig. 11.

Fig. 11
figure 11

Change curve of Mok with ν.

Full size image

Taking the long side as an example, the effect of Poisson’s ratio on the absolute value of the control bending moment at the midpoint is studied. It can be known from Fig. 11 that when the Poisson’s ratio is 0.2, the absolute value of the control bending moment at the midpoint of the long side is 43.44 MN. When the Poisson’s ratio is 0.3, the absolute value of the control bending moment at the midpoint of the long side is 43.44 MN, indicating that with the increase of the Poisson’s ratio, the absolute value of the control bending moment at the midpoint of the long side does not increase significantly. The absolute value of the control bending moment at the midpoint of the long side varies approximately in a horizontal straight line with the Poisson’s ratio, meaning that the Poisson’s ratio has almost no effect on the absolute value of the control bending moment at the midpoint of the long side.

Under the same Poisson’s ratio, the absolute value of the control bending moment at the midpoint of the long side is the largest, and the absolute value of the control bending moment at the midpoint of the short side is the smallest, indicating the main roof breaks first from the midpoint of the long side. As the coal mining face advances, the midpoint of the middle and the midpoint of the short side break successively.

Verification of the rupture law of the main roof

The coal mining face underground is dynamically migrating. As the propulsion distance of the working face increases, the coal mining face continuously approaches the upper and lower slopes of the mining area or the main transportation roadway. Based on the rupture direction and rupture sequence of each region of the main roof, the rupture law of the main roof can be determined, as shown in Fig. 12.

Fig. 12
figure 12

Primary rupture law of main roof.

Full size image

As can be seen from Fig. 12, as the working face advances, the control bending moment at the midpoint of the long side reaches the ultimate bending moment. The midpoint of the long side breaks first, and then extends along the length direction of the working face to both sides. The working face continues to advance, the control bending moment at the midpoint of the middle reaches the ultimate bending moment. The midpoint of the middle begins to break and then extends along the length of the working face to both sides. As the working face advances further, the control bending moment at the midpoint of the short side reaches the ultimate bending moment. The midpoint of the short side begins to break, and then extends to both sides along the propulsion direction of the working face, eventually forming an O-X type rupture morphology.

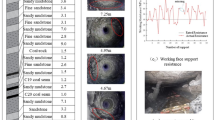
Based on the engineering overview of the 1304 working face of a certain coal mine of China Coal Group, Wang et al.36set the periphery of the thin plate as the fixed boundary and applied uniform loads until rupture. The rupture morphology of the main roof with fixed support on all four sides is shown in Fig. 13.

Fig. 13
figure 13

Rupture morphology of main roof36.

Full size image

It can be known from Fig. 13 that the main roof shows a typical O-X type rupture. The rupture line cuts the main roof into blocks with a trapezoidal middle and triangular sides36. The test results show a certain degree of consistency with the results of the theoretical analysis in this paper, verifying the correctness of the theoretical analysis.

Conclusion

Accurately understanding the primary rupture law of main roof in long-wall face has important theoretical and practical significance. By establishing and visualizing new rupture index, the rupture direction of each region of the main roof was theoretically analyzed, the rupture sequence of each region of the main roof was explored, and the rupture law of the main roof was verified based on the relevant model experiment.

(1) The rupture of the long-side region of the main roof extends along the length direction of the working face starting from the midpoint of the long side, the rupture of the middle region extends along the length direction of the working face starting from the midpoint of the middle, and the rupture of the short-side region extends along the propulsion direction of the working face starting from the midpoint of the short side.

(2) Under various influencing factors, the absolute value of the control bending moment at the midpoint of the long side is the largest, and the absolute value of the control bending moment at the midpoint of the short side is the smallest. The main roof breaks first from the midpoint of the long side. As the coal mining face advances, the midpoint of the middle and the midpoint of the short side break successively, eventually forming an O-X type rupture morphology.

(3) The propulsion distance of the working face and the lateral load mainly affect the control bending moment at the midpoint of the long side and the middle of the main roof, and have a relatively small influence on the control bending moment at the midpoint of the short side. The length of the working face and Poisson’s ratio hardly affect the control bending moments at the midpoint of the long side, the middle and the short side.

In this paper, PBM is taken as the new rupture index, and the rupture law of the main roof with fixed support on all four sides is obtained. The main roof breaks from the midpoint of the long side and then extends along the length direction of the working face. To prevent spillage in the rupture area, the hydraulic support in the rupture area should increase the supporting resistance, thereby ensuring the safe production of the working face. The rupture law of the main roof in this paper is obtained based on the boundary conditions of fixed support on all four sides. However, the immediate roof and coal seam in reality are not rigid bodies in the complete sense. The subsequent studies should focus on the rupture law of the main roof under other boundary conditions.