Nonlinear behavior of dispersive solitary wave solutions for the propagation of shock waves in the nonlinear coupled system of equations

Abstract

In this paper, the nonlinear coupled system of partial differential equations named the Wu–Zhang system investigated by applying the new auxiliary equation method. The Wu–Zhang system help us to investigate the various nonlinear wave propagation phenomena physically including the width and amplitude of solitons, physically form of shock, traveling and solitary wave structures in fiber optics, fluid dynamics, plasma physics, nonlinear optics, these nonlinear wave equations play significant role in these phenomenas. In this regard, the dispersive long wave is described by the Wu–Zhang system, from which a number of solitons and solitary wave structure are formally extracted as an accomplishment. On the basis of the computational program Mathematica, soliton and many other solitary wave results have been obtained with the ability to use an analytical approach. Consequently, various solutions in solitons and solitary waves are generated in rational, trigonometric, and hyperbolic functions and displayed within contour, two–dimension and three–dimension plotting by using the numerical simulation. The soliton solutions are obtained including bright and dark solitons, anti–kink wave solitons, peakon bright and dark solitons, kink wave soliton, periodic wave solitons, solitary wave structure, and other mixed solitons. In order to comprehend the significance of investigating various nonlinear wave phenomena in engineering and science, including soliton theory, nonlinear optics, fluid mechanics, material energy, water wave mechanics, mathematical physics, signal transmission, and optical fibers, all research outcomes are required. With precise analytical results, shed light that the applied approach to be more powerful, dependable, and accurate.

Introduction

The nonlinear evolution equations (NLEEs) are used in various domains as a mathematical tool. These equations play a significant role in various applied sciences and engineering including nonlinear dynamics, fiber optics, nonlinear optics, fluid dynamics, communication system, electronic engineering, computing engineering and ocean engineering^1,2,3. Researchers are increasingly investigating the exact solutions of NLEEs to understand complex physical phenomena. Analytical solutions to the NLEEs are crucial in nonlinear sciences, particularly in nonlinear physical sciences, as they play significant role in physical information and lead to further applications. The researchers from the various domains of physics, mathematics, and engineering having the great interest to investigate the nonlinear models in various fields, including soliton wave theory, nonlinear dynamics, ion acoustic wave phenomena, nonlinear optics, bio–mathematics, optical fibers, ocean engineering, chemical engineering, electronic engineering, computing engineering, communication system, artificial engineering, kinematics, plasma physics, geochemistry, geophysics, solid sate physics, mathematical physics, computer networking and elastic media. The development of nonlinear science has also increased interest among young scientists^4,5,6. The process of solving nonlinear equations is frequently difficult, and numerous methods have been developed to handle the analysis of these kinds of systems. Applications of solitons and nonlinear waves include soliton dynamics, fiber optics, biomedical issues, fluid dynamics, engineering, and industrial phenomena. There is a growing interest in studying the propagation of nonlinear waves, which tend to travel through dynamical systems. Numerous scientific and engineering fields, such as electro-chemistry, electromagnetic theory, nonlinear dynamics, cosmology, soliton wave theory, acoustics, atomic physics, astrophysics, geo-physics, transmission system, can benefit from their use. The researchers have been investigated the various kind of analytical soliton solution to solve complex physical models due to a lack of work on nonlinear problems^7,8,9,10.

Over the course of the past ten decades, numerous groups of academics, scientists, and mathematicians have developed a wide variety of effective methods for solving nonlinear partial differential equations. The name of some important methods are, the new auxiliary equation technique¹¹, the first integral technique¹², the lumped Galerkin technique¹³, exp$(-\Phi (\eta ))-$function approach¹⁴, the auxiliary equation technique^15,16, improved $\left( \frac{G^{\prime }}{G}+G+A\right) -$expanded technique¹⁷, extended simple equation technique^18,19,20,21, the modified sardar sub equation technique²², new Kudryashov scheme²³, tanh coth scheme²⁴, the the $(G^{\prime }/G^{2}-)$expanded scheme²⁵, general exponential rational function technique^26,27, Darboux transformation²⁸, extended direct algebraic technique^29,30,31, extended simple equation technique^32,33, sine cosine technique³⁴, extension of auxiliary equation mapping technique^35,36,37,38, modified extended auxiliary equation mapping technique^{39,40,41,42,43}, improved tanh function technique⁴⁴, and improved F–expansion technique^45,46. The investigation into the solutions, structures, interactions, and additional properties of soliton received a great deal of attention, and a number of significant results were successfully derived as a result of this investigation.

A nonlinear wave equation that is well-known is called the Wu–Zhang system. The nonlinear Wu–Zhang system given^51,52 as

$$\begin{aligned} \nonumber&U_{t }+ V_{x}+ U U_{x}=0, \\&V_{t}+\frac{1}{3} U_{xxx}+\left( U V \right) _{x}=0. \end{aligned}$$

(1)

In the Eq.(1), the $U_{t}$ is representing to the elevation of water and $V_{t}$ is representing to the surface velocity of water. In order to investigate the various nonlinear wave propagation phenomena physically including the width and amplitude of solitons, physically form of shock, traveling and solitary wave structures in fiber optics, fluid dynamics, plasma physics, nonlinear optics, these nonlinear wave equations play significant role in these phenomenas. The transformations of the examined wave solutions, into shock wave profiles are analysed. The time coefficient functions contained in the equation and the effects of the parameters in the solutions are discussed by considering the physically form of shock waves, width and amplitude of solitons, and wave dispersion process. In the previous studies, researchers explored the various analytical and numerical solutions under different methods for the nonlinear Wu–Zhang system. Triki et al. explored the topological and non–topological solitons solutions for the Wu–Zhang equation using the ansatz method⁴⁷. Hosseini et al. utilized the first integral method and secured precise solitary wave solutions of the nonlinear Wu–Zhang equation⁴⁸. Mustafa et al. found the singular, solitary, and multi–solitons for the Wu–Zhang equation by applying two different techniques, namely extended tanh and Hirota approaches⁴⁹. Kaplan et al. utilized the modify simple equation and exponential rational function techniques to precisely describe the traveling wave solutions to the Wu–Zhang equation⁵⁰. Eslami et al. utilized the first integral approach and extracted exact solitons of the Wu–Zhang equation⁵¹. Khater et al. found the solutions in dispersive long wave form of nonlinear Wu–Zhang system under modify auxiliary equation technique⁵². But, in this study examined the soliton and many other solitary wave solutions to the nonlinear Wu–Zhang system under new auxiliary equation method. The examined solutions are more interested, novel and generalized in the various soliton and solitary wave structure.

The arrangement of this investigation given in these section: the introduction describe with literature review about the governing equation in section 1. In section 2, explain the proposed methodology with all steps. We extracted the novel results in soliton and solitary wave structures to the nonlinear Wu–Zhang system under proposed technique in section 3. In section 4, comparing and disusing the extracted results. The concluding remarks describing of this investigation at the end.

Summery of utilized approach

The nonlinear system of equation given as

$$\begin{aligned}&L_{1}(u,~v,~u_{t},~v_{t},~u_{x},~v_{x},~ u_{xx},~v_{xx},~u_{tt},~v_{tt},~u_{xxx},~v_{xxx},...... )=0,\nonumber \\&M_{1}(u,~v,~u_{t},~v_{t},~u_{x},~v_{x},~ u_{xx},~v_{xx},~u_{tt},~v_{tt},~u_{xxx},~v_{xxx},...... )=0. \end{aligned}$$

(2)

Where $L_{1},~M_{1}$ are the polynomial functions for unknown functions u and v. Consider the transformation for Eq.(2) as

$$\begin{aligned} u ( x,t )= w( \varsigma ), \quad v ( x,t )= q( \varsigma ), \quad \quad \varsigma = x + \mu t. \end{aligned}$$

(3)

Through Eq.(3), get the system of nonlinear equations with ordinary derivatives as

$$\begin{aligned}&L_{2}\left( w,~q,~w^{\prime },~q^{\prime },~ w^{\prime \prime },~ q^{\prime \prime },~w^{\prime \prime \prime },~ q^{\prime \prime \prime }, ...\right) =0,\nonumber \\&M_{2}\left( w,~q,~w^{\prime },~q^{\prime },~ w^{\prime \prime },~ q^{\prime \prime },~w^{\prime \prime \prime },~ q^{'''}, ...\right) =0. \end{aligned}$$

(4)

While $L_{2},~M_{2}$ are the polynomial functions for unknown functions w, q and their derivatives. In Eq.(4) prime represent to the ordinary derivative with respect to $\varsigma .$

Under the mathematical calculations the system of nonlinear ordinary differential equations (NLODEs) change into ordinary differential equation as

$$\begin{aligned} H\left( w,~w^{\prime },~ w^{\prime \prime },~w^{'''}, ...\right) =0. \end{aligned}$$

(5)

The generalized solution to the Eq.(5) given as

$$\begin{aligned} w(\varsigma )=a_{0}+\sum _{k=1}^N \left( a_k \varphi ^{k} (\varsigma )+b_k \varphi ^{-k} (\varsigma ) \right) . \end{aligned}$$

(6)

Where $a_{0}, a_{k}, b_{k}~(k=1,2,3,....)$ are constants which calculate be later. Utilizing the homogeneous scheme on Eq.(5) to securing N. The $\varphi (\varsigma )$ satisfy the following Riccati equation.

$$\begin{aligned} \left( \frac{d \varphi }{d \varsigma }\right) = \varphi ^{2}(\varsigma )+c. \end{aligned}$$

(7)

Where c is constant. The nine exact solutions for Eq.(6) are given as belows:

When $c<0,$ the hyperbolic solutions for Eq.(6) are

$$\begin{aligned} & \varphi _{1}(\varsigma )=\frac{\sqrt{-\left( p^2+q^2\right) c}-p\sqrt{-c} \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}, \end{aligned}$$

(8)

$$\begin{aligned} & \varphi _{2}(\varsigma )=\frac{-\sqrt{-\left( p^2+q^2\right) c}-p\sqrt{-c} \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}, \end{aligned}$$

(9)

$$\begin{aligned} & \varphi _{3}(\varsigma )=\sqrt{-c}+\frac{-2 p\sqrt{-c} }{p+\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }, \end{aligned}$$

(10)

$$\begin{aligned} & \varphi _{4}(\varsigma )=-\sqrt{-c}+\frac{-2 p\sqrt{-c} }{p+\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }. \end{aligned}$$

(11)

When $c>0,$ the trigonometric solutions for Eq.(6) are

$$\begin{aligned} & \varphi _{5}(\varsigma )=\frac{\sqrt{\left( p^2-q^2\right) c}-p\sqrt{c} \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}, \end{aligned}$$

(12)

$$\begin{aligned} & \varphi _{6}(\varsigma )=\frac{-\sqrt{ \left( p^2-q^2\right) c}-p\sqrt{c} \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}, \end{aligned}$$

(13)

$$\begin{aligned} & \varphi _{7}(\varsigma )=i \sqrt{c}+\frac{-2 p i \sqrt{c} }{p+\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }, \end{aligned}$$

(14)

$$\begin{aligned} & \varphi _{8}(\varsigma )=-i \sqrt{c}+\frac{2 p i \sqrt{c} }{p+\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }. \end{aligned}$$

(15)

When $c=0,$ the rational solution for Eq.(6) given as

$$\begin{aligned} \varphi _{9}(\varsigma )=-\frac{1}{\varsigma +\varsigma _{0}}. \end{aligned}$$

(16)

Where p, q and r in Eqs.(7)–(15) are constants. Setting Eq.(6) in Eq.(5) with Eq.(7), and combing the every factors of $\varphi ^{k}(\varsigma ) (k=1,2,3,...),$ and make them equal to zero. Then securing the set of equations and solve them by any computing software to extract the unknown values. Setting these values and $\varphi (\varsigma )$ into Eq.(6) and secured required results to the system of nonlinear equations.

Solitary wave solutions of nonlinear Wu–Zhang system

The wave transformation for Eq.(1), consider as

$$\begin{aligned} U ( x, t )= W( \varsigma ), \quad V ( x, t )= Q( \varsigma ), \quad \quad \varsigma = x + \mu t. \end{aligned}$$

(17)

Substitute Eq.(17) into Eq.(1), we obtained as

$$\begin{aligned} & \mu W^{\prime } + W W^{\prime }+Q^{\prime }=0. \end{aligned}$$

(18)

$$\begin{aligned} & \mu Q^{\prime } + W^{\prime } Q + W Q^{\prime }+\frac{1}{3} W^{'''}=0. \end{aligned}$$

(19)

Integrating once yields the Eq.(18), and secure the integration constant to be zero.

$$\begin{aligned} Q=-\mu W -\frac{1}{2} W^{2}. \end{aligned}$$

(20)

Putting the value of Q in Eq.(19), secure as

$$\begin{aligned} \mu ^{2} W^{\prime } -3 \mu W W^{\prime }+\frac{3}{2} W^{2} W^{\prime }-\frac{2}{3} W^{'''}=0. \end{aligned}$$

(21)

Integrate once the Eq.(21), finally get as

$$\begin{aligned} 6 \mu ^{2} W -9 \mu W^{2}+3 W^{3}-2 W^{\prime \prime }{\prime \prime }=0. \end{aligned}$$

(22)

Where taken the integration constant to be zero. Utilizing the homogeneous technique on Eq.(22), secured $N=1.$ The exact solution to the Eq.(22), given as

$$\begin{aligned} W (\varsigma ) =a_{0}+a_{1}{\varphi (\varsigma )}+\frac{b_{1}}{\varphi (\varsigma )}. \end{aligned}$$

(23)

Substitute Eq.(23) along with Eq.(6) in Eq.(22) and collect the every factors to the $\varphi ^{k}(\varsigma ), (i=1,2,3,...),$ and make them equal to zero. Then securing the set of equations in constant parameters $a_{0}, a_{1}, b_{1},$ and $\mu .$ These parameters values in the set of equations are solved by Mathematica software to obtain the following solutions cases.

Family–I

$$\begin{aligned} a_0=a_0,~~a_1= 0,~~b_1= -\frac{1}{2} \sqrt{3} a_0^2,~~\mu = a_0,~~c= -\frac{1}{4} \left( 3 a_0^2\right) . \end{aligned}$$

(24)

Substitute Eq.(24) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–I with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{1}(x,t)= \frac{1}{2} a_0 \left( 2-\frac{\sqrt{3} a_0 \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }\right) , \end{aligned}$$

(25)

$$\begin{aligned}&U_{2}(x,t)=\frac{1}{2} a_0 \left( \frac{\sqrt{3} a_0 \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }+2\right) , \end{aligned}$$

(26)

$$\begin{aligned}&U_{3}(x,t) =\frac{\sqrt{3} a_0^2 \sqrt{-c}}{2 c-\frac{4 c p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}}+a_0, \end{aligned}$$

(27)

$$\begin{aligned}&U_{4}(x,t)=\frac{\sqrt{3} a_0^2 \sqrt{-c}}{-\frac{4 c p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-2 c}+a_0. \end{aligned}$$

(28)

Where $\varsigma = x + \mu t.$

We consider the case–2 as $c>0$ and using the family–I with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{5}(x,t) =a_0-\frac{\sqrt{3} a_0^2 \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{2 \left( \sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }, \end{aligned}$$

(29)

$$\begin{aligned}&U_{6}(x,t) =\frac{\sqrt{3} a_0^2 \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{2 \left( \sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }+a_0, \end{aligned}$$

(30)

$$\begin{aligned}&U_{7}(x,t) =a_0+\frac{\sqrt{3} i a_0^2}{\sqrt{c} \left( 2-\frac{4 p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }, \end{aligned}$$

(31)

$$\begin{aligned}&U_{8}(x,t) =a_0-\frac{i \sqrt{3} a_0^2}{\sqrt{c} \left( 2-\frac{4 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }. \end{aligned}$$

(32)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–I with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned}&U_{9}(x,t) =\frac{1}{2} \sqrt{3} a_0^2 (\varsigma +\varsigma _{0})+a_0. \end{aligned}$$

(33)

Where $\varsigma = x + \mu t.$

Family–II

$$\begin{aligned} a_0=a_0,~~a_1= -\frac{2}{\sqrt{3}},~~b_1= 0,~~\mu = a_0,~~c= -\frac{1}{4} \left( 3 a_0^2\right) . \end{aligned}$$

(34)

Substitute Eq.(34) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–II with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{10}( x,t)=a_0-\frac{2 \left( \sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }, \end{aligned}$$

(35)

$$\begin{aligned}&U_{11}(x,t)=a_0+\frac{2 \left( \sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }, \end{aligned}$$

(36)

$$\begin{aligned}&U_{12}(x,t)=a_0+\frac{2 \sqrt{-c} \left( \frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1\right) }{\sqrt{3}}, \end{aligned}$$

(37)

$$\begin{aligned}&U_{13}(x,t)=a_0+\frac{2 \sqrt{-c} \left( \frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}+1\right) }{\sqrt{3}}. \end{aligned}$$

(38)

Where $\varsigma = x + \mu t.$

We consider the case–2 as $c>0$ and using the family–II with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{14}( x,t)=a_0-\frac{2 \left( \sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }, \end{aligned}$$

(39)

$$\begin{aligned}&U_{15}(x,t)=a_0+\frac{2 \left( \sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }, \end{aligned}$$

(40)

$$\begin{aligned}&U_{16}(x,t)=a_0-\frac{2 i \sqrt{c} \left( 1-\frac{2 p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }{\sqrt{3}}, \end{aligned}$$

(41)

$$\begin{aligned}&U_{17}(x,t)=a_0+\frac{2 i \sqrt{c} \left( 1-\frac{2 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }{\sqrt{3}}. \end{aligned}$$

(42)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–II with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{18}(x,t)=a_0+\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(43)

Where $\varsigma = x + \mu t.$

Fig. 1

Visualization of $U_{2}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to anti–kink wave soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0} =0.2, \mu =1.5, a_{0}=-3$.

Fig. 2

Visualization of $U_{4}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to kink wave soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Family–III

$$\begin{aligned} a_0= -2 \sqrt{\frac{2}{3}} \sqrt{c},~~a_1= -\frac{2}{\sqrt{3}},~~b_1= -\frac{2 c}{\sqrt{3}},~~\mu = -2 \sqrt{\frac{2}{3}} \sqrt{c}. \end{aligned}$$

(44)

Substitute Eq.(44) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–III with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{19}( x,t)=\frac{2 \left( \frac{\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\sqrt{-c \left( p^2+q^2\right) }}{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}-\frac{c \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }-\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(45)

$$\begin{aligned}&U_{20}(x,t)=\frac{2 \left( \frac{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }-\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(46)

$$\begin{aligned}&U_{21}(x,t)=\frac{2\left( 2 \sqrt{-c} p-\sqrt{2} \sqrt{c}\right. \left( \frac{1}{-\sinh \left( 2 \sqrt{-c} (r+\mu t+x)\right) +\cosh \left( 2 \sqrt{-c} (r+\mu t+x)\right) +p}\right. }{\sqrt{3}} \nonumber \\&\left. \left. -\frac{1}{\sinh \left( 2 \sqrt{-c} (r+\mu t+x)\right) -\cosh \left( 2 \sqrt{-c} (r+\mu t+x)\right) +p}\right) \right) , \end{aligned}$$

(47)

$$\begin{aligned}&U_{22}(x,t)= \frac{2\left( 2 \sqrt{-c} p-\sqrt{2} \sqrt{c}\right. \left( \frac{1}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right. }{\sqrt{3}} \nonumber \\&\left. \left. +\frac{1}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +3 p}\right) \right) . \end{aligned}$$

(48)

Where $\varsigma = x + \mu t.$

Fig. 3

Visualization of $U_{5}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 4

Visualization of $U_{6}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=3$.

We consider the case–2 as $c>0$ and using the family–III with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{23}( x,t)=\frac{2 \left( \frac{\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\sqrt{c \left( p^2-q^2\right) }}{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\sqrt{c \left( p^2-q^2\right) }}-\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(49)

$$\begin{aligned}&U_{24}(x,t)=\frac{2 \left( \frac{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} ((\varsigma +\varsigma _{0}))\right) }-\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(50)

$$\begin{aligned}&U_{25}(x,t)=\frac{2 \sqrt{c} \left( \frac{i}{1-\frac{2 p}{-i \sin \left( 2 \sqrt{c} ((\varsigma +\varsigma _{0}))\right) +\cos \left( 2 \sqrt{c} ((\varsigma +\varsigma _{0}))\right) +p}}+\frac{2 i p}{-i \sin \left( 2 \sqrt{c} ((\varsigma +\varsigma _{0}))\right) +\cos \left( 2 \sqrt{c} ((\varsigma +\varsigma _{0}))\right) +p}-i-\sqrt{2}\right) }{\sqrt{3}}, \end{aligned}$$

(51)

$$\begin{aligned}&U_{26}(x,t)=\frac{2 \sqrt{c} \left( -\frac{i}{1-\frac{2 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}}-\frac{2 i p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}+i-\sqrt{2}\right) }{\sqrt{3}}. \end{aligned}$$

(52)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–III with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{27}(x,t)=\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(53)

Where $\varsigma = x + \mu t.$

Fig. 5

Visualization of $U_{7}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=8, p=1, q=1, \varsigma _{0}=0.2, \mu =1.5, a_{0}=3$.

Fig. 6

Visualization of $U_{8}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=1, q=1, \varsigma _{0}=0.2, \mu =1.5, a_{0}=3$.

Family–IV

$$\begin{aligned} a_0= 2 \sqrt{\frac{2}{3}} \sqrt{c},~~a_1= \frac{2}{\sqrt{3}},~~b_1= \frac{2 c}{\sqrt{3}},~~\mu = 2 \sqrt{\frac{2}{3}} \sqrt{c}. \end{aligned}$$

(54)

Substitute Eq.(54) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–IV with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{28}( x,t)=\frac{2 \left( \frac{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }+\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(55)

$$\begin{aligned}&U_{29}(x,t)=\frac{2 \left( -\frac{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}-\frac{c \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }+\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(56)

$$\begin{aligned}&U_{30}(x,t)=\frac{2 \left( 2 \sqrt{-c} p \left( \frac{1}{\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-\frac{1}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) +\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(57)

$$\begin{aligned}&U_{31}(x,t)=\frac{2 \left( 2 \sqrt{-c} p \left( \frac{1}{\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -3 p}-\frac{1}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) +\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}. \end{aligned}$$

(58)

Where $\varsigma = x + \mu t.$

Fig. 7

Visualization of $U_{10}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to anti–kink wave soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 8

Visualization of $U_{11}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to mixed dark–bright soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

We consider the case–2 as $c>0$ and using the family–IV with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{32}( x,t)=\frac{2 \left( \frac{\sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }+\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(59)

$$\begin{aligned}&U_{33}(x,t)=\frac{2 \left( -\frac{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}-\frac{c \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }+\sqrt{2} \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(60)

$$\begin{aligned}&U_{34}(x,t)=\frac{2 \sqrt{c} \left( -\frac{i}{1-\frac{2 p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}}-\frac{2 i p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}+i+\sqrt{2}\right) }{\sqrt{3}}, \end{aligned}$$

(61)

$$\begin{aligned}&U_{35}(x,t)=\frac{2 \sqrt{c} \left( \frac{i}{1-\frac{2 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}}+\frac{2 i p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}-i+\sqrt{2}\right) }{\sqrt{3}}. \end{aligned}$$

(62)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–IV with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{36}(x,t)=-\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(63)

Where $\varsigma = x + \mu t.$

Fig. 9

Visualization of $U_{13}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to anti–kink wave soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 10

Visualization of $U_{14}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Family–V

$$\begin{aligned} a_0= \frac{4 i \sqrt{c}}{\sqrt{3}},~~a_1= -\frac{2}{\sqrt{3}},~~b_1= \frac{2 c}{\sqrt{3}},~~\mu = \frac{4 i \sqrt{c}}{\sqrt{3}}. \end{aligned}$$

(64)

Substitute Eq.(64) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–V with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{37}( x,t)=\frac{2 \left( \frac{\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\sqrt{-c \left( p^2+q^2\right) }}{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }+2 i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(65)

$$\begin{aligned}&U_{38}(x,t)=\frac{2 \left( \sqrt{-c \left( p^2+q^2\right) }+i \sqrt{c} p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +i \sqrt{c} q\right) ^2}{\sqrt{3} \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) \left( \sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) \right) }, \end{aligned}$$

(66)

$$\begin{aligned}&U_{39}(x,t)= \frac{2\left( \sqrt{-c}+2 i \sqrt{c}\right. \left( -\frac{1}{1-\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}}-1\right. }{\sqrt{3}}\nonumber \\&\left. \left. +\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) \right) , \end{aligned}$$

(67)

$$\begin{aligned}&U_{40}(x,t)= \frac{2\left( \sqrt{-c}+2 i \sqrt{c}\right. \left( 1-\frac{1}{-\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1}\right. }{\sqrt{3}}\nonumber \\&\left. \left. +\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) \right) . \end{aligned}$$

(68)

Where $\varsigma = x + \mu t.$

We consider the case–2 as $c>0$ and using the family–V with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{41}( x,t)=\frac{2 \left( \frac{\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\sqrt{c \left( p^2-q^2\right) }}{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}+\frac{c \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }+2 i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(69)

$$\begin{aligned}&U_{42}(x,t)=\frac{2 \left( \sqrt{c \left( p^2-q^2\right) }+i \sqrt{c} p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +i \sqrt{c} q\right) ^2}{\sqrt{3} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) \left( \sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }, \end{aligned}$$

(70)

$$\begin{aligned}&U_{43}(x,t)=\frac{8 i \sqrt{c} p^2}{\sqrt{3} \left( \sin ^2\left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +i \sin \left( 4 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\cos ^2\left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p^2\right) }, \end{aligned}$$

(71)

$$\begin{aligned}&U_{44}(x,t)=\frac{8 \sqrt{c} \left( \sin \left( 4 \sqrt{c} (\varsigma +\varsigma _{0})\right) -i \cos \left( 4 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( \sin ^2\left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -i \sin \left( 4 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\cos ^2\left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p^2\right) }. \end{aligned}$$

(72)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–V with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{45}(x,t)=\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(73)

Where $\varsigma = x + \mu t.$

Family–VI

$$\begin{aligned} a_0= -\frac{2 i \sqrt{c}}{\sqrt{3}},~~a_1= 0,~~b_1= -\frac{2 c}{\sqrt{3}},~~\mu = -\frac{2 i \sqrt{c}}{\sqrt{3}}. \end{aligned}$$

(74)

Substitute Eq.(74) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–VI with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{46}( x,t)=\frac{2 \sqrt{c} \left( -\frac{\sqrt{c} \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }-i\right) }{\sqrt{3}}, \end{aligned}$$

(75)

$$\begin{aligned}&U_{47}(x,t)=\frac{2 \sqrt{c} \left( \frac{\sqrt{c} \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }-i\right) }{\sqrt{3}}, \end{aligned}$$

(76)

$$\begin{aligned}&U_{48}(x,t)=\frac{2 \sqrt{c} \left( \frac{\sqrt{-c}}{\sqrt{c} \left( 1-\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) }-i\right) }{\sqrt{3}}, \end{aligned}$$

(77)

$$\begin{aligned}&U_{49}(x,t)=\frac{2 \sqrt{c} \left( \frac{\sqrt{-c}}{\sqrt{c} \left( -\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1\right) }-i\right) }{\sqrt{3}}. \end{aligned}$$

(78)

Where $\varsigma = x + \mu t.$

We consider the case–2 as $c>0$ and using the family–VI with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{50}( x,t)=\frac{2 \sqrt{c} \left( \frac{\sqrt{c} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\sqrt{c \left( p^2-q^2\right) }}-i\right) }{\sqrt{3}}, \end{aligned}$$

(79)

$$\begin{aligned}&U_{51}(x,t)=\frac{2 \sqrt{c} \left( \frac{\sqrt{c} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }-i\right) }{\sqrt{3}}, \end{aligned}$$

(80)

$$\begin{aligned}&U_{52}(x,t)=-\frac{4 i \sqrt{c} p}{\sqrt{3} \left( i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p\right) }, \end{aligned}$$

(81)

$$\begin{aligned}&U_{53}(x,t)=\frac{4 i \sqrt{c} \left( \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( -i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p\right) }. \end{aligned}$$

(82)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–VI with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{54}(x,t)=-\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(83)

Where $\varsigma = x + \mu t.$

Fig. 11

Visualization of $U_{15}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 12

Visualization of $U_{16}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=1, q=1, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Family–VII

$$\begin{aligned} a_0= -\frac{2 i \sqrt{c}}{\sqrt{3}},~~a_1= -\frac{2}{\sqrt{3}},~~b_1= 0,~~\mu = -\frac{2 i \sqrt{c}}{\sqrt{3}}. \end{aligned}$$

(84)

Substitute Eq.(84) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case-1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–VII with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{55}( x,t)=\frac{2 \left( \frac{\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) -\sqrt{-c \left( p^2+q^2\right) }}{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}-i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(85)

$$\begin{aligned}&U_{56}(x,t)=\frac{2 \left( \frac{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}-i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(86)

$$\begin{aligned}&U_{57}(x,t)=\frac{2 \left( \sqrt{-c} \left( \frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1\right) -i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(87)

$$\begin{aligned}&U_{58}(x,t)=\frac{2 \left( \sqrt{-c} \left( \frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}+1\right) -i \sqrt{c}\right) }{\sqrt{3}}. \end{aligned}$$

(88)

Where $\varsigma = x + \mu t.$

We consider the case-2 as $c>0$ and using the family–VII with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{59}( x,t)=\frac{2 \left( \frac{\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) -\sqrt{c \left( p^2-q^2\right) }}{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}-i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(89)

$$\begin{aligned}&U_{60}(x,t)=\frac{2 \left( \frac{\sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) }{p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q}-i \sqrt{c}\right) }{\sqrt{3}}, \end{aligned}$$

(90)

$$\begin{aligned}&U_{61}(x,t)=\frac{2 \sqrt{c} \left( \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +i \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +3 i p\right) }{\sqrt{3} \left( -i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p\right) }, \end{aligned}$$

(91)

$$\begin{aligned}&U_{62}(x,t)=\frac{2 i \sqrt{c} \left( 3 i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +3 \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p\right) }{\sqrt{3} \left( i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p\right) }. \end{aligned}$$

(92)

Where $\varsigma = x + \mu t.$

According to case-3 as $c=0$ and using the family–VII with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{63}(x,t)=\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(93)

Where $\varsigma = x + \mu t.$

Fig. 13

Visualization of $U_{67}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to kink wave soliton with $c=-2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 14

Visualization of $U_{68}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 15

Visualization of $U_{69}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=0.5, q=0.5, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Fig. 16

Visualization of $U_{70}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=2, p=1, q=1, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

Family–VIII

$$\begin{aligned}&a_0=a_0,~~a_1= \frac{2}{\sqrt{3}},~~b_1= \frac{1}{8} \sqrt{3} a_0^2,~~\mu = a_0,~~c=-\frac{1}{16} \left( 3 a_0^2\right) . \end{aligned}$$

(94)

Substitute Eq.(94) in Eq.(23), solitary wave structures to the Eq.(1), extracted below as:

By according to the case–1 as $c<0$ of the new AEM and utilizing parameter values arranged in family–VIII with Eq.(7) to Eq.(10) in Eq.(23), then secure the hyperbolic solutions for Eq.(1) as:

$$\begin{aligned}&U_{64}( x,t)=\frac{1}{24}\left( \frac{16 \sqrt{3} \left( \sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) \right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}+24 a_0+\right. \nonumber \\&\left. \frac{3 \sqrt{3} a_0^2 \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }-\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }\right) , \end{aligned}$$

(95)

$$\begin{aligned}&U_{65}(x,t)=\frac{1}{24}\left( 24 a_0-\frac{16 \sqrt{3} \left( \sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) \right) }{p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q}\right. \nonumber \\&\left. -\frac{3 \sqrt{3} a_0^2 \left( p \sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +q\right) }{\sqrt{-c \left( p^2+q^2\right) }+\sqrt{-c} p \cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) }\right) , \end{aligned}$$

(96)

$$\begin{aligned}&U_{66}(x,t)= a_0+\frac{2 \sqrt{-c} \left( 1-\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) }{\sqrt{3}}+\nonumber \\&\frac{\sqrt{3} a_0^2}{8 \sqrt{-c} \left( 1-\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}\right) }, \end{aligned}$$

(97)

$$\begin{aligned}&U_{67}(x,t)= a_0+\frac{2 \sqrt{-c} \left( -\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1\right) }{\sqrt{3}}+\nonumber \\&\frac{\sqrt{3} a_0^2}{8 \sqrt{-c} \left( -\frac{2 p}{-\sinh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +\cosh \left( 2 \sqrt{-c} (\varsigma +\varsigma _{0})\right) +p}-1\right) }. \end{aligned}$$

(98)

Where $\varsigma = x + \mu t.$

We consider the case–2 as $c>0$ and using the family–VIII with the help of Eq.(11) to Eq.(14) in Eq.(23) and secure the trigonometric solutions of Eq.(1) as:

$$\begin{aligned}&U_{68}( x,t)=\frac{2 \left( \sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }+a_0+\nonumber \\&\frac{\sqrt{3} a_0^2 \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{8 \left( \sqrt{c \left( p^2-q^2\right) }-\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }, \end{aligned}$$

(99)

$$\begin{aligned}&U_{69}(x,t)=a_0-\frac{2 \left( \sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }{\sqrt{3} \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }-\nonumber \\&\frac{\sqrt{3} a_0^2 \left( p \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +q\right) }{8 \left( \sqrt{c \left( p^2-q^2\right) }+\sqrt{c} p \cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) \right) }, \end{aligned}$$

(100)

$$\begin{aligned}&U_{70}(x,t)=a_0+\frac{2 i \sqrt{c} \left( 1-\frac{2 p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }{\sqrt{3}}-\nonumber \\&\frac{i \sqrt{3} a_0^2}{\sqrt{c} \left( 8-\frac{16 p}{-i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }, \end{aligned}$$

(101)

$$\begin{aligned}&U_{71}(x,t)= a_0-\frac{2 i \sqrt{c} \left( 1-\frac{2 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }{\sqrt{3}}+\nonumber \\&\frac{i \sqrt{3} a_0^2}{\sqrt{c} \left( 8-\frac{16 p}{i \sin \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +\cos \left( 2 \sqrt{c} (\varsigma +\varsigma _{0})\right) +p}\right) }. \end{aligned}$$

(102)

Where $\varsigma = x + \mu t.$

According to case–3 as $c=0$ and using the family–VIII with the help of Eq.(15) in Eq.(23) and secure the rational solutions of Eq.(1) as:

$$\begin{aligned} U_{72}(x,t)=-\frac{1}{8} \sqrt{3} a_0^2 (\varsigma +\varsigma _{0})+a_0-\frac{2}{\sqrt{3} (\varsigma +\varsigma _{0})}. \end{aligned}$$

(103)

Where $\varsigma = x + \mu t.$

Fig. 17

Visualization of $U_{71}(x,t)$ in contour, two–dim and three–dim plotting demonstrated to periodic wave soliton with $c=4, p=1, q=1, \varsigma _{0}=0.2, \mu =1.5, a_{0}=-3$.

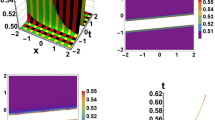
Remarks: The examined solitary wave solutions for the nonlinear coupled system of equations through unified integrated approach are novel, interested and different from the existing literature. The Figures 1–17, represented to physical structure of some solutions in the form of solitary waves, bright solitons, dark solitons, kink wave solitons, mixed bright–dark solitons, peakon solitons, periodic wave solitons, singular solitons, and anti–kink wave solitons.

Results and discussion

In this part of the proposed investigation, the determined results are more interesting and novel in the form of soliton and many solitary wave structure. The generated solutions are novel and more generalized through efficient analytical method. Now elucidate the similarities and differences between our generated results for the nonlinear Wu–Zhang system and those previously determined in the literature. In the past studies researchers have discovered a variety of results for nonlinear Wu–Zhang system. These results examined in elliptic, exponential, trigonometric and hyperbolic functions solutions and having physical structure in traveling waves and solitons. Such as Triki et al. explored the topological and non-topological solitons solutions for the Wu–Zhang equation using the ansatz method⁴⁷. Hosseini et al. utilized the first integral method and secured precise solitary wave solutions of the nonlinear Wu–Zhang equation⁴⁸. Mustafa et al. found the singular, solitary, and multi–solitons for the Wu-Zhang equation by applying two different techniques, namely extended tanh and Hirota approaches⁴⁹. Kaplan et al. utilized the modify simple equation and exponential rational function techniques to precisely describe the traveling wave solutions to the Wu–Zhang equation⁵⁰. Eslami et al. utilized the first integral approach and extracted exact solitons of the Wu–Zhang equation⁵¹. Recently Khater et al. found the solutions in dispersive long wave form of nonlinear Wu–Zhang system under modify auxiliary equation technique⁵². Our constructed results in this study for the nonlinear Wu–Zhang system having a different physical structure. We can see in the Figures 1–17, in the form of solitary waves, bright solitons, dark solitons, kink wave solitons, mixed bright–dark solitons, periodic wave solitons with different structure, peakon bright and dark solitons, mixed singular solitons, and anti–kink wave solitons. The remaining solutions are represent to the varieties of nonlinear wave phenomena such as peakon bright, peakon dark, kink wave, anti–kink wave, kink bright wave, kink dark wave, singular, mixed periodic wave, and singular periodic waves. The graphical representation of the explored solutions prove the ancientness and effectiveness of our proposed methodology. The proposed approach has a capability to investigate the complex problems by using the advance symbolic computation tool.

The examined results for nonlinear governing system are shed light that our proposed method is dependable, more powerful, straightforward, successful, and efficient to use. As a result of the relationship described above and the brief discussion that followed, we are able to be certain that the solutions that were obtained are novel and have not been elaborated by other approaches in the existing literature.

Conclusion

In the current research, investigated the nonlinear Wu–Zhang system on the based of new auxiliary equation method. The various soliton and solitary wave solutions to this nonlinear system are constructed in a variety of different structure. The auxiliary equation approach is a reliable tool to examine the nonlinear models for constructing the enriched exact solutions. Furthermore, after comparing it to various methods and discovering that it encompasses all of them, not only does it cover them all, but it also has the ability to obtain novel solutions that are superior to those methods. The examined solutions through this new technique are interested, more generalized, and did not formulated in the existing literature. Furthermore, the secured results having different physical structure in various soliton, traveling and solitary waves such as kink wave, peakon bright solitons, singular bright and dark solitons, peakon dark solitons, peridic wave solitons within different physical structure, and anti–kink wave solitons. A few of the solutions that obtained plotted within contour, two–dimensional and three–dimensional using the numerical simulation to demonstrate some of their characteristics. It is also a very efficient, powerful, and effective approach. It can also be applied to many different kinds of nonlinear partial differential equations.