Introduction

The global energy landscape is undergoing a paradigm shift toward decentralized, renewable-powered systems, with microgrids emerging as critical enablers of sustainable electrification1,2,3,4. As nations such as China intensify their clean-energy commitments, the integration of variable resources, particularly wind power, into microgrid architectures has become both a technical imperative and an economic challenge5,6,7,8. Day-ahead economic dispatch, which optimizes generation, storage, and consumption schedules 24 h in advance, increasingly embeds carbon-trading signals and multi-energy couplings to suit real-time pricing regimes9,10,11. While renewable integration cuts carbon footprints, the intermittency of wind energy and rigid demand patterns create complex trade-offs between cost efficiency, grid stability, and user satisfaction. This dual challenge motivates advanced dispatch frameworks that harmonize generation assets, storage systems, and demand-side flexibility12,13,14,15.

Effective day-ahead dispatch in wind-integrated microgrids faces three interrelated challenges: (1) temporal mismatch between stochastic wind generation and load profiles, (2) price volatility in electricity markets requiring dynamic cost and risk assessments, and (3) conflicting objectives of minimizing cost while maximizing renewable utilization and user comfort16,17,18,19. Additional operational concerns such as voltage unbalance, inertia support, and islanded-mode reliability further complicate control design for rooftop-photovoltaic (PV) and hybrid microgrids20,21,22,23. Forecast uncertainty, often 10 to 20% mean absolute error even with federated deep-reinforcement-learning predictors24,25, can heighten reliance on costly grid power during deficit periods. At the same time, small-data topology-estimation techniques are beginning to improve prediction robustness and dispatch resilience26,27,28,29. Energy-storage deployment helps but introduces charge-discharge losses and lifecycle costs30,31.

Prior research offers diverse dispatch strategies. Single-objective models that focus solely on cost minimization or renewable-utilization maximization laid the groundwork but overlooked key stakeholder interactions32,33,34. Stochastic programming and deep-learning methods hedge wind uncertainty35,36, whereas game-theoretic formulations incentivize demand response (DR)37. Hosting-capacity assessments and distributed-generation planning studies highlight network constraints that must also be respected in dispatch optimization38. Storage integration has delivered measurable cost savings in islanded microgrids39, and price-elastic DR schemes achieve notable peak-load reduction40. Hybrid DR mechanisms that merge incentive payments with price-based elasticity41 and multi-timescale storage-dispatch rules that consider degradation and adaptive operating modes42,43, together with particle swarm optimization-based strategies for optimal power injection5, mark important progress. Cross-sector investigations into building-level robust scheduling and multi-stage optimization further validate the value of coordinated control under uncertainty29,31,43.

Despite this progress, critical gaps remain: (1) partial resource coordination as most studies optimize wind, storage, or DR in isolation, (2) oversimplified DR modeling that neglects user-comfort trade-offs, and (3) static scenario analysis lacking unified comparative metrics31. Grid-resiliency studies for data centers using spatial and temporal regulation1,29 and distributed optimal dispatch for smart distribution networks20,34,38 underscore the need for holistic, scenario-rich evaluation frameworks. For instance, while Li et al. demonstrated DR-driven cost benefits40 and Sun et al. quantified storage’s renewable-buffering capacity39, no prior work systematically compares scenarios ranging from conventional dispatch to full wind-storage-DR integration. Moreover, recent data-driven voltage-regulation and stability-assessment methods reveal that coordinated multi-timescale interventions can significantly enhance power-quality indices34,41,42.

This paper addresses these limitations through a novel day-ahead economic-dispatch framework featuring:

1) Five operational scenarios comparing conventional, wind-only, wind-storage, wind-DR, and full wind-storage-DR configurations.

2) Hybrid DR that fuses incentive-based load adjustments with dynamic price elasticity via a tariff-scaling-factor approach.

3) Triple-metric evaluation covering cost efficiency, renewable utilization (curtailment rates), and user comfort (load-adjustment frequency and magnitude).

Key innovations include:

● The first comparative analysis of incremental wind-storage-DR benefits under real-time pricing.

● A two-stage DR mechanism balancing grid needs (through incentives) and consumer economics (via price elasticity).

● Practical quantification of comfort-compensated DR potential using peak-reduction, valley-filling, and user- tolerance indices.

The remainder of the paper is organized as follows. Section "Day-ahead economic dispatch model for microgrids considering wind power, energy storage and demand response" describes the day-ahead economic dispatch model for microgrids incorporating wind power, energy storage, and demand response. Section "Evaluation metrics for demand-side response in microgrids" defines the evaluation metrics used to assess demand-side response performance. Section "Case study and simulation analysis" presents the case study and simulation analysis across multiple scenarios, comparing cost distribution, renewable curtailment, and user comfort. Finally, Section "Conclusion" concludes the paper with key findings on optimal coordination strategies for microgrid operation.

Day-ahead economic dispatch model for microgrids considering wind power, energy storage and demand response

Baseline model: microgrid without wind, storage, or demand response participation

In the baseline scenario, the microgrid operates without the integration of wind power, energy storage systems, or DR mechanisms. Under these conditions, there are no restrictions on power exchange with the main grid, and no renewable generation contributes to the microgrid’s supply. Consequently, the entire energy demand must be fulfilled by purchasing electricity directly from the grid. The system only needs to satisfy basic power balance constraints.

The corresponding objective function for this baseline model is presented in Eq. (1):

$${C_1}{\text{=}}\sum\limits_{{i=1}}^{T} {{P_{{\text{zi}}}}} {C_{{\text{z}}i}}$$
(1)

The operational constraints governing this scenario are detailed in Eq. (2):

$$\begin{gathered} {P_{{\text{zi}}}}={P_{li}}, \hfill \\ {P_{{\text{vi}}}}{\text{=}}{P_{wi}}={P_{ci}}=0 \hfill \\ \end{gathered}$$
(2)

Modeling of wind power participation

When wind or solar generation is incorporated, the microgrid faces surplus and shortfall situations. If generation exceeds the load demand, the surplus power can be sold to the main grid; if it falls short, the deficit must be purchased from the main grid. Partial curtailment of wind and solar power is permitted under this model. Additionally, constraints are imposed on the amount of power that can be exchanged between the microgrid and the main grid.

The objective function for this scenario is formulated in Eq. (3), with associated constraints detailed in Eq. (4).

$${C_2}{\text{=}}\sum\limits_{{i=1}}^{{24}} {({P_{vi}}{C_{vi}}+{P_{wi}}{C_{wi}}+{P_{zi}}} {C_{gi}}{y_i} - {P_{zi}}{C_{mi}}(1 - {y_i}))$$
(3)
$$\begin{aligned} &{P_{wi}}+{P_{vi}}+{P_{zi}}={P_{li}} \\&s.t.\,0 \leqslant {P_{wi}} \leqslant {P_{wi\hbox{max} }}\,\,;\,\,\,0 \leqslant {P_{vi}} \leqslant {P_{vi\hbox{max} }}\,\,;\,\,0 \leqslant \left| {{P_{zi}}} \right| \leqslant {P_{z\hbox{max} }} \end{aligned}$$
(4)

Modeling of wind power and energy storage participation

When both wind generation and battery storage are active in the system, the battery’s state-of-charge (SOC) must be maintained within defined upper and lower bounds. The battery’s charging and discharging powers are also limited per unit time. Similar to the previous model, constraints on power exchange with the main grid and partial renewable energy curtailment are enforced.

The objective function under this combined setup is presented in Eq. (5), while the operational constraints are described in Eq. (6).

$${C_3}{\text{=}}\sum\limits_{{i=1}}^{{24}} {({P_{wi}}{C_{wi}}+{P_{vi}}{C_{vi}}+{P_{zi}}} {C_{gi}}{y_i} - {P_{zi}}{C_{mi}}{\text{(1-}}{{\text{y}}_i}{\text{)+}}{P_{ci}}{C_{ci}})$$
(5)
$$\begin{aligned} &{P_{wi}}+{P_{vi}}+{P_{zi}}={P_{li}}{\text{+}}{P_{ci}} \\&s.t.\,0 \leqslant {P_{wi}} \leqslant {P_{wi\hbox{max} }}\,\,;\,\,0 \leqslant {P_{vi}} \leqslant {P_{vi\hbox{max} }}\,\,;\,\,0 \leqslant \left| {{P_{zi}}} \right| \leqslant {P_{z\hbox{max} }}\,\,;\, \hfill \\ \,\\&0 \leqslant \left| {{P_{ci}}} \right| \leqslant {P_{c\hbox{max} }}\,\,;\,\,SO{C_{\hbox{min} }} \leqslant SO{C_i} \leqslant SO{C_{\hbox{max} }} \hfill \\ \end{aligned}$$
(6)

Modeling of wind power and demand response participation

Price-based demand response

In price-based DR, customer electricity consumption behavior is influenced by the elasticity of electricity prices. The price elasticity coefficient describes how sensitive electricity demand is to price fluctuations. The relationship between electricity consumption and price is captured using the elasticity factor, which measures the ratio of the percentage change in load to the percentage change in price, as shown in Eq. (7).

$$\xi =\frac{{\Delta P}}{P} \cdot \frac{c}{{\Delta c}}$$
(7)

In practical scenarios, electricity consumption is influenced by both the current period’s price changes and the future periods’ expected price variations, leading to immediate load adjustments as well as load shifting across time periods. Therefore, a comprehensive model must consider both immediate and time-shifted DRs.

$$\xi _{{ii}} = \frac{{\Delta P_{i} }}{{P_{i} }} \cdot \frac{{c_{i} }}{{\Delta c_{i} }}$$
(8)
$$\xi _{{ij}} = \frac{{\Delta P_{i} }}{{P_{i} }} \cdot \frac{{c_{j} }}{{\Delta c_{j} }}$$
(9)
$$\zeta = \left( {\begin{array}{*{20}c} {\xi _{{ff}} } & {\xi _{{fp}} } & {\xi _{{fg}} } \\ {\xi _{{pf}} } & {\xi _{{pp}} } & {\xi _{{pg}} } \\ {\xi _{{gf}} } & {\xi _{{gp}} } & {\xi _{{gg}} } \\ \end{array} } \right)$$
(10)
$${\Delta }{\mathbf{P}} = \left[ {\begin{array}{*{20}c} {p_{f} } & 0 & 0 \\ 0 & {p_{p} } & 0 \\ 0 & 0 & {p_{g} } \\ \end{array} } \right]\zeta \left[ {\begin{array}{*{20}c} {\frac{{{\Delta c}_{f} }}{{c_{f} }}} & {\frac{{{\Delta c}_{p} }}{{c_{p} }}} & {\frac{{{\Delta c}_{g} }}{{c_{g} }}} \\ \end{array} } \right]^{T}$$
(11)

To illustrate the structure of the tariff scaling matrix ζ, consider a simplified case with three time intervals (f, p, g), where price changes affect demand elasticity across intervals. For example, if ξff = 1.2, ξfp = − 0.3, and ξfg = 0.1, it means a 10% increase in period f’s price leads to a 12% drop in f’s demand, a 3% increase in p’s demand, and a 1% increase in g’s demand. This interaction captures both direct and spillover effects of pricing signals on consumption behavior.

After considering DR, the adjusted load demand matrix at each time step is represented by P’, as defined in Eq. (12).

$$P^{'} = P + \Delta P$$
(12)

Incentive-based demand response

Incentive-based DR targets controllable loads, which can be shifted across time periods based on agreements between users and the dispatch center. Uncontrollable loads, such as lighting and essential communication equipment, must always be prioritized during scheduling. Controllable loads, like washing machines and rice cookers, can be deferred from peak periods to off-peak periods or periods with abundant renewable energy availability. Users participating in incentive-based DR are compensated for shifting their loads.

The objective function for incentive-based DR is given in Eq. (13), with the associated compensation mechanism detailed in Eq. (14), and constraints outlined in Eq. (15).

$$C_{4} {\text{ = }}\sum\limits_{{i = 1}}^{{24}} {(P_{{wi}} C_{{wi}} + P_{{vi}} C_{{vi}} + P_{{zi}} } C_{{gi}} y_{i} - P_{{zi}} C_{{mi}} (1 - y_{i} )){\text{ + }}C_{{DR}}$$
(13)
$$C_{{DR}} = \mathop \sum \limits_{{i = 1}}^{{24}} \lambda p_{{in.i}} = \mathop \sum \limits_{{t = 1}}^{{24}} \lambda p_{{out.i}}$$
(14)
$$\begin{aligned} &P_{{wi}} + P_{{vi}} + P_{{zi}} = P_{{_{{li}} }}^{'} + P_{{Di}} \\&s.t.\,\,0 \le P_{{wi}} \le P_{{wi\max }} \,\,;\,\,0 \le P_{{vi}} \le P_{{vi\max }} \,\,;\,\,0 \le \left| {P_{{zi}} } \right| \le P_{{z\max }} \,\,;\,\,\\&0 \le P_{{in.i}} \le P_{{in.\max }} \,\,;\,\,0 \le P_{{out.i}} \le P_{{out.\max }}\end{aligned}$$
(15)

Modeling of combined wind, storage, and demand response participation

Finally, the comprehensive model that jointly incorporates renewable energy generation, energy storage systems, and DR strategies is formulated. This integrated objective function is presented in Eq. (16), with the corresponding operational constraints provided in Eq. (17).

$$C_{5} {\text{ = }}\sum\limits_{{i = 1}}^{{24}} {(P_{{wi}} C_{{wi}} + P_{{vi}} C_{{vi}} + P_{{zi}} } C_{{gi}} y_{i} - P_{{zi}} C_{{mi}} {\text{(1 - y}}_{i} {\text{) + }}P_{{{\text{C}}i}} C_{{{\text{C}}i}} + P_{{Di}} C_{{Di}} )$$
(16)
$$\begin{aligned}&{P_{wi}}+{P_{vi}}+{P_{zi}}=P_{{_{{li}}}}^{\prime }+{P_{Di}} \\&s.t.\,\,\left\{ \begin{gathered} 0 \leqslant {P_{wi}} \leqslant {P_{wi\hbox{max} }}\,\,;\,\,0 \leqslant {P_{vi}} \leqslant {P_{vi\hbox{max} }}\,\,;\,\,0 \leqslant \left| {{P_{zi}}} \right| \leqslant {P_{z\hbox{max} }} \hfill \\ SO{C_{\hbox{min} }} \leqslant SO{C_i} \leqslant SO{C_{\hbox{max} }} \hfill \\ 0 \leqslant {P_{in.i}} \leqslant {P_{in.\hbox{max} }}\,\,;\,\,0 \leqslant {P_{out.i}} \leqslant {P_{out.\hbox{max} }} \hfill \\ \end{gathered} \right.\end{aligned}$$
(17)

Evaluation metrics for demand-side response in microgrids

Demand-side response (DSR) aims to optimize electricity consumption patterns by encouraging users to adjust their usage behavior. This includes reducing consumption during peak periods, improving end-use efficiency, and shifting demand to align with renewable generation availability. In the context of microgrid operation, DSR plays a key role in flattening peak loads and enhancing the utilization rate of renewable energy sources such as wind and solar power. To quantitatively assess the effectiveness of DSR strategies, four key performance indicators are proposed.

Load factor

The load factor reflects how evenly electrical load is distributed over a given period. Effective demand-side management reduces peak-hour load intensity, thereby easing operational stress on the grid. An increased load factor indicates a smoother demand curve and better system performance. The load factor is calculated as shown in Eq. (18).

$$L{F_{DSM}}=\frac{1}{T}\mathop \sum \limits_{{i=1}}^{T} \frac{{{l_i}}}{{{l_{\hbox{max} }}}}$$
(18)

Renewable energy utilization rate

A well-structured DSR strategy can align electricity demand with periods of high renewable energy output. By shifting loads to coincide with renewable generation peaks, the overall consumption of wind and solar energy increases, reducing dependence on conventional sources. The renewable energy utilization rate is expressed in Eq. (19).

$${M_{rei}}=\frac{{{P_{gr}}}}{{{P_{gi}}}}$$
(19)

User comfort index

While DSR offers technical and economic benefits, it may impact user comfort. Electricity consumption behavior is influenced by pricing signals, but users tend to favor stable and convenient consumption patterns. DSR may alter these patterns, potentially reducing comfort levels. Therefore, user comfort is included as an important evaluation metric, which can be quantified using the formulation in Eq. (20).

$${C_{{\text{com}}}}=1 - \frac{{\sum\limits_{{i=1}}^{{24}} {\left| {{P_{Gi}} - {P_{Li}}} \right|} }}{{\sum\limits_{{i=1}}^{{24}} {{P_{Li}}} }}$$
(20)

The load values used in Eq. (20) represent post-DR demand profiles, ensuring that the computed comfort index dynamically reflects the true deviation from user baseline preferences after implementation of DR strategies.

This index captures the aggregate deviation between scheduled and forecasted consumption, normalized over the planning horizon. A lower value indicates less disruption to expected user behavior. It reflects both the frequency and intensity of load shifts imposed by DR, providing a measure of how comfortably users can adapt to the new schedule. A comfort score above 90% indicates minimal inconvenience, supporting the feasibility of demand-side flexibility in practice.

Daily peak load and peak-to-Valley load ratio

In microgrid systems, excessive peak loads can reduce reserve margins and increase fluctuations, threatening system stability. According to the Cauchy-Schwarz inequality, system losses are directly related to the ratio between the maximum and minimum daily load. A smaller peak-to-valley ratio reduces line losses and improves both load balancing and equipment utilization.

These two indicators, daily peak load and the ratio of maximum to minimum daily load, jointly reflect the apparent power supply stress within the system. Lower values suggest more stable grid operation and higher supply capacity efficiency. This ratio is defined in Eq. (21).

$$\left\{ \begin{gathered} \hbox{min} {{p^{\prime}}^{}}_{{\hbox{max} - f}} \hfill \\ \hbox{min} \left( {{{p^{\prime}}^{}}_{{\hbox{max} - (f - g)}}} \right) \hfill \\ \end{gathered} \right.$$
(21)

Case study and simulation analysis

System overview and scenario setup

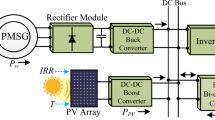
The structure of the microgrid under study is shown in Fig. 1, which includes wind turbines, PV systems, battery energy storage, and residential loads.

Fig. 1
figure 1

Structural Diagram of the Wind–Solar–Storage–Load Microgrid System.

Full size image

The installed wind turbine capacity is 360 kW with an operation and maintenance (O&M) cost of 0.52 CNY/kWh. The PV system has an installed capacity of 260 kW and an O&M cost of 0.75 CNY/kWh. The energy storage system has a rated capacity of 700 kWh, operating within a SOC range of [0.4, 0.9]. The initial SOC is set at 0.4, and the round-trip cost (charge–discharge) is 0.1 CNY/kWh. The maximum charging/discharging power is 20% of the rated energy capacity per hour.

The microgrid is permitted to exchange power with the main grid, subject to a maximum limit of 200 kW. The hourly electricity purchase and sale prices for the 24-hour day-ahead market are summarized in Table 1.

Table 1 Day-ahead electricity purchase and sale prices (CNY/kWh).
Full size table

The forecasted output profiles of wind and PV generation, along with the day-ahead load prediction, are illustrated in Fig. 2a. The net load, calculated as the difference between load and renewable generation, is shown in Fig. 2b, providing insight into the microgrid’s external power demand after internal generation is utilized. Negative net load values indicate that generation exceeds local demand. In such cases, the excess is either stored (subject to battery SOC and power limits), exported to the main grid within allowable exchange constraints, or curtailed if neither option is available. This behavior is modeled dynamically in the dispatch framework.

Fig. 2
figure 2

Forecasted Energy and Load Profiles: (a) Predicted Wind, PV Output, and Load Demand, (b) Net Load After Renewable Generation (negative values denote export potential or surplus subject to curtailment or storage).

Full size image

Solution approach for Wind–Solar participation only

In the absence of renewable sources, the microgrid relies entirely on grid-supplied electricity, with energy cost directly calculated by multiplying the load with corresponding time-of-use prices. However, as shown in simulation results (not displayed here), this configuration leads to a violation of the grid power exchange limit.

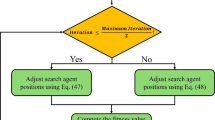
When wind and solar generation are included, power variables become dynamic and cannot be solved analytically. To address this, a PSO algorithm is applied to determine the optimal power allocation while respecting grid constraints and maximizing economic efficiency. In this study, the particle swarm optimization (PSO) algorithm is used to solve the nonlinear dispatch optimization problem. Each particle represents a potential solution, encoded with variables such as SOC, transferable loads, and renewable dispatch. The fitness function is defined by the total operational cost, while penalty terms are applied to particles violating constraints. During iteration, particles update their velocities and positions based on individual and global best solutions, converging toward the optimal dispatch configuration under the defined system constraints. The solution process is outlined in Fig. 3a.

Solution approach for Wind–Storage participation

This model introduces battery storage alongside wind and solar energy. The objective function is revised to account for both energy cost and unmet load penalties. Wind power, being the most economical source, is prioritized. Excess renewable energy can be curtailed (i.e., wind and PV curtailment is allowed) if it exceeds demand or system constraints.

The optimal dispatch strategy ensures that if wind and PV cannot fully meet the load, the shortfall is compensated by either storage or the main grid, depending on availability. Penalty factors are applied for exceeding power limits. The complete solution process follows the same structure as in Fig. 3a. To ensure feasibility during optimization, a hard penalty is applied within the PSO fitness function whenever a particle violates constraints such as SOC limits, power bounds, or system balance. Specifically, the SOC constraints are treated as hard boundaries. Any solution candidate (particle) violating the SOC bounds is immediately assigned an infinite fitness value. This discourages exploration of infeasible zones and accelerates convergence toward feasible, optimal dispatch configurations.

Wind and demand response participation model

To model DR, the K-Means clustering algorithm is first applied to segment the daily load into three periods: peak, flat, and valley, as shown in Table 2. The selection of K = 3 was validated using the silhouette coefficient method, which confirmed strong cluster separability. Moreover, this value aligns with real-world electricity tariff structures that commonly divide daily periods into peak, flat, and valley segments. Price-based DR is used to reshape the load curve according to electricity prices, while incentive-based DR shifts flexible loads to low-cost periods via direct control, offering compensation in return. In this model, transferable loads replace battery discharge functions, following a similar optimization path as in the wind–storage scenario. The solution process is illustrated in Fig. 3b.

Table 2 Load period classification results using k-means clustering.
Full size table
Fig. 3
figure 3

Optimization Flowcharts: (a) Wind–Solar–Storage Participation Model, (b) Wind–DR Participation Model.

Full size image

Integrated model: wind, storage, and demand response participation

The final scenario combines wind power, PV, battery storage, and both types of DR. By integrating the strategies from Sections C and D, the system leverages all available flexibility mechanisms to optimize economic dispatch while maintaining operational stability. The comprehensive solution procedure is shown in Fig. 4.

Fig. 4
figure 4

Integrated Solution Flowchart for Wind, Storage, and DR Participation.

Full size image

Comparison of results analysis

To comprehensively evaluate the impact of different microgrid strategies, simulation results are compared across grid-only, renewable integration, energy storage, and DR participation. The key findings are summarized through Figs. 5, 6 and 7. As shown in Fig. 5, when the microgrid operates with only the main grid Fig. 5a, it experiences sharp load peaks, causing significant stress on external power procurement. With the integration of predicted wind and solar generation Fig. 5b, renewable energy reduces grid reliance but introduces variability. By adding energy storage to the system Fig. 5c, fluctuations are significantly mitigated, leading to a smoother and more stable supply profile. In Scenario 2, curtailment events occurred in 4 out of 24 time intervals, resulting in approximately 46 kWh of unused wind energy due to grid exchange constraints. This led to an estimated opportunity cost of 37.7 CNY, highlighting the potential benefit of energy storage and DR mechanisms to absorb or shift excess generation.

These improvements offer significant benefits to microgrid operators. The 23.4% cost reduction enhances economic viability, while the improved load factor (by 17.6%) enables more stable and efficient grid operation with reduced peak-demand penalties. The high renewable utilization (> 88%) and consistent user comfort (> 90%) ensure compliance with decarbonization goals without compromising consumer satisfaction, thereby supporting resilient and sustainable energy planning.

Fig. 5
figure 5

Comparison of Power Supply Strategies in Microgrid Models: (a) Grid-only operation without renewables or DR; (b) Wind-solar generation with partial grid support; (c) Wind–solar–storage dispatch with grid coordination. Each scenario shows the evolution of load and supply coordination.

Full size image
Fig. 6
figure 6

Impact of Price-Based DR on Load Curve. The modified load profile under DR shows significant flattening and peak shifting compared to the original demand, improving system flexibility.

Full size image
Fig. 7
figure 7

System Performance Under Full Integration: (a) Coordinated output with DR (case 1); (b) Load adjustment profile for case 1; (c) Output dispatch with DR (case 2); (d) Load adjustment profile for case 2. Full integration results in better peak flattening and load–generation coordination.

Full size image

Figure 6 highlights the effect of implementing electricity price-based DR. Compared to the original load curve, DR effectively flattens the load profile, shifting consumption away from peak pricing periods and enhancing system flexibility. The most comprehensive improvements are seen in Fig. 7. In Fig. 7a, the coordinated dispatch of renewable sources, storage, and the grid optimizes overall power allocation, while Fig. 7b shows effective load adjustment through DR. Figure 7c and d further illustrate another case where the system achieves even better load balancing and smoother load curves, highlighting the robustness of combining renewable generation, energy storage, and both price- and incentive-based DR. Overall, the results demonstrate that full integration of renewables, storage, and demand-side participation significantly enhances microgrid stability, minimizes grid stress, and improves renewable energy utilization.

Conclusion

This study proposes an advanced day-ahead economic dispatch framework for wind-integrated microgrids, utilizing coordinated energy storage and a hybrid DR strategy. Five distinct scenarios were analyzed: grid-only dispatch (Fig. 5a), wind participation without storage or DR (Fig. 5b), wind coordinated with energy storage (Fig. 5c), wind with price-based DR (Fig. 6), and full integration of wind, storage, and both price- and incentive-based DR strategies (Fig. 7a–d). Among these, the fully integrated model demonstrated the highest efficiency, achieving a 23.4% reduction in operational cost, a 17.6% improvement in load factor, and over 88% utilization of renewable energy. The unmet load ratio was reduced to below 1.5%, while user comfort remained above 90% across all time intervals. Visual comparisons show that load peaks were significantly flattened and renewable intermittency was smoothed most effectively when all resources were coordinated. These results validate the practicality and robustness of the proposed dispatch strategy, providing a cost-effective and resilient scheduling solution for next-generation microgrids operating under dynamic pricing environments.