A magnetized protostellar jet launched from the innermost disk at the truncation radius

Abstract

Protostellar jets form when part of the accreting material is energetically ejected from the vicinity of protostars. Understanding where and how they are launched and collimated is crucial to determining their role in the accretion process. The HH 211 jet is a highly collimated, magnetized jet associated with a rotating disk around a young protostar. With Atacama Large Millimeter/submillimeter Array, we have resolved a pristine molecular spine at its base down to the disk. This spine has a high velocity of ~ 107 ± 8 km s⁻¹ but a slow rotation with a specific angular momentum of ~ 4 ± 1 au km s⁻¹, suggesting it to be launched at ~ 0.021 ± 0.005 au in the disk, providing the most stringent constraint yet on current magneto-centrifugal theories of jet production. Quantitative modeling supports the interpretation that the molecular spine represents the dense central component of a magnetized radial wind. This wind, launched by magneto-centrifugal force at the innermost edge of the disk—the truncation radius, removes residual angular momentum from the disk, enabling disk material to accrete onto the protostar. The toroidal field strength to collimate the dense spine in the model also agrees with that previously measured in the jet.

Protostellar jets are believed to play an important role in star formation, carrying away angular momentum from the innermost disk region, allowing disk material to fall onto the central protostars. Their launching mechanism is still undetermined because the launching regions are within ~ 0.1 au of the protostars and thus too small to be resolved with current instruments. Two popular jet-launching models, the X-wind model¹ and the disk-wind model², have been proposed to explain where and how they are launched from the disks by magneto-centrifugal force. In the X-wind model, a wide-angle radial wind is launched from the innermost disk region at the truncation radius called the “X-point” and the jet is only the dense central spine of the wind. In the disk-wind model, an extended wind is launched from a range of disk radii and the jet is the innermost wind launched from a range of the innermost disk radii, with the velocity being mainly poloidal. Thus, these two models can be used to account for the jets with different amounts of specific angular momentum and different degree of radial expansion, especially at the jet base. In particular, the X-wind model has been used to explain the jets with small specific angular momentum and large radial expansion^3,4, while the disk-wind model has been used to explain the jets with small to large specific angular momentum^5,6,7,8. However, current measurements of specific angular momentum of the jets are quite uncertain due to shock contamination and insufficient spatial and velocity resolutions. Besides, accurate measurements of jet velocity and radial expansion are also needed to determine the jet-launching mechanism.

The HH 211 protostellar system is located in Perseus at $\sim$ 321 pc away. It is one of the youngest protostellar systems⁹, with a gravitational collapse age of only $\sim$ 35,000 yrs¹⁰. The central protostar currently has a mass of only $\sim$ 0.06 ± 0.02 $M_\odot$^10,11 and is expected to grow into a star like our Sun⁹. It is associated with an outflow, consisting of a highly collimated jet propagating supersonically along the outflow axis and outflow cavity walls around the jet^12,13,14. The jet lies close to the plane of the sky¹⁵, optimal for measuring radial expansion and jet rotation. More importantly, the jet has been found to be magnetized¹⁶, supporting the role of magnetic field in the launching and collimation. Previous observations with Atacama Large Millimeter/submillimeter Array (ALMA) at $\sim$ 6 au resolution also spatially resolved an accretion disk around the protostar¹¹, connecting the jet launching to the disk accretion.

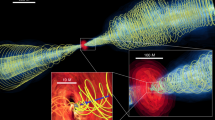
Figure 1a presents the recent JWST composite map of the HH 211 outflow in H$_2$ and CO (taken on 2022 August 28) in near infrared at 30−45 au resolution¹⁷, showing the overall structure of the outflow, with a collimated jet surrounded by outflow cavity walls. The outflow is bipolar with a southeastern (SE) component on the approaching (blueshifted) side and a northwestern (NW) component on the receding (redshifted) side^13,18. As shown in Fig. 1b, although the jet is detected in H$_2$ (red image) at a distance larger than $\sim$ 1000 au away from the protostar, no jet emission is detected in the inner region due to dust extinction by the surrounding dusty envelope.

Fig. 1

JWST composite image and ALMA SiO and CO images of the HH 211 outflow. (a) The JWST composite image: blue for F335M (several H$_2$ lines and continuum nebulosity), green for F460M (4.69 μm H$_2$ line, CO rotational-vibrational band head emission, and continuum nebulosity), and red for F470N (4.69 μm H$_2$ line) filters. The cross marks the position of the protostar located at ICRS $\alpha _{(2000)}=3^\textrm{h} 43^\textrm{m} 56^\textrm{s}_{^{.}} 808$ and $\delta _{(2000)}=32^{\circ }00^{\prime }50^{\prime \prime }_{^{.}}1535$¹¹. (b) Zooms in to the inner region in the JWST image. (c) The ALMA SiO image (green) with the JWST image. (d) The ALMA CO image (green) with the JWST image. The CO map is obtained with $v_\text {rel}\sim -30$ to $-16$ km s⁻¹ for the SE component and 19 to 32 km s⁻¹ for the NW component to avoid any significant contamination of the shells, where $v_\text {rel}$ is the radial velocity relative to the systemic velocity of $\sim$ 9.2 km s⁻¹. The insert shows the innermost part of the CO jet with the continuum map of the disk (gray image) reported before¹¹. The resolutions are $\sim$ 10 au for SiO and CO in panels c and d, and $\sim$ 7.5 au for CO in the insert.

In the following, we present our ALMA observations in SiO J = 8-7 and CO J = 3-2 at submillimeter wavelengths at a few times higher resolution of $\sim$ 10 au (i.e., $0^{\prime \prime }_{^{.}}033$) (taken on 2021 August 29 and September 27, 29) to study this inner region. In addition, a velocity resolution of $\sim$ 0.42 km s⁻¹ is used to study its kinematics. Without suffering from dust extinction, the jet is clearly detected in SiO (green in Fig. 1c) and CO (green in Fig. 1d) at submillimeter wavelengths down to the protostar connecting to that detected in H$_2$. Here the CO jet is from the emission at high velocity (as discussed in Methods). The previously identified reflection-symmetric wiggle^19,20 can also be seen down to the protostar in the SiO and CO jets.

The SiO jet consists of a chain of knots with a (transverse) width growing with the distance from the protostar. These knots are roughly equally spaced and associated with a broad range of velocities, and appear as bow-like structures at low velocity (see Methods), supporting that they trace the internal shocks produced by a semi-periodical variation in jet velocity^21,22,23. The CO jet shows a similar knotty structure to the SiO jet. Nonetheless, within $\sim$ 600 au of the protostar, the CO jet is narrower and passes through the center of the SiO jet, and thus can be considered as the central spine of the jet. As shown in the insert in Fig. 1d at $\sim$ 7.5 au resolution, the CO jet can be seen down to the center of the disk (gray image) to within $\sim$ 10 au of the protostar, with the innermost part further in blocked by the disk. More importantly, the CO jet there is roughly continuous and well collimated with a roughly constant radius (i.e., a half of the transverse Gaussian FWHM) estimated to be $R_j\sim$ 13 au, much smaller than those measured further away in atomic lines²⁴.

Figure 2 shows the intensity maps and position-velocity (PV) diagrams of the SiO jet and CO jet within $\sim$ 200 au of the protostar to study the kinematics at the base. The first SiO knots E1 and W1 (as marked by the red line segments) are located at $\sim$ 100 au in the SE jet component and $-160$ au in the NW jet component, respectively. They are associated with a broad range of velocities of $\sim$ 40 km s⁻¹ (see panels b and d), supporting that they are internal shocks formed in the jet. They appear as wide bow structures at low velocities as shown in Figures S1c and S1d. Moreover, a double-peak line profile characteristic of a bow shock^25,26 is also seen for knot W1 (see Fig. 3b), with one peak at high velocity and the other at low velocity. Only a single-peak line profile is seen for knot E1 at high velocity (see Fig. 3a) because the emission at low velocity is much fainter and does not show a clear peak. Therefore, they are likely wide internal bow shocks. However, since their SiO emission is faint in the bow wings, they appear as knots in the total intensity maps shown in Fig. 2, tracing the bow tips. Near the protostar, the SiO emission traces the V-shaped base of the shells around the jet (see Figs. S1c and S1d for clearer structures). They are associated with a broad range of velocities of $\sim$ 50 km s⁻¹, and thus whatever is driving them must have a significant radial velocity component at the base.

Fig. 2

Intensity maps and PV diagrams of the SiO and CO jets at the base. The jet is rotated to be aligned with the vertical direction. Red image and red contours are for SiO, while green image and gray image with gray contours are for CO. The first SiO knots are marked with E1 and W1 on the SE and NW side, respectively. Contours start from 3 $\sigma$ with a step of 3 $\sigma$ for CO and a step of 4 $\sigma$ for SiO, where $\sigma =7$ K. Black vertical dashed lines mark the systemic velocity. The velocity resolution in the PV diagrams is $\sim$ 0.42 km s⁻¹.

Fig. 3

Line profiles of the SiO and CO emission towards knots E1 and W1. The line profiles are obtained by integrating the emission over a circular region with a diameter of 30 au. The profiles have been smoothed with a hanning factor of 5.

On the other hand, the CO jet inner to the first SiO knots traces the pristine jet without any clear sign of shocks (i.e., a localized broad range of velocities) in the PV diagrams. The NW jet component has a mean radial velocity of $\sim$ 22.6 km s⁻¹ (see Methods). It has a velocity range increasing from the first knot W1 to the base, as outlined by the green curves, indicating that the radial component of the jet velocity increases towards the base. This behavior has been seen before in HH 212 and can be attributed to a radial expansion of the jet at the base⁴. Around the mean jet radial velocity, the peak emission also shows a sinusoidal PV structure that could be due to a semi-periodical variation in jet velocity with a wavelength of $\sim$ 50-60 au. On the other hand, the SE jet component has a mean radial velocity of $\sim$ −20 km s⁻¹ (see Methods). Although no clear PV structure can be identified around that velocity, the velocity range of the jet also appears to increase towards the base from the first knot E1. At knots E1 and W1, the CO emission is also associated with a range of velocities around the mean jet radial velocity, but not as broad as that seen in SiO. However, it is difficult to determine if the CO emission there also shows a double-peak line profile (see Fig. 3), because the emission at low velocity is contaminated by the internal shells and resolved out by the interferometry. Therefore, the CO emission there could trace the postshock gas or weakly shocked jet material.

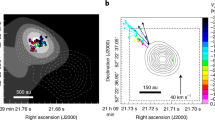
Jet rotation can be measured from the PV diagrams cut across the jet axis. Figure 4 shows such PV diagrams constructed from the CO jet roughly midway between the protostar and the first SiO knots, i.e., 50 au in the SE jet component and −64 au in the NW jet component (with the cuts indicated with the white lines in Fig. 2a,c, respectively), where the jet is not significantly affected by internal shocks and contaminated by shell emission. To increase the sensitivity, we first convolved the map of the jet with a beam of $\sim$ 32 au $\times$ 6.4 au ($0^{\prime \prime }_{^{.}}1$$\times$ $0^{\prime \prime }_{^{.}}02$) elongated along the jet axis with position angle (P.A.) $\sim$ 116$^\circ$ and then produced the PV diagrams. As shown in Fig. 4b, the NW jet component can be seen around the mean jet radial velocity of $\sim$ 22.6 km s⁻¹ and be roughly separated from the shells. A linear velocity gradient with $m\sim 0.81\pm 0.11$ au (km s⁻¹)$^{-1}$ (as indicated by the cyan line) centered at $\sim$ 23 km s⁻¹ from $\sim$ 20.8 to 25.4 km s⁻¹ with the redshifted velocity in the northeast (NE) and blueshifted velocity in the southwest (SW) is seen across the jet axis. At each velocity channel, the white open box and the error bar (smaller than the box) indicate the peak position and the associated uncertainty obtained from a Gaussian fit to the intensity profile (see Table 1). The velocity gradient was then obtained by performing a linear fit to the peak positions, taking into account their uncertainties, with a reduced $\chi ^2$ of $\sim$ 0.7. As shown in Fig. 5, this velocity gradient, although very small, can still be seen in the maps at the two velocity ends of the velocity gradient along the cut (marked by the black line). The red and blue curves show the peak positions of the redshifted and blueshifted emission, respectively, derived from the Gaussian fitting. The blueshifted emission beyond $\sim$ −90 au is excluded because it is contaminated by shell emission, forming a V-shaped structure that opens away from the central protostar. As can be seen, the position shift between the redshifted and blueshifted emission decreases towards the protostar and becomes unresolved closer in. This behavior has been seen before in the spinning jet HH 212⁴ because the velocity range of the jet increases with the decreasing distance toward the protostar due to a radial expansion, as found earlier. The velocity gradient has the same velocity sense as that seen in the disk and envelope¹⁰, and is thus likely arising from rotation in the jet. It is detected with a velocity range $\triangle v$ $\sim$ 4.6 km s⁻¹ across the cut position, thus the jet is estimated to have a specific angular momentum $l_j \sim m (\triangle v /2)^2 \sim 4\pm 1$ au km s⁻¹ about the jet axis. On the blueshifted side, no clear jet emission can be identified around the mean jet radial velocity of $\sim$ −20 km s⁻¹ likely because the jet and shell merge in the velocity (see Fig. 4a).

Fig. 4

PV diagrams in CO cut across the jet axis to search for jet rotation. (a) The PV diagram for the SE jet component cut at 50 au and (b) The PV diagram for the NW jet component cut at -64 au. In (b), the cyan line marks the linear velocity gradient seen across the jet axis in the NW jet component, with the redshifted velocity in the northeast (NE) and blueshifted velocity in the southwest (SW). The contours start from 25 K with a step of 10 K. At each velocity channel, the white open box and the error bar (smaller than the box) indicate the peak position and the associated uncertainty obtained from a Gaussian fit to the intensity profile (see Table 1). The velocity gradient was then obtained by performing a linear fit to the peak positions, taking into account their uncertainties.

Fig. 5

CO Channel maps at the two velocity ends of the linear velocity gradient across the jet axis. The black line indicates the cut position. Blue contours for the velocity $v_\text {rel}\sim 21{-}22$ km s⁻¹ while red contours for the velocity $v_\text {rel}\sim 24{-}25$ km s⁻¹. Red contours start from 20 K with a step of 10 K. Blue contours start from 22 K with a step of 11 K. The thick contours indicate the highest intensity levels and highlight the velocity gradient. The red and blue curves show the peak positions of the redshifted and blueshifted emission, respectively, derived from the Gaussian fitting. The ellipse shows the beam size.

Table 1 Best-fit parameters for the centroids in the PV diagram using a Gaussian Profile with $A \exp [-(4\ln 2)(x-x_0)^2/\text {FWHM}^2]$.

Independent of the uncertain launching conditions, for a jet launched by magneto-centrifugal force from a rotating disk, the launching radius at the foot point of the jet in the disk can be derived assuming a conservation of energy and angular momentum along the field line⁶. In particular, it can be derived from the observed velocity ($v_j$) and specific angular momentum ($l_j$) of the jet at a large distance from the launching point and the mass of the protostar ($M_*$). With $M_*\sim$ $0.06\pm 0.02$ $M_\odot$^10,11, $v_j \sim$ $107\pm 8$ km s⁻¹ (see Methods), and $l_j \sim 4\pm 1$ au km s⁻¹, the launching radius is estimated to be $r_L\sim$ $0.021\pm 0.005$ au, where the specific angular momentum $l_o \sim 1.06\pm 0.12$ au km s⁻¹. Here, Equation 2 in Lee et al.²⁷, which was derived for a small $l_j$ value as estimated here, was used to estimate the $r_L$ value. Since the protostar has a theoretical radius of $\sim$ $2R_\odot \sim$ 0.01 au²⁸, which is $\sim$ half of the launching radius, the jet is likely launched at the innermost edge of the disk truncated by the stellar field¹. The magnetic lever arm parameter, which determines the efficiency of acceleration and transport of angular momentum, is $\lambda \sim l_j/l_o \sim 3.8\pm 0.5$. Therefore, the Alfvén radius within which most of the acceleration is achieved is $r_A = \sqrt{\lambda } r_L \sim 0.042\pm 0.010$ au.

We can further constrain the jet-launching models by comparing our results to the models more quantitatively. Since the CO jet in HH 211 is launched from the innermost edge of the disk, we adopt the asymptotic X-wind model²⁹ for which analytic solutions exist and $\lambda \sim$ 3.7. We defer comparing our results with the disk-wind model, because it is not clear if a large widening factor of $\sim R_j/r_L \gtrsim$ 620 to produce the observed jet radius is feasible for a small $\lambda$⁸.

Figure 6 shows the density, velocity, and streamlines of the wind in the X-wind model. To mimic the observations, we also include a dusty disk to block the innermost jet and impose an outer boundary of the wind defined by the observed CO shell (see Methods) as outlined by the red curve. As can be seen, the model launches a radial wind with a dense spine along the outflow axis. The tenuous wide-angle radial wind component is expected to produce the observed broad range of velocities for the V-shaped SiO shells at the base and the wide bow structures³⁰ for the first knots W1 and E1, although simulations are needed to confirm these. This model is self-similar and scaled with the mass of the protostar $M_*$, the radius of the launching point $R_x$, and the mass-loss rate of the wind $\dot{M}_w$. To achieve the observed jet velocity, it requires $R_x\sim$ 0.017 au, similar to the estimated $r_L$ value. Assuming that the accretion rate in the disk is smaller than the infall rate in the envelope, which is $M_{\text {inf}}\sim 4.3\times 10^{-6}$ $M_\odot$ $\textrm{yr}^{-1}$$^($¹⁰$^)$, we have $\dot{M}_w \lesssim M_{\text {inf}}/\lambda \lesssim (1.1\pm 0.2)\times 10^{-6}$ $M_\odot$ $\textrm{yr}^{-1}$. Here we set $\dot{M}_w\sim 10^{-6}$ $M_\odot$ $\textrm{yr}^{-1}$.

Fig. 6

The X-wind model for the jet. Left panel shows the density distribution (color image), velocity field (vectors), and streamlines (black curves) of the wind in our model. Thick red curves mark the CO shell for the outer boundary of the wind. Black hashed region shows the dusty disk. Right panel shows the model in 3D created with VisIt. It also shows the magnetic field at the base.

Figure 7 shows the model results. We only model the NW jet component because the kinematics of the SE jet component is contaminated by the shells. For comparison, we also show the observed intensity of the jet in Fig. 7a. As can be seen, this model can readily produce the key features in the observations, e.g., a highly collimated jet structure with roughly similar intensity (see Fig. 7b), a velocity range increasing toward the base (see Fig. 7c), and a linear velocity gradient across the jet axis (see Fig. 7d). Nonetheless, comparing to the observed jet, the jet in the model is narrower and has a broader velocity range away from the base. This implies that the streamlines of the wind in the model are required to be more collimated away from the base with less expansion velocity perpendicular to the jet axis. Further work is needed to determine if this can be achieved by fine-tuning the values and the functional forms of the specific angular momentum and ratio of magnetic field to mass-flux carried on a streamline in the X-wind model²⁹.

Fig. 7

Model results in comparison with the observations in CO for the NW jet component at the base. (a,b) The observed and model intensity maps of the jet, respectively. The first SiO knot is marked with W1. (c) The PV diagram along the jet axis, as shown in Fig. 2d. (d) The PV diagram along the jet axis, as shown in Fig. 4b. Red contours are from the model.

Previously, SiO line polarization was detected in this jet at a distance of 300−500 au and the field strength was estimated to be $\sim$ 15 mG assuming a density of $n(\text{H}_2)\sim 2\times 10^6$ $\textrm{cm}^{-3}$$^($¹⁶$^)$. In this model, the toroidal field is dominant over the poloidal field at large distance and has a field strength $B_\phi \sim 6 \frac{R_x}{R}$ G at those distances. The cylindrical radius of the wind at the assumed $n(\text {H}_2)$ is $R \sim$ 10 au (see Fig. 6) and thus the field strength is $B_\phi \sim$ 10 mG, also roughly in agreement with the observed value.

In summary, the X-wind model can provide a reasonable match to the observations of the CO jet at the base, supporting that the jet is only the dense central spine of the wide-angle radial wind. The wind removes residual angular momentum from the disk, enabling disk material to accrete onto the protostar. This model has also been used to reproduce the radial expansion and rotation of the knots detected in SiO at the base of the HH 212 jet^4,27. However, the SiO knots can be affected by shocks. In addition, SiO emission traces only the densest spine of the wind due to its high critical density. On the other hand, the CO jet base here in HH 211 appears not to be affected by shocks. It also appears wider due to the lower critical density of the CO emission, and thus covering more streamlines of the wind, providing stronger constraint on the model, especially on the collimation. On the other hand, since we defer comparing our results with the disk-wind model due to a lack of appropriate analytical formulation available, further work is needed to check whether the disk-wind model could also provide a possible interpretation.