Introduction

As mineral resource extraction progresses, mining operations are increasingly moving to deeper underground levels. Chute transportation of ore has become prevalent in large and medium-sized metal mines, resulting in significant dust generation during ore discharge, particularly in high chutes with multiple intermediate discharge points. The descent of ore through the chute generates a powerful air blast, accompanied by the production and dispersion of substantial dust quantities, severely compromising the air quality in ore discharge chambers and adjacent tunnels. In recent years, due to heightened emphasis on mine safety and stringent implementation of environmental protection regulations, dust control in high chute mines has emerged as a critical research focus within the mining industry.

Hemeon1 pioneered the study of airflow generated during the free fall of small-particle materials, conceptualizing the resulting impact airflow as the sum of airflows generated by individual particles falling in stationary air. Plinke et al.2,3 investigated the impact force produced by freely falling objects, elucidating the effects of factors such as fall height, mass flow rate, particle size, moisture content, and material type on the force magnitude. Cooper et al.4 conducted experimental research, building upon previous studies, to calculate air entrainment during material falling at conveyor belt transfer points and its influencing factors. Uchiyama5 employed a two-dimensional vortex method to simulate particles falling from a slit into stationary air, examining the effects of particle diameter and density on airflow. The study revealed maximum airspeed at the jet centerline, with particle speed exceeding the free fall velocity of individual particles. Wypych et al.6 performed both experimental and theoretical studies on dust generation and air entrainment mechanisms during material free fall, analyzing the effects of fall height and temperature. They concluded that the volume of entrained air is proportional to the 5/3 power of the fall height. Ansart et al.7 utilized PIV (Particle Image Velocimetry) technology to examine the diameter of falling airflow, concluding that reducing particle size increases jet diameter, albeit only considering fine particles ranging from 34 to 97 μm. In 20118, image analysis technology was employed to study the impact of fall height on fine particle flow diameter and intensity, indicating that increased fall height resulted in larger jet diameter and decreased core intensity. Esmaili9 conducted simulations and experiments, using PIV technology to measure coarse materials’ free fall velocity, comparing particle and air velocity, and air entrainment readings with Ansys CFX simulations and theoretical formulas. Wang et al.10 investigated pressure difference, airflow velocity, and their influencing factors at multi-segment high shaft mine unloading ports from an energy conservation and exchange perspective. Wang et al.11 employed the CFD-DEM method to simulate energy transfer and impact airflow velocity variations during mineral falling, deriving a mathematical model for impact airflow velocity through multiple nonlinear regression. Wang et al.12,13 utilized CPFD software and similar experiments to examine the effects of unloading conditions and time intervals on airflow and dust transport in chutes, finding that primary dust generation locations and dust concentration are inversely proportional to particle size and proportional to unloading height, while increasing unloading intervals can reduce dust accumulation. Wang et al.14 studied dust diffusion patterns through numerical simulations and established an SSA-ELM prediction model, proposing high-pressure air curtains for dust pollution control. After parameter optimization, dust removal efficiency reached 87.3%, with air curtain angle decreasing as air supply angle increased. Nie et al.15 investigated and optimized a new wind-assisted spray device through experimental and numerical simulation methods, aiming to solve high-concentration coal dust pollution in a fully mechanized working face, and achieved efficient dust reduction with the device when operated at specific parameters (30-degree deviation, 6 MPa spray pressure, 90 L/min air output), effectively suppressing dust pollution. However, dust control in high chute mine unloading presents greater challenges, influenced by factors such as unloading flow rate, height, and impact airflow size. The complex and variable dust distribution pattern, affected by multiple factors, poses difficulties for traditional analytical methods in comprehensively and accurately revealing underlying relationships.

This paper establishes an experimental model for high chute mines, aiming to investigate the factors influencing dust distribution and their interrelationships through Grey Relational Analysis (GRA). The study aims to uncover the underlying patterns of dust distribution and provide a theoretical foundation for proposing targeted dust control measures in high chute ore discharge operations. The research presented herein offers significant theoretical value and provides robust technical support for enhancing the underground working environment and protecting miners’ health.

Establishment of the similar experimental model

Analysis of impact airflow similarity criteria

The descent of ore within the chute represents a two-phase flow involving both gas and solid phases. The similarity criteria for this process can be derived using dimensionless analysis. This analysis reveals that the primary physical quantities influencing the impact airflow velocity v and dust generation during ore discharge in high chutes include: the density of air \(\rho_{{\text{g}}}\), the air viscosity \(\mu\), the diameter of the ore \(d_{p}\), the diameter of the chute D, ore mass flow rate \(M_{p}\), the acceleration of gravity g, the mineral density \(\rho_{p}\), unloading mining height H, time t, and sneak wellhead local ventilation resistance coefficient \(\xi\). The functional relationship between these factors and the impact of airflow in high discharge chutes can be expressed as \(f(v,\rho_{g} ,\mu ,H,d_{p} ,D,M_{p} ,g,\rho_{p} ,t,\xi ) = 0\). (In the formula, v is the size of the impact airflow, m/s; \(\rho_{{\text{g}}}\), \(\rho_{p}\) respectively, are the densities of air and mineral, kg/m3; \(\mu\) is the air viscosity, m/s; H is the unloading mining height, m; \(d_{p}\) and D are the diameters of ore and the chute, m; \(M_{p}\) is the ore unloading flow rate, kg/s; g is the acceleration of gravity, m/s2; t is time, s; ζ is the local ventilation resistance coefficient of the ore pass mouth.) According to the PI theorem of dimensional analysis, \(\rho_{{\text{g}}}\) ,\(\mu\) and H are chosen as the basic physical quantity group for dimensional analysis: \(\pi_{1} = \frac{{\rho_{g} vH}}{\mu }\), \(\pi_{2} = \frac{{d_{p} }}{H}\), \(\pi_{3} = \frac{D}{H}\), \(\pi_{4} = \frac{{M_{p} }}{H\mu }\), \(\pi_{5} = \frac{{H^{3} \rho_{g}^{2} g}}{{\mu^{2} }}\), \(\pi_{6} = \frac{{\rho_{p} }}{{\rho_{g} }}\), \(\pi_{7} = \frac{\mu t}{{H^{2} \rho_{g} }}\), \(\pi_{8} = \xi\). From \(\pi_{1}\) and \(\pi_{7}\) , we can derive: \(\pi_{1} \pi_{3} = \frac{{\rho_{g} \nu D}}{\mu } = Re\) (Reynolds number criterion); From \(\pi_{1}\)、\(\pi_{7}\) , we obtain: \(\pi_{1} \pi_{7} = \frac{vt}{H} = H_{0}\) (time-sharing criteria); From \(\pi_{2}\),\(\pi_{4}\),\(\pi_{5}\), and \(\pi_{6}\), we derive: \(\frac{{\pi_{4} }}{{\pi_{2} \pi_{5}^{1/2} \pi_{6} }} = \frac{{M_{p} }}{{\rho_{p} d_{p} g^{1/2} H^{3/2} }}\) (mass flow criteria). (In the formula, \(M_{p}\) is the ore unloading flow rate, kg/s; \(\rho_{p}\) is the density of mineral, kg/m3; \(d_{p}\) is the diameter of ore, m; g is the acceleration of gravity, m/s2; H is the unloading mining height, m.)

The similarity principle dictates that to establish similarity between an experimental model and its prototype, geometric, kinematic, and dynamic similarities must be achieved. A comparable experimental model was constructed using a geometric size ratio of 10:1 between the prototype and the model. Consequently, the pass diameter D, unloading height H, and the particle size similarity ratio of the ore all maintained this 10:1 ratio. Furthermore, if Re, HO, and \(\frac{{M_{p} }}{{\rho_{p} d_{p} g^{1/2} H^{3/2} }}\) criteria are equivalent, the model can replicate impact airflow phenomena similar to those observed in the prototype.

The number of HO criteria remains constant. Given that t is a dependent variable of H, as demonstrated by the free-falling body equation \(t_{y} /t_{m} = \sqrt {H_{y} /H_{m} } = \sqrt {10} /1\), the velocity ratio between the prototype and model can be expressed as \(v_{y} /v_{m} = \sqrt {10} /1\).

Given that \(v_{y} /v_{m} = \sqrt {10} /1\), \(\mu_{y} /\mu_{m} = 1/1\), and \(D_{y} /D_{m} = 10/1\) do not satisfy the Reynolds number criterion equality, it is important to note that under the current experimental conditions, calculations of the Reynolds number indicate that both the prototype and the model are within the same self-mode region. Consequently, the similarity requirement for the Reynolds number criterion can be disregarded in this context16.

When the number of criteria \(\frac{{M_{p} }}{{\rho_{p} d_{p} g^{1/2} H^{3/2} }}\) is equal, the prototype and model satisfying the number of criteria \(\left( {M_{p} } \right)_{y} /\left( {M_{p} } \right)_{m} = 100\sqrt {10} /1\) can be determined through \(\left( {\rho_{p} } \right)_{y} /\left( {\rho_{p} } \right)_{m} = 1/1\), \(\left( {d_{p} } \right)_{y} /\left( {d_{p} } \right)_{m} = 10/1\), \(g_{y} /g_{m} = 1/1\), and \(H_{y} /H_{m} = 10/1\).

Given that the resistance coefficient ξ is dimensionless, its power cannot be determined through dimensional analysis. To minimize its influence, the resistance coefficient of the experimental model should ideally match that of the actual entity.

Design of the experimental similarity model

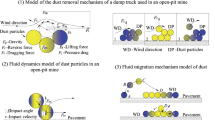
The prototype of the Li Lou Iron Mine No. 24 High Chute serves four levels: -325 m, -350 m, -375 m, and -400 m, each with a height of 25 m, resulting in a total chute height of 100 m. The chute has a diameter of 3 m, with an inclined section measuring 2.5 m in diameter and set at a 45° angle. For experimental purposes, a geometric scale model is constructed with a scale ratio of \(C_{y} /C_{m} = 10/1\). As illustrated in Fig. 1, the experimental model of the chute ore discharge system comprises four sections, labeled from top to bottom as Sects. 1, 2, 3, and 4. The main body of the chute model utilizes PVC pipes with a 0.3 m diameter, while the inclined section employs PVC pipes with a 0.25 m diameter. The total height of the model chute is 10 m.

Fig. 1
figure 1

Chute ore discharge experimental similarity model.

Full size image

The experimental apparatus comprises several components: the chute model body, ore discharge funnel, outlet cross-section adjustment plate, ore storage section, airflow measurement pipe, and anemometer. The ore discharge funnel regulates the ore flow rate by modifying the outlet cross-section. An adjustable cross-sectional area plate at the inclined chute outlet allows for alteration of the outlet resistance coefficient. The ore storage pipe functions as a repository and release mechanism for ore that descends to the chute model’s base. The study employs a JFY-4 type multi-parameter ventilation detection instrument as the anemometer. Its probe, inserted into the inclined chute via the airflow measurement pipe, quantifies the impact airflow generated during ore discharge. Furthermore, an LD-5C microcomputer laser dust sampler is utilized for continuous monitoring of dust concentration at the exits of each chute model section.

Experimental methods and measurement of parameters

The experimental ore is sourced from the Li Lou Iron Mine. During underground ore discharge, the actual size of the ore is less than 500 mm. An XPC-60 × 100 jaw crusher is utilized to reduce the ore size to below 50 mm. Following the crushing process, the ore is classified into five distinct grades using screening meshes with the following specifications: 1 mesh (aperture approximately 25 mm), 2 mesh (aperture approximately 10 mm), 4 mesh (aperture approximately 5 mm), and 16 mesh (aperture approximately 1 mm). The resulting five ore grades are as follows: 25 mm < D ≤ 50 mm, 10 mm < D ≤ 25 mm, 5 mm < D ≤ 10 mm, 1 mm < D ≤ 5 mm, and D ≤ 1 mm.

The resistance coefficient of the chute was measured on-site, with values ranging from approximately 10 to 1500 as the opening of the ore discharge point was gradually adjusted from fully open to nearly completely closed. The top opening of the chute model was connected to the inlet of a small extraction fan. Through a series of extraction experiments, the resistance coefficient of the chute model was determined under varying outlet cross-sectional conditions. By adjusting the outlet cross-sectional area and establishing an appropriate air volume, the static pressure at the fan inlet was measured using a differential pressure sensor. The airflow velocity at each outlet was measured using an anemometer. Based on these measurements, the resistance coefficient of the model was calculated for various conditions.

The monitoring process utilized a JFY-4 type multi-parameter ventilation detection instrument and an LD-5C microcomputer laser dust sampler. Monitoring points were established at the exit of each chute section. During ore discharge, the airflow velocity monitoring instruments and dust samplers were activated concurrently. Data was recorded at one-second intervals, with continuous measurements taken for a total of 60 s at each monitoring point.

Results and analysis of the similarity experiment

Drawing from the aforementioned similarity theory and a comprehensive review of pertinent literature, it becomes apparent that the primary factors influencing the generation of impact airflow and dust dispersion during ore discharge in high chutes are the discharge height H, discharge flow rate Mp, ore particle size D, ore moisture content W, and chute resistance coefficient ξ. Through the adjustment of these parameters during ore discharge, continuous monitoring of the impact airflow velocity at the discharge point can be implemented. This process enables the determination of the maximum impact wind speed and the average dust concentration over a 60-s interval at the chute discharge point, thereby elucidating the linear and nonlinear relationships among these factors.

Relationship between maximum impact wind speed, average dust concentration, and ore discharge flow rate

The primary driver of airflow during ore discharge in the chute is the weight of the ore itself. Furthermore, higher discharge flow rates incorporate more fine particles, resulting in elevated initial dust concentrations. To investigate the effects of varying ore discharge flow rates on impact wind speed and dust concentration, the discharge funnel was adjusted to regulate the ore flow rate at 2 kg/s, 4 kg/s, 6 kg/s, 8 kg/s, and 10 kg/s. Figures 2 and 3 depict the resulting curves for maximum impact wind speed and average dust concentration at the discharge points of four distinct chute sections, at various heights. These curves demonstrate how the maximum impact wind speed and dust concentration vary with different ore discharge flow rates in each section of the chute.

Fig. 2
figure 2

Trend of impact wind speed with changes in ore discharge flow rate.

Full size image
Fig. 3
figure 3

Trend of dust mass concentration with the change in unloading flow rate.

Full size image

Figures 2 and 3 demonstrate that, at a constant discharge height, the maximum impact wind speed increases with a rise in ore discharge flow rate. However, the rate of increase in maximum impact wind speed gradually diminishes as the discharge flow rate continues to escalate.

The relationship between impact wind speed and ore discharge flow rate approximates a power-law function, with the exponent varying according to discharge height. The exponent increases with greater discharge heights, ranging experimentally from 0.593 to 0.732. The diminishing rate of increase in impact wind speed as discharge flow rate rises can be attributed primarily to the continuous collision of ore particles during descent. These collisions reduce particle-air interactions. As the discharge flow rate increases, the larger volume of falling ore results in fewer particles contacting the surrounding air, thereby reducing the ore’s influence on airflow within the chute. Moreover, increased discharge height provides more space for ore dispersion, facilitating greater particle-air interaction. This expanded space enhances ore-air contact, rendering the impact airflow more responsive to discharge flow rate variations. Consequently, as discharge height increases, alterations in discharge flow rate exert a more pronounced effect on the impact airflow.

With a fixed discharge height, the average dust concentration at the discharge point exhibits a continuous increase as the discharge flow rate rises, with an accelerating rate of increase. This phenomenon occurs because higher discharge flow rates generate stronger impact airflow, which subsequently entrains a greater quantity of fine particles from the ore, thereby augmenting the dust source.

Relationship between maximum impact wind speed, average dust concentration, and ore

The law of conservation of energy dictates that the potential energy of falling ore particles transforms into the kinetic energy of air, the kinetic energy of the ore itself, and energy dissipated through collisions and friction. The discharge height directly influences the amount of energy transferred to the air within the chute. To investigate the relationship between discharge height and both impact wind speed and dust concentration in the chute, ore discharge experiments were conducted at various heights: 1st section (H = 10 m), 2nd section (H = 7.5 m), 3rd section (H = 5 m), and 4th section (H = 2.5 m). Figures 4 and 5 illustrate the resulting curves, depicting the maximum impact wind speed and average dust concentration at the discharge point for different ore particle size distributions in relation to discharge height.

Fig. 4
figure 4

Trend of impact wind speed with the change in unloading height.

Full size image
Fig. 5
figure 5

Trend of dust concentration with the change in unloading height.

Full size image

Figures 4 and 5 demonstrate that, with a constant ore particle size, the maximum impact wind speed generated during ore discharge increases significantly as the discharge height increases. This relationship adheres to an exponential function, suggesting that within a specific range, the trend of increasing maximum impact wind speed becomes more pronounced with greater discharge heights. Within this range, the ore remains in a relatively high acceleration phase. As the discharge height increases, the space available for ore dispersion expands, consequently enhancing the ore’s capacity to induce airflow within the chute. Consequently, the increase in maximum impact airflow becomes more substantial with increasing discharge height.

The relationship between particle size and the exponent of the function describing maximum impact wind speed variation with discharge height exhibits a non-linear pattern for ores of different size ranges. Initially, as particle size decreases, the exponent increases, followed by a subsequent decrease. This trend suggests that within a specific particle size range, smaller particles demonstrate a more pronounced change in maximum impact wind speed as discharge height increases. However, due to air resistance, ore particles below a certain size threshold rapidly attain a uniform velocity within the discharge height range. Consequently, for these smaller particle sizes, the correlation between maximum impact wind speed and discharge height becomes less significant.

With a fixed ore particle size, the average dust concentration at the discharge point exhibits a linear increase as the discharge height increases. Analysis of the curves representing various ore particle size distributions reveals that smaller particle size distributions correspond to steeper slopes in the linear function. This indicates that as particle size decreases, the variation in dust concentration becomes more sensitive to changes in discharge height.

Relationship between maximum impact wind speed, average dust concentration, and ore particle size

The force exerted by ore particles on the air within the chute during discharge is directly proportional to their projected area perpendicular to the airflow. For a given mass, smaller particle sizes result in a greater number of particles, thus increasing the total projected area. This amplifies the force exerted by the ore particles on the airflow inside the chute. However, the relationship between projected area and particle size is not strictly linear due to continuous collisions, friction, and other interactions among falling particles. To investigate the influence of varying ore particle sizes on impact wind speed and dust concentration during discharge, ore samples from different size ranges were released at the 1st section of the chute (H = 10 m) with a discharge rate of 6 kg/s. Figures 6 and 7 illustrate the resulting curves, depicting the maximum impact wind speed and average dust concentration at the discharge point for different ore particle size distributions as a function of discharge flow.

Fig. 6
figure 6

Trend of impact wind speed with ore particle size.

Full size image
Fig. 7
figure 7

Trend of dust concentration with ore particle size.

Full size image

Figures 6 and 7 demonstrate that for a constant discharge flow rate, the maximum impact airflow decreases as the ore particle size range increases. This reduction in maximum impact airflow becomes more pronounced with larger particle sizes. Conversely, when the particle size range remains constant, the maximum impact airflow increases with rising discharge flow, albeit at a diminishing rate as the discharge flow rate escalates. Furthermore, this reduction in the rate of increase becomes more evident with smaller particle sizes. Analysis of the ore particle falling process reveals that as the discharge flow rate increases and the particle size range decreases, the likelihood of particle collisions and contact also increases. Consequently, this leads to a reduced rate of increase in the maximum impact wind speed, as the heightened particle interactions diminish the sensitivity of the impact wind speed to further increases in discharge flow.

At a constant discharge flow rate, the average dust concentration exhibits an inverse relationship with the ore particle size range. A narrower particle size distribution leads to increased airborne particles, resulting in elevated dust concentrations within the chute. This trend becomes more pronounced as the ore flow rate increases.

Relationship between maximum impact wind speed, average dust concentration, and water content of the ore

To investigate the influence of varying ore moisture contents on impact wind speed and dust concentration during ore unloading in a chute, measurements were taken of the maximum impact wind speed and average dust concentration at ore moisture contents of w = 0.41%, 1.39%, 2.36%, 3.31%, 4.24%, and 5.15%. Figure 8 illustrates the variation curves of maximum impact wind speed and average dust concentration in relation to ore moisture content at the unloading port of the fourth section.

Fig. 8
figure 8

Trends of impact airflow and dust concentration with ore moisture content.

Full size image

Figure 8 illustrates a linear decrease in maximum impact airflow as ore moisture content increases. However, this change in maximum impact airflow is relatively minor. The primary reason for this is that the increase in ore moisture content only causes agglomeration of some fine particles, partially reducing the specific surface area of the ore in contact with air during its descent. The average dust concentration, on the other hand, is more significantly influenced by ore moisture content, particularly when it falls below approximately 3%. Within this range, the average dust concentration decreases rapidly with increasing moisture content. However, when the moisture content surpasses 3.5%, further increases in moisture content have a less pronounced effect on reducing the average dust concentration.

Relationship between maximum impact wind speed and average dust concentration with the chute resistance coefficient

During the ore unloading process in the chute, the air within the structure gains energy, primarily utilized to overcome the resistance generated by the chute and the external tunnels parallel to its inlet and outlet. When resistance-enhancing measures, such as placing a cover at the chute opening, are implemented, the cover’s sealability directly influences the magnitude of the impact airflow. In the experimental process, the resistance coefficient of the entire chute model was modified by altering the cross-sectional area of the chute opening. The measured resistance coefficients were 21, 53, 215, 533, and 1260. Figure 9 illustrates the variation curves of the maximum impact wind speed and average dust concentration at the unloading port of Sect. 4, under different chute resistance coefficients.

Fig. 9
figure 9

Trends of impact wind speed and dust concentration with the resistance coefficient of the ore pass.

Full size image

Figure 9 illustrates that both the maximum impact wind speed and the average dust concentration decrease as the chute resistance coefficient increases, following a power function relationship. At low chute resistance levels, the maximum impact wind speed and dust concentration exhibit significant variations with changes in the resistance coefficient. However, once the chute resistance reaches a certain threshold, the changes in both parameters become less pronounced as the resistance coefficient increases.

The chute resistance coefficient exerts a more substantial influence on the maximum impact wind speed compared to dust concentration. This phenomenon primarily stems from the direct effect of the resistance coefficient on the magnitude of the impact wind speed. Conversely, the reduction in dust concentration observed with increasing resistance is predominantly attributed to the diminished intensity of the impact airflow.

Correlation analysis

In investigating dust distribution patterns in high chute mining shafts, GRA is utilized to assess more precisely the influence of various factors on dust distribution. GRA serves as an effective approach for addressing issues with limited data and uncertainty. By examining the geometric proximity, both micro and macro, between relevant factors, GRA determines the closeness of their relationships, thereby elucidating the mutual influence among factors within the system.

Initially, the data for each influencing factor and the reference sequence undergo preprocessing, including dimensionless normalization and standardization, to ensure the accuracy and reliability of the analysis results. The examination of the influence degree of the five factors on the maximum shock wind speed and average dust concentration provides valuable insights for controlling shock airflow generation and reducing dust levels during high chute ore unloading. Utilizing the relationships between the maximum shock wind speed, average dust concentration, and the influencing factors obtained from the experiments, the GRA method from grey theory is applied to evaluate the impact of various factors on these parameters. In this analysis, X01 denotes the maximum shock wind speed at the chute opening, X02 represents the average dust concentration within 60 s at the chute opening, and X1, X2, X3, X4, and X5 correspond to the five main influencing factors: unloading height H, unloading flow Mp, ore particle size D, ore moisture content W, and chute resistance coefficient ξ. X01 and X02 are designated as reference sequences, while the influencing factors serve as comparison sequences. The grey relational degrees between the maximum shock wind speed, average dust concentration, and the influencing factors are calculated using the established formula for grey relational degree.

The initial value of the sequence is established as \(X = (X_{0} ,X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} ) = \left( {\begin{array}{*{20}c} {x_{0} (1)} & {x_{1} (1)} & \cdots & {x_{5} (1)} \\ {x_{0} (2)} & {x_{1} (2)} & \cdots & {x_{5} (2)} \\ \vdots & \vdots & \vdots & \vdots \\ {x_{0} (72)} & {x_{1} (72)} & \cdots & {x_{5} (72)} \\ \end{array} } \right)\). Each element in the matrix is then normalized by dividing it by the first number, resulting in a new matrix \(X^{{^{\prime } }} = (X_{0}^{{^{\prime } }} ,X_{1}^{{^{\prime } }} ,X_{2}^{{^{\prime } }} ,X_{3}^{{^{\prime } }} ,X_{4}^{{^{\prime } }} ,X_{5}^{{^{\prime } }} )\), where \(X_{i}^{{^{\prime } }} = X_{i} /x_{i} (1) = (x_{i}^{{^{\prime } }} (1),x_{i}^{{^{\prime } }} (2), \cdots x_{i}^{{^{\prime } }} (n)),n = 0,1,2 \cdots ,72,i = 1,2, \cdots ,5\).

The sequence difference is computed by calculating the absolute difference between each element of the comparison sequence and its corresponding element in the reference sequence, denoted as \(\left| {x_{0} (k) - x_{i} (k)} \right|\). This process yields the sequence difference matrix \(R = (\zeta_{1} (k),\zeta_{2} (k),\zeta_{3} (k),\zeta_{4} (k),\zeta_{5} (k))^{T}\).

The range of the sequence is determined by calculating the difference between the highest and lowest values of \(M = \mathop {\max }\limits_{i} \mathop {\max }\limits_{k} \Delta _{i} (k)\) and \(m = \mathop {\min }\limits_{i} \mathop {\min }\limits_{k} \Delta _{i} (k)\)

The correlation coefficient is calculated utilizing \(\zeta_{i} (k) = \frac{m + \rho \cdot M}{{\Delta_{i} (k) + \rho \cdot M}}\) to derive the corresponding gray correlation coefficient matrix \(R_{i} = (\zeta_{1} (k),\zeta_{2} (k),\zeta_{3} (k),\zeta_{4} (k),\zeta_{5} (k))^{T}\). In this formula, ρ represents the distinguishing coefficient, with a value range of (0, 1). A smaller ρ value results in a greater differentiation between correlation coefficients, thus enhancing the distinguishing capability. Conventionally, ρ is assigned a value of 0.5.

The gray correlation degree is calculated using the formula \(\zeta_{i} = \frac{1}{n}\sum\limits_{k = l}^{n} {\zeta_{i} } (k),i = l,2,3,4,5;k = 1,2, \cdots ,72\). Upon substituting the data, the correlation degrees between the maximum impact wind speed and each factor are determined as: \(\overline{{R_{i} }} = (\zeta_{1} ,\zeta_{2} ,\zeta_{3} ,\zeta_{4} ,\zeta_{5} )\) = (0.951, 0.870, 0.857, 0.741, 0.926). Similarly, the correlation degrees between the average dust concentration and each factor are calculated as: \(\overline{{R_{i} }} = (\zeta_{1} ,\zeta_{2} ,\zeta_{3} ,\zeta_{4} ,\zeta_{5} )\) = (0.938, 0.869, 0.846, 0.941, 0.919). The specific relationship is illustrated in Fig. 10.

Fig. 10
figure 10

The correlation between maximum impact wind speed, average dust concentration, and various factors.

Full size image

The analysis of the gray correlation model reveals a hierarchy of influence among the five factors affecting the maximum impact wind speed at the unloading port. The order of correlation degree is as follows: X1 > X5 > X2 > X3 > X4. This sequence indicates that the unloading height and the resistance coefficient of the sluice exert the most significant influence on the impact wind speed. The unloading flow rate and ore particle size follow in importance, while the ore moisture content demonstrates a comparatively minor effect on the generated impact airflow.

The correlation degree of influencing factors on the average dust concentration at the unloading port follows the order: X4 > X1 > X5 > X2 > X3. This analysis indicates that ore moisture content and unloading height are the primary factors affecting dust concentration at the unloading port during the unloading process. Secondary factors include the high chute mines resistance coefficient, ore unloading flow rate, and ore particle size.

The correlation degree analysis results provide a robust foundation for dust control in high-sluice mining operations. Several measures can be implemented to mitigate the generation of impact airflow. Firstly, the unloading height can be reduced by excavating an independent ore sluice in the lower middle section and increasing ore storage height in a multi-section sluice, thereby lowering the unloading height in the upper middle section. Secondly, the sluice resistance coefficient can be increased primarily by enhancing resistance at the unloading port, such as installing sealing devices. Thirdly, if the unloading amount remains constant, extending the unloading time can help reduce the unloading flow rate. To minimize dust generation, increasing ore moisture content through water spraying during unloading is an effective method. Furthermore, reducing the content of fine ore particles is also a viable approach. The implementation of these measures will contribute to enhancing the mine’s working environment, safeguarding miners’ health, and improving production efficiency.

Main conclusions

Utilizing the principles of similarity theory, this study derived similarity criteria for the generation of impact airflow and dust during high chute mine unloading. A similar experimental model for multi-section high-slope shafts was constructed, enabling experimental investigations into the generation of impact airflow and the distribution characteristics of dust concentration. Additionally, the study examined the factors influencing these phenomena.

The study demonstrates that both the maximum impact wind speed and average dust concentration exhibit a positive correlation with increases in unloading flow rate and height. Conversely, larger ore particle size ranges and higher chute mines resistance coefficients result in reduced impact airflow and lower dust concentrations. Additionally, the research indicates that dust concentration decreases rapidly as moisture content increases; however, this effect becomes less pronounced when moisture content exceeds 3.5%.

The GRA unveiled the correlation degrees linking the maximum impact wind speed to the five principal influencing factors—unloading height (H), unloading flow rate (Mp), ore particle size (D), ore moisture content (W), and chute resistance coefficient (ξ)—as 0.951 for H, 0.870 for ξ, 0.857 for Mp, 0.741 for D, and 0.926 for W. Similarly, when examining the average dust concentration, the correlation degrees with these factors were found to be 0.938 for W, 0.869 for H, 0.846 for ξ, 0.941 for Mp, and 0.919 for D. These numerical values quantitatively reflect the magnitude of the relationships between each factor and the dust distribution parameters, namely the maximum impact wind speed and the average dust concentration. A higher correlation degree implies a more pronounced influence of the respective factor on the dust distribution dynamics.

The analysis reveals that unloading height and the resistance coefficient of high chute mines exert the most significant influence on impact wind speed. These factors are followed in importance by unloading flow rate and ore particle size. The moisture content of the ore demonstrates a comparatively minor effect on the generation of impact airflow. Regarding dust concentration at the unloading port of high chute mines, ore moisture content and unloading height emerge as the primary determinants. Secondary factors affecting dust concentration include the resistance coefficient of high chute mines, unloading flow rate, and ore particle size.

The findings offer a robust theoretical framework for devising tailored dust control strategies in high chute ore discharge scenarios. By strategically reducing the unloading height or augmenting the chute resistance coefficient, one can effectively mitigate both the impact wind speed and dust concentration levels. Furthermore, enhancing the ore moisture content via water spraying proves to be a highly effective method for substantially curbing dust concentration, particularly when the moisture content remains below the critical threshold of 3.5%.

Limitations

The limitations of this study primarily lie in the scope and conditions of the experimental setup. Firstly, the similarity model used in the experiments was designed based on a specific geometric scaling ratio, which may not fully capture the complexities of real-world high ore pass operations. Secondly, the study focused on a limited range of influencing factors, such as unloading height, flow rate, particle size, moisture content, and resistance coefficient, while other potential factors (e.g., ore composition, chute surface conditions) were not explored. Additionally, the experimental data were collected under controlled laboratory conditions, which might not fully reflect the variability and unpredictability of actual mining environments. Future research could benefit from expanding the range of experimental conditions, incorporating more diverse factors, and conducting field studies to validate the findings in real mining scenarios.