An improved numerical model for landslide-induced waves and its application to the Huangtian landslide in the XW reservoir, China

Abstract

Landslides are one of the most common types of geological disasters. However, the waves generated by landslides often cause more severe damage than the landslides themselves. This paper proposes an improved numerical model for landslide-induced waves. The model’s governing equations are derived from the equilibrium of forces acting on columns and principles of fluid dynamics. It can rapidly and effectively simulate the entire process of landslide-induced wave generation. Moreover, the model improves computational efficiency through the use of fixed computational cells, particularly in mountainous regions. The model was validated using a case study by Fernández-Nieto and then applied to simulate the Huangtian landslide-induced waves in the XW reservoir, China. The simulated landslide deposit closely matches the digital surface model obtained from unmanned aerial vehicle surveys. Simulated results showed a maximum wave height of 40.85 m, a maximum run-up height on the opposite bank of 34.1 m, and a wave height of 3.75 m near the dam. The fixed computational cells, which accounted for approximately 22% of the total cells, led to a four-fold improvement in computational efficiency over a full grid approach. Even with the additional cost of the preliminary simulation, the overall method still achieved a 3.7-fold improvement in computational efficiency over a full grid approach.

Introduction

Landslides are among the most common types of geological hazards^1,2. However, the waves induced by landslides can be even more devastating than the landslides themselves^3,4. In 1958, the Lituya Bay landslide in Alaska generated a wave with a height of 524 m^5,6. In 1963, the Vajont Dam landslide in Italy produced a catastrophic surge that overtopped the dam, inundated downstream villages, and resulted in approximately 2,000 fatalities^7,8. On September 30, 2018, an Mw 7.5 strike-slip earthquake struck Palu Bay, Indonesia, triggering landslides and a tsunami that caused about 4,340 deaths^9,10. In recent years, other notable landslide-induced surge events, including the Baige landslide¹¹, the Todos los Santos Lake landslide¹², and the Anak Krakatau Island landslide¹³, have also caused significant casualties and financial losses. Consequently, the analysis of wave propagation remains crucial for disaster prevention and mitigation efforts.

Numerous numerical models have been developed to simulate landslide-induced waves events. These models can be broadly categorized into three groups: (1) Eulerian methods based on grids, including depth-averaged models that employ the finite difference method (FDM)^14,15, finite element method (FEM)¹⁶, and finite volume method (FVM)¹⁷. For instance, Wang¹⁸ used Fluent to simulate landslide-generated waves in a flume, modeling the landslide as a rigid body. A significant limitation of this approach was its inability to account for landslide deformation. Furthermore, while Wang¹⁹, Hu¹¹, and Chen¹⁷ employed FLOW-3D to respectively simulate landslide-generated waves from the RS landslide (RM reservoir), the Baige landslide (Jinsha River), and the Wangjiashan landslide (Baihetan reservoir), these valuable site-specific simulations were consistently limited to domains of 3–8 km in extent, potentially restricting their applicability for predicting far-field characteristics, such as wave height decay along the propagation path, wave travel time, and the maximum run-up on distant shores—critical parameters whose reliable prediction is essential for the development of safe and cost-effective preventive measures. (2) Lagrangian methods based on particles, such as smoothed particle hydrodynamics (SPH)²⁰ and the material point method (MPM)²¹. These methods discretize both the fluid and the landslide into particles, effectively addressing fluid-soil interactions and large deformation problems. For example, Dai²² simulated the movement of the Baiyun landslide in the South China Sea using the SPH method, but the 50 m particle radius employed was too coarse for effectively modeling landslide-induced waves in reservoir. Currently, the MPM is primarily employed to investigate the dynamics of landslide-generated waves within 2D profiles. For instance, Zhao²³ utilized the MPM to study landslide-generated waves in a flume cross-section, and further examined the influence of various slide material parameters on the resulting impulse waves. (3) The coupling methods of solid mechanics and hydrodynamics provide detailed characterizations of landslide motion and wave generation through various equations. Wang²⁴ utilized an FDEM-SPH (finite-discrete element method- smoothed particle hydrodynamics) method to simulate a landslide-generated wave case in the Three Gorges reservoir area, and Wu²⁵ employed an MPM-SPH approach for the Wangjiashan landslide-induced wave event in the Baihetan reservoir area. However, a critical issue in these studies was that the landslide motion was firstly computed and then used as an initial condition for the subsequent wave simulation. This one-way coupling methodology inherently neglects the mutual interaction between the slide material and the water body.

Despite these advancements, several problems persist in the current research landscape for simulating landslide-induced waves. These include (i) simplifications such as the rigid body assumption, (ii) the substantial computational cost entailed by modeling landslide-induced waves in 3D, which limits the feasible computational domain, impacting far-field predictions, and (iii) the one-way coupling approaches that do not fully capture the dynamic interplay between the landslide and the water.

Addressing the need for computationally rapid simulations of large-scale engineering scenarios within acceptable error tolerances, this paper presents a coupled modelling approach. It integrates LS-Rapid^26,27,28, a model for landslide motion, with COMCOT^29,30, a model for tsunami simulation, both of which are based on Shallow Water Equations. The interaction between the landslide mass and the water body is represented by the drag force^31,32, enabling the coupled model to simulate the complete landslide disaster chain, encompassing “Motion→ Wave induction→ Wave propagation”. The paper is structured as follows: Sect. 2 introduces an improved numerical model for simulating landslide-induced waves and details its validation tests. Section 3 applies this model to the Huangtian landslide in the XW reservoir, China, describing the engineering geological characteristics of the landslide and the setup for numerical simulation. Section 4 presents the numerical results of the Huangtian landslide-induced waves. Section 5 evaluates the model’s effectiveness in simulating the Huangtian landslide-induced wave events, discusses its computational efficiency, and outlines potential directions for future research. Finally, Sect. 6 summarizes the key findings.

Methodology

Description of the model

The model is conceptualized as a three-layer structure, comprising a fixed sliding surface, a movable sliding mass, and an overlying water body (Fig. 1a). The model employs a Cartesian coordinate system and is discretized into a series of vertical columns oriented perpendicular to the XOY plane, which include both soil and water columns. As shown in Fig. 1b, the forces acting on each soil column consist of gravity (${G_2}$), lateral pressure (${P_2}$), frictional resistance (${S_2}$), support force (${N_2}$), buoyancy (B), and the drag force (${D_2}$) exerted by the water. Similarly, the forces acting on each water column include gravity (${G_1}$), lateral pressure (${P_1}$), frictional resistance (${S_1}$), support force (${N_1}$), and drag force (${D_1}$).

Fig. 1

Model schematic and force analysis. (a) Schematic diagram of the model; (b) Force analysis on the soil and water columns. The forces acting on the columns include gravity (${G_n}$), support force (${N_n}$), frictional resistance (${S_n}$), lateral pressure (${P_n}$), and buoyancy (B). $n=1$ and $n=2$ represent the water body and sliding mass, respectively. $\alpha$ and $\beta$represent the angles of the ground surface with respect to the XOZ plane and the YOZ plane, respectively. $\Delta x$ and $\Delta y$ denote the cell sizes in the x- and y-directions, respectively.

Governing equations

The governing equations of the model comprise one continuity equation and two momentum equations to describe landslide motion, as well as one continuity equation and two momentum equations to characterize wave propagation. These equations are derived based on the principles of fluid dynamics and the equilibrium of forces acting on the columns, as described by Sassa²⁶. Therefore, the model is suited for simulating waves induced by flow slides³³ in a static water environment. The detailed derivation process is presented in the following section.

Derivation of the continuity equations

The sliding mass and water body are assumed to be incompressible. Based on mass conservation within each column, the continuity equations for landslide motion and wave propagation are described by Eqs. (1) and (2), respectively.

$$\frac{{\partial {h_2}}}{{\partial t}}+\frac{{\partial {Q_{2x}}}}{{\partial x}}+\frac{{\partial {Q_{2y}}}}{{\partial y}}=0$$

(1)

$$\frac{{\partial \eta }}{{\partial t}}+\frac{{\partial {Q_{1x}}}}{{\partial x}}+\frac{{\partial {Q_{1y}}}}{{\partial y}}= - \frac{{\partial Z}}{{\partial t}}$$

(2)

Where ${h_2}$ represents the thickness of the sliding mass; ${Q_{2x}}={v_{2x}}{h_2}$ and ${Q_{2y}}={v_{2y}}{h_2}$; ${v_{2x}}$ and ${v_{2y}}$ denote the average velocities of the sliding mass in the x- and y-directions, respectively; $\eta$is the water surface elevation; ${Q_{1x}}={v_{1x}}{h_1}$ and ${Q_{1y}}={v_{1y}}{h_1}$; ${h_1}$ is the water depth; ${v_{1x}}$ and ${v_{1y}}$ represent the average velocities of the water body in the x- and y-directions, respectively; Z is the bed elevation.

Derivation of the momentum equations

The momentum equations for landslide motion and wave propagation are derived based on the conservation of momentum in the x- and y-directions. A detailed derivation for the x-direction is presented below, with the y-direction following a similar approach. The equilibrium equations for the sliding mass and the water body are given as Eqs. (3) and (4), respectively.

$${a_{2x}}=\frac{{d{P_{2x}}+{N_{2x}} - {S_{2x}} - {D_{2x}}}}{{{m_2}}}$$

(3)

$${a_{1x}}=\frac{{d{P_{1x}} - {S_{1x}} - {D_{1x}}}}{{{m_1}}}$$

(4)

Where ${a_{1x}}$ and ${a_{2x}}$ are the acceleration of the water body and the sliding mass in the x-direction, respectively; ${m_1}={\rho _1}{h_1}\Delta x\Delta y$ and ${m_2}={\rho _2}{h_2}\Delta x\Delta y$; ${\rho _1}$ and ${\rho _2}$ represent the density of the water body and the sliding mass, respectively; ${P_{1x}}$ and ${P_{2x}}$ are the lateral pressures acting on the water column and the soil column in the x-direction, respectively; ${S_{1x}}$ and ${S_{2x}}$ the components of the frictional resistance acting on the water column and the soil column in the x-direction, respectively; ${D_{1x}}$ and ${D_{2x}}$ are the component of the drag forces acting on the water column and the soil column in the x-direction, respectively. Note that these forces act in opposite directions; ${N_{2x}}$ is the component of the support force acting on the soil column in the x-direction.

Suppose that the horizontal velocities along the column are identical³⁴, then ${a_{1x}}$ and ${a_{2x}}$ can be written as

$${a_{1x}}=\frac{{\partial {v_{1x}}}}{{\partial t}}+{v_{1x}}\frac{{\partial {v_{1x}}}}{{\partial x}}+{v_{1y}}\frac{{\partial {v_{1y}}}}{{\partial y}}$$

(5)

$${a_{2x}}=\frac{{\partial {v_{2x}}}}{{\partial t}}+{v_{2x}}\frac{{\partial {v_{2x}}}}{{\partial x}}+{v_{2y}}\frac{{\partial {v_{2y}}}}{{\partial y}}$$

(6)

Landslide motion

The accelerations of the sliding mass induced by the support force, lateral pressure, and frictional resistance in the x-direction are detailed in Sassa²⁶ and are represented by Eqs. (7), (8), and (9), respectively.

$$\frac{{{N_{2x}}}}{{{m_2}}}=g\frac{{\tan \alpha }}{{{h_2}\sqrt {q+1} }}$$

(7)

$$\frac{{d{P_{2x}}}}{{{m_2}}}= - kg\frac{{\partial {h_2}}}{{\partial x}}$$

(8)

$$\frac{{{S_{2x}}}}{{{m_2}}}=\frac{{{D_x}}}{{\sqrt {q+1} }}(g\tan {\phi _a}+\frac{{c(q+1)}}{{{\rho _2}{h_2}}})$$

(9)

Where g is the gravitational acceleration; $q={\tan ^2}\alpha +{\tan ^2}\beta$; $k=1 - \sin {\phi _a}$; ${\phi _a}$ is the apparent friction angle of the sliding surface soil; c represent the cohesion of the sliding surface soil; ${D_x}=\frac{{{v_{2x}}}}{{\sqrt {v_{{2x}}^{2}+v_{{2y}}^{2}+v_{{2z}}^{2}} }}$, ${v_{2z}}={v_{2x}}\tan {\alpha _2}+{v_{2y}}\tan {\beta _2}$.

The drag force, generated by the friction between the water body and the sliding mass, can be described as a function³¹ of the relative velocity between the sliding mass and the water, the frontal area of the sliding mass, and the drag coefficient^35,36. Specifically, the drag force ${D_2}$ can be written as

$${D_2}=\frac{1}{2}{\rho _1}{C_D}({v_2} - {v_1})\sqrt {{{({v_2} - {v_1})}^2}} \Delta x\Delta y$$

(10)

Where ${C_D}$ is the drag coefficient; ${v_1}$ and ${v_2}$ denote the average velocities of the water body and the sliding mass, respectively.

Therefore, the acceleration of the sliding mass in the x-direction, induced by the drag force ${D_2}$, can be expressed as

$$\frac{{{D_{2x}}}}{{{m_2}}}=\frac{{{C_D}}}{{2{h_2}}}\frac{{{\rho _1}}}{{{\rho _2}}}({v_{2x}} - {v_{1x}})\sqrt {{{({v_{2x}} - {v_{1x}})}^2}}$$

(11)

By substituting Eqs. (5), (7), (8), (9), and (11) into Eq. (3) and multiplying the result by ${h_2}$, the following momentum equation for landslide motion in the x-direction is obtained:

$$\begin{gathered} \frac{{\partial {Q_{2x}}}}{{\partial t}}+\frac{{\partial (Q_{{2x}}^{2}/{h_2})}}{{\partial x}}+\frac{{\partial ({Q_{2x}}{Q_{2y}}/{h_2})}}{{\partial y}}=g{h_2}\frac{{\tan \alpha }}{{{q_2}+1}} - kg{h_2}\frac{{\partial {h_2}}}{{\partial x}} - \frac{{{D_x}}}{{\sqrt {q+1} }}(g{h_2}\tan {\phi _a}+\frac{c}{{{\rho _2}}}(q+1)) \hfill \\ {\text{ }} - \frac{1}{2}\frac{{{\rho _1}}}{{{\rho _2}}}{C_D}({v_{2x}} - {v_{1x}})\sqrt {{{({v_{2x}} - {v_{1x}})}^2}} \hfill \\ \end{gathered}$$

(12)

Similarly, the momentum equation for landslide motion in the y-direction can be expressed as follows:

$$\begin{gathered} \frac{{\partial {Q_{2y}}}}{{\partial t}}+\frac{{\partial ({Q_{2x}}{Q_{2y}}/{h_2})}}{{\partial x}}+\frac{{\partial (Q_{{2y}}^{2}/{h_2})}}{{\partial y}}=g{h_2}\frac{{\tan \beta }}{{q+1}} - kg{h_2}\frac{{\partial {h_2}}}{{\partial y}} - \frac{{{D_y}}}{{\sqrt {q+1} }}(g{h_2}\tan {\phi _a}+\frac{c}{{{\rho _2}}}(q+1)) \hfill \\ {\text{ }} - \frac{1}{2}\frac{{{\rho _1}}}{{{\rho _2}}}{C_D}({v_{2y}} - {v_{1y}})\sqrt {{{({v_{2y}} - {v_{1y}})}^2}} \hfill \\ \end{gathered}$$

(13)

Where ${D_y}=\frac{{{v_{2y}}}}{{\sqrt {v_{{2x}}^{2}+v_{{2y}}^{2}+v_{{2z}}^{2}} }}$.

Wave propagation

The accelerations of the water body induced by the lateral pressure and frictional resistance in the x-direction are detailed in Liu^29,37 and are represented by Eqs. (14) and (15), respectively.

$$\frac{{d{p_{1x}}}}{{{m_1}}}= - g\frac{{\partial {h_1}}}{{\partial x}}$$

(14)

$$\frac{{{S_{1x}}}}{{{m_1}}}=\frac{{g{n^2}{v_{1x}}\sqrt {{{({v_{1x}}+{v_{1y}})}^2}} }}{{h_{1}^{{10/3}}}}$$

(15)

Where n is Manning’s roughness coefficient.

The drag forces are equal in magnitude and opposite in direction, resulting from the friction between the sliding mass and the water body. According to Newton’s third law of motion, the drag force ${D_1}$ can be expressed as

$${D_1}= - \frac{1}{2}{\rho _1}{C_D}({v_2} - {v_1})\sqrt {{{({v_2} - {v_1})}^2}} \Delta x\Delta y$$

(16)

Therefore, the acceleration of the water body in the x-direction, induced by the drag force ${D_1}$, can be expressed as

$$\frac{{{D_{1x}}}}{{{m_1}}}= - \frac{{{C_D}}}{{2{h_1}}}({v_{2x}} - {v_{1x}})\sqrt {{{({v_{2x}} - {v_{1x}})}^2}}$$

(17)

By substituting Eqs. (6), (14), (15), and (17) into Eq. (4) and multiplying the result by ${h_1}$, the following momentum equation for wave propagation in the x-direction is obtained:

$$\begin{gathered} \frac{{\partial {Q_{1x}}}}{{\partial t}}+\frac{{\partial (Q_{{1x}}^{2}/{h_1})}}{{\partial x}}+\frac{{\partial ({Q_{1x}}{Q_{1y}}/{h_1})}}{{\partial y}}= - g{h_1}\frac{{\partial \eta }}{{\partial x}} - \frac{{g{n^2}{Q_{1x}}\sqrt {Q_{{1x}}^{2}+Q_{{1y}}^{2}} }}{{h_{1}^{{7/3}}}} \hfill \\ {\text{ }} - \frac{1}{2}{C_D}({v_{1x}} - {v_{2x}})\sqrt {{{({v_{1x}} - {v_{2x}})}^2}} \hfill \\ \end{gathered}$$

(18)

Similarly, the momentum equation for wave propagation in the y-direction can be expressed as follows:

$$\begin{gathered} \frac{{\partial {Q_{1y}}}}{{\partial t}}+\frac{{\partial ({Q_{1x}}{Q_{1y}}/{h_1})}}{{\partial x}}+\frac{{\partial (Q_{{1y}}^{2}/{h_1})}}{{\partial y}}= - g{h_1}\frac{{\partial \eta }}{{\partial y}} - \frac{{g{n^2}{Q_{1y}}\sqrt {Q_{{1x}}^{2}+Q_{{1y}}^{2}} }}{{h_{1}^{{7/3}}}} \hfill \\ {\text{ }} - \frac{1}{2}{C_D}({v_{1y}} - {v_{2y}})\sqrt {{{({v_{1y}} - {v_{2y}})}^2}} \hfill \\ \end{gathered}$$

(19)

Numerical scheme

The governing equations are discretized using the finite difference method and solved within rectangular cells²⁷. Here, h denotes the thickness of the landslide and the water surface elevation at the center of a cell (i, j). The flow rates ${Q_x}$ and ${Q_y}$ are defined at the boundaries of each cell in the x- and y-directions, respectively (Fig. 2). Consequently, the continuity equations are solved within each cell, while the momentum equations are solved at the cell boundaries.

Fig. 2

Schematic diagram of the discretized cells³⁴.

The boundary conditions in this model adopt the open and moving boundaries employed in the COMCOT model^30,38. To ensure model stability, the model limits fluid flow to adjacent cells within each time step. Consequently, the time step must satisfy the following condition.

$$\Delta t \leqslant \hbox{min} \left( {\frac{{\Delta x}}{{\omega \hbox{max} \left| {{v_x}} \right|}},\frac{{\Delta y}}{{\omega \hbox{max} \left| {{v_y}} \right|}}} \right)$$

(20)

Where $\omega =5$, ${v_x}=\hbox{max} \left\{ {{v_{1x}},\left. {{v_{2x}}} \right\}} \right.$, ${v_y}=\hbox{max} \left\{ {{v_{1y}},\left. {{v_{2y}}} \right\}} \right.$.

Computational scheme

When simulating real-world landslide-induced wave disasters, the simulation domain is often extensive. Consequently, a large number of cells may remain empty and are unnecessary for computation. However, traditional computational schemes still include these empty cells in the calculations^34,39, resulting in inefficient use of computational resources. Although the dynamic computational cell method proposed by Shen⁴⁰ helps maintain model stability, its contribution to improving computational efficiency remains limited.

To enhance the computational efficiency of the model, this paper proposes conducting calculations exclusively within fixed computational cells (Fig. 3). These cells primarily cover the regions impacted by landslide-induced wave disasters, as depicted in Fig. 3. Empty cells are retained solely for spatial positioning purposes. By reducing the number of computational cells involved in the calculations, the model achieves a significant improvement in computational efficiency, especially in mountainous regions.

Prior studies indicate that the maximum wave heights occur near landslide sources⁴¹. Accordingly, preliminary simulations were conducted for the relevant area, maintaining the target grid resolution, to estimate the landslide’s area of movement and the maximum wave height. The fixed computational domain was subsequently defined: it encompassed the landslide movement area, expanded horizontally by several hundred meters, with its upper boundary set approximately 100 m above the highest simulated wave elevation. Because there is inherently no mass exchange across the boundaries of the fixed domain, the numerical accuracy is not compromised.

Fig. 3

Schematic diagram of the fixed computational cells.

Solution procedure

The solution procedures for the model are outlined as follows.

• 1. The predicted flow rates ${Q_{2x}}$ and ${Q_{2y}}$ of the landslide for the next time step are obtained using Eqs. (12) and (13).

• 2. The predicted landslide thickness ${h_2}$ and bed elevation Z for the next time step are determined using Eq. (1).

• 3. The predicted water surface elevation $\eta$ and water depth ${h_1}$ for the next time step are computed using Eq. (2).

• 4. The predicted flow rates ${Q_{1x}}$ and ${Q_{1y}}$ of the water for the next time step are determined using Eqs. (18) and (19).

• 5. The above procedures are iteratively repeated until the entire computational process is completed.

Validation test

The model was developed based on the LS-Rapid and COMCOT models and incorporates the drag force resulting from the friction between the landslide mass and the water body to capture their mutual interactions. The model was subsequently implemented using the Fortran programming language. To validate the effectiveness of the model, we conducted a validation test by comparing our simulation results with Fernández-Nieto’s simulation results⁴² of landslide-induced waves in a water tank. The model setup and the physical parameters were consistent with those used by Fernández-Nieto⁴².

Figure 4 illustrates the model setup for the landslide-induced wave in a water tank. The model consists of a water tank measuring 10 m in length, 0.6 m in width, and 1 m in height. The bottom of the tank comprises a 5-m-long inclined plane with a slope angle of 11.31° on the left side and a 5-m-long horizontal plane on the right. The tank is bounded by two 1-m-high vertical sidewalls, and its right end features an open boundary. The thickness of the sliding mass is determined using Eq. (21), and the tank is initially filled with 0.4 m of quiescent water. The numerical model is employed to simulate wave generation resulting from the sliding mass descending the slope and entering the water. The A-A’ profile is specifically established to capture the dynamics of landslide motion and wave propagation. The computational domain is divided into 200 cells in the x-direction and 12 cells in the y-direction; therefore, $\Delta x=0.05{\text{ m}}$ and $\Delta y=0.05{\text{ m}}$.

$${h_2}(x)=\left\{ \begin{gathered} 0.2x - 0.3{\text{, if }}1.5 \leqslant x \leqslant 2.5 \hfill \\ 0{\text{ , otherwise}} \hfill \\ \end{gathered} \right.$$

(21)

Fig. 4

Schematic diagram of the model setup for the landslide-induced wave in a water tank. (a) Side view; (b) Top view. A-A’ denotes the longitudinal section of the model.

As depicted in Fig. 5, the sliding mass descends along a slope and ultimately deposits on the bottom of the tank. Initially, the leading edge of the sliding mass moves rapidly, reaching a position at 6.45 m by 3.0 s, due to its unobstructed position. This initial deposit effectively obstructs the subsequent sliding mass from moving further forward along the water tank. The final deposit, shown in the stationary state of the sliding mass in Fig. 5, features a leading edge at 6.45 m and a maximum thickness of 0.85 m. When the sliding mass comes into contact with the water, waves are generated. Between 0 and 3.0 s, these waves propagate in the same direction as the sliding mass. By 4.0 s, the waves begin to propagate in the opposite direction to the sliding mass, with a maximum wave height of 0.04 m. The simulated results show good agreement with the numerical simulation by Fernández-Nieto⁴².

Fig. 5

Comparison of simulation results with those of Fernández-Nieto⁴² along the A-A’ profile.

Application to the Huangtian landslide-Induced waves

This section employs the proposed numerical model to investigate the hazards of Huangtian landslide-induced waves in the XW reservoir, China. The XW reservoir spans 178 km and has a water level variation of 60 m, which is twice the range of variation in the Three Gorges reservoir²⁵. As a result, the XW reservoir area faces significant challenges in addressing geological hazards. The Huangtian landslide, which is a typical case, occurred during the construction of a hydropower station in the XW reservoir and for which field measurements of wave heights are available. By comparing the simulation results with the monitoring data, it is validated that the model can effectively simulate real-world landslide-generated waves, with a high degree of accuracy and reliability.

Geographic and geological setting

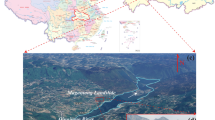
The Huangtian landslide is located in Lincang County, Yunnan Province, China, in the downstream region of the Lancang River (24°44’8’’ N, 100°1’40’’ E) (Fig. 6). The study area lies within the tectonic collision zone between the Indian and Eurasian Plates, which has shaped a landscape characterized by numerous mountains and valleys. The topography features higher elevations in the northwest, gradually descending towards the south, with several peaks exceeding 3,000 m in altitude. Major rivers flowing through the study area include the Lancang River, Nu River, Jinsha River, and Heihui River, with the Lancang River traversing the region in a north-south direction (Fig. 6). The region serves as a transitional climate zone between cold and subtropical climates, with average annual precipitation ranging from 650 mm to 1,100 mm and maximum daily rainfall exceeding 100 mm. The average annual temperature ranges from 5 °C to 16 °C.

The fault zones in the study area primarily include the Lancangjiang Fault Zone (LCFZ), Honghe Fault Zone (HHFZ), Nantinghe Fault Zone (NTFZ), and Wanding Fault Zone (WDFZ). According to historical records of major earthquakes, over a hundred earthquakes (M ≥ 5) have occurred in the area in the past century, including 23 major earthquakes (M ≥ 6).

Fig. 6

Location and tectonics of the study area. (a) Location of the study area (the red dashed line box indicates the area shown in Fig. b); (b) Location of the Huangtian landslide, showing historical earthquakes and major fault zones. (LCFZ: Lancangjiang Fault Zone; HHFZ: Honghe Fault Zone; NTFZ: Nantinghe Fault Zone; WDFZ: Wanding Fault Zone).

Characteristics of the Huangtian landslide

The characteristics of the Huangtian landslide were investigated using Google Earth imagery, field surveys, and digital surface model (DSM) with a resolution of 0.04 m, obtained from an unmanned aerial vehicle (UAV) in April 2024.

The Huangtian landslide is located on the right bank of the lower reaches of the Lancang River, approximately 9.5 km from the dam (Fig. 7). Following several days of heavy rainfall, on July 20, 2009, during the dam construction, the landslide occurred suddenly at a water level of 1,125 m. The debris entered the water, generating significant impact waves. Since the landslide occurred at night, the maximum wave height within reservoir, which could only be inferred from the wave traces left on the shore, were estimated to be between 30 and 40 m⁴¹. Meanwhile, the maximum wave height near the dam was recorded as approximately 3.0 m⁴³.

Fig. 7

Google Earth imagery of the study area. The white dashed-line box indicates the location of the Huangtian landslide. εwl¹ represents the Wuliangshan Group, Cambrian; T_2 − 3 represents the Middle Triassic. (LCFZ: Lancangjiang Fault Zone).

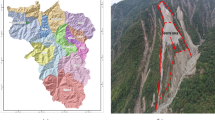
The Huangtian landslide is approximately 780 m in length and 450 m in width, with a volume of 9.5 Mm³ (Fig. 8). The landslide outlet is located at an elevation of approximately 1,080 m, while the headscarp is situated at around 1,550 m (Fig. 8). Following the failure, the back wall of the sliding surface is approximately 140 m in height and 300 m in width (Fig. 9). The deposited material forms a platform and a steep slope. The platform is located at an elevation of 1,400 m, and the steep slope, with an angle ranging from 50° to 60°, lies between elevations of 1,200 m and 1,400 m (Fig. 9).

Fig. 8

Plan view and cross-section of the Huangtian landslide. (a) Plan view of the Huangtian landslide. The black line (B-B’) indicates the location of the cross section; (b) Cross section of the Huangtian landslide. The normal storage level of the reservoir is 1,240 m, while the water level during the landslide event was 1,125 m. (LCFZ: Lancangjiang Fault Zone). This figure was generated using ArcGIS Pro 3.1.6 (https://www.esri.com/) and Microsoft Excel 2021 (https://www.microsoft.com/).

Fig. 9

Photographs of the Huangtian landslide. (a) Front view of the Huangtian Landslide, with the deposit outline indicated by a black line; (b) Side view of the Huangtian Landslide, with the deposit outline indicated by a black line.

Numerical simulation

Numerical model setting

The initial topography of the numerical model was constructed using a digital elevation model with a resolution of 12.5 m from the Alaska Satellite Facility through their Data Search platform. The sliding surface of the Huangtian landslide was determined using DSM with a resolution of 0.04 m, obtained by an industrial UAV in April 2024.

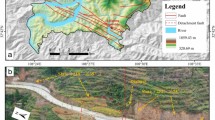
Figure 10 illustrates the model used to simulate the Huangtian landslide-induced waves. The landslide thickness is significantly greater in the upper section compared to the lower section, with the maximum thickness reaching 87.5 m (Fig. 10a). The simulation domain, measuring 18 km in length and 8.9 km in width, is divided into 1,440 cells in the x-direction and 712 cells in the y-direction. The fixed computational domain was determined from preliminary simulations of the area shown in Fig. 10a. The fixed computational cells primarily cover the landslide movement area and regions below an elevation of 1,300 m (Fig. 10b), comprising 230,172 grid cells, which accounts for approximately 22% of the total cells. Within the model, 11 monitoring points are spaced at 2 km intervals to track wave heights.

Fig. 10

The model for simulating the Huangtian landslide-induced waves. (a) Initial distribution of landslide thickness; (b) Layout of the model. The red box denotes the area covered by fixed computational cells. Monitoring points P1–P11 are distributed within the area.

Physical parameters

In this study, the parameters adopted in the simulation of the Huangtian landslide-induced waves were determined through back-analysis of the limit equilibrium state of the Huangtian landslide slope, as well as through geotechnical laboratory tests on samples from the Xinminbazi landslide⁴⁴ within the XW reservoir. The laboratory tests⁴⁴ revealed that the steady-state friction angles of the sliding belt soil were 23.49° in the natural state and 20.3° in the saturated state.

Based on the DSM, the back-analysis of the limit equilibrium state of the Huangtian landslide slope, and the geotechnical laboratory tests of the Xinminbazi landslide, we inferred that the effective friction coefficient (${H \mathord{\left/ {\vphantom {H L}} \right. \kern-0pt} L}$, where H and L denote the vertical drop and horizontal travel distance of the landslide, respectively) for the Huangtian landslide is approximately 0.5. Consequently, the apparent friction angle adopted in the simulation is approximately 25°, which is slightly higher than the steady-state friction angle of the sliding belt soil of the Xinminbazi landslide by approximately 1.5°.

Additionally, laboratory tests of the Xinminbazi landslide indicated that the steady-state friction angle of the sliding belt soil in the saturated state is approximately 86% of that in the natural state. Therefore, once the landslide entered the water, the apparent friction angle was adjusted to 22° in the simulation, corresponding to 88% of its initial value. Notably, the cohesion was assumed to be zero during the landslide movement. Settings for the Manning roughness coefficient and the drag coefficient drew upon the findings of Bosa⁷ and Pudasaini³¹, respectively. The specific parameters adopted in the simulation are detailed in Table 1.

Table 1 Physical parameters adopted in the simulation of the Huangtian landslide-induced waves⁴⁵.

Analysis of simulated results

Landslide motion

Figures 11, 12 and 13 illustrate the simulated results of the Huangtian landslide-induced waves at different times. Upon initiation of the simulation, the sliding mass rapidly descends along the slope. At 30 s, the landslide velocity reaches its maximum value of 34.09 m/s. Subsequently, the velocity decreases, with the upper and lower sections of the landslide stopping first. By 80 s, the landslide near the water surface also stops. The submerged volume of the deposit is approximately 4.35 Mm³, and the river remains unblocked (Figs. 13 and 14). The simulated deposit is in good agreement with the DSM obtained via UAV surveys in April 2024 (Figs. 15 and 16).

Fig. 11

Simulated thickness of the sliding mass at different times in 3D.

Fig. 12

Simulated velocity of the sliding mass at different times in 3D.

Fig. 13

Simulated results of landslide-induced waves at different times along the B-B’ cross section.

Fig. 14

Volume change of the Huangtian landslide over time.

Fig. 15

Comparison of the simulated deposit with the DSM obtained from an UAV in 3D.

Fig. 16

Comparison of the simulated deposit with the DSM obtained from an UAV along the B-B’ cross section.

Waves propagation

Figure 17 depicts the simulated water surface elevation at different times. At 30 s, the wave reached the opposite bank. Within the study area, the maximum wave height was recorded at 40.85 m, while the maximum run-up height on the opposite bank was measured at 34.1 m (Fig. 19). This is consistent with the results of the field survey (Fig. 20). Subsequently, the wave height decreased as the propagation distance increased (Figs. 18, 19 and 20). At 380 s, the wave reached the dam. Owing to the obstruction by the dam, the wave height at P10 was elevated to 3.75 m (Figs. 18 and 20).

Fig. 17

Simulated water surface elevation at different times in 3D.

Fig. 18

Simulated water surface elevation at monitoring points P1–P11 over time.

Fig. 19

Simulated maximum wave height for each cell in 3D.

Fig. 20

Comparison of the simulated wave height with the survey data along the river^41,43.

Discussion

Characteristics of the numerical model for landslide-induced waves

The numerical model was employed to simulate landslide-induced waves in a water tank, and the results were found to be in good agreement with those reported by Fernández-Nieto. Subsequently, the model was applied to simulate the Huangtian landslide-induced waves. The simulated landslide deposit closely matched the DSM obtained from UAV surveys. Field observations recorded maximum wave heights ranging from 30 to 40 m within the river channel, diminishing to approximately 3 m at the dam site situated 9.5 km downstream. The numerical model developed in this study predicted a maximum wave height of 40.85 m and a wave height of 3.75 m at the dam site. The simulated wave height at the dam site is approximately 0.75 m higher than the observation. This discrepancy likely stems from our model’s inability to fully represent the three-dimensional geometry of the hyperbolic arch dam. Nevertheless, an absolute error of this magnitude can be deemed acceptable in many engineering contexts.

In the preliminary simulation for the local area of the Huangtian landslide-generated surge (Fig. 10a), the landslide stopped at 80 s, and the wave height in the river channel dropped below 3 m by 200 s, with the simulation requiring a computation time of about 8 min. The simulation of the entire domain using a fixed computational grid (Fig. 10b) required approximately 100 min for the surge wave to propagate to the dam site. In contrast, Huang⁴¹ utilized an SPH model, simulating a maximum wave height of 48 m within a limited domain covering only 3 km near the landslide, thus not encompassing the dam site, with a reported computation time of 24 h.

In the simulation of the Huangtian landslide-induced waves, fixed computational cells accounted for approximately 22% of the total cells, which led to a four-fold improvement in computational efficiency over a full grid approach. Even with the additional cost of the preliminary simulation, the overall method still achieved a 3.7-fold improvement in computational efficiency over a full grid approach. Asunción⁴⁶ found that integrating a load balancing algorithm with multiple GPUs improved speedup by only up to 12% over a single GPU. Therefore, the use of a fixed computational grid demonstrates a highly effective method for enhancing computational performance in these types of simulations.

Applications and future studies of the model

The model is based on the principles of fluid dynamics and the equilibrium of forces acting on columns, as described by Sassa²⁶. Therefore, the model could be used to predict the scale and intensity of flow-slide-generated wave hazards, but it cannot capture the rock mass fragmentation and separation.

In this study, the apparent friction angle was treated as a constant. When simulating the Huangtian landslide-induced waves, the apparent friction angle for the submerged landslide material was adjusted to 22°, corresponding to 88% of its initial value. However, this approach is unable to provide a mechanistic description of the dynamic variations in material strength that occur during landslide motion. Yavari-Ramshe and Ataie-Ashtiani¹⁴ have shown that the constitutive behavior of the material significantly influences the deformation pattern and magnitude of landslides, as well as the propagation characteristics of landslide-induced waves. Future research should incorporate the dynamic variations in material strength during landslide movement into numerical models.

Conclusions

This study introduces an improved numerical model for simulating landslide-induced waves. The model is based on the LS-Rapid and COMCOT models and accounts for drag forces due to friction between the landslide mass and the water body. To validate the model’s effectiveness, it is employed to simulate a validation test of landslide-induced waves in a water tank. The simulated results show good agreement with those reported by Fernández-Nieto⁴². Subsequently, the model is employed to simulate a typical case of the Huangtian landslide-induced wave in the XW reservoir, China. The primary findings of this research are discussed in the following sections.

• (1) In the simulation of the Huangtian landslide-induced waves, based on the experimental data from the Xinminbazi landslide⁴⁴ within the XW reservoir, the apparent friction angle of the submerged landslide material was adjusted to 22°, which corresponds to 88% of its initial value. The simulated landslide deposit closely matched the DSM obtained from UAV surveys.

• (2) In the simulation of the Huangtian landslide-induced waves, the maximum wave height was recorded at 40.85 m, while the maximum run-up height on the opposite bank was measured at 34.1 m. The wave height decreased with increasing propagation distance. However, due to the obstruction by the dam, the wave height near the dam increased from 1.57 m to 3.75 m.

• (3) This model has advantages in rapidly analyzing landslide-induced waves. In the simulation of the Huangtian landslide-induced waves, fixed computational cells accounted for approximately 22% of the total cells, which led to a four-fold improvement in computational efficiency over a full grid approach. The maximum wave height used to assess the hazards associated with these waves only requires a computational time of approximately 100 min.