Realistic wave-optics simulation of X-ray dark-field imaging at a human scale

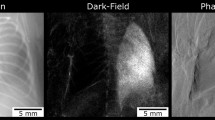
Abstract

X-ray dark-field imaging (XDFI) has been explored as a superior alternative to conventional X-ray imaging for diagnosing many pathologic conditions. However, a simulation tool capable of reliably predicting clinical XDFI images at a human scale, is currently lacking. In this paper, we demonstrate, to the best of our knowledge, the first human-scale XDFI simulation. Using the developed simulation tool, we illustrate the strengths and limitations of XDFI for the diagnosis of emphysema, fibrosis, atelectasis, edema, and pneumonia. We augment the XCAT phantom with Voronoi grids to simulate the alveolar substructure responsible for the lung’s dark-field signal, assign material properties to each tissue type, and simulate X-ray wave propagation through the augmented XCAT phantom using a multi-layer wave-optics propagation. By altering the density and thickness of the Voronoi grids, as well as the material properties, we simulate XDFI images of normal and diseased lungs. Our simulation framework can generate realistic XDFI images of a human chest with normal or diseased lungs. The simulation confirms that the normal, emphysematous, and fibrotic lungs produce clearly distinct dark-field signals. It also shows that alveolar fluid accumulation in pneumonia, wall thickening in interstitial edema, and deflation in atelectasis all result in similar reductions in dark-field signal. It is feasible to augment XCAT with pulmonary substructure and generate realistic XDFI images using multi-layer wave optics. By providing the most realistic XDFI images of lung pathologies to date, the developed simulation framework enables in-silico clinical trials and the optimization of both hardware and software for XDFI.

Introduction

In conventional X-ray imaging, the image contrast arises from the attenuation of X-rays due to photoelectric absorption and Compton scattering. X-rays are weakly absorbed by low-atomic-number (low-Z) materials such as soft tissues. Thus, conventional X-ray imaging is unable to distinguish them despite providing excellent contrast for high-Z materials such as bones and metallic implants. Alternative approaches utilizing complementary contrast mechanisms to improve contrast in soft tissues have been explored for several decades. For example, X-ray phase-contrast imaging (XPCI) exploits X-ray refraction caused by local variations in the electron density¹. It is well established that XPCI has significantly higher soft-tissue contrast than traditional attenuation-based X-ray imaging². X-ray dark-field imaging (XDFI) utilizes ultra-small-angle scattering of coherent X-ray wavefronts induced by microscopic structural inhomogeneities^3,4. XDFI has been shown to provide superior performance over the conventional X-ray imaging for the diagnosis of many pathologic conditions such as pulmonary fibrosis and other pulmonary diseases^5,6,7,8,9. Early methods for XPCI and XDFI required a highly coherent X-ray source such as synchrotron^{10,11,12,13,14}. Consequently, their incorporation into routine medical imaging has been very difficult. Recent developments of Talbot-Lau interferometry have lifted this serious restriction¹⁵ and it has become possible to build a tabletop XPCI/XDFI system using a conventional X-ray source^16,17. Although early XPCI/XDFI systems were only suitable for small ex-vivo specimens¹⁸ and small animals¹⁹, considerable progress has been made to scale up the size of these systems for human imaging^20,21. One of the key technical limitations in this endeavor is the lack of a reliable method for predicting the performance of these systems at a human scale.

A typical X-ray simulation framework consists of two parts: a numerical phantom that provides a detailed description of human anatomy and a forward model that implements the image formation process. Simulating XPCI/XDFI at human scale poses challenges for both parts of the simulation framework. For the simulation of medical X-ray imaging, voxelated numerical phantoms are typically used with the voxel size about the same as the detector pitch. For XPCI/XDFI simulation, the boundaries between the coarse voxels can generate strong diffraction artefact, which is hard to separate from a true XPCI/XDFI signal. In contrast, the 4D extended cardiac-torso (XCAT) phantom represents various organs using non-uniform rational B-spline (NURBS) surfaces^22,23, which can be used to generate a voxelated phantom at arbitrarily high resolution.

The forward model describes the interaction of incident X-rays with various anatomic structures in the numerical phantom as well as X-ray optical components. For XPCI simulation, ray tracing²⁴ or Monte Carlo methods²⁵, which are commonly used in conventional attenuation-based X-ray simulation, have been extended to calculate the X-ray refraction. Wave optics simulation can best model the wave phenomena such as coherent scattering and diffraction of X-rays; however, it usually requires large computational resources. We previously demonstrated a fast, yet accurate wave-optics simulation of XPCI using a forward model built upon the first-order Rytov approximation^26,27,28, which is valid when the refractive index difference at the boundary is small and thus can be safely used in the XPCI simulation²⁹. The so-called full-wave Rytov (FWR) method allows for fast yet accurate wave-optics simulation of XPCI using NURBS-defined models as well as geometric primitives and a voxelated phantom.

The first-order approximation, however, ignores multiple scattering within an imaged specimen, which can be problematic for XDFI simulation. This is because the image contrast of XDFI originates from the multiple scattering of X-rays by a microstructure such as the lung alveoli. Thus, for XDFI simulation, a multi-layer wave propagation method has been dominantly used^30,31,32, which can handle multiple scattering. In this method, a numerical phantom is divided into an axial stack of slices, and a wave propagation is performed across the axial stack consecutively. For the numerical propagation through each layer, the beam-propagation method (BPM) has been dominantly used, which uses the angular-spectrum scalar wave theory together with the projection approximation. With the projection approximation, the axial variation of the refractive index is ignored within the layer’s volume. Although the angular-spectrum scalar wave theory can be implemented very efficiently using the Fourier transform³³, the grid size for the calculations must be sufficiently small to resolve the wave field distortions introduced by microstructure. This requirement significantly increases the computational cost. Thus, the XDFI simulation using the BPM has been mostly applied to a small phantom of relatively simple geometry such as a box filled with spheres^30,31.

For the numerical phantom, we generate a high-resolution voxelated phantom from the NURBS-defined XCAT model. The phantom is augmented by adding small air voids to the lung region in each slice, which generates the ultra-small angle X-ray scattering by alveoli, and thus the dark-field signal for lungs. For the forward model, we use a multi-layer wave propagation method as described in Methods.

Methods

Extended cardiac-torso (XCAT) phantom to simulate lung microstructure

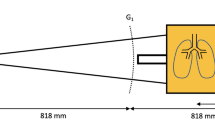
Figure 1 shows the simulation geometry used in this study. In a multi-layer wave-optics simulation, the numerical phantom is divided into an axial stack of layers, and the X-ray wave propagates through the layers in a sequential manner. For the numerical phantom, we use the XCAT phantom, which represents various organs with about 2800 NURBS surfaces^22,23and thus can accurately model the complex human anatomy such as the lungs, skeleton, muscles, bronchial tree, and vasculature³⁴. Due to its realism and computational efficiency, the XCAT phantom has been widely adopted to simulate various imaging modalities. Using the XCAT (Duke University, ver. 2), we produced 2505 coronal slices of 100 μm intervals. Each slice contained 4096 × 4096 pixels of 100 μm with the pixel value representing the organ identification number (ID) stored as a 16-bit integer.

Fig. 1

Schematic diagram of the simulation geometry used in this study. The 3D rendering was created using MATLAB (MathWorks, Inc., version R2021b). G1, G2: gratings; and D: detector. The numbers 1 through 5 in the circles refer to the planes where Eqs. (6) through (9) were calculated.

Fig. 2

Augmentation of the XCAT phantom for the XDFI simulation. (a) shows an example slice of the XCAT, 4096 × 4096 pixels with the pixel size of 100 μm. The numbers in the figure correspond to the organ identifier (ID) labels. (b) and (c) show the real (δ) and imaginary (β) parts of the refractive index after assigning the material properties. (d) shows an example of the lung microstructure, which is modeled using Voronoi grids. Scale bars: 5 cm in (a) through (c) and 1 mm in (d).

Figure 2a shows an example coronal slice produced by the XCAT. Based on the organ ID, we have assigned the complex refractive index value $\:n\left(x,y,z\right)$ to each organ for the X-ray energy (i.e., wavelength) used for the simulation.

The complex refractive index, an input to the XPCI/XDFI simulation, is typically written in the form $\:n\left(x,y,z\right)=1-\delta\:\left(x,y,z\right)+i\beta\:\left(x,y,z\right)$.

$$\:\delta\:=\frac{{N}_{el}{r}_{e}{\lambda\:}^{2}}{2\pi\:},$$

(1)

$$\:\beta\:=\frac{\lambda\:\mu\:\left(\lambda\:\right)}{4\pi\:},$$

(2)

where $\:\lambda\:$ is the wavelength of X-ray, $\:{r}_{e}$ is the classical radius of electron (2.818 × 10^− 15 m). The electron density $\:{N}_{el}$ and the linear attenuation coefficient $\:\mu\:\left(\lambda\:\right)$ were obtained from the data for adult human tissues³⁵. Figures 2b,c show $\:\delta\:$ and $\:\beta\:$, respectively, assigned to the coronal slice shown in Fig. 2a, for the X-ray energy of 50 keV.

The alveoli of human lungs have a mean diameter of 200 μm, and the lung parenchyma occupies about 92% of the total lung volume³⁶. To model the microstructure of lungs, Taphorn et al. used 2D Voronoi grids³⁷which we adopted in this study. To embed the Voronoi cell in the voxelated phantom, we upsampled each XCAT slice by a factor of 80 before incorporating the Voronoi tessellation. After upsampling, the pixel resolution was 1.25 μm—one-eighth of the grating period. Next, we replaced the regions identified as lungs with 2D Voronoi grids, then dilated the individual edges by the number of pixels corresponding to the wall thickness. Figure 2d shows an example of 2D Voronoi grids that we incorporated into the XCAT phantom. We assigned the material properties for lung tissue to the alveolus wall (i.e., Voronoi boundaries) and air to the inner region of each Voronoi cell (Table 1). The alveolar density varies with the height (i.e., the distance from the diaphragm) in the lungs. McDonough et al. provided the alveolar density of $\:y=-2.5015x+34.983$, where $\:y$ equals the number of alveoli and $\:x$ is the lung height (range, 1–5; 1: lung apex, 5: lung base); the alveolar density is 31.6 ± 3.4 alveoli/mm³ in the lung apex and 21.2 ± 1.6 alveoli/mm³ in the lung base. We have adopted the formula to assign 37 different values of alveolar density to the lungs depending on the height, so that the average alveolar density is 31.6 alveoli/mm³ in the upper one-fifth region and 21.2 alveoli/mm³ in the lower one-fifth region. Notably, in our multi-layer simulation, we incorporated 2D Voronoi grids into each layer, each thinner than the mean chord length of the Voronoi cells. The number of 2D Voronoi cells was set to ensure that X-rays interacted with the same number of Voronoi structures per unit thickness as in 3D Voronoi grids with grid spacing matching the target alveolar density described above.

Fig. 3

Examples of the microstructures incorporated into the XCAT phantom are shown for normal (a), emphysematous (b), and fibrotic (c) lungs. The scale bar (1 mm) in (a) also applies to (b) and (c).

Figure 3 shows examples of the Voronoi grids for normal, emphysematous, and fibrotic lungs. For emphysematous lungs, the alveolar density was reduced to 80%, 50%, and 20% to simulate mild, moderate, and severe degree of emphysema, respectively, which resulted in enlarged alveoli correspondingly. For fibrotic lungs, the alveolar density was reduced to 1/4, and the wall thickness increased by 40 times. Further, we simulated atelectasis, edema, and pneumonia by augmenting the left lung of the XCAT phantom. For atelectatic lungs, the volume of the left lung was reduced by 10% along all the three dimensions, while maintaining the total number of alveoli. The lung was shrunk by modifying the control points of the NURBS model, from which the XCAT slices were generated.

Fig. 4

Simulation of pulmonary atelectasis in the augmented XCAT phantom. (a) and (b) show the 3D rendered lung models before and after atelectasis-induced parenchymal volume loss in the left lung, respectively. The 3D renderings were created using MATLAB (MathWorks, Inc., version R2021b). (c) and (d) show examples of XCAT slices before and after the introduction of atelectasis in the left lung, respectively. Scale bars in (a) through (d): 5 cm.

Figures 4a,b show 3D rendered views of the lungs before and after shrinking the left lung by 10%, respectively. Figures 4c,d show the XCAT slices before and after the augmentation, respectively. To model interstitial edema in edematous lungs, the thickness of the alveolus wall for the left lung was increased by 20% without changing the alveolar density. Figure 5a shows examples of the Voronoi grids for normal (i) and edematous (ii) lungs. For pneumonic lungs, 10% of the alveoli in the left lung were randomly selected and assigned the material properties for pus (similar to blood), without changing the alveolar density or the wall thickness. Figure 5b shows an example of the Voronoi grids for pneumonic lungs after the augmentation.

Fig. 5

Examples of the lung microstructure simulated with Voronoi grids for (a) pulmonary edema and (b) patchy alveolar pneumonia. In (a), (i) represents normal lungs, which is shown together for comparison, and (ii) represents pulmonary edema with 20% increase in the interstitial wall thickness. In (b), 10% of randomly selected alveoli were assigned the material properties for blood (same as pus) to simulate alveolar pneumonia. The values shown in the figure represent the real part ($\:\delta\:$) of the refractive index. Scale bars in (a) and (b): 1 mm.

Table 1 Material properties used in the simulation at 50 kev X-ray energy. The refractive index ($\:\delta\:$ and $\:\beta\:$) was calculated using Eqs. (1) and (2), based on the linear attenuation coefficient and electron density obtained from data on adult human tissues³⁵.

Multi-layer wave-optics simulation of X-ray propagation through the augmented XCAT phantom and gratings

Suppose that a planar X-ray wave of the energy 50 keV is propagating in the $\:z$ direction and incident onto the phantom perpendicular to the coronal plane (Fig. 1). For the $\:N$-th layer, the transmittance function $\:{T}_{N}\left(x,y\right)$ is defined as follows

$$\:{T}_{N}\left(x,y\right)=\text{exp}\left\{i\left(\frac{2\pi\:}{{\lambda\:}}\right)\left[\frac{n\left(x,y;N\right)\:}{{{n}_{0}\:}}-1\right]\varDelta\:z\right\},$$

(3)

where $\:n\left(x,y;N\right)$ and $\:{n}_{0}$ are the complex refractive index of the $\:N$-th layer and the immersion medium (air), respectively, $\:\varDelta\:z$ is the thickness of each layer, and $\:{\lambda\:}$ is the wavelength of the X-ray in the immersion medium (2.4797 × 10^− 11 m). Using axial averaging, $\:n\left(x,y;N\right)$ is averaged over multiple slices when $\:\varDelta\:z$ is increased. Assuming a plane wave, the wave field incident onto the first layer can be simply set as $\:{U}_{0}\left(x,y\right)=1$. The wave field after the $\:N$-th layer can be calculated using the angular-spectrum scalar wave theory, as given by Eq. (4), (Eq. 1.25 in Chap. 1.3 of Paganin¹).

$$\:{U}_{N}\left(x,y\right)={F}^{-1}\left\{H\left(u,v;\varDelta\:z\right)F\left\{{U}_{N-1}\left(x,y\right){T}_{N}\left(x,y\right)\right\}\right\},$$

(4)

where $\:{U}_{N}\left(x,y\right)$ is the wave field after the $\:N$-th layer; $\:H\left(u,v;\varDelta\:z\right)$ is the transfer function defined in Eq. (5); $\:F$ and $\:{F}^{-1}$ represent the 2D Fourier transform and the 2D inverse Fourier transform, respectively. The transfer function is given as follows.

$$\:H\left(u,v;\varDelta\:z\right)=\text{exp}\left\{i2\pi\:\varDelta\:zw\left(u,v\right)\right\}$$

(5)

where $\:\varDelta\:z$ is the thickness of each layer, and $\:\left(u,v\right)$ are the spatial frequency components corresponding to $\:\left(x,y\right)$, respectively, and $\:w\left(u,v\right)=\sqrt{{\left(1/\lambda\:\right)}^{2}-{u}^{2}-{v}^{2}}$.

The wave field after the last layer of the phantom, $\:{U}^{\left(1\right)}\left(x,y\right)$, is incident onto the absorption grating G₁ of 10 μm period, which is in direct contact with the phantom (Fig. 1). The wave field right after G1 can be written as.

$$\:{U}^{\left(2\right)}\left(x,y\right)={U}^{\left(1\right)}\left(x,y\right)\left[\text{rect}\left(\frac{x}{p}\right)*\text{comb}\left(\frac{x}{p}\right)\right],$$

(6)

where $\:p$ is the grating period, and $\:\text{rect}\left(x\right)=1$ (for $\:\left|x\right|<\frac{1}{2}$); $\:\frac{1}{2}$ (for $\:\left|x\right|=\frac{1}{2}$); and 0 otherwise. The comb function is defined as $\:\text{comb}\left(x\right)={\sum\:}_{m=-\infty\:}^{\infty\:}\delta\:\left(x-m\right)$, where $\:\delta\:\left(x\right)$ is the Dirac delta function. The amplitude grating G₂ has the same period as G₁. Typically, G₂ is placed at a fractional Talbot distance from the grating G₁, which would correspond to 2.0164 m for the simulation condition used in this study. However, in the recent demonstrations of XDFI using a pig³⁸ and humans³⁹ G₂ was placed at a much shorter distance, which rendered the system to be much more compact yet different from a standard Talbot-Lau setup. In this simulation study, we place G₂ at the distance of $\:d$ = 0.25 m from G₁, similar to these experimental demonstrations. The propagation of X-ray between G₁ and G₂ can be calculated using the angular-spectrum scalar wave theory³³. The wave field right before G₂ can be written as

$$\:{U}_{3}\left(x,y\right)={F}^{-1}\left\{{\stackrel{\sim}{U}}^{\left(2\right)}\left(u,v\right)H\left(u,v;d\right)\right\},$$

(7)

where $\:{F}^{-1}$ represents the 2D inverse Fourier transform, $\:{\stackrel{\sim}{U}}^{\left(2\right)}\left(u,v\right)$ is the 2D Fourier transform of $\:{U}^{\left(2\right)}\left(x,y\right)$, and $\:H\left(u,v;d\right)=\text{exp}\left\{i2\pi\:dw\left(u,v\right)\right\}$ is the transfer function for the light-field propagation over $\:d$. The intensity measured at the position is given by $\:{I}^{\left(3\right)}\left(x,y\right)={\left|{U}^{\left(3\right)}\left(x,y\right)\right|}^{2}$.

To acquire the absorption, the differential phase, and the normalized visibility, 8 images are recorded while translating G₂ by different amounts. For the $\:k$-th position ($\:k$ = 1, 2, ..., $K$), the intensity after G₂ is given by.

$$\:{I}^{\left(4\right)}\left(x,y;k\right)={I}^{\left(3\right)}\left(x,y\right)\left[\text{rect}\left(\frac{x}{p}\right)*\text{comb}\left(\frac{x}{p}-\frac{k}{K}\right)\right]$$

(8)

The penumbral blurring due to the finite focal spot size of the X-ray source is modeled as an asymmetric Gaussian function, which is applied in the Fourier space. In the direction parallel to the grating lines, the width of the blurring function is determined by projecting the X-ray focal spot size (1.2 mm) onto the detector plane. In the direction orthogonal to the grating lines, the width of the blurring function is determined by projecting one period of the source grating G₀ (70 μm) onto the detector plane. Since the coherence length of X-rays generated by a conventional source is extremely short, penumbral blurring—arising from the finite focal spot size—can be modeled by summing the contributions from an ensemble of spatially shifted coherent sources. However, modeling the penumbral blurring as a convolution operation (i.e., multiplication in Fourier space) assumes shift invariance, which is not strictly valid when the simulated object is thick. Nonetheless, this convolution approach can reproduce penumbral blurring with high computational accuracy and has therefore been adopted in previous works (e.g., Pogany et al.⁴⁰).

Notably, to capture small-angle X-ray diffraction from the lung alveoli, we perform the X-ray propagation from Eq. (3) through (8) using an upsampled grid of 1.25 μm resolution, which is 80 times higher than that used for the XCAT simulation. Because the size of each upsampled image is too large, we divide the computation domain to 32 × 32 overlapping tiles, each 10,880 × 10,880 pixels. Then, to expedite the wave-optics simulation, we average every 20 slices along the beam propagation direction. The axial averaging converts 2505 slices to 126 layers, 2 mm thick each. For the 50 keV X-rays diffracted by a periodic structure of the 200 μm period, the diffraction angle is only 0.124 µrad. The X-ray image will be laterally shifted only by 0.248 nm after 2 mm, which is about 3 orders of magnitude smaller than the pixel resolution of our wave-optics simulation.

The detector, which comprises 1024 × 1024 pixels of 400 μm pixel size, is located right after G₂. Assuming a detector array of $\:{N}_{d}$×$\:{N}_{d}$ pixels, each of which is a square with dimensions $\:\varDelta\:$×$\:\varDelta\:$, and no dead space between pixels, the intensity recorded with the detector can be written at the ($\:i,j$)-th pixel ($\:i$, $\:j$ = 1, 2, …, $\:{N}_{d}$) as

$$\:{I}^{\left(5\right)}\left[i,j;k\right]=\left(D{I}^{\left(4\right)}\left(x,y;k\right)\right)\left[i,j\right]:={\int\:}_{-\varDelta\:/2}^{\varDelta\:/2}{\int\:}_{-\varDelta\:/2}^{\varDelta\:/2}{I}^{\left(4\right)}\left(i\varDelta\:+\xi\:,j\varDelta\:+\eta\:;k\right)d\xi\:d\eta\:,$$

(9)

where $\:D$ represents an integration downsampling operator. The augmentation of lungs using Voronoi grids is the most computationally intensive step. Using parallel processing on 16 CPUs, with 24 GB memory for each, it took about 11 days on average to complete the computation. The computation for the fibrosis case, which involves increasing the alveolus thickness (i.e., Voronoi boundaries), took about 1.5 months. Currently, the augmentation using Voronoi grids is done on the fly, as it would require a lot of disk space to save all the augmented slices. One idea to overcome this challenge is to use a preselected set of Voronoi patterns (20–30), instead of using a completely random pattern for every slice. Figure 6 shows an example of 8 images recorded for different values of $\:k$.

Extraction of absorption, differential phase, and dark-field images from the raw images for various positions of G₂

From the 8 raw images, the absorption, the differential phase, and the dark-field images were calculated using the standard Fourier retrieval method⁴¹. For each pixel, a phase stepping curve was acquired, which is the intensity $\:{I}^{\left(5\right)}\left[i,j;k\right]$ as a function of the G₂ step position, $\:k=1,\:2,\dots\:,\:8$. These phase step curves sample the sinusoidal intensity pattern over one period of length $\:K$ (Eq. 8). For each pixel index, a 1D discrete Fourier transform was performed with respect to step index $\:k$. The X-ray intensity can be calculated from the zeroth order Fourier coefficient ($\:{a}_{0}$). The absorption due to the phantom, presented as relative transmission $\:T$, can be calculated as the ratio of $\:{a}_{0,s}$, measured with the sample, and $\:{a}_{0,r}$, the reference (i.e., without the sample).

$$\:T=\frac{{a}_{0,s}}{{a}_{0,r}}$$

(10)

The X-ray refraction in the direction perpendicular to the grating grooves can be quantified as the transverse shift of the interference fringes, which can be calculated from the phase of the first Fourier component, $\:{\varphi\:}_{1}$. The X-ray refraction due to the phantom can be obtained from the relative phase shift between the sample and reference measurements.

$$\:\varphi\:=\frac{\lambda\:d}{p}\frac{\partial\:\varPhi\:}{\partial\:x}={\varphi\:}_{1,s}-{\varphi\:}_{1,r}$$

(11)

where $\:x$ is the phase stepping direction. The ultra-small angle scattering of X-rays can be quantified as the change in the visibility, which is given as the ratio of the first ($\:{a}_{1}$) and the zeroth ($\:{a}_{0}$) order Fourier coefficients. The scramble of the wavefront due to the microstructure in the phantom can be obtained from the normalized visibility, the ratio of the visibility measured with the sample and the reference (i.e., without the sample).

$$\:{V}_{norm}=\frac{{V}_{s}}{{V}_{r}}=\frac{{a}_{1,s}/{a}_{0,s}}{{a}_{1,r}/{a}_{0,r}}$$

(12)

Results and discussions

Wave-optics simulation of XPCI and XDFI using the XCAT human phantom

Fig. 6

Simulation of a grating-based XPCI/XDFI system using the augmented XCAT phantom: simulated intensity images for 8 different positions of G₂. The scale bar (5 cm) in (a) also applies to the images (b) through (h).

Figure 6 shows an example of the raw images simulated for 8 different positions of G₂ or for different values of $\:k$ representing different phases sampled from the Talbot pattern. Because the incident X-ray wave was assumed to have uniform amplitude of one, the values shown in Figs. 6a through h correspond to the intensity normalized with the background. As expected, the intensity values change with the grating position being the highest in Fig. 6a, where G₁ and G₂ are in phase, and the lowest in Fig. 6e, where G₂ is shifted with respect to G₁ by half the period. The amount of modulation in intensity also varies by the multiple scattering properties of the imaged tissue. In soft tissues of the mediastinum and abdomen there is a large modulation ranging from 0.45 in Fig. 6a to 0.047 in Fig. 6e. However, due to the multiple-scattering interfaces of the lung, the modulation of the X-ray intensity in the lungs between Fig. 6a,e is greatly reduced relative to other tissues. This is illustrated by the residual lung transmission in Fig. 6e despite being absent in other tissues. Figure 7a shows the absorption (i), phase (ii), and dark-field (iii) images extracted from the 8 images shown in Fig. 6 using the standard Fourier analysis (see Methods). The absorption image shows the absorbance, the negative logarithm of the transmittance with base 10, comparable to a conventional chest X-ray imaging. The phase image and the dark-field image are additional images provided by the grating-based XPCI and XDFI methods, respectively.

Fig. 7

Absorption (i), differential phase contrast (ii), and dark-field (iii) images for the XCAT phantoms simulating normal lungs (a), emphysema (b), and pulmonary fibrosis (c), respectively. The scale bars (5 cm) in (i) also apply to (ii) and (iii).

Dependence of absorption, phase, and dark-field signals on the microstructure of lungs

Using the developed method, we have simulated the dark-field image of human lungs affected by fibrosis and emphysema. The diseased lungs were modeled by varying the cell number and edge thickness of Voronoi grids, as described in Methods. Figures 7a through c show the absorbance, phase, and dark-field images for normal, emphysematous, and fibrotic lungs. Figure 7a illustrates how the different signal contrasts available in grating interferometry vary by tissue type. The primary signal in absorption image (i) comes from the X-ray absorbing bones and soft tissues of the mediastinum and the thorax. The differential phase image (ii) shows strong gradient at tissue interfaces while the lungs appear as a high frequency noise due to the abundance of multiple-scattering interfaces that prevent reliable phase retrieval. However, this strong multiple scattering signal from the lung parenchyma provides abundant signal in the dark-field image (iii) with less anatomic background from the bones and heart shadow.

The effects of emphysema are illustrated in Fig. 7b. The reduced lung density in emphysema, modeled here as a lower density Voronoi grid, results in subtle reduction in absorption compared to the healthy absorption image. Conversely, there is a greater visual difference in signal between the emphysema and healthy dark-field images compared to the subtle difference in absorption images. The fibrotic lungs, modeled as a Voronoi grid with lower density and thicker wall, show clearer changes in both the absorption and dark-field images, as shown in Fig. 7c. The enhanced sensitivity to structural changes in the lungs of X-ray dark-field is also supported by comparing the histograms of healthy and diseased lungs as well as the mean signals in the lungs in Fig. 8.

Fig. 8

Comparison of absorption (a) and dark-field (b) signals for normal, emphysematous, and fibrotic lungs. Probability density distributions and boxplots within the lung region are shown for all the three cases. In each box plot, the central mark represents the median value, and the bottom and top edges represent the 25th and 75th percentiles, respectively.

Figure 8a shows the probability distributions and boxplots of the attenuation signal (i.e., absorbance) within the lung region for the normal, emphysematous, and fibrotic cases. For the attenuation signal, the normal and emphysematous lungs produce wide distributions that are almost overlapping. The median values are also about the same: 1.342 and 1.319 for the normal and emphysematous lungs, respectively. The fibrotic lung produces a narrow distribution with a peak at 1.61, which is clearly distinguished from the other two cases, and a significantly higher median value of 1.741. Figure 8b shows the probability distributions and boxplots of the dark-field signal within the lung region for the same conditions. The normal, emphysematous, and fibrotic lungs show clearly distinct distributions on the histogram. The median absorbances for the three cases are 0.135, 0.122, and 0.103, respectively. Figure 9a shows the probability distributions of the dark-field signal within the lung region for emphysema at different severity levels: normal, mild, moderate, and severe.

Fig. 9

Comparison of dark-field signals for emphysematous lungs at different levels of severity (a) and for normal, atelectatic, edematous, and pneumonic lungs (b). Probability density distributions of the dark-field signal in the lung region are shown for the different cases.

We have also simulated atelectatic, edematous, and pneumonic lungs. Figure 9b shows the probability distribution of the dark-field signal within the lung region for these different disease states. This figure illustrates the limitation of using dark field signal alone in characterizing lung pathology. As can be seen, pathophysiologic alterations in lung structure induced by alveolar fluid accumulation in pneumonia, wall thickening in interstitial edema, and deflation in atelectasis all result in a reduction in dark-field signal. Therefore, using the dark-field image in isolation can be misleading. Signal alteration by emphysema and fibrosis is manifested by drop in dark-field signal relative to healthy lung, as seen in Fig. 8, and observation that agrees with experimental findings⁴². One should regard the absorption and dark field signals as complementary to each other, providing information about very different aspects of the lung. To enhance the sensitivity and specificity of X-ray imaging, researchers have proposed methods that combine both signals into a normalized scatter contrast for visualizing different lung pathologies⁵.

The performance of grating interferometer X-ray dark-field and absorption contrasts at distinguishing different tissue properties is strongly dependent on the acquisition factors such as X-ray tube voltage (kV) and phase stepping as well as grating geometry. While some studies have demonstrated optimizing grating interferometer setups experimentally⁴³, doing so is challenging and time-consuming as each geometry requires careful alignment, depends on the available gratings, and varies with the application. By incorporating a multi-layered wave-based approach to model multiple scattering in X-ray dark-field imaging, the proposed framework enables system simulation and acquisition optimization of X-ray grating interferometers across a range of grating geometries and acquisition settings to optimize parameters for maximal performance in any given application.

While the study presented in this work featured a system geometry and set of acquisition parameters based on an experimental system³⁹, once the numerical phantom is precomputed multiple system geometries and acquisitions can be rapidly investigated to find the optimal geometry and parameter set to maximize disease sensitivity and specificity. Further, 3D implementations of the dead leaves super formula could offer a more computationally efficient method for reproducing modeled lung parenchyma⁴⁴. Availability of such modeling approaches can be used to design and optimize X-ray grating interferometers more rapidly for new and improved applications.