Investigating reservoir-triggered seismicity in the Koyna–Warna region through nodal ambient noise tomography

Ranjan, Pratul; Kumar, Prakash; Mandal, Biswajit; Karuppannan, Periyasamy

doi:10.1038/s41598-025-12099-z

Download PDF

Article
Open access
Published: 20 July 2025

Investigating reservoir-triggered seismicity in the Koyna–Warna region through nodal ambient noise tomography

Pratul Ranjan^1,2,
Prakash Kumar^1,2,
Biswajit Mandal^1,2 &
…
Periyasamy Karuppannan¹

Scientific Reports volume 15, Article number: 26323 (2025) Cite this article

1332 Accesses
Metrics details

Subjects

Abstract

The Koyna–Warna region in southern India is a unique case of dual Reservoir-Triggered Seismicity (RTS), surrounding impoundments on Koyna and Warna rivers. In this study, we perform ambient noise surface wave tomography using data from a temporary dense deployment of three-component geophones in order to understand the origin of RTS. To achieve this objective, surface wave dispersion curves from noise cross-correlations in rotated coordinates were used to create group velocity maps in 0.5–5 s periods. The group velocity dispersions from map bins were inverted for shear wave velocity ($V_s$) and $V_s$ radial anisotropy ($\xi$) maps down to 5 km depth. The $V_s$ and $\xi$ till 1 km depth are correlated with topographical features in agreement with the basement depth estimates. Large earthquakes in the region are marked by negative $\xi$ with negative $V_s$ anomaly or $V_s$ anomaly contrast, suggesting shear strength could be an important control on their genesis. A large negative $V_s$ anomaly southwest of the Koyna reservoir is linked with reservoir water migration to greater depths, part of a larger interconnected system of pathways extending across the reservoirs. These results, set decades post reservoir impoundment, can help understand the evolution of RTS around dam sites elsewhere.

Advanced monitoring of tailings dam performance using seismic noise and stress models

Article Open access 30 November 2022

Detection of urban hidden faults using group-velocity ambient noise tomography beneath Zhenjiang area, China

Article Open access 13 January 2021

Reservoir impoundment-triggered seismicity in Brazil: the case of M4.0 Nova Ponte earthquake

Article Open access 14 December 2023

Introduction

The RTS has been evidenced in different parts of the world such as Lake Mead (USA), Xinfengjiang reservoir (China), Kariba reservoir (Zambia–Zimbabwe Border), Kremasta (Greece), Koyna (India) etc.¹. Among these, the Koyna–Warna region is characterized by one of the largest RTS event ever recorded ($M_w$ 6.3) around the world. In addition, unlike the remaining RTS sites, the Koyna–Warna is a multi-reservoir system, which provides a unique opportunity for understanding the impact of multiple impoundments on the aquifers in a broad area. The insights from the seismic velocity structure in such a complex RTS region would help scientists and engineers in the planning of future dam sites globally.

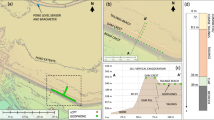
On 10th December 1967, an $M_w$ 6.3 earthquake occurred south-west of the Koyna Dam, which is located on the Koyna river in Maharashtra, India (Fig. 1a,b). It caused widespread damage in the nearby town of Koynanagar, with houses completely destroyed and over 200 people killed². Such a large earthquake was unprecedented in this region with no record of seismicity prior to the start of the dam construction in 1956. After the associated reservoir was filled in 1962, seismicity started in the Koyna region, which could be recorded at the seismological station in Pune, 120 km away³. The minor seismicity culminated in the occurrence of the Koyna earthquakes of 1967^4,5,6. Later when the neighbor Warna reservoir was filled after the creation of Warna dam in 1985, seismicity started to appear around Warna reservoir as well. Over the last 60 years, more than 20 earthquakes with M > 5 and 200 earthquakes with M > 4 earthquakes have occured in the Koyna–Warna region⁷.

The origin of the seismicity pattern in the Koyna–Warna region is still debated, however some understanding has been established. The emergence of minor seismicity around the time of the first impoundment of Koyna and Warna dams was later investigated, and a high correlation between water level changes in the reservoirs and seismicity rate was found^13,14. However, water level changes are not the only factors determining the seismicity pattern, as stress transfer between local faults can explain some of the focal mechanisms, suggesting that the region is divided into multiple tectonic blocks^15,16,17. Currently, the consensus is that the seismicity in this region is “triggered” along a network of local faults by the diffusion of pore pressure, due to reservoir water filling cycle^1,8,14,18

The Koyna–Warna region is part of the Western ghats (stepped terrain) in the Deccan Volcanic Province (DVP), which formed due to the passage of the Indian plate over the Reunion hotspot about 65 Ma ago¹⁹. In this region, the DVP is composed of nearly horizontal simple tholeiitic lava flows with thickness up to 1.2 km, underlain by a granitic-granitoid basement²⁰. As part of the scientific deep drilling project, nine cored boreholes were drilled in the Koyna–Warna region (Fig. 1a,b), which shed new light on the stratigraphy²¹. The basement granite-granitic gneiss is inter-layered with migmatitic gneiss, in addition, evidences of fluid-rock interaction that has led to mineralization along micro-fractures has been found^22,23. Using results from these cored boreholes, a deep research borehole was drilled recently down to 3 km depth with the purpose of well logging²⁴.

The Koyna–Warna region hosts multiple NE-SW faults along with NW-SE structural lineaments. The 1967 Koyna earthquake (M 6.3) occurred along a NNE-SSW fault and generated surficial fissures up to 4 km SSE of Donichawadi (Fig. 1b). Focal mechanism solutions of the mainshock and the aftershocks revealed a left-lateral strike-slip fault extending SSE of the Koyna reservoir^4,17,25. Aeromagnetic maps also indicate a NNE-SSE magnetic lineament side-by-side this fault zone²⁶. This NNE-SSW lineament along with the Donichawadi fault is referred to as the Koyna River Fault Zone (KRFZ) or Koyna Seismogenic Zone (KSZ) in literature^16,27. By combining aeromagnetic, SAR interferometry and bouger gravity anomaly maps, the NNE-SSW lineament has been found to be a shallow feature and seems to be connected to deeper NW-SE lineaments²⁸. The majority of the seismicity near the Koyna reservoir originates in 7–13 km depth range of mainly strike-slip mechanisms, in contrast to the Warna region where majority of the seismicity is shallow (< 7 km) with normal faulting mechanisms^8,9,17,29.

The subsurface structure in the Koyna–Warna region has been imaged using multiple geophysical tools such as seismic, gravity, magnetotelluric methods etc. Deep seismic sounding along two roughly E–W profiles bounding the Koyna reservoir in the north and the south, revealed a low-velocity layer between 6 and 11.5 km depth³⁰. The 2D gravity models indicate a gravity low at Koyna, which is attributed to isostatic adjustment that leads to thickened crust³¹, or an additional low density layer at 5–15 km depth³². The 2D magnetotelluric image along a WNW-ESE profile across the Koyna Seismogenic Zone reveals a shallow (< 10 km) conductive anomaly interspersed between very high resistive blocks that are likely Deccan basalts³³. The first detailed P and S velocity maps of the Warna region was performed using 343 local earthquakes around the Warna reservoir³⁴. Zones of high $V_p$/$V_s$ and low $V_s$ were observed beneath the Warna reservoir at less than 1.5 km depth and extending down to 7 km depth in lateral sections.

Despite decades of research in the Koyna–Warna region, the linkage between the genesis of large earthquakes and the shallow structure is not well understood, partly because it has only been studied in a small area of the Koyna–Warna region. Due to non-uniform distribution of earthquakes, past travel time tomography has yielded resolution limited to the Warna reservoir^34,35. Ambient noise tomography is based on measuring phase or group velocity changes of the surface wave arrivals that emerge after cross-correlating ambient noise waveforms from pairs of stations³⁶. Because ambient noise sources are abundant around the globe, this technique allows better spatial resolution in regions with non-uniform or sparse earthquake distribution³⁷. It has also been shown that at shorter periods (< 10 s), stacking of 1 month of cross-correlations provides high enough SNR for ambient noise tomography and the required number of stacked days reduces with decreasing period^38,39. Ambient noise cross-correlations of vertical–vertical and transverse–transverse components are used to compute Rayleigh wave and Love wave group velocities respectively, from which the shear wave vertical velocity ($V_{sv}$) and shear wave horizontal velocity ($V_{sh}$) as well as shear wave radial anisotropy ($\xi$) are derived. Conventionally, $\xi$ is negative for vertically aligned structures such as dykes, faults etc. and positive for horizontally aligned structures such as lava flows, sedimentary layering etc.^40,41,42. So far ambient noise cross-correlations have only been used to derive 1D shear wave velocity model for the whole Koyna-Warna region⁴³.

In this study, we use waveform data from ninety seven 4.5 Hz three-component geophone nodes installed in the Koyna–Warna region between January 2010 and May 2010 in order to compute cross-correlations of seismic noise waveforms recorded on the vertical as well as transverse components. We measure the the fundamental mode Rayleigh wave group velocity dispersion curves from the stacked vertical–vertical (ZZ) cross-correlations and the fundamental mode Love wave dispersion curves from the stacked transverse-transverse (TT) cross-correlations using all station pairs. After that, we invert the Rayleigh and Love-wave group velocity dispersion measurements to obtain 2-D group velocity maps. Finally, by separately inverting the group velocity maps from ZZ and TT cross-correlations, the shear wave radial anisotropy and the isotropic shear wave velocity maps are also generated.

Results

The isotropic shear wave velocity ($V_s$) in the upper 1 km of the Koyna–Wanra region indicates strong correlation with the topographical features (Fig. 2a,b). In 0 km depth lateral section, towards the west of the Western ghats escarpment, negative $V_s$ anomalies are observed that seem to follow the Western ghats escarpment. Similarly, negative $V_s$ anomaly beneath the Warna reservoir and the southern part of the Koyna reservoir is observed. In addition, moderately negative $V_s$ anomalies are also observed beneath the Morana reservoir. On the other hand, positive $V_s$ anomalies are observed in the eastern part of the Koyna-Warna region. In 1 km depth lateral section, similar correlation between $V_s$ anomalies and the topographical features are observed, although the low $V_s$ beneath the Warna reservoir shifts towards the Warna dam in the east and the Western ghats escarpment in the west (Fig. S1).

From 2 km depth onwards, a negative $V_s$ anomaly is observed beneath the central part of the Western ghats escarpment down to 5 km depth. One of the earthquakes in the 1967 Koyna earthquake sequence also occurred in this region (Fig. 2c). Apart from that, negative $V_s$ anomaly is only observed directly beneath the north-western part of Warna reservoir down to 2 km depth. At greater depths, moderately positive $V_s$ anomalies are observed directly beneath the reservoir, however these are surrounded by negative $V_s$ anomalies. The majority of the seismicity in 0–5 km depth also occurs outside the boundaries of the Warna reservoir, mainly towards the south-west.

The $V_s$ radial anisotropy ($\xi$) is mostly positive down to 1 km depth (Fig. 3a, Fig. S1), which means at these depths $V_{sh}$ is higher than $V_{sv}$. At greater depths however, a negative $\xi$ is observed overall. At depths $\ge$ 2 km, negative $\xi$ is localized around the 1967 Koyna earthquake epicenters, the northern part of Warna reservoir, and between Warna and Morana reservoirs.

The cross-sections in the central part of the Koyna–Warna region reveal evolution of seismicity in the region across several $V_s$ and $\xi$ anomaly zones (Fig. 4a–g). The depth resolution is not uniform across the cross-sections. It varies between 5 and 6.5 km after topographic adjustment depending on the wavelength content of the dispersion data (see Methods section).

$V_s$ estimated locally around the Warna reservoir using local earthquake tomography³⁴ agree well with the results in the present study. At 1.5 km depth, low $V_s$ beneath the northern part of the Warna reservoir, found previously, correlates with the negative $V_s$ anomaly at 2 km depth (Fig. 2b) and 1.5 km depth (Fig. S1) in the present study. In addition, it was observed that most of the of the seismicity occurred in low velocity zones that were present outside the reservoir boundaries³⁴, similar to present study. Furthermore, they also observed that the low $V_s$ zones close to the Warna reservoir migrated northwards at greater depths. This pattern could be related to the negative $V_s$ anomaly that we observe in the central part of the western ghats escarpment in lateral sections at 2 km depth and deeper (Fig. 2b–d).

The shallow structure in the Koyna–Warna region is dominated by Deccan basalts, which are found to be 800–1200 m thick across the region based on borehole data²² and magnetotelluric experiments²⁷. These formed as a result of large scale melting when the Indian plate passed over the Reunion hotspot¹⁹. Most of the lava flow in this region is characterized by rubbly pahoehoe type that consists of a thick sheet like smooth flow base up and a thin rubbly top with slabs of lava embedded in it⁴⁷. This sheet like geometry of the Deccan lava flow can explain the positive $\xi$ observed in the top 1 km depth (Fig. 3a, Fig. S1)

Large earthquakes in Koyna–Warna and the strain budget

Large earthquakes globally exhibit two major patterns in terms of seismic velocities of the source zones: either they occur at the transition between high and low velocity lithology or they occur in a low velocity zone indicating a fractured medium allowing migration of fluids from a deeper source^48,49. The occurrence of these large earthquakes mostly control the strain budget in a region.

Two main theories have been proposed to explain the strain budget in the Koyna–Warna region. First theory states that the geometrical orientations of faults allow stress transfer such that the release of stress due to a large earthquake on one of the faults destabilizes another fault. The stress triggering due to earthquakes in the Koyna region generates earthquakes in the Warna region and has resulted in continued seismicity until now¹⁶. This theory may explain the occurrence of a normal faulting earthquake ($M_w$ 5.6) following the strike-slip earthquake ($M_w$ 6.3) a few days apart, in the 1967 sequence^4,5,6. The second theory advocates for alternating phases of strike-slip and normal faulting earthquake predominance in the region due to periodic changes in the regional stress pattern⁸. However, most of the large earthquakes following the 1967 sequence have been normal faulting type with the fewer strike slip earthquakes also having a significant normal component. Therefore, stress transfer due to geometric orientation of faults as well as periodic variation in stress levels may not fully explain the seismicity pattern.

The source zones of the first two earthquakes in the 1967 sequence are characterized by transition from mostly positive to slightly negative $V_s$ anomaly (Fig. 4a), while highly negative $\xi$ (Fig. 4b). The highly negative $\xi$ is correlated with the predominantly strike-slip mechanism of the two earthquakes on steeply dipping fault planes. Steeply dipping fault planes result in lower $V_{sh}$ compared to $V_{sv}$, hence negative $\xi$. The $V_s$ anomaly pattern suggests that the earthquakes occurred at a structural boundary. The third earthquake in the sequence is characterized by a negative $V_s$ anomaly and slightly positive to negligible $\xi$ (Fig. 4c,d). The negative $V_s$ anomaly indicates a weakened crust before or after the earthquake. A similar pattern can be observed near the Warna reservoir, where some of the earliest recorded large earthquakes happened in a neutral zone (1974 event; Fig. 2d) and at a structural boundary marked by transition between high and low $V_s$ anomaly (1976 event; Fig. 2c). The source zones of both events lie in a negative $\xi$ zone (Fig. 3c,d). The subsequent large earthquakes occurred in negative $V_s$ anomaly zones with moderately negative $\xi$ (Figs. 3c,d, 4e,f). An exception is the 1975, Mw 5.0 event that occurred in a negative $V_s$ zone with highly positive $\xi$ at 0.1 km depth (Figs. 2a, 3a). The unusual depth of this event i.e. above the basement, along with its position close to the western ghats escarpment, away from the reservoirs, suggests either poor event location or unknown extremely shallow fault activity.

Theoretical models of earthquake nucleation on both slip-weakening and rate-and-state faults indicate that critical nucleation length after which the quasi-static slip develops into a dynamic rupture is proportional to the shear wave modulus or shear strength, and it is particularly significant for slip-weakening faults^50,51. In addition, numerical experiments on earthquake nucleation in presence of a precursory drop in shear wave velocity suggests that the velocity anomaly can lead to reduction in nucleation size as well as earlier nucleation. Thus, such precursory velocity drop can lead to earlier onset of large earthquakes⁵².

The distribution of smaller earthquakes across the cross-sections suggests a net southward migration of seismicity from Koyna reservoir towards Warna reservoir in the last 60 years (Fig. 4). The recent seismicity (year > 2000) at shallow depth (< 5–6 km) is concentrated around the negative $V_s$ anomaly zones particularly in the central and southern part of Koyna-Warna region (Fig. 4a,e,f). Measurements of geodetic strain rates indicate low annual tectonic deformation of 0.2–0.3 $\pm$ 0.04 mm/year in the region, much lower than that of Indian plate⁵³. Even with such low deformation rates, seismicity has continued in this region till date. In recent years, it has concentrated in the negative $V_s$ anomaly zones likely due to their low shear strength. This also means that the accumulated stress is more frequently released in the south-central part compared to the northern part that is close to the Koyna reservoir. Therefore, there is a probability of higher stress accumulation and hence a greater chance that the next large earthquake may occur close to the Koyna reservoir. On the other hand, seismicity near the Warna reservoir would likely continue but become smaller with further decrease in shear strength.

Influence of reservoir impoundment on the $V_s$ structure

The immediate effect (< few years) of reservoir impoundment on the $V_s$ structure has been observed in the form of compaction beneath the reservoir, leading to higher velocities⁵⁴. However, over time, water infiltration to greater depths has also been evidenced by increased seismicity levels along with lower shear wave velocity⁵⁵. In this section, we study after-effects of reservoir impoundment on recent shear wave velocity structure of the Koyna–Warna region.

A large negative $V_s$ anomaly is observed in the spatial maps as well as the cross-sections SW of the Koyna reservoir and extending westwards across the western ghats escarpment (Figs. 2b–d, 4a,g). This anomaly continues from 2 km depth down to the 5 km depth and possibly beyond (Fig. 4a) and it is marked by moderately negative to negligible $\xi$ (Figs. 3b–d, 4b). The isotropic nature of this velocity anomaly suggests that the structure underneath exhibits multi-directional deformation. At shallow depths, this anomaly seems to be linked to the Koyna reservoir (Fig. 4a; “K”). Fluid migration pathways from shallow levels down to greater depths along weakened zones may explain the lateral and depth continuity of this anomaly.

Increased pore pressure diffusion to greater depths due to annual filling and emptying cycle of the Koyna and Warna reservoirs, and release after the occurrence of a large earthquake, has been identified as a possible mechanism of seismicity in the region^1,14,18. Well logs in a 3 km pilot research borehole (KFD1) at a nearby site, indicate higher water content in 1.5–3 km depth that suggest deeper penetration of reservoir water⁵⁶. Besides, mineralogical and geochemical analyses of the cores from KBH1 borehole near the pilot borehole have identified precipitation of ferruginous and siliceous minerals along fractures at different depth levels (800–1200 m), which indicate percolation of water to greater depths^23,57. Evidence of fluid migration SW of the Koyna reservoir has also been found in the form of a westward dipping conductive zone in an E-W MT profile passing south of the 1967 Koyna earthquake ($M_w$ 6.3) epicenter²⁷. Shallow parts of the dipping conductive structure roughly coincides with the negative $V_s$ anomaly zone especially around 4–5 km depth. Therefore, the conductive zone could be a downward continuation of the negative $V_s$ anomaly.

The spatio-temporal distribution of seismicity reveals that the earliest earthquakes in the region occurred very close to the Koyna reservoir (Fig. 4a) likely due to reservoir loading and subsurface compaction. The smaller fractures developed due to this seismicity may have facilitated reservoir water migration. The left lateral slip along with a small normal faulting component during the 1967 Koyna earthquake ($M_w$ 6.3) might have weakened the structure SW of the Koyna reservoir that allowed reservoir water to migrate downwards and southwestwards over several decades aided by smaller earthquakes (Fig. 4e,f). The downward migrating water under higher pressure and temperature would have induced chemical alterations in the structure which is evidenced as negative $V_s$ anomaly.

Tectonic link between Koyna and Warna reservoirs

The $V_s$ anomalies provide insights into how the RTS in the Koyna–Warna region may have evolved. The first two 1967 Koyna earthquakes ($M_w$ 5.9 and $M_w$ 6.3) produced left-lateral strike slip movement leading to the transfer of stress southwards and westwards (Fig. 4a). The regions surrounding the two epicenters were weakened due to the reservoir water migration, evidenced by negative $V_s$ anomalies with low degree of anisotropy (Fig. 4a,b). The stress transfer may have pushed the already weakened zones beyond the critical limit, allowing small fractures to develop into large earthquakes⁵⁸, the first of which occurred 2 days after the 1967 main shock with a normal faulting mechanism (Figs. 2c, 3c, 4c,d). Over time the stress may have transferred further southwards, leading to the 1974–1976 Warna earthquakes in a region of relative higher shear strength, evidenced by moderately positive $V_s$ anomaly (Figs. 2c, 3c). After the Warna reservoir got filled in late 80s–early 90s, the reservoir water migration likely started occurring near Warna reservoir, similar to the Koyna reservoir case. This phenomena produced weakened shear strength in the surrounding regions (Figs. 4e, 5) and coupled with stress transfer, likely generated the 2009 Warna earthquake sequence with normal faulting earthquakes (Figs. 4e,f, 5). Thus, Koyna–Warna region may represent an interconnected aquifer system, where reservoir water migrates from shallow to deeper levels as well as laterally, generating zones of weakened shear strength (Fig. 5).

Conclusion

We performed ambient noise tomography of the Koyna–Warna region using data from 97 three-component geophone nodes installed for a 5 month period between Jan 2010 and May 2010. Examining the spectrogram and power spectral density of the waveforms as well as manual picking of the group velocity dispersion curves, provided reliable measurements between 0.5 and 5 s period. Inversion of the dispersion curves in this period range allowed estimation of 1D $V_s$ model down to 5 km depth across the region. The 1D $V_s$ models were interpolated to generate 2D lateral and cross-section maps of $V_s$ as well as $\xi$. The $V_s$ anomalies correlate with topographical features down to 1 km depth and the basement depth below the Deccan basalts is identified using $\xi$ values, in agreement with the previous results. The source zones of large earthquakes in the region exhibit $V_s$ anomaly contrast or negative $V_s$ anomaly, consistent with global occurrences as well as theoretical and numerical models, suggesting structural shear strength changes as an important factor in assessing potential for future large earthquakes. Negative $V_s$ anomaly SW of the Koyna reservoir close to the location of KFD1 and KBH1 boreholes provides seismic evidence of reservoir water percolation to 5 km depth and beyond. Extended $V_s$ anomalies in depth and laterally, indicate an interconnected system of water migration pathways between Koyna, Warna, and Morana reservoirs, and their associated rivers. Further studies on the temporal variation of $V_s$ can enhance our understanding of the evolution of these water migration pathways and their implications for seismic hazard.

Methods

Preprocessing and computation of cross-correlations

A network of ninety-seven 3-component geophones (Geospace GS-11D) of 4.5 Hz natural frequency coupled with Taurus dataloggers was deployed in the Koyna–Warna region from January 2010 to May 2010 to record the local seismicity³⁴. Spectrogram of waveforms indicate high noise levels below 0.1 s period and above 2 s period, however variations in the noise are detectable at shorter periods as well as longer periods (Fig. 6a). The power spectral density of the waveforms shows that the noise amplitudes lie between the global noise models up to 7 s period (0.14 Hz) and down to 0.1 s period or shorter (> 10 Hz) (Fig. 6b).

Considering this analysis, the waveforms were deconvolved using their instrument responses and then bandpass filtered between 0.16 and 12 Hz. Next, the waveforms were decimated from 100 Hz sampling frequency to 40 Hz. After that, the daily waveforms were divided into 2 h time windows and spectrally whitened to flatten spurious events in the waveforms. Finally, the waveforms were cross-correlated with max lag of 1 h and all cross-correlations were linearly stacked for the entire duration of the installation. Using this process, cross-component and same component cross-correlations: North-North (NN), East-East (EE), East-North (EN), North-East(NE), and Vertical-Vertical(ZZ) were computed. The waveform preprocessing and computation of cross-correlations was performed using MSNoise version-1.3⁴⁴. All the cross-correlations of horizontal components were rotated to radial and transverse coordinates: Radial-Radial(RR), Transverse-Transverse (TT), Radial-Transverse (RT), and Transverse-Radial (TR)⁶². In total, 4050 ZZ cross-correlations and 3989 TT as well as RR cross-correlations were obtained.

Computation of dispersion curves

Group velocity dispersion curves were computed using Frequency-Time ANalysis (FTAN) of the cross-correlations that involves simultaneously analyzing the cross-correlations in both frequency and time domains⁶³. The Rayleigh wave dispersion curves were computed using the ZZ cross-correlations, while the Love wave dispersion curves were computed using TT cross-correlations. After an automatic computation of dispersion curves, these were manually re-picked one by one in order to remove discrepancies and the FTAN normalized amplitudes of the picks were recorded to determine the quality of picks (see Fig. S2 for FTAN illustration). At short distances, the dispersion measurements of long periods are not reliable. Therefore, measurements were only made for periods corresponding to inter-station distances that are larger than one wavelength. At this stage, 2912 dispersion curves from TT cross-correlations and 3066 dispersion curves from ZZ cross-correlations were obtained.

By simultaneously plotting dispersion curves from all the cross-correlations in the form of heat map, their average trend and the scatter in the measurements can be observed (Fig. 6c,d). In general, Love wave group velocities are higher than Rayleigh wave group velocities. For periods less than 1 s, larger scatter in the dispersion curves is observed, which could be due to the incoherent noise, possibly human-induced, interfering with the coherent noise sources⁶⁴. On the other hand, measurements at periods longer than 3 s also show large scatter, however this is likely due to fewer measurements made at those periods. In order to purge measurements that may potentially be erroneous, we only consider period range of 0.5 s onward for further analysis. In addition, the standard deviations of the measurements obtained using all the station pairs will be used to quantify relative uncertainty during depth inversion (see “Inversion for shear wave velocity” section).

Ambient noise group velocity maps and resolution tests

The data from dispersion curves were transformed to group velocities in a 2D grid using damped least squares inversion. The group velocities at each period were forward modeled based on ray theory and superposition principle, where the arrival time of a surface wave group in a cross-correlation waveform is the sum of its travel times in 2D bins along the station pair path. For each path, the traveltime perturbation with respect to the reference traveltime in mean model depends linearly on the path length and the relative group velocity perturbation with respect to mean group velocity in each 2D bin. Then the L2 norm of the misfit between observed and modeled group velocities are inverted linearly using damped least squares. The forward modeling and the inversion methodology is well described and implemented in a plugin of MSNoise (MSNoise-Tomo)^44,65. The 2D grid for inversion was defined by dividing the Koyna-Warna region into 2.5 km $\times$ 2.5 km bins, and the weights for damping and smoothing were calculated for each period using l-curve⁶⁶ (Fig. S3). The data covariance matrix was diagonally populated with FTAN amplitudes of the dispersion picks calculated (see “Computation of dispersion curves” section), in order to assign weights to the measurements based on the quality of the picks. The parameters for the generation of group velocity maps using MSNoise-Tomo are provided in Tables Fig. S1, Fig. S2, and Fig. S3.

In order to test the resolution of the group velocity maps, we performed spike resolution tests at each period using $\pm 10 \%$ spike anomalies of size 5 km $\times$ 5 km each, separated by 5 km. The spike resolution tests or sparse checkerboard allow clear identification of the distortion in anomaly shapes compared to conventional checkerboards⁶⁹. Smearing of the anomalies is observed near the boundaries of the region at all periods for both Rayleigh and Love wave maps (Fig. 7a–d). The well-recovered region gradually shrinks in size with increasing period, such that at 5.0 s period only the central part of the Koyna-Warna region comprising of the Warna reservoir and southern Koyna reservoir is well-recovered. The resolution is roughly similar for both Rayleigh and Love wave maps. The amplitude of the anomalies also decreases with increasing period. This pattern is likely due to fewer available station-pair paths at longer periods (Fig. S4).

Based on the resolution test, the poorly recovered regions at all periods have been masked during the generation of group velocity maps (Fig. 7e–h). In addition, regions that show abnormally high group velocities for shorter periods (> 3.75 km/s for Love wave and > 3.50 km/s for Rayleigh wave) that are unrealistic for crustal scale from regional studies^70,71 have been masked. In general, the Love wave velocities are higher than Rayleigh wave velocities across all periods. In most parts of the region, the group velocities increase with increasing period because longer period waves sample greater depths and the subsurface seismic velocities tend to generally increase with depth.

Inversion for shear wave velocity

The dispersion curve obtained from each bin of the group velocity maps was used to invert for 1D shear wave velocity in depth. In total, 667 bins of 2.5 km $\times$ 2.5 km size from Rayleigh wave maps and 664 bins from Love wave maps maps were used. The depth inversion was performed using the nearest neighbor algorithm⁷², which is implemented in the dinver program of the Geopsy software package for ambient noise processing⁴⁶. The dispersion curves obtained from Rayleigh wave maps and Love wave maps were separately inverted for shear wave velocity in vertical direction ($V_{sv}$) and shear wave velocity in horizontal direction ($V_{sh}$) respectively. The relative standard deviations of the dispersion curves (Fig. 6c,d) across different periods were used as standard errors during the inversion.

As with other inversion problems in earth sciences, the inversion of surface wave dispersion curves for shear wave velocity is ill-posed and suffers from non-uniqueness of the solution. In order to overcome these challenges to a certain extent, a workflow wherein resampling of the dispersion curves based on wavelength and experimenting with multiple parametrization of the 1D $V_s$ model has been suggested⁷³. Following this workflow, each dispersion curve was resampled in terms of wavelength ($\lambda$) and six different parameterizations (three based on fixed number of layers and three based on fixed thickness ratio of successive layers) for 1D $V_s$ model were defined using swprepost package⁴⁵. The resampled dispersion curve was inverted in geopsy-dinver by applying the nearest neighbor algorithm to a starting $V_s$ model generated following each parametrization. At the end of 6 inversions for each dispersion curve, 20 lowest misfit models from the 6 types of parameterizations were weighted-averaged with respect to their misfits to obtain the best-fit 1D $V_s$ model. This process was followed for both 1D $V_{sv}$ and $V_{sh}$ inversions. The full list of parameters related to the 1D $V_s$ model inversions are provided in Table S4.

After best-fit $V_{sh}$ and $V_{sv}$ 1D models were obtained for each lateral bin, the isotropic $V_s$ model ($V_s^{iso}$) and the radial anisotropy ($\xi$) were calculated as follows:

$$\begin{aligned} V_s^{iso} = \left( \frac{V_{sv}*\varepsilon _{sv} + V_{sh}*\varepsilon _{sh} }{\varepsilon _{sh}+\varepsilon _{sv}}\right) , \end{aligned}$$

(1)

$$\begin{aligned} \xi = \left( \frac{V_{sh} - V_{sv}}{V_s^{iso}}\right) , \end{aligned}$$

(2)

where $\varepsilon _{sv}$ and $\varepsilon _{sh}$ are the misfit errors of $V_{sv}$ and $V_{sh}$ model estimations respectively.

The $V_s^{iso}$ models and the $\xi$ for all the bins were smoothed in the lateral direction using a 2D Gaussian smoothing with kernel width of 2 bins (5 km), which is equivalent to the spatial resolution found laterally (Fig. 7a-d). In the vertical direction, a 1D Gaussian smoothing with a width of 300 m was applied. This width is less than the minimum resolvable layer thickness of the 1D model ($\lambda _{min}/3$)⁷⁴, which also corresponds to the vertical resolution. The fundamental mode surface waves are not sensitive to depths larger than $\lambda _{max}/2$⁷⁵, therefore, this value was used as the maximum resolvable depth. Finally, a topographical correction based on Scripps’ SRTM15+V2.6 grid⁷⁶ was applied to the $V_s^{iso}$ and $\xi$ results using pygmt. The model volume was sliced laterally and vertically to obtain the horizontal sections and the vertical cross-sections respectively. In the previous sections, $V_s^{iso}$ has been referred as just $V_s$.

Data availability

The Supplementary Material for this article includes four additional figures, four tables and a description of the contents. It also contains description of all the datasets and scripts necessary to generate the figures, which are uploaded to figshare.org at https://figshare.com/s/e739c54537ba304ee0f3.

References

Gupta, H. K. Artificial water reservoir-triggered seismicity (rts): Most prominent anthropogenic seismicity. Surv. Geophys. 43, 619–659. https://doi.org/10.1007/s10712-021-09675-z (2022).
Article ADS Google Scholar
Narain, H. & Gupta, H. Koyna earthquake. Nature 217, 1138–1139. https://doi.org/10.1038/2171138a0 (1968).
Article ADS Google Scholar
Guha, S., Gosavi, P., Padale, J. & Marwadi, S. An earthquake cluster at Koyna. Bull. Seismol. Soc. Am. 61, 297–315. https://doi.org/10.1785/BSSA0610020297 (1971).
Article Google Scholar
Langston, C. A. A body wave inversion of the Koyna, India, earthquake of December 10, 1967, and some implications for body wave focal mechanisms. J. Geophys. Res. 1896–1977(81), 2517–2529. https://doi.org/10.1029/JB081i014p02517 (1976).
Article ADS Google Scholar
Langston, C. A. Source inversion of seismic waveforms: The Koyna, India, earthquakes of 13 September 1967. Bull. Seismol. Soc. Am. 71, 1–24. https://doi.org/10.1785/BSSA0710010001 (1981).
Article Google Scholar
Langston, C. A. & Franco-Spera, M. Modeling of the Koyna, India, aftershock of 12 December 1967. Bull. Seismol. Soc. Am. 75, 651–660. https://doi.org/10.1785/BSSA0750030651 (1985).
Article Google Scholar
Gupta, H. K. Review: Reservoir triggered seismicity (rts) at Koyna, India, over the past 50 yrs. Bull. Seismol. Soc. Am. 108, 2907–2918. https://doi.org/10.1785/0120180019 (2018).
Article Google Scholar
Rao, N. P. & Shashidhar, D. Periodic variation of stress field in the Koyna–Warna reservoir triggered seismic zone inferred from focal mechanism studies. Tectonophysics 679, 29–40. https://doi.org/10.1016/j.tecto.2016.04.036 (2016).
Article ADS Google Scholar
Shashidhar, D. et al. A catalogue of earthquakes in the Koyna–Warna region, western India (2005–2017). J. Geol. Soc. India 93, 7–24. https://doi.org/10.1007/s12594-019-1115-y (2019).
Article Google Scholar
Guha, S. et al. Catalogue of earthquakes (>= m 3.0) in peninsular India. Atomic Energy Regulatory Board—Technical Reports. https://inis.iaea.org/records/04xwa-pdq75 (1993).
Uieda, L. et al. PyGMT: A Python Interface for the Generic Mapping Tools. https://doi.org/10.5281/zenodo.7772533 (2023).
Inkscape Project. Inkscape Vector Graphics Editor, Version 1.2.2. https://inkscape.org (2022).
Gupta, H. K., Rastogi, B. K. & Narain, H. Common features of the reservoir-associated seismic activities. Bull. Seismol. Soc. Am. 62, 481–492. https://doi.org/10.1785/BSSA0620020481 (1972).
Article Google Scholar
Pandey, A. P. & Chadha, R. Surface loading and triggered earthquakes in the Koyna–Warna region, western India. Phys. Earth Planet. Inter. 139, 207–223. https://doi.org/10.1016/j.pepi.2003.08.003 (2003).
Article ADS Google Scholar
Catchings, R. D., Dixit, M. M., Goldman, M. R. & Kumar, S. Structure of the Koyna–Warna seismic zone, Maharashtra, India: A possible model for large induced earthquakes elsewhere. J. Geophys. Res. Solid Earth 120, 3479–3506. https://doi.org/10.1002/2014JB011695 (2015).
Article ADS Google Scholar
Gahalaut, V. K., Kalpna, A. & Singh, S. K. Fault interaction and earthquake triggering in the Koyna–Warna region, India. Geophys. Res. Lett. 31, 818. https://doi.org/10.1029/2004GL019818 (2004).
Article Google Scholar
Talwani, P. Seismotectonics of the Koyna–Warna area, India. Pure Appl. Geophys. 150, 511–550. https://doi.org/10.1007/s000240050091 (1997).
Article ADS Google Scholar
Durá-Gómez, I. & Talwani, P. Hydromechanics of the Koyna–Warna region, India. Pure Appl. Geophys. 167, 183–213. https://doi.org/10.1007/s00024-009-0012-5 (2010).
Article ADS Google Scholar
Courtillot, V. et al. Deccan flood basalts at the cretaceous/tertiary boundary? Earth Planet. Sci. Lett. 80, 361–374. https://doi.org/10.1016/0012-821X(86)90118-4 (1986).
Article ADS CAS Google Scholar
Patro, B. P. K. & Sarma, S. V. S. Trap thickness and the subtrappean structures related to mode of eruption in the deccan plateau of India: Results from magnetotellurics. Earth Planets Space 59, 75–81. https://doi.org/10.1186/BF03352679 (2007).
Article ADS Google Scholar
Gupta, H. et al. Investigations related to scientific deep drilling to study reservoir-triggered earthquakes at Koyna, India. Int. J. Earth Sci. 104, 1511–1522. https://doi.org/10.1007/s00531-014-1128-0 (2015).
Article CAS Google Scholar
Misra, S. et al. Granite-gneiss basement below deccan traps in the Koyna region, western India: Outcome from scientific drilling. J. Geol. Soc. India 90, 776–782. https://doi.org/10.1007/s12594-017-0790-9 (2017).
Article ADS CAS Google Scholar
Halder, P., Shukla, M. K., Kumar, K. & Sharma, A. Understanding the mechanism of shallow crustal fluid-rock interaction in the deccan trap basement rocks and its significance in the koyna-warna seismogenic region, western india. Phys. Chem. Earth A/B/C. https://doi.org/10.1016/j.pce.2025.103870 (2025).
Article Google Scholar
Goswami, D., Hazarika, P. & Roy, S. In situ stress orientation from 3 km borehole image logs in the koyna seismogenic zone, western India: Implications for transitional faulting environment. Tectonics 39, e2019005647. https://doi.org/10.1029/2019TC005647 (2020).
Article ADS Google Scholar
Modak, K., Rohilla, S., Podugu, N., Goswami, D. & Roy, S. Fault associated with the 1967 m 6.3 koyna earthquake, India: A review of recent studies and perspectives for further probing. J. Asian Earth Sci. X 8, 100123. https://doi.org/10.1016/j.jaesx.2022.100123 (2022).
Article Google Scholar
Agrawal, P., Pandey, O. & Chetty, T. Aeromagnetic anomalies, lineaments and seismicity in Koyna–Warna region. J. Indian Geophys. Union 8, 229–242 (2004).
Google Scholar
Borah, U. K. et al. Role of fluid on seismicity of an intra-plate earthquake zone in western India: An electrical fingerprint from magnetotelluric study. Earth Planets Space 75, 149. https://doi.org/10.1186/s40623-023-01905-5 (2023).
Article ADS Google Scholar
Arora, K. et al. Lineaments in deccan basalts: The basement connection in the Koyna–Warna rts region. Bull. Seismol. Soc. Am. 108, 2919–2932. https://doi.org/10.1785/0120180011 (2018).
Article Google Scholar
Gupta, H. K. et al. Location of the pilot borehole for investigations of reservoir triggered seismicity at Koyna, India. Gondwana Res. 42, 133–139. https://doi.org/10.1016/j.gr.2016.10.014 (2017).
Article ADS Google Scholar
Krishna, V. G., Kaila, K. L. & Reddy, P. R. Synthetic seismogram modeling of crustal seismic record sections from the Koyna dss profiles in the western India. In Properties and Processes of Earth’s Lower Crust 143–157. https://doi.org/10.1029/GM051p0143 (American Geophysical Union (AGU), 1989).
Tiwari, V., Vyaghreswara Rao, M. & Mishra, D. Density inhomogeneities beneath deccan volcanic province, India as derived from gravity data. J. Geodyn. 31, 1–17. https://doi.org/10.1016/S0264-3707(00)00015-6 (2001).
Article Google Scholar
Vasanthi, A. & SatishKumar, K. Understanding conspicuous gravity low over the Koyna–Warna seismogenic region (Maharashtra, India) and earthquake nucleation: A paradigm shift. Pure Appl. Geophys. 173, 1933–1948. https://doi.org/10.1007/s00024-015-1237-0 (2016).
Article ADS Google Scholar
Patro, P. K., Borah, U., Babu, G. A., Veeraiah, B. & Sarma, S. V. S. Ground electrical and electromagnetic studies in Koyna–Warna region, India. J. Geol. Soc. India 90, 711–719. https://doi.org/10.1007/s12594-017-0780-y (2017).
Article Google Scholar
Dixit, M. M. et al. Seismicity, faulting, and structure of the Koyna–Warna seismic region, western India from local earthquake tomography and hypocenter locations. J. Geophys. Res. Solid Earth 119, 6372–6398. https://doi.org/10.1002/2014JB010950 (2014).
Article ADS Google Scholar
Kumar, S. & Kumar, P. One-dimensional velocity model, station correction and earthquake relocation of local earthquakes in the koyna-warna region, india. Pure Appl. Geophys. 176, 4761–4782. https://doi.org/10.1007/s00024-019-02264-7 (2019).
Article ADS Google Scholar
Shapiro, N. M. & Campillo, M. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett. 31, 491. https://doi.org/10.1029/2004GL019491 (2004).
Article Google Scholar
Ranjan, P. & Stehly, L. Estimation of seismic attenuation from ambient noise coda waves: Application to the hellenic subduction zone. Bull. Seismol. Soc. Am. 114, 2065–2082. https://doi.org/10.1785/0120230265 (2024).
Article Google Scholar
Lehujeur, M. et al. Reservoir imaging using ambient noise correlation from a dense seismic network. J. Geophys. Res. Solid Earth 123, 6671–6686. https://doi.org/10.1029/2018JB015440 (2018).
Article ADS Google Scholar
Wang, Y., Lin, F.-C., Schmandt, B. & Farrell, J. Ambient noise tomography across mount st. helens using a dense seismic array. J. Geophys. Res. Solid Earth 122, 4492–4508. https://doi.org/10.1002/2016JB013769 (2017).
Article ADS Google Scholar
Esteve, C. et al. The seismic signature and geothermal potential of the Schwechat depression in the Vienna basin, Austria, from ambient noise tomography. Geothermics 127, 103211. https://doi.org/10.1016/j.geothermics.2024.103211 (2025).
Article Google Scholar
Jiang, C. & Denolle, M. A. Pronounced seismic anisotropy in kanto sedimentary basin: A case study of using dense arrays, ambient noise seismology, and multi-modal surface-wave imaging. J. Geophys. Res. Solid Earth 127, e2022024613. https://doi.org/10.1029/2022JB024613 (2022).
Article ADS Google Scholar
Wu, S.-M. et al. Crustal characterization of the hengill geothermal fields: Insights from isotropic and anisotropic seismic noise imaging using a 500-node array. J. Geophys. Res. Solid Earth 129, e2024028915. https://doi.org/10.1029/2024JB028915 (2024).
Article Google Scholar
Rohilla, S., Rao, N. P., Gerstoft, P., Shashidhar, D. & Satyanarayana, H. V. S. Shear-wave velocity structure of the Koyna–Warna region in western India using ambient noise correlation and surface-wave dispersion. Bull. Seismol. Soc. Am. 105, 473–479. https://doi.org/10.1785/0120140091 (2015).
Article Google Scholar
Lecocq, T., Caudron, C. & Brenguier, F. Msnoise, a python package for monitoring seismic velocity changes using ambient seismic noise. Seismol. Res. Lett. 85, 715–726. https://doi.org/10.1785/0220130073 (2014).
Article Google Scholar
Vantassel, J. jpvantassel/swprepost: v2.0.0. https://doi.org/10.5281/zenodo.6558333 (2022).
Wathelet, M. et al. Geopsy: A user-friendly open-source tool set for ambient vibration processing. Seismol. Res. Lett. 91, 1878–1889. https://doi.org/10.1785/0220190360 (2020).
Article Google Scholar
Duraiswami, R. A. et al. Volcanology and lava flow morpho-types from the Koyna–Warna region, western deccan traps, India. J. Geol. Soc. India 90, 742–747. https://doi.org/10.1007/s12594-017-0785-6 (2017).
Article CAS Google Scholar
Hua, Y., Zhao, D., Toyokuni, G. & Xu, Y. Tomography of the source zone of the great 2011 Tohoku earthquake. Nat. Commun. 11, 1163. https://doi.org/10.1038/s41467-020-14745-8 (2020).
Article ADS PubMed PubMed Central Google Scholar
Ranjan, P. & Konstantinou, K. Local earthquake tomography of the aegean crust: Implications for active deformation, large earthquakes, and arc volcanism. Tectonophysics 880, 230331. https://doi.org/10.1016/j.tecto.2024.230331 (2024).
Article Google Scholar
Rubin, A. M. & Ampuero, J.-P. Earthquake nucleation on (aging) rate and state faults. J. Geophys. Res. Solid Earth 110, 686. https://doi.org/10.1029/2005JB003686 (2005).
Article Google Scholar
Uenishi, K. & Rice, J. R. Universal nucleation length for slip-weakening rupture instability under nonuniform fault loading. J. Geophys. Res. Solid Earth 108, 681. https://doi.org/10.1029/2001JB001681 (2003).
Article Google Scholar
Thakur, P. & Huang, Y. The effects of precursory velocity changes on earthquake nucleation and stress evolution in dynamic earthquake cycle simulations. Earth Planet. Sci. Lett. 637, 118727. https://doi.org/10.1016/j.epsl.2024.118727 (2024).
Article CAS Google Scholar
Pandey, A., Gahalaut, V. K., Yadav, R. K., Catherine, J. K. & Naidu, M. S. Conundrum of sustained seismicity and low deformation in the Koyna–Warna region, India. Bull. Seismol. Soc. Am. https://doi.org/10.1785/0120240196 (2025).
Article Google Scholar
Ebrahimi, M., Tatar, M., Aoudia, A. & Guidarelli, M. Loading effects beneath the Gotvand-e olya reservoir (south-west of Iran) deduced from ambient noise tomography. Geophys. J. Int. 212, 229–243. https://doi.org/10.1093/gji/ggx411 (2017).
Article ADS Google Scholar
Dong, S. et al. Seismic evidence for fluid-driven pore pressure increase and its links with induced seismicity in the Xinfengjiang reservoir, South China. J. Geophys. Res. Solid Earth 127, e2021023548. https://doi.org/10.1029/2021JB023548 (2022).
Article ADS Google Scholar
Podugu, N., Goswami, D., Akkiraju, V. V. & Roy, S. In-situ physical and elastic properties of archaean basement granitoids in the Koyna seismogenic zone, western India from 3 km downhole geophysical well logs: Implications for water percolation at depth. Tectonophysics 848, 229725. https://doi.org/10.1016/j.tecto.2023.229725 (2023).
Article Google Scholar
Modak, K. Evidence of water percolation in granitoid basement in koyna seismogenic zone: Implications for reservoir triggered seismicity. J. Earth Syst. Sci. 133, 163. https://doi.org/10.1007/s12040-024-02380-6 (2024).
Article Google Scholar
Kato, A. & Ben-Zion, Y. The generation of large earthquakes. Nat. Rev. Earth Environ. 2, 26–39. https://doi.org/10.1038/s43017-020-00108-w (2021).
Article ADS Google Scholar
Peterson, J. R. Observations and Modeling of Seismic Background Noise. https://doi.org/10.3133/ofr93322 (1993).
Krischer, L. et al. ObsPy: A bridge for seismology into the scientific python ecosystem. Comput. Sci. Discov. 8, 014003 (2015).
Article Google Scholar
Hunter, J. D. Matplotlib: A 2d graphics environment. Comput. Sci. Eng. 9, 90–95. https://doi.org/10.1109/MCSE.2007.55 (2007).
Article Google Scholar
Lin, F.-C., Moschetti, M. P. & Ritzwoller, M. H. Surface wave tomography of the western united states from ambient seismic noise: Rayleigh and love wave phase velocity maps. Geophys. J. Int. 173, 281–298. https://doi.org/10.1111/j.1365-246X.2008.03720.x (2008).
Article ADS Google Scholar
Levshin, A. et al.Recording, Identification, and Measurement of Surface Wave Parameters 131–182 (Springer, 1989).
Schwardt, M., Pilger, C., Gaebler, P., Hupe, P. & Ceranna, L. Natural and anthropogenic sources of seismic, hydroacoustic, and infrasonic waves: Waveforms and spectral characteristics (and their applicability for sensor calibration). Surv. Geophys. 43, 1265–1361 (2022).
Article ADS PubMed PubMed Central Google Scholar
Mordret, A. et al. Near-surface study at the valhall oil field from ambient noise surface wave tomography. Geophys. J. Int. 193, 1627–1643. https://doi.org/10.1093/gji/ggt061 (2013).
Article ADS Google Scholar
Calvetti, D., Morigi, S., Reichel, L. & Sgallari, F. Tikhonov regularization and the l-curve for large discrete ill-posed problems. J. Comput. Appl. Math. 123, 423–446. https://doi.org/10.1016/S0377-0427(00)00414-3 (2000).
Article ADS MathSciNet MATH Google Scholar
NOAA National Centers for Environmental Information. ETOPO 2022 15 Arc-Second Global Relief Model (2022).
Wessel, P. et al. The generic mapping tools version 6. Geochem. Geophys. Geosyst. 20, 5556–5564. https://doi.org/10.1029/2019GC008515 (2019).
Article ADS Google Scholar
Rawlinson, N. & Spakman, W. On the use of sensitivity tests in seismic tomography. Geophys. J. Int. 205, 1221–1243. https://doi.org/10.1093/gji/ggw084 (2016).
Article ADS Google Scholar
Dey, S., Ghosh, M. & Mitra, S. 3d shear-wave velocity structure of the crust and upper mantle beneath India, Himalaya and Tibet. J. Geophys. Res. Solid Earth 129, e2023028292. https://doi.org/10.1029/2023JB028292 (2024).
Article Google Scholar
Ghosh, M., Dey, S. & Mitra, S. Love-wave group-velocity tomography of India–Tibet: Insights into radially anisotropic s-wave velocity structure. Geophys. J. Int. 241, 901–918. https://doi.org/10.1093/gji/ggaf074 (2025).
Article Google Scholar
Sambridge, M. Geophysical inversion with a neighbourhood algorithm—i. Searching a parameter space. Geophys. J. Int. 138, 479–494. https://doi.org/10.1046/j.1365-246X.1999.00876.x (1999).
Article ADS Google Scholar
Vantassel, J. P. & Cox, B. R. Swinvert: A workflow for performing rigorous 1-d surface wave inversions. Geophys. J. Int. 224, 1141–1156. https://doi.org/10.1093/gji/ggaa426 (2020).
Article ADS Google Scholar
Cox, B. R. & Teague, D. P. Layering ratios: A systematic approach to the inversion of surface wave data in the absence of a priori information. Geophys. J. Int. 207, 422–438. https://doi.org/10.1093/gji/ggw282 (2016).
Article ADS Google Scholar
Garofalo, F. et al. Interpacific project: Comparison of invasive and non-invasive methods for seismic site characterization. Part i: Intra-comparison of surface wave methods. Soil Dyn. Earthq. Eng. 82, 222–240. https://doi.org/10.1016/j.soildyn.2015.12.010 (2016).
Article Google Scholar
Tozer, B. et al. Global bathymetry and topography at 15 arc sec: Srtm15+. Earth Space Sci. 6, 1847–1864. https://doi.org/10.1029/2019EA000658 (2019).
Article ADS Google Scholar

Download references

Acknowledgements

The digital seismic waveform data, collected using the 3-Component Taurus Standalone recording system, belongs to the CSIR-National Geophysical Research Institute (NGRI), and permission for its use has been granted vide reference no. Lib/2025/Pub-42. We acknowledge the contributions of the Controlled Source Seismic (CSS) field crew in data acquisition. The financial assistance provided by the Ministry of Earth Sciences (MoES), New Delhi, is gratefully acknowledged. The authors extend their special thanks to Dr. H. K. Gupta for his encouragement and kind support in facilitating this study as a pilot project and Dr. M.M. Dixit for successfully executing the pilot project. We also thank Dr. Rahul Biswas for his valuable comments, which helped improve the manuscript. Finally, we are thankful to the two anonymous reviewers for their constructive comments that helped improve the manuscript.

Author information

Authors and Affiliations

CSIR-National Geophysical Research Institute (NGRI), Hyderabad, Telangana, 500007, India
Pratul Ranjan, Prakash Kumar, Biswajit Mandal & Periyasamy Karuppannan
Academy of Scientific and Innovative Research (AcSIR), Ghaziabad, Uttar Pradesh, 201002, India
Pratul Ranjan, Prakash Kumar & Biswajit Mandal

Authors

Pratul Ranjan
View author publications
Search author on:PubMed Google Scholar
Prakash Kumar
View author publications
Search author on:PubMed Google Scholar
Biswajit Mandal
View author publications
Search author on:PubMed Google Scholar
Periyasamy Karuppannan
View author publications
Search author on:PubMed Google Scholar

Contributions

P.R. conducted the analysis and wrote the initial manuscript draft as well as revised the manuscript. P.K. conceived idea for the analysis and provided computational resources. B.M. and P.K prepared the data, reviewed the results, and prepared some of the figures. All authors revised the initial manuscript draft.

Corresponding author

Correspondence to Pratul Ranjan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary Information.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Ranjan, P., Kumar, P., Mandal, B. et al. Investigating reservoir-triggered seismicity in the Koyna–Warna region through nodal ambient noise tomography. Sci Rep 15, 26323 (2025). https://doi.org/10.1038/s41598-025-12099-z

Download citation

Received: 23 April 2025
Accepted: 15 July 2025
Published: 20 July 2025
DOI: https://doi.org/10.1038/s41598-025-12099-z