A modified EWMA signed rank control chart for enhanced quality monitoring in the automobile industry

Abstract

Control charts may aid in maintaining and improving the efficiency of manufacturing and industrial processes. Nonparametric control charts are more dependable and practical than parametric charts when it is unclear how the data will be distributed. Also, when the distribution of the underlying process is unknown or uncertain, nonparametric control charts are required. The nonparametric charts are a reliable alternative that also can quickly detect shifts in process parameter(s). For effective process location monitoring, we have developed a nonparametric extended exponentially weighted moving average chart based on the Wilcoxon signed rank test under ranked set sampling (hereafter named REEWMA_WSR). The performance of the proposed REEWMA_WSR chart has been evaluated by calculating the run-length properties using the Monte Carlo simulations approach. The in-control and out-of-control run-length profiles of the proposed chart are also investigated under normal, non-normal, and contaminated normal distributions. Performance comparison of the proposed REEWMA_WSR chart is done with various usual and nonparametric charts. The proposed chart’s practical implementation is also illustrated using a real-life application.

Introduction

Control charts serve as crucial tools in the statistical process control (SPC) toolkit, playing a vital role in monitoring process parameters to enhance the quality of final products (cf. Montgomery¹). Memoryless and memory charts are the two main categories based on their design structure. Memoryless charts that adhere to (cf. Shewhart’s²) structures work well for significant process changes. Memory-type control charts are intended for the quick identification of minor to moderate process shifts. The cumulative sum (CUSUM) chart by (cf. Page³), the exponentially weighted moving average (EWMA) chart by (cf. Roberts⁴), the double EWMA chart by (cf. Shamma and Shamma⁵), and the progressive mean (PM) chart by (cf. Abbas et al.⁶) are all examples of these types of charts. Currently, the parametric control chart is extensively used to spot changes in the process mean or standard deviation by using a parameter. However, a drawback of parametric control charts lies in their reliance on assumptions regarding normality, homogeneity of variances, and independence, impacting the properties of these charts. In practical scenarios, the distribution of data collected from the production process is often unknown or only partially identified, lacking precise parameter values. To address these challenges, the nonparametric (NP) control chart has been introduced as an alternative, aiming to overcome the limitations associated with the assumptions made by parametric control charts. Notably, NP charts, introduced by Graham et al.⁷, Chakraborti, and Graham⁸, demonstrate robustness and heightened sensitivity compared to parametric charts, particularly under heavy-tailed distributions of the quality characteristic of interest.

Control charts based on NP statistics must be implemented as a result. Researchers have focused on the EWMA and CUSUM control structures, which are based on different NP statistics. This has resulted in the creation of new NP control charts. For asymmetrical distributions, (cf. Park⁹) suggested Wilcoxon signed rank (WSR) charts and Shewhart sign charts. Amin and Searcy¹⁰ used the WSR statistic to investigate the characteristics of the EWMA chart. A thorough analysis of NP control charts was carried out by Chakraborti et al.¹¹, Bakir¹² used sign rank-like statistics and signed ranks to develop an NP control chart. A variety of NP control charts were provided by Chakraborti and Graham¹³, while Chakraborti and Eryilmaz¹⁴ suggested an NP Shewhart-type signed rank control chart. An NP control chart was created by (cf. Das and Bhattacharya¹⁵ for monitoring process variability. Two NP equivalents of the CUSUM and EWMA control charts, based on the WRS test, were presented by (cf. Li et al.¹⁶). Based on these rules, Human et al.¹⁷ created NP Shewhart-type sign control charts. Recent developments in univariate and multivariate NP charts were described by (cf. Graham et al.¹⁸).

Charts constructed on the ranked set sampling (RSS) scheme prove to be more sensitive and often more cost-effective than the aforementioned extensions, all of which are based on the simple random sampling (SRS) scheme. The RSS method not only offers a more economical alternative but also yields more effective results, aligning with the needs of quality practitioners in such scenarios. Researchers, aiming for optimal analytical precision within budgetary and time constraints, often encounter challenges in industrial and environmental systems. Obtaining real measurements for a dataset can be arduous due to high costs or specific data types. To address these challenges, McIntyre¹⁹ introduced the cost-effective and efficient RSS scheme. Especially useful when dealing with measures involving time, money, or potentially harmful data types, the RSS system operates efficiently by relying on rankings instead of actual measurements. Sample selection criteria in RSS schemes pose no issues, resembling the principles of stratified random sampling, wherein the entire population is divided into subgroups characterized by homogeneous items within and heterogeneous objects between them.

Initially, Salazar and Sinha²⁰ pioneered the development of control charts through the use of the range of subgroup sample and median RSS schemes. By utilizing several RSS algorithms, (cf. Muttlak and Al-Sabah²¹) also contributed to the construction of control charts. Al-Omari and Haq²² suggested control charts utilizing the double RSS scheme, whereas Abujiya and Muttlak²³ presented a control chart based on several DRSS schemes. By adding different types of RSS procedures, (cf. Abujiya et al.²⁴) improved the performance of the EWMA control charts. Repetitive sampling was used to propose an EWMA sign chart by Aslam et al.²⁵. Asghari et al.²⁶ created a sign control chart based on RSS, whereas Lu²⁷ introduced the NP EWMA sign control chart. Mehmood et al.²⁸ evaluated process mean fluctuations with control charts that used several RSS techniques. Further improvements to CUSUM control charts were made by Abujiya et al.²⁹ to better analyze process dispersion with different RSS methods. Haq et al.³⁰ presented a new type of synthetic control chart that uses different RSS forms to evaluate the process mean and dispersion. Using the RSS technique, Abid et al.³¹ created an NP CUSUM control chart that included a sign test. Three NP control charts based on the RSS approach were proposed by Tapang et al.³². Under the RSS approach, Abid et al.³³ investigated the performance of NP EWMA control charts by using Wilcoxon signed-rank statistic.

Rasheed et al.³⁴ constructed a triple EWMA WSR control chart based on RSS. Ali et al.³⁵ suggested an NP double EWMA chart by utilizing the sign test statistic. Taboran and Sukparungsee³⁶ examined that the MEWMA-sign control chart was more responsive to slight shifts than the EWMA-sign control chart during their examination of it for process mean monitoring under anomalous distributions. Abbas et al.³⁷ introduced the NP progressive mean control chart based on the WSR statistic. Petcharat and Sukparungsee³⁸ provided a novel EWMA WSR chart to evaluate changes in the mean parameter. Recently, Talordphop et al.³⁹ enhanced the performance of the extended EWMA (EEWMA) chart by using the WSR statistic under the SRS scheme.

Initially, EEWMA chart was introduced by Naveed et al.⁴⁰ and showed that the EEWMA chart is more effective than traditional Shewhart and EWMA charts for detecting small shifts in the process location. Many researchers have enhanced the performance of the EEWMA chart under different scenarios. Naveed et al.⁴¹ developed the EEWMA chart by adopting the multiple dependent state technique. Karoon et al.⁴² assessed the exact run length of the EEWMA chart in case of seasonal autoregressive process. Naveed et al.⁴³ improved the performance of the EEWMA under chart under repetitive sampling method. Recently, Naveed et al.⁴⁴ evaluated the performance of the combined EEWMA-MA chart under auxiliary and non-auxiliary information.

By taking motivation from the work of Talordphop et al.³⁹, in this study we suggest an NP EEWMA chart using WSR statistic under the RSS scheme (hereafter named as $R{EEWMA}_{WSR}$) to monitor the changes in the process location. The in-control (IC) and out-of-control (OOC) performance of the proposed $R{EEWMA}_{WSR}$ chart is investigated under normal (standard normal), non-normal (student’s t, logistic, Laplace), and contaminated normal (CN) environments. The key advantages of the proposed $R{EEWMA}_{WSR}$ chart are as: (i) The proposed $R{EEWMA}_{WSR}$ chart is easy-to-use, less-expensive and more robust (ii) The suggested REEWMA-WSR chart is very effective by handling the heavy-tailed distributions (iii) The proposed $R{EEWMA}_{WSR}$ chart is revealed better performance as compared to its counterpart charts.

The subsequent sections of this article are outlined as follows: Section “Design structure of the existing and proposed charts” explains the design structure of the existing and proposed charts. IC and OOC performance evaluation of the proposed $R{EEWMA}_{WSR}$ chart is presented in section “Performance evaluation”. Comprehensive comparison of the proposed chart and its competitors are presented in section “Comparison between proposed and existing charts”. Utilizing an authentic dataset, section “Real-life application” furnishes a numerical example. The article concludes with summary and concluding thoughts.

Design structure of the existing and proposed charts

In this section, we have provided the design structure of the existing and proposed control charts.

The classical EWMA control chart

Consider a sequence of independently distributed random variables, denoted as ${X}_{1}, {X}_{2},.. {X}_{i},\dots$ drawn from a normal population with a mean $\mu$ and variance ${\sigma }^{2}$. Introducing a smoothing constant $\lambda$, the EWMA statistic ${Z}_{i}= \lambda {X}_{i}+\left( 1- \lambda \right){Z}_{i-1}$ where ${Z}_{i}$ stands represents the EWMA statistic, and λ range is 0 to 1. A lower value of $\lambda$ implies that the previous statistic’s value carries more weight, while the current variable of interest is given less weight. When $\lambda =1.$, the EWMA statistic becomes a representation that solely relies on recent data. The initial value ${Z}_{0}$ serves as the mean or average of preliminary data from a Phase I sample. The variable ${Z}_{i}$ denotes the prior value of the statistic. The mean and variance of the EWMA statistic can be derived, as discussed by Roberts⁴, particularly in the context of an (IC) process.

$$E\left({Z}_{i}\right)= {\mu }_{0},$$

(1)

$$Var\left({Z}_{i}\right)={\sigma }^{2} \left[\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\right]$$

(2)

In this context, we denote the target mean and variance of ${X}_{i}$ as ${\mu }_{0}$ and ${\sigma }^{2}$, respectively. If these parameters are not known, we derive estimates from initial samples. As a result, the control constraints of the EWMA chart are as follows:

$$\left.\begin{array}{c}{UCL}_{i}={\mu }_{0}+\text{L }\sqrt{{\sigma }^{2} \left[\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\right] }\\ CL= {\mu }_{0}\\ {LCL}_{i}={\mu }_{0}-\text{L }\sqrt{{\sigma }^{2} \left[\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\right]}\end{array}\right\}$$

(3)

The process is considered to be in $(IC)$ state if the ${W}_{i}$ falls inside of the ${UCL}_{i}$ and ${LCL}_{i}$, otherwise, it is stated to be $(OOC).$

The classical EEWMA control chart

The plotting statistic of EEWMA after applying a smoothing constant ${\lambda }_{1}$ and ${\lambda }_{2}$ is defined as (cf. Naveed et al.⁴⁰):

$${W}_{i}= {\lambda }_{1}{X}_{i}- {\lambda }_{1}{X}_{i-1}+\left( 1- {\lambda }_{1}+ {\lambda }_{1}\right){W}_{i-1}; \,\text{where}\, 0 < {\lambda }_{1} \le 1\, \text{and} \,0 \le {\lambda }_{2} < {\lambda }_{1}$$

The suggested statistic, denoted as ${W}_{i}$, ensures a total weight of one across its components. Here, ${X}_{i-1}$ signifies the prior value of the variable, and ${W}_{i-1}$ represents the prior value of the statistic. The determination of the target mean relies on the values of ${W}_{0}$. The mean and variance of the EEWMA statistic have been reported by Naveed et al.⁴⁰ in the following manner:

$$E\left(Wi\right)= {\mu }_{0}$$

(4)

$$Var ({W}_{i})={\sigma }^{2}\left[\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\right]$$

(5)

In this scenario, the mean and variance of ${X}_{1}$ are represented by ${\mu }_{0}$ and ${\sigma }^{2}$, respectively. Setting ${\lambda }_{2}$ = 0, transforms it into the variance of the EWMA statistic instead of the EEWMA statistic. When ${\lambda }_{1}$ is equal to ${\lambda }_{2}$ the variance of the EEWMA statistic tends toward infinity; however, when ${\lambda }_{2}$ is greater than ${\lambda }_{1}$ the variance of the EEWMA statistic produces undesirable results. Conversely, when ${\lambda }_{2}$ is less than ${\lambda }_{1}$, the variance of the EEWMA statistic provides valid results. Consequently, the control limits for the EEWMA chart are outlined as follows (cf. Naveed et al.⁴⁰):

$$\left.\begin{array}{c}{UCL}_{i}= {\mu }_{0}+L \sqrt{{\sigma }^{2}\left[\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\right]}\\ CL={\mu }_{0}\\ {LCL}_{i}={\mu }_{0}-L \sqrt{{\sigma }^{2}\left[\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\right]}\end{array}\right\}$$

(6)

The EWMA WSR control chart under SRS

The WSR statistic is a well-known substitute for the one sample t-test for constructing confidence intervals and testing median hypotheses for symmetrical continuous data distribution. For the t- test, the assumption of normality is necessary, but not for the SR statistic. According to (cf. Gibbons and Chakraborti⁴⁵) the SR to t-test has an asymptotic relative efficiency of at least 0.864. Graham et al.⁷ suggested the EWMA control chart using WSR statistic under the SRS scheme (from here named as ${\text{EWMA}}_{\text{WRS}}$) and found that it performs much better than the NPEWMA-SN chart for monitoring process location. The methodology of the ${\text{EWMA}}_{\text{WRS}}$ chart is as follows: Assume ${X}_{i1}, {X}_{i2}, {X}_{i3}, \dots , { X}_{in,}$ represents the ${i}^{th} \left(i=\text{1,2},3, \dots \right)$ rational subclass of independent observations with size $n >1$ assuming that the known median value to be monitored is ${M}_{0}$. Let ${R}_{it}^{+}$ ranks of absolute observations of differences from the median, i.e. $\left|{X}_{it}- {M}_{0}\right|$ for $t=1, 2, 3, \dots , n$.

The WSR statistic is defined as follows:

$${WSR}_{i}= \sum_{i=1}^{n}sign\left|{X}_{it}- {M}_{0}\right| {R}_{it}^{+}$$

here, $i=\text{1,2},3, \dots$ and $t=\text{1,2},3, \dots , n$ and

$$sign\left( {X_{it} - M_{0} } \right) = \left( {\begin{array}{*{20}c} 1 & {if,X_{it} - M_{0} > 0 } \\ 0 & {if,X_{it} - M_{0} = 0} \\ { - 1} & {if,X_{it} - M_{0} < 0} \\ \end{array} } \right)$$

(7)

Gibbons and Chakraboti⁴⁵ proved that the WSR statistic is linearly associated with another statistic ${V}_{n}^{+}$ with a following relationship ${WSR}_{i}=2 {V}_{n}^{+}- \frac{n\left(n+1\right)}{2}$. Based on the above relationship between WSR and ${V}_{n}^{+}$, the mean and variance of ${WSR}_{i}$ are $E\left({SR}_{i}\right)=0$, and $Var\left({SR}_{i}\right)= \frac{n(n+1)(2n+1)}{6}$, respectively (cf. Graham et al.⁷).

The ${\text{EWMA}}_{\text{WSR}}$ plotting statistic is as follows:

$${\text{EWMA}}_{{{\text{WSR}}_{i} i}} = ~\lambda \left( {WSR_{i} } \right) + \left( {1 - \lambda } \right){\text{EWMA}}_{{{\text{WSR}}_{{i - 1}} }} ~\;\;0~ < ~\lambda ~ \le 1$$

(8)

The mean and variance of ${\text{EWMA}}_{{\text{WSR}}_{i}}$ are $E({\text{EWMA}}_{{\text{WSR}}_{i}})=$ 0, & ${\text{Var}(\text{EWMA}}_{{\text{WSR}}_{i}})=$ $\frac{\lambda }{2-\lambda }\left(1-{\left(1-\lambda \right)}^{2i}\right)$ $\left(\frac{n(n+1)(2n+1)}{6}\right),$where control limits of the ${\text{EWMA}}_{\text{WRS}}$ chart using ${E(Z}_{i})$ and ${Var (Z}_{i})$ are written as:

$$\left.\begin{array}{c}{UCL}_{i}={\mu }_{0}+\text{ L }(\sqrt{\left(\frac{n(n+1)(2n+1)}{6}\right)\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i}) }\\ CL= 0\\ {LCL}_{i}={\mu }_{0}-\text{L }(\sqrt{\left(\frac{n(n+1)(2n+1)}{6}\right)\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})}\end{array}\right\}$$

(9)

$L$ is the ${\text{EWMA}}_{\text{WSR}}$ chart’s smoothing constant in Eq. (9). If the plotting statistic given in Eq. (9) is outside the range of limits given in equations ${LCL}_{i}$, and ${UCL}_{i}$., respectively, the ${\text{EWMA}}_{\text{WSR}}$ chart indicates a shift in the process mean.

The EWMA WSR control chart under RSS

Abid et al.³³ first designed the EWMA control chart based on WSR statistic by utilizing the RSS technique (hereafter named as ${\text{REWMA}}_{\text{WSR}}$) and showed that their proposed chart has a quicker shift detection ability than its counterpart charts. The design structure of the ${\text{REWMA}}_{\text{WSR}}$ is as follows: Consider ${X}_{\left(it\right)k}$ as the quality characteristic under investigation, where the process median is denoted as ${M}_{0}$. Let $i=1, 2, 3,\dots$,& $t=1, 2,\dots , n,$. Additionally, let $k=1, 2,\dots , m$, indicating the number of cycles from which $n,$ size samples are independently drawn. For each sample, the ranks of absolute deviations of the RSS observations from ${M}_{0}$, denoted as ${R}_{\left(it\right)m}^{+}$ (i.e., ${R}_{\left(it\right)m}^{+}=\left|{X}_{\left(ij\right)k}-{M}_{0}\right|$, are determined.

Assuming $r$ equals the product of $n$ and $(r=nm)$, indicating the number of iterations of cycles for the RSS techniques. The WSR test statistic under RSS scheme is given as:

$$\begin{aligned} & WSR_{{RSS_{i} }} = \mathop \sum \limits_{t = 1}^{n} \mathop \sum \limits_{k = 1 }^{m} sign \left( {X_{{\left( {it} \right)k}} - M_{0} { }} \right) R_{{\left( {it} \right)k}}^{ + } \\ & sign\left( {X_{{\left( {it} \right)k}} - M_{0} { }} \right) = \left( {\begin{array}{*{20}c} 1 & {if \left( {X_{{\left( {it} \right)k}} - M_{0} { }} \right){ } > 0 } \\ 0 & {if \left( {X_{{\left( {it} \right)k}} - M_{0} { }} \right){ } = 0} \\ { - 1} & {if \left( {X_{{\left( {it} \right)k}} - M_{0} { }} \right) < 0} \\ \end{array} } \right) \\ \end{aligned}$$

(10)

The mean and variance of $W{SR}_{{RSS}_{i}}$ reported by (cf. Abid et al.³³) are as follows: $E\left(W{SR}_{{RSS}_{i}}\right)=0$ and $Var\left(W{SR}_{{RSS}_{i}}\right)=\left(\frac{r (r+1)(2r+1)}{6}\right){\delta }_{0}^{2}$, respectively, where ${\delta }_{0}^{2}$ is a key factor for gaining efficiency of RSS over SRS and it is defined as (cf. Kim and Kim⁴⁶):

$$\delta_{0}^{2} = 1 - \left( {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}} \right)\mathop \sum \limits_{t = 1}^{n} \left( {F_{t} \left( 0 \right) - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)^{2} .$$

The values of ${F}_{t}\left(0\right), t=\text{1,2},\dots ,n,$ are found by estimating the incomplete beta integral i.e.,

$${F}_{t}\left(0\right)=\frac{r!}{\left(t-1\right)!\left(r-t\right)!}\underset{-\propto }{\overset{0}{\int }}F{\left(v\right)}^{t-1}{\left(1-F\left(v\right)\right)}^{r-t}f\left(v\right)dv.$$

So, the ${\text{REWMA}}_{\text{WSR}}$ plotting statistic is written as (cf. Abid et al.³³):

$${REWMA}_{W{SR}_{{RSS}_{i}}}=\lambda W{SR}_{{RSS}_{i}}+\left(1-\lambda \right){REWMA}_{W{SR}_{{RSS}_{i-1}}},$$

(11)

The initial value of the monitoring statistic ${REWMA}_{W{SR}_{{RSS}_{0}}}$ is established as equal to the target median when the process is under $(IC)$ state,

that is, ${REWMA}_{W{SR}_{{RSS}_{0}}}={M}_{0}$. Hence, the $(IC)$ mean and variance of ${REWMA}_{W{SR}_{{RSS}_{i}}}$ is written as [cf. Abid et al.³³) are $E({REWMA}_{W{SR}_{{RSS}_{i}}})=0$ and $Var({REWMA}_{W{SR}_{{RSS}_{i}}})$ $\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\left(\frac{r (r+1)(2r+1)}{24}\right){\delta }_{0}^{2}$.

Therefore, the control limits of the ${REWMA}_{WRS}$ reported by (cf. Abid et al.³³) are as under:

$$\left.\begin{array}{c}{UCL}_{i}={\mu }_{0}+\text{ L }\sqrt{\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\left(\frac{r (r+1)(2r+1)}{24}\right){\delta }_{0}^{2}. }\\ CL= 0\\ {LCL}_{i}={\mu }_{0}-\text{L }\sqrt{\frac{\lambda }{2-\lambda }(1-{\left(1-\lambda \right)}^{2i})\left(\frac{r (r+1)(2r+1)}{24}\right){\delta }_{0}^{2} }.\end{array}\right\}$$

(12)

If the value of ${REWMA}_{W{SR}_{{RSS}_{i}}}$ exceeds the lower or upper control limits defined above, the process is identified as $(OOC$), prompting an investigation for assignable causes. Conversely, if the value falls within the control limits, the process is deemed $(IC)$ and the charting procedure proceeds accordingly.

The EEWMA WSR control chart under SRS

Recently, Talordphop et al.³⁹ developed the EEWMA chart by using the WSR statistic (hereafter named as ${\text{EEWMA}}_{\text{WSR}}$). The plotting statistic of the ${\text{EEWMA}}_{\text{WSR}}$ control is given below:

$${\text{EEWMA}}_{{WSR}_{i}} = {\lambda }_{1}W{SR}_{{SRS}_{i}} - {\lambda }_{2} W{SR}_{{SRS}_{i-1}}+\left(1- {\lambda }_{1}- {\lambda }_{2}\right){\text{EEWMA}}_{{WSR}_{i-1}}$$

(13)

where $0 < {\lambda }_{1}< {\lambda }_{2} \le 1 \,\,\text{and}\, 0 \le {\lambda }_{2} < {\lambda }_{1}$.

The mean and variance of ${\text{EEWMA}}_{{WSR}_{i}}$ are: $E\left({\text{EEWMA}}_{{WSR}_{i}}\right)=0$, and $Var\left({\text{EEWMA}}_{{WSR}_{i}}\right)$$= \left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}$$-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\left(\frac{n (n+1)(2n+1)}{6}\right)$, respectively (cf. Talordphop et.al.³⁹).

Therefore, the control limits of the ${\text{EEWMA}}_{{WRS}_{i}}$ are:

$$\left.\begin{array}{c}{UCL}_{i}={\mu }_{0}+\text{ L }\sqrt{\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\left(\frac{n(n+1)(2n+1)}{24}\right) }\\ CL= 0\\ {LCL}_{i}={\mu }_{0}-\text{L }\sqrt{\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\left(\frac{n (n+1)(2n+1)}{24}\right) }.\end{array}\right\}$$

(14)

In Eq. (14), the upper, middle, and lower control limits are shown as ${LCL}_{i}$, $CL$, and ${UCL}_{i}$, respectively. If the plotting statistic given in Eq. (13) goes beyond the limits set by Eq. (14), the chart shows that the process is $(OOC)$. On the other hand, the process is thought to be in an $(IC)$ state if the plotting statistic stays within the control limits.

The proposed REEWMA WSR control chart under RSS

This section presents the design structure of the proposed $R{EEWMA}_{WSR}$ chart. By adopting the same procedure reported in section “The EWMA WSR control chart under RSS”, the plotting statistic of the proposed $R{EEWMA}_{WSR}$ chart is defined as:

$$\begin{aligned} & {REEWMA}_{W{SR}_{{RSS}_{i}}} = {\lambda }_{1}W{SR}_{{RSS}_{i}} - {\lambda }_{2} W{SR}_{{RSS}_{i-1}}\\&\quad +\left(1- {\lambda }_{1}- {\lambda }_{2}\right){REEWMA}_{W{SR}_{{RSS}_{i-1}}}.\end{aligned}$$

(15)

where $0 < \lambda_{1} < \lambda_{2} \le 1 \;{\text{and}} \;0 \le \lambda_{2} < \lambda_{1}$ and $W{SR}_{{RSS}_{i}}$ is already defined above.

The $(IC)$ mean and variance of the plotting statistic ${REEWMA}_{W{SR}_{{RSS}_{i}}}$ for the proposed $R{EEWMA}_{WRS}$ chart are defined as:

$E({REEWMA}_{W{SR}_{{RSS}_{i}}})=0$ and $Var({REEWMA}_{W{SR}_{{RSS}_{i}}})$ $=\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)$  $\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}$ $-2a{\lambda }_{1}{\lambda }_{2}$ $\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}$ $\left(\frac{r (r+1)(2r+1)}{24}\right)$ ${\delta }_{0}^{2}$, respectively.

Therefore, the control limits of the proposed $R{EEWMA}_{WSR}$ chart is written as:

$$\left.\begin{array}{c}{UCL}_{i}={\mu }_{0}+\text{ L }\sqrt{\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\left(\frac{r (r+1)(2r+1)}{6}\right){\delta }_{0}^{2}. }\\ CL= 0\\ {LCL}_{i}={\mu }_{0}-\text{L }\sqrt{\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}\right)\left\{\frac{1-{(1-{\lambda }_{1}-{\lambda }_{2})}^{2i}}{2\left({\lambda }_{1}-{\lambda }_{2}\right)-{\left({\lambda }_{1}-{\lambda }_{2}\right)}^{2}}\right\}-2a{\lambda }_{1}{\lambda }_{2}\left\{\frac{1- {(1-{\lambda }_{1}-{\lambda }_{2})}^{2i-2} }{2\left({\lambda }_{1}{-\lambda }_{2}\right)-{\left({\lambda }_{1}{-\lambda }_{2}\right)}^{2}}\right\}\left(\frac{r (r+1)(2r+1)}{6}\right){\delta }_{0}^{2} }.\end{array}\right\}$$

(16)

The upper, middle, and lower control limits to be calculated in Eq. (16) are represented as ${LCL}_{i}$, $CL$, and ${UCL}_{i}$ respectively. If the plotting statistic, as per Eq. (15), falls outside the bounds set by Eq. (16), the resulting chart signals an $(OOC$) condition. On the contrary, if the plotting statistic stays within the control limits, it is inferred that the process is in an $(IC$) state.

Performance evaluation

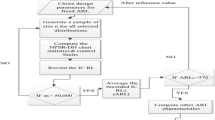
The total number of observations in the sample must be acquired before the chart alarm, known as $RL$, is determined, and the expected value of $RL$ is represented by $ARL$. The ($IC$) and ($OOC$) $RL$ are defined as ${ARL}_{0}$ and ${ARL}_{1}$, respectively. A chart is deemed effective if it exhibits a lower ${ARL}_{1}$ value during a specific shift. To gauge the efficiency of the suggested chart, various measures such as the standard deviation of $RL$($SDRL)$, ${P}_{5}, {P}_{25}, {P}_{50} (MDRL), {P}_{75}$ and ${P}_{95},$ are considered due to the skewed distribution of $RLs$. The properties of the suggested chart’s $RL$ are calculated using the Monte Carlo simulations method, and $R$ programming language codes are generated through 20,000 iterations. The algorithm for calculating the $RL$ profiles of the proposed chart $R{EEWMA}_{WSR}$ is outlined as follows:

We utilize NP scheme to generate $RL$, $\left(SDRL\right)$, and percentiles for different sample sizes $(n)$ and smoothing parameter values ${(\lambda }_{1}{,\lambda }_{2}) .$ The selection of $L$ and smoothing parameters ${(\lambda }_{1}{,\lambda }_{2})$ is done for a given ${ARL}_{0}$, and each group is plotted using the $R{EEWMA}_{WSR}$ statistic from the Eq. (15). The process is observed until reaching an ${ARL}_{1}$ point. The multiplier’s value for ${ARL}_{0}$ is set to achieve the desired $({ARL}_{0}\cong$ 200, 370, 500). The $RL$ profiles of the process are estimated by repeating these procedures 20,000 times.

In Table 1, we present $L$ values corresponding to different scenarios involving the choice of $n$ (5, 6, 7, and 8), various combinations of ${(\lambda }_{1}{,\lambda }_{2})$ (0.1, 0.03), (0.2, 0.07), (0.3, 0.15), and (0.5, 0.25), and different ${ARL}_{0}$ values (200, 370, and 500). It is observed that increasing the value of $n$ results in a decrease in the $L$ value, holding ${(\lambda }_{1}{,\lambda }_{2})$, and ${ARL}_{0}$ fixed. For instance, when $n=5,$ $L=2.43,$ and $n=10,$ $L= 2.073$ for ${(\lambda }_{1}, {\lambda }_{2})$ $\left(0.1, 0.03\right)$ and ${ARL}_{0}\cong 370$ (cf. Table 1). Conversely, an increasing trend is noticed in the $L$ value when changing ${(\lambda }_{1}{,\lambda }_{2})$ against a fixed value of $n$ and ${ARL}_{0}$. For example, with ${(\lambda }_{1}{,\lambda }_{2})$ $=\left(0.1, 0.03\right), L=2.43,$ and ${(\lambda }_{1}{,\lambda }_{2})$ $=\left(0.5, 0.25\right),$ $L= 2.764$ for $n=5$ and ${ARL}_{0}\cong 370)$ (cf. Table 1). Additionally, the $L$ value increases as the ${ARL}_{0}$ value rises, keeping $n$ and ${(\lambda }_{1}{,\lambda }_{2})$ constant. For instance, when ${ARL}_{0}\cong 200, L=1.892,\text{ and }{ARL}_{0}\cong 500, L=2.167\text{ for }n=10,\text{ and }{(\lambda }_{1}{,\lambda }_{2})=\left(0.1, 0.03\right)$ (refer to Table 1). The information provided in Table 1 is valuable for the practical implementation of the proposed scheme.

Table 1 Values of $L$ with different combination of $n$ and ${(\lambda }_{1}{,\lambda }_{2}$) for ${ARL}_{0}$ $\approx$ 200, 370 and 500.

Normal and non-normal environments

The performance of the proposed chart is assessed under normal and non-normal distributions. For the purpose of this investigation, the continuous symmetric distribution was used of the following components: (a) A bell-shaped, symmetrical Normal Distribution characterized by mean and variance, represented as N(0,1); (b) A platykurtic-shaped symmetrical Student’s t-distribution with (υ = 4) degrees of freedom and a heavy tail; (c) The double exponential (Laplace) distribution, denoted as DE (0, 1/$\sqrt{2}$); (d) Logistic Distribution, LOG(0,$\sqrt{3}$/π); and (e) The contaminated normal distribution (CN) is utilized to assess the performance in the presence of outliers.

For the sake of comparison, all the mentioned distributions have been standardized with a mean of zero and a standard deviation of one. These distributions have been employed to evaluate the proposed scheme’s resilience to changes in the underlying distribution. The density functions for these distributions are presented in Table 2.

Table 2 Density functions of the continuous distributions that are used.

IC robustness performance of the proposed and existing charts

Table 3 presents the $(IC RL)$ performance of the proposed $R{EEWMA}_{WSR}$ chart and the existing charts such as: ${EEWMA}_{WSR}$, EEWMA, ${EWMA}_{WSR}$, $R{EWMA}_{WSR}$, and EWMA charts. To assess the $(IC RL)$ robustness of both proposed and existing charts, four distinct sets of parameters ${(\lambda }_{1}{,\lambda }_{2})$: (0.1, 0.03), (0.2, 0.07), (0.3, 0.15), and (0.5, 0.25) are employed against a fixed ${ARL}_{0}$ value of 370. The first row in Table 3 displays the $(IC ARL)$ and $SDRL$ values, while the second row presents $(IC)$ values for ${P}_{5}, {P}_{25}, {P}_{50}, {P}_{75},$ and ${P}_{95}$, respectively. Table 3 illustrates that the proposed $R{EEWMA}_{WSR}$ chart exhibits $(IC)$ robustness across all considered distributions, precisely achieving the expected ${ARL}_{0}=370$. In comparison, the $R{EEWMA}_{WSR}$ chart demonstrates higher sensitivity than the $E{EWMA}_{WSR}, {EWMA}_{WSR},$ and $R{EWMA}_{WSR}$ charts (cf. Table 3). Consequently, the proposed chart stands out as a preferable option for practitioners due to its ability to approximate nominal ${ARL}_{0}$ values closely when compared to the ${EWMA}_{WSR}$ and $R{EWMA}_{WSR}$ charts.

Table 3 The $\text{IC RL}$ profiles of the proposed and existing charts for $n=10$ and ${ARL}_{0}$ $\approx$ 370.

The EEWMA and EWMA charts exhibit limited robustness in terms of $(IC)$, displaying increased variation in RL distribution. Their $(IC RL)$ properties show significant variation across different continuous distributions. For instance, considering ${ARL}_{0}$ as a reference measure of location for the EEWMA chart, its value is 369 for N(0,1), 312.12 for CN, 174.92 for t(4) distribution, 303.23 for Logistic, and 184.52 for Laplace, all against the parameter values ${(\lambda }_{1}{,\lambda }_{2},L$): (0.5, 0.25, 2.9895) (cf. Table 3). In contrast, for the EWMA chart, the ${ARL}_{0}$ values are 369.38, 195.56, 317.42, 265.32, and 327.23 for N(0,1), t(4), Logistic, Laplace, and CN, respectively, against ${(\lambda }_{1}L$): (0.5,2.9790) (cf. Table 3). Both the EEWMA and EWMA charts demonstrate suboptimal $(IC)$ performance, particularly in the case of t(4) (cf. Table 3). Furthermore, the ${ARL}_{0}$ values of EEWMA and EWMA charts underscore their inadequacy for non-normal distributions, potentially leading to an increased likelihood of false alarms.

OOC performance of the proposed $\mathrm{REEWMA}_\mathrm{WSR}$ chart

This section discusses the $(OOC)$ performance evaluation of the $R{EEWMA}_{WSR}$ charts proposed in this study. The $(OOC)$ performance assessment involves the exploration of various combinations of ${(\lambda }_{1}{,\lambda }_{2})$, $n$ and different shift values $(C)$. In this study, efficiency is measured based on the consideration that a chart with a smaller ${ARL}_{1}$ value is deemed effective for a given shift.

Effect of $({\lambda}_{1},{\lambda}_{2})$ and ${n}$ on ${ARL}_{1}$ performance

Table 4 presents the ${ARL}_{1}$ and ${SDRL}_{1}$ values for the proposed $R{EEWMA}_{WSR}$ chart across different parameter choices, specifically ${(\lambda }_{1}{,\lambda }_{2})$ = (0.1,0.03),(0.2,0.07), (0.3,0.15), and (0.5,0.25). Notably, the performance of the proposed chart exhibits superior ${ARL}_{1}$ and ${SDRL}_{1}$ metrics when smaller values of ${(\lambda }_{1}{,\lambda }_{2})$ are employed. For instance, with $n=5, C=0.2$, using ${(\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03),$ results in ${ARL}_{1}$ and ${SDRL}_{1}$ = 9.83, while with ${(\lambda }_{1}{,\lambda }_{2})$ = (0.3,0.15), the values are ${(ARL}_{1}=41.08$, ${SDRL}_{1}37.29$) (cf. Table 4). Furthermore, the analysis reveals that the proposed $R{EEWMA}_{WSR}$ chart demonstrates lower ${ARL}_{1}$ and ${SDRL}_{1}$ values for larger values of $n$, holding ${(\lambda }_{1}{,\lambda }_{2})$ constant. For example, with $C=0.3$, ${(\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$ when $n=5,$ the values are ${ARL}_{1}=7.57$,and ${SDRL}_{1}=4.48$ compared to $n=10$, where the values become ${ARL}_{1}=2.69$, ${SDRL}_{1}=1.29$) (cf. Table 4).

Table 4 The ${ARL}_{1} \text{and} {SDRL}_{1}$ values of the proposed $R{EEWMA}_{WSR}$ under different choices of ${(\lambda }_{1}{,\lambda }_{2}$) and $n$ with ${ARL}_{0}$ $\approx$ 370.

To gain a deeper understanding of the study, we constructed the ${ARL}_{1}$ curve for various combinations of ${(\lambda }_{1}{,\lambda }_{2})$, and $n$. From analysis of Fig. 1a–d reveals that increasing the values of ${(\lambda }_{1}{,\lambda }_{2})$ also increases the ${ARL}_{1}$ values, while keeping $n$ constant. Conversely, an increase in the value of $n$ results in a decrease in ${ARL}_{1}$ for a fixed value of ${(\lambda }_{1}{,\lambda }_{2})$ (cf. Fig. 2a–d).

Fig. 1

The ${ARL}_{1}$ values of the proposed against different choice of (${\lambda }_{1}{,\lambda }_{2})$ for (a) $n=5$, (b) $n=6$, (c) $n=8$ and (d) $n=10$ at ${ARL}_{0}\cong 370.$

Fig. 2

The ${ARL}_{1}$ values of the proposed against different choice of $n$ for (a) (${\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$, (b) (${\lambda }_{1}{,\lambda }_{2})=(0.2, 0.07)$, (c) (${\lambda }_{1}{,\lambda }_{2})=(0.3, 0.15)$, and (d) (${\lambda }_{1}{,\lambda }_{2})=(0.5, 0.25)$ at ${ARL}_{0}\cong 370.$

Distributional effect on ${ARL}_{1}$ performance

To evaluate the distributional effect on $(OOC)$ performance of the proposed ${EEWMA}_{WSR}$ , we calculate the ${ARL}_{1}$ and ${SDRL}_{1}$ values for each continuous distribution being examined. These values are computed across different selections of ${(\lambda }_{1}{,\lambda }_{2}$) and $n$, and the results are presented in Tables 5 and 6.

Table 5 The ${ARL}_{1} \text{and} {SDRL}_{1}$ values of the proposed $R{EEWMA}_{WSR}$ under different choices of ${(\lambda }_{1}{,\lambda }_{2}$) and $n=5$ for all distributions with ${ARL}_{0}$ $\approx$ 370.

Table 6 The ${ARL}_{1} \text{and} {SDRL}_{1}$ values of the proposed $R{EEWMA}_{WSR}$ under different choices of $n$ and ${(\lambda }_{1}{,\lambda }_{2})=(\text{0.1,0.03}$) for all distributions with ${ARL}_{0}$ $\approx$ 370.

The key findings are as follows:

• The ${ARL}_{1}$ and ${SDRL}_{1}$ values for the proposed $R{EEWMA}_{WSR}$ chart show an increase as the ${(\lambda }_{1}{,\lambda }_{2}$) values are increased while keeping $n$ constant across all distributions considered (refer to Table 5). For instance, when ${n=5 ,\text{ C}=0.25, (\lambda }_{1}{,\lambda }_{2})=\left(0.1, 0.03\right),$ the (${ARL}_{1}, {SDRL}_{1})$ values for normal distribution are (10.3, 6.37), for t(4) distribution are (7.39, 4.44), for logistic distribution are (8.99, 5.59), for Laplace distribution are (6.92, 4.11), and for CN distribution are (10.52, 6.76). On the other hand, for ${(\lambda }_{1}{,\lambda }_{2}$) = (0.5,0.25), the ${ARL}_{1}$, ${SDRL}_{1}$ values for normal distribution are (25.51, 21.50), t(4) distribution are (15.79, 12.24), logistic distribution are (20.83, 17.12), Laplace distribution are (13.76, 10.47), and CN distribution are (26.97, 22.85) (cf. Table 5).

• The ${ARL}_{1}$ and ${SDRL}_{1}$ metrics of the proposed $R{EEWMA}_{WSR}$ chart exhibit a decreasing trend as the value of $n$ increases, while maintaining a fixed value of ${(\lambda }_{1}{,\lambda }_{2}$) across all examined distributions (refer to Table 6). For instance, when ${\text{C}=0.3, (\lambda }_{1}{,\lambda }_{2})=\left(0.1, 0.03\right), n=5$ the ${(ARL}_{1}, {SDRL}_{1})$ values for normal distribution are (7.57, 4.48), for t(4) distribution are (5.62, 3.15), for logistic distribution are (6.81, 3.96), for Laplace distribution are (5.38, 3.06), and for CN distribution are (7.86, 4.71). However, for n = 10, the (${ARL}_{1}, {SDRL}_{1})$ values shift to (2.69, 1.29) for normal, (2.12, 0.96) for t(4), (2.46, 1.15) for logistic, (2.09, 0.96) for Laplace, and (2.79, 1.38) for CN, respectively (cf. Table 6).

• The $R{EEWMA}_{WSR}$ chart, as suggested, exhibits a faster shift detection capability when confronted with the Laplace distribution in comparison to other distributions, across various combinations of ${(\lambda }_{1}{,\lambda }_{2})$ and $n$ (cf. Tables 5 and 6).

Comparison between proposed and existing charts

Tables 7 display the ${ARL}_{1}$ value of proposed and existing charts including ${EEWMA}_{WSR}$, usual $EEWMA$, $R{EWMA}_{WSR}$, ${EWMA}_{WSR}$ and usual $EWMA$ charts, under various magnitudes of shifts. The shifts are examined across five distributions, Normal, t(4), Logistic, Laplace, and CN with results reported for both $(IC)$ and $(OOC)$ $ARL$ values have been computed for all process shifts and used for comparisons. Additionally, an alternative metric, expected ARL $(EARL)$, following the formulation provided below, has been employed for overall performance comparisons between proposed and existing charts (cf. Malela-Majika et al.⁴⁷).

Table 7 The ${ARL}_{1} \text{and} {SDRL}_{1}$ comparison between proposed and existing charts for ${(\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03$) and $n=10$ at ${ARL}_{0}$ $\approx$ 370.

$$EARL= \frac{1}{c} \sum_{i=1}^{c}{ARL}_{i}$$

$\mathrm{REEWMA}_\mathrm{WSR}$ versus $\mathrm{EEWMA}_\mathrm{WSR}$

The concept of ${\text{EEWMA}}_{\text{WSR}}$ was initially introduced by (cf. Talordphop et al.³⁹). Within the scope of this study, the proposed methodology demonstrates greater efficacy compared to the ${\text{EEWMA}}_{\text{WSR}}$ control chart across various continuous distributions. Specifically, the proposed ${\text{REEWMA}}_{\text{WSR}}$ charts trigger alarms at 14.59, 10.44, 12.82, 9.6, and 15.02 points, respectively. In contrast, the existing ${\text{EEWMA}}_{\text{WSR}}$ charts sound alarms at 57.74, 40.81, 50.33, 36.96, and 61.67 points, respectively, in the event of a 10% increase in the process location. These calculations are performed under the design parameters for the Normal Distribution, Student t distribution, Logistic distribution, Laplace distribution, and CN distribution, with $n$ = 10, ${(\lambda }_{1}{,\lambda }_{2}) =\left[\left(0.1, 0.03\right)\left(0.1, 0.03\right)\right],$ and ${ARL}_{0}=370,$. The $(EARL)$ values for the ${\text{REEWMA}}_{\text{WSR}}$ and ${\text{EEWMA}}_{\text{WSR}}$ under normal, logistic, t(4), Laplace, and CN distributions are (5.96, 19.41), (4.29, 14.82), (5.10, 17.48), (3.99, 13.72), and (5.92, 20.34), respectively (cf. Table 7). Hence, the proposed chart outperforms well against the ${\text{EEWMA}}_{\text{WSR}}$ chart.

${\mathrm{REEWMA}}_{\mathrm{WSR}}$ versus EEWMA

The concept of EEWMA was first introduced by (cf. Naveed et al.⁴⁰). The proposed chart, with parameters $n$=10, and ${(\lambda }_{1}{,\lambda }_{2}) =\left(0.1, 0.03\right),$ exhibits the ${ARL}_{1}$ values are 7.53, 10.44, 5.55, 6.66, and 5.20 for the normal, t(4), logistic, Laplace, and CN distributions, respectively. The $EEWMA$ chart, with these parameters, yields ${ARL}_{1}$ values of 26.21, 28.41, 26.54, 26.97, and 30.09 for the same distributions if we increase $C$= 1.5. It has been observed that the proposed methods outperform the traditional $EEWMA$ chart. The corresponding $(EARL)$ values of the proposed $R{EEWMA}_{WSR}$ chart for the normal, t(4), logistic, Laplace, and CN distributions are $EARL=$ 5.96, 4.29, 5.10, 3.99, and 5.92, while the $EEWMA$ chart of $EARL$ = 17.55, 18.90, 18.06, 18.25, and 19.60, for normal, t(4), logistic, Laplace, and CN distributions, respectively (cf. Table 7). So, the performance of the proposed $R{EEWMA}_{WSR}$ is relatively better than $EEWMA$ chart.

$\mathrm{REEWMA}_\mathrm{WSR}$ versus $\mathrm{REWMA}_\mathrm{WSR}$

The ${ARL}_{1}$ values for the proposed ${\text{REEWMA}}_{\text{WSR}}$ and ${\text{REWMA}}_{\text{WSR}}$ under various distributions normal, t(4), logistic, Laplace, and CN are (46.62, 52.23), (33.4, 36.11), (41.08, 45.7), (29.98, 32.66), and (48.78, 54.42), respectively, with design parameters set at $n=10,$ ${ARL}_{0}=370$, [${(\lambda }_{1}{,\lambda }_{2})$ = (0.1,0.03)] and $C=0.05$. The $(EARL)$ values for the ${\text{REEWMA}}_{\text{WSR}}$ and ${\text{REWMA}}_{\text{WSR}}$ under normal, t(4), logistic, Laplace, and CN distributions are (5.96, 6.03), (4.29, 4.42), (5.10, 5.38), (3.99, 4.11), and (5.92, 6.26), respectively. Minor differences in EARL values can be observed between the ${\text{REEWMA}}_{\text{WSR}}$ and ${\text{REWMA}}_{\text{WSR}}$ charts (cf. Table 7).

$\mathrm{REEWMA}_\mathrm{WSR}$ versus $\mathrm{EWMA}_\mathrm{WSR}$

The concept of ${\text{EWMA}}_{\text{WSR}}$ was initially introduced by (cf. Garaham et al.⁷). Within the study, the proposed methodology demonstrates greater efficacy compared to the ${\text{EWMA}}_{\text{WSR}}$ control chart across various continuous distributions. Specifically, the proposed ${\text{REEWMA}}_{\text{WSR}}$ charts trigger alarms at 14.59, 10.44, 12.82, 9.6, and 15.02 points, for normal, t(4), logistic, Laplace, and CN distributions, respectively. In contrast, the existing ${\text{EWMA}}_{\text{WSR}}$ charts sound alarms 65.24, 45.55, 56.56, 40.32 and 69.18 points, for normal, t(4), logistic, Laplace, and CN distributions, respectively, when $C=0.1$. The $(EARL)$ values for the ${\text{REEWMA}}_{\text{WSR}}$ and ${\text{EWMA}}_{\text{WSR}}$ under normal, t(4), logistic, Laplace, and CN distributions are (5.96, 20.81), (4.29, 15.85), (5.10, 18.26), (3.99, 14.35), and (5.92, 21.80), respectively (cf. Table 7). Therefore, the proposed ${\text{REEWMA}}_{\text{WSR}}$ chart shows better performance than ${\text{EWMA}}_{\text{WSR}}$ chart.

$\text{REEWMA}_\mathrm{WSR}$ versus EWMA

Roberts⁴ presented the classical (EWMA) chart as a method for monitoring the means of certain processes. Compared to the $EWMA$ chart, the proposed ${\text{REEWMA}}_{\text{WSR}}$ chart demonstrates superior performance. When $C$ = 0.1, the ${\text{REEWMA}}_{\text{WSR}}$ chart triggers alarms at 14.59, 10.44, 12.82, 9.6, and 15.02 points, for normal, t(4), logistic, Laplace, and CN distributions, respectively. In contrast, the existing $EWMA$ charts increase alarms at 57.92, 65.31, 62.50, 62.55, and 69.57 for normal, t(4), logistic, Laplace, and CN distributions, respectively. The corresponding $(EARL)$ values for the ${\text{REEWMA}}_{\text{WSR}}$ chart are $EARL$  = 5.96, 4.29, 5.10, 3.99, and 5.92, while the $EWMA$ chart produces values of $EARL$  = 19.11, 21.90, 20.48, 20.83, and 22.73 for normal, t(4), logistic, Laplace, and CN distributions, respectively (cf. Table 7). So, the proposed ${\text{REEWMA}}_{\text{WSR}}$ chart demonstrates far better performance against $EWMA$ chart.

To deepen our comprehension of the research, we have generated the ${ARL}_{1}$ based bar chart between proposed and existing charts. From Fig. 3, shows the $n$ = 10, ${(\lambda }_{1}{,\lambda }_{2})$  = [(0.1,0.03)] for (a) Normal (b) t(4) (c) Logistic, (d) Laplace, and (e) CN distributions at ${ARL}_{0}=370.$ It is noted that the proposed chart performs better against all distributions in comparison to the existing charts such as ${EEWMA}_{WSR}$, usual $EEWMA$, $R{EWMA}_{WSR}$, ${EWMA}_{WSR}$ and usual $EWMA$ (cf. Fig. 3). Moreover, the proposed ${\text{REEWMA}}_{\text{WSR}}$ indicates better performance in case of t(4) distribution as compared to other distributions considered in this study (cf. Fig. 3).

Fig. 3

The ${ARL}_{1}$ comparison between proposed and existing charts against (${\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$ and $n=10$ for Normal, t(4), Logistic, Laplace, and Contaminated normal Distribution at ${ARL}_{0}\cong 370.$

Real-life application

An automobile sector case study demonstrates how well the charts suggested in this research can identify shifts in process monitoring. Automotive construction relies heavily on piston rings, especially when it comes to keeping the engine’s pressure stable. These three rings, which are housed in the piston’s outer diameter, have different functions. With an average size of 74 mm + 0.05 for automotive engines, accuracy in measuring the outside and inside diameters of the piston and piston ring is essential to the engine’s efficient operation. The practical implementations of the proposed methodologies highlight the significance of the inside diameter of piston rings as a significant variable, based on data from (cf. Montgomery 1). This data collection consists of the first 25 $(IC)$ and the remaining 15 $(OOC)$ sample observations, each with a size of 5. The first 20 sample observations are collected in a retrospective analysis stage to see if the process is statistically $(IC)$. These $(IC)$ samples are utilized to estimate unknown parameters and track the piston ring’s internal diameter. The monitoring stage illustrates the recommended techniques with the 15 $(OOC)$ samples given below. Based on the WSR Test, a Non-Parametric Exponentially Weighted Moving Average (${\text{REEWMA}}_{\text{WSR}}$) chart is used for the suggested schemes, Along with the design criteria for these charts include $L=2.43$, ${(\lambda }_{1}{,\lambda }_{2})$ for the ${\text{REEWMA}}_{\text{WSR}}$ chart, $L=2.7151$ for EEWMA, $L=2.69$ for ${\text{REWMA}}_{\text{WSR}}$, $L=2.073$ for ${\text{EWMA}}_{\text{WSR}}$ & $L=2.6950,$ EWMA at ${ARL}_{0}=370$, we used $n=5$. The monitoring statistics and associated control limits, based on the mentioned constants, are plotted in Figs. 4, 5, 6 and 7. According to the output of all the charts, the suggested chart shows the initial $(OOC)$ signal following the 32^st point, in accordance with the ${\text{REEWMA}}_{\text{WSR}}$ chart. Compared to the EEWMA, ${\text{REWMA}}_{\text{WSR}}$, ${\text{EWMA}}_{\text{WSR}}$ and EWMA control charts, which show the $(OOC)$ signal after the 37^th point, this is more consistent. These findings demonstrate that, in comparison to alternative methods, the recommended charts are more successful in quickly spotting $(OOC)$ signals.

Fig. 4

A real-life application of the proposed $R{EEWMA}_{WSR}$ chart for (${\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$, $L=2.43$, and $n=5$ at ${ARL}_{0}\cong 370$.

Fig. 5

A real-life application of the proposed ${EEWMA}_{WSR}$ chart for (${\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$, $L=2.66$, and $n=5$ at ${ARL}_{0}\cong 370$.

Fig. 6

A real-life application of the EEWMA chart for (${\lambda }_{1}{,\lambda }_{2})=(0.1, 0.03)$, $L=2.7150$, and $n=5$ at ${ARL}_{0}\cong 370.$

Fig. 7

A real-life application of the EWMA chart for ${\lambda }_{1}=0.1$, $L=2.6950$, and $n=5$ at ${ARL}_{0}\cong 370.$

Conclusions and recommendations

In order to identify anomalous variations in process parameters, control charts are crucial statistical process control (SPC) instruments. Although the normalcy assumptions of the process are the foundation upon which these charts are often built, there are times when these assumptions are not met or the process distribution is unidentified. Nonparametric control charts are useful in these situations because they are distribution-free and show consistent in-control run length $(IC RL)$ characteristics over a range of continuous distributions. In this study, a new NP monitoring method namely, ${\text{REEWMA}}_{\text{WSR}}$, is proposed based on the WSR statistic. The IC and OOC performance of the proposed ${\text{REEWMA}}_{\text{WSR}}$ chart is evaluated under normal and non-normal situations. The OOC performance comparisons of the proposed ${\text{REEWMA}}_{\text{WSR}}$ is done with various existing charts such as: ${EEWMA}_{WSR}$, usual $EEWMA$, $R{EWMA}_{WSR}$, ${EWMA}_{WSR}$ and usual $EWM$. The proposed ${\text{REEWMA}}_{\text{WSR}}$ chart shows its superiority over competitor’s charts. The proposed chart is also triggered quick OOC signal as compared to the existing charts considered in this study based on data set related to the substrate production process. It concludes that the proposed method has performed better than other methods. Moreover, the proposed ${\text{REEWMA}}_{\text{WSR}}$ chart performs significantly better in case of Laplace distribution and it is less efficient in case of contaminated normal process is. This study can be enhanced by using joint monitoring and multivariate methods in NP scenario. Future enhancements to this study could involve the incorporation of joint monitoring and multivariate methods in NP scenarios.