Quantum computation for robot posture optimization

Abstract

Quantum computing has gained attention for its potential to surpass classical computing in large-scale computations. In this study, we propose a method for solving the inverse kinematics of a robot using quantum computing. The approach leverages the ability of qubits to represent points on a sphere in three-dimensional space. Forward kinematics calculations are performed using qubits that encode the posture of each robot link, while inverse kinematics solutions are obtained through iterative optimization on a classical computer. Furthermore, we demonstrate that the robot’s end-effector position can be effectively represented using a 2-qubit rotation gate, where the root joint angle influences the tip joint angle, resulting in accelerated convergence during inverse kinematics optimization. The proposed method was validated on an actual quantum computer, confirming its feasibility and efficiency. These findings suggest that hybrid quantum-classical approaches can enhance robotic motion planning and optimization in future quantum computing applications.

Introduction

In recent years, quantum computing has made significant strides, with the potential to outperform classical computers in large-scale computation tasks. Quantum research has primarily focused on two key areas: improving the performance of quantum hardware and developing algorithms that can solve specific computational problems upon the realization of scalable quantum computers. While much of the attention has been on fundamental areas like quantum algorithms, there is growing interest in applying quantum computing to real-world applications across various domains.

In parallel, robotics has also witnessed remarkable advancements, with robots increasingly playing a central role in various sectors. Robotics poses a wide range of computational challenges, such as joint control, inverse kinematics calculations, and trajectory planning. In particular, inverse kinematics, the central focus of this study, can be solved using various methods in both robotics and computer graphics¹. However, a robot is a highly complex system where the movements of multiple joints are interdependent. As the number of joints increases, the computational time required for solving these problems also increases significantly. This challenge is especially pronounced in redundant manipulators, where multiple joint configurations yield identical end-effector positions. In such cases, a single analytical solution is generally not possible. The ability to quickly determine a valid joint angle combination from many possibilities is critical for enabling flexible and responsive robotic motion, which requires high-speed computation. Given the growing potential of quantum computing, we argue that it is essential to explore its application in robotics calculations. Quantum computing holds the promise of significantly accelerating computations, potentially enabling faster and more efficient solutions to inverse kinematics and other robotics challenges, especially when quantum computers become widely available in the future.

Inverse kinematics, the calculation of joint angles required to achieve a robot’s target end-effector position, poses a significant challenge in robotics, especially for a general 6-degree-of-freedom (DOF) robot, as an analytical solution is not feasible. In practical applications, robots are often designed with 6 DOF (3 for posture control and 3 for position control) to ensure the existence of an analytical solution². However, such robots face difficulties in obstacle avoidance and workability, prompting some designs to incorporate additional redundant DOFs. Despite this, inverse kinematics for these robots remains analytically unsolvable. To address this, numerical methods, such as linear programming³, gradient descent⁴, conjugate gradient methods⁵, and other optimization techniques⁶, are commonly employed to find solutions. Notably, Yang et al. proposed an efficient solver for obtaining inverse kinematics solutions of complex manipulators under certain constraints⁷.

In recent years, quantum computing has attracted growing interest in diverse domains, including molecular simulation, chemical modeling, and financial optimization^8,9,10,11. Alexeev et al. explored the opportunities, challenges, and community needs driving the development of quantum computing for scientific applications⁸. Teo et al. reviewed GaN-based devices for potential applications in power electronics, RF electronics, and quantum computing⁹. Egger et al. provided a comprehensive survey on quantum computing’s potential for computationally difficult finance problems¹⁰, while Sato et al. proposed Hamiltonian simulation for hyperbolic partial differential equations¹¹.

In robotics, quantum computing has been explored for accelerating computational tasks, particularly through methods like Quantum Approximate Optimization Algorithm (QAOA) and quantum annealing, aimed at solving combinatorial optimization problems more efficiently. Schuetz et al. presented versatile random-key algorithms enhanced with model stacking and ensemble techniques, as well as path relinking for solution refinement¹². Otani et al. demonstrated that quantum annealing can be applied to robot end-effector trajectory calculation, significantly improving computational speed¹³. Furthermore, Luo et al. proposed an improved quantum particle swarm optimization algorithm, applied to robot trajectory planning¹⁴. Despite these advancements, practical research on the application of quantum computers in fields beyond combinatorial optimization remains limited¹⁵. Fazilat et al. proposed a quantum-based kinematic model for determining the position and orientation of a six-jointed robotic arm¹⁶. Moreover, Fazilat et al., presented a quantum-inspired sliding-mode control method of an articulated industrial robotic arm¹⁷. Dahassa et al., proposed a novel motion planning method using optimal control-based Grover’s algorithm¹⁸. Cao et al. presented an improved quantum particle swarm optimization (IQPSO) algorithm to solve inverse kinematics problems¹⁹. Chen et al., proposed trajectory optimization for obstacle avoidance using multi-group ant colony and quantum-behaved particle swarm optimization algorithms²⁰. Zhang et al., proposed an IQPSO algorithm for searching the global optimal solution compared with the QPSO and PSO algorithms²¹. Numbi et al., also proposed Proportional-Derivative control using a QPSO for trajectory tracking of a mobile robot²² and a quantum teleportation for remote control of a car-like mobile robot²³. Fazilat et al., explore the application of quantum-inspired neural networks to address the inverse kinematics problem of robotic arms²⁴.

In this study, we propose a novel approach to solving the inverse kinematics problem using quantum computing. The key insight is that qubits, the fundamental units of quantum computing, can represent points on a sphere in three-dimensional space, which aligns naturally with the requirements of kinematic calculations. Using quantum computing, forward kinematics calculations are performed by encoding the posture of each robot link as qubits, while the inverse kinematics solution is obtained using classical optimization algorithms. This hybrid approach leverages the strengths of both quantum and classical computing to solve the inverse kinematics problem more efficiently. Additionally, we demonstrate that the position of the robot’s end-effector can be represented using a 2-qubit rotation gate, where the root joint angle influences the angle of the joint connected to the end effector, leading to faster convergence in the iterative process. To further validate the method, we implemented and verified the approach on an actual quantum computer, demonstrating the feasibility and effectiveness of quantum-based solutions in robotics.

Methods

Qubit operation and Bloch sphere representation

A quantum bit, or qubit, is the fundamental unit of information in quantum computing. Unlike a classical bit, which can represent only one of two discrete values (0 or 1), the state of a qubit can exist in an infinite number of possible values. This is because a qubit’s state is a linear combination of the two basis states, denoted by $|\left. 0 \right\rangle$ and $|\left. 1 \right\rangle$ as expressed in Eq. (1)²⁵.

$$|\left. q \right\rangle =a|\left. 0 \right\rangle +b|\left. {\text{1}} \right\rangle$$

(1)

Where α and β are the probability amplitudes of the qubit state. The eigenstates $|\left. 0 \right\rangle$ and $|\left. 1 \right\rangle$ can also be expressed in two-dimensional vector space in Eqs. (2) and (3)²⁶.

$$a\,=\,R{e_{|\left. 0 \right\rangle }}+iI{m_{|\left. 0 \right\rangle }}$$

(2)

$$b\,=\,R{e_{|\left. {\text{1}} \right\rangle }}+iI{m_{|\left. {\text{1}} \right\rangle }}$$

(3)

Where $Re_{{|\left. 0 \right\rangle }}$ and $Im_{{|\left. 0 \right\rangle }}$ are the real and imaginary components of α, $Re_{{|\left. {\text{1}} \right\rangle }}$ and $Im_{{|\left. {\text{1}} \right\rangle }}$ are the real and imaginary components of β, and i is an imaginary number, such that i² = − 1.

Several quantum operators are capable of manipulating a qubit’s state. These quantum operators, often referred to as gates, can be represented using four fundamental Hermitian matrices, known as the Pauli matrices. The Pauli matrices are defined in Eq. (4) through (7) and serve as the building blocks for many quantum operations.

$${\sigma _0}=\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)$$

(4)

$${\sigma _x}=\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right)$$

(5)

$${\sigma _y}=\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)$$

(6)

$${\sigma _z}=\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)$$

(7)

A single qubit state is represented in the 3D space using the Bloch sphere^27,28 (Fig. 1). Rotations by angles λ, θ, $\:\varphi\:$ and around the x, y, and z axis, are performed using the transformation matrix defined in Eqs. (8) through (10), also expressed using the Pauli matrices.

$$RX\left( \lambda \right)=cos\frac{\lambda }{2}{\sigma _0} - isin\frac{\lambda }{2}{\sigma _x}$$

(8)

$$RY\left( \theta \right)=cos\frac{\theta }{2}{\sigma _0} - isin\frac{\theta }{2}{\sigma _y}$$

(9)

$$RZ\left( \varphi \right)=cos\frac{\varphi }{2}{\sigma _0} - isin\frac{\varphi }{2}{\sigma _z}$$

(10)

Fig. 1

Bloch sphere representation (image adapted from²⁶).

Forward kinematics calculations with quantum circuits

We propose a method for performing forward kinematics calculations using the Bloch sphere representation of qubits. The Bloch sphere allows qubits to represent points in three-dimensional space, and by utilizing this property, we can represent the posture of each link in a robot, which typically consists of multiple links, using qubits. As discussed in previous works^15,16, this approach leverages the inherent geometric properties of quantum states to map robotic movements into a quantum framework, enabling new possibilities for efficient calculations in robotic control systems. This enables the representation of the positions of the tips of each link as seen from the root of the robotic structure. By summing the coordinate representations of the qubits corresponding to each link, we can effectively perform a forward kinematics calculation. The corresponding equations for the forward kinematics of a simple manipulator with two links are given in Eqs. (11) and (12).

$$x\,=\,{L_{\text{1}}}{\text{cos}}{\theta_{\text{1}}}\,+\,{L_{\text{2}}}{\text{cos}}({\theta_{\text{1}}}\,+\,{\theta_{\text{2}}})$$

(11)

$$y\,=\,{L_{\text{1}}}{\text{sin}}{\theta_{\text{1}}}\,+\,{L_{\text{2}}}{\text{sin}}({\theta_{\text{1}}}\,+\,{\theta_{\text{2}}})$$

(12)

where L1 is the length of the link 1, L2 is the length of the link 2, θ1 is the joint angle of the joint 1 in the horizontal plane and θ2 is the joint angle of the joint 2 from the link 1 in the horizontal plane.

We designed a quantum circuit to perform forward kinematics calculations by assigning a qubit to each link of a two-link manipulator. Specifically, qubits q0 and q1 represent the posture of link 1 and link 2, respectively. To match the orientation vector of the robot’s links in 3D space with the corresponding vector in the Bloch sphere representation, we applied rotation gates to the qubits. These gates perform rotations in the Roll (X), Pitch (Y), and Yaw (Z) directions within the 3D space, thereby rotating the qubit vectors. In cases where a joint can rotate in multiple directions, the rotation gates in each direction are applied sequentially, as outlined in Eq. (13). Quantum rotations are typically executed as unitary operations on quantum states, with the sandwich product being used when calculating the expectation value or the measured value of the system. This method ensures that the quantum representation of the manipulator’s posture in 3D space remains consistent with the physical behavior of the robot.

$${q_{0 - rotated}}=RX({\lambda_0}) * RY({\theta_0}) * {q_0}$$

(13)

For a serial link manipulator, the absolute position of the tip of a given link is determined by the rotation of all preceding joints. Therefore, the state of the qubit representing the second link must account for the rotation of the first link. Accordingly, the qubit representing the tip position of the second and subsequent links in absolute space, as observed from the root, corresponds to the cumulative effect of all rotation gates involved. This includes the rotation gate of the root link, and the overall transformation is represented by the product of these rotation gates, applied in sequence as detailed in Eq. (14). The sequence of operations, including the quantum rotation gates, reflects the coupled nature of quantum states that represent each link’s posture in the manipulator, which is integral to solving forward kinematics using quantum computing methods.

$${q_{{\text{1}} - rotated}}=RX({\lambda_0}) * RY({\theta_0}) * RY({\theta_{\text{1}}}) * {q_{\text{1}}}$$

(14)

If the posture of a link is represented by a qubit, the expected value of the qubit’s state, when measured with respect to the X, Y, and Z rotation gates, corresponds to coordinates on the Bloch sphere. Given that the radius of the Bloch sphere is unity in this representation, the link distance in absolute space is calculated on a classical computer by multiplying the expected value derived from the qubit by the link length associated with that qubit. As outlined earlier, each link’s posture is encoded by a qubit, and on a conventional computer, the expected values for each qubit are multiplied by their respective link lengths and summed to compute the end-effector position of the manipulator (Fig. 2). In this study, the quantum circuits were implemented using Qiskit, a widely used library for quantum circuit computation²⁹.

Fig. 2

Quantum Circuit for representing 2-link manipulator.

Inverse kinematics calculations with a quantum optimization algorithm (QOA)

For solving inverse kinematics, the conventional inverse matrix method is applicable only when the robot has a small number of degrees of freedom and a unique inverse kinematics solution exists. In contrast, the pseudo-inverse matrix method, which employs optimization techniques, is used to identify the inverse kinematics solution that best satisfies additional constraints in the case of multiple solutions, typically for robots with a higher number of degrees of freedom. This research was inspired by the capability to perform forward kinematics calculations using quantum circuits, and it is hypothesized that faster inverse kinematics calculations for robots could reduce the computational time required for numerous inverse kinematics evaluations during the generation of complex robotic movements.

We propose a method for inverse kinematics computation leveraging forward kinematics quantum circuits and a quantum optimization algorithm. In the field of quantum algorithms, various methods such as Variational Quantum Eigensolver (VQE) and Quantum Approximate Optimization Algorithm (QAOA) have been explored for practical quantum computing applications. These methods typically partition the computational tasks between quantum circuits for solving the quantum mechanical components and classical algorithms for evaluating the results, due to the current limitations of quantum circuits, which are not yet capable of performing long calculations on their own.

In the method proposed in this paper, the inverse kinematics calculation is performed by combining forward kinematics calculations using quantum circuits with convergence determination via classical optimization. First, the quantum circuit is employed to compute the forward kinematics of a robot for a given set of joint angles. Second, the difference between the target end-effector position, calculated classically, and the position obtained from the quantum circuit is evaluated. Third, the joint angles that minimize this difference are computed, and the quantum computation is repeated iteratively until the difference becomes less than a specified threshold. While there are various optimization methods available, this study utilizes COBYLA (Constrained Optimization BY Linear Approximation) as the optimization solver for the quantum optimization algorithm, primarily because it integrates seamlessly with Qiskit. Since the optimization step is carried out classically, additional terms such as energy minimization³⁰ and obstacle avoidance³¹ can be incorporated into the objective function.

Entangled quantum circuit with RXX, RYY, RZZ gates

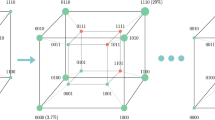
For more practical applications, it would be desirable to solve the problem even when the robot has a larger number of degrees of freedom. However, as previously mentioned, inverse kinematics calculations for robotic arms with more than three degrees of freedom cannot be solved geometrically due to the existence of multiple solutions. Therefore, the optimization approach utilizing quantum circuits proposed in this study may offer a promising solution. In the case of a robotic arm with three degrees of freedom per joint and two joints, resulting in a total of six degrees of freedom, a quantum circuit can be constructed as described in Eqs. (15) and (16) (Fig. 3).

$${q_{0 - rotated}}=RX({\lambda_0}) * RY({\theta_0}) * RZ(\varphi ) * {q_0}$$

(15)

$${q_{{\text{1-}}rotated}}=RX({\lambda_0}) * RY({\theta_0}) * RZ(\varphi_{\text{0}}) * RX({\lambda_{\text{1}}}) * RY({\theta_{\text{1}}}) * RZ(\varphi_{\text{1}}) * {q_{\text{1}}}$$

(16)

Fig. 3

Quantum circuit for representing 2-link 6-DOF manipulator.

However, to fully exploit the potential of quantum computing, entanglement is crucial, as calculations with two independent qubits cannot fully leverage the advantages of quantum computation. In previous approaches, rotation gates that represent the rotation of each link in different directions were applied independently to each qubit. However, in our approach, we utilize the RXX, RYY, and RZZ gates, which apply the same rotation gate to two qubits simultaneously (Fig. 4). For instance, the RXX gate is defined as in Eq. (17).

$$RXX\left( \lambda \right)={\text{exp}}\left( { - i\frac{\lambda }{2}{\sigma _x} \otimes {\sigma _x}} \right)$$

(17)

where ${\sigma _x}$ is the Pauli-X operator, and λ is the rotation angle. The RXX gate acts on two qubits simultaneously, applying the Pauli-X operator to both qubits. This operation introduces a correlation between the two qubits. The Eq. (17) can be transformed to Eq. (18).

$$RXX\left( \lambda \right)=\cos \frac{\lambda }{2}{\sigma _0} \otimes {\sigma _0} - i\sin \frac{\lambda }{2}{\sigma _x} \otimes {\sigma _x}$$

(18)

Entanglement arises between the two qubits due to their inability to behave independently of each other. Specifically, the qubit representing the first link becomes entangled with the qubit representing the second link. This entanglement facilitates a natural representation of a scenario where the rotation of the parent link influences the child link, which in turn reduces the overall computation time. The RX, RY, RZ, RXX, RYY, and RZZ gates, parameterized by angles $\lambda$, $\theta$, $\varphi$, and acting around the x, y, and z axes, are described by equations (19) through (24). While a single-qubit arbitrary rotation gate can be represented as a 2 × 2 unitary matrix, a two-qubit arbitrary rotation gate is generally represented by a 4 × 4 unitary matrix. This enables the manipulation of two qubits in arbitrary ways, allowing for the generation of complex entanglements and interactions.

$$RX\left( \lambda \right)=\left( {\begin{array}{*{20}{c}} {\cos \frac{\lambda }{2}}&{ - i\sin \frac{\lambda }{2}} \\ { - i\sin \frac{\lambda }{2}}&{\cos \frac{\lambda }{2}} \end{array}} \right)$$

(19)

$$RY\left( \theta \right)=\left( {\begin{array}{*{20}{c}} {\cos \frac{\theta }{2}}&{ - \sin \frac{\theta }{2}} \\ {\sin \frac{\theta }{2}}&{\cos \frac{\theta }{2}} \end{array}} \right)$$

(20)

$$RZ\left( \varphi \right)=\left( {\begin{array}{*{20}{c}} {{e^{ - i\frac{\varphi }{2}}}}&0 \\ 0&{{e^{i\frac{\varphi }{2}}}} \end{array}} \right)$$

(21)

$$RXX\left( \lambda \right)=\left( {\begin{array}{*{20}{c}} {\cos \frac{\lambda }{2}}&0&0&{ - i\sin \frac{\lambda }{2}} \\ 0&{\cos \frac{\lambda }{2}}&{ - i\sin \frac{\lambda }{2}}&0 \\ 0&{ - i\sin \frac{\lambda }{2}}&{\cos \frac{\lambda }{2}}&0 \\ { - i\sin \frac{\lambda }{2}}&0&0&{\cos \frac{\lambda }{2}} \end{array}} \right)$$

(22)

$$RYY\left( \theta \right)=\left( {\begin{array}{*{20}{c}} {\cos \frac{\theta }{2}}&0&0&{i\sin \frac{\theta }{2}} \\ 0&{\cos \frac{\theta }{2}}&{ - i\sin \frac{\theta }{2}}&0 \\ 0&{ - i\sin \frac{\theta }{2}}&{\cos \frac{\theta }{2}}&0 \\ {i\sin \frac{\theta }{2}}&0&0&{\cos \frac{\theta }{2}} \end{array}} \right)$$

(23)

$$RZZ\left( \varphi \right)=\left( {\begin{array}{*{20}{c}} {{e^{ - i\frac{\varphi }{2}}}}&0&0&0 \\ 0&{{e^{i\frac{\varphi }{2}}}}&0&0 \\ 0&0&{{e^{ - i\frac{\varphi }{2}}}}&0 \\ 0&0&0&{{e^{i\frac{\varphi }{2}}}} \end{array}} \right)$$

(24)

Fig. 4

Quantum Circuit for representing 2-link 6-DOF manipulator with RXX, RYY, and RZZ gates.

Mathematically, if the state of a two-qubit system cannot be represented as a single tensor product of the individual qubit states, it is considered to be in an entangled state. As shown in Eq. (18), the RXX gate transforms the system into a state that is a superposition of tensor products, which is an entangled state. The degree of entanglement, quantified by the concurrence³², varies depending on the angle λ³³. Notably, when λ equals π/2, the system is in a Bell state, which represents the maximum entangled state. In Qiskit, the implementation of a two-qubit rotational gate is achieved through a decomposition into a series of Hadamard, CNOT, and RZ gates. This decomposition is advantageous because it allows for efficient execution on quantum hardware that natively supports these fundamental gates. The corresponding unitary transformation can be realized through the following gate sequence:

• 1. Apply Hadamard gates to both qubits.

• 2. Apply a CNOT gate with the first qubit as the control and the second as the target.

• 3. Apply an RZ​ gate to the target qubit.

• 4. Apply another CNOT gate.

• 5. Apply Hadamard gates to both qubits again.

Results

2-joint 6-DOF arm simulation

For a multi-degree-of-freedom (DOF) robotic arm that has multiple inverse kinematics solutions and requires optimization, we examined the convergence behavior of the proposed quantum circuit both with and without quantum entanglement. These results were then compared to those obtained using conventional optimization techniques. A two-link robot model was used in our simulations, where the root of Link 1, Joint 1, has three rotational degrees of freedom (DOF) in the X, Y, and Z directions, and the root of Link 2, Joint 2, similarly has three rotational DOFs (Fig. 5). Table 1 shows D-H parameters of the robot model. In this setup, we focused solely on the positional inverse kinematics of the robot’s three primary joints, as the orientation of the end effector was controlled via an additional joint with three DOFs, akin to a wrist joint. Two variants of the quantum circuit—one with entanglement and one without—were designed for a 6-DOF robotic arm, with 3 DOFs in each of the two joints. The target end position was specified, and inverse kinematics calculations were performed iteratively through optimization techniques.

The simulations were conducted using both a local PC environment and a Fujitsu quantum simulator. On the local machine, the calculations were implemented using Qiskit within a Jupyter Notebook environment on a Windows 11 PC, which runs a Linux-based setup through WSL2. As a quantum simulator, a hybrid quantum computing platform integrating a 40-qubit quantum simulator was used to enable optimized quantum computations. The mpiQulacs³⁴, running within the Fujitsu simulator, is a quantum simulator.

Table 1 Robot model D-H parameters.

Fig. 5

Schematic view of a 6-DoF arm robot.

based on Qulacs that facilitates multi-process, multi-node parallel processing, enabling the execution of large-scale quantum circuits at high speed. The qiskit-qulacs package allows users to leverage mpiQulacs as a backend for Qiskit. Users can write quantum programs via the API provided by the Qiskit SDK, with mpiQulacs executing the quantum circuits. The parameters for the COBYLA solver used in the optimization calculations are summarized in Table 2. Additionally, in order to assess the differences from general optimization calculations, simulations were performed in the same computing environment, where conventional forward kinematics calculations using homogeneous transformation matrices were carried out in place of quantum circuit-based forward kinematics, and the optimization process was also executed using COBYLA.

Table 2 Optimization condition.

In Fig. 6, the horizontal axis represents the number of iterations performed during the calculation, while the vertical axis shows the difference between the target and the calculated end-effector positions of the robot at each iteration. Table 3 summarizes the results of the computation. By comparing the simulation outcomes with and without entanglement, it is observed that the error remains at 0.5 m after 30 iterations when no entanglement is used, whereas the error significantly decreases after only 8 iterations when entanglement is utilized. Furthermore, comparing the conventional method with the entangled approach, it is evident that the entanglement-based method converges with fewer iterations, leading to a more accurate solution. In addition, comparing the results from the Local environment and the quantum simulator, there is no significant difference in the number of iterations required to converge, but the quantum simulator converges more accurately.

Fig. 6

Comparison with sum of squared errors of end effector position with 6-DOF arm.

Experiment with a real quantum machine

The same verification as in the previous simulation was performed using an actual quantum computer. We used a 64-qubit superconducting quantum computer developed by RIKEN RQC-Fujitsu Collaboration Center. This system operates at an ultra-low temperature (around 20 millikelvin) and utilizes microwave signals in the 8 GHz range to control qubits.

The experimental results are shown in Fig. 7 and summarized in Table 4. As in the simulation results, the quantum circuit with entanglement has a reduced error compared to the case without entanglement.

Table 3 Comparison with sum of squared errors of end effector position with 6-DOF arm.

Fig. 7

Comparison with sum of squared errors of end effector position with 6-DOF arm.

Table 4 Comparison with sum of squared errors of end effector position with real machine calculation.

Discussion

In the simulation and experiment, we demonstrated that both forward and inverse kinematics calculations can be performed using entangled qubits to represent the posture of each link in a robot manipulator with multiple joints. From the simulation results shown in Table 3, it is evident that the quantum circuit with entanglement (RXX, RYY, RZZ) achieves significantly better accuracy than the circuit without entanglement. After 30 iterations, the total Euclidean error in the X-Y-Z coordinates was approximately 1.85 m without entanglement and 1.18 m with entanglement, representing a 36% reduction in overall positional error. This indicates that entanglement enables a more coherent representation of the linkage dependency, leading to improved convergence in inverse kinematics optimization. Interestingly, the simulator-based quantum circuit with entanglement achieved nearly the same level of accuracy in just 10 iterations (total error: 1.17 m) as in 30 iterations (1.21 m). This suggests that entanglement contributes most strongly to the early phase of optimization, pointing to a potential for reduced computational load in time-sensitive robotic applications. However, the slight increase in total error at 30 iterations may reflect the presence of local minimal or overfitting behavior within the classical optimizer.

Comparing the results from the local environment and the quantum simulator (Table 3), both configurations with entanglement achieved convergence within 30 iterations. The quantum simulator demonstrated more balanced error across all axes, with X: 0.56 m, Y: 1.06 m, and Z: 0.16 m. This suggests that the quantum simulator may offer more stable convergence across a broader workspace, even if local accuracy in some axes appears slightly lower. On the other hand, in the real quantum hardware experiment (Table 4), the circuit with entanglement again outperformed the non-entangled variant. After 30 iterations, the total error was reduced from approximately 1.84 m to 1.04 m, corresponding to a ~ 43% improvement. Despite the presence of noise, the quantum hardware demonstrated the feasibility of this entanglement-based inverse kinematics optimization.

However, one limitation of this approach is that this method cannot be applied to robots that operate only with prismatic (linear) joints (i.e., Cartesian robots), because its formulation is based on representing rotational joints with quantum circuits. Another limitation is that, although the proposed method utilizes entanglement, it captures only unidirectional dependency from parent to child links and does not fully exploit bidirectional entanglement interactions. It does not fully exploit quantum computational techniques involving entanglement, which have been explored in other quantum computing approaches. Therefore, incorporating techniques such as the quantum Fourier transform³⁵, where rotational angle information is encoded in qubits as phase information and represented by multiple qubits, is considered a promising direction for further enhancement.

This study confirms the validity of the proposed method not only through theoretical analysis and simulation but also through experimental verification on actual quantum computers. It was observed that the accuracy of the proposed method on real quantum computers is lower than in the simulation due to noise-related issues, which is a known challenge in practical quantum computation. Ongoing research is focusing on improving the noise tolerance of quantum devices, and significant advancements are expected in the future. Since the proposed method requires only one qubit per link, it is feasible to verify its effectiveness with current NISQ (Noisy Intermediate-Scale Quantum) devices. Additionally, the proposed method has the potential to speed up computations by parallelizing tasks, which could contribute to the development of practical quantum computing applications in robotics.

Conclusions

In this study, we presented a novel approach to inverse kinematics calculation using quantum circuits for forward kinematics. Our work contributes to the field of quantum and robotics in two significant ways. First, we showed that by entangling two qubits, the computation converges more quickly and accurately compared to non-entangled qubits. This entanglement represents how a change in the parent link’s posture influences the child links. Notably, our method allows for the representation of robot postures using a minimal number of qubits; for example, a manipulator with three links requires three qubits, while a humanoid robot with 16 links can be modeled with 16 qubits. Considering the present-day hardware constraints—typically fewer than 100 usable qubits—our method remains well within feasible implementation range. Second, we validated our results on an actual quantum computer, providing valuable insights into the practical application of quantum computing in robotics. By leveraging quantum circuits for forward and inverse kinematics, our approach offers a promising path toward scalable and efficient robotic computation, with further enhancement expected through advanced entanglement-based quantum algorithms.