Introduction

China possesses abundant coal resources alongside substantial coalbed methane (CBM) reserves1. As shallow coal resources diminish, mining operations are progressively shifting towards deeper deposits. This transition is accompanied by increasingly complex geological conditions at depth, including elevated in-situ stress, gas pressure, and temperature, which have intensified gas disasters, compromising both safety and mining efficiency2. Efficient CBM extraction constitutes a fundamental approach to mitigating such disasters. The gas flow process, encompassing adsorption, desorption, and seepage, is intrinsically linked to coal deformation (swelling/shrinking), significantly impacting extraction effectiveness3,4. Consequently, establishing optimal CBM extraction parameters necessitates a thorough understanding of the coupled characteristics of gas flow and coal deformation throughout the entire extraction process.

Gas adsorption and desorption in coal constitute a thermodynamically reversible process. Consequently, the associated coal swelling (during adsorption) and shrinkage (during desorption) are fundamentally reversible phenomena. Significant research has investigated CBM sorption characteristics and the resulting coal deformation. Baran et al.5 experimentally demonstrated anisotropic coal deformation during gas adsorption and desorption under varying gas pressures, establishing a corresponding deformation model consistent with empirical data. Similarly, Ren6, Zhang7 and Nie8 analyzed deformation patterns induced by gas adsorption-desorption and developed mathematical models relating sorption to coal strain. Complementary studies by Tang9, Lin10 and Bergen11 examined the temporal dynamics of gas adsorption in shale/coal and associated anisotropic deformation behavior. In contrast, Liu’s experimental work12,13 under multiple gas pressures revealed a linear relationship between adsorbed gas volume and coal deformation magnitude. Ma14, Liang15, and Wei16 experimentally quantified the influence of effective stress on coal deformation throughout complete gas adsorption-desorption. Complementing this empirical work, George17 and Espinoza3 developed theoretical models elucidating the mechanistic relationship between gas desorption dynamics and coal deformation.

Similarly, coal experiences deformation during gas seepage processes. Wei18, Chen19, and Li20 conducted stress-seepage experiments demonstrating that external stress exerts significant control over coal permeability, which exhibits strong coupling with coal deformation. Complementing this research, Jiang21 and Li22 quantified deformation behavior during gas seepage under varying temperatures. Their findings reveal that elevated temperatures amplify pore and fracture deformation, consequently driving substantial permeability evolution in coal matrices.

In summary, existing studies frequently overlook coal deformation dynamics throughout the entire CH4 flow process. During gas extraction, effective stress within the coal seam continuously evolves due to declining gas pressure. Furthermore, mining-induced stresses at the working face create highly dynamic loading conditions, characterized by complex axial/radial stress evolution23. Consequently, CH4 flow in coal represents a tightly coupled multi-physics phenomenon involving stress, seepage, and thermal fields. Despite this interdependence, current research rarely integrates stress-seepage coupling when analyzing CH4 adsorption/desorption behavior under varying stress states.

To address this gap, the authors employed a self-developed coal solid-gas coupling test apparatus to conduct CH4 flow experiments under controlled multi-axial stress states. This approach enabled quantitative characterization of coal deformation dynamics throughout the complete CH4 flow cycle (adsorption, desorption, and seepage). Based on these observations, a novel strain model incorporating CH4 flow-induced deformation mechanisms was formulated to enhance CBM extraction efficiency.

Experimental protocols

The collection and Preparation of coal sample

Coal samples were obtained from a newly exposed seam in the Qinshui Basin, Shanxi Province, China. Following immediate on-site sealing, specimens were transported to the laboratory for processing. Cylindrical cores (Φ50 mm × 100 mm) were prepared using a diamond core drill, with all surface precision-ground to achieve parallelism and smoothness. To ensure experimental reproducibility, specimens underwent rigorous selection based on diameter, height, weight, wave velocity, and compressive strength, et al. Ten specimens meeting these criteria were ultimately selected and surface-degreased using anhydrous ethanol prior to testing.

Strain gauges (25 mm gauge length) were mounted at symmetrical mid-height positions on opposing sample faces to measure axial and radial deformation, respectively. Prior to testing, specimens were radially encapsulated in heat-shrink sleeves and subjected to vacuum dehydration. This involved placing samples in a vacuum oven at 70 °C for over 24 h until mass stabilization (< 0.1% variation over 1 h). Figure 1 illustrated this preparation sequence.

Fig. 1
figure 1

Experimental sample preparation and selection.

Full size image

Experimental equipment

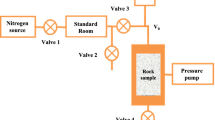
A self-developed coal solid-gas coupling test apparatus (Fig. 2) was employed for this investigation. The system integrates five critical functions of triaxial stress application via independent radial/axial hydraulic pumps, vacuum processing capabilities, CH₄ flow characterization, full-field strain monitoring, automated data acquisition24. CH4 adsorption characteristics were quantified using the high-pressure volumetric method, while triaxial strain measurements were obtained through positioned resistance strain gauges. Crucially, the apparatus enables simultaneous monitoring of CH4 transport dynamics and coal deformation throughout testing cycles.

Fig. 2
figure 2

System diagram of self-developed coal solid-gas coupling test apparatus.

Full size image

Experimental procedure and protocol

CH4 isothermal adsorption experiments followed Chinese National Standard GB/T 19,560 − 2008 (High-pressure isothermal adsorption testing of coal), while CH4 seepage experiments complied with Coal Industry Standard MT/T 223–1990 (Method for determination of coal and rock permeability)7. According to the working front stress state in the gas pre-extraction stage25, this paper utilized the control variable method to analyze the gas flow and coal deformation characteristics under different stress loading ratio, and the details of specific experimental condition settings were shown in Table 1. Figure 3 documented the experimental workflow and specific testing conditions.

Table 1 Designing for gas pressure and external stress.
Full size table
Fig. 3
figure 3

Experimental procedure and conditions setting. (a) Experimental flow chart. (b) Experimental conditions for gas adsorption. (c) Experimental conditions for seepage.

Full size image

The adsorption capacity of CH4 in coal can be calculated using equation of state.

$$\frac{{{P_0}{V_0}}}{{{Z_0}}}=\frac{{{P_t}({V_0}+{V_c}+{V_a})}}{{{Z_t}}}$$
(1)

Where, V0 was the reference tank volume (in cm3). P0 and Z0 was the gas pressure (in MPa) and compression coefficient in the tank prior to adsorption, respectively. Vc was the total volume of the coal pores and pipeline (in cm3). Va was the CH4 adsorption amount (in cm3). Pt and Zt was the gas pressure (in MPa) and compression coefficient in the reference tank at time t, respectively. The pipeline volume was 13.75 cm3.

The steady-state method was used to measure coal permeability under varying stress conditions, and the flow was found to conform to Darcy’s law26.

$$K=\frac{{2\mu q{P_a}L}}{{A(P_{1}^{2} - P_{2}^{2})}}$$
(2)

Where, K was the coal permeability (in m2). µ was the gas viscosity coefficient (in Pa∙s). q was the gas flow (in cm3/s). Pa was the atmospheric pressure (in MPa). L was the height of coal (in cm). A was the cross-sectional area of coal sample (in cm2). P1 and P2 were the gas pressure in the inlet and outlet respectively (in MPa).

The test of coal porosity

The gas expansion method was employed to determine coal porosity under varying confining stresses, following the experimental procedure outlined in Fig. 2. The experimental procedure commenced by loading the coal sample into the triaxial stress chamber and applying confining stress via valves V4 and V6. Helium was then introduced into the reference tank by opening valve V1 and adjusting pressure reducer V7 until a stable pressure of 1 MPa was achieved. Following pressure stabilization, valve V1 was closed and the initial reference tank pressure (P0) was recorded. Gas injection into the coal sample was initiated by opening valve V2. The equilibrium pressure (P1) in the reference tank was recorded after stabilization of both the reference tank and outlet pressures. All pressure measurements adhered to Boyle’s law.

$${P_0}{V_0}={P_1}\left( {{V_0}+{V_c}+{V_v}} \right)$$
(3)

The coal porosity ϕ at different levels of stress can be obtained using the following Eq. 

$$\phi =\frac{{{V_v}}}{V} \times 100\%$$
(4)

Where, Vv and V was the volume of pore and coal (in cm3), respectively.

Figure 4 illustrated the evolution of coal porosity under varying stress conditions. Increasing radial/axial stress ratios induced progressive compaction of native pores and fractures, resulting in systematically reduced porosity.

Fig. 4
figure 4

Test results of coal porosity under different stress ratios.

Full size image

Timeliness analysis of gas flow and coal strain

Gas adsorption and coal strain

Figure 5 presented the temporal evolution of CH4 adsorption capacity and sorption kinetics, while Fig. 6 quantified induced coal strain, where negative values represented shirking and positive values represented swelling. Both CH4 adsorption and coal deformation kinetics followed Langmuir-type behavior6,27, as confirmed by nonlinear regression of experimental data (Table 2). The governing equations were as follow.

$${Q_n}=\frac{{{a_n}{b_n}{t_n}}}{{1+{b_n}{t_n}}}$$
(5)
$${\varepsilon _n}=\frac{{{A_n}{B_n}{t_n}}}{{1+{B_n}{t_n}}}$$
(6)

Where, n = x, j, s. n = x represented the process of CH4 adsorption, n = j represented the process of CH4 desorption, n = s represented the process of CH4 seepage. Qn was CH4 amount (in cm3/g). an was the ultimate amount (in cm3/g). bn was the constant associated with time (in 10−3/s). εn was the strain of coal within tn (in 10−2). An was the ultimate strain of coal (in 10−2). Bn was the strain constant associated with time (in 10−3/s). tn was time (in 103s).

Fig. 5
figure 5

The amount and rate of CH4 adsorption as a function of adsorption time.

Full size image
Fig. 6
figure 6

Coal strain as a function of adsorption time.

Full size image
Table 2 The fitting result of CH4 adsorption amount and coal strain with time.
Full size table

Where, εx−X was the radial strain of coal during adsorption process, 10−2. εx−Y was the axial strain, 10−2. εx−V was the volumetric strain, 10−2.

CH4 adsorption exhibited three stages of kinetics with adsorption time: an initial rapid uptake, followed by a decelerated increase, culminating in equilibrium10,28. Coal strain demonstrated congruent evolution, with volumetric strain exceeding radial strain, which surpassed axial strain. Under low-pressure conditions, elevated CH4 concentration gradients and limited molecular mean free paths within the coal matrix29 promoted surface diffusion dominance in micropores9. This mechanism drove accelerated adsorption and concurrent strain accumulation.

As adsorption progressed, increasing mean pore pressure reduced CH₄ concentration gradients within the coal matrix while extending molecular mean free path. These changes diminished diffusive transport, causing adsorption kinetics and induced strain to asymptotically approach equilibrium. Under triaxial stress conditions, hydrostatic pore pressure exerted equal radial and axial loading. However, axial expansion is suppressed relative to radial expansion due to the high confining stresses along the axial direction.

Gas desorption and coal strain

Figure 7 quantified the temporal evolution of CH4 desorption capacity, kinetics, and velocity, while Fig. 8 documented corresponding coal strain. Both gas desorption and coal strain followed Langmuir-type decay patterns. Experimental data were fitted using nonlinear regression, with parameters tabulated in Table 3.

Fig. 7
figure 7

Variation of CH4 desorption amount, rate and velocity with desorption time.

Full size image
Fig. 8
figure 8

Strain variation of coal with desorption time.

Full size image
Table 3 The fitting result of CH4 desorption amount and coal strain with time.
Full size table

Where, εj−X was the radial strain of coal during desorption process, 10−2. εj−Y was the axial strain, 10−2. εj−V was the volumetric strain, 10−2.

CH4 desorption kinetics and associated strain evolution exhibited temporal symmetry with adsorption processes. During initial desorption, steep pressure gradients between the coal matrix and external environment drove rapid gas release via pore desorption and fracture seepage. This abrupt pressure decline induced instantaneous matrix contraction, manifesting as transient compressive strain. As pore pressure equilibrated with atmospheric boundary conditions (0.1 MPa), seepage fluxes decayed asymptotically. Consequently, both desorption rates and strain magnitudes approached equilibrium.

The desorption rate (defined as the rate of desorption amount to equilibrium adsorption amount) and velocity exhibited kinetics congruent with cumulative desorption. Volumetric strain dominated the deformation response during desorption, manifesting as pronounced matrix contraction. Due to higher axial confinement stress, axial strain remained suppressed relative to radial direction throughout both adsorption (swelling) and desorption (shirking).

Gas seepage and coal strain

Figure 9 characterized gas seepage dynamics and concurrent coal strain evolution under incremental confining stresses. During CH4 seepage, coal deformation exhibited Langmuir-type kinetics congruent with and yet magnitude-constrained relative to adsorption-phase strain. Nonlinear regression confirmed Langmuir behavior for seepage-induced strain, with fitting parameters documented in Table 4.

Fig. 9
figure 9

Variation of coal strain with gas seepage time.

Full size image
Table 4 The fitting results of strain of coal with time during CH4 seepage.
Full size table

Where, εs−X was the radial strain of coal during seepage process, 10−2. εs−Y was the axial strain, 10−2. εs−V was the volumetric strain, 10−2.

During CH4 seepage, gas transport encompassed concurrent adsorption and desorption processes. Upon achieving steady-state flow, adsorption-induced swelling dominated over desorption-induced shirking, resulting in volumetric shrinking of coal matrix. This differential strain response originated from greater adsorption site occupancy versus limited desorption coverage under equivalent pressure conditions.

Effect of axial/radial stress ratio on the coal strain

Effect of axial/radial stress ratio on the coal strain during CH4 adsorption

Adsorption-induced pore pressure elevation and surface interactions caused omnidirectional coal swelling. Figure 10 demonstrated the Langmuir-type correlation between volumetric strain and CH4 adsorption capacity across tested stress states. Nonlinear regression confirmed superior Langmuir model fidelity, with fitting parameters tabulated in Table 5.

$${\varepsilon _n}=\frac{{{\eta _n}{\gamma _n}{Q_n}}}{{1+{\gamma _n}{Q_n}}}$$
(7)

Where, ηn and γn were the fitting parameters during CH4 adsorption/desorption process, and the units of the two parameters were 10−2 and g/cm3, respectively.

Fig. 10
figure 10

Variation of coal strain with CH4 adsorption amount.

Full size image
Table 5 The fitting results of CH4 adsorption amount and coal strain.
Full size table

Both CH4 equilibrium adsorption amount and coal strain decreased with increasing axial/radial stress ratio (σ%). At σ% = 1.5, the equilibrium adsorption amount of CH4 was 3.42 cm3/g, and the corresponding axial, radial and volumetric strain of coal were 1.32 × 10−2, 0.18 × 10−2 and 2.84 × 10−2, respectively. At σ% = 3.5, the equilibrium adsorption amount of CH4 was 2.84 cm3/g, and the corresponding axial, radial and volumetric strain of coal were 1.06 × 10−2, 0.12 × 10−2 and 2.26 × 10−2, respectively. This represented reductions of 16.96% (adsorption), 19.70% (εx−X), 33.33% (εx−Y), and 20.42% (εx−V) respectively with increased stress anisotropy.

These reductions originated from two stress-dependent mechanisms. (1) Lower stress ratios preserved greater micropore surface area, providing enhanced adsorption site density and pronounced matrix swelling. Increasing axial stress induced progressive micropore closure, reducing accessible adsorption sites and constraining strain development. (2) Elevated stress anisotropy impeded CH4 diffusion through constricted pore networks, reducing the Knudsen diffusion coefficient. Concurrently, diminished gas-matrix collision frequency lowered adsorption kinetics, further suppressing CH4 uptake and associated swelling.

Coal strain anisotropy emerged from the coupled effects of fracture pattern, anisotropic stress states, and pore pressure. Linear regression analyses (Fig. 11) quantified directional strain sensitivity to adsorption under increasing stress anisotropy. Volumetric strain exhibited the strongest adsorption dependence, followed by radial and axial strains, confirming progressive mechanical constraint along the highly stressed axial direction.

Fig. 11
figure 11

Coal strain induced by gas adsorption under stresses.

Full size image

Effect of axial/radial stress ratio on the coal strain during CH4 desorption

Coal exhibited shirking deformation due to gas desorption. The relationship between coal strain and gas desorption amount was presented in Fig. 12, with corresponding fitting results detailed in Table 6.

Fig. 12
figure 12

Variation of strain of coal with CH4 desorption amount.

Full size image
Table 6 The fitting results of CH4 desorption amount and coal strain.
Full size table

At σ% = 1.5, the CH4 desorption amount was 2.87 cm³/g with a desorption rate of 83.93%. The corresponding axial, radial, and volumetric strains of the coal were 1.03 × 10⁻², 0.14 × 10⁻², and 2.18 × 10⁻², respectively. When σ% increased to 3.5, the equilibrium CH4 desorption amount decreased by 19.50% to 2.31 cm³/g, while the desorption rate declined by 3.0–81.41%. Concurrently, the axial, radial, and volumetric strains decreased to 0.91 × 10⁻², 0.06 × 10⁻², and 1.88 × 10⁻², which were reduced by 11.65%, 57.14% and 13.76%, respectively.

These reductions originated from two mechanisms, ① Elevated stress diminished coal matrix surface energy, suppressing CH4 desorption and consequent shrinkage16. ② Compression of micropores and fractures under external stress restricted CH4 desorption/seepage pathways, thereby inhibiting shrinkage strain and rate development. Linear regression analysis of stress-dependent strain data (Fig. 13) confirmed consistent stress sensitivity patterns between desorption and adsorption processes.”

Fig. 13
figure 13

Coal strain induced by gas desorption under stresses.

Full size image

Effect of axial stress/radial stress ratio on the coal deformation during CH4 seepage

Coal exhibited non-elastic behavior30, resulting in stress-dependent permeability variations. As shown in Fig. 14, coal strain and permeability evolved with increasing stress ratios. At σ% = 1.5, permeability measured 4.53 × 10⁻¹⁷ m², accompanied by axial, radial, and volumetric strains of 0.84 × 10⁻², 0.12 × 10⁻², and 1.81 × 10⁻², respectively. When σ% increased to 3.5, permeability declined by 53.86% to 2.09 × 10⁻¹⁷ m², while strains decreased to 0.37 × 10−2, 0.05 × 10−2 and 0.79 × 10−2, which were reduced by 55.95%, 58.33% and 56.36%, respectively. This systematic reduction indicated the experimental coal transitions through compression and elastic deformation stages under elevated stress31.

Fig. 14
figure 14

Coal strain and permeability under different stresses.

Full size image

During gas seepage in coal, deformation manifested through dual-scale mechanisms15: macroscopically as volumetric strain variation, and microscopically as pore-fracture-matrix reorganization. Assuming constant seepage parameters and pore pressure during initial conditions, coal deformation primarily results from synergistic effects of increasing axial stress and methane advection. As seepage progresses, compression of pores and fractures inhibits CH₄ flow, reducing both flow velocity and internal pressure per unit time. This process macroscopically reduces permeability while simultaneously inducing matrix swelling. Linear regression analysis (Fig. 14) revealed strain sensitivity followed the hierarchy: volumetric > radial > axial strain.

Discussion

Time-dependent analysis of coal strain during CH4 flow revealed stress-ratio-dependent deformation patterns (Fig. 15). Using adsorption-desorption kinetic equations, a residual strain model capturing hysteresis effects in coal matrices was derived.

$$\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{\text{x}}}=\frac{{{A_{\text{x}}}{B_{\text{x}}}{t_{\text{x}}}}}{{1+{B_{\text{x}}}{t_{\text{x}}}}}} \\ {{\varepsilon _{\text{j}}}=\frac{{{A_{\text{j}}}{B_{\text{j}}}{t_{\text{j}}}}}{{1+{B_{\text{j}}}{t_{\text{j}}}}}+\Delta \varepsilon } \end{array}} \right.$$
(8)

Where, Δε was the residual coal strain.

Fig. 15
figure 15

Analysis of coal strain coal in the entire process of gas flow.

Full size image

Residual strain

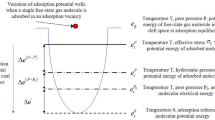
Residual strain generation during gas adsorption-desorption represents a critical manifestation of the complex coal-gas interactions, governed primarily by elastic deformation, pore structure evolution, and adsorption-desorption hysteresis.

As a heterogeneous and non-ideal elastic medium, coal exhibits inherent strength variations. During adsorption-induced swelling, localized plastic deformation may occur in high-stress regions. During subsequent desorption-shrinkage, the stress state within these regions cannot fully recover to its initial condition due to constraints imposed by surrounding elastic zones32. Furthermore, while matrix swelling may close primary fractures, the complete reopening of fractures during shrinkage is impeded by frictional resistance and debris infilling. This irreversibility manifests macroscopically as residual strain.

The swelling-shrinking forces generated during gas adsorption and desorption continuously modify the microstructure of coal. Irreversible deformation of pores and fractures directly contributes to residual strain development33. Under cyclic force loading, weak pore walls undergo compaction or permanent dilation, altering pore morphology and volume. Concurrently, stress concentrations during adsorption-swelling can exceed the strength of coal, generating new micro-fractures and propagating existing ones34. Debris production from fracture wall abrasion further modifies fracture geometry through infilling or roughness alteration. These competing mechanisms—fracture propagation (increasing void volume and contributing to residual expansion strain) versus pore collapse and debris occlusion (reducing effective porosity and enhancing shrinkage)—collectively determine the evolution of pore and fracture and the magnitude of residual volumetric strain.

Adsorption-desorption hysteresis constitutes another primary factor in residual strain. The prevalence of ink-bottle shaped pores (characterized by narrow necks and wide bodies) in coal impedes desorption through capillary condensation effects at pore throats35. Additionally, strong interactions between CH4 molecules and the coal surface necessitate higher energy barriers for desorption, resulting in retained gas. This retained gas sustains matrix support and swelling pressure, preventing the coal from fully reverting to its initial state before adsorption.

Permeability evolution

Coal permeability dynamics are fundamentally governed by micropore architecture and its response to multiphysical processes during gas extraction. Disruption of in-situ stress equilibrium initiates critical restructuring of internal pores and fractures through stress redistribution36. Porosity and permeability—key parameters in stress-seepage coupling—evolve under triaxial constraints of external stress, pore pressure, and coal mechanical properties37.

During elastic deformation under increasing effective stress, coal undergoes sequential compaction phases. Initial fracture closure and matrix compression reduce pore volume and specific surface area, diminishing equilibrium gas adsorption capacity16. This microstructural collapse impairs CH₄ flow through three concurrent mechanisms: (1) seepage pathway constriction, (2) pore pressure gradient reduction, and (3) increased flow resistance, culminating in macroscopic permeability decline38.

Concurrently, CH4 adsorption-desorption induces matrix swelling/shrinking, directly modulating permeability through interdependent stress mechanisms: adsorbed CH4 generates compressive stress causing reverting elastic matrix deformation, while free-phase gas exerts swelling stress triggering unrecoverable plastic deformation through structural displacement39. This prevents full restoration of pre-adsorption pore-fracture geometry. Residual gas further provides structural reinforcement and sustained swelling pressure, with resulting irreversible strain impairing subsequent gas seepage.

During CBM extraction, thermo-hydro-mechanical (THM) coupling continuously modifies pore-fracture network architecture, governing gas transport through a dynamically coupled system integrating matrix deformation, skeletal restructuring, and gas flow40. Elucidation of stress-dependent deformation and transport mechanisms provides critical foundations for optimizing CBM extraction parameters and advancing multiphysics coupling theory, facilitating precision methane recovery and geohazard mitigation.

Conclusion

(1) CH4 adsorption and desorption in coal exhibited three stages of rapid-increase, slow-increase, and plateau stages. Both adsorbed/desorbed gas amount decreased with increasing axial/radial stress ratio. Higher stress ratios further reduced CH₄ adsorption/desorption rates compared to lower ratios.

(2) CH4 flow induced variable magnitudes of coal swelling/shrinking. During initial flow stages, volumetric strain increased rapidly before equilibrating as gas transport stabilized.

(3) Temporal evolution of both gas flux and coal strain followed Langmuir-type kinetics. Adsorption/desorption amount similarly exhibited Langmuir relationships with coal strain. Increasing stress promoted linear decay of coal strain.

(4) Irreversible residual strain developed during CH4 adsorption-desorption, exhibiting inverse correlation with axial/radial stress ratios. The established model incorporated this deformation hysteresis through a time-dependent constitutive framework with residual strain quantification across all process stages.