Introduction

The precision of dose delivery is the focus of many medical physics studies in radiotherapy, as inaccurate radiation dose administration can lead to a reduced therapeutic index and significantly alter treatment outcomes1. Hence, for advanced treatments, the quality of the radiation delivery2 should be monitored accurately, and the treatment plan should ensure state of the art radiation dose assessment and patient-specific quality assurance prior to the treatment3,4.

Microbeam Radiation Therapy (MRT) is a disruptive dose delivery method that consists of a spatial fractionation of low-to-medium-energy synchrotron-generated X-rays into an array of intense, quasi-parallel microbeams5,6. This approach pushes the concept of the dose-volume effect to its theoretical limits7, offering a unique method for radiotherapy. The dose distribution specific to MRT is entirely different from that observed in conventional radiotherapy. It features high-dose regions (peaks- several tenth of Gy) in the form of microbeams, each 25–100\(\upmu\)m wide, separated by low-dose regions (valleys- 5–7\(\%\) of peak dose) with a pitch of 100–400\(\upmu\)m. Peak doses are found to be linked to the treatment efficacy8 whereas the valley doses seem to be linked to toxicity in healthy tissue9.

The choice of dosimeter for treatment quality control in MRT is challenging due to several factors: (1) the spatial fractionation, which results in a micrometrically resolved pattern of peak and valley dose regions, requiring high spatial resolution; (2) the need for a wide dynamic dose range, as the dose in valley regions is only 5–7\(\%\) of the peak dose, making it difficult to achieve accurate simultaneous measurements in both peaks and valleys with a single dosimeter10; (3) the high dose rate of synchrotron-generated X-rays (up to 16 kGy/s)11; and (4) the use of orthovoltage photon energy12,13,14. At the biomedical beamline (ID17) of the European Synchrotron Radiation Facility (ESRF), absolute reference dosimetry under broad beam conditions is performed using an ionization chamber, based on the recommendations of TRS-39815,16,17. As a result, the development of detectors and dosimetry methods to address this challenge has been the focus of many studies. Semiconductor detectors such as MOSFETs and silicon strip detectors offer excellent spatial resolution (around 1\(\upmu\)m and 10\(\upmu\)m, respectively), but they are not tissue-equivalent and exhibit strong energy dependence5,18,19,20. Gel dosimeters and PRESAGE materials are 3D dosimeters with a resolution limited to the resolution of the imaging method (CT scan) and require a complex read-out procedure12,21. Plastic scintillators coupled with optical fibers are tissue-equivalent; however, they are highly sensitive to light and require a dark room22. Thermoluminescent dosimeters (TLDs) are also tissue-equivalent but have limited resolution (around 100 \(\upmu\)m) and a complex read-out process23. Diamond detectors, such as the commercial microDiamond PTW 60019, offer excellent resolution (1\(\upmu\)m in edge-on mode); however, their response is dependent on angular orientation, making detector alignment challenging24. Additionally, scanning an MRT field with this detector requires translating it within the beam in micrometer steps across the horizontal plane to measure all the peaks and valleys in the field, resulting in a time-consuming process.

Gafchromic films are currently the gold standard for treatment quality control in MRT translational trials25. Despite of requiring a read-out procedure, Gafchromic films are commonly favored because they are tissue-equivalent 2D dosimeters with high spatial resolution (less than 25\(\upmu\)m) and are available in various models with different dynamic ranges26,27. For MRT film dosimetry using dedicated readout methods, the spatial resolution of the measured dose maps can range from approximately 1–10\(\upmu\)m, depending on the specific read-out method (flatbed scanner, microscope and microdensitometer)26,27,28.

To measure peak and valley doses using Gafchromic films, two approaches were commonly employed so far : (1) the use of two different types of films to separately measure peak and valley doses10,27, and (2) the use of high dose range films to simultaneously measure peak and valley doses on the same film26. The latter approach requires scaling up the prescribed dose by a factor (typically five to ten) to ensure both peak and valley doses remain within the dynamic range of the film. This scaling up method is performed using several vertical scanning of the phantom in the beam12 with the additional uncertainty brought by the fact that the microbeams could not overlap perfectly. This method differs significantly from real treatment conditions, where each beam is delivered with a single vertical movement of the stage. The two films type method requires two sets of irradiations for peak and valley dose measurements, along with two sets of calibrations films. Together with prohibitive experiment times, quantification issues and inaccuracies in the dose data extraction are also an issue with this method due to an increased noise on the peak films and non-linearities on the valley films because of saturated zones. Moreover, the literature shows that, regardless of the method, a difference of up to 30\(\%\) has been observed, between peak and valley doses calculated using Monte Carlo (MC) methods and those measured using films29.

As both peak and valley doses are key parameters linked to the treatment quality30, it would add significant value to be able to experimentally assess these indicators simultaneously within accurate patient specific QA dedicated methods. The goal of this study was to identify the most suitable Gafchromic film type for MRT patient specific QA where peak and valley doses would be measured simultaneously at the treatment depth, with clinical doses relevant to the ongoing translational studies25,31. Broad beam and MRT dose distributions, including peak and valley doses, were experimentally evaluated and compared to calculated doses. The aim of the study was also to compare the response of four different types of Gafchromic films (EBT-3, EBT-XD, MD-V3, and HD-V2) with a reference dosimeter —the microDiamond detector for MRT, as a well-established 1D high-resolution detector for MRT24,32, and the ionization chamber for broad beam reference dosimetry, aligned with reference dosimetry protocols16,17—and to compare the measured doses with calculated doses from two independent dose calculation engines33,34.

Methods

This study was conducted as part of translational MRT trials on canine patients carried out on the ID17 biomedical beamline at the ESRF25,31. The same beam quality as that used during the veterinary treatments was employed for both experimental methods and dose calculations (average energy 121 keV, see full spectrum on Figure 2.A in8).

Experimental dosimetry

Three types of dosimeters were used in this study:

  • The PinPoint PTW 31014 Ionization Chamber (IC) (PTW, Freiburg, Germany) with a sensitive volume of 0.015 cm³ was used to obtain the reference dose rates in a homogeneous 2 \(\times\) 2 \(\hbox {cm}^{2}\) field within a water-equivalent phantom. The IC was placed in a RW3 phantom inside a specific insert filled with water at a depth of 2 cm, centered in the middle of the field, and vertically scanned at a speed of 20 mm/s according to the absolute dosimetry protocols for synchrotron-generated X-rays16,17. Reference dose rates at 2 cm were obtained in the range 60–5400 Gy/s by attenuating the treatment beam with PMMA slabs.

  • The PTW microDiamond (PTW 60019, PTW, Freiburg, Germany) is a synthetic single-crystal diamond with a small sensitive volume of 0.004 mm³ (diameter = 2.2 mm, thickness = 1 \(\upmu\)m). This detector was chosen for its near water-equivalence and minimal perturbation to the absorbed dose in water for small field dosimetry. Additionally, it has shown promising results in small field irradiation using orthovoltage photons in Small Animal Radiation Research Platform (SARRP) units35 and in MRT dosimetry32. This detector was used in edge-on mode, where it achieves micrometric resolution, to measure peak and valley doses in MRT. The alignment of the microDiamond was first verified using a CCD camera. Then, the microbeams were shaped using a Multislit collimator29. The detector was first centered on a peak. Peak and valley doses were alternatively measured by translating the detector in 206.5 \(\upmu\)m steps, the nominal distance between peak and valley centers.

  • Radiochromic films (RCFs) are high resolution, self-developing, two- dimensional dosimeters which are widely used in quality assurance and dose verification. RCFs contain an organic compound of diacetylene monomers which are incorporated into a gelatine matrix and coated onto a polyester base. The irradiation triggers a polymerization reaction which causes the coloration of polymer chain36. The degree of polymer chain coloration is strictly proportional to the absorbed dose. RCFs used today in medical physics are manufactured under the commercial name of Gafchromic films (Ashland, Bridgewater, NJ, USA)37. In this study, four types of Gafchromic films were tested: EBT-3 with a dynamic range of 0.1–20 Gy, EBT-XD with a dynamic range of 0.1–60 Gy, MD-V3 with a dynamic range of 1–100 Gy, and HD-V2 with a dynamic range of 10–1000 Gy. As the prescribed valley doses in canine trials were 2.8 Gy and 4.9 Gy25, which are below the dynamic range of the HD-V2 film, these films were exclusively used to measure peak doses.

Gafchromic film preparation, irradiation and readout

Gafchromic film sheets were cut into \(4 \times 4\;\hbox { cm}^{2}\) pieces for calibration, broad beam, and MRT dose measurements. Each film was labeled and marked to ensure that all pieces were irradiated and read in the same orientation. A non-irradiated film was kept for each type of film to serve both for optical density normalization and as the zero Gy dose point in the calibration curve. For film calibration and absolute dose measurements (broad beam and MRT), films were placed perpendicular to the beam direction inside the RW3 phantom, as shown in Fig. 1. MRT peak and valley continuous depth dose curves were obtained using EBT-XD films as it is the best compromise in dynamic range to ensure the measurement of peak and valley doses from the surface to 3.5 cm depth. These peak and valley doses were measured by placing the film parallel to the beam direction.

Fig. 1
figure 1

Configuration for measuring the absolute dose in synchrotron radiation broad beam therapy (top) and MRT (bottom) and using Gafchromic films.

Full size image

Films were calibrated under reference conditions by irradiating them with a given absorbed dose from a \(2 \times 2\;\hbox { cm}^{2}\) broad beam, measured at a depth of 2 cm16. Calibration doses were selected based on the film’s dynamic range and an estimation of the MRT doses to be measured. Table  1 shows the calibration doses for each film type along with the desired dose metrics to be measured. Based on the publication by Borca et al.38 and to extend the dynamic range, calibration points were taken beyond the nominal range to investigate the possibility of measuring both peak and valley doses on the same piece of film. The dose rate in the synchrotron is a function of the current in the storage ring, and the total absorbed dose is calculated using Eq. (1)39:

$$\begin{aligned} D = \frac{\dot{D} \times h \times I}{v} \end{aligned}$$
(1)

here, \(\dot{D}\) is the dose rate in Gy/s/mA, h is the beam vertical aperture, I is the current and v is the vertical scanning speed in mm/s. During the canine patient trials, a beam aperture of 520 \(\upmu\)m was used, with a storage ring current around 200 mA. Under this configuration, the typical dose rate at the reference condition16 (field size \(2 \times 2 \hbox { cm}^{2}\), scan speed 20 mm/s) was approximately 27 Gy/s/mA. Given that the maximum vertical scan speed allowed by the motors was around 80 mm/s, delivering doses lower than 35 Gy for calibration films was practically impossible.

Table 1 Calibration doses used for different types of the films.
Full size table

To address this, PMMA slabs with thicknesses up to 26 cm were used to reduce the dose rate. This is an adequate approach considering studies suggesting that the energy dependence of the film response is negligible within the energy range used in this study37,40. Films were vertically scanned at speeds ranging from 10 to 80 mm/s, the speed being adjusted to deliver the desired calibration doses.

Films were then irradiated with square broad beam fields or MRT fields of \(2 \times 2 \hbox { cm}^{2}\) at various depths. Additionally, they were exposed to conformal fields corresponding to the treatment beams used for the canine patients trial; at 2 cm and at the treatment depth in RW3 solid water (5–10 cm).

During the canine trials, film dosimetry was conducted a day prior to treatment. Given studies showing the relative stability of film response 6 h after irradiation38, an accelerated protocol was employed instead of the recommended 24 h delay between exposure and readout. This protocol involved recording the exact exposure times for each piece of film and ensuring that the same timing was maintained for the readout process (typically between 10 and 12 h post irradiation).

The information recorded within the film polymer is extracted as Optical Density (OD), meaning the films are exposed to a light source, and the quantity of transmitted light is collected by a detector. In this study, two types of readout instruments were used: Zeiss Axio-Vision optical microscope (Oberkochen, Germany) equipped with red filter and coupled with a CCD camera (AxioCam MRm Rev. 3 FireWire, Zeiss) with a pixel size of 1.3 \(\upmu\)m26 and Epson Perfection V750 flatbed scanner (Epson, Suwa, Japan) with a pixel size of 10.8 \(\upmu\)m27. The responses were corrected for both the heterogeneity of the light source and baseline signal from non-irradiated film, and the calibration curves were established based on protocols fully described by Ocadiz et al.27. Given the 10.8 \(\upmu\)m resolution of the flatbed scanner, there is a potential for partial volume averaging effects when analyzing peaks with a width of 50 \(\upmu\)m; however, this resolution is sufficient for valley analysis. In contrast, the microscope with its 1.3 \(\upmu\)m resolution is suitable for analyzing both peaks and valleys. Therefore, in the results section the readouts from the microscope were primarily analyzed for peak and valley extraction. In the discussion section the readouts from both the scanner and the microscope were compared to assess the impact of the readout methods on the extracted values.

MRT films analysis

The pixel values were converted to dose values using calibration curves. The resulting dose maps were automatically realigned by applying a rotation to ensure the beams were perfectly vertical. Misalignment of peaks can lead to underestimation or overestimation of the extracted peak and valley dose values, respectively.

The centers of the peaks and valleys were automatically detected. Then, macro pixels values were created by averaging the dose values within regions of 10 \(\upmu \hbox {m }\times 400 \upmu \hbox {m}\) for peaks and \(100\,\upmu \hbox {m } \times 400\,\upmu \hbox {m}\) for valleys38. This method was applied to create separate peak and valley dose maps with a resolution of \(400 \times 400 \upmu \hbox {m}^{2}\) (see Figure 3 in27). Finally, average peak and valley doses were obtained on these separate maps using a \(2 \times 2 \hbox { mm}^{2}\) zone at the center of each dose map, encompassing 5 peaks or 5 valleys. Averaging over multiple peaks or valleys was employed to mitigate the effects of the inhomogeneities of the film responses at the micrometric level.

Dose calculation methods

The two dose calculation methods used in this study were the hybridDC dose calculation algorithm33 and penMRT34. The hybridDC algorithm employs a MC method (Geant4) for simulating photon transport and convolution-based methods for electron transport. This approach generates separate peak and valley dose maps with sub-millimetric voxel resolution or micrometric resolution dose maps at the voxel level41. In contrast, penMRT is a high-resolution, purely MC code based on the PENELOPE MC code42, providing micrometric resolution capable of resolving peaks and valleys. Thus, the continuous depth dose profiles of a peak and a valley in an MRT field were compared to the 3D dose maps calculated by penMRT, as the hybrid method only provides separate average peak and valley 3D dose maps.

For the canine patient trials dose prescription was performed using the hybrid algorithm to determine the necessary treatment time. In MRT treatment, the irradiation time (equivalent to monitor units) is expressed as a reference dose. This reference dose represents the broad beam dose at a reference depth (2 cm) required to achieve the prescribed MRT peak or valley dose at the depth of interest. Thus, the reference dose value calculated by hybridDC was then applied to the dose maps calculated by penMRT to extract the dose values in Gy. In this way, the measured doses using different types of films were compared with the calculated doses from these two methods, which use different calculation cores (Geant4 versus PENELOPE). Separate peak and valley dose maps can also be obtained from penMRT high-resolution dose maps with the following method: macropixels were built within a \(2 \times 2 \hbox { mm}^{2}\) zone at the center of the field for peaks by averaging pixel values over \(10\, \upmu \hbox {m} \times 400 \upmu \hbox {m}\) region of interest and for valleys by averaging pixel values over \(100 \upmu \hbox {m} \times 400\,\upmu \hbox {m}\). Average values from these macrovoxels were used to determine the peak and valley doses. For hybridDC, peak and valley doses were extracted by averaging pixel values within a \(2 \times 2 \hbox { mm}^{2}\) zone at the center of the field from the separate peak and valley dose maps.

Comparison methods

This study includes comparisons of absolute dose measurements in both broad beam and MRT fields in between film, IC, and microDiamond measurements, as well as the two dose calculation methods at discrete points. For point-to-point comparisons, the relative differences were calculated using one of the following equations:

$$\begin{aligned} \begin{aligned} \delta&= \frac{D_{\text {film}} - D_{\text {ref}(\mu \text {Diamond or IC})}}{D_{\text {ref}(\mu \text {Diamond or IC})}} \\ \delta&= \frac{D_{\text {measured}} - D_{\text {ref(calculated)}}}{D_{\text {ref(calculated)}}} \\ \delta&= \frac{D_{\text {hybrid}} - D_{\text {ref(penMRT)}}}{D_{\text {ref(penMRT)}}} \end{aligned} \end{aligned}$$
(2)

here, \(\delta\) represents the relative difference, and D is the measured absolute dose using film, ionization chamber (IC), microDiamond, or the calculated dose using hybridDC or penMRT.

Uncertainty analysis

Uncertainties were calculated for the relative differences between film-measured and reference-measured doses or calculated doses, evaluated separately for each film type and at each measurement depth. When multiple measurements were performed using the same film type under identical irradiation conditions at a specific depth, the relative differences between the film and the reference dosimeter or calculation were computed for each set of measurement. The resulting values were then averaged, and the associated uncertainty was calculated using error propagation, based on the standard deviations of the individual relative differences using following equation.

$$\begin{aligned} \begin{aligned} \sigma _{\text {total}} = \frac{\sqrt{\sum _{i=1}^{n} \sigma _i^2}}{n} \end{aligned} \end{aligned}$$
(3)

where \(\sigma _i\) is the standard deviation of relative difference in the \(i^{\text {th}}\) measurement, and n is the number of measurements for that film type and configuration.

Determining the sources of discrepancies between measured and calculated dose values

Based on a previous study where some discrepancies between measurements and calculations were attributed to imperfections in the multislit collimator blades29, we investigated the dose profiles of single and multiple microbeams using HD-V2 films. This analysis aimed to determine whether these imperfections significantly affect the measured peak and valley doses.

Results

Depth dose measurement

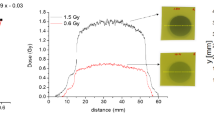
Broad beam doses in a \(2 \times 2 \hbox { cm}^{2}\) field were measured at different depths using the IC and EBT-3 films, with the films placed perpendicular to the beam (as shown in Fig. 2a,b), and were compared to calculated doses using the hybrid DC and penMRT dose calculation algorithms (Fig. 2b,c). The measured and calculated values were found to be in satisfactory agreement, with relative differences of less than 5\(\%\). When compared to the reference dose measured using the IC, the EBT-3 films showed a slight tendency to overestimate the dose by approximately 2\(\%\) compared to IC. The calculated values from penMRT and the hybridDC algorithms were in good accordance with the IC measurements, showing relative differences of less than 1\(\%\) and 2\(\%\), respectively.

Fig. 2
figure 2

Depth dose comparisons in a broad beam field with a prescribed dose of 5 Gy at a depth of 2 cm: (a) and (b) illustrate the setup where the films were placed perpendicular to the incident beam. (c) presents the absolute doses measured using the IC and EBT-3 film, alongside the doses calculated using penMRT and hybridDC methods. (d) shows the relative differences between the measured dose values, the calculated values, and comparisons between the measured and calculated doses. Standard deviations are shown in 1 sigma (error propagation was used).

Full size image

For continuous depth dose measurements in a \(2 \times 2 \hbox { cm}^{2}\) MRT square field, the central peak and central valley doses -averaged over 10 \(\upmu\)m and 100 \(\upmu\)m, respectively- were obtained using EBT-XD films placed parallel to the beam axis inside the phantom (Fig. 3a,b). Using \(4 \times 4 \hbox { cm}^{2}\) film pieces and excluding the damaged margins during the cutting process, depth doses were measured continuously over a range of 3.4 cm. The measured and calculated peak doses were normalized to the dose value at a depth of 2 cm (Fig. 3c,e). The relative differences showed satisfactory agreement, with less than 5\(\%\) for the peak and less than 10\(\%\) for the valley, except for depths less than 2 mm (Fig. 3d,f). The higher relative differences in the valley were attributed to increased statistical uncertainties in both measured and calculated values.

Fig. 3
figure 3

Continuous depth dose measurement in a \(2 \times 2 \hbox { cm}^{2}\) MRT square field. (a) EBT-XD films were placed parallel to the beam axis between the RW3 slabs. (b) Depth doses were measured over a range of 3.4 cm. (c) and (d) The central peak doses, both measured and calculated using penMRT, were averaged over 10 \(\upmu\)m, normalized to the dose at a depth of 2 cm, and the relative differences were calculated. (e) and (f) The central valley doses, both measured and calculated using penMRT, were averaged over 100 \(\upmu\)m, normalized to the dose at a depth of 2 cm. The normalization depth is indicated by the cyan arrow. The relative differences were calculated with a step of 1 mm. The standard deviation in penMRT calculated values is shown as 1 sigma, while it is not shown for the film case due to high statistical uncertainties that would obscure the figure.

Full size image

Comparison of responses: MicroDiamond, Gafchromic films and calculated doses

For a prescribed valley dose of 1 Gy at a depth of 7 cm in a \(2 \times 2 \hbox { cm}^{2}\) MRT square field, comparing different film types with microDiamond measurements highlighted the limitations and advantages of each film (Fig. 4a,b). In Fig. 4a, HD-V2 films demonstrated high statistical uncertainty in peak dose measurements, with relative differences increasing up to 60\(\%\) as the depth increased and the dose decreased. EBT-3 (not shown) and EBT-XD films both experienced saturation in peak dose measurements at 2 cm, around 60 Gy. In contrast, MD-V3 films demonstrated good agreement, with relative differences of approximately up to 10\(\%\). In Fig. 4b, both EBT-3 and EBT-XD films showed satisfactory agreement with microDiamond in valley dose measurement, with relative differences around 2\(\%\) and less than 6\(\%\), respectively. MD-V3 films also showed satisfactory agreement within the error bars, with relative differences of less than 9\(\%\). However, this relative difference increased with depth as the valley dose approached the lower dynamic range of the film (valley dose of around 1 Gy at 7 cm). When comparing the Peak-to-Valley Dose Ratio (PVDR) in Fig. 4c, the best agreement was observed with MD-V3 films, except at a depth of 7 cm. Both EBT-XD and EBT-3 films also showed good agreement around 7 cm, with relative differences of less than 5\(\%\).

Fig. 4
figure 4

Comparison of (a) and (d) peak doses, (b) and (e) valley doses, and (c) and (f) Peak-to-Valley Dose Ratios (PVDR) measured by HD-V2, EBT-3, EBT-XD, and MD-V3 films, and calculated by hybridDC and penMRT, respectively, against measurements obtained with microDiamond in a \(2 \times 2 \hbox { cm}^{2}\) MRT square field, with a prescribed valley dose of 1 Gy at a depth of 7 cm. Standard deviations are represented as 1 sigma (error propagation was used).

Full size image

The comparison of calculated doses using hybridDC and penMRT with the measured peak and valley doses as well as PVDRs using the microDiamond detector showed that with the exception of 7 cm the hybridDC and penMRT predicted lower peak doses than those measured by the microDiamond (Fig. 4d). At 7 cm the highest and lowest relative differences in peak doses were noted with a relative difference of around 16\(\%\) and 5\(\%\) for hybridDC and penMRT, respectively. The overall microDiamond measurements for valley doses were between 30\(\%\) and 37\(\%\) higher than the computed values (Fig. 4e). For PVDR, since the differences in valley doses are relatively consistent, the peak dose differences have the most significant impact on PVDR values. Consequently, the largest discrepancy of about 30–33\(\%\) was observed at a depth of 7 cm (Fig. 4f). In general, both calculation methods demonstrated satisfactory agreement with each other, showing a relative difference of less than 10\(\%\) in peak doses and less than 5\(\%\) in valley doses, with hybridDC predicting slightly higher values.

Comparison of measured and calculated peak and valley doses using four different film types

To evaluate the dosimetric performance, reproducibility and repeatability of each film type, all measurements were performed under consistent experimental conditions. The same phantom setup, source-to-phantom distance, beam spectra, irradiation geometry, and film readout protocol were used throughout the study. The only parameters that varied were the prescribed dose and the measurement depth. Each film type was tested multiple times to evaluate the reliability of the results. In Fig. 5, peak and valley doses were measured using four different types of films and were calculated using penMRT, based on prescribed doses for canine patients to achieve valley doses of 2.8 or 4.9 Gy at depths of 5–10 cm with various conformal shapes (refer to Table 1 in25 for an example of field shapes). Due to the similarity in calculated doses between hybridDC and penMRT, as observed in the previous section, only the penMRT-calculated doses are shown in the figure. The same prescribed doses were used to irradiate films through a \(2 \times 2 \hbox { cm}^{2}\) square field as the reference shape. For square fields when measuring peak doses, as shown in Fig. 5a: (1) HD-V2 films exhibited high uncertainties and overestimated doses by up to 50\(\%\); (2) MD-V3 showed satisfactory agreement with a relative difference of less than 8\(\%\); (3) for EBT-3 and EBT-XD, the agreement between calculations and measurements improved with increasing depth, except at 2 cm, where doses around 40 Gy caused saturation in these films. At greater depths, the relative difference mostly decreased to less than 20\(\%\). The difference between measured and calculated valley doses for all film types ranged from 20 to 40\(\%\) (Fig. 5b). An example of dose distribution for a square field on Gafchromic films is shown in Fig. 5c.

Fig. 5
figure 5

Relative differences in peak and valley doses measured using EBT-3, EBT-XD, MD-V3, and HD-V2 compared to calculations with penMRT. Left column (\(2 \times 2 \hbox { cm}^{2}\) square field) (a) peak dose comparison: film vs. penMRT; (b) valley dose comparison: film vs. penMRT; (c) dose distribution for a square field on the Gafchromic film. Right column (Conformal fields): (d) peak dose comparison: film vs. penMRT; (e) valley dose comparison: film vs. penMRT. (f) Dose distribution for a conformal field on the Gafchromic film. Standard deviations are represented as 1 sigma (error propagation was used).

Full size image

For peak doses in the conformal fields shown in Fig. 5d, the best agreement was observed between MD-V3 and penMRT, with a relative difference of less than 4\(\%\). For EBT-3 and EBT-XD, agreement with calculated values improved with increasing depth, with overall relative differences of less than 13\(\%\). In the case of valley doses (Fig. 5e), MD-V3 exhibited satisfactory agreement with a relative difference of less than 10\(\%\) at 6 cm. However, at 8 cm, where the valley dose approached or fell below the lower dynamic range of MD-V3, the relative difference increased to about 78\(\%\). For EBT-3 and EBT-XD, similar to the square field measurements, discrepancies ranged from 9 to 40\(\%\). An example of dose distribution for a conformal field on Gafchromic films is shown in the Fig. 5f.

Investigating discrepancies between measured and calculated peak and valley doses

An observation of typical CT scan images of the RW3 phantom revealed the presence of a 1.25 mm air gap at a depth of 1 cm (Fig. 6a). Analysis of the central peak and central valley of a square MRT field simulated on these CT images indicated that where the films were positioned, a maximum underestimation of 70\(\%\) in the peak dose (Fig. 6b) and an overestimation of 40\(\%\) in the valley dose (Fig. 6c) might occur.

Fig. 6
figure 6

Beam profile study: (a) Dose map measured using HD-V2 films, averaged over 0.5 mm to reduce statistical uncertainties. (b) Dose profile in a field composed of 5 microbeams, with a distorted valley highlighted by a pink rectangle. (c) In a single microbeam field, the amplitude of the distorted valley or “false” peak (called P2) is quantified.

Full size image

The beam profiles of single and multiple microbeam fields were measured and averaged over 0.5 mm to reduce statistical uncertainties (Fig. 6d). Analysis of these profiles, as shown in Fig. 6e,f, revealed the appearance of a distorted valley resembling a “false” peak. To quantify its amplitude, the integral under the real peak (P1) and the false peak (P2) in Fig. 6f were calculated, resulting in an integral ratio of 32\(\%\) for P2 to P1.

Discussion

This study took place in the context of MRT translational research and aimed to identify the film offering the best compromise for simultaneously measuring peak and valley doses under treatment-relevant conditions. It also revealed several factors that have an impact on film dosimetry and the accuracy of dose calculations.

According to Fig. 2, in depth dose measurements using EBT-3 films, the broad beam absolute dose measurements showed satisfactory agreement, with deviations of less than 3.8\(\%\) for penMRT and less than 5.4\(\%\) for the hybrid method, indicating strong consistency between the measurements and calculations. These minor deviations can be attributed to the inherent statistical uncertainties of Gafchromic films43,44. The best agreement was observed between the doses calculated by penMRT and those measured by the IC. In Fig. 3, the slight increase in relative differences for MRT depth dose measurements, where the films were positioned parallel to the beam axis (approximately \(<5 \%\) for peak and \(<10 \%\) for valley), can be explained by the increased attenuation of the beam within the film material compared to water-equivalent materials45. These agreements could be an indicator of the accuracy of the beam spectrum used for dose calculation.

From Fig. 4, the comparison between four different types of films and the microDiamond detector revealed that MD-V3 films provided the best agreement for peak doses. For valley doses, satisfactory agreement was observed within the error bars. However, at increased depths, where the measured doses fell below the dynamic range of the MD-V3 films, this limitation impacted the results. When comparing doses measured using microDiamond to those calculated by both dose calculation methods, the measured doses were consistently higher than the calculated values. This discrepancy may be due to the microDiamond being used in edge-on mode, where scattered photons interacting with both the edge and the face of the detector might lead to dose overestimation. Furthermore, the agreement between the two dose calculation methods allows us to use these tools interchangeably.

Base on the data in Fig. 5, peak doses measured by HD-V2 films were significantly higher than the calculated values, likely because HD-V2 films have a wide dynamic range up to 1000 Gy. However, when measuring doses near the lower end of this range, the data can become very noisy, making these films unsuitable for patient quality control. On the other hand, peak doses measured by MD-V3 showed a coincidence within 8\(\%\) with both penMRT and hybridDC calculated values, especially in conformal fields. In the case of peak doses, for EBT-3 and EBT-XD films, significant differences were observed at depths of 2–7 cm, with discrepancies decreasing as the depth increased. This suggests that peak doses at shallower depths may exceed the films’ dynamic range. Overall, an underestimation of approximately 5–15\(\%\) was observed. The measured valley doses using EBT-3, EBT-XD, and MD-V3 were generally significantly higher than the calculated values, with an average discrepancy ranging from 20 to 35\(\%\).

Several hypotheses can be proposed to explain these differences between calculated and film-measured doses: (1) Both dose calculation engines, hybrid and penMRT, assume ideal multislit collimators where transmission, reflection, and scattering of X-ray beams through the collimator blades are neglected, which can impact valley regions10. Misalignments and imperfections on the collimator blades can also cause distorted valleys, as observed in this study and shown in Fig. 6b,c. According to Pellicioli et al.29, the 10–30\(\%\) discrepancies between measurements and calculations were attributed to the neglect of physical interactions between photon beams and blades, as well as blade imperfections. While refining physical models to account for photon-blade interactions is possible at the cost of time-consuming simulations10,12, identifying and quantifying defective blade surfaces remains challenging, and only a nearly perfect manufacturing process can ensure their quality10,46. (2) Microscope readings may cause an overestimation of valley doses due to issues with focal point and light scattering of non-absorbed light. This results in the detector receiving less light, leading to higher values being extracted by the film data processing program compared to the actual doses. Comparisons between valley values read by the microscope and a flatbed scanner showed an average overestimation of about 7\(\%\) when using the microscope (see Table 2). (3) Another hypothesis is the potential spreading of the film polymer over distances of a few hundred microns due to the high concentration of activated color centers within the films inside the microbeam passages. Measuring valley doses is analogous to measuring out-of-field doses in broad beams. Several studies have investigated small fields dose distribution using Gafchromic films and compared them to MC simulations. While satisfactory agreement was observed for in-field doses, an overestimation of doses was noted at distances of some hundred microns from the field edges47,48,49, supporting the hypothesis of potential polymer spreading. A recent study also demonstrated an increase in film resolution, in terms of Full Width at Half Maximum (FWHM), with increasing deposited energy in the UV wavelength range, which may also apply to X-rays50. To investigate this effect, it would be interesting to study the impact of dose escalation in peak and valley regions, as well as the lateral resolution as a function of the absorbed dose. (4) Based on the literature51, air gaps in between RW3 slabs—where the films are inserted—can lead to underestimation pf peak doses by approximately 3\(\%\), as shown in Pellicioli et al.51 with a 30 \(\upmu\)m air gap and overestimation of valley doses up to 15–20\(\%\). These discrepancies can be minimized with improved experimental setups, particularly by ensuring tight fixation between the RW3 slabs to eliminate air gaps as much as possible.

Table 2 Relative differences in valley dose values read by microscope compared to flatbed scanner.
Full size table

In this study (Fig. 5), we have shown, EBT-3 films are well-characterized38, with a reproducibility across all depths and field shapes, and were found, in our experience, to be easy to cut. This is supported by the small error bars observed in both peak and valley dose comparisons, and by the stable relative differences across multiple measurements, indicating their repeatability. EBT-XD films also showed reasonably good reproducibility for peak dose measurements, though with slightly larger uncertainties compared to EBT-3. For valley dose evaluations, however, EBT-XD showed greater variability, particularly at deeper depths, suggesting higher sensitivity to dose levels. Additionally, we observed that EBT-XD films were more prone to damage during the cutting process. Both EBT-3 and EBT-XD films are prone to saturation due to their limited dynamic range in peak dose measurements. MD-V3 films can be used for both peak and valley dose measurements, depending on the prescribed dose for MRT treatment. However, based on our observations, they were more difficult to cut, as the polyester layers tended to separate and expose the active layer during cutting. This cutting behavior may be related to the film’s internal structure, in which the adhesive layer is present only on one side between the active layer and the protective polyester layer52. Two independent dose calculation engines, hybridDC and penMRT, showed consistent levels of discrepancies with film-measured peak and valley doses. Given their agreement, they can be used redundantly for fast and high-resolution dose calculations, respectively. However, for a safe clinical transfer of MRT, both calculation engines might not yet be mature enough, and further development is still needed to improve the accuracy of dose calculation in this complex treatment modality. For patient quality control prior to treatment, a potential solution could be to obtain PVDRs at various depths using a microDiamond detector. Following this, peak doses can be verified using MD-V3 films, while valley doses can be inferred from the PVDRs obtained with the microDiamond. These findings support the integration of MD-V3 films into clinical MRT QA workflows, particularly for verifying peak dose delivery with high spatial resolution. Regarding dose calculation systems, both penMRT and hybridDC consistently underestimated valley doses, independent of depth. Given the established correlation between valley dose and normal tissue toxicity9, treatment planning or prescription based on valley doses calculated by these engines should include an appropriate safety margin to reduce the risk of complications.

The next step of this work is to perform a detailed simulation of the multislit collimator, integrating the slight divergence of the synchrotron X-ray beam, and to study their effects on the calculated valley doses. This will help determine whether observed discrepancies can be due to the simplifications made in the calculation algorithms. Additionally, the use of a flatbed scanner with higher spatial resolution for reading both peak and valley doses, along with quantifying the differences compared to microscope-read values, will be studied.

Conclusion

In this study, we tested four types of Gafchromic films and compared the results to microDiamond measurements as well as hybridDC and penMRT calculated doses. In broad beam dosimetry, penMRT demonstrated better agreement with measurements and offered the advantage of high-resolution dose map representation, enabling the detailed study of individual peaks and valleys. Cross-validation of calculated doses with measured doses in MRT fields showed an acceptable agreement within uncertainty intervals for peak doses, with a relative difference up to 8\(\pm 0.1\)% in the case of MD-V3 film. However, a systematic difference between calculated and measured valley doses was observed, with several hypotheses proposed to explain these discrepancies. Despite these differences, MD-V3 films showed strong potential for MRT dose assessment at the prescribed doses used in MRT translational and clinical trials.